Investigating the relevance of Environmental Kuznets curve hypothesis in Saudi Arabia: towards energy efficiency and minimal carbon dioxide emission

Abstract

The Saudi economy is driven by the energy sector which mainly derived from petroleum-based resources. Besides export, the Kingdom’s consumption of this resource showed a significant increase which linearly promoting CO₂ emission increment. Therefore, it is essential to model the Kingdom’s energy consumption to estimate the profile of her future energy consumption. This work explores modelling and multi-step-ahead predictions for energy use, gross domestic product (GDP), and CO₂ emissions in Saudi Arabia using previous data (1980–2018). The dynamic interrelationship of the variable’s nexus was tested using the Granger causality and cointegration method in the short-run and long-run. In the long-run, the models reveal an inverted U-shape relation between CO₂ emissions and GDP, validating Environmental Kuznets curve. When energy consumption is increased by 1%, there will be an increase in CO₂ emissions by 0.592% at constant GDP, and when GDP is increased by 1%, there will be an increase in CO₂ emissions by 0.282% at constant energy used. CO₂ emissions appear to be both energy consumption and income elastic in Saudi Arabia in the long-run equilibrium. Granger causality based on vector error correction method reveals unidirectional causality from income to CO₂ emissions, and bidirectional causality from CO₂ emissions to energy consumption and vice versa in the short-run. In the long-run, bidirectional causality from income to CO₂ emissions and vice versa and unidirectional causality from the used energy to CO₂ emissions were observed. Also, there is a bidirectional causality from GDP to energy used and vice versa in the short-run, meaning that GDP and energy consumption are interdependent. Saudi Arabia needs to increase energy infrastructure investments and increase energy efficiency by implementing energy management policies, reducing environmental pollution, and preventing the negative effect on economic growth.

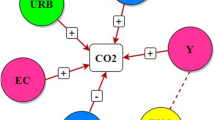
Graphical abstract

Introduction

There has been a dramatic increase in world energy consumption recently and will yet increase in the future due to economic development and population growth (Aydin 2015; Rosen 2021). Hydrocarbon constitutes the largest part of the world’s energy consumption in the past forty years, with 185% increase in consumption between 1970 and 2012 (Aydin et al. 2016). For instance, fossil fuels account for ~ 90% (29.4% coal, 23.8% natural gas, and 34.8% oil) of the global primary energy consumption in 2010 (Aydin 2014). Inadequate supply of affordable and reliable modern-day energy is a significant challenge in social and economic development worldwide. Saudi Arabia is gifted with massive fossil fuel resources, culminating in excess energy consumption and massive emissions of CO₂. Therefore, it is imperative to study the relationship between CO₂ emissions, used energy and gross domestic product (GDP) in Saudi Arabia. In 2012, Saudi Arabia was reported as the leading oil producer globally, holding the second-largest reserves of crude oil, making her the wealthiest country in the Arab world. Based on the report of the Organization of the Petroleum Exporting Countries (OPEC), the economy of Saudi Arabia mainly depends on fossil fuels. Around 90% of Saudi export total revenues in 2011 is from Fossil fuel (Alshehry and Belloumi 2015).

Recently, Saudi Arabia has enjoyed a speedy GDP growth alongside a firmly positive balance of trade without public debt (Samargandi 2017). In 2011, the total per capita energy consumption is over 3 times greater than the global average (Saudi Arabia: 6.5 toe/capita, world average: 1.9 toe/capital). Due to the rapid increase in population, strong GDP, and continuous pressure on natural resources, there has been an inherent drive, which has complicated international responsibilities to ensure a safer environment for sustainable development planning.

In the last five decades, CO₂ emission from Saudi Aramco, the Kingdom-owned petroleum giant is substantially higher than other major petroleum company on earth. Although the emissions reduced recently due to the COVID-19 pandemic, Saudi Arabia exhibits extremely weak capacity to reduce CO₂ emission and resistance to climate action has made it a pariah in global efforts to reduce greenhouse gas (GHG) (DW 2020). However, the country has a 20 years vision to improve energy efficiency by embarking on massive technological advancement towards a green and sustainable economy.

Moreover, Saudi Arabia's government has shown a commitment to reducing annual CO₂ emissions by ~ 130 tonne by 2030 using energy efficiency policies that could facilitate the pursuit of economic diversification from oil and contribute to a reduction of GHG and adaptation to climate change (Krarti et al. 2017). The Kingdom updated the guidelines for the Saudi Electricity Company (SEC) and established the Saudi Energy Efficiency Center (SEEC) towards promoting energy efficiency across sectors. The SEEC initiated Saudi Energy Efficiency Programme (SEEP) in 2012 to give incentives and make improvements to lower energy demand across sectors (DW 2020; SEEC 2015). SEEP enacted over 35 policies, including improved building standards (like enforcement of insulation in new buildings), energized public awareness campaign, higher efficiency demands for cooling/heating equipment (by updating the standards of thermal insulation products), and the creation of the Center of Excellence in Energy Efficiency at King Fahd University of Petroleum and Minerals, and new energy efficiency programmes and certifications at technical universities (DW 2020; U.S.-Saudi-Business-Council 2021). Smart Metering Project (SMP) was enacted to micromanage electrical usage, billing, and monitoring for businesses and homes to meet its digitalization goals of Vision 2030. SMP will enable electricity users to monitor their usage in real time via their smartphones (U.S.-Saudi-Business-Council 2021).

Saudi Arabia is unique due to the rapid growth in GDP, energy consumption, energy extraction, and subsidised energy prices. Although several researchers have studied the authenticity of the Environmental Kuznets curve (EKC) (Alshehry and Belloumi 2015; Kacprzyk and Kuchta 2020; Samargandi 2017), considering the pollution and the energy consumption in Saudi Arabia, it is essential to reanalyse the validity of EKC for Saudi Arabia. The EKC theory propounded by Grossman and Krueger (1995) claim that the early phase of the real GDP progress exhibits adverse effects on the environment, which reduce with increasing growth rate beyond a particular limit. Brock and Taylor (2005) claim that the soundness of EKC theory is mainly determined by three factors: the production volume, the structure of means of production, and the utilisation of technology in industries. It is essential to contextualise the relevant factors that could authenticate or nullify the EKC theory in leading oil producers like Saudi Arabia.

In Saudi Arabia, the energy sector contributes ~ 41% to the GDP, while the agricultural sector contributes ~ 2%. Despite the global mandate for the alleviation of GHG for sustainable development, Saudi Arabia experiences a continuous increase in emissions of CO₂ due to the growth pattern of the real GDP. To achieve the ambitious sustainable development goal, it is crucial to significantly reduce GHG emissions, especially CO₂ (Alshehry and Belloumi 2015). There are several reports on the relationship between real GDP and CO₂ emissions but rarely agree on the exact nature of the relationship. Alshehry and Belloumi (2015) explored this phenomenon by investigating if the EKC theory is valid for Saudi Arabia, if CO₂ emissions are sensitive to energy consumption and income, and if innovation could reduce CO₂ emissions. They reported the existence of at least a long-run relationship between income, energy price, CO₂ emissions, and energy used. Several authors have examined the first proposal confirming the nexus between production scale and CO₂ emissions covering different countries and regions (Omri 2013). Omri (2013) reported that the scale of production and CO₂ emissions are monotonically related, assuming other factors are constant. A similar report was published by Pao and Tsai (2011) for Brazil, Alam et al. (2017) for India, Lotfalipour et al. (2010) for Iran, and Ang (2008) and Azlina and Mustapha (2012) for Malaysia. However, several studies have reported conflicting results, claiming that the relation between CO₂ emissions and production scale depicts an inverted U-shaped EKC for upper-middle-income and high-income countries (Al-Mulali et al. 2015), Italy and Denmark (Ozturk and Acaravci 2010), Tunisia (Shahbaz et al. 2014), Malaysia (Saboori et al. 2012; Sohag et al. 2015).

Taher and Hajjar (2014) and Liu et al. (2012) focussed on Saudi Arabia. Taher and Hajjar (2014) explored the policy simulations using the Australian dynamic integrated model of climate and the economic structure to study the effect of three hypothetical policies. For instance, a 1% reduction in energy consumption, a 5% reduction in CO₂ emissions and a 0.5% point on economic growth. Taher and Hajjar (2014) report revealed that EKC is not valid for Saudi Arabia when they used the cumulative sum of regression residuals (CUSUM) and squared of CUSUM methods. Liu et al. (2012) investigated the effects of CO₂ capture and storage to formulate policy for future energy in Saudi Arabia. They examined the stakeholder's perceptions regarding the effects of carbon storage on Saudi Arabia energy policy by running a survey amongst oil and gas professionals that work in the Middle East and North Africa (MENA) region. Their report shows that the major limitations to carbon storage are technical uncertainty and high capital costs. However, Liu et al. (2012) did not explore the validity of EKC using CUSUM and CUSUM-squared methods. Eventually, their work scope does not include the three hypotheses of EKC proposed by Brock and Taylor (2005). However, some authors have a U-shaped relationship between production scale and CO₂ emissions, invalidating the EKC theory (Luo et al. 2017; Shahbaz and Sinha 2019). For instance, Begum et al. (2015), Roca et al. (2001) and Caviglia-Harris et al. (2009) reported that increasing the GDP growth continuously increases CO₂ emissions. The above conflicting reports have compelled the need to explore the relation between CO₂ emissions and energy production scale in Saudi Arabia.

This paper explores the validity of the Environmental Kuznets curve (EKC) hypothesis in Saudi Arabia using previous data (1980–2018). The relevance of EKC was tested using the econometric method. With this method, we check the dynamic interrelationship of the variable’s nexus using the Granger causality and cointegration method in the short-run and long-run and test the validity of EKC theory for CO₂ emission and energy consumption. Rather than CO₂ emissions per capita, we used total CO₂ emissions, following the Kyoto Protocol (Friedl and Getzner 2003), towards reducing the percentage of CO₂ emissions. The outcome of this study will help in policy planning and implementation to examine economic growth and proffer solution to environmental problems.

Data

Testing the applicability of EKC for Saudi Arabia, the annual report from 1980 to 2018 was used based on availability. The data for CO₂ emissions are in a million tonne, energy consumption is in Quadrillion Btu, and GDP is in billion US$ and is obtained from WORLD DATA ATLAS (WDI 2021a, b, c).

Table 1 presents the descriptive statistics of the three parameters. Figure 1 gives the series trend for Saudi Arabia. They increased across time, with the GDP demonstrating the most correlated variant (revealed by the coefficient of variation (CV)). Energy consumption is the least correlated variant. Table 2 presents the average growth rates (%) along the periods to 2018 for each series. The growth rates for 15, 10, and 5 years are computed as the growth between 2003 and 2018, 2008 and 2018, and 2013 and 2018. In the last five years (2013–2018), Saudi Arabia has experienced the lowest growth rate in energy consumption (0.78%) and GDP (1%) and more significant growth rates in CO₂ emission (7.7%) than the world percentage growth rate for related parameters. The last 5 years global growth rates in CO₂ emissions, energy consumption, and economic growth are 5.51, 1.33, and 2.26%, respectively. The decline in the growth rate in the CO₂ emissions and energy consumption could be due to the gradual deployment of alternative energy like atomic and renewable energy in Saudi Arabia (Tlili 2015). This could be responsible for the stagnation in CO₂ emissions and reduction in energy consumption in recent years (Fig. 1). Although Saudi Arabia is a leading oil producer nation, the kingdom realised the urgent need to attain energy security, which could only be achieved by promoting renewable energy.

Table 1 Descriptive statistics of the variables for Saudi Arabia, 1980–2018

Fig. 1

Time series plots of the CO₂ emissions, energy consumption and real GDP, 1980–2018

Table 2 Percentage average growth rate for each parameter

Before the empirical analysis, the variables were transformed to natural logarithms format to ensure smoothness. Therefore, the series can be explained based on growth, considering the first difference.

Model and methodology

EKC model

Testing the applicability of the EKC theory, a long-run correlation between CO₂ emissions, energy consumption, and GDP in quadratic form of the natural logarithm (obtained from the empirical literature in energy economics) is expressed as follows (Pao and Tsai 2011):

$${\text{LNCO2}}_{t} = \beta_{0} + \beta_{1} {\text{LNGDP}}_{t} + \beta_{2} {\text{LNGDPSQ}}_{t} + \beta_{3} {\text{LNEC}}_{t} + u_{t}$$

(1)

LNGDP, LNGDPSQ, LNEC and LNCO2 signify the natural logarithms of the GDP, GDP square, CO₂ emissions, and energy consumption. Energy consumption is supposed to have a positive sign since an increase in energy consumption is expected to boost economic activity, promoting CO₂ emissions. For the EKC theory to be valid, the signs of the coefficient β₁ and β₂ must be positive and negative, reflecting the upturned U-shape pattern. The income level of β₁/2β₂ represents the turning point. Suppose the value of β₂ is statistically insignificant. The turning point is higher than the highest GDP in the data series. In that case, there is a monotonic boost in the correlation between GDP and CO₂ emissions (Pao and Tsai 2011). Lastly, the error term (u_t) is assumed to be autonomous and identically distributed with constant variance and a zero mean.

The independent variables may be remarkably but not perfectly correlated among themselves, making the regression result inaccurate. This occurrence is called multicollinearity, and consequently, the null hypothesis cannot be rejected, where it should be rejected. This means that multicollinearity can prevent the suitability of the t-statistics and associated p values for the assessment and the significance of the independent variables. The following expression is employed to test the multicollinearity in Eq. (1):

$${\text{LNEC}}_{t} = a_{0} + a_{1} {\text{LNGDP}}_{t} + a_{2} {\text{LNGDPSQ}}_{t} + u_{t}$$

(2)

If the result of the model indicates multicollinearity, the following expression is employed to test the EKC hypothesis validity:

$${\text{LNCO2}}_{t} = \beta_{0} + \beta_{1} {\text{LNGDP}}_{t} + \beta_{2} {\text{LNGDPSQ}}_{t} + u_{t}$$

(3)

If the turning point is higher than the highest GDP value in the data series or β₂ is not significant statistically, the correlation between CO₂ emissions, energy consumption and GDP, in the long-run, is specified as follows:

$${\text{LNCO2}}_{t} = \alpha_{0} + \alpha_{1} {\text{LNEC}}_{t} + \alpha_{2} {\text{LNGDP}}_{t} + u_{t}$$

(4)

Econometric methodology

Equations (1) or (4) can estimate the empirical analysis tests for the short-run connection between the variables. In contrast, the long-run relationship can be obtained using the vector error-correction model (ECM). All the econometrics analysis were done using EViews 10. The analysis can be achieved in three steps. The first is the verification of the integration order of the variables since the validity of the cointegration tests could only be ascertained if the variants have a similar integration order. Three different unit root tests, namely Kwiatkowski-Phillipse-Schmidt-Shin (KPSS) (Kwiatkowski et al. 1992), Philip Perron (PP) (Phillips and Perron 1988) and Augmented Dickey–Fuller (ADF) (Dickey and Fuller 1981), are engaged to examine the stationarity and the integration order of the variables. However, the test is designed based on the null hypothesis that a series with 1st differential [I(1)] has a low power to reject the null hypothesis. To achieve remarkable results, KPSS is occasionally employed as a complement to PP and ADF tests.

Having ensured that all the series are incorporated in a similar order, the Johansen maximum-likelihood technique (Johansen and Juselius 1990) is employed in the second step to investigate the cointegration relationship between the parameters in Eqs. (2)–(4). If there is cointegration between the variables, the ordinary least square (OLS) method applied in estimating Eqs. (2)–(4) does not result in a false regression result. Moreover, the variables obtained by OLS are highly reliable (Alves and da Silveira Bueno 2003). The cointegration presence signifies a long-run equilibrium relationship amongst the parameters and further indicates Granger causality amongst the parameters at least in one direction (Engle and Granger 1987; Oxley and Greasley 1998).

Finally, suppose all the variables are of the same order and cointegrated. In that case, the ECM is employed to rectify any uncertainty in the cointegration relationship, computed in the form of an error-correction term (ECT). This will enable short-run and long-run causality test between the cointegrated parameters. The ECM of Eq. (4) is expressed below:

$$\begin{aligned} \Delta {\text{LNCO2}}_{t} & = \gamma_{10} \mathop \sum \limits_{i = 1}^{{m_{1} }} \gamma_{11i} \Delta {\text{LNCO2}}_{t - 1} \\ \quad + \mathop \sum \limits_{i = 1}^{{n_{1} }} \gamma_{12i} \Delta {\text{LNGDP}}_{t - 1} \\ &\quad + \mathop \sum \limits_{i = 0}^{{k_{1} }} \gamma_{13i} \Delta {\text{LNEC}}_{t - 1} + \delta_{1} {\text{ECT}}_{t - 1} + \mu_{1t} \\ \end{aligned}$$

(5)

$$\begin{aligned} \Delta {\text{LNGDP}}_{t} & = \gamma_{20} \mathop \sum \limits_{i = 1}^{{m_{2} }} \gamma_{21i} \Delta {\text{LNCO2}}_{t - 1} \\ \quad + \mathop \sum \limits_{i = 1}^{{n_{2} }} \gamma_{22i} \Delta {\text{LNGDP}}_{t - 1} \\ &\quad + \mathop \sum \limits_{i = 0}^{{k_{2} }} \gamma_{23i} \Delta {\text{LNEC}}_{t - 1} + \delta_{2} {\text{ECT}}_{t - 1} + \mu_{2t} \\ \end{aligned}$$

(6)

$$\begin{aligned} \Delta {\text{LNEC}}_{t} & = \gamma_{20} \mathop \sum \limits_{i = 1}^{{m_{3} }} \gamma_{31i} \Delta {\text{LNCO2}}_{t - 1} \\ \quad + \mathop \sum \limits_{i = 1}^{{n_{3} }} \gamma_{32i} \Delta {\text{LNGDP}}_{t - 1} \\ & \quad + \mathop \sum \limits_{i = 0}^{{k_{3} }} \gamma_{33i} \Delta {\text{LNEC}}_{t - 1} + \delta_{3} {\text{ECT}}_{t - 1} + \mu_{3t} \\ \end{aligned}$$

(7)

where

$${\text{ECT}}_{t - 1} = {\text{LNCO2}}_{t - 1} - \alpha_{0} - \alpha_{1} {\text{LNGDP}}_{t - 1} - \alpha_{2} {\text{LNEC}}_{t - 1}$$

(8)

is obtained from the long-run cointegration relationship defined in Eq. (4). The sign Δ represents the first-difference operator; m_i is the maximum lag length, n_i and k_i are estimated using Akaike’s information criteria (AIC), and µ_it are the error terms that are not serially correlated. The parameter δ₁ represents the coefficient of adjustment speed, which estimates the speed of adjustment at which LNCO2 return to long-run equilibrium levels if LNCO2 contravenes the long-run equilibrium connection. The negative sign of the obtained coefficient of adjustment speed agrees with the convergence towards the long-run equilibrium.

The ECM presented in Eqs. (5)–(8) incorporates the dependent variables (with their lags) and the preceding uncertainty represented by ECT_t-1. This could be used to test the long-run and short-run causality amongst cointegrated parameters using a Wald test. Considering Eqs. (5) and (6), the short-run causality will be tested from GDP to CO₂ emissions and vice versa. If the joint null hypothesis, coefficient γ_12i = 0, ʉ_i is rejected and the causality direction is from GDP emissions to CO₂, while the causality direction is from CO₂ emissions to GDP if the joint null hypothesis γ_21i = 0, ʉ_i is rejected. For long-run causality, if the null hypothesis, δ₁ = 0 is rejected, CO₂ emissions react to deviation from the long-run uncertainty. If the null hypothesis δ₂ = 0 is rejected, the real GDP reacts to divergences from the long-run equilibrium.

Lastly, GDP strongly Granger causes CO₂ emissions if the null hypothesis, γ_12i = δ₁ = 0, ʉ_i is rejected. In contrast, CO₂ emissions strongly Granger causes GDP if the null hypothesis γ_21i = δ₂ = 0, ʉ_i is rejected. In the same vein, the causality between the GDP and energy consumption could be determined using Eqs. (6) and (7) and the causality between energy used and CO₂ emissions using Eqs. (5) and (7). The cointegration test was also examined using autoregressive distributed lag (ARDL) model by Pesaran et al. (2001). Pesaran et al. (2001) resolved time series data non-stationary concern and developed the model regardless of the stationary properties of the data. ARDL model is appropriate provided all parameters are stationary at level [I(0)] or solely I(1) or I(0) and I(1) together.

Empirical findings

The yearly time-series records of the form 1980 and 2018 were employed in estimating Eqs. (1)–(2) and the outcomes are presented in Table 3. The variance inflation factors (VIF) obtained reveal the existence of multicollinearity in Eq. (1). Therefore, Eq. (2) was applied for the cointegration test between energy use and the GDP. Equation (3) was applied for the cointegration test between CO₂ emissions and GDP, and Eq. (4) was applied for the cointegration test among GDP, emissions, and energy use.

Table 3 Long-run coefficients of Eqs. (1)–(4) and multicollinearity test using variance inflation factors (VIF)

Unit roots and cointegration

Table 4 gives the unit root tests outcomes using three different models, PP, ADF, and KPSS. All of the variables exhibit a unit root in their levels [I(0)] but are integrated (stationary) in their first differential [I(1)], signifying that they are stationary at I(1) (order one). Table 5 gives the outcomes of the cointegration test for the variables in Eqs. (2)–(4) using the Johansen test. The hypothesis of no cointegrating using trace statistics and maximum Eigen statistics tests rejected equations at a 1% significance level for Eqs. (2)–(4). The results show that the data series LNEC, LNGDP and LNGDP2 have at most two cointegration model without lags (panel 1 of Table 5). The estimated cointegration vector normalised for LNEC (2, 3.418, − 0.259) is presented in Table 3. LNGDPSQ and LNGDP exhibit significant negative and positive signs in the long-run, which validates the EKC theory. Meaning that the energy use level first rises with increasing LNGDP; it further stabilises and subsequently declines. This indicates the presence of an inverse U-shaped relationship between energy use and income, with a turning point of about 6.59 (in natural logarithm) of the economic growth (Fig. 2), where the elasticity of energy used based on GDP is 3.418–0.519 × LNGDP in the long-run. The reports of Ahmad et al. (2017) and Pao and Tsai (2011) broadly corroborate this report.

Table 4 Results of unit roots tests

Table 5 Johansen’s cointegration test

Fig. 2

Long-run environmental Kuznets curve shape for CO₂ emissions and energy consumption. The coloured vertical lines represent the turning points for CO₂ emissions and energy consumption

The series LNCO2, LNGDP and LNGDP2 have one cointegration equation without lags (panel 2 of Table 5). The obtained cointegration vector normalised for LNCO2 is (1, 21.858, − 1.715), according to Table 3. In the long-run, GDP and GDPSQ exhibit substantial positive and negative signs, which validates the EKC theory, which means that CO₂ emissions firstly rises with increasing GDP. It further stabilises and subsequently declines. This indicates the presence of an inverse U-shaped relationship between CO₂ emissions and income, with a turning point of around 6.37 (in natural logarithm) of GDP (Fig. 2), where the elasticity of CO₂ emissions based on GDP is 21.858–3.431 × LGDP in the long-run. The reports of (Ahmad et al. 2017) for Croatia, (Apergis and Payne 2010) for 11 commonwealth nations with independent states, (Ozturk and Acaravci 2013) for Turkey, (Saboori et al. 2012) for Malaysia, (Wang et al. 2011) for (Yavuz 2014) for Turkey, broadly corroborate this report. However, the results do not corroborate with the reports of (Pao and Tsai 2011) for Russia, (Ozturk and Acaravci 2010) for Turkey, (Acaravci and Ozturk 2010) for nineteen European countries. Contradictory results could be attributed to the sensitivity of EKC to the choice of parameters to study (CO₂ emissions per capita or total CO₂ emissions), country, duration, methods, and sample size.

Figure 3 presents the effect of economic growth on CO₂ emissions and energy consumption. GDP is seen to have a significant effect on CO2 emissions and energy consumption due to over reliance on fossil fuel and the subsidy added to fossil-based energy source coupled with inability of the kingdom to implement the energy efficient policy duly. The results indicate that the relationships of both CO₂ emissions-economic growth and energy consumption-economic growth exhibit a monotonic decrease since the turning point value (6.37 and 6.59) of LNGDP is less than the highest value (6.67) of LNGDP in Saudi Arabia. Therefore, CO₂ emissions appear to be both energy consumption and GDP elastic in Saudi Arabia in the long-run equilibrium. The series LNCO2, LNGDP and LNEC in panel 3 in Table 5 also exhibit cointegration vectors normalised for LNCO2, which are (1, 0.282, 0.592) in Table 3. The coefficient possesses the anticipated signs of the long-run relationship. The outcomes show that when energy consumption is increased by1%, there will be an increase in CO₂ emissions by 0.592% at constant GDP, and when GDP is increased by 1%, there will be an increase in CO₂ emissions by 0.282% at constant energy used. Since both variables are statistically significant, both real income and energy consumption are important determinants of CO₂ emissions in Saudi Arabia. This report is contrary to that of Pao and Tsai (2011), which reported that energy consumption is a more vital contributing factor to CO₂ emissions in Brazil.

Fig. 3

Effect of GDP on CO₂ emissions and energy consumption for Saudi Arabia, 1980–2018

VECM granger causality inference

ARDL was used as an ideal method for testing cointegration among variables and the validity of EKC in Saudi Arabia (Alshehry and Belloumi 2015). Table 6 presents the results of cointegration using ARLD and Bounds test. Using ARLD test uses p value to test for cointegration, while Bounds test uses F-statistics. The results show that only Eqs. (2) and (4) exhibit cointegration, while the result of Eq. (3) is inconclusive. Nevertheless, it does not describe the causality amongst the variables (meaning which variable causes which variable). Granger (Granger 1969) causality method is a viable method that can show which variable causes which variable both in the short- and long-run. If no cointegration, the traditional VAR can be employed to test for causality amongst the parameters.

Table 6 Results of ARDL and bounds test for cointegration (bounds test null hypothesis: no long-run relationships exist)

On the other hand, if there is cointegration, VAR results can be misleading (Saboori and Sulaiman 2013). If the series cointegrates, it is vital to ensure the stationarity of the variables (as presented in Table 4) before use for VECM (Enders and Walter 2015). If cointegration exists among the parameters, the residuals from the long-run equation and the lagged residuals must be obtained as additional regressor before the VECM approach can be used. The significance and the negative sign of the pace of adjustment indicate long-run causality, while the short-run causal relationship was tested using the F-statistics of Wald test.

Table 7 presents the outcomes of the Granger causality test. The results show that when CO₂ emissions are the dependent parameters, the GDP coefficient is positive, whereas energy consumption is negative. Both exhibit a 1% level of statistical significance in the short-run. Moreover, the variables exhibit long-run relation since the coefficient of ECT is negative and extremely significant. It reveals that the disturbance in the system exhibits 36% speed of adjustment in the first quarter, which is quite fast. This means that intrusions in the system will take about 2.78 years to attain an equilibrium path in the long-run.

Table 7 Granger causality outcomes

Furthermore, when energy consumption is the dependent variable, the coefficient of CO₂ emissions is negative and significant at a 1% level of significance in the short-run. At the same time, the coefficient of GDP is positive and not statistically significant. For GDP, CO₂ emissions have a negative relation with GDP and significant at a 5% significance level in the short-run. At the same time, energy consumption is positive and exhibits no statistical significance in the short-run. We can clearly say that the model for CO₂ emissions and GDP exhibits strong long-run cointegration. In contrast, the model for energy consumption has a weak cointegration, judging by the speed of adjustment. Therefore, at the instance of deviation from long-term equilibrium, LNCO, LNGDP and LNEC can take as much as just over 2.78, 17.24 and 2.94 years to revert to equilibrium. The average adjustment speed is 7.65 years.

In summary, the following are inferred:

• 1. A bidirectional causality exists from CO₂ emissions to energy consumption and vice versa in the short-run, meaning that CO₂ emissions and energy used are co-dependent on each other.

• 2. A bidirectional causality exists from LNGDP to LNEC and vice versa in the short-run, meaning that GDP and energy consumption are interdependent.

• 3. There is unidirectional causality from LNGDP to LNCO2.

• 4. A bidirectional causality exists from CO₂ emissions to energy consumption and vice versa, in the long-run, meaning that CO₂ emissions and energy used are co-dependent on each other. This indicates that an increase in economic growth will reduce CO₂ emissions, and a decline in CO₂ emissions will boost the GDP in the future, meaning that EKC is valid.

Table 8 confirms that the model for CO₂ emission is correctly specified, but the model's errors are not serially correlated. The residuals are normally distributed, and the model has heteroskadesticity challenge based on Breusch-Pagan-Godfrey but Homoskedastic based on ARCH test. Heteroskadesticity problem means that the variability of the random disturbance differs across the vector elements. The model is not correctly specified for energy consumption at a 5% significant level but at a 10% level of significance, and the errors in the model are not serially correlated. Like the CO₂ model, the residuals are normally distributed, and the model has heteroskadesticity challenge based on Breusch-Pagan-Godfrey but homoskedastic based on ARCH test. Figure 4 presents the CUSUM and CUSUMSQ for all the dependent variables. The results reveal that the model parameters are stable over a long time since the critical bounds are within the bounds of a 5% level of significance. Therefore, all the models are reliable and perfect for policy purpose.

Table 8 Analytical tests for CO₂ emissions and energy consumption model

Fig. 4

Plots of both the CUSUM and CUSUMSQ for dependent variable a LNCO2, b LNEC and c LNGDP, 1980–2018

Variance decomposition and impulse response function

VECM gives the granger causality within the sample but cannot clarify out of sample causality (Ahmad et al. 2017). This means that it does not investigate the behaviour of one variable in the reaction to shocks from other variables in the long-run. The response of a variable to other variables outside the sample could be investigated using variance decomposition and impulse response function (Ahmad et al. 2017). Therefore, variance decomposition and impulse response function was employed to investigate out of sample causality. Engle and Granger (1987) reported that the variance decomposition method offers remarkable results in the VAR environment. Therefore, the VAR model was used in investigating variance decomposition. Variance decomposition describes how much one parameter contributes to explaining other parameters. In contrast, the impulse response function describes how one parameter reacts to the shocks of other parameters, as well as its shock (Engle and Granger 1987).

Table 9 presents the outcomes of variance decomposition. The results reveal that in the short-run (period 1–5), CO₂ emissions contribute about 65.96% to itself. The contribution of GDP and energy consumption in the description of CO₂ emissions are 1.45 and 24.87%, respectively. Although the contribution of GDP is insignificant, GDP square (7.71%) is more significant. In the long-run (5–10 period), it clear that CO₂ emissions were self-explanatory at around 41.83%. The influence of energy consumption, GDP, and GDPSQ on CO₂ emissions are 35.64, 2.67 and 19.86%, respectively. Moving further to the future, the impact of energy used, GDP and GDPSQ on CO₂ emissions increase significantly, but the contribution of energy consumption starts to decline after period 12.

Table 9 Variance decomposition analysis

Variance decomposition of energy consumption reveals that in the short-run (period 1–5), energy consumption describes itself around 93.80%. The contribution of GDP and CO₂ emissions in describing energy consumption are 0.09 and 1.46%, respectively. Although the contribution of GDP is insignificant, the GDP square (4.64%) is more significant. In the long-run (5–10 periods), it clear that energy consumption self-explanatory at around 78.54%. The contribution of CO2 emissions, GDP and GDPSQ to energy consumption are 4.58%, 2.21% and 14.68%, respectively. Moving further to the future, the contribution of energy consumption, GDP and GDPSQ to energy consumption increase significantly.

Variance decomposition of GDP reveals that GDP contributes about 56.38% to itself, whilst energy used, CO₂ emissions and GDP square contribute to GDP about 15.15, 24.80 and 3.68% in the short-run (period 1–5). The GDP contribution to itself decreases significantly, while the contributions of CO₂ emissions, energy consumption and GDP square increase significantly. At period 20, GDP contributes about 25.54% itself and energy consumption and CO₂ emissions contribute 27.76 and 20.12% to GDP. Likewise, variance decomposition of GDPSQ reveals that in the short-run, GDP contributes the most (64.24%), and the second contribution is from CO₂ emissions followed by energy consumption. In the long-run, the contribution of GDP declines considerably, while the contribution of energy consumption and CO₂ emissions increased, but the contribution of CO₂ emissions starts to decline after period 10.

Figure 5 shows the outcomes of the impulse response function of the variables. The results reveal that a one SD shock (innovation) to energy consumption positively promotes CO₂ emissions. In contrast, GDP contributes insignificantly to CO₂ emissions in the short-run (1–5 period), although with a positive impact in periods 1 and 2. In the long-run, energy consumption has a positive influence on CO₂ emissions, and economic growth negatively affects CO₂ emissions, as seen in the second and third image of the first row of Fig. 5. CO₂ emissions positively contribute to energy consumption, whereas GDP contributes insignificantly to energy used in the short-run (period 1–4). In the long-run, a one SD shock on CO₂ emissions positively impacts energy consumption. However, GDP innovation negatively influences energy consumption, as seen in the first and third image of the second row of Fig. 5.

Fig. 5

Impulse response function (IRF). Impulses: LNCO2 LNEC LNGDP LNGDPSQ; responses: LNCO2 LNEC LNGDP LNGDPSQ

Moreover, an innovation to GDP square contributes negatively to energy consumption and CO₂ emissions in the short- and long-run. These conclusions are like those of VECM for causality and ARDL for EKC. Therefore, the variables exhibit comparable behavioural pattern, even the out of sample.

Conclusion and policy suggestions

This work investigates the long-run equilibrium relationship between economic growth, energy consumption, and carbon emissions in Saudi Arabia from 1980 to 2018. A multicollinearity test (using variance inflation factor (VIF)) and ARDL bounds test were employed for cointegration test among the variables to test the validity of EKC. When energy consumption is increased by 1%, there will be an increase in CO2 emissions by 0.592% at constant GDP. When GDP is increased by 1%, there will be an increase in CO2 emissions by 0.282% at constant energy used. CO₂ emissions appear to be both energy consumption and GDP elastic in Saudi Arabia in the long-run equilibrium. The dynamic causal relationships amongst GDP, energy consumption, and CO₂ emission in Saudi Arabia were examined using the Johansen cointegration method using energy consumption and CO₂ emissions as control variables. The outcomes reveal that there is at least a long-run equilibrium relationship between economic growth, energy consumption, and CO₂ emissions. A unidirectional causality was observed from GDP to CO₂ emissions for Saudi Arabia in the short-run.

Furthermore, energy used and GDP cause CO₂ emissions in the long-run. A bidirectional causality was observed from CO₂ emissions to energy use and vice versa in the short-run and long-run, meaning that CO₂ emissions and energy consumption are co-dependent. Also, there is a bidirectional causality from GDP to energy used and vice versa in the short-run, meaning that GDP and energy consumption are interdependent.

The three parameters are equally defined and influenced in the long-run. At the instance of innovation in the system, each variable adjusts in the short-run to reinstate the long-run equilibrium. The average speed of adjustment is about 7.65 years. This shows that Saudi Arabia needs to include environmental considerations in her macroeconomic policies more passionately to cut the emissions of pollutant and to ensure economic growth. This is an indication that increases in GDP could reduce CO₂ emissions, and a decline in CO₂ emissions will boost the GDP in the future, meaning that EKC is acceptable for Saudi Arabia.

Nevertheless, the variance decomposition analysis result reveals that about 15% (in the short-run, 5 years) and 28% (in the long-run, 20 years) contribution of energy consumption to explain economic growth in Saudi Arabia. The findings suggest that a policy for reduction of fossil-based energy utilization, which automatically minimizes CO₂ emissions, may lead to a declining GDP in the future when energy efficient system is not employed. Therefore, Saudi Arabia needs to remove subsidies from fossil fuels and strategize on boosting energy efficiency by minimising environmental impacts related to different energy use. In 2014, Saudi Arabia generated about US$ 5.81 of economic output per kg of oil, which is by far below the global average (US$ 7.57), according to the WDI database. The high level of per capita energy consumption (9401.37 kWh, about 4.89 times the global average (1922 kWh) in 2014) and low prices for local supply of fossil fuel consumed led to the rising intensity of energy economic activities. Fossil fuels (natural gas and oil) are the primary sources of energy consumption in Saudi Arabia, making it one of the biggest environment polluters on earth. Carbon dioxide emission per capita is about 18 tonne in 2018, in comparison with the world average of 4.9 tonne.

Saudi Arabia can attain CO₂ emission abatement towards sustainable economic growth by massive investment in clean energy, considering renewable energy resources like wind, solar, geothermal and waste-to-energy and implement energy efficiency measures. Saudi Arabia energy policy must be strictly adhered to, giving incentives towards improving lower energy demand in buildings, transportation and industry, which account for 90% of the Kingdom’s energy consumption. The use of electric vehicle with solar charging will help to lower the energy consumption in transportation. Moreover, various sectors should be persuaded to embrace advanced technologies to reduce pollution. Energy-efficient technologies, in combination with the use of renewable energy source, could increase economic growth.

This study was performed based on the available data. We hereby recommend future study using more recent data if possible.