Exergetic optimization of solar water collectors using computational intelligence techniques

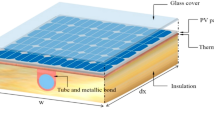
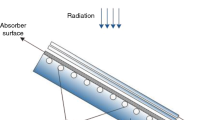
Abstract

This article proposes a model to determine the optimal performance and design conditions for a flat plate solar water collector. The model uses the hourly solar irradiation data over a year for humid subtropical climatic conditions for estimating the thermal, optical, and exergy efficiency. The proposed model has been validated with the data in the literature. Six single-objective computational intelligence (CI) techniques are used to determine the maximum exergy efficiency by optimizing the plate area of the absorber, mass flow rate, and inlet temperature of the working fluid. The statistical analysis shows that the performance of water cycle algorithm is superior in every statistical parameter. Six multi-objective CI techniques are used to evaluate the trade-off solutions between the conflicting objectives of maximizing exergy efficiency and minimizing the area of the absorber plate. Three of these algorithms are able to determine the maximum exergy efficiency with the minimum absorber plate area. A MATLAB-based GUI has also been provided to help in determining the optimal values of the decision variables under various scenarios.

Graphic abstract

Appendices

Appendix 1

Nomenclature
$A_{p}$	Area of absorber plate (m2)	$\overline{I}_{d}$	Monthly average of the hourly diffuse radiation on a horizontal surface (W/m2)	$T_{\text{in}}$	Inlet fluid temperature (K)
$a_{1}$	Constant	$\overline{I}_{g}$	Monthly average of the hourly global radiation on a horizontal surface (W/m2)	$T_{av}$	Average temperature (K)
$a$	Constant	$\overline{I}_{o}$	Monthly average of the hourly extraterrestrial radiation on a horizontal surface (W/m2)	$T_{sky}$	Temperature of sky (K)
$b_{1}$	Constant	$j$	j factor	$U_{b}$	Bottom heat loss coefficient (W/m2 K)
$b$	Constant	$k_{a}$	Thermal conductivity of air (W/m K)	$U_{s}$	Side heat loss coefficient (W/m2 K)
$C_{p}$	Specific heat of fluid (kJ/Kg K)	$k_{i}$	Thermal conductivity of the insulation (W/m K)	$U_{l}$	Overall heat loss coefficient (W/m2 K)
$c_{p - a}$	Specific heat of air (kJ/Kg K)	$k_{p}$	Thermal conductivity of the absorber plate (W/m K)	$U_{t}$	Top heat loss coefficient of (W/m2 K)
$D_{e}$	Equivalent diameter of the channel (m)	$L$	Depth of the channel (m)	$V_{f}$	Fluid velocity (m/s)
$D_{i}$	Inner diameter of the tube (m)	$L_{1}$	Absorber plate length (m)	$V_{\text{wind}}$	Wind velocity (m/s)
$D_{o}$	Outer diameter of the tube (m)	$L_{2}$	Absorber plate width (m)	$W$	Center-to-center distance between two fins (m)
$\dot{E}_{d}$	Destroyed exergy rate (kJ)	$L_{3}$	Height of the collector (m)	$X$	Solution from algorithm
$\dot{E}_{\text{in}}$	Inlet exergy rate (kJ)	$L_{a}$	Latitude of Guwahati (o)	$\alpha_{p}$	Absorptivity of plate
$\dot{E}_{l}$	Leakage exergy rate (kJ)	$\dot{m}$	Mass flow rate (kg/s)	$\beta$	Tilt angle (o)
$E_{l}$	Elevation of Guwahati (kms)	$Nu$	Nusselt number	$\delta_{a}$	Thickness of adhesive
$\dot{E}_{\text{out}}$	Outlet exergy rate (kJ)	$\Delta P$	Pressure drop due to fluid friction (Pa)	$\delta_{b}$	Thickness of the back insulation (m)
$\dot{E}_{s}$	Stored exergy rate (kJ)	$\Delta P_{\text{in}}$	Pressure drop due to fluid friction (Pa)	$\delta_{c1 - c2}$	Distance between the first glass cover and the second glass cover (m)
$\dot{E}_{{d,\Delta T_{f} }}$	Exergy rate due to temperature difference between the plate and working fluid (kJ)	$\Delta P_{\text{out}}$	Pressure drop at the outlet (Pa)	$\delta_{p - c1}$	Distance between the absorber plate and the first glass cover (m)
$\dot{E}_{d,\Delta P}$	Exergy rate due to pressure drop due to friction in the flow channel (kJ)	$\Pr$	Prandtl number	$\delta_{s}$	Thickness of the side insulation (m)
$\dot{E}_{{d,\Delta T_{s} }}$	Exergy rate due to temperature difference between the plate and the sun (kJ)	$Q_{u}$	Useful heat gain (W)	$\delta_{p}$	Thickness of the absorber plate (m)
$\dot{E}_{in,Q}$	Absorbed solar radiation exergy rate by the heater (kJ)	$q_{t}$	Heat loss from the top (W/ m2)	$\varepsilon_{p}$	Emissivity of absorber plate
$\dot{E}_{in,f}$	Inlet exergy rate with fluid flow (kJ)	$Ra$	Rayleigh number	$\varepsilon_{c}$	Emissivity of the covers
$\dot{E}_{out,f}$	Outlet exergy rate with fluid flow (kJ)	${\text{Re}}$	Reynolds number	$\varepsilon_{b}$	Emissivity of bottom plate
$f_{c}$	Normalizing factor	$r_{b}$	Tilt factor for beam radiation	$\eta_{o}$	Optical efficiency (%)
$F_{R}$	Heat removal factor	$r_{d}$	Tilt factor for diffuse radiation	$\eta_{th}$	Thermal efficiency (%)
$F^{^{\prime}}$	Collector efficiency factor	$r_{r}$	Tilt factor for reflected radiation	$\eta_{ex}$	Exergy efficiency (%)
$\overline{H}_{d}$	Monthly average of the daily diffuse radiation (W/m2)	$S$	Absorbed radiation flux by the absorber plate (W/m2)	$\rho_{d}$	Diffusive reflectivity of the cover system
$\overline{H}_{g}$	Monthly average of the daily global radiation on a horizontal surface (W/m2)	$\overline{SH}$	Monthly average of the sunshine hours per day (hr)	$\rho$	Density of fluid (kg/m3)
$\overline{H}_{o}$	Monthly average of the daily extraterrestrial on a horizontal surface radiation (W/m2)	$\overline{SH}_{\max }$	Monthly average of the maximum possible sunshine hours per day (hr)	$\sigma$	Stefan–Boltzmann constant (W/m2 K4)
$h_{r}$	Equivalent radiative heat transfer coefficient (W/m2 K)	$T_{a}$	Ambient temperature (K)	$\tau \alpha$	Transmissivity absorptivity factor
$h_{w}$	Heat transfer coefficient between first cover and surrounding air (W/m2 K)	$T_{p}$	Temperature of absorber plate (K)	$\left( {\tau \alpha } \right)_{b}$	Transmissivity absorptivity factor based on beam radiation
$h_{f}$	Inside wall individual fluid convection heat transfer coefficient (W/ m2 K)	$T_{fm}$	Mean fluid temperature (K)	$\left( {\tau \alpha } \right)_{d}$	Transmissivity absorptivity factor based on diffuse radiation
$h_{{c_{1} - c_{2} }}$	Heat transfer coefficient between first and second glass cover (W/m2 K)	$T_{s}$	Temperature of Sun (K)	$\left( {\tau \alpha } \right)_{p}$	Transmissivity absorptivity factor of absorber plate
$h_{{p - c_{1} }}$	Heat transfer coefficient between absorber plate and first cover (W/m2 K)	$T_{{C_{1} }}$	Temperature of first glass cover (K)	$\mu_{f}$	Viscosity of the fluid (kg/m s)
$I_{T}$	Flux incident on the absorber plate (W/m2)	$T_{{C_{2} }}$	Temperature of second glass cover (K)	$\omega$	Hour angle at sunrise or sunset (o)
$\overline{I}_{b}$	Monthly average of the hourly beam radiation (W/m2)	$T_{\text{out}}$	Outlet fluid temperature (K)	$\omega_{s}$	Hour angle at sunrise or sunset (o)

Single-objective case

The results obtained from the optimization toolkit for designing a flat plate solar water collector are explained in this section. Section "Introduction" describes the results obtained for a single-objective optimization case to maximize exergetic efficiency as an objective. The results obtained for solving the multi-objective problem are explained in Section "Mathematical modeling and simulation" of this appendix.

Section 1

The results explained in this section are generated using the following conditions for the single-objective optimization problem.

Selected objective: Maximize mean exergetic efficiency

Selected CI techniques: SHTS, SHO, WCA

Maximum function evaluations: 200

No. of runs: 3

After completing all the selected optimization simulations, the toolkit reports the results using graphs and spreadsheets. The results are also saved in MATLAB compactable '.mat' files. A brief explanation regarding the results provided by the toolkit is given below.

Convergence curve

A snapshot of the graph in '.jpeg' format for the selected optimization problem is shown below. The graph provides the convergence of the best solution for the defined termination criteria for each selected algorithm. The x-axis represents the number of function evaluations, and the y-axis reports the corresponding mean exergy efficiency. The graph is saved in '.jpeg' and MATLAB compactable '.fig' formats.

Optimal solution of all the runs for each algorithm

The optimal solutions for each run, reported by each algorithm, are provided in a spreadsheet. A snapshot of the sheet showing the solutions of three runs for the SHO algorithm is given below. The sheets SHTS and WCA contain the solutions reported by the algorithms SHTS and WCA for all three runs, respectively.

Best solution among all runs

Sheet titled 'BestSol' provides the best solution reported by the selected algorithms among the multiple runs. A snapshot of the sheet representing the best solutions reported by SHTS, SHO, and WCA for the optimization problem is given below.

Statistical results for all simulations

The statistical analysis of the optimized results determined by each algorithm is provided in the spreadsheet named 'Stats'. A snapshot of the statistical results sheet is shown below.

Simulation results

The toolkit saves all the individual simulation results in MATLAB compactable '.mat' files for all the selected algorithms. A snapshot of the folder with all the results, including graphs, spreadsheets, and '.mat' files, is shown below

Section 2

This section explains the toolkit results for solving multi-objective optimization model for a flat plate solar water collector system. Similar to single-objective results, the multi-objective model results are also reported using graphs and spreadsheets. The results explained here are generated using the below-mentioned conditions for the multi-objective optimization problem.

Selected techniques: MODE, MOGA, FYYPO

Maximum function evaluations: 200

No. of runs: 3

Pareto front determined by all algorithms and global Pareto front

The Pareto front corresponding to each selected algorithm and the global Pareto front are presented in a graph and are saved in '.jpeg' and MATLAB compactable '.fig' files. A snapshot of the graph generated for the selected optimization conditions is given below.

Pareto solutions determined by each algorithm

The Pareto solutions determined by each algorithm are provided in a spreadsheet. Each sheet represents the results of the corresponding algorithm while considering all the performed runs.

Global Pareto solutions

The global Pareto solutions obtained in the multi-objective model are provided in a sheet titled 'GLOBAL'. The global Pareto solutions are obtained by selecting the non-dominated solutions from all the simulation instances.

Corner points determined by each algorithm

The corner points determined by each algorithm are provided in a sheet titled 'corner'. A snapshot of the sheet for the selected optimization conditions is given below.

Simulation results

The individual simulation results are saved in MATLAB compactable '.mat' files for all the selected algorithms. A snapshot of the folder with all the results, including graphs, spreadsheets, and '.mat' files, is shown below.