Introduction

Wolf [1] first introduced PVT (photovoltaic/thermal) technology in 1976, to increase total solar efficiency and jointly produce thermal and electrical energy. Additionally, because some of the waste heat is eliminated, the working temperature of the PV cells is reduced and as a result increases their electrical efficiency. PVT modules of all types, such as heat pipe PVT modules, air PVT modules [2], water PVT modules [3, 4], and nanofluid PVT modules [5, 6], have been developed over many years [7]. However, the intermittent nature of solar irradiance still limits the performance of the aforementioned PVT systems. Additionally, the temperature impact causes a greater output thermal energy level (and, thus, a higher module temperature) result in a lower electrical efficiency, so there is a conflict between that level and electrical efficiency [8]. There are two ways to identify each PV/T system’s optimal performance point: conducting several experiments and utilizing sophisticated computer techniques. Nowadays, computer approaches direct us to quickly and correctly find the optimal solution for each complex system [9]. In an air PV/T system, Shahsavar et al.'s [10] study concentrated on a number of certain variables, such as the channel's depth, length, and width as well as the output air temperature for system optimizing, and report the finest cases, based on NSGA.

Cao et al. [11] examined the cooling of a PV system using a nanofluid in a different investigation. They looked into the effects of three key changes in the mass flow rate, solar irradiation, as well as the nanofluid characteristics. The adaptive neuro-fuzzy inference system (ANFIS) was used to optimize the system, and the estimated procedure's optimum electrical efficiency was calculated. In 2013, Karathanassis et al. [12] developed a novel optimization approach for particular usage in a micro-channel. Khaki et al. [13] employed the genetic algorithm to improve both the energy efficiency and exergy efficiency of building integrated photovoltaic/thermal (BIPV/T) systems. Vera et al. [14] put up a mathematical model and made both experimental and mathematical predictions regarding the building integrated photovoltaic/thermal (BIPV/T) system's efficiency. To determine the best selection criteria that would affect the system's mechanism and overall performance, they used the GA. Air gap, collector length, aspect ratio, mass flow rate, collector count, and storage tank capacity were the factors that were examined. The use of GA in conjunction with optimization goals was the main focus of Singh et al. study [15]. Sohani et al. [16] performed a multi-objective optimization of a building integrated photovoltaic/thermal (BIPV/T) system using phase change material (PCM) in the context of Tehran's weather conditions The optimization process incorporated energy efficiency, ecological impact, and economic factors to achieve a balanced outcome. Therefore, 77.2 mm was determined to be the ideal PCM thickness for the test conditions. Additionally, the energy payback period of the system was determined to be 3.3 years., and its annual CO2 emissions were 17.7% fewer than they were been in the basic case.

A PV/T arrangement was examined by Sarhaddi et al. [17]. They demonstrated a novel method for examining the design specifications of an average air PV/T system Moreover, electrical, thermal, and environmental aspects were considered in the total energy analysis of an air PV/T configuration. Their results demonstrated that the system under investigation had total energy, electrical, and thermal efficiency of around 45%, 10%, and 17.18%, respectively. In 2022, Sattar et al. [18] conducted the most recent study and created an analytical model for a solar module that was paired with airflow to provide cooling. The main parameters that were considered were mass flow rate, irradiation, temperature, and duct geometrical requirements. Additionally, the main optimization objective was to increase the electrical output power. A multi-objective multivariable optimization was used on the system to accomplish this goal [19].

This paper focused on studying the parameters design (the mass flow rate of fluid (m.), tube spacing (W), tube diameter (D), absorber conductivity (Kabs), and packing factor (S)) effect on both electrical and thermal efficiencies of a PVT collector with different types of meta-heuristic algorithms: moth flame optimization (MFO), ant-lion optimization (ALO), dragonfly algorithm (DA), grey wolf optimization (GWO), particle swarm optimization (PSO), multiverse optimization (MVO), and genetic algorithm (GA). The algorithms for sine–cosine algorithm (SCA) and whale optimization (WOA) were selected and applied on multi-objective optimization problem to obtain the optimal solution of design parameters. The algorithms were built and validated using MATLAB software, comparing these algorithms' results to obtain the most accurate and useful result for collector designing. Finally, the effect of these parameters was studied as a feasibility study on the PVT collector performance represented in thermal and electrical efficiencies and mean plate temperature. Moreover, the influence of air temperature as well as solar radiation regarding the average plate temperature and both efficiencies of the PV/T collectors was studied.

The paper structure is divided into the following parts: Part 2 introduces the detailed mathematical modeling of PV/T collector. Part 3 explains the problem formulation and the different used algorithms. Part 4 discusses the optimization algorithms used in this study. Part 5 displays and talks about the results obtained from each algorithm and a comparison of the temperatures of the hybrid PV/T collector and PV modules in different environmental conditions. Finally, “Conclusions” Section presents the conclusions and recommendations.

Mathematical model

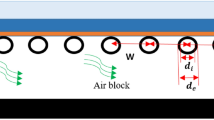
Here, a water PV/T system’s mathematical model was created using the energy balances of its many parts. Due to the system’s symmetrical geometry, differential elements with length (dx) as well as width (w) were used (Fig. 1).

Fig. 1
figure 1

PV/T system schematic view [20]

Full size image

The collector’s useful energy output is [21]:

$$ \begin{aligned} Q_{{\text{u}}} & = S \cdot A_{{{\text{PV}}/{\text{T}}}} F_{{\text{R}}} \left[ {G \left( {\tau \alpha } \right)_{{{\text{eff}}}} - U_{{\text{L}}} \left( {T_{{\text{i}}} - T_{{\text{a}}} } \right)} \right] \\ & \quad + \left( {1 - S} \right)\left[ {A_{{{\text{PV}}/{\text{T}}}} F_{{\text{R}}} \left[ {G \left( {\tau \alpha } \right)_{{{\text{eff}}}} - U_{{\text{L}}} \left( {T_{{{\text{pm}}}} - T_{{\text{a}}} } \right)} \right]} \right], \\ \end{aligned} $$
(1)

where the area of PV/T collector is APV/T, the PV plate average temperature is Tpm, the ambient temperature is represented by Ta, the heat removal factor is given by FR, the solar irradiance is represented as G, Ti represents the water input temperature, S is the area of the PV/T module covered with the PV cell, and the total heat loss coefficient is given by UL. The heat removal factor is determined as follows [22]:

$$ F_{{\text{R}}} = \frac{{m C_{{\text{p}}} }}{{A_{{{\text{PV}}/{\text{T}}}} U_{{\text{L}}} }}\left[ {1 - \frac{{\frac{Z}{{U_{{\text{l}}} }} - \left( {T_{{\text{o}}} - T_{{\text{a}}} } \right)}}{{\frac{Z}{{U_{{\text{L}}} }} - \left( {T_{{\text{i}}} - T_{{\text{a}}} } \right)}}} \right], $$
(2)

where Z is the solar energy absorbed, To is the temperature of the outlet water, Ti is temperature of the inlet water, m· is the water flow rate, and Cp is the specific heat coefficient of water (constant pressure). The overall heat loss coefficient is [23]:

$$ U_{{\text{L}}} = U_{{\text{t}}} + U_{{\text{b}}} + U_{{\text{e}}} , $$
(3)

where Ue is the edge’s heat loss coefficient, the backside’s heat loss coefficient is Ub, and Ut is the front side’s total heat loss coefficient. The next equation can calculate the total efficiency, electrical efficiency, and thermal efficiency [22, 23]:

$$ \eta_{{{\text{th}}}} = \frac{{Q_{{\text{u}}} }}{{A_{{{\text{PV}}/{\text{T}}}} \cdot G}} , $$
(4)
$$ \eta_{elect} = \eta_{e,ref} \left[ {1 - {\text{B}}\left( {T_{cell} - T_{a,ref} } \right)} \right], $$
(5)
$$ \eta_{T } = \eta_{th} + \frac{{\eta_{elect } }}{{\eta_{plant} }}, $$
(6)

where Tcell is the PV cells ‘temperature, \(T_{{{\text{a}},{\text{ref}}}}\) indicates the temperature under standard conditions (298.15 K), B indicates the PV temperature coefficient (0.0045), ηe,ref is the solar cell's efficiency under STC, ηT indicate the total efficiency, the thermal efficiency is ηth, and ηelect indicates the total efficiency, and ηplant is the average efficiency of producing electrical power and is taken as 38%.

The study was performed in the city of Cairo (30.06° N, 31.23° E). The monthly solar radiation as well as air temperature of Cairo, Egypt, is indicated in Fig. 2. Table 1 illustrates the parameters of PV/T collector [23].

Fig. 2
figure 2

Monthly environmental condition of Cairo a solar radiation b air temperature [24]

Full size image
Table 1 Configuration parameters of PV/T collector
Full size table

Problem formulation

Several valuable studies have been conducted to optimize PV/T collectors design parameters (the fluid flow rate (m·), tube space (W), absorber conductivity (Kabs), tube diameter (D), and packing factor (S) using various techniques. Certain studies revised the optimization algorithms to improve PV/T collector performance and efficiency. This study enhanced the PV/T collectors’ effectiveness, with several optimization techniques (GA, PSO, GWO, ALO, MVO, DA, MFO, SCA, and WOA) for obtaining the desired optimal system design corresponding to the highest efficiency. Using optimization methods, the optimized operating parameters for PV/T collectors were found with high thermal and electrical efficiency as the objective. There are five factors in the desired PV/T collector, which are represented as:

$$ x_{i}^{\min } \le \, x_{i } \le x_{i}^{\max } ; i \, = \, 1, \, 2, \, 3, \, 4, \, 5 $$
(7)

where x = (m·, D, W, Kabs, S).

The optimal values of xi were determined by maximizing the thermal and electrical efficiencies of the PV/T collector in which the objective function is given by:

$$ f\left( x \right) = \max \left\{ {\begin{array}{*{20}c} {\eta_{{{\text{e}},{\text{ref}}}} \left[ {1 - B\left( {T_{{{\text{cell}}}} - T_{{{\text{a}},{\text{ref}}}} } \right)} \right]} \\ {\frac{{Q_{{\text{u}}} }}{{A_{{{\raise0.7ex\hbox{${{\text{PV}}}$} \!\mathord{\left/ {\vphantom {{{\text{PV}}} {\text{T}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{T}}$}}}} G}}} \\ {\eta_{{{\text{th}}}} + \frac{{\eta_{{{\text{elect}} }} }}{{\eta_{{{\text{plant}}}} }}} \\ \end{array} } \right. $$
(8)

The objective functions for maximizing the provided efficiencies are determined as follows:

$$ f\left( x \right)_{\min } = \min \left( {\frac{1}{f\left( x \right)}} \right) $$
(9)

As the provided objective function is minimized, the efficiencies will be maximized.

Optimization algorithms

Genetic algorithm

A GA is a popular and extensively utilized tuning technique based on natural selection and genetics. Furthermore, it is often employed as a baseline for assessing sophisticated algorithms. The Global Optimization Toolbox in MATLAB was used in this study for GA optimization. It is a versatile tool to find results rapidly and efficiently.

Particle swarm optimization

This algorithm is initiated by a swarm of particles (the initial population). Particles use precise formulas to search across the search region. Particles attend their finest-recognized places after conducting the study in the field of search. Next, the ideal position is determined, and the particles control the movement of extra particles. The exploration of the field of search is repeated until a proper result is recognized. The swarm is fine-tuned according to the equations below for each iteration [25]:

$$ v_{i}^{t + 1 } = I*v_{i}^{t } + c_{1} *r_{1} *\left( {p_{i}^{t} - x_{i}^{t} } \right) + c_{2} *r_{2} *\left( {g_{i}^{t} - x_{i}^{t} } \right), $$
(10)
$$ x_{i}^{t + 1} = x_{i}^{t} + v_{i}^{t + 1} , i = 1,2, \ldots ,n $$
(11)

where I indicates the weighted inertia, positive constants are c1 and c2, n indicates number of particles, plus t indicates the iterations’ number, and r1 and r2 are two random variables that diverge within the interval 0 and 1. The particle's finest location is pi, while its biggest particle is gi.

Grey wolf optimization algorithm

This algorithm is stimulated by means of the headship construction and shooting performance of grey wolves (Canis Lupus) in their normal habitation. The headship construction in the model simulation is separated into four wolf classifications: alpha, delta, beta, and omega. The stages of shooting are as follows: looking for a target, rotating it, and attacking it [26]. The rightest result is observed in the alpha (α) that mathematically simulated the social hierarchy of wolves in GWO. Subsequently, the results indicate that beta (β) and delta (δ) are the second and third highest scores. Omega (ω) is expected for the outstanding probable results. The GWO algorithm’s optimization is guided by α and β; these wolves are followed by means of the ω wolves [27]. The next is a short-lived description of the mathematical model. The circling routine of the grey wolves is mathematically denoted by [28]:

$$ \overrightarrow {D } = \left| {\overrightarrow {c. } \overrightarrow {{x_{{\text{p}}} }} \left( {{\text{iter}}} \right) - \overrightarrow {{x\left( {{\text{iter}}} \right)}} } \right|, $$
(12)
$$ \vec{x} \left( {{\text{iter}} + 1} \right) = \vec{x}_{p} \left( {{\text{iter}}} \right) - \vec{A} $$
(13)

The position vectors of the prey and grey wolves are represented by \(\overrightarrow {{x_{p} }}\) and \(\vec{x}\), respectively. The current iteration is iter. Coefficient vectors \(\vec{A}\) and \(\vec{B}\) are estimated as follows [29]:

$$ \vec{A} = 2 \vec{a}\overrightarrow {{r_{1} }} - \vec{a}, $$
(14)
$$ \vec{C} = 2 \overrightarrow {{r_{2} }} , $$
(15)

where \( \overrightarrow {{r_{1} }} , {\text{and}}\; \overrightarrow {{r_{2} }} \) are the random vectors with values between 0 and 1. Through the iterations, the components of a are progressively lowered from 2 to 0. Grey wolf hunting is mathematically modeled as follows [29]:

$$ \vec{D} = \left| {\overrightarrow {{b_{1} }} \overrightarrow {{x_{a} }} - \vec{x}} \right| , \overrightarrow {{D_{\beta } }} = \left| {\overrightarrow {{b_{2} }} \overrightarrow {{x_{\beta } }} - \vec{x}} \right| , \overrightarrow {{D _{\delta } }} = \left| {\overrightarrow {{c_{3} }} \overrightarrow {{x_{\delta } }} - \vec{\alpha }} \right|, $$
(16)
$$ \overrightarrow {{x_{1} }} = \overrightarrow {{x_{a} }} + \overrightarrow {{A_{1} }} \left( {\overrightarrow {{D_{a} }} } \right) , \overrightarrow {{x_{2 } }} = \overrightarrow {{x_{\beta } }} + \overrightarrow {{A_{2} }} \left( {\overrightarrow {{D_{\beta } }} } \right) , \overrightarrow {{x_{3} }} = \overrightarrow {{x_{\delta } }} + \overrightarrow {{A_{3} }} \left( {\overrightarrow {{D_{\delta } }} } \right), $$
(17)
$$ \vec{x}\left( {{\text{iter}} + 1} \right) = \left( {\overrightarrow {{x_{1} }} + \overrightarrow {{x_{2} }} + \overrightarrow {{x_{3} }} } \right)/3, $$
(18)

Iteratively, α, β, and δ estimate the potential target location and update the distance. The best outcomes are then used to force the other agents to update their locations. Potential solutions often converge on prey if |A|< 1, or flee from prey if |A|> 1.

Ant-lion optimization algorithm

This algorithm is built on the hunting machinery of ant-lions also includes a random way of walking exploration and haphazard agent selection. The six basic processes of the haphazard wandering of ants, catching in ant-lion pits, creating traps in ant-lions, sliding ants near ant-lions, gathering prey, and repairing traps are elitism. The elite ant-lion is selected from each iteration’s greatest ant-lion. Using a stochastic movement, ants can readily detect the food location. The following equations mathematically express this phenomenon [30]:

$$ y\left( t \right) = \left[ {\begin{array}{*{20}c} {0, {\text{cumsum}}\left( {2r\left( {t_{1} } \right) - 1} \right), {\text{cumsum}}\left( {2r\left( {t_{2} } \right) - 1} \right), \ldots } \\ {{\text{cumsum}}\left( {2r\left( {t_{n} } \right) - 1} \right)} \\ \end{array} } \right], $$
(19)

where y (t) represents random ant walks, the variables n, t, and r (t) indicate the iterations’ maximum number, random walk steps, as well as the function built as follows [30]:

$$ r \left( t \right) = \left\{ {\begin{array}{*{20}c} 1 & {{\text{rand}} > 0.5} \\ 0 & {{\text{rand}} \le 0.5} \\ \end{array} } \right., $$
(20)

where the symbol rand indicated a uniformly distributed random number in the range 0 and 1[31].

Multiverse optimization algorithm

Concerning the multiverse theory, there was more than just one enormous bang, but also numerous big bangs occurred, each of which birthed a novel universe. It is concluded that there are numerous other worlds besides the Earth. There is also a chance that these different universes will strike; Consequently, MVO draws inspiration for solving the optimization problem from the ideas behind worm holes, black holes, and white holes. This algorithm needs to track these optimization criteria [32].

  1. 1.

    The high inflation rate results in a lot of white holes.

  2. 2.

    Black holes are likely to exist if the rate of inflation is high.

  3. 3.

    If the pace of inflation in the universe is high, objects will be hurled into white holes.

  4. 4.

    If the rate of inflation of the universe is low, objects will be captured by black holes.

  5. 5.

    Objects can randomly go through wormholes to the best universe, regardless of the rate of inflation.

The following is the expression for the MVO algorithm's basic mathematical model [33]:

$$ x_{i }^{j } = \left\{ {\begin{array}{*{20}c} {x_{k}^{j} } & {r_{1} < {\text{NI}}\left( {U_{{\text{i}}} } \right)} \\ {x_{i}^{j} } & {r_{1 } \ge {\text{NI}}\left( {U_{{\text{i}}} } \right)} \\ \end{array} } \right., $$
(21)

where NI (Ui) indicates the normalized inflation rate of the ith universe, \(x_{k}^{j}\) indicates the jth object of the kth universe, a random number within 0 and 1 is r1, and \(x_{i}^{j}\) is the jth object of the ith universe. The equation stated \(x_{i}^{j}\) is [32]:

$$ x_{i}^{j} = \left\{ {\begin{array}{*{20}c} {\left( {X_{j} + {\text{TDR}} \times \left( {{\text{ub}}_{j} - {\text{lb}}_{j} } \right) \times r_{4} + {\text{lb}}_{j} } \right),} & { r_{3} < 0.5} \\ {\left( {X_{j} - {\text{TDR}} \times \left( {{\text{ub}}_{j} - {\text{lb}}_{j} } \right) \times r_{4} + {\text{lb}}_{j} } \right),} & {r_{3} \ge 0.5, r_{2} < {\text{Web}},} \\ {X_{i}^{j} } & {r_{2} \ge {\text{WEP}}} \\ \end{array} } \right. $$
(22)

where TDR and WEP are coefficients, ub indicate the upper limit, lb indicate the lower bound, Xj indicate the jth parameter of the best universe discovered so far, as well as (r2, r3, and r4) are values randomly selected within 0 and 1. Adaptive factors like WEP and TDR are employed to create exploitation. WEP is used to improve exploitation near the greatest result found so far, and TDR is used to improve exploitation near the finest result found so far. The following are the WEP and TDR coefficient adaptive formulas [33]:

$$ {\text{WEP}} = \min + l \times \left( {\frac{{\left( {\max - \min } \right)}}{L}} \right), $$
(23)
$$ {\text{TDR}} = \left( {1 - \frac{{l_{\frac{1}{p}} }}{{L^{\frac{1}{p}} }} } \right), $$
(24)

The smallest and greatest values are characterized by min and max, in turn; l indicates the current iteration, and L is the iterations’ maximum number. The exploitation factor is represented by p.

Dragonfly algorithm

This algorithm built on swarm intelligence established by Mirjalili at Griffith University in 2016. It draws inspiration from the natural dragonfly’s static and dynamic behaviors [34]. Dragonflies’ dynamic swarming behavior generates a variety of solutions in DA, enhancing the algorithm’s exploration capabilities. The exploitation capacity of the algorithm is indicated by the static swarm [35].

The separation’s mathematical model is computed as follows [34]:

$$ S_{i} = - \mathop \sum \limits_{j = 1}^{N} X - X_{j} , $$
(25)

where N indicates the neighboring individuals’ number, Xj indicates the jth neighboring individual position, and X indicates the current position. Alignment (A) is represented as [34]:

$$ A_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{N} V_{j} }}{N}, $$
(26)

where Vj indicates the individual velocity of the jth neighbor. Cohesion (C) is computed as follows [33]:

$$ C_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{N} X_{j} }}{N} - X $$
(27)

A food source’s (F) attractiveness is ascertained by [34]:

$$ F_{i} = X^{ + } - X $$
(28)

The following determines how to divert an adversary (E) externally [35]:

$$ E_{i} = X^{ - } + X, $$
(29)

in which the adversary position is denoted by X− and the food source position by X+.

The dragonfly’s position is updated in a search space and analysis based on its movement step vectors (ΔX) and position (X) vectors. Because DA’s step vector and PSO’s step vector are identical, the movement direction is indicated by DA’s step vector as [35]:

$$ \Delta X_{t + 1} = \left( {nS_{i} + aA_{i} + dC_{i} + fF_{i} + eE_{i} } \right) + r\Delta X_{t} , $$
(30)

where the variables t, f, e, r, n, d, and A represent the number of iterations, food factor, enemy factor, weight of inertia, separation weight, cohesion weight, and alignment of the ith individual. Calculating the location vectors is done as [35]:

$$ X_{t + 1} = X_{t} + \Delta X_{t + 1} $$
(31)

When there are no nearby alternatives, dragonflies adopt the Lévy flight walk to increase the randomness of their flight. As a result, updates the dragonfly’s position by [36]:

$$ X_{t + 1} = X_{t} + {\text{Levy}}\left( d \right) \times X_{t} , $$
(32)
$$ {\text{Levy}}\left( x \right) = 0.01 \times \frac{{\sigma_{{\text{d}}} r_{1} }}{{\left| {r_{2} } \right|^{{\frac{1}{\beta f}}} }}, $$
(33)
$$ \sigma_{{\text{d}}} = \left( {\frac{{\Gamma \left( {1 + \beta f} \right) \times \sin \left( {\frac{\pi \beta f}{2}} \right)}}{{\Gamma \left( {\frac{1 + \beta f}{2}} \right) \times \beta f \times 2^{{\left( {\frac{\beta f - 1}{2}} \right)}} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\beta f}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\beta f}$}}}} , $$
(34)
$$ \Gamma \left( x \right) = \left( {x - 1} \right), $$
(35)

where the location vectors’ dimension is indicated by the letter d. With respect to [0, 1], r1 and r2 are random values, while βf is a constant (1.5) [35].

Moth-flame optimization algorithm

The first step in MFO is the randomly generated building of moths across the solution space. Each moth's fitness value, or position, is then calculated, and the ideal position is flame-tagged. The locations of the moths are then updated by a spiral movement function for achieving the well locations tagged by a flame, then, until the termination requirements are satisfied, updating the novel finest solitary locations and repeating the earlier steps (i.e., updating the moth positions and creating new positions) [37]. The MFO mathematical model consists of two parts: flames and moths. The real search agents that traverse the search space are moths, and the best sites for moths to be found that have been found so far are fires. [38]. The following equations explain the algorithm [37]:

$$ {\text{No}}.\;{\text{ of}}\;{\text{flame}}\; = \,{\text{round}} \left( {N - I *\frac{N - I}{T} } \right) , $$
(36)

where I denotes the current iteration, T and N denotes the maximum number of iterations and the maximum number of flames. One can determine the distance, Di, between the jth moth (Mj) and the matching jth flame (Fj) by referring to [38]:

$$ Di = \left| {Fj - Mj } \right| $$
(37)

Sine–cosine algorithm

This algorithm [34] is motivated by sine and cosine functions. The technique searches the candidate solution space using a mathematical model to catch the optimized solution. In the search space, the particle positions are updated as [39]:

$$ J_{t + 1} = J_{t} + r_{1} \cdot \sin r_{2} \cdot \left| {r_{3 } p - J_{t} } \right| $$
(38)
$$ J_{t + 1} = J_{t} + r_{1} \cdot \cos r_{2} \cdot \left| {r_{3 } p - J_{t} } \right| $$
(39)

The updated position is Jt+1; r1, r2, and r3 are the random variables; and the desired location is Pi. Depending on if the random number is larger or smaller than 0.5, these two equations are employed accordingly. To identify the optimized solution, the particle variation in the search space is related to sine or cosine functions.

Whale optimization algorithm

A school of little fish moving close to the water surface is hunted by a humpback whale, according to Mirjalili and Lewis, who first created this algorithm in 2016. By reducing its circle, the whale creates bubbles, which can be referred to as 9-shaped routes [40]. This algorithm is split into two sections. The first step is exploration, which includes a random approach to finding prey. The spiral bubble-net attack can be used to encircle prey in the second phase, also known as the exploitation phase [41].

If P < 5 where P indicates a random number within 0 and 1 and if \(\left| {\vec{A}} \right|\)< 1, use the encircling prey approach to update the position [41]:

$$ \overrightarrow {{X\left( {t + 1} \right)}} = \overrightarrow {{X^{*} \left( t \right)}} - \left( {\vec{A} \vec{D}} \right) $$
(40)
$$ \vec{A} = \left( {2 \vec{a} \vec{r}} \right) - \left( {\vec{a}} \right), $$
(41)
$$ \vec{D} = \left| {\left( {2 \vec{r} \overrightarrow {{X^{*} \left( t \right)}} } \right) - \overrightarrow {X\left( t \right)} } \right|, $$
(42)

where \( \overrightarrow {{X\left( {t + 1} \right) }}\) represents the updated position, \(\overrightarrow {X\left( t \right)}\) represents the best solution position, \(\vec{a}\) is a random vector between 2 and 0 depending on the maximum iteration number consuming shrinking encircling, and \(\vec{r}\) denotes a random vector in between [0, 1].

If |\(\vec{A}\) |> 1, update the position by exploring the phase method that [42]:

$$ \overrightarrow {{X\left( {t + 1} \right)}} = \overrightarrow {{X^{{{\text{rand}}}} }} - \left( {\vec{A} \vec{D}} \right) $$
(43)
$$ \vec{D} = \left| {2 \vec{r} \overrightarrow {{X^{{{\text{rand}}}} }} - \overrightarrow {{X^{* } \left( t \right)}} } \right| $$
(44)

where \(\overrightarrow {{X^{{{\text{rand}}}} }}\) is a random position vector.

If P > 1, position is updated by updating the spiral as [43]:

$$ \overrightarrow {{X\left( {t + 1} \right)}} = \left( {\vec{D} e^{bi} \cos 2 \pi l} \right) \overrightarrow {X\left( t \right),} $$
(45)

where L indicates a random value between − 1 and 1, and b characterizes the logarithmic spiral shape [41].

$$ \vec{D} = (\overrightarrow {{X^{*} \left( t \right)}} - \left( {\overrightarrow {X\left( t \right)} } \right) $$
(46)

The flowchart introduces the steps of the previous algorithms and the explanation is shown in Fig. 3; the first step determines the optimization technique inputs parameters such as initial population, max iteration, boundary limit, and position after the calculation of PV/T parameters (m·, D, W, S, Kabs) and calculate the objective function thermal and electrical efficiencies, set the fitness value for each search agent and update these positions, at max. Iteration evaluates the solutions with respect to objective function. Table 2 illustrates the range of variation and input parameters for optimization algorithms and approaches.

Fig. 3
figure 3

Flow chart of proposed optimization algorithms for PV/T collector

Full size image
Table 2 The range of variation and input parameters for optimization approaches
Full size table

Results and discussion

This paper optimized five dissimilar PV/T collector parameters which affect the PV/T collectors overall performance. The additional design parameters remained unchanged, while these five parameters were optimized. Several design criteria should be chosen to turn a PV module with a certain size and electrical qualities into a PV/T collector. A comparison of the optimization algorithms’ outcomes is displayed in Table 3. The primary design parameters are the fluid flow rate of fluid (m·), tube spacing (W), tube diameter (D), absorber conductivity (Kabs), and packing factor (S). A comparison was made of the thermal, electrical, and overall efficiency. It was observed that ALO, SCA, and WOA produced the best fluid flow rates that are 0.025 kg/s, 0.028 kg/s, and 0.024kg/s, respectively, compared with those of other algorithms, but the SCA had the least thermal and electrical efficiencies that are 46.89%, and 14.28% respectively, compared with those of ALO and WOA, ALO efficiencies are 52.08% and 14.28, WOA efficiencies are 51.75% and 14.26%. The best tube diameter results were obtained from the PSO and MFO algorithms that is 0.01m; however, the MFO algorithm produced the best thermal and electrical efficiency that are 52.04% and 14.28%, respectively. Moreover, ALO and WOA produced optimal tube spacings, which is 0.0869 m for ALO and 0.09 m for WOA, with convergent electrical and thermal efficiencies. The absorber conductivity of copper material was obtained from the SCA optimization with thermal efficiency of 46.89% and electrical efficiency of 14.13%, and the MVO algorithm produced aluminum as an absorber material with thermal efficiency is 51.99% and electrical efficiency is 14.28%. The MVO algorithm had the highest thermal and electrical efficiencies are 51.99% and 14.28%, respectively, but copper is more cost-effective than aluminum. The optimal packing factor was obtained from the optimization results achieved using the GA, PSO, and SCA, which are 0.989, 1, and 0.9387, respectively. As shown, the GA algorithm had the worst thermal and electrical efficiencies are 41.41% and 13.85%. After the optimization process, the DA algorithm offered a better thermal efficiency is 41.89%, compared with that of the GA algorithm; however, when DA's performance was contrasted with other algorithms, it was worse. The PSO algorithm had a better tube diameter and optimized packing factor; however, it had low thermal and electrical efficiencies that are 42.44% and 13.93%, respectively. Although the SCA had good results for the flow rate, absorber conductivity, and packing factor, in addition, its thermal and electrical efficiency were poor when contrasted with other methods. With respect to the table, the electrical and thermal efficiencies of the WOA and MVO were approximately close, but the WOA values were better than the MVO values; however, they both did not have the optimal design for the PV/T collector. Finally, the MFO, ALO, and GWO algorithms had the optimized values for the both efficiencies, and the GWO algorithm had the optimal values for the design parameters. Thus, the optimized PV/T design was obtained from the GWO algorithm.

Table 3 PV/T design parameters based on different optimization techniques
Full size table

After applying the resulting optimized parameters in the simulation for each optimization algorithm, the figures of electrical and thermal efficiencies with reduced temperature were introduced. Figures 4, 5 and 6 show the comparison of each algorithm's thermal, electrical, and total efficiencies. GWO and ALO algorithms show the same and highest electrical and thermal efficiencies, but the GWO algorithm parameters were more effective than that of the ALO algorithm.

Fig. 4
figure 4

Variation in thermal efficiency of PV/T for all algorithms

Full size image
Fig. 5
figure 5

Variation in electrical efficiency of PV/T for all algorithms

Full size image
Fig. 6
figure 6

Total PV/T efficiency variation for all algorithms

Full size image

As shown from the results, the three algorithms GA with thermal efficiency of 41.41% and electrical efficiency 13.85%, PSO with thermal efficiency of 42.44% and electrical efficiency 13.39%, and DA with thermal efficiency of 41.89% and electrical efficiency 13.67%, introduce the minimum thermal and electrical efficiency values. The DA and GA had the worst values for thermal and electrical efficiencies, although GA and PSO had the maximum and most effective packing factors that are 0.095 and 1, respectively.

The thermal efficiency of the MFO and MVO algorithms was good but lower than that of the GWO and ALO algorithms. In addition, the electrical efficiency of the MFO and MVO algorithms was high but not suitable, compared with that of the GWO algorithm. The WOA algorithm efficiencies curves were high and exhibited good results, but the optimized parameters are not the most valuable values. The SCA algorithm efficiencies values were not the worst or maximum values, compared with those of other algorithms, although it had a good packing factor. Unfortunately, the other SCA parameters were not the best values. Finally, the GWO algorithm recorded the best-optimized parameters with the optimized electrical and thermal efficiencies and good design parameters.

Tables 4, 5 and 6 introduce the effectiveness of the flow rate, packing factor, and tube spacing based on the thermal and electrical efficiencies of the PV/T collector concerning the change in solar radiation. The figures show a comparison of the IV curves of a stand-alone PV and the IV curves of a PV/T collector concerning this effect at air temperature (25 °C). As shown in Table 4, it was observed that with an increase in radiation, the flow rate also increased, resulting in higher thermal and electrical efficiencies. Table 5 shows that an increase in packing factor to radiation resulted in thermal efficiency decrease and an increase in electrical efficiency, but the tube spacing has a different effect on the flow rate and packing factor as it decreased the electrical and thermal efficiencies because of an increase in plate temperature. Table 6 shows the thermal, electrical, and PV/T temperature with tube width variation.

Table 4 The electrical, thermal, and PV/T temperature with mass flow variation
Full size table
Table 5 The electrical, thermal, and PV/T temperature with packing factor variation
Full size table
Table 6 The thermal, electrical, and PV/T temperature with tube width variation
Full size table

Figures 7 and 8 show similar currents in the stand-alone PV module and PV/T collector but a small change and an increase in voltage increased the flow rate and packing factor. For the stand-alone PV module, the packing factor and mass flow were less than those in the PV/T collector. Figure 9 denotes the matching currents in the stand-alone PV and PV/T collectors. However, an increase in voltage occurred in the PV/T collector and caused a decrease in tube spacing.

Fig. 7
figure 7

PV/T collector I–V curves with mass flow rate (Kg/s) variation at STC

Full size image
Fig. 8
figure 8

PV/T collector I–V curves with packing factor variation at STC

Full size image
Fig. 9
figure 9

PV/T collector I–V curves with tube spacing (m) variation at STC

Full size image

Table 7 shows the comparison of the present results of the optimization design with the reported results. For the GWO algorithm result (the best results obtained), Fuentes et al. [28] achieved approximately the same electrical and thermal efficiencies as those of the present efficiencies, but the total efficiency of the GWO algorithm was more effective. Compared with the other papers, the thermal, electrical, and total efficiencies of the GWO algorithm were better and more effective. Thus, the GWO algorithm had an excellent result, compared with those of the previous studies. By comparing our previous work [22] with the present study; the new algorithms overcome the lakes and disadvantages such as; inefficiency in large-scale continuous situations; great accuracy requires proper parameter adjustment, random selection of seeds and positions, and increase in complexity time, so the new algorithm achieved high and more accurate efficiency within low simulation time as shown in Table 7.

Table 7 Comparing PV/T efficiency with the previous works
Full size table

Conclusions

The design parameters for PV/T collectors that aim to produce the maximized thermal and electrical efficiency were presented in this study. The PV/T collector performance is built on numerous design factors that include the fluid flow rate (m·), tube diameter (D), spacing between tubes (W), absorber material (Kabs), and packing factor (S). With the aim of determining the ideal values for the design parameters, the PV/T collector performance was computed using meta-heuristic optimization techniques, including GA, PSO, GWO, ALO, MVO, DA, MFO, SCA, and WOA. The PV/T collector parameters were optimized with each optimization algorithm, and the obtained parameters were compared with each other, tested, and validated using MATLAB software. The results showed that the most effective optimization algorithms were GWO, ALO, and MFO because they produced the highest thermal and electrical efficiencies. The values of the parameters optimized with the GWO algorithm were the most effective and highest efficiencies; thus, they were considered the most suitable design parameters for PV/T collectors, the results that compared the efficiencies for each algorithm were introduced and discussed. A study of mass flow rate, packing factor, and tube diameter effect with the variation of radiation on the thermal and electrical efficiencies was discussed. Another point also was introduced in this paper that from the electrical behavior as the comparison between stand-alone PV temperature and hybrid PV/T collector temperature, there is a good enhancement in IV curves of the hybrid PV/T collector over the IV curve of stand-alone PV module. In future, we will study the ability to use machine learning and artificial intelligence in PV/T system control and design.