Techno-economic assessment of microalgae cultivation in a tubular photobioreactor for food in a humid continental climate

Abstract

Fish as the primary source for the essential n − 3 fatty acids eicosapentaenoic acid (EPA) and docosahexaenoic acid (DHA) cannot cover the global demand for these important nutrients resulting in a supply gap of currently 1.1 million tons of EPA + DHA annually. A further exploitation of natural fish stocks is linked to great damage to ecosystems. Oleaginous microalgae are a natural source for EPA and DHA and could possibly contribute to closing this gap. The cultivation in photobioreactors (PBR) in a ‘cold-weather’ climate showed that microalgae compare favorably to aquaculture fish. The present study assesses the economic potential of microalgae for food in such system model. Techno-economic assessment was conducted on the basis of a dynamic system model for the cultivation of Nannochloropsis sp. in industrial scale in Central Germany over a time span of 30 years. The net present value (NPV) and return-on-investment (ROI) were obtained for a number of scenarios in which technic and economic parameters were altered. Taking the size of the PBR considered into account, the cultivation of Nannochloropsis sp. yielded a positive NPV of EUR 4.5 million after 30 years which translates to an annualized ROI of 1.87%. The sensitivity analysis overall resulted in annualized ROIs between 1.12 and 2.47%. Major expenditures comprised the PBR infrastructure, maintenance and labor cost. An extended cultivation season by four weeks was responsible for an NPV surplus of almost one third (32%). An increase in the selling price by 15% was responsible for a 47% higher NPV. In comparison with Atlantic salmon (Salmo salar) raised in aquaculture, EPA from Nannochloropsis sp. resulted in about halved cultivation costs (− 44 to − 60%). In this study we could show that microalgae from photoautotrophic cultivation not only have the potential to supply humans with essential nutrients, but they are also a lucrative investment, even in a ‘cold-weather’ climate where cultivation cannot take place year round.

Graphic abstract

Introduction

Fish is by far the biggest source of n − 3 long-chain polyunsaturated fatty acids (PUFA), more specifically the fatty acids eicosapentaenoic acid (EPA) and docosahexaenoic acid (DHA) (de Oliveira Finco et al. 2016). The consumption of n − 3 long-chain PUFAs has been linked to cardio-vascular benefits, a support of the nervous system and a regulatory effect on inflammatory conditions (Adarme-Vega et al. 2014; García et al. 2017). These nutrients are otherwise only found in human milk, cultivated marine algae, marine mammals and krill [EFSA Panel on Dietetic Products Nutrition and Allergies (NDA) 2012] and cannot be converted by the human body in sufficient amounts (Galán et al. 2019). The question is not if alternative sources can substitute fish as the primary source for EPA and DHA, but which sources could possibly complement fish already today. Exploitation of wild-caught fish cannot be expanded without depleting natural resources and ecosystems (Adarme-Vega et al. 2014; de Oliveira Finco et al. 2016). Aquaculture fish on the other side has to rely on terrestrial fodder plants and thus competes with other food groups for arable land. Besides, the diet of aquaculture fish is enriched with wild-caught fish and fish oil to enhance its PUFA content (Adarme-Vega et al. 2014) leading to over 70% of the available fish oil being used for fish feed production (Tocher 2015; Galán et al. 2019). As a result, it has been found that fish currently only contributes around 15% of the global demand for EPA and DHA, and krill as an alternative source adds 0.3% (Salem and Eggersdorfer 2015). The annual global gap of EPA and DHA supply thus presently reaches 1.1 million tons (Schade et al. 2020), and the world population keeps on growing.

Microalgae have been studied in numerous application contexts as a source of, e.g., biofuels, fertilizers, synthetic materials, food and nutraceuticals. The exploration of alternative fuels has long driven microalgae research. However, it has been shown that from an economic and technical point of view, microalgae cannot compete with fossil fuels and are most profitable for food and feed (Barsanti and Gualtieri 2018; Walsh et al. 2018). As such, microalgae are considered the most abundant primary producers of high-value nutrients like n − 3 long-chain PUFAs and carotenoids (Adarme-Vega et al. 2014). Moreover, microalgae contain additional valuable compounds for human nutrition, such as dietary fiber which is assumed to have a positive influence on cardio-vascular diseases and an anticancer effect (Mišurcová et al. 2012). Further health-promoting compounds in microalgae comprise carotenoids, phycobiliproteins and sterols (García et al. 2017). Nannochloropsis sp. is an oleaginous microalga with an average EPA content of 4.2% under light-saturated, non-stressed conditions (Schade and Meier 2020). It favors temperatures between 21 and 25 °C (Chini Zittelli et al. 1999; Ma et al. 2016).The microalga has moreover been authorized by the US Food and Drug Administration and the European Novel Food Regulation for the application as a food (Qiu et al. 2019). Nannochloropsis sp. was selected for its suitable nutritional profile with a comparatively high lipid and protein levels. Likewise, Phaeodactylum tricornutum shows high lipid and protein contents and contains both EPA and DHA.

The photoautotrophic production of microalgae avoids using limited resources for the production of nutrients. More specifically, not only the pressure on the global fish stock is released, but compared to heterotrophic production of microalgae, no arable land must be used for the cultivation of feed for algae (Keller et al. 2017). Land as a scarce, non-renewable resource is a key indicator for the environmental viability of the global food system (Meier 2017; Rockström et al. 2020). Naturally grown land is considered as the basis of biodiversity and as such regulates the climate, adjusts the air and water quality and provides food and room for recreation (Frischknecht and Büsser Knöpfel 2013). Photobioreactors (PBR) reportedly perform better than open raceway ponds (ORP) concerning the production cost and productivity (Barsanti and Gualtieri 2018). Moreover, they are possibly more suitable for a humid continental climate than ORP because they exploit the forthcoming solar insolation optimally without any dark zones as they can exist in an ORP (Schade and Meier 2019). At the same time, they might be more efficiently operated in a humid continental climate to prevent exorbitant cooling costs (Schade and Meier 2019). Additionally, the strongest argument for the usage of a PBR over ORP is the much lower risk of contamination with bacteria, protozoa or other microalgae (García et al. 2017), which is crucial for the production of edibles. Compared to fish as the main source for PUFAs, the environmental impacts of microalgae cultivation are similar to those from wild-caught fish, and often smaller than those from aquaculture fish depending on the fish species and the exact production system or catching method (Schade et al. 2020).

PBRs have hardly been assessed with regard to cost analysis, economic risks or benefits (Zhu et al. 2018). In particular, tubular PBR cost analyses are scarce, and such investigations with the application of microalgae for food have barely been conducted. If microalgae are to be used as an alternative source for EPA and DHA globally, it is necessary to evaluate their cultivation under different climatic conditions. As such, to the best of our knowledge, cultivation cost of microalgae production has not been assessed yet in a humid continental climate. The humid continental climate has first been defined by Wladimir Köppen in 1900 in his quantitative classification of the earth’s climate zones, which is still widely applied today (Belda et al. 2014). The humid continental climate in Central Germany is hence characterized by seasonal changes. Temperatures in the coldest month must be below − 3 °C and mean temperatures must equal or exceed 10 °C in at least 4 months of the year (Peel et al. 2007). The chosen region is moreover described by an absence of a dry season, and has a warm summer (Peel et al. 2007). The cold climate, which is the superordinate category of the humid continental climate, is the dominant climate zone in Europe (44.4%), North America (54.4%) and Asia (43.8%) (Peel et al. 2007), which shows that it is rather important to explore such locations for the production of microalgae.

In this study, a techno-economic assessment was conducted to evaluate costs and benefits occurring during the production of microalgae in a tubular photobioreactor in a ‘cold-weather’ climate. The cultivation system was based on a previous study of the authors (Schade and Meier 2020) and followed a ‘top–down’ approach to assess major processes in the cultivation model. From the established net cash flow table, the net present value (NPV) (discounted cash flow) was calculated, along with the return-on-investment (ROI). Upon the alteration of different technical and economic parameters, a sensitivity analysis was conducted to analyze critical factors in industrial scale microalgae production for food.

Materials and methods

General approach

The techno-economic assessment was performed in accordance with Zimmermann et al. (2020) in order to construct the methodology section as transparent and coherent as possible. This TEA guideline allows TEA to be conducted in parallel to life cycle assessment (LCA) which emerges in aligned vocabulary and assessment steps, and it applies many concepts from ISO 14,044 (ISO Organisation 2006). TEA should cover the process steps illustrated in Fig. 1. Similar to LCA, the construction of TEA is an iterative process.

Fig. 1

Process steps in TEA according to Zimmermann et al. (2020) and reference to study chapters

Goal and scope clarified the context of the study and the reasons for carrying it out. Moreover, the methodological framework was assessed in this section (e.g., functional unit, system boundaries). The inventory was covered by the establishment of the microalgae cultivation model used in this study. The cost assessment examined investment cost and operating cost as well as the NPV and the ROI as significant indicators for the economic potential of the model. Price forecasts for the most important input materials during the whole lifetime of the facility were conducted. A following scenario analysis considered the variation of both relevant economic and technical system parameters.

Goal, scope and target product

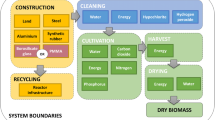
The overall goal of this study was to evaluate the economic potential of microalgae biomass production for food in a tubular photobioreactor in a humid continental climate. For that matter, the costs for generic industrial scale microalgae cultivation were assessed in a techno-economic assessment (TEA) applying the NPV and the ROI. Furthermore, major economic and technical hurdles were identified in a scenario analysis where relevant alterations of system parameters were tested. System-boundaries comprised all relevant processes and input materials of the cultivation stage up to the dry biomass (target product) (Fig. 2). One scenario considered EPA-rich microalgae oil and residual protein-rich biomass as the final products. This scenario thus moreover comprised an oil extraction stage. The evaluation of the economic potential was conducted in EUR. The inputs in Fig. 2 refer to the baseline scenario and the scenario considering microalgae oil as the target product.

Fig. 2

System-boundaries and input data of microalgae cultivation (baseline scenario and microalgae oil scenario)

Microalgae cultivation model

Input flows of microalgae cultivation were based on the design model of a previous study of the authors which evaluated the environmental impacts of cultivation processes in a hypothetical 628 m³ tubular photobioreactor located in Halle/Saale, Central Germany (Schade and Meier 2020). Dry biomass for human nutrition was produced in borosilicate glass tubes with a diameter of 40 mm (baseline scenario) and a wall thickness of 2 mm. Borosilicate glass as the material for the tubes was contemplated as superior over other possible tube materials, such as polymethyl methacrylate or silicone as it has a long lifespan of at least 50 years (Schultz and Wintersteller 2016). Moreover, it has an excellent translucence, which does not degrade under solar radiation to enable the photoautotrophic process (Schultz and Wintersteller 2016), and it is a safe material to use for the production of edibles. Further construction materials (aluminum, steel, synthetic rubber) were designed in accordance with the study by Pérez-López et al. (2017). Cultivation took place from mid-April until mid-October, because an evaluation of the climatic characteristics of the location suggested this period to be most efficient for the cultivation of microalgae, taking into account maximum, minimum and mean daily temperatures as well as solar insolation.

The calculation of the yields and productivity was based on the climatic conditions of the site, which were drawn from detailed satellite data provided by the NASA Power Data Access Viewer (NASA—National Aeronautics and Space Administration 2019). The location shows temperatures slightly below − 3 °C in the coldest months of the year (January and February) and average temperatures between 14.5 and 20.3 °C from May until September. April and October portray mean temperatures of slightly below 10 °C which is why it was assumed that on average, half of these months, cultivation was feasible. Solar insolation is highest from May until August with 16.1–18.2 MJ/m²/day and still reaches 14.1 MJ/m²/day in April and 10.8 MJ/m²/day in September. The month with the lowest radiation during the cultivation season is October with 5.6 MJ/m²/day on average. Table 1 lists the essential system parameters and input materials of all scenarios, which were based on a technical variation in the system (for scenario overview see chapter 2.6 Sensitivity analysis). All other scenarios that are not portrayed in Table 1 relied on a variation of economic parameters and thus were equal to the baseline scenario. The plant was modeled with a lifespan of 30 years. The system model relied on a combination of sources. Resource consumptions of major processes during the cultivation were based on own calculations and literature data. Additionally, some input parameters relied on expert advice. More specifically, the nutritional values of the microalgae species considered in this study are mean values compiled from the literature. Likewise, the photoconversion efficiency (PCE) is a mean value, which was obtained from several studies that had all applied a similar cultivation system and taken into account all relevant restraining parameters. Those parameters comprised light saturation and photoinhibition, practical losses through reflection, inactive absorption, respiration, and high oxygen rates (Lundquist et al. 2010; Posten 2012; Skarka 2012; Benemann 2013; De Vree et al. 2015).

Table 1 Parameters and input materials in microalgae cultivation scenarios (the origin of the values presented are described in the text)

The nutrient demand was calculated according to the protein content of the microalgae species under implementation of the nutrient-to-protein conversion factor, which was adopted from the literature (Templeton and Laurens 2015). The carbon dioxide demand was in accordance with the literature, too (Chisti 2007; Patil et al. 2008; Lardon et al. 2009; Ma et al. 2016). Usage of hydrogen peroxide and hypochlorite was estimated after Pérez-López et al. (2017). The electricity consumption and demand for natural gas resulted from different processes in the cultivation model, which were all based on own calculations. These processes comprised water pumping, aeration with CO₂, mixing of the suspension in the tubes, centrifugation and drying of the algae biomass (Schade and Meier 2020). Total uncertainty of the electrical processes is 1.07, and total uncertainty of the remaining foreground processes (photobioreactor materials, nutrients, water use, land use) is 1.13. The complete system model can be accessed in the previous study of the authors (Schade and Meier 2020).

Cost assessment

For the compilation of the cost assessment, a net cash flow table for the construction phase and the first 30 years of operation was established in order to calculate the NPV (discounted cash flow) and the ROI from it. The net cash flow is obtained by subtracting all cost paid from the received benefits while including cost for a capital loan, such as capital payback and interest rate (Lauer 2008). The first two years were supposed to be the construction phase of the plant without incoming benefits. Investment costs were evenly spread over these two years. For the following first 6 years of cultivation, a reduced production was modeled to account for the starting phase of the plant with the benefits doubling in the second year of production and a growth of 6% for each of the subsequent five years until full production is achieved. A bank loan covered the investment cost with an interest rate of 2.05% (average interest rate of the months 01/2019 to 09/2019 for Germany) (Trading Economics 2019). The net present value of a given time period NPV_n is calculated from Eq. 1 (Short et al. 1995) where NCF is the net cash flow of a time period n, and d is the nominal discount rate, which also covers inflation and is set here to 12% (Thomassen et al. 2016; Walsh et al. 2018).

$${\text{NPV}}_{n} = \frac{{{\text{NCF}}}}{{\left( {1 + d} \right)^{n} }}$$

(1)

For better comparability between the assessed scenarios, the ROI is calculated in addition to the NPV. The ROI indicates the percentage of a net value that is received from an investment over a given period of time and was calculated from the NPV of a given period of time n (Eq. 2) (Chen 2020a).

$${\text{ROI}} = \frac{{\mathop \sum \nolimits_{3}^{n} {\text{NPV}}_{n} - C_{{{\text{tot}}}} }}{{C_{{{\text{tot}}}} }}$$

(2)

The ROI is estimated for every year of plant operation, starting from the third year when facility operation begins. For every time period n, the sum of the net present values from year three to year n is calculated. The total costs C_tot represent the sum of payments assigned in the first and second year when all investment costs were paid. Since the investment project covers a timeframe of 30 years and the ROI does not consider length of time, the calculation of the annualized ROI_A gives a more representative result. The ROI can be annualized following Eq. 3 (Chen 2020b) where n is the number of years for the investment.

$${\text{ROI}}_{A} = \left[ {\left( {1 + {\text{ROI}}} \right)^{\frac{1}{n}} - 1} \right] \times 100\%$$

(3)

Although the facility was modeled as an ‘nth’ plant which presupposes a mature state of facility design and technique, there can still be contingencies that have not been accounted for in the model. In order to avoid an underestimation of the costs in the TEA and get a too optimistic result, a contingency factor of 1.25 was put on the overall costs (Lauer 2008).

Price forecasts for input materials

Prices for input materials that are constantly required in a great amount over the lifetime of the facility were analyzed in a forecast. Since the facility is supposed to run with a 30-year-lifespan, analyses of future prices intended to portray—as accurately as possible—representative prices at a given point in time. Historical prices were obtained for a 15-year period from 2004 to 2019, except electricity, for which the annual price was observed from 2000 to 2018. Prices were recorded for the materials ammonium, phosphate fertilizer and natural gas (World Bank 2019), as well as electricity (Eurostat 2019). The prices for carbon dioxide were investigated using the commodity price index (U.S. Bureau of Labor Statistics 2019) and a reference year price from 2016 (Thomassen et al. 2016). Concerning electricity, location-specific prices for Germany were applied. For natural gas, European prices were utilized. When prices were given in US-Dollar, they were converted based on the respective monthly currency rate [UKForex Limited (OFX) 2019]. It was relied on the Geometric Brownian Motion (Eq. 4) in order to estimate future prices of required resources (Hilpisch 2014).

$$\Delta S\left( t \right) = S_{t - 1} \mu \Delta t + S_{t - 1} \sigma \varepsilon \sqrt {\Delta t}$$

(4)

ΔS(t) is the price change of a respective resource over a given time period which changes as a function of the drift ($\mu$), the volatility ($\sigma$) and a Wiener process of random values (ε). The time period t comprises one month. The calculation is based on a starting price S_t−1. Whereas the drift indicates the deterministic trend of the process, the volatility controls the influence that coincidence has on the process S(t). The drift and volatility are both constants and are estimated from the mean and standard deviation of historical returns ($\mu_{t}$), which in return are drawn from the price (s_t) of each time period (Eq. 5).

$$\mu_{t} = \frac{{s_{t} - s_{t - 1} }}{{s_{t - 1} }} \times 100$$

(5)

The simulation with the Geometric Brownian motion was repeated 1000 times for each commodity and future prices analyzed according to their mean, median and 90% confidence interval. A 90% confidence interval was considered appropriate, given that these results are meant to be used in the sensitivity analysis. Thus, they should not be characterized by extreme values at the lower and upper end. A timespan of 30 years in the future was portrayed by means of monthly prices (Fig. 3).

Fig. 3

Historical and predicted future prices of commodities used during microalgae cultivation. Colors indicate a random selection of scenarios from the calculation of the Geometric Brownian Motion

Sensitivity analysis

The sensitivity analysis was based on both changes in technic and economic parameters in order to analyze the volatility of the system model. Besides the earlier described baseline scenario, the following alterations were made to the model.

Min/max commodity prices

In the baseline scenario, the mean predicted commodity prices calculated in the forecast were used for the cost assessment. However, forecasts, especially over a long time period, are rather volatile and subject to a great amount of unpredictable parameters. In order to evaluate the influence of possibly higher or lower developments of the commodity prices, the upper and lower ends of the 90% confidence intervals were included in the assessment.

Long/short production periods

The selected location in Central Germany as part of the humid continental climate zone is subject to variations in seasonal temperatures. As a result, cultivation season lengths can fluctuate drastically with a focus on the months April and October. Both can be rather warm and thus suitable for microalgae cultivation, or cold on too many days of the month with minimum temperatures dropping below 0 °C. The system model was thus evaluated applying constantly longer and shorter cultivation periods. As can be seen in the inventory table (Table 1), the length of the production period influenced the yield tremendously. Even though productivity decreases in spring and fall due to a lower solar insolation, a longer cultivation season is favorable and expands the yield. This climatic dependence was considered a key element of the cultivation in a ‘cold-weather’ climate and was hence analyzed in the cost assessment, too.

Tube price

The borosilicate glass tubes used in the photobioreactor are one of the main materials needed for microalgae cultivation and constitute one of the biggest investments concerning the whole facility. Consequently, it was tested how a fluctuation in the cost of a rather big share of the investment affects the whole cost assessment of the plant.

Variations in selling price

The agreement on a specific reasonable selling price is a crucial step in the cost assessment as it here generates the only source for benefits. The selling price used in this study was determined according to values found in the literature. Yet, a sample analysis on microalgae biomass products on the German market was conducted which revealed great fluctuations in the selling price. Price variations within the same product were due to package size where a bigger size generated a discount. Among the different products, prices differed at times tremendously without evident reason. At the same time, it was not obvious where and how the biomass had been produced. However, even with the economy of buying the biggest package, industry net selling prices still outnumbered the selling price suggested in the literature to a great extent with the literature price of EUR 38 per kg dry mass hardly being in the low range of the 90% confidence interval (Fig. S1). However, the mean value of the market analysis resulted in a net selling price (EUR 109 per kg)—equaling 187% of the literature price. The results of the market analysis can be found in the supplementary material (Tab. S1, Fig. S1). Consequently, these possible variations were accounted for in the sensitivity analysis by altering the selling price of the biomass by 5% and 15%.

Alternative microalgae species

In a previous study of the authors, it has been shown how the choice of microalgae species can alternate the environmental impacts, depending on the target product (Schade et al. 2020). For that matter, the cost assessment was repeated using P. tricornutum as the cultivated species in the PBR. Phaeodactylum tricornutum also is an oleaginous microalga with a nutritional profile that is similar to Nannochloropsis sp. However, in comparison with the latter, P. tricornutum possesses a higher percentage of protein (36.4%) (Rebolloso-Fuentes et al. 2007) and slightly less EPA + DHA (3.25%) (Zhukova and Aizdaicher 1995; Ryckebosch et al. 2014). The cultivation of another microalga with a comparable nutritional profile not only illuminates possible changes in the outcome due to taxonomical reasons. Because of the similar profile, information can be obtained about how sensitively the system reacts if the composition of one and the same alga fluctuate like it naturally does.

Microalgae oil

In another scenario, it was tested how the choice of a different goal product affects the NPV. In the baseline scenario, the whole biomass was considered as the target product. However, whole microalgae biomass only procures a fraction of the selling price compared to more refined products such as extracted lipids or antioxidants. Thus, the production of microalgal oil from Nannochloropsis sp. as a source for EPA was modeled with the residual protein-rich biomass being sold as an alternative to soybean meal. It was assumed that the whole lipid content of the biomass was extracted using supercritical CO₂. In order to extract 1 kg of microalgae oil, 11.7 kg CO₂ (Wang et al. 2016) and 58.6 MJ electricity (Shimako et al. 2016) were needed. Based on the inventory data for microalgae cultivation used in this study, 1 kg DM contains 206 g lipids and 42 g EPA. The yearly microalgae oil yield would accordingly add up to 13,225.2 kg lipids with an EPA content of 20.39%. Microalgae omega-3 oil has been reported to realize a net market price between USD 80 and 160 (Borowitzka 2013; Matos 2017; Barkia et al. 2019) which roughly corresponds to EUR 72–144. Yet, a sample market analysis of microalgae oil products for omega-3 PUFAs for the German market resulted in much higher net prices between EUR 240 and 900 (mean: EUR 452) per kg microalgae oil with an EPA + DHA share of 40–50%. Remarkably, the prices for microalgae oil were not correlated with the actual concentration of EPA and DHA in the product which provoked a massive fluctuation of the EPA + DHA net price across the products with around EUR 530–2300 (mean: EUR 1025) per kg EPA + DHA. In order to obtain a reasonable selling price, the mean value of the EPA + DHA kilogram prices was multiplied with the percentage of EPA contained in the microalgae oil. Hence, a net selling price of EUR 209 per kg microalgae oil was estimated in this study. For each kilogram microalgae oil, 3.85 kg protein-rich residual biomass was generated. The unit price for the residual protein-rich biomass was assumed to amount to 0.44 EUR/kg DM (van der Voort et al. 2017). The results of the market analysis on microalgae oil products can be accessed in the supplementary material (Tab. S2, Fig. S2). In order to conduct a profound analysis, the cost assessment for microalgae oil as the target product was repeated using the highest price suggested in the literature (144 EUR/kg oil).

Results

Investment cost and operating cost

The proportionate distribution of investment costs is shown in Fig. 4 with all components contributing more than EUR 100,000 being portrayed. In three scenarios, investment costs differed from the baseline scenario. All other scenarios equaled the baseline scenario regarding investment costs and were thus not portrayed here. The cost for the glass tube system was the biggest share and made up between 24 and 31%. Only when the glass tube price was diminished by 20%, the system was exceeded in its costs by the price for the drying system (21–24% of all investment costs). The third biggest cost component was the construction of all buildings needed for the cultivation system (18–21% of all investment costs.). All other investments contributed only 7% or less to the total investment sum.

Fig. 4

Percental component contribution to investment costs

The proportional distribution of the operating costs (Fig. 5) varied for every scenario (excluding selling price change scenarios) and was clearly dominated by labor cost, which contributed between 39 and 42% to the overall operating costs. This position was mostly followed by costs for the maintenance of the mechanical and electrical equipment. However, when commodity prices develop at the maximum end, costs for carbon dioxide exceeded these maintenance costs. The scenario using microalgae oil as the target product was also characterized by relatively high carbon dioxide costs due to the lipid extraction with supercritical carbon dioxide. Administration usually made up approximately 10% or less of the operating costs. The smallest share was constituted by the overall fuel costs and maintenance of the photobioreactor (cleaning). Even in the scenario with maximum commodity prices, fuel costs only contributed a minor share of the operating costs. Electricity processes, which are usually the main drivers in environmental assessments of microalgae cultivation, only had an insignificant share of the operating costs. They ranged from almost 2% in the minimum commodity prices scenario to 5.81% in the microalgae oil scenario, which had an expressively higher energy use.

Fig. 5

Percental component contribution to operating costs

The total investment and operating cost per kilogram dry microalgae biomass are portrayed in Table 2, assuming a lifespan of 30 years. Around 80% of the costs in all scenarios was produced by infrastructure, labor cost and maintenance cost. However, with commodity prices reaching their maximums, and in the microalgae oil scenario also fuel costs became significant. Overall, investment and operating costs summed up to EUR 8.63–11.00 per kilogram of dry biomass. The most favorable scenario in terms of production cost was the one with extended cultivation seasons, which was even more desirable than commodity prices dropping to a minimum. The highest production costs were generated when microalgae oil was the target product. However, also short cultivation seasons were highly critical and generated production costs almost as high as when microalgae oil was produced.

Table 2 Total investment and operating cost in EUR per kg dry microalgae biomass (excluding interests and contingency factor)

Net present value

The NPV puts the costs in ratio to the benefits, while it also considers a diminution of the cash flow over the years, thus taking into account the time value of money. Additionally, the contingency factor and interests are included in the calculation of the NPV. The baseline scenario results in a positive NPV of EUR 4.5 million after 30 years, which indicates that the investment in the microalgae photobioreactor in this region is profitable. The effects of the variation of certain technical and economic parameters are shown in Fig. 6. Despite the partially extensive changes in the NPV, the results remained always positive indicating an overall profitable investment. The least change in the NPV was given with the variance of commodity prices which only lessened the NPV by 3.9% when prices develop at the maximum end, and effected a rise of the NPV by 2.9% when commodity prices were set to a minimum. The cultivation of another microalgae species, namely P. tricornutum, caused a positive shift with a 7.3% higher NPV. Moreover, the change in the kilogram costs for the production of P. tricornutum (Table 2) differed only by 2.4%. The change of the glass tube price by 20%, which was considered tremendous, only affected the NPV to an acceptable extent, causing a shift of around 12%. The selling price, on the other side, had a great effect on the NPV with a 5% shift resulting in an NPV change of around 15.5% and a 15% selling price change causing an alteration in the NPV of approximately 47%, which makes the consideration of the selling price a major issue. The choice of EPA-rich oil in combination with the production of protein-rich dry biomass as the target products also needs to be evaluated carefully. The maximum net selling price for microalgae oil which was found in the literature (EUR 144) resulted in a reduction in the NPV by more than 90%. Another scenario with microalgae oil as the target product was calculated using a net selling price (EUR 209) that was planned according to the average market price of EPA + DHA in microalgae oil. This scenario provoked an NPV increase of 19%. The effect of the length of the cultivation period on the NPV was also rather substantial. Continuously shorter or longer cultivation periods altered the NPV by almost one third compared to the baseline scenario, which is a significant impact taking into account that, for instance, longer periods implied that production was just two weeks extended in both April and October.

Fig. 6

Effects of parameter variation on the NPV of the photobioreactor

Return-on-investment

The ROI not only gives information about how lucrative an investment will be but also at which point in time returns are to be expected. The annual ROI of the microalgae cultivation scenarios is depicted in Fig. 7. The baseline scenario showed an ROI of 80.66% after the 30-year lifespan, while positive returns were to be expected after ten years and six months. The least attractive scenario was microalgae oil as the target product in combination with an application of the selling price suggested in the literature. This scenario only had an ROI of 6.41% after the whole lifespan and did not portray a positive ROI before more than 24 years. Two more scenarios were relatively unprofitable with an ROI below 55%, namely the short period scenario (54.59%) and the scenario with the selling price dropping by 15% (42.92%). These scenarios had positive returns after 12 years and 5 months, and after 13 years and 9 months respectively. The most profitable scenario was the one with the selling price rising by 15%, which resulted in an ROI of 118.21% and positive returns after 9 years. The scenario with constantly long cultivation periods followed. Here, an ROI of 106.62% could be expected, with positive returns after 9 years and 3 months.

Fig. 7

Annual return-on-investment for microalgae cultivation scenarios

However, since the investment duration covers a rather long timeframe of 30 years, a more robust analysis of the ROI can be obtained by annualizing the value. The annualized ROI is illustrated in Fig. 8 for all scenarios. The baseline scenario in this case accomplished returns of 1.87% per year. All scenarios yielded returns between 1.1 and 2.5% per year, except for the microalgae oil scenario applying the literature selling price which only had returns of 0.19% per year and thus was rather unprofitable. Besides a 15% rise in the net selling price, the most lucrative scenario was the one with extended production periods from April until October. This scenario accounted for 2.29% of annual returns.

Fig. 8

Annualized return-on-investment in % for the different microalgae cultivation scenarios

Discussion

To the best of our knowledge, here for the first time, in this techno-economic analysis we assessed the expenditures and revenues of cultivating microalgae for food in a humid continental climate in order to determine the NPV and the ROI. A set of different scenarios comprising the alteration of technic and economic parameters to the system was analyzed to identify critical processes.

The biggest share of the investment cost was held by the costs for the glass tubes system, the dryer and the buildings of the facility. All other costs were under 10% of the investment. Concerning operating cost, a great portion was due to labor (around 40%), followed by costs for the maintenance of the mechanical and electrical equipment. All costs excluding interests and the contingency factor summed up to EUR 9.60 per kilogram dry biomass of which 80% were made up by infrastructure, labor cost and maintenance cost. In the context of the PBR considered, this resulted in an NPV of EUR 4.5 million and positive returns in year eleven with an annualized ROI of 1.87%. Beside the application of the literature price for microalgae oil, which hardly yielded a positive value, the least favorable scenarios were the net selling price reduction by 15% (− 47% NPV) and continuously short cultivation seasons (− 32% NPV). The best options, in return, included a net selling price increase of 15% that augmented the NPV by 47% and continuously long cultivation periods which accounted for a 32% higher NPV. Alterations in the glass tube price, commodity prices and microalgae species all affected the NPV to less than 12%. With regard to the ROI, all scenarios yielded positive returns of annually 1.1–2.5%. Only microalgae oil as the target product sold for the price drawn from the literature had very little returns of 0.19% annually.

The sensitivity analysis revealed that the NPV of the microalgae cultivation system always stayed positive. However, the profit varied drastically at times. In particular, the parameters, which withdraw from outer control to a certain extent, must be considered carefully. In particular, the influence of cultivation season length showed an immense impact in our analysis. Both constantly short and long cultivation periods altered the NPV by almost one third, which poses a great concern keeping in mind that this is a parameter, which is dependent on the climatic conditions. With EUR 10.48, the total cost per kilogram dry biomass was almost as high in the short period scenario as in the microalgae oil scenario (EUR 11.00) in which a whole new process step was added. Another surprising factor was the alteration provoked through a change in the microalgae species cultivated. P. tricornutum induced an NPV rise of 7.3%, which is immense considering that the nutritional profile of the microalga is similar to this one of Nannochloropsis sp. This implies that comparable alterations can also occur within the cultivation of one species, as certain fluctuations in the nutritional profile and growth performance are natural, even when cultivation processes and parameters are optimized. Both these fluctuations attributable to the microalgae themselves and the climatic conditions should be reflected in the selling price, which could be used to absorb any instabilities to a certain extent due to uncontrollable cultivation parameters and thus function as a ‘buffer.’

The market analysis showed that the net selling price for microalgae biomass drawn from the literature was rather at the lower end of actual market prices. In fact, selling prices varied tremendously but were disguised through the use of different packaging sizes and content units. In the European Union, there are only few microalgae species, which have already been approved for human consumption by regulators, in terms of either the whole biomass or concerning certain metabolites. Chlorella vulgaris and Arthrospira platensis have been consumed in reasonable amounts prior to the Novel Food Act and were as such approved by implication. Moreover, Odontella aurita and Tetralsemis chuii have been approved (European Commission 2018) as well as algae oil from Ulkenia sp., Schizochytrium sp and Crypthecodinium cohnii (European Commission 2018; Molino et al. 2018) and antioxidants from Haematococcus pluvialis, Nannochloropsis gaditana and Dunaliella (Enzing et al. 2014; European Commission 2018). The compound market value of microalgae products is assumed to reach a market value of USD 3.32 billion by 2022 (Molino et al. 2018). Dry biomass is still mainly produced from Arthrospira and Chlorella and sold as a whole. However, besides the extraction of n − 3 PUFAs, the market for antioxidants from microalgae is promising, with astaxanthin achieving a market price of USD 2500–7000 per kilogram (Panis and Carreon 2016) and β-carotene realizing USD 300–1500 per kilogram (Barkia et al. 2019). DHA is currently largely produced in heterotrophic cultivation from Cryptothecodininum cohnii and Schizochytrium limacinum (Barkia et al. 2019). Taking into account the restraints of heterotrophic cultivation, above all concerning land use, the here modeled system could provide an environmentally friendly alternative. The environmental analysis of the cultivation system also showed that microalgae production in a humid continental climate is feasible concerning environmental impacts. The carbon footprint and energy use compared well to wild-caught fish and favorable to aquaculture fish, whereas the latter was specifically characterized by a relatively high land use rate. Costs for Atlantic salmon (Salmo salar) aquaculture production, the third most consumed fish species in Europe (EUMOFA 2018) and the globally largest single fish commodity by value (FAO 2018), have been increasing over the last years mainly due to higher costs for feed as well as increasing labor costs and depreciation (Iversen et al. 2020). Production costs varied between USD 4.35 and 5.93 (EUR 3.92–5.35) per kilogram depending on the country of origin (Iversen et al. 2020). Presupposed an EPA + DHA content of 7.43 g/kg edible salmon (Schade et al. 2020), this results in an EPA + DHA price of 0.52–0.72 EUR/g. Nannochloropsis sp. contains 42 g EPA/kg dry biomass. If the costs for interests and the contingency factor are added to the production costs, it needs EUR 12.43 to cultivate one kilogram of biomass. Consequently, this accounts for an EPA price of 0.29 EUR/g, which makes microalgae a superior source for n − 3 PUFAs in economic terms, too. As a final point, microalgae are able to serve the market for vegan products and as such represent the only extensive vegan source for EPA and DHA.

At some points in the cost model of the system, assumptions had to be made due to a lack of data, which can be tracked in the summary of the cost model in the supplementary material (Tab. S3). Moreover, a major constraint was the diversity of net selling prices on the market and in the literature. However, these points were addressed by introduction of the contingency factor.

The here conducted analysis poses a first calculation of economic profitability in a ‘cold-weather’ climate and can thus function as a primary reference for stakeholders who consider investing in such a system. The system model used in this study introduces the photoautotrophic cultivation of EPA from Nannochloropsis sp. In particular the production of n − 3 PUFAs largely relies on heterotrophic cultivation which results in a competition with other food production systems for arable land. It would be remarkable to compare these systems in a techno-economic assessment for economic profitability, and in a life cycle assessment for their environmental impacts. Heterotrophic production has hardly been studied in the literature and analyses on its economic value a scarce. Considering the growing market for n − 3 PUFAs, especially EPA and DHA, such investigation would be of high interest. Here, to our knowledge for the first time, we showed that microalgae cultivation in a ‘cold-weather’ climate is feasible, which enlarges the possible production area for microalgae tremendously. While a great part of global microalgae production is based in Asia where it is cultivated in open ponds, PBRs in a ‘cold-weather’ climate could be a save alternative, especially regarding the risk of contamination. The preferred application of PBRs in a colder climate, such as the humid continental climate, could possibly lead to the establishment of a whole new industry in these climates.

However, the risks deriving from the climatic preconditions need to be assessed carefully, given that constantly short cultivation periods over a few years could seriously hamper the economic viability of such cultivation plants. The adjustment of the selling price of the final products definitely should consider these aspects.

Conclusion

Distinct microalgae species have the potential to complement human nutrition with health-promoting and disease suppressing nutrients and metabolites. It has been shown that microalgae cultivation is profitable in a humid continental climate, a so-called ‘cold-weather’ climate. Yet, the climatic preconditions can influence the economic profitability distinctly which should be reflected in the selling price of the target product. Given the abundance of essential nutrients in microalgae resulting in beneficial effects on human health, it is probable that their cultivation becomes a massive industry (Probst et al. 2015) even more so since they are still considered as a ‘poorly explored natural source for a healthy diet’ (Sathasivam et al. 2019). Finally, the exploitation of microalgae could help reduce pressure on natural fish stocks.