Abstract
A wide variety of different (fixed-point) iterative methods for the solution of nonlinear equations exists. In this work we will revisit a unified iteration scheme in Hilbert spaces from our previous work [16] that covers some prominent procedures (including the Zarantonello, Kačanov and Newton iteration methods). In combination with appropriate discretization methods so-called (adaptive) iterative linearized Galerkin (ILG) schemes are obtained. The main purpose of this paper is the derivation of an abstract convergence theory for the unified ILG approach (based on general adaptive Galerkin discretization methods) proposed in [16]. The theoretical results will be tested and compared for the aforementioned three iterative linearization schemes in the context of adaptive finite element discretizations of strongly monotone stationary conservation laws.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we analyze the convergence of adaptive iterative linearized Galerkin (ILG) methods for nonlinear problems with strongly monotone operators. To set the stage, we consider a real Hilbert space X with inner product \((\cdot ,\cdot )_X\) and induced norm denoted by \(\Vert \cdot \Vert _X\). Then, given a nonlinear operator \(\mathsf {F}:\,X\rightarrow X^\star \), we focus on the equation
where \(X^\star \) denotes the dual space of X. In weak form, this problem reads
with \(\left<\cdot ,\cdot \right>_{X^\star \times X}\) signifying the duality pairing in \(X^\star \times X\). For the purpose of this work, we suppose that \(\mathsf {F}\) satisfies the following conditions:
-
(F1)
The operator \(\mathsf {F}\) is Lipschitz continuous, i.e. there exists a constant \(L_\mathsf {F}>0\) such that
$$\begin{aligned} \left| \left<\mathsf {F}(u)-\mathsf {F}(v),w\right>_{X^\star \times X}\right| \le L_\mathsf {F}\left\| u-v\right\| _X \left\| w\right\| _X, \end{aligned}$$for all \(u,v,w \in X\).
-
(F2)
The operator \(\mathsf {F}\) is strongly monotone, i.e. there is a constant \(\nu >0\) such that
$$\begin{aligned} \nu \left\| u-v\right\| _X^2 \le \left<\mathsf {F}(u)-\mathsf {F}(v),u-v\right>_{X^\star \times X}, \end{aligned}$$for all \(u,v \in X\).
Given the properties (F1) and (F2), the main theorem of strongly monotone operators states that (1) has a unique solution \(u^\star \in X\); see, e.g., [20, §3.3] or [23, Theorem 25.B].
1.1 Iterative linearization
The existence of a solution to the nonlinear equation (1) can be established in a constructive way. This can be accomplished, for instance, by transforming (1) into an appropriate fixed-point form, which, in turn, induces a potentially convergent fixed-point iteration scheme. To this end, following our approach in [16], for some given \(v\in X\), we consider a linear and invertible preconditioning operator \(\mathsf {A}[v]:\,X\rightarrow X^\star \). Then, applying \(\mathsf {A}[u]^{-1}\) to (1) leads to the fixed-point equation
For any suitable initial guess \(u^0\in X\), the above identity motivates the iteration scheme
Equivalently, we have
For given \(u^n\in X\), we emphasize that the above problem of solving for \(u^{n+1}\) is linear; consequently, we call (3) an iterative linearization scheme for (1). Letting
we may write
In order to discuss the weak form of (5), for a prescribed \(u\in X\), we introduce the bilinear form
Then, based on \(u^n\in X\), the solution \(u^{n+1}\in X\) of (5) can be obtained from the weak formulation
Throughout this paper, for any \(u\in X\), we assume that the bilinear form \(a(u;\cdot ,\cdot )\) is uniformly coercive and bounded. The latter two assumptions refer to the fact that there are two constants \(\alpha ,\beta >0\) independent of \(u \in X\), such that
and
respectively. In particular, owing to the Lax-Milgram Theorem, these properties imply the well-posedness of the solution \(u^{n+1}\in X\) of the linear equation (7), for any given \(u^n\in X\).
Let us briefly review some prominent procedures that can be cast into the framework of the linearized fixed-point iteration (7): For instance, we point to the Zarantonello iteration given by
with \(\delta >0\) being a sufficiently small parameter; cf. Zarantonello’s original report [21], or the monographs [20, §3.3] and [23, §25.4]. A further example is the Kačanov scheme which reads
in the special case that \(g=\mathsf {A}[u]u-\mathsf {F}(u)\) is independent of u. Finally, we mention the (damped) Newton method which is defined by
for a damping parameter \(\delta (u^n)>0\). Here \(\mathsf {F}'\) signifies the Gâteaux derivative of \(\mathsf {F}\) (provided that it exists). For any of the above three iterative procedures, we emphasize that convergence to the unique solution of (1) can be guaranteed under suitable conditions; see our previous work [16] for details. In addition, we note that more general iterative procedures such as, e.g., Newton-like methods, fit into the approach of the unified iteration scheme (7), see [16, Remark 2.9].
1.2 The ILG approach
Consider a finite dimensional subspace \(X_N\subset X\). Then, the Galerkin approximation of (2) in \(X_N\) reads as follows:
We note that (13) has a unique solution \(u_{N}^\star \in X_N\) since the restriction \(\mathsf {F}|_{X_N}\) still satisfies the conditions (F1) and (F2) above. The iterative linearized Galerkin (ILG) approach is based on discretizing the iteration scheme (7). Specifically, a Galerkin approximation \({u}_N^{n+1} \in X_N\) of \(u_{N}^\star \), based on a prescribed initial guess \({u}_N^{0} \in X_N\), is obtained by solving iteratively the linear discrete problem
for \(n\ge 0\). For the resulting sequence \(\{u_N^n\}_{n\ge 0}\subset X_N\) of discrete solutions it is possible, based on elliptic reconstruction techniques (cf., e.g., [17, 18]), to obtain general (abstract) a posteriori estimates for the difference to the exact solution, \(u^\star \in X\), of (1), i.e. for \(\Vert u^\star -u_N^{n+1}\Vert _X\), \(n\ge 0\), see [16, §3]. Based on such a posteriori error estimators, an adaptive ILG algorithm that exploits an efficient interplay of the iterative linearization scheme (14) and automatic Galerkin space enrichments was proposed in [16, §4]; see also [6]. We refer to some related works in the context of (inexact) Newton schemes [1, 2, 9, 10], or of the Kačanov iteration [4, 13].
1.3 Goal of this paper
The convergence of an adaptive Kačanov algorithm, which is based on a finite element discretization, for the numerical solution of quasi-linear elliptic partial differential equations has been studied in [13]. Furthermore, more recently, the authors of [12] have proposed and analyzed an adaptive algorithm for the numerical solution of (1) within the specific context of a finite element discretization of the Zarantonello iteration (10). The latter paper includes an analysis of the convergence rate which is related to the work [5] on optimal convergence for adaptive finite element methods within a more general abstract framework. This work has been advanced further in the recent article [11]. The purpose of the current paper is to generalize the adaptive ILG algorithm from [12] to the framework of the unified iterative linearization scheme (5); furthermore, arbitrary (conforming) Galerkin discretizations will be considered. In order to provide a convergence analysis for the ILG scheme (14) within this general abstract setting, we will follow along the lines of [12], however, we emphasize that some significant modifications in the analysis are required. Indeed, whilst the theory in [12] relies on a contraction argument for the Zarantonello iteration, this favourable property is not available for the general iterative linearization scheme (5). To address this difficulty, we derive a contraction-like property instead. This observation will then suffice to establish the convergence of the adaptive ILG scheme, and to (uniformly) bound the number of linearization steps on each (fixed) Galerkin space similar to [12]; we note that the latter property constitutes a crucial ingredient with regards to the (optimal) computational complexity of adaptive iterative linearized finite element schemes.
1.4 Outline
Section 2 contains a convergence analysis of the unified iteration scheme (5). On that account we will encounter a contraction-like property, which is key for the subsequent analysis of the convergence rate of the adaptive ILG algorithm in Sect. 3. Here, in addition, a (uniform) bound of the iterative linearization steps on each discrete space will be shown. In Sect. 4, we will test our ILG algorithm in the context of finite element discretizations of stationary conservation laws. Finally, we add a few concluding remarks in Sect. 5.
2 Iterative linearization
The goal of this section is to establish a contraction-like property and to prove the convergence of the iteration (5). In the sequel, we shall focus on the case where the solution of (1) appears as the (unique) minimizer of an associated potential \(\mathsf {H}\). This is relevant in many applications, where \(\mathsf {H}\) plays the role of a physical energy.
2.1 Potential
We begin by introducing two additional assumptions that relate the operator \(\mathsf {F}\) to a potential \(\mathsf {H}\).
-
(F3)
There exists a Gâteaux differentiable functional \(\mathsf {H}:X \rightarrow {\mathbb {R}}\) such that \(\mathsf {H}'=\mathsf {F}\).
In addition to (F3), we impose a monotonicity condition (which corresponds to an energy reduction in the context of physical models) on the sequence generated by the iterative linearization scheme (5).
-
(F4)
There exists a constant \(C_\mathsf {H}>0\) such that the sequence defined by (5) fulfils the bound
$$\begin{aligned} \mathsf {H}(u^{n-1})-\mathsf {H}(u^{n}) \ge C_\mathsf {H}\left\| u^{n}-u^{n-1}\right\| _X^2 \qquad \forall n \ge 1, \end{aligned}$$(15)where \(\mathsf {H}\) is the potential of \(\mathsf {F}\) introduced in (F3).
Let us provide some remarks on the assumption (F4). Suppose that the assumptions (F1)–(F3) are satisfied, and consider the sequence \(\{u^n\}_{n \ge 0}\) generated by the iteration (5). For fixed \(n \ge 1\), and \(\epsilon ^n:=u^n-u^{n-1}\), we define the real-valued function \(\varphi (t):=\mathsf {H}(u^{n-1}+t\epsilon ^n)\), for \(t \in [0,1]\). Taking the derivative leads to
Appealing to the fundamental theorem of calculus yields
Using (4) and (7), we note that
Hence,
Consequently, for any given \(u \in X\), if the bilinear form \(a(u;\cdot ,\cdot )\) is uniformly coercive with constant \(\alpha > \nicefrac {L_\mathsf {F}}{2}\), cf. (8), where \(L_\mathsf {F}\) refers to the Lipschitz constant occurring in (F1), then we obtain
i.e. (15) is satisfied with \(C_\mathsf {H}=\alpha - \nicefrac {L_\mathsf {F}}{2}>0\).
Proposition 1
If \(\mathsf {F}\) satisfies (F1)–(F3), and the bilinear form \(a(\cdot ;\cdot ,\cdot )\) from the unified iteration scheme (5) is coercive with coercivity constant \(\alpha > \nicefrac {L_\mathsf {F}}{2}\), cf. (8), then (F4) holds true.
Remark 1
For the Zarantonello iteration scheme (10) we note that \(a(u;v,w)=\delta ^{-1}(v,w)_{X}\), for \(u,v,w \in X\), in (6). Then, we have that \(a(u;v,v)=\delta ^{-1}\left\| v\right\| _X^2\), for \(u,v \in X\), which, upon using Proposition 1, shows that (F4) is satisfied for any \(\delta \in (0,\nicefrac {2}{L_\mathsf {F}})\). Under suitable assumptions, a similar observation can be made for the Newton method (12) provided that the damping parameter \(\delta (u^n)\) is chosen sufficiently small; cf. [16, Theorem 2.6].
Remark 2
The above Proposition 1 delivers a sufficient condition for (F4). We note, however, that it is not necessary. In particular, if the coercivity constant \(\alpha \) in (8) is much smaller than the Lipschitz constant \(L_\mathsf {F}\) from (F1), then the bound on \(\alpha \) in Proposition 1 is violated. Nonetheless, in that case, we can still satisfy (15) by imposing alternative assumptions; cf., e.g., (K2) in [16].
2.2 Contractivity and convergence
For the sake of proving the main result of this section, we require some auxiliary results. The first is an a posteriori error estimate.
Lemma 1
Consider the sequence \(\{u^n\}_{n\ge 0}\subset X\) generated by the iteration (5). If \(\mathsf {F}\) satisfies (F1)–(F2), and \(a(u;\cdot ,\cdot )\), for \(u \in X\), fulfils (8)–(9), then it holds the bound
for any \(n\ge 1\).
Proof
By invoking (F2), and since \(u^\star \) is the (unique) solution of (1), for \(n\ge 1\), we find that
Employing (4), (7), and (9), we further get
and thus
By the triangle inequality, this leads to
which completes the proof. \(\square \)
Remark 3
We note that the above result equally holds if (2) and (5) are restricted to any closed subspace of X.
Next, we will present a relation between the norm \(\Vert \cdot \Vert _X\) and the potential \(\mathsf {H}\). This result is also stated in [12, Lemma 5.1], and generalizes [7, Lemma 16] and [14, Theorem 4.1]. In the present work we will give a shorter and more elementary proof.
Lemma 2
Suppose that the operator \(\mathsf {F}\) satisfies (F1)–(F3), and denote by \(u^\star \in X\) the unique solution of (1). Then, we have the estimate
In particular, \(\mathsf {H}\) takes its minimum at \(u^\star \).
Proof
Similarly as in the proof of Proposition 1, for fixed \(u \in X\), we define the real-valued function \(\varphi (t):=\mathsf {H}(u^\star +t(u-u^\star ))\), for \(t \in [0,1]\). Then, by invoking the fundamental theorem of calculus, and implementing (1), we obtain
Applying the assumptions (F1) and (F2) we can bound the integrand from above and below, respectively. Indeed, the strong monotonicity (F2) implies that
and therefore,
Likewise, by invoking (F1) instead of (F2), we find that
Combining the above bounds leads to (17). \(\square \)
Before formulating and proving our main result, we state one more auxiliary observation.
Lemma 3
Consider a sequence \(\{a_j\}_{j=1}^\infty \subset [0,\infty )\) which satisfies the estimate
for some constant \(c>0\). Then, it holds the bound \(a_j\le c^{-1}(1+c)^{2-j}a_1\), for any \(j\ge 2\).
Proof
Let us define the sequence \(b_k:=\sum _{j=k}^\infty a_j\), \(k\ge 1\). Using (18), we note that
for all \(k\ge 1\). By induction, this implies that \(b_2\ge (c+1)^{k-2}b_{k}\) for any \(k\ge 2\). Therefore, we infer that
Rearranging terms completes the proof. \(\square \)
Theorem 1
Suppose that (F1)–(F4) are satisfied. Furthermore, let the bilinear form \(a(\cdot ;\cdot ,\cdot )\) from (7) be coercive and bounded, cf. (8) and (9), respectively. Then, for any \(k\ge 1\), the sequence \(\{u^n\}_{n\ge 0}\) from (5) satisfies the estimate
with
Moreover, the contraction-like property
holds true for any \(n\ge 2\). In particular, the sequence \(\{u^n\}_{n\ge 0}\) converges to the unique solution \(u^\star \in X\) of (1).
Proof
Let \(n>k\ge 1\) be arbitrary. Then, we note the telescope sum
Thus, by virtue of (15), we infer that
We aim to bound the left-hand side. To this end, we employ Lemma 2, which implies that
This, together with Lemma 1, leads to
Combining (22) and (23) yields
Letting \(n\rightarrow \infty \), we obtain (19). Moreover, upon setting \(c:=C_{20}^{-1}\) and \(a_j:=\Vert u^{j}-u^{j-1}\Vert ^2_X\), \(j\ge 1\), the bound (19) takes the form (18). Hence, applying Lemma 3, we deduce (21), which immediately implies that \(\left\| u^n-u^{n-1}\right\| _X\) vanishes. Consequently, by Lemma 1, the sequence \(\{u^n\}_{n \ge 0}\) converges to \(u^\star \). \(\square \)
Remark 4
The convergence statement from Theorem 1 can be proved under slightly different assumptions, cf. [16, Proposition 2.1]. In particular, properties (F1), (F3), and (F4) can be replaced by assuming that the mappings \(u \mapsto a(u;u,\cdot )\) and \(u \mapsto \text {F}(u)\) are continuous from X into its dual space \(X^\star \) with respect to the weak topology on \(X^\star \), and that the sequence \(\{u^{n}\}_{n \ge 0}\) defined by the iteration (5) satisfies \(\Vert u^{n}-u^{n-1}\Vert _X\rightarrow 0\) as \(n\rightarrow \infty \).
3 Adaptive ILG discretizations
In this section, following the recent approach [12], we will present an adaptive ILG algorithm that exploits an interplay of the unified iterative linearization procedure (5) and abstract adaptive Galerkin discretizations thereof, cf. (14). Moreover, we will establish the (linear) convergence of the resulting sequence of approximations to the unique solution of (1), and comment on the uniform boundedness of the iterative linearization steps on each discrete space. We proceed along the ideas of [12, §4 and §5], and generalize those results to the abstract framework considered in the current paper. Throughout this section, we will assume that any iterative linearization is of the form (7), with (8) and (9) being satisfied.
3.1 Abstract error estimators
We generalize the assumptions on the finite element refinement indicator from [12, §4]. Let us consider a sequence of hierarchical finite dimensional Galerkin subspaces \(\{X_N\}_{N\ge 0}\subset X\), i.e.
For any \(N\ge 0\), suppose that there exists a computable error estimator
and constants \(C_{25},C_{26} \ge 1\) independent of N such that the ensuing conditions are satisfied:
-
(A1)
For all \(u,v \in X_N\) it holds that
$$\begin{aligned} |\eta _N(u)-\eta _N(v)| \le C_{25} \left\| u-v\right\| _X. \end{aligned}$$(25) -
(A2)
The error of the discrete solution \(u_{N}^\star \in X_N\) from (13) is controlled by the a posteriori error bound
$$\begin{aligned} \left\| u^\star -u_{N}^\star \right\| _X \le C_{26} \eta _N(u_{N}^\star ), \end{aligned}$$(26)where \(u^\star \in X\) is the exact solution of (1).
The following result shows that the two estimators for \({u}_N^{n}\) and \(u_{N}^\star \) are equivalent once the linearization error is small enough. This result coincides with [12, Lemma 4.9], however, in the original proof, the bound from [12, Eq. (3.3)] needs to be replaced by (16) from Lemma 1 in our work. As a consequence, here and in the sequel, the constants in our analysis are slightly different, and the proofs from [12] require some minor adaptations. Since these modifications are fairly obvious to incorporate, we will omit the proofs and merely refer the corresponding results in [12]; see also [15] for details.
Lemma 4
([12, Lemma 4.9]) Suppose that \(\mathsf {F}\) satisfies (F1)–(F2), and that the a posteriori estimator fulfils (A1). Furthermore, for some \(n\ge 1\), assume that
with a constant \(\lambda \in (0, C_{27}^{-1})\), where
Then, we have that
Moreover, the two error estimators \(\eta _N({u}_N^{n})\) and \(\eta _N(u_{N}^\star )\) are equivalent in the sense that
3.2 Adaptive ILG algorithm
We focus on the adaptive algorithm from [12], which was studied in the context of finite element discretizations of the Zarantonello iteration (10). It is closely related to the general adaptive ILG scheme in [16]. The key idea is the same in both algorithms: On a given Galerkin space, we iterate the linearization scheme (14) as long as the linearization error dominates. Once the ratio of the linearization error and the a posteriori error bound is sufficiently small, we enrich the Galerkin space in a suitable way.

Remark 5
We emphasize that we do not know (a priori) if the while loop of Algorithm 1 always terminates after finitely many steps. Moreover, it may happen that \(\eta _N(u_N)=0\), for some \(N \ge 0\), i.e. the algorithm terminates; here, for each \(N\ge 0\), we denote by \(u_N\) the final guess on the corresponding Galerkin space \(X_N\) from Algorithm 1. Let us provide two comments on this issue, cf. [12, Proposition 4.4 & 4.5]:
-
(a)
Suppose that there is an enrichment \(X_N\) of \(X_0\) generated by the above Algorithm 1 such that \(\Vert {u}_N^{n}-{u}_N^{n-1}\Vert _X > \lambda \eta _N({u}_N^{n})\) for all \(n \ge 0\); in this situation, the while loop will never end. Given the assumptions of Theorem 1, it follows from (21) that \(\Vert {u}_N^{n}-{u}_N^{n-1}\Vert _X \rightarrow 0\) as \(n\rightarrow \infty \). In addition, by virtue of Theorem 1 (applied to the discrete setting (13) and (14)), we have that \({u}_N^{n} \rightarrow u_{N}^\star \) as \(n \rightarrow \infty \). Then, invoking the reliability (A2) and the continuity (A1), we conclude that
$$\begin{aligned}&\left\| u^\star -u_{N}^\star \right\| _X \le C_{26} \eta _N(u_{N}^\star ) = C_{26}\lim _{n \rightarrow \infty } \eta _N({u}_N^{n}) \le C_{26} \lim _{n \rightarrow \infty } \lambda ^{-1} \Vert {u}_N^{n}-{u}_N^{n-1}\Vert _X=0. \end{aligned}$$It follows that \(u^\star =u_{N}^\star \), and therefore \({u}_N^{n} \rightarrow u^\star \) as \(n \rightarrow \infty \). In particular, Algorithm 1 will generate an approximate solution which, for sufficiently large n, is arbitrarily close to the exact solution of (1).
-
(b)
If, for some \(n,N \in {\mathbb {N}}\), the while loop terminates, then we have the bound \(\Vert {u}_N^{n}-{u}_N^{n-1}\Vert _X\le \lambda \eta _N({u}_N^{n})\). Thus, in the special situation where \(\eta _N(u_N^n)=0\), we directly obtain that \(\Vert {u}_N^{n}-{u}_N^{n-1}\Vert _X=0\). Then, employing Lemma 1 and Remark 3, we find that \(\left\| u_{N}^\star -{u}_N^{n}\right\| _X\le C_{16} \Vert {u}_N^{n}-{u}_N^{n-1}\Vert _X=0\), i.e. \(u_{N}^\star ={u}_N^{n}\). Consequently, recalling (A2), we deduce that
$$\begin{aligned} \Vert u^\star -{u}_N^{n}\Vert _X=\Vert u^\star -u_{N}^\star \Vert _X \le C_{26} \eta _N(u_{N}^\star ) =C_{26} \eta _N({u}_N^{n})=0. \end{aligned}$$We obtain that \({u}_N^{n}=u^\star \), i.e. the exact solution of (1) is found.
3.3 Convergence
We will now turn to the proof of the convergence of Algorithm 1. More precisely, we will show that the sequence \(u_N\) generated by the above ILG procedure converges, under certain assumptions, to the exact solution \(u^\star \) of (1). In view of Remark 5, given the assumptions (F1)–(F4), we may assume that the while loop always terminates after finitely many steps with \(\eta _N(u_N)>0\) for all \(N \ge 0\).
We begin with the following result, which extends [12, Proposition 4.10] from the specific context of finite element discretizations to general Galerkin spaces. Within this broader setting an additional assumption is imposed, see the perturbed contraction property (30). We underline that this condition is satisfied for the finite element method, which is proved in [12, Proposition 4.10].
Proposition 2
Let (F1)–(F2) and (A1) be satisfied, and \(\lambda \in (0,C_{27}^{-1})\) be given. Moreover, for each \(N\ge 0\), assume that the while loop of Algorithm 1 terminates after finitely many steps, thereby yielding an output \(u_N\in X_N\), with \(\eta _N(u_N) >0\). Furthermore, suppose that there are constants \(0< q_{30} <1\) and \(C_{30}>0\) such that it holds the perturbed contraction bound
where \(u_{N}^\star \in X_N\) is the unique solution of (13). Then, we have that \(\eta _N(u_N) \rightarrow 0\) as \(N \rightarrow \infty \).
Combining the above Proposition 2 and Lemma 4 leads to the following result.
Corollary 1
Given the same assumptions as in Proposition 2 and, additionally, (A2), then \(u_N \rightarrow u^\star \) for \(N \rightarrow \infty \), where the sequence \(\{u_N\}_{N\ge 0}\) is generated by the Algorithm 1, and \(u^\star \) is the unique solution of (1).
Proof
Let \(u_N={u}_N^{n}\in X_N\), \(n\ge 1\), be the output of Algorithm 1 based on the Galerkin space \(X_N\). Then, by virtue of (28), and due to (A2) and (29), we have
with
Applying Proposition 2 completes the proof. \(\square \)
3.4 Linear convergence
In this section we show the linear convergence of the output sequence \(\{u_N\}_{N \ge 0}\) generated by Algorithm 1. To this end, under the perturbed contraction assumption (30), and with altered constants, we extend the result from [12, Theorem 5.3] to the setting of general Galerkin spaces. Let
with \(\nu >0\) from (F2), and introduce the quantity
where \(u^\star \in X\) and \(u_{N}^\star \in X_N\) are the (unique) solution of (1) and its Galerkin approximation from (13), respectively. By virtue of Lemma 2, provided that (F1)–(F3) hold, we observe that
Theorem 2
([12, Theorem 5.3]) Let \(\mathsf {F}\) satisfy (F1)–(F3), and assume (A1)–(A2). Furthermore, suppose that there are constants \(0< q_{30} <1\) and \(C_{30} >0\) such that (30) holds true. Then, upon setting
with \(\gamma \) from (33), and with \(\lambda \in (0,C_{27}^{-1})\), the following contraction property holds: If the while loop of Algorithm 1 terminates after finitely many steps with \(\eta _N(u_N) >0\), for all \(N \ge 0\), then we have the (linear) contraction property
Moreover, there exists a constant \(C_{35}>0\) such that
i.e. the error estimators decay at a linear rate.
Remark 6
If the error estimator \(\eta _N\) from (24) is both reliable (cf. (26)) and efficient in the sense that
with \(C_{27}\) independent of N, then Theorem 2 implies the linear convergence of the error. Indeed, by invoking (31), (35), (29), and (36), we obtain
In addition, applying Galerkin orthogonality, and recalling the Lipschitz continuity (F1) and strong monotonicity (F2) of \(\mathsf {F}\), the Céa type estimate
can be derived immediately. Then, combining the above inequalities leads to the estimate
which yields the linear convergence of the error.
3.5 Uniform bound for the number of linearization steps
Assuming that the while loop of Algorithm 1 terminates after finitely many steps for all \(N \ge 0\), the result below states that the number of iterative linearization steps (14) on each Galerkin space \(X_N\), denoted by \(\# \mathrm {It}(N)\), can be (uniformly) bounded. This observation could potentially serve as a key ingredient for the analysis of the computational complexity of the ILG Algorithm 1. The proof can be carried out along the lines of [12, Propoition 4.6], with obvious adaptations, in particular, taking into account the contraction-like property (21).
Proposition 3
([12, Proposition 4.6]) Assume (F1)–(F4) and (A1)–(A2). Let \(\lambda \in (0,C_{27}^{-1})\) be the adaptivity parameter from Algorithm 1. Suppose that the while loop of Algorithm 1 terminates after finitely many steps with \(\eta _N(u_N)>0\) for all \(N \ge 0\). Then, the number of iterative linearization steps \(\# \mathrm {It}(N)\) on \(X_N\) satisfies the estimate
for all \(N\ge 1\), where the constants
are independent of N.
Remark 7
We note that Proposition 3 does not assert a uniform bound for the number of linearization steps since the right-hand side of (37) depends on N due to the ratio of the estimators on two consecutive spaces. For many problems and sensible error estimators, however, it holds the contraction property
for N large enough, with a contraction constant \(0<q_{38}<1\) independent of N. Furthermore, if we additionally assume the reliability and efficiency estimate (36), then combining (38), (36), and (29), we obtain \(\eta _N(u_N) \simeq \eta _{N-1}(u_{N-1})\). Consequently, a uniform bound on the number of linearization steps on each Galerkin subspace \(X_N\) is guaranteed.
4 Numerical experiments
In this section we test our ILG Algorithm 1 with two numerical experiments in the context of finite element discretizations of stationary conservation laws.
4.1 Model problem
On an open, bounded and polygonal domain \(\varOmega \subset {\mathbb {R}}^2\), with Lipschitz boundary \(\varGamma =\partial \varOmega \), we consider the following second-order elliptic partial differential equation in divergence form:
Here, we choose \(X:=H^1_0(\varOmega )\) to be the standard Sobolev space of \(H^1\)-functions on \(\varOmega \) with zero trace along \(\varGamma \); the inner product and norm on X are defined, respectively, by \((u,v)_X:=(\nabla u,\nabla v)_{L^2(\varOmega )}\) and \(\left\| u\right\| _X:=\Vert \nabla u\Vert _{L^2(\varOmega )}\), for \(u,v\in X\). Partial differential equations of the form (39) are widely used in mathematical models of physical applications including, for instance, hydro- and gas-dynamics, or plasticity, see [22, §69.2–69.3] and [3, §1.1] for a discussion of the physical meaning. We suppose that \(g \in X^\star =H^{-1}(\varOmega )\) in (39) is given, and the diffusion parameter \(\mu \in C^1([0,\infty ))\) fulfils the monotonicity property
with constants \(M_\mu \ge m_\mu >0\). Under this condition the nonlinear operator \(\mathsf {F}:\,H^1_0(\varOmega )\rightarrow H^{-1}(\varOmega )\) from (39) can be shown to satisfy (F1) and (F2), with \(\nu =m_{\mu }\) and \(L_\mathsf {F}=3M_{\mu }\); see [23, Proposition 25.26]. Moreover, \(\mathsf {F}\) has a potential \(\mathsf {H}:X \rightarrow {\mathbb {R}}\) given by
where \(\psi (s):=\nicefrac 12\int _0^s \mu (t) \,\mathsf {d}t\), \(s\ge 0\), i.e. (F3) is satisfied as well. The weak form of the boundary value problem (39) in X reads:
In [16, §5.1] the convergence of the Zarantonello, Kačanov, and Newton iteration for the nonlinear boundary value problem (39) was examined. In particular, if \(\mu \) satisfies (40) and is monotonically decreasing, then the assumption (F4) is satisfied for all of these three iterations schemes (for appropriate damping constants). We will provide some more details in §4.3.3.
4.2 Discretization and refinement indicator
For the sake of discretizing (41), and thereby of obtaining an ILG formulation for (39), we will use a conforming finite element framework. We consider a sequence of hierarchical, regular and shape-regular meshes \(\{\mathcal {T}_N\}_{N\ge 1}\) that partition the domain \(\varOmega \) into open and disjoint triangles \(T \in \mathcal {T}_N\) such that \(\overline{\varOmega }=\bigcup _{T \in \mathcal {T}_N} \overline{T}\). Moreover, we consider the finite element space
where we signify by \(\mathcal {P}_1(T)\) the space of all affine functions on \(T \in \mathcal {T}_N\). The mesh refinements in Algorithm 1 are obtained by means of the newest vertex bisection and the Dörfler marking strategy, see [19] and [8], respectively.
For an edge \(e \subset \partial T^+ \cap \partial T^{-}\), which is the intersection of (the closures of) two neighbouring elements \(T^{\pm } \in \mathcal {T}_N\), we signify by \(\llbracket {\textit{\textbf{v}}}\rrbracket |_e={\textit{\textbf{v}}}^{+}|_e \cdot {\textit{\textbf{n}}}_{T^+}+{\textit{\textbf{v}}}^{-}|_e\cdot {\textit{\textbf{n}}}_{T^{-}}\) the jump of a (vector-valued) function \({\textit{\textbf{v}}}\) along e, where \({\textit{\textbf{v}}}^{\pm }|_e\) denote the traces of the function \({\textit{\textbf{v}}}\) on the edge e taken from the interior of \(T^{\pm }\), respectively, and \({\textit{\textbf{n}}}_{T^{\pm }}\) are the unit outward normal vectors on \(\partial T^{\pm }\), respectively. For \(u \in X_N\) we define the local refinement indicator, for each \(T \in \mathcal {T}_N\), and the global error indicator, respectively, by
This error estimator satisfies the assumptions (A1)–(A2) for the problem under consideration; we refer to [12, §8.3] for details.
4.3 Experiments
We revisit two experiments from [16], whereby we test the (modified) adaptive ILG Algorithm 1. We consider the L-shaped domain \(\varOmega =(-1,1)^2 \setminus ([0,1] \times [-1,0])\), and start the computations with an initial mesh consisting of 192 uniform triangles. The procedure is run until the number of elements exceeds \(10^6\). Moreover, we will always choose the initial guess \(u_0^0 \equiv 0\).
4.3.1 Smooth solution
We consider the nonlinear diffusion coefficient \(\mu (t)=(t+1)^{-1}+\nicefrac {1}{2}\), for \(t \ge 0\), and select g in (39) such that the analytical solution of (41) is given by the smooth function \(u^\star (x,y)=\sin (\pi x) \sin (\pi y)\). It is straightforward to verify that \(\mu \) fulfils the bounds (40) so that the assumptions (F1)–(F3) are satisfied. In addition, the convergence of the Zarantonello (10), Kačanov (11), and Newton (12) schemes are guaranteed for appropriate choices of the damping parameters, see [16]; here, we choose \(\delta =0.85\) and \(\delta =1\) in case of the Zarantonello and Newton method, respectively. A priori, for the Newton method, we remark that choosing the damping parameter \(\delta =1\) (potentially resulting in quadratic convergence of the iterative linearization close to the solution) might lead to a divergent iteration for the given boundary value problem; for this reason, a prediction and correction strategy, which guarantees convergence (and which does not cause any correction of the damping parameter in the current experiments), is presented in [16, Remark 2.8].
In Fig. 1 we plot the error estimators (solid lines) and true errors (dashed lines) of our three linearization schemes against the number of elements \(|\mathcal {T}_N|\) in the triangulation. In addition, the dashed line without any markers is the graph of the function \(|\mathcal {T}_N|^{-\nicefrac {1}{2}}\). We observe the optimal convergence rate \(\mathcal {O}(|\mathcal {T}_N|^{-\nicefrac {1}{2}})\) for both (almost) uniform and adaptive mesh refinements corresponding to the parameters \(\theta _*=0\) and \(\theta _*=0.5\), respectively, in the Dörfler marking strategy, see [8, §4.2, Eq. (\(\hbox {M}_*\))].
Experiment 4.3.1: Convergence rates. Left: Adaptively refined meshes. Right: (Almost) uniform meshes. The solid and dashed lines correspond to the estimator and the error, respectively
In Fig. 2 we can observe the uniformly bounded number of linearization steps on a given mesh for any of the three considered fixed-point methods, and for both choices of the adaptivity parameter \(\lambda =0.1\) and \(\lambda =0.001\) in Algorithm 1. For the value \(\lambda =0.1\), the number of linearization steps on a given mesh does not differ essentially between the three considered iteration schemes. However, there is a remarkable difference for the choice \(\lambda =0.001\). The Newton iteration clearly outperforms the other two fixed-point methods, which is not surprising because of the local quadratic convergence regime. In addition, we can also observe that the Kačanov method is superior to the Zarantonello iteration in view of the number of linearization steps.
Experiment 4.3.1: Number of iterations
4.3.2 Nonsmooth solution
In our second experiment, we consider the nonlinear diffusion parameter \(\mu (t)=1+\mathrm {e}^{-t}\), for \(t \ge 0\). Again, it is easily seen that \(\mu \) satisfies (40). Moreover, it can be shown that the three linearization schemes under consideration will converge for appropriate choices of the parameter \(\delta \), see [16]. We choose g in (39) such that the analytical solution is given by
where r and \(\varphi \) are polar coordinates. This is the prototype singularity for (linear) second-order elliptic problems with homogeneous Dirichlet boundary conditions in the L-shaped domain; in particular, we note that the gradient of \(u^\star \) is unbounded at the origin. We let \(\delta =0.5\) for the Zarantonello iteration, and use the damping parameter \(\delta =1\) for the Newton method as in the experiment before.
For the choice \(\theta _*=0.5\) in Dörfler’s marking procedure we retain the (almost) optimal convergence rate for both the error and the estimator. Due to the singularity, however, the convergence rate is reduced when the mesh is (almost) uniformly refined (i.e. corresponding to the value \(\theta _*=0\)), see Fig. 3. For the number of linearization steps on each Galerkin space, we can make the same observations as for the smooth case from before (Fig. 4).
Experiment 4.3.2: Convergence rates. Left: Adaptively refined meshes. Right: (Almost) uniform meshes. The solid and dashed lines correspond to the estimator and the error, respectively
Experiment 4.3.2: Number of iterations
4.3.3 Numerical verification of the constant \(C_\mathsf {H}\) from (F4)
In this last section we aim to numerically investigate the lower bound
cf. (15), for the two previous experiments, and for any of the three iteration schemes (10)–(12). It can be shown that the Zarantonello iteration satisfies (F4) with
for \(\delta \in \left( 0,\nicefrac {2}{3 M_\mu }\right) \), cf. Remark 1. Moreover, for the Kačanov scheme it holds
cf. [16, §2.3.2, eq. (18)]. Finally, for the (damped) Newton method, cf. [16, Rem. 2.8], we have
For the Experiment 4.3.1 it is straightforward to verify that \(m_\mu =\nicefrac {3}{8}\) and \(M_\mu =\nicefrac {3}{2}\). This leads to the lower bounds \(C_\mathsf {H}^Z\ge 0.25\) for \(\delta =0.4\), \(C_\mathsf {H}^K\ge \nicefrac {3}{16}\), and \(C_\mathsf {H}^N\ge \nicefrac {3}{32}\). Furthermore, in Experiment 4.3.2 it holds \(m_\mu =1-2\exp (-\nicefrac {3}{2})\) and \(M_\mu =2\), which yields the bounds \(C_\mathsf {H}^Z\ge 1\) for \(\delta =0.25\), \(C_\mathsf {H}^K\ge \nicefrac {1}{2}-\exp (-\nicefrac {3}{2})\), and \(C_\mathsf {H}^N\ge \nicefrac {1}{4}-\nicefrac {1}{2}\exp (-\nicefrac {3}{2})\).
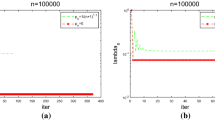
In Fig. 5, for \(n=1\), we plot the upper bound
against the number of space enrichments N. Here, we run the algorithm with identical initial space \(X_0\) and initial guess \(u_0^0\) as in the experiments before, and until the number of elements exceeds \(10^6\). On any given Galerkin space \(X_N\), we perform one iterative step in order to obtain \(u_N^1\) from \(u_N^0\), and, subsequently, enrich our space adaptively using the Dörfler parameter \(\theta _*=0.5\). As we can see from Fig. 5, the numerical ratio (42) is never violated for any of the three iterative linearization methods. In addition, we note that the lower bound for \(C_\mathsf {H}^Z\) is much smaller than the ratio (42) observed in the experiments, which is likely due to the rough upper estimate for the Lipschitz constant \(L_\mathsf {F}= 3 M_\mu \).
5 Conclusions
We have established a contraction-like property of the unified iteration scheme (5), which is key for the convergence analysis of the adaptive ILG Algorithm 1. In particular, we were able to generalize some of the results from [12] including the linear convergence of the general ILG procedure and the (uniform) boundedness of the number of linearization steps on each Galerkin space. We underline that the latter property constitutes an important stepping stone for the analysis of optimal computational complexity, cf. [12, §6 and §7] and [11, Theorem 7].
References
Amrein, M., Wihler, T.P.: An adaptive Newton-method based on a dynamical systems approach. Commun. Nonlinear Sci. Numer. Simul. 19(9), 2958–2973 (2014)
Amrein, M., Wihler, T.P.: Fully adaptive Newton-Galerkin methods for semilinear elliptic partial differential equations. SIAM J. Sci. Comput. 37(4), A1637–A1657 (2015)
Astala, K., Iwaniec, T., Martin, G.: Elliptic partial differential equations and quasiconformal mappings in the plane. Princeton Mathematical Series, vol. 48. Princeton University Press, Princeton, NJ (2009)
Bernardi, C., Dakroub, J., Mansour, G., Sayah, T.: A posteriori analysis of iterative algorithms for a nonlinear problem. J. Sci. Comput. 65(2), 672–697 (2015)
Carstensen, C., Feischl, M., Page, M., Praetorius, D.: Axioms of adaptivity. Comput. Math. Appl. 67(6), 1195–1253 (2014)
Congreve, S., Wihler, T.P.: Iterative Galerkin discretizations for strongly monotone problems. J. Comput. Appl. Math. 311, 457–472 (2017)
Diening, L., Kreuzer, C.: Linear convergence of an adaptive finite element method for the \(p\)-Laplacian equation. SIAM J. Numer. Anal. 46(2), 614–638 (2008)
Dörfler, W.: A convergent adaptive algorithm for Poisson’s equation. SINUM 33, 1106–1124 (1996)
El Alaoui, L., Ern, A., Vohralík, M.: Guaranteed and robust a posteriori error estimates and balancing discretization and linearization errors for monotone nonlinear problems. Comput. Methods Appl. Mech. Engrg. 200(37–40), 2782–2795 (2011)
Ern, A., Vohralík, M.: Adaptive inexact Newton methods with a posteriori stopping criteria for nonlinear diffusion PDEs. SIAM J. Sci. Comput. 35(4), A1761–A1791 (2013)
Gantner, G., Haberl, A., Praetorius, D., Schimanko, S.: Rate optimality of adaptive finite element methods with respect to the overall computational costs. Tech. Rep. 2003.10785, arxiv.org (2020)
Gantner, G., Haberl, A., Praetorius, D., Stiftner, B.: Rate optimal adaptive FEM with inexact solver for nonlinear operators. IMA J. Numer. Anal. 38(4), 1797–1831 (2018)
Garau, E.M., Morin, P., Zuppa, C.: Convergence of an adaptive Kačanov FEM for quasi-linear problems. Appl. Numer. Math. 61(4), 512–529 (2011)
Garau, E.M., Morin, P., Zuppa, C.: Quasi-optimal convergence rate of an AFEM for quasi-linear problems of monotone type. Numer. Math. Theory Methods Appl. 5(2), 131–156 (2012)
Heid, P., Wihler, T.P.: On the convergence of adaptive iterative linearized Galerkin methods. Tech. Rep. (2019). arXiv:1905.06682
Heid, P., Wihler, T.P.: Adaptive iterative linearization Galerkin methods for nonlinear problems. Math. Comp. p. in press (2020)
Lakkis, O., Makridakis, C.: Elliptic reconstruction and a posteriori error estimates for fully discrete linear parabolic problems. Math. Comp. 75(256), 1627–1658 (2006)
Makridakis, C., Nochetto, R.H.: Elliptic reconstruction and a posteriori error estimates for parabolic problems. SIAM J. Numer. Anal. 41(4), 1585–1594 (2003)
Mitchell, W.: Adaptive refinement for arbitrary finite-element spaces with hierarchical basis. J. Comput. Appl. Math. 36, 65–78 (1991)
Nečas, J.: Introduction to the Theory of Nonlinear Elliptic Equations. Wiley, New Jersey (1986)
Zarantonello, E.H.: Solving functional equations by contractive averaging. Tech. Rep. 160, Mathematics Research Center, Madison, WI (1960)
Zeidler, E.: Nonlinear functional analysis and its applications. IV. Springer, New York (1988). Applications to mathematical physics, Translated from the German and with a preface by Juergen Quandt
Zeidler, E.: Nonlinear Functional Analysis and its Applications. II/B. Springer, New York (1990)
Acknowledgements
Open access funding provided by University of Bern
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors acknowledge the financial support of the Swiss National Science Foundation (SNF), Grant No. 200021_182524.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Heid, P., Wihler, T.P. On the convergence of adaptive iterative linearized Galerkin methods. Calcolo 57, 24 (2020). https://doi.org/10.1007/s10092-020-00368-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10092-020-00368-4
Keywords
- Numerical solution methods for quasilinear elliptic PDE
- Monotone problems
- Fixed point iterations
- Linearization schemes
- Kačanov method
- Newton method
- Galerkin discretizations
- Adaptive mesh refinement
- Convergence of adaptive finite element methods