Introduction

Since the ratio of the aged-class forest area of Japan increases annually, there is a need to ensure such mature forest resources are used sustainably. In line with this increase, the supply of large-diameter logs is also expected to expand. Sugi (Cryptomeria japonica D. Don) is one of the major planted species in Japan, with various applications thanks to its lightness, straight grain, and ease of processing. In recent years, the required quality of sawn lumber as structural members has risen; hence, the need to produce lumber which meets demands in terms of strength, moisture content, and shape stability.

The wood properties of Sugi vary significantly, due to the many cultivars [1–5] and the variation in the growing environment caused by wide stand locations [6–10]. Determining the variation in wood properties among logs and sorting logs according to usage would help improve lumber production efficiency. Wood properties also vary widely within a log [1, 11–15]. If sawing patterns were optimized according to the variation in wood properties within a log, not only according to log shape but also targeting maximum volume yield, it would be useful to produce lumber capable of meeting the end-use requirements.

In the Japanese Agricultural Standards for Logs [16], logs with top-end diameters of less than 14 cm, 14 to less than 30 cm and 30 cm or more are defined as small, medium and large logs, respectively. The major diameter classes presently in distribution range from 18 to 22 cm for mainly kiln-dried squared lumber, with the next size up from 24 to 28 cm [17]. However, the ratio of large-diameter logs of 30 cm or more would increase with the expansion of the aged-class forest area. A previous study [18] showed the potential to efficiently produce lumber suitable for end use by sorting logs by Young’s modulus and moisture content and sawing them using optimal sawing patterns for medium-diameter Sugi logs. Little is known about the variation in wood properties in large Sugi logs [19], and few studies exist on lumber quality based on data obtained in actual sawing tests.

In Japan, however, squared lumber is a major sawn product used for building members when constructing wooden houses. As one example of the variation in sawing patterns in large Sugi logs, several squared pieces of lumber without pith could be produced in this study. It is important to clarify the relationship between the wood properties of logs and the quality of the sawn lumber. The purposes of this study include accumulating fundamental data on wood properties within large Sugi logs and taking applicable variations in wood properties into consideration for sorting logs and sawing patterns.

Materials and methods

Materials

A total of 35 large Sugi logs grown in Ibaraki Prefecture were used in this study, 32–42 cm in diameter and 3.65 or 4 m long. Since these logs were sold for lumber production in the log market, their quality reflects the general quality of large-diameter logs available for lumber production in the North Kanto region, Japan. Although the height of each log was unclear, they were predicted from the first to third logs because of the trend in these diameter classes in that market.

Discs from the top and butt ends of all 35 logs were cut to determine the wood properties, whereupon the remaining logs 3 m long were used for the sawing test. After debarking, the lengths, short and long diameter of the top and butt ends, heartwood percentage, number of growth rings, warp, taper, and eccentricity of the 24 logs used for the sawing test were all measured. The heartwood percentage was the ratio of the heartwood radius to the short radius through the pith on the top end, while the number of growth rings was counted on the top end. Warp was calculated as the chord height per short diameter of the top end, while taper was calculated as the difference between the top- and butt-end diameters per log length. Eccentricity was calculated as the distance between the pith and the geometric center per short diameter.

The natural frequency of log vibration was measured using a longitudinal vibration method and Young’s modulus of the logs was calculated using Eq. (1):

$$ E_{\text{{\it fr}}} = 4 \times L^{2} \times {\text{{\it fr}}}^{2} \times \rho \times 10^{ - 9} $$
(1)

where E fr (GPa) is Young’s modulus, L (m) the length, fr (Hz) the natural vibration frequency, and ρ (kg/m3) the bulk density, respectively.

Measurement of the wood properties

The wood properties of all 35 logs were measured. Strips 40 mm wide and 30 mm thick were cut from the discs of the top and butt ends of the log. These strips were then split into small pieces at intervals of 20 mm from pith to bark, parallel to the growth layers and the green weight and volume of each piece were measured using an electronic densimeter MD-300S (ALFA MIRAGE). The oven-dry weight was obtained by drying at 105 °C for 24 h. The basic density was calculated as the oven-dry weight per green volume, while the moisture content was calculated as the water-weight per oven-dry weight. The basic density and moisture content were measured with the same piece. The area-weighted mean, based on distance from the pith, was calculated as the mean value of the basic density and moisture content of the discs, sapwood, and heartwood in the top and butt ends, respectively, while the arithmetic mean value of the top and butt ends was calculated as a mean value for the logs. The growth ring width of the butt end was measured using 2D image analysis software Win ROOF (MITANI CORPORATION). The microfibril angle (MFA) of the butt end was measured every 5–6 growth rings by a technique using the slit-like pit aperture directions. The angle between the slit-like pit aperture directions of tangential pittings and the axis of the tracheid was consistent with the MFA of the S2 layer of a single macerated latewood tracheid in Sugi [20]. The latewood slice was macerated in Schulze solution (KClO3 + 60 % HNO3), and then soaked in hot water for 2–3 days and dyed with safranin. Images of the slit-like pit aperture in the tangential wall of the latewood were obtained via a digital camera, and the angle between the cell longitudinal axis and the slit-like pit aperture was determined as the MFA value using Win ROOF. The MFA at three points per tracheid were measured and the mean value of twenty tracheids was calculated as the MFA of that ring. The mean MFA of the log was the arithmetic mean of the values measured for every 5–6 growth rings.

Sawing test

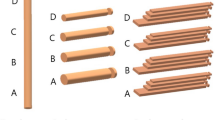
In the sawing test, 24 large-diameter Sugi logs randomly selected from a group of 35 were used. A 1,200 mm band mill with an auto feed carriage and a 1,100 mm auto-roller table band resaw installed in the Forestry and Forest Products Research Institute, Japan were also used in this study. Logs were sawn using the three sawing patterns shown in Fig. 1. The main product was squared lumber without pith, 13.0 cm wide and thick. Several pieces of squared lumber were sawn depending on the diameter of the logs. Two squared lumber sections were produced in sawing pattern II (SP-II), three squared lumber sections in sawing pattern III (SP-III), and four squared lumber sections in sawing pattern IV (SP-IV), respectively. The squared lumbers without pith were dried in a conventional steam heated kiln at a temperature of 70–80 °C and relative humidity of 48–73 % for 15 days.

Fig. 1
figure 1

Sawing patterns. SP-II sawing pattern II which produced two squared lumber sections, SP-III sawing pattern which produced three squared lumber sections, SP-IV sawing pattern IV which produced four squared lumber sections. The size of squared lumber was 13.0 cm wide and thick. Each dot shows the position of pith

Full size image

Lumber quality

Immediately after sawing, the squared lumber was weighed and its width, thickness, and length were measured. The natural frequency of the lumber vibration was measured using a longitudinal vibration method and Young’s modulus of the lumber was calculated using Eq. (1). The chord height of the lumber was measured in units of 1 mm using a thread and ruler, and the lumber warp was calculated using Eq. (2).

$$ W_{1} = \left( {{{H_{1} } \mathord{\left/ {\vphantom {{H_{1} } {L_{1} }}} \right. \kern-0pt} {L_{1} }}} \right) \times 100 $$
(2)

Here, W 1 (%) was the lumber warp, H 1 (mm) the chord height, and L 1 (mm) the length. The lumber warp was measured in two directions, and the larger value was deemed to be the lumber warp. A specimen 20 mm thick was cut from the middle of each lumber after kiln-drying to determine the moisture content, which was calculated as the water-weight per oven-dry weight (at 105 °C for 24 h). The moisture content of the lumber after sawing was calculated from the ratio of the weight after sawing to that after kiln-drying. Data of Young’s modulus, warp, and moisture content were obtained after sawing and kiln-drying.

Results and discussion

Log specifications

The specifications of the 24 logs used for the sawing test were shown in Table 1. One of the characteristics of the large-diameter logs was the increased percentage of heartwood [21]. The mean percentage of heartwood in the large Sugi logs used in this study was 69.4 %, which certainly exceeded the 61.1 % reported in middle-diameter Sugi logs of similar origin [18]. The warp of the logs, meanwhile, was 4.0 %, which was smaller than the 8.3 % reported for middle-diameter Sugi of similar origin [22]. The reason for this is the tendency of the diameter to expand with the decreasing ratio of chord height relative to the top end diameter. The tendencies in the 24 logs showed an increased percentage of heartwood and a decline in large-diameter log warp. However, more data must be accumulated to prove such tendencies in Sugi logs.

Table 1 Specifications of the logs for the sawing test
Full size table

Basic density

The mean basic densities of the logs, sapwood, and heartwood are shown in Table 2. The mean basic density of heartwood exceeded that of sapwood, as a general tendency for Sugi [23]. The mean basic density of the logs used in this study was 0.290 g/cm3, which was lower than that reported by previous studies [6–8, 11, 12]. Generally, the basic density tended to be high at the top of trees within the trunk [4, 8, 12]. The reason for the lower mean basic density is the fact that the logs used in this study were first to third logs; but those in previous studies were whole trees, including the tops. In addition, since the materials in those reports were planted at different times from those of this study, wood properties such as the basic density would differ owing to the difference in the growing environment and forest management. The mean basic density in this study was lower than the values of plus tree clones planted at a similar time [23] and the value measured at breast height in younger and older stands [24, 25]. Since large-diameter logs are considered to comprise a smaller proportion of juvenile wood with comparatively high density for whole-log volume compared to small- or middle-diameter logs, the mean basic density could be lower than smaller logs. The coefficient of variation (CV) of the basic density among logs was 0.073, which was within the range of that within a cultivar in previous reports [2, 3].

Table 2 The mean basic density and the moisture content of log, sapwood, and heartwood
Full size table

The instances of the profile of basic density in the radial direction of the top end are shown in Fig. 2. The basic density decreased outward from the pith, similar to the tendency in previous studies [1, 8, 9, 11, 12]. The CV of the basic density in a radial direction within a log ranged from 0.04 to 0.15, while in certain logs, e.g. nos. 101 and 122, there were only limited variations in basic density within logs. Conversely, in other logs, e.g. nos. 125 and 220, the internal variations were considerable. Where the CV of basic density was high, the difference between the basic density near the pith and that in the outer position was considerable. Although the differences in basic density near the pith and that at the outer position varied widely, the ratio of the stable density portion was expected to rise with increasing log diameter.

Fig. 2
figure 2

Profile instances of basic density in the radial direction. The figure showed the measurement of the top end

Full size image

Moisture content

The mean moisture content of the logs, sapwood, and heartwood is shown in Table 2, the values of which resembled those reported in some papers [4, 5, 13, 23]. Larger variations among logs were obtained for the moisture content in heartwood rather than sapwood. Although the moisture content in sapwood was close to the maximum moisture content affected by basic density [13], the moisture content of heartwood, regardless of basic density, was distributed over a wide range [5, 13, 23, 26], a tendency confirmed in this study. The CV of the moisture content in heartwood exceeded that of sapwood.

Profile instances of moisture content in the radial direction of the top end are shown in Fig. 3, where several distribution patterns of heartwood moisture content can be seen [27–29]. Three patterns were observed in this study, namely consistently low moisture content (type-A), high near the pith and decreasing in the radial direction (type-B), and high irregularly (type-C). Although certain type-C logs showed a difference in the mean moisture content of heartwood between the top and butt ends, no logs were classified as other types in terms of the moisture content pattern in the top and butt ends. The number of logs of types-A, B, and C were 7, 13, and 15, respectively. In most type-C logs, an area of high moisture content appeared at the outer portion of the heartwood. The figures for the mean moisture content of heartwood for types-A, B and C were 69.1, 88.6, and 159.7 %, respectively. In almost all logs with high mean moisture content of heartwood, it was predicted that the distribution of the high moisture content area would be irregular, as for type C.

Fig. 3
figure 3

Profile instances of moisture content in the radial direction. The arrows show the borders of heartwood in each log. The figure showed the measurement of the top end

Full size image

Growth ring width

The variations in the mean growth ring width of the top and butt ends of logs are shown in Table 3. The mean growth ring width of the intra-log ranged between 2.84 and 5.27 mm.

Table 3 The variations in the mean growth ring width of the top and butt ends of logs
Full size table

The growth ring width and distance from the pith in relation to the ring number from the pith at the butt end of three typical logs are shown in Fig. 4. The 25 logs showed a tendency similar to that for the no. 104 log, namely a large growth ring width near the pith, which decreased steeply in later years, and stabilized after the 10th or 15th ring. This tendency resembled that reported for certain cultivars [4] and plus-tree clones [26, 30]. The growth rate of these logs would have been high in the early years. For the remaining 10 logs, although the growth ring width near the pith was similarly large, it gradually declined in later years, e.g. the no. 115 log, or no clear tendency was defined, e.g. for no. 101 shown in Fig. 4. A declining tendency in later years also emerged in the result of some plus-tree clones [26, 30]. The maximum growth ring width intra-log appeared before the 10th ring in almost all logs and within 6 cm or so from the pith. The mean ring numbers with maximum width at the top and butt ends were 4.7 and 5.2, respectively.

Fig. 4
figure 4

The growth ring width and distance from the pith in relation to the ring number from the pith at the butt end

Full size image

Microfibril angle

The MFA is shown in relation to the ring number from the pith of certain logs in Fig. 5. In all logs, the MFA peaked near the pith, tending to decline in later years and stabilize toward the bark. This tendency also emerged in other studies [20, 31, 32]. Hirakawa and Fujisawa [20] indicated that the MFA variation pattern of the S2 layer in latewood tracheids from pith to bark was almost the same in all six clones, while the value of the angles in the mature wood region differed among individual clones. The growth ring number reaching a constant value of MFA was defined as the portion whereby the change of MFA became 2.5° or less, referring to the previous paper [31]. In most logs in this study, the MFA reached a constant value before the 15th ring, as shown in Fig. 5a. In only three logs, the ring numbers of constant MFA ranged between 18th and 25th, as shown in Fig. 5b. Kijitani and Kitahara [14], Hirakawa and Fujisawa [31], and Fukunaga et al. [33] reported a tendency to reach the constant value of MFA earlier with increasing height above ground. Even if the log diameters were the same, the growth ring number of reaching constant MFA would differ according to the height above ground. In the first logs, the area of large MFA could be wide.

Fig. 5
figure 5

The MFA in relation to the ring number from the pith of some logs. The MFA was measured in butt end

Full size image

Based on utilization as sawn lumber, consideration of MFA in relation to distance from the pith was reasonable. A histogram of distance from the pith of reaching constant MFA is shown in Fig. 6. The mode ranged between 6.0 and 8.0 cm, peaking at a distance of 10.4 cm, while the MFA in relation to the distance from the pith of some logs is shown in Fig. 7. The constant value of MFA ranged between about 15 and 20°.

Fig. 6
figure 6

The histogram of distance from the pith of reaching a constant MFA

Full size image
Fig. 7
figure 7

The MFA in relation to distance from the pith of some logs. The MFA was measured in butt end

Full size image

The relationship between the mean MFA and E fr of logs is shown in Fig. 8, while a negative correlation was found between the mean MFA and E fr of log (r = −0.693, P < 0.01). Cave and Walker [34] showed that the MFA were important determinants of stiffness. Yamashita et al. [35] showed that the E fr variation among cultivars was regarded as effectively explained by MFA characteristics. In large-diameter logs, since the area of stable smaller MFA could widely exist, it would be advantageous in terms of producing reliable large-or small-sized lumber in bulk with high Young’s modulus.

Fig. 8
figure 8

The relationship between the mean MFA and E fr of log. Two asterisks indicates significant at the 1 % level

Full size image

Wood properties and lumber quality

The correlation coefficients between lumber quality both after sawing and kiln-drying and wood properties were shown in Table 4.

Table 4 Correlation coefficients of between lumber quality both after sawing and kiln-drying and wood properties
Full size table

A positive correlation was found between the moisture content of heartwood and that of lumber (r = 0.896, P < 0.01). The correlation coefficient between the mean moisture content of logs and that of lumber, meanwhile, was 0.705, which was smaller than the former, since the squared lumber without pith was sawn from large logs comprised a high proportion of heartwood. Although the moisture content varied according to the sawing position, it was reasonable to estimate the moisture content of lumber based on that of heartwood rather than that of the whole log, in the case of large-sized lumber. The relationship between the mean moisture content of heartwood and the moisture content of squared lumber without pith after kiln-drying is shown in Fig. 9. A positive correlation was found between the mean moisture content of heartwood and the moisture content of squared lumber without pith after kiln-drying (r = 0.769, P < 0.01). If logs of type-A or B in the moisture content pattern, shown in Fig. 3, and with mean moisture content of heartwood of less than about 120 % were selected, almost all the lumber moisture content after kiln-drying was less than 25 %, which indicates that the incidence of inferior kiln-dried products could be reduced. Sorting lumber by weight before it is kiln-dried was already executed in some sawmills, and improved the efficiency of the kiln-drying process. In addition, sorting logs by heartwood moisture content before sawing would enable energy and cost savings for kiln-drying and upgrade the quality of the kiln-dried lumber.

Fig. 9
figure 9

The relationship between the mean moisture content of heartwood and the moisture content of squared lumber without pith after kiln-drying. The x axis indicates the area weighted mean moisture content of heartwood of log calculated based on distance from the pith. Type A, B, and C refers to Fig. 3. Two asterisks indicates significant at the 1 % level

Full size image

The relationship between the E fr of logs and that of squared lumber without pith after sawing is shown in Fig. 10. A positive correlation was found between the E fr of log and that of lumber (r = 0.832, P < 0.01). This suggests that sorting logs by E fr would be useful, especially to produce reliable sawn lumber from large logs efficiently. Significant negative correlations were observed between the lumber E fr after sawing and kiln-drying and the mean and the constant value of MFA. Since the E fr was affected by the MFA, it might be possible to produce lumber with higher E fr than that of logs using a sawing pattern avoiding the area near the pith with large MFA.

Fig. 10
figure 10

The relationship between the E fr of log and that of the squared lumber without pith after sawing. Two asterisks indicates significant at the 1 % level

Full size image

The lumber warp was considered attributable to the bending stress induced by the longitudinal stresses in the log [36]. The growth strain was shown to be affected by the growth rate and related to the basic density, and MFA [37]. Yamamoto et al. [38] showed that contractive-released strains increased with decreasing MFAs in Sugi. Since a significant negative correlation was observed between the lumber warp after sawing and the constant value of MFA (P < 0.05), the MFA would be considered one of the causes of lumber warp after sawing.

The mean lumber warps after sawing and kiln-drying, respectively, are shown in Fig. 11. The mean moisture contents of squared lumber after sawing and kiln-drying were 113.5 % (SD 31.8 %) and 21.3 % (SD 7.8 %), respectively. The statistical difference was determined by a two-sided paired t test (P < 0.01), while the lumber warp after kiln-drying significantly exceeded that after sawing. A positive correlation was found between the lumber warp after sawing and kiln-drying (r = 0.383, P < 0.01). Since lumber warp rose with decreasing moisture content, it is important to minimize the lumber warp after sawing. Lumber warp after kiln-drying was caused by significant longitudinal shrinkage and its gradients, which were affected by MFA [39]. A significant negative correlation was observed between the lumber warp after kiln-drying and both the growth ring number and distance from the pith of reaching constant MFA (P < 0.05). The area range for reaching constant MFA was predicted to be related to the warp of squared lumber after kiln-drying. Adapting the sawing pattern considering the area with high MFA gradients around the pith or enlarging the size of the rough sawn anticipating the large warp could be effective in improving the lumber quality. It is necessary to examine the influence of sawing patterns on the relationship between the area for reaching constant MFA and the lumber quality in detail. The relationship between the sawing patterns and the quality of squared lumber without pith will be investigated in our other studies on sawing tests using a greater number of logs.

Fig. 11
figure 11

The mean lumber warp after sawing and after kiln-drying. The error bars shows standard deviation. Two asterisks indicates significant at the 1 % level

Full size image

Application of wood properties to sawing patterns

The distance from the pith of reaching constant MFA was within 10 cm or so. Lumber outside this area is expected to be reliable. From a volume yield perspective, SP-III exceeded SP-II. However, the quality of squared lumber without pith could potentially increase despite the lower volume yield, if SP-II used in relatively large logs was to avoid the central part of logs with large MFA. It is desirable for the lumber sawn from the central part to be, e.g., boards not needing to be particularly sturdy as nonstructural members.

If the log diameter were sufficient, it would be possible to produce several squared lumber sections without pith and not containing any of the large MFA. As an additional experiment, one log was sawn using sawing pattern V (SP-V) shown in Fig. 12. In this sawing pattern, four squared lumber sections without pith were produced, except the central one with pith. The short diameter of the top end of this log was 43.8 cm, while the E fr of the log was 6.14 GPa. The MFA in this log reached a constant value within the 10th growth ring and 6.1 cm from the pith, and the constant MFA was 20°. Since the diameter of reaching a constant MFA was about 12 cm, which was included in the center squared lumber with pith, four squared lumber without pith could be produced from the area of stable MFA in the log. The E fr of the four squared lumber sections without pith ranged from 6.48 to 7.60 GPa, while that of the central item was 6.11 GPa. In this sawing pattern, it would be possible to produce squared lumber, for which a higher E fr from the outer position of the log, by selecting a log above the E fr , would be required. If the area of reaching constant MFA was small, the squared lumber with higher E fr would be obtained more reliably. Although the sawing work efficiency of sawing would be expected to decline, the potential for lumber production with target Young’s modulus could increase dramatically.

Fig. 12
figure 12

The illustration of sawing pattern considering the pattern of MFA. A dot shows the position of pith. The size of squared lumber was 13.0 cm wide and thick. Shaded part indicates the area of reaching constant MFA

Full size image

In the case of the top-end diameter exceeding 43 cm or so, such an SP-V would be recommended to produce reliable squared lumber for structural use. It is important to consider the distance from the pith of reaching constant MFA. In addition, if the moisture content of heartwood is high, it is desirable for the lumber sawn from the central part to be small-dimension lumber like boards to improve the kiln-drying efficiency. A method must be developed to predict the moisture content and MFA of logs easily. To improve the lumber quality, not only one but also multiple wood properties must be applied to the sawing pattern. A sawing pattern considering each of the wood properties and corresponding to the lumber quality for end use would improve the yield of reliable lumber.

Conclusions

Variation in basic density and moisture content in the radial direction in large Sugi logs was shown in this study. The greater the log diameter, the more the ratio of stable portion of density is expected to increase. Three patterns of heartwood moisture content were observed. It was reasonable to estimate the moisture content of lumber based on that of heartwood rather than that of the whole log, especially in terms of the production of large-sized lumber. The MFA reached a constant value before the 15th ring and within about 10 cm or so in terms of distance from the pith. Since the E fr was affected by the MFA, it might be possible to produce lumber with a higher E fr than that of logs using a sawing pattern avoiding the area near the pith with large MFA. In large-diameter logs, since the area of stable smaller MFA could exist widely, it would be advantageous for producing reliable large-sized lumber. The area range for reaching constant MFA was predicted to be related to the warp of squared lumber after kiln-drying. A sawing pattern considering each of the wood properties corresponding to the lumber quality for end use would improve the yield of reliable lumber.