Introduction

Rockfalls are one of the most common types of landslides in mountain areas. They are characterised by a destructive potential, which derives from their high speed and high energy and lack of early warning indicators (Broili 1973; Guzzetti et al. 2002; Agliardi and Crosta 2003; Dorren 2003; Frattini et al. 2008). Furthermore, the detached rock blocks can vary in a wide range of volumes, from less than 1 m3 to more than 105 m3 (Rochet 1987; Hungr and Evans 1988; Hungr et al. 1999; Ruiz-Carulla and Corominas 2020).

The geometry of a rockfall is represented by a source or release area, a propagation area, and a deposition area (Losasso et al. 2017; Rossi et al. 2021). The identification of the potential source areas is challenging and in most cases with inaccessible and rough topography. Rockfall source areas are determined by several geological factors, including lithology, slope angle, rock mass strength, network of discontinuities, and vegetation (Sturzenegger et al. 2007; Messenzehl et al. 2017; Sarro et al. 2018; Rossi et al. 2021).

Rockfall phenomena are difficult to predict due to the lack of precursors and the complex trigger mechanisms (Feng et al. 2021). The latter can be represented by an earthquake (Kobayashi et al. 1990), the rainfall and freeze-and-thaw cycles (Matsuoka and Sakai 1999), or the progressive weathering of the rock mass and the development of the discontinuities. Moreover, several investigation techniques are applied in the literature for the understanding of rockfall processes. These include 2D and 3D trajectory analyses, kinematic analysis, and numerical simulations (Sari (2022) and references therein). Furthermore, the rockfall hazard and risk assessments are of major societal interest and their investigation is commonly approached with physically based modelling methods (Sturzenegger et al. 2007; Frattini et al. 2008; Sarro et al. 2018; Akin et al. 2021; Alvioli et al. 2021; Sari 2022; Schilirò et al. 2022). Additionally, rockfalls are characterised by long run-out distances, depending on the kinetic energy of the blocks and the topographic characteristics of the area (Giacomini et al. 2009; Hungr et al. 2014). Therefore, an ideal rockfall predictive analysis should include the identification of the potential release areas and the assessment of trajectories of falling blocks (Hantz et al. 2021). Moreover, the use of Unmanned Aerial Vehicles (UAV) represents an asset for landslide hazard studies, especially for outcrops difficult to access on the field (Francioni et al. 2020; Forte et al. 2021; Mineo et al. 2021; Pignalosa et al. 2022; Zhang et al. 2022).

In general, the numerical simulation approach presents some limitations regarding the modelling itself. These include (i) the definition of the source areas that are seldom not based on direct field observations but defined with a stochastic approach, (ii) the assignment of the coefficient of restitution that represents an oversimplification and is not always defined by back analysis of past rockfalls, and (iii) the fragmentation process which is rarely accounted for in the simulations (Frattini et al. 2008; Matas et al. 2017).

In this study, the risk of rockfall invasion in the residential area of Frassitelli, Ischia Island, was investigated. This was carried out with an integrated approach consisting of (i) the study of the potential release areas with the structural investigation of a Green Tuff exposure, and (ii) the simulation of the trajectories and run-out of the rock blocks with numerical models.

The investigated slopes of Mt. Epomeo show evidence of instability, as demonstrated by the presence of numerous rock blocks at the foothill and in the residential area. These rock blocks were characterised by orthophotos and field surveys, collecting information on their position and volume. Furthermore, the two outcrops are located at 280 and 420 m a.s.l. and, due to their inaccessibility, the structural analysis was carried out by means of Virtual Outcrop Models (VOMs) following drone-derived photo acquisition. The collected data were validated with field measurements from the nearby area. Subsequently, kinematic models were performed with the gathered discontinuity dataset against the slope faces of the two outcrops.

The numerical modelling of the rockfall trajectories was performed with the module ‘Rockfall’ of the software RAMMS (RApid Mass MovementS), developed by Leine et al. (2014). Several scenarios of potential rock volumes and shapes were simulated. The results of the simulated rockfall trajectories were quantified and compared between the models. The following parameters showed to play a primary influence on the rockfall trajectory pathways:

  • the volume and shape of the rock blocks;

  • the topographic position of the source area;

  • the geomorphological features of the propagation area.

Finally, the risk of rockfall with respect to the nearby residential area was evaluated in a range of scenarios, and the potential mitigation measures were considered.

Study area

Geological setting

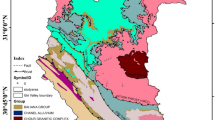
Ischia Island, located in the Gulf of Naples, is part of a complex volcanic field, covering an area of about 42 km2. The geological and geomorphological features characterising the Island determine a high susceptibility to instability events and processes. These include earthquakes, flow-like landslides, rockfalls, flash floods, and tsunamis, creating a multi-hazard environment (Selva et al. 2019). The main lithologies outcropping are trachytes and latite-phonolites lavas, as well as pyroclastic soils and ancient mudflow deposits (Chiesa et al. 1987; Orsi et al. 1998), emplaced after the Green Tuff eruption (about 55 ka). The latter forms the core of Mt. Epomeo and is a trachytic ignimbrite characterised by a green colour due to seawater alteration.

Frassitelli village is a residential, tourist, and agricultural area located at the foothill of the southwestern slope of Mt. Epomeo. The latter is characterised by W-SW facing slopes constituted by fault scarps with high gradients. In general, the combination of volcanic lithologies, steep walls along the main gullies and cliffs, and the occurrence of erosion processes and seismic activity have led to frequent rockfall events (Del Prete and Mele 1999, 2006; Di Martire et al. 2012).

This study focussed on two outcrops composed of Green Tuff (GT, Fig. 1), bordered by highly dipping fault scarps, located at 280 and 420 m a.s.l. and forming a 400-m-wide and 345-m-high exposure. Henceforth, we refer to the outcrop located at 420 m a.s.l. as ‘Cliff A’ and to the one located at 280 m a.s.l. as ‘Cliff B’. The former has a maximum height (peak-to-ground distance) of about 160 m, while the latter of about 70 m.

Fig. 1
figure 1

Geolithological and geomorphological photo-mosaic and maps of the study area. GT, Green Tuff; HGT, Hydrothermalised Green Tuff; dt, detrital talus

Full size image

The tuff locally occurs highly hydrothermalised (HGT, Fig. 1) as a result of the upward migration of hydrothermal fluids that affect the tuff mineralogy, which is composed of oxidised and reddish minerals with finer grain size. Furthermore, the area is characterised by a wide paleo-surface, probably of volcano-tectonic origin, which divides the two outcrops. Additionally, the area is bounded by two deeper gullies. Finally, the frequent occurrence of past rockfalls is testified by the presence of a detrital talus (dt) and large isolated rock blocks. The presence of weathered and hydrothermalised rocks, as well as the numerous faults characterising these slopes, can explain why the area suffered frequent rockfalls.

Data and methods

3D models

The VOM of the two analysed outcrops were built following high-resolution image acquisition performed by means of a drone. The latter was a DJI™ Phantom 4 quadrotor UAV platform equipped with a 4 K video camera with a 1/2.3″ CMOS sensor, 94-degree field of view, 12.4 MP images, and a focal length of 3.6 mm.

The images were acquired with a minimum overlap of 70% and were then georeferenced and processed with the Structure from Motion (SfM) computer vision techniques. During this stage, a dense point cloud is developed, from which the Digital Surface Model (DSM), and the nadir and oblique orthomosaic images were obtained. The orthomosaic images enabled the identification of the rock blocks at the base of the slopes from past rockfalls and the estimation of their volumes. The field measurement of such features was not possible due to the inaccessibility of the outcrops.

Additionally, the Digital Terrain Model (DTM) of the investigated area was derived from the 2009 to 2012 1 × 1 m LiDAR survey (https://sit.cittametropolitana.na.it/index.php) and imported for the rock trajectory simulations. This choice was determined by the large presence of high vegetation in the drone-derived DSM.

Structural analysis

Faults and fractures dataset

The structural analysis was aimed to characterise the potential rockfall source areas on the two investigated outcrops by identifying the discontinuity sets and evaluating their impact on the stability of the rock mass.

The two outcrops are inaccessible for direct data collection. Therefore, the field surveys were carried out in the nearby area, characterising the background fractures and the major faults of the Green Tuff fm., while the VOMs enabled the remote data collection from the outcrops that were successively analysed with the software OpenPlot (Tavani et al. 2011).

The VOMs were also used to reconstruct the geometry of the exposure, with the plugin ‘Facets’ in CloudCompare v2.10.2. Subsequently, the different data were combined to perform the kinematic analysis of the potential failure mechanisms.

OpenPlot software was applied to extract the fracture sets affecting the analysed outcrops. It is an open-source software used for the analysis of geostructural features in a 3D environment (Tavani et al. 2011). By importing the developed VOMs into the software, the fracture planes are derived following the digitisation of their traces along the outcrop. The software computes the best-fit plane from the digitised polyline and the outcrop topography (Hodgetts et al. 2004), and the fracture planes are directly displayed in the 3D view on the dense point cloud. Each fracture plane is characterised by different parameters, including coordinates (X, Y, Z), dip, and dip direction. Successively, the dataset is sorted by attitude with stereographic equal-area projections and the fracture sets affecting the rock mass are defined.

The CloudCompare v2.10.2 plugin ‘Facets’ enables the automatic measurement of the slope faces of the analysed model, allowing the reconstruction of the outcrop geometries, as described by Dewez et al. (2016). The cloud is divided into sub-families of points according to user-defined parameters of co-planarity. The results are a mosaic of planar polygons (facets) defined as mesh surfaces (with contour, extent, centroid, and normal values) and adjusted to fit the original 3D point cloud. Each facet is characterised by a measure of dip and dip direction, which allows to organise them into sets, represented in a stereoplot diagram.

The plugin can be alternatively applied with a Kd-Tree (Kd) or a Fast Marching (FM) method, both based on a least-square fitting algorithm (Fernández 2005). The former recursively divides the cloud into small planar patches, whereas with the latter the subdivision is systematic (Dewez et al. 2016). We applied the fast marching (FM) method, which requires the definition of the following parameters: octree level, max distance at n%, min points per facet, max edge length.

Kinematic analysis

The kinematic analysis represents a straightforward approach to identifying the structurally controlled failures in rock masses, where the discontinuity systems are adversely oriented with respect to the slope (Sari 2022). It was performed with the software DIPS (Rocscience Inc. 2020), investigating the potential failure mechanisms. The input data are the slope faces obtained from CloudCompare and the fracture sets collected via field surveys and from the VOMs with OpenPlot software (Schilirò et al. 2024).

Different failure mechanisms were considered, including planar sliding, wedge sliding, direct toppling, and flexural toppling. For each potential failure mechanism, the percentage of critical intersections within the fracture network with respect to the individual slope face was computed. The percentage of critical intersections defines the failure mechanisms with higher levels of susceptibility.

Numerical modelling

The simulation of the potential rockfall trajectories was performed with the module ‘Rockfall’ of the software RAMMS. The rock is assumed as a three-dimensional rigid body, with three translational and three rotational degrees of freedom (Leine et al. 2014). The rockfall simulation technique is based on a probabilistic model which considers the uncertainties of the trajectories. The modelling of the rock-soil interaction is based on hard contact laws taking into account the role of the rock shape. The Rockfall module utilises hard-contact, rigid-body mechanics to model rockfall trajectories in general three-dimensional terrains. This approach determines that contact forces are applied to the edges and corner points of the rock (Leine et al. 2014).

The LiDAR-based DTM, with a 1 × 1 m cell size, was used as input for the rockfall simulation. In addition, the different lithologies or vegetation outcropping on the slope were determined by photointerpretation of the UAV-derived orthomosaic maps. Based on a qualitative approach, each lithology was assigned to a ‘Terrain Category’, while the types of vegetation were assigned to a ‘Forest Category’, as summarised in Table 1. The former refers to eight terrain categories corresponding to different physical parameters, while the latter is defined in terms of stem wood area per hectare (basal area). The friction parameters of the terrain categories generally vary with respect to the block size. In our case, the considered rock block scenarios fall within the same range of terrain categories suggested by the software User Manual v1.7 (last access: December 2023, available at: http://ramms.slf.ch/ramms/downloads/RAMMS_ROCK_Manual.pdf). This allowed us to set the same conditions between the different scenarios.

Table 1 Friction parameters for the terrain categories used in the simulations, where \({\mu }_{{\text{min}}}\) is the initial friction encountered at the contact, \({\mu }_{{\text{max}}}\) is the maximum value of friction reached during the sliding, \(\beta\) controls the rate at which friction decreases after the contact, \(k\) controls how quickly the friction increases from \({\mu }_{{\text{min}}}\) to \({\mu }_{{\text{max}}}\), and \({C}_{v}\) is the drag coefficient which describes the hardness of the terrain material
Full size table

Furthermore, the software enables the setting of the release zone as a point, line, or area. We defined a linear release zone for both Cliff A and Cliff B following the structural analysis results. The polylines defined for the two outcrops were composed of 218 (Cliff A) and 105 (Cliff B) release points since Cliff A is wider and characterised by a more complex geometry. For each release point, the number of random orientations was arbitrarily set to 20, with a total of 6460 launched rock blocks per model (4360 from Cliff A, 2100 from Cliff B). Moreover, the initial velocity and rotation velocity were set to zero, aiming at simulating the rock block instabilities under gravity (Yan et al. 2023).

The input parameters regarding the rock blocks, namely volume and shape, were defined by the structural analysis. The shape of the rocks is critical in rockfall dynamics, influencing several parameters of the rock block trajectories, including run-out distance, jump height, and lateral spreading (Leine et al. 2014; Nagendran and Ismail 2019). In RAMMS, the rock block is modelled as a polyhedron with a convex hull. Three predefined rock shapes are available (‘Long’, ‘Equant’, and ‘Flat’), with a set of subcategories depending on the ratio between the dimensions of the rock itself. The shapes used in the simulations are summarised in Table 2 with their associated geometrical and physical parameters. RAMMS trajectory simulations do not take into account the fragmentation processes.

Table 2 Physical and geometrical properties of the block shapes used in the simulated scenarios
Full size table

The outputs of the rockfall simulations in RAMMS are the maps of the trajectories representing physical parameters, including velocity (m s−1), kinetic energy (kJ), jump height (m), number of deposited blocks, and a statistics summary.

The different scenarios were quantitatively compared with each other based on the physical properties displayed in the urban area at the base of the slope. This area was delimited including all the buildings at the base of the slope and following the geomorphological features. Subsequently, only the portions of the rockfall trajectories within the urban area were considered to analyse the average values of velocity, kinetic energy, and jump height. Also, the percentage of blocks deposited in the urban area with respect to the total launched blocks was calculated for each model. In addition, the Rockfall Hazard Vector (RHV) magnitude (Crosta and Agliardi 2003) was calculated by using the number of blocks, jump height, and kinetic energy.

Results

UAV survey

The high-resolution images acquired via drones enabled the elaboration of the orthomosaic maps of the area and the VOMs of the investigated outcrops. The orthomosaic maps allowed the data collection of the rock blocks of past rockfalls at the base of the cliffs. Their volumes were estimated from the frontal and zenith orthomosaic maps (Fig. 2), with a minimum threshold of 2 m3. The results show that about 75% of the blocks have a volume between 2 and 5 m3 while about 16% fall in the 5–20 m3 class. Moreover, some blocks with a volume between 20 and 60 m3 were measured (about 7% of the total) and the maximum volume found was about 107 m3. However, these data should be analysed considering that the fragmentation occurred during the fall and, therefore, even larger volumes were mobilised from the examined outcrops.

Fig. 2
figure 2

Example of rock blocks deposited at the base of the scarps measured from the top-view orthomosaic map, with their frequency distribution (%)

Full size image

Structural analysis

The structural analysis aimed at characterising the potential rockfall source areas on the two investigated outcrops.

Fracture network

On the VOMs of the two analysed outcrops, a total of 128 fractures were digitised with the software OpenPlot (Fig. 3a). The collected data were integrated with the field measurements and sorted by attitude, defining the occurrence of three main fracture sets (Fig. 3b), striking N-S (J1), NW-SE (J2), and NE-SW (J3). All the sets are characterised by steeply dipping fractures, with average dips of 72°, 75°, and 80° for J1, J2, and J3, respectively.

Fig. 3
figure 3

a Digital mapping of the fracture planes on the VOMs of the two analysed outcrops with b Schmidt equal-area stereographic projection (lower hemisphere) of the fractures collected from field and remote surveys

Full size image

Slope geometry

The geometry of the slopes was reconstructed with ‘Facets’ plugin in CloudCompare software. The parameters used for the application of the fast marching (FM) method were defined with a trial-and-error approach and are summarised in Table 3.

Table 3 User-defined cell fusion parameters for the ‘Facets’ model. The ‘retro-projection error for propagation’ was enabled
Full size table

Three main slope faces were individuated defining the geometries of the two cliffs (Fig. 4), striking N-S, NE-SW, and NW-SE and having average dips of 61°, 57°, and 55°, respectively. In both outcrops, the N-S slope face represents the main striking direction, whereas the NE-SW and the NW-SE are defined by several pinnacles, especially in Cliff A (mainly represented by fault surfaces).

Fig. 4
figure 4

Results of the ‘Facets’ analysis in CloudCompare along with the respective stereographic projection. Three main slope faces were defined, striking N-S, NE-SW, and NW-SE

Full size image

Kinematic analysis

The fracture sets identified from the structural analysis of Cliffs A and B are used to perform the kinematic analysis of the potential failure mechanisms on each of the three main slope faces extracted with ‘Facets’.

The failure modes considered were planar sliding, wedge sliding, direct toppling, and flexural toppling. Each failure mechanism was tested by considering the three individuated fracture sets with respect to the three main slope faces. The models are calculated assuming the Green Tuff fm. with an internal friction angle of 28.8° (Alvioli et al. 2022).

The results are graphically shown in stereoplot projections with the critical zones highlighted for each failure mechanism (wedge sliding is shown in Fig. 5, while the failure mechanisms direct toppling, flexural toppling, and planar sliding are available as Online Resource 1) and are quantified as the percentage of critical intersections of the fracture network with respect to the individual slope directions (Fig. 6).

Fig. 5
figure 5

Stereographic projections of the kinematic analysis performed on the three main slope faces for the potential failure mechanisms of wedge sliding

Full size image
Fig. 6
figure 6

Kinematic analysis results quantified as the percentage of critical intersections within the fracture network calculated for each slope face

Full size image

The wedge sliding is the most critical failure mechanism on all the slope faces, with percentages of critical intersections of 23.2%, 20.8%, and 10.9% on the N-S, NE-SW, and NW-SW slope faces, respectively. Comparable values of critical intersections are observed only for the planar sliding (9.4% on the N-S slope face and 7.4% on the NE-SW slope face) and for the flexural toppling (8.7% on the NW-SE slope face).

Rockfall simulations

The rockfall trajectories modelling included different scenarios by combining the rock volumes and shapes previously identified. The former values were established following the analysis of the fallen rock blocks of the study area. As shown in Fig. 2, the volumes span in a 2–107 m3 range. The 5 m3, 20 m3, and 60 m3 scenarios were simulated.

The block shapes were defined from a qualitative investigation of the rock blocks isolated by fractures in Cliffs A and B (Fig. 7). Two main shapes were individuated in the software as more representative, namely ‘equant’ and ‘long’ (Table 2). Additionally, the shape ‘flat’ was included in the simulated scenarios for a complete evaluation of the shape impact on the simulated trajectories.

Fig. 7
figure 7

Example of rock blocks isolated by fractures and qualitatively identified as ‘equant’ and ‘long’ for the set-up of the block shapes in the rock fall simulations

Full size image

The combination of the defined rock volumes and shapes determined nine different scenarios (Table 4), which were simulated with fixed input parameters (Table 2) to ensure equal comparison between the models.

Table 4 Input parameters and setup specifics of the nine rockfall scenarios simulated in RAMMS
Full size table

Comparison between scenarios

The nine simulated scenarios showed qualitative and quantitative differences in the trajectory maps. The latter were analysed with the distribution of kinetic energy (kJ), velocity (m s−1), and jump height (m) developed along the paths (Fig. 8). The analysis of the different trajectory maps enabled us to qualitatively compare the results between the simulated scenarios.

Fig. 8
figure 8

Example of trajectory maps with the values of kinetic energy (kJ), velocity (m s−1), and jump height (m) displayed along the rockfall paths (the scenarios Equant-5, Flat-20, and Long-60 are shown as examples). The kinetic energy, velocity, and jump height of all nine scenarios are available in Online Resource 2

Full size image

In addition, the maps of the deposited blocks were analysed with a focus on the residential area. The percentage of rock blocks (with respect to the 6460 launched in each model) reaching the residential area was calculated and the locations of the deposited blocks are shown on-map (Fig. 9). This result highlights the influence of the morphological features of the slope on the rock trajectories. A small percentage of blocks are deposited in the gullies with high vegetation in the northern and southern sectors, while the main arresting areas are represented by the top and the base of Cliff B. Therefore, these features represent natural barriers for the buildings with respect to potential rockfalls. Nevertheless, a relevant percentage of rock blocks reaches the urban area in the simulated scenarios (Fig. 9).

Fig. 9
figure 9

Maps of the deposited blocks for the nine scenarios simulated showing the final location of the launched rock blocks and the percentage of blocks reaching the urban area (highlighted in light green with the buildings in dark grey). Red: blocks from Cliff A; blue: blocks from Cliff B

Full size image

In detail, the Long-20 scenario (rock blocks shape: ‘long’, volume: 20 m3) displays the highest percentage (25%), while the Flat-60 scenario has the lowest (3%). In general, within the same volume class, the shape ‘long’ produces a higher chance of reaching the residential area, followed by ‘equant’ and ‘flat’. On the other hand, the increase in rock volume enhances the propagation of the blocks only up to 20 m3, while the percentage of blocks reaching the urban area decreases with 60 m3. The difference between the ‘equant’ and ‘long’ scenarios is reduced with increasing volume.

The physical properties shown along the rockfall trajectories were quantified as the average value registered for each scenario within the urban area. These values were compared between the models (Fig. 10) and the influence of volumes and shapes of the rock blocks on the rockfall trajectories was investigated. Additionally, the differences between the blocks falling from Cliff A and B were highlighted (Fig. 10). The following results are observed:

  • the volume of the blocks has a critical positive influence on the kinetic energy (Fig. 10b) but a limited impact on the velocity and jump height (Fig. 10a, c). In particular, from 5 to 20 m3 both velocity and jump height increase, while with further increase in volume (60 m3), the velocity reduces, and the jump height slightly increases;

  • the shape of the blocks strongly influences the trajectory simulations, with the shape ‘long’ displaying the highest values and the shape ‘flat’ the lowest (Fig. 10d, e, f);

  • the rock blocks falling from Cliff A show higher values of velocity, energy, and jump height in the urban area with respect to those falling from Cliff B (Fig. 10).

Fig. 10
figure 10

Quantitative output data (average values) of the rockfall trajectories within the residential area for the nine scenarios simulated. a Velocity (m s−1), b kinetic energy (kJ), and c jump height (m) versus volume (m3), and d velocity (m s−1), e kinetic energy (kJ), and f jump height (m) versus the shape of the rock blocks

Full size image

Finally, the physical parameters obtained from the rockfall simulations enabled the calculation of the RHV as proposed by Crosta and Agliardi (2003). The properties involved in the calculation are kinetic energy, jump height, and number of blocks deposited. In this case, only the shapes ‘equant’ and ‘long’ (as identified from the structural analysis) and the volumes 5 and 20 m3 (as defined by the volume analysis, Fig. 2) were investigated. The obtained results are shown in terms of RHV magnitude divided into three classes (Fig. 11), namely low rockfall hazard (1.732 ≤ RHV ≤ 3), intermediate rockfall hazard (3 ≤ RHV ≤ 4.359), and high rockfall hazard (4.359 ≤ RHV ≤ 5.196).

Fig. 11
figure 11

Trajectory maps displaying the RHV magnitude for the Equant-5, Long-5, Equant-20, and Long-20 scenarios. The urban area is indicated in light grey and the buildings in dark grey

Full size image

Discussion

In this study, we investigated the potential rockfall source areas of two outcrops and simulated the trajectory and run-out of the rock blocks with respect to the nearby residential area. The latter, is one of the most hazardous sectors for rockfall triggering and invasion, as shown by Alvioli et al. (2022), which investigated the rockfall risk on the whole island.

Source areas

The analysis of the rockfall source was conducted with a structural analysis of Cliff A and Cliff B and led to the identification of the main fracture sets characterising the outcrops and the definition of the potential failure mechanisms. The wedge sliding resulted in the most likely failure mechanisms, with 23% and 21% of critical intersections on the N-S and on the NE-SW slope faces, respectively. Additionally, the analysis of the blocks deposited at the base of the cliffs identified rock volumes up to 107 m3, with about 75% of the rock blocks having a volume between 2 and 5 m3. Considering that these rocks underwent fragmentation during impact, it can be assumed that the starting volumes were even larger. However, the rockfall simulations with RAMMS did not consider the fragmentation of the blocks and, for these reasons, three classes of volumes were simulated: 5, 20, and 60 m3.

Rockfall trajectories

The rockfall trajectory simulations were performed by considering different rock shapes and volumes. The latter had a critical impact on the kinetic energy along the trajectory while showing a minor influence on the velocity and the jump height (Fig. 10). The shape ‘long’ showed the best properties in the rockfall trajectories while the shape ‘flat’ has lower values, especially with increasing volumes.

This aspect is well reflected in the percentage of rock blocks reaching the urban area (Fig. 9): the larger volumes from 5 to 20 m3 determine a remarkable increase in the ‘equant’ and ‘long’ scenarios (from 15 to 19% and from 21 to 25%, respectively). On the other hand, a further increase in volume (60 m3) produces a reduction in the percentages.

It derives that larger volumes can be more dangerous up to a certain volume. In fact, the response of the underlying terrain is different with increasing rock volumes and is responsible for the reduction of the velocity in the 60 m3 scenarios. Also, the jump height of the 60 m3 blocks shows a lower increase than expected, due to the lower rebound of rock blocks with such volumes.

The influence of the block shapes is testified by the low percentages observed in the ‘flat’ scenarios (about 3–4%). Although the reduced probability of reaching the urban area, the rock blocks of 60 m3 show the highest values of energy and jump height (Fig. 10).

In general, the simulated rockfall scenarios would impact the residential area with values of kinetic energy in the order of 102 to 104 kJ (Fig. 10). In detail, considering the Equant and Long scenarios, the average kinetic energy in the residential area spans from about 970 kJ (Equant-5) to about 7200 kJ (Long-20) and up to 17600 kJ (Long-60).

Moreover, the RHV magnitude maps (Fig. 11) enabled a comparison between the simulated scenarios encompassing multiple parameters. The percentage of urban area falling into the three classes of RHV was calculated to quantify the level of hazard occurring in each scenario (Fig. 12a). Also, the individual contribution of Cliff A and Cliff B to the RHV magnitude (Fig. 12a) and to the percentage of blocks reaching the urban area (Fig. 12b) were calculated.

Fig. 12
figure 12

a Percentage of urban area with low, medium, and high RHV with respect to the total urban area with the individual contributions of Cliff A (plain) and Cliff B (dotted), and b percentage of rock blocks reaching the urban area for Cliff A and Cliff B for the four selected scenarios

Full size image

All the scenarios display about 25% of the urban area affected by the rockfall trajectories, except for the Equant-5 scenario (about 17%). In the Long-5 and Equant-20 models, about 11% of the urban area displays high RHV, while only 1% in the Long-20 model.

Considering the percentage of urban area showing high or medium RHV, the impact of the rock volume is critical. In fact, the Equant-20 and the Long-20 scenarios have the highest values (about 23% and 20%, respectively), while in Equant-5 and Long-5, only the 9% and 15%, respectively, of the urban area fall into the two categories of higher hazard. Therefore, the Equant-20 scenario can be considered the most hazardous for the residential area, followed by the Long-20 and the Long-5.

The increase in rock volume is critical for the equant scenarios while showing a lower impact with the long shape. The rock blocks with equant shapes are more rounded and maintain their capability to roll, whereas the long shape is more developed in two dimensions and the increase in volume reduces the runout distances despite the high values of energy and jump height.

Moreover, the analysis of the data shown in Figs. 9 and 12 allows us to derive useful information on the individual impact of Cliff A and Cliff B:

  • The residential area can be divided into a southern and a northern sector. The former is mainly affected by the blocks falling from Cliff B, while the latter from Cliff A;

  • in all the scenarios except Equant-5, Cliff A determines a higher RHV magnitude with respect to Cliff B;

  • the percentages of rock blocks reaching the urban area are always higher for Cliff B than for Cliff A.

The Cliff A blocks have longer distances and more natural barriers (Fig. 9) on their way to the urban area, but the kinetic energy, velocity, and jump height of their trajectories are much higher than those developed by the blocks of Cliff B (Fig. 10). For this reason, the fewer blocks coming from Cliff A are more hazardous than those from Cliff B, especially for the northern sector of the urban area. This is in agreement with what was found by Alvioli et al. (2022), which additionally highlighted the impact on the roads and trails. Moreover, the N-S and the NE-SW slope faces resulted in the most likely to fail from the kinematic analysis (Fig. 6). The latter slope faces point towards the northern part of the urban area, which can be considered, therefore, as the most critical zone regarding the risk of rockfalls.

Conclusion

In this study, the potential rockfall scenarios affecting two outcrops of Mt. Epomeo (Ischia Island) were investigated with an integrated approach. The structural analysis was aimed at identifying the potential source areas, and the trajectory simulations were performed to evaluate the rockfall impact with respect to the residential area in different scenarios. From the structural analysis resulted that the most likely failure mechanism is the wedge sliding on the N-S and NE-SW slope faces. On the other hand, the trajectory simulations highlighted that, although some geomorphological barriers are present in the propagation area, the percentage of rock blocks reaching the urban area spans from 15 to 25%. Moreover, the rock blocks reach the residential area with average kinetic energy spanning from 102 to 104 kJ in the 5 m3 and 20 m3 models, respectively. Finally, it was observed that the northern part of the residential area of Frassitelli is mainly affected by the rock blocks falling from Cliff A. The latter develops the highest average velocity, energy, and jump height values.

In conclusion, the integrated approach performed at the local scale enabled the detailed definition of the rockfall hazard affecting the residential area. In detail, such a hazard could be mitigated by applying artificial barriers with rock volume scenarios up to 20 m3, while with higher volumes involved, a timely evacuation would represent the only suitable action. Moreover, considering the seismic activity characterising the study area, future work should be aimed at simulating the occurrence of earthquake-induced rockfalls by including the seismic input in the simulations.