Introduction

The detailed characterization of the thermo-hydro-mechanical-chemical (THMC) properties of rocks and the interactions of the rock-fluid-matrix is crucial for a comprehensive understanding of the behavior of any type of reservoir (e.g., gas or oil). The characterization of rocks properties is complex as they depend on the interaction of large amount of local and regional geological factors, including the stress regime, rock composition, weathering, and alteration effects (Gupta and Seshagiri-Rao 2000; Aydan and Ulusay 2013; Pola et al. 2012, 2016; Siratovich et al. 2016; Navelot et al. 2018; Khalil et al. 2020). One of the most important parameters in reservoir engineering is rock permeability. Simultaneously, this property depends, among others, on the porosity and pore characteristics (whether matrix porosity or fracture porosity) of the rock mass. The interaction between rocks and fluids not only alters the fabric and mineral composition of rocks but also creates and propagates pores and fractures (e.g., Mielke et al. 2015, 2016, 2017; Verati et al. 2016; Heap et al. 2017; Heap 2019). Particularly, hydrothermal alteration and high fractured density zones are characteristics of active geothermal areas (e.g., active calderas) (Chabani et al. 2021; Zosseder et al. 2022). Active calderas have proven to be good targets for geothermal exploitation. Examples include the Campi Flegrei in Italy (Carlino et al. 2016), Rotorua in New Zeland (Scott et al. 2015), and Los Humeros and Acoculco in Mexico (Arzate et al. 2017; Bolós et al. 2022), which are geothermal fields in active caldera zones. Particularly, the Acoculco caldera has been classified as a hot dry reservoir (HDR). The fluid circulation is null or too low and stimulation techniques have been proposed (e.g., hydraulic fracturing or acidification) (López-Hernández et al. 2009; Sánchez-Córdova et al. 2020). Another important factor to highlight in active calderas is the role of the petrophysical parameters (e.g., porosity, permeability, alteration degree) of the overlying volcanic units. The connections between the volcanic layers and the fracture system of the underlying reservoir rocks control the fluid pathways (Tescione et al. 2020). Thus, the characterization of these volcanic units with different alteration degrees and fractured reservoir units (sedimentary or plutonic rocks) is essential to have a better understanding of the rock-fluid-fractures interactions. On the one hand, hydrothermal alteration modifies rock properties through interactions with hydrothermal fluids, leading to changes in the pore system and other characteristics of the rock, such as permeability, mechanical strength, and chemical composition (Meller and Kohl 2014). On the other hand, fracture network gains importance when the matrix porosity and permeability are poor and non-feasible for fluid flow (Ashwell et al. 2015; Heap and Kennedy 2016; Lamur et al. 2017).

The study of rock properties and their interactions with different fluids can be studied in the laboratory by simulating conditions and creating empirical equations. Previous investigations in hydrothermally altered rocks (e.g., Farquharson et al. 2015; Heap et al. 2019) have shown that high permeability values (k ˃ 1×10−16 m2) are often associated with good pore and fracture connectivity. On the contrary, denser rocks such as welded ignimbrites, non-altered volcanic rocks, intrusive rocks, and sedimentary rocks (tight sandstones or limestones) have most of the time, poor porosity, and low matrix-permeability values. In these cases, the permeability relies mostly on the fracture network of the rock mass. The influence of fractures on the permeability of rocks has been previously studied under laboratory conditions by inducing shear or tensile fractures in cylindrical specimens (e.g., Hassanzadegan et al. 2013; Heap et al. 2017; Lamur et al. 2017; Eggertsson et al. 2020). These results have demonstrated that the permeability of fractured rocks depends on various factors, including experimental conditions (e.g., confining pressure, temperature, shear displacements) and fracture characteristics (e.g., rugosity, separation, tortuosity). Permeability tends to increase with fracture thickness and shear displacement. However, increases in confining stress, tortuosity, and rugosity lead to a significant reduction of permeability. One parameter not considered in previous studies is the missing material resulting from the fracturing process. After inducing fractures, some material is removed from the fracture walls. This detached material can be assumed as an increase of the effective porosity by creating new voids within the fracture walls, facilitating the fluid flow. In this work, this missing material is assumed as an increase in the effective porosity of the rock, and it is compared with permeability changes before and after fracturing.

Rock properties constitute the basis for elaborating conceptual and numerical models of geological structures, including a wider range of pressure, temperature, and flow scenarios (Milsch et al. 2016; Kluge et al. 2017; Blöcher et al. 2019). It is important to emphasize that assigning properties to these models is not simple, primarily due to the very complex heterogeneous and isotropic nature of rocks. Some useful tools, such as empirical equations and the creation of international extensive databases derived from many laboratory tests have been constructed (Bär et al. 2020; Weydt et al. 2018, 2021; Weinert et al. 2021). However, the assignment of properties for the construction of any model must be done based on an adequate upscaling and complemented with studies at different scales (Heap and Kennedy 2016).

The primary objective of this study is to analyze the physical, mechanical, and hydric properties of the main lithologies of the Acoculco Caldera Complex (ACC) (Mexico). Special attention is given to the influence of the alteration degree and fractures on the strength and permeability of rocks. Rock properties variation are evaluated in terms of porosity, including both pore matrix (porous system of the non-fractured rock volume) and fractures. The present investigation is part of the GEMex project (Cooperation in Geothermal energy research Europe-Mexico for development of Enhanced Geothermal Systems and Superhot Geothermal Systems). In this context, the resulting data and equations will become part of an extensive database essential for the construction of different conceptual geothermal models. These models, in conjunction with other studies (e.g., geophysical studies) could aid in identifying new zones of geothermal interest.

Geological context and materials

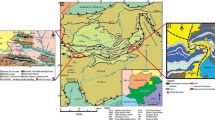
The Acoculco Caldera Complex (ACC) is situated in the eastern part of the Trans-Mexican Volcanic Belt. The volcanic activity of the ACC, including the emission of domes and ignimbrite eruptions covers a period of 2.64 Ma from 2.7 to 0.06 Ma (Sosa-Ceballos et al. 2018; Avellán et al. 2019 and 2020). The central portion of the complex consists of hydrothermally altered rhyodacite ignimbrites, basaltic andesite lava flows, and dacitic to rhyolitic domes (Fig. 1a) (Canet et al. 2010 and 2015). Outcrops of hydrothermal altered andesitic and rhyolitic units can be observed throughout the inner caldera, better exposed all around Acoculco and Pedernales villages (Fig. 1a).

Fig. 1
figure 1

Panoramic view of the most representative outcrops. a Acb10 volcanic outcrop with hydrothermal alteration near Acoculco village. Physical hydrothermal alteration features as the loss of color of rocks are clearly identified. Structural information represents fractures in the inner caldera. b Panoramic view of sedimentary rocks. Stratification of the sequence is represented by a set of fractures K1 and K2 (orientation varies according to the geometry of the folds). Some other sets of fractures oriented almost perpendicular to the stratification of the sequence are related to tensile fractures due to folding (e.g., diagonal, transverse, longitudinal). c Completed folded sedimentary sequence. Different types of folds resulting from the combination of several kinematical mechanisms, such as chevron are recognizable

Full size image

The general description of the outcrops suggests an activity of recrystallized amorphous silica; pervasive bleaching and silicification processes in different degrees are common in all the hydrothermally altered samples. The basement of the Caldera is composed of a series of folded upper Jurassic to Upper Cretaceous limestones belonging to the Sierra Madre Oriental, which are exposed along the eastern part of the complex, extending between Chignahuapan and Zacatlan villages (Fig. 1b). General characteristics of the outcrops in this zone include parallel stratified micritic limestones with lents or nodules of black flint, affected by at least seven sets of fractures, including those associated to the bedding sequence. All limestone sequences exhibit pronounced folding sequences (chevron folds) (Fig. 1c).

A total of twelve rocks with approximate sizes of 30×40×40 cm were collected. These collected blocks include limestone, andesitic lavas, and rhyolitic lavas. Limestone blocks were selected based on their homogeneity, while volcanic blocks were chosen according to observable degrees of hydrothermal alteration. The study materials are described as follows, utilizing hand specimens, petrographic optical microscopy, and X-ray diffraction.

Fresh to slightly altered volcanic samples

This group is represented by Acb2, Ac66, Ac264, and Ac265 samples. They are slightly altered with gray color. It presents a porphyritic texture with plagioclase (from 0.05 to 0.1 mm in size), quartz, amphibole, oxides, chlorite, and epidote in minor proportions. The Ac66 sample presents fractures and pores filled by oxides; its groundmass is made by oriented phenocrysts of albite (Fig. 2a).

Fig. 2
figure 2

a Microscopic view of fractured plagioclase phenocrysts in fresh to slightly altered volcanic samples (Ac66). b Scanning electron microscope view of interconnected pores and fractures in hydrothermal altered samples (Ac31). Filled pores and some recrystallized minerals are also observed. c SEM-EDS analysis in hydrothermal altered volcanic samples (Ac50). d Pyroxene in a plagioclase matrix in sample Ac50, it can be observed the affections of the micro-fractures. e Scanning electron microscope view of sinuous fractures in hydrothermal altered samples (Ac50). Some of them are filled by fine-grained material. f microscopic view of filled and shear displaced fractures in sample Acb3. g Microscopic view of gastropod in sample Acb7. h Scanning electron microscope view of fractures cutting the grains and throat and chamber fractures type in limestones samples (Acb7). Pl=Plagioclase, Px=Pyroxene, mPl= microlite of plagioclase, Ga= Gastropod, Ff= Filled fractures, Fd= displaced fractures, Fs= sinuous fracture, Ca= carbonate grain, TC= throat and chamber fracture type, IP=interconnected pores, and RM= recrystallized minerals

Full size image

Hydrothermal altered volcanic samples

This group is represented by Ac31, Ac50, and Acb10 samples. They are a very altered white sample and slightly gray and yellow stained. Samples are very fractured with an aphanitic recrystallized amorphous silica texture (vuggy silica), and interconnected pores and fractures (Fig. 2b). The groundmass is almost all recrystallized, composed predominantly of glass and amorphous silica; phenocryst shapes are hardly recognizable. According to X-ray powder diffraction, the major constituents of samples are quartz (from ~60 to ~65 %) and cristobalite (from ~30 to ~35 %), and some samples, including Ac50 and Acb10, could be constituted also by sanidine and albite in minor proportion (<5 %). SEM-EDS analysis also identifies the content of iron, sulfur, barium, and zircon (<2 %) (Fig. 2c). Ac50 and Acb10 samples present a not clear porphyritic texture, composed predominantly of phenocrysts of feldspar, pyroxene, quartz, epidote, oxides, and pores filled by oxides (Fig. 2d), with sinuous fractures (from 2 to 50 μm in aperture) filled by fine-grained material (Fig. 2e). Despite the high degree of alteration in sample Acb10 some minerals such as plagioclase (from 0.8 to 1 mm in size), biotite (from 0.05 to 0.1 mm in size), amphibole, and quartz are recognizable.

Limestones samples

This group is represented by AcPc, Acb3, Acp2, and Acb7 samples. They are gray with observable veins and fractures, sub-perpendicular to the lamination (60 to 70° with respect to the lamination axis), some of which are filled with carbonate and some others converge with each other. Thin sections description showed, in all the samples, a matrix-supported texture, the presence of ellipsoidal carbonate grains (from 5 to 100 μm in size), stylolites displacing refilled fractures, and bioclast (gastropods) in minor proportion (from 1 to ~10% for Acb7 sample) (Fig. 2f, g). Particularly, sample Acb7 exhibits a dominant characteristic in terms of secondary structure: it shows fractures cutting the grains and some opaque minerals with hexagonal and cubic shapes (Fig. 2h) and throat and chamber fractures type.

Methods

A total of 220 cylindrical specimens with different diameters (26, 32, and 53 mm ∅) and heights (2.0 to 2.2 times ∅; ASTM D4543-19 2019) were drilled from the collected 12 blocks, considering the perpendicular direction of the horizontal plane of the outcrop. Comprehensive physical and mechanical characterizations, including density, percentage of porosity, and strength, were conducted on all cylindrical specimens.

Matrix permeability measurements were carried out on 150 specimens with a diameter of 26 mm. Subsequently, all these specimens were fractured in a point load device. To create a fracture along the vertical axis, the point load conical steel platens were placed at the top and bottom of the rock, and the specimens were jacketed in a neoprene membrane to prevent material loss due to fragmentation. After this process, only specimens with a single vertical fracture were selected for measuring fracture permeability.

The basic physical characteristics of each specimen were determined following various international standards. Grain density (ρg) was determined using a Helium gas pycnometer (model Ultrapyc 1200e) on powder samples (ASTM D5550-14 2014), while the bulk density (ρb) was determined by direct measuring of the dimensions and the mass of each specimen (ASTM D7263-21 2021). Effective porosity (ηe) was measured by two different methods: 1) gas-pycnometry (UNE-EN 1936- 2007) and 2) mercury intrusion technique. The gas pycnometry technique covers a pore size range of 0.05–10,000 μm but no information about the pore size distribution is obtained. On the other hand, the mercury intrusion method determines not only the effective porosity but also the throat pore size diameter and their distribution in a size range of 0.001–100 μm.

Matrix and fracture permeability (KL) were calculated in a GasPerm AP-123-002-0 gas permeameter. The device operates based on the Darcy equation, assuming ideal horizontal laminar flow of gas under steady-state isothermal conditions . When gas is used as fluid flow, it flows toward the downstream end of a core specimen, its pressure decreases, the gas expands, and its velocity will increase. This effect is known as the Klinkenberg effect (Fink et al. 2017) and it was calculated with Eqs. 1 to 3:

$${K}_g=\frac{\mu {P}_b{Q}_bL}{A\Delta P{P}_{mean}}$$
(1)
$${K}_g={K}_L\ \left(\frac{m}{P_{mean}}\right)$$
(2)
$$m=0.614{K}_g^{0.647}$$
(3)

where Kg is the permeability to gas (Da), μ is the viscosity of the gas (Cp), Pb is the atmospheric pressure (atm), L is the length of the specimen (cm), A is the cross-sectional area of the cylinder (cm2), Qb is the atmospheric gas flow rate at Pb (cm/s), ΔP is the differential pressure (Atm), Pmean is the mean core gas pressure (Atm), and m is the Klinkenberg correction factor. The permeameter operates at a maximum pore pressure of 150 psi (~1 MPa) and a confining pressure up to 400 psi (~2.8 MPa). It can operate in two different modes: (1) forward, where the user can control the inlet pressure while the outlet pressure is open to the atmosphere and (2) backwards, where the user can control inlet as well as outlet pressure using a metering valve. All the tests were implemented in forward-mode with 350 psi (~2.4 MPa) of confining pressure. To take into account the Klinkenberg effect, a graph was constructed under the next known characteristics: gas permeability (Y-axis) was obtained at five different differential pressures (ΔP) and plotted against reciprocal mean pressure (1/Pm) on the X-axis, the KL is obtained by projecting a trend line until the reciprocal mean pressure is zero (see ASTM D6539-13 2013 for detail). Moreover, all the permeability experiments were checked for the Forchheimer correction (Farquharson et al. 2015; Kushnir et al. 2018; Heap et al. 2018, 2019). To ensure a laminar regime and account for diffusion and slippage effects during the permeability measurements, both fractured and non-fractured specimens were assessed for the Knudsen number (Kn). The Knudsen number is utilized to classify the flow regime in porous media and is defined as the ratio between the molecular mean free path of the fluid (λ) and the pore radius (r) of the sample, which is obtained from the Mercury intrusion test:

$${K}_n=\frac{\lambda }{r}$$
(4)

Knudsen defined four ranges for the equation above. (1) The viscous flow regime (Kn < 0.01), where the conventional fluid dynamic equations are valid, and no permeability correction is needed. (2) The slip flow regime (0.01 < Kn < 0.1), where the conventional fluid dynamic equations remain valid but a correction for the slipping phenomena, such as the Klinkenberg or Knudsen correction, is needed. (3) The transition flow regime (0.1 < Kn < 10), where slip and diffusion flows are present. Although regular fluid dynamics equations may be used, it is recommended to use the Knudsen diffusion equations for permeability calculations, especially for values near to 10. 94) The Knudsen flow regime (Kn > 10), where the classic dynamic fluid equations fail, and diffusion-based formulations must be applied instead (Ziarani and Aguilera 2012). For this work, only Klinkenberg and Forchheimer (e.g., in fractured specimens) correction were used.

To compare the differences between permeability values before and after fracturing, the same pressure conditions were applied in fractured specimens for the permeability measurement. Shear displacement was assumed as zero since the end caps in the gas permeameter are flat and parallel. After fracturing each specimen, the mass was registered to quantify the loss of material during the test. This loosed material was considered as an increase in effective porosity using equation (5):

$${\eta}_{ef}\left(\%\right)=\left[\frac{\left({m}_0-{m}_f\right)\ast 100}{m_0}\right]+{\eta}_e$$
(5)

where ηef is the effective porosity after fracturing (%), m0 is the initial mass before fracturing (g), and mf is the mass after fracturing (g). Volcanic samples with the highest alteration degree (Ac50 and Ac31) were not used for the point load test since the conical steel plates of the device penetrate through the surface of the specimen and inducing a fracture was not possible. A multiple linear regression analysis was conducted to assess the simultaneous influence of multiple parameters on the fracture permeability of the tested specimens. Fracture permeability was used as the response variable. Bulk and grain density, total porosity, effective porosity, and effective porosity after fracturing (5) were selected as independent variables. The resulting equation was evaluated in terms of the adjusted coefficient of determination or R2 and the probability value (p-value). R2 values range from 0 to 1.0 values. An R2 of 0.6 refers that in the analyzed equation, 60% of the variation of the dependent variable (in our case fracture permeability) can be explained by the independent variables (e.g., density, effective porosity, total porosity). Since the analysis involves more than one independent variable, the R2 cannot be employed in isolation, and the interpretation of the results should be complemented with another statistical parameter. The p-value explains the significance of the equation in terms of the probability of occurrence of an extreme event. The lower the p-value, the more unlikely the possibility of erroneous scenarios. P-values ≤ 0.0001 represent a model with low uncertainty and good significance. In turn, p-values between 0.0001 and 0.5 indicate a model with intermediate uncertainty and significance. P-values ˃ 0.5 represent the worst case with high uncertainty and low or null significance models. Finally, rock strength is obtained by uniaxial compressive tests on 70 cylindrical specimens with diameters of 32 and 53 mm following standard procedures (ASTM D7012-10 2010), on a 250-kN GDS VIS servo-controlled hydraulic testing frame at a constant displacement rate of 0.05 mm/min.

Results and discussions

Porosity and permeability in volcanic and sedimentary rocks

The mean measured values of porosity (effective and total) and permeability of volcanic and sedimentary rocks are presented in Table 1. Limestone showed homogeneous values for the petrophysical parameters. Total porosity values range from 8.37 ± 0.29 to 11.76 ± 0.12 %. Effective porosity values (determined through Helium pycnometry and Mercury intrusion techniques) range from 0.76 ± 0.10 to 1.37 ± 0.62 % and 0.18 ± 0.07 to 0.44 ± ˂0.01%, respectively. In contrast, volcanic samples showed significant heterogeneity. For example, the total porosity of the unit Ac50 (high alteration grade) was 50.79 ± 3.50%, and effective porosity of 49.21 ± 3.54% using Helium pycnometry. On the other hand, Acb2 (fresh rock) has a total porosity of 6.35 ± 0.82% and effective porosity of 1.97 ± 1.15%. Figure 3 a displays the throat pore size diameter distribution determined through Hg-porosimetry of each rock specimen. In general, limestone specimens have a homogenous pore throat ranging from 15 to 90 μm (f1), and only one exception in specimen Acb7-01 which presents two distinct populations, ranging from ~0.01 to 2 (f1) and from ~15 to 90 μm (f2). On the other hand, hydrothermal altered volcanic rocks show two distinct populations, ranging from ~0.010 to 2 (f1) and from ~11 to 80 μm (f2) (Fig. 3a). The interpretation of results from Mercury intrusion in volcanic rocks, particularly in altered units must consider an extra aspect. The measurement rate of this technique is limited to pores between 0.001 and 100 μm diameter. Therefore, some pores in the altered samples (> 10 mm) did not account for the measurements. This phenomenon explains the different effective porosity values obtained from Mercury intrusion and Helium pycnometry (range of measurements from 0.05 to 10,000 μm) for the same rock specimen (Acb10, Ac31, Ac50) (Table 1). The above situation also should be considered for the calculation of the flow regime (Kn). The calculated Kn for volcanic altered samples was > 10. According to Ziarani and Aguilera (2012), corrections due to diffusion and slippage should be applied to the permeability values. However, the Mercury intrusion results do not show all the spectra of pore sizes, and only corrections for slippage effects (Klinkenber and Forchheimer correction) were applied to permeability values.

Table 1 Summary of properties for limestones and volcanic rocks
Full size table
Fig. 3
figure 3

Percentage of incremental intruded volume as a function of throat pore size diameter of (a) hydrothermal altered volcanic and (b) limestones. Note that the pore size distribution of two specimens of each rock sample are included. Pore families are identified by a thick line: orange for family 1 (f1) and blue for family 2 (f2)

Full size image

Permeability values measured on limestone specimens are generally low, with no significant variations observed. Permeability rated from ≤ 9.87×10−19 m2 (the lower acquisition limit of the device) to 3.5×10−18 m2 (Table 1). These values are perfectly in accordance with the low effective porosity values (ηe ˂ 1.37%) and it is similar to the values from the same area (Weydt et al. 2018, 2021). As well as porosity values, permeability values on volcanic specimens show high variability, dependent on the alteration degree. It rates from a maximum value of 2.6×10−12 m2 to a minimum value of 1.3×10−18 m2, from hydrothermally altered (Ac31) to fresh to slightly altered samples (Ac66), respectively. To put our data into a global context, the permeability values of volcanic rocks were compared with values of similar rocks published previously (Fig. 4a) (Farquharson et al. 2015; Heap and Kennedy 2016; Lamur et al. 2017; Colombier et al. 2017; Weydt et al. 2018, 2021; Mordensky et al. 2018). Figure 4a illustrates the relationship between effective porosity and permeability. As the trend line shows, there is a significant exponential relationship with an R2=0.65 of our data, like those established by different authors of similar rocks (e.g., Lamur et al. 2017; Colombier et al. 2017; Heap et al. 2018).

Fig. 4
figure 4

a Liquid permeability (KL) as a function of effective porosity values obtained by mercury intrusion (ηeHe). b Uniaxial Compressive Strength as a function of ηT for volcanic rock units. Limestones rock units are not included because values do not present significant variation, not even a clear tendency or pattern. Values from bibliography are also included (Farquharson et al. 2015; Heap and Kennedy 2016; Lamur et al. 2017; Colombier et al. 2017; Weydt et al. 2018, 2021; Mordensky et al. 2018)

Full size image

The permeability values of the analyzed hydrothermally altered rhyolite specimens (Ac31 and Acb10) are in good accordance with the values of effusive rhyolites reported by Colombier et al. (2017). In contrast,the hydrothermally altered andesite samples, despite having similar effective porosity values, exhibit lower permeability, especially in the most altered unit (Ac50), which does not align with those reported by the same author. As expected, the grade of hydrothermal alteration in volcanic samples influences the relationship between properties. Particularly, the distribution of data included in Fig. 4a indicates that the porosity and permeability values increase with the increase in the degree of alteration. On the contrary, some data does not fit in this general trend, showing higher permeability values. For example, Ac50 and Ac31 samples exhibit similar values of effective porosity, but Ac31 has higher permeability. This difference in permeability is attributed to the intrinsic characteristics of the pore system, such as pore size, geometry, and spatial distribution.

At the reservoir scale, our results suggest that the poor porosity and low matrix permeability values of the limestone unit function as a barrier for fluid circulation from top to bottom. On the contrary, porosity and permeability values obtained for volcanic units suggest that these units allow fluid circulation, evidenced by the observed alterations of the different collected units. The origin of the fluids affecting the volcanic units is not included in this work (for detailed information consult Pandarinath et al. 2020). However, based on the porosity characteristics of limestone and volcanic units, it can be assumed that hydrothermal fluids are not affecting the limestone unit. Even when the thickness of the volcanic units can reach up to 800 m (Avellán et al. 2019, 2020; Guerrero-Martínez et al. 2020; Viggiano-Guerra et al. 2011), the temperature gradient is not sufficient to consider them as a potential target for exploitation (100°C). On the contrary, at depths of 2000 m, where the limestone unit is located, the temperature rises to 300 °C (measured temperature in wells EAC-1 and EAC-2, Guerrero-Martínez et al. 2020). This temperature is more than sufficient for geothermal exploitation; however, fluid circulation is poor or null, as shown in our results. Thus, as well described in previous investigations (Deb et al. 2020; López-Hernández et al. 2009), the ACC is a good candidate for using stimulation techniques such as hydraulic fracturing.

Mechanical behavior of studied rocks

Table 1 displays the UCS values for both volcanic and limestone specimens. Figure 5a and b show the stress-strain relationship of limestones and hydrothermally altered volcanic samples, respectively. UCS values of limestones range from 88.32 to 150.96 MPa, while for hydrothermal altered volcanic samples range from 3.12 to 31.86 MPa (Fig. 5b). The influence of the intensity of hydrothermal alteration on the strength values is evident if we compare them with the values of fresh to slightly altered samples, where there are values greater than 150 MPa. In addition, as shown in Fig. 4 b, the strength values decrease by an increment of both the percentage of total porosity and the pore size due to the hydrothermal alteration processes. Particularly, the strength reduction related to porosity is due to both (García-del-Cura et al. 2011; Baud et al. 2014): (1) the distribution and pore geometry cause a reduction of the load sample section; and (2) the pores act as stress concentration points, being the strength lower as the pore diameter increase (Heap and Kennedy 2016; Davis et al. 2017; Avar and Hudyma 2022), this is evident in the Ac31 sample, where pores of centimetric measurements and vuggy texture were recognized. On the other hand, the strength values variability in limestones is due to the presence of discontinuities as stylolites in every single specimen, as well as their characteristics, including thickness, filling, previous displacement, orientation with respect to the load axis, and in the case that the specimen contains two or more discontinuities it will also depend on their geometrical arrangement, persistence, and their nature of termination, including horizontally and vertically intersecting fracture. For example, the content of parallel and subparallel discontinuities in each group, is responsible for the reduction of the maximum strength, for sample: AcP2 the strength varies from 182 to 78 MPa, which represents a decrease of more than 50% and it is the same scenario for more homogeneous specimens, including samples Acb7 and Acb3 (Fig. 5a, c). On the contrary, several specimens from the AcPc rock sample show the lowest value of strength basically because of the presence of sub-perpendicular fractures to the load axis (Fig. 5a, c). Particularly, the AcPc-04 specimen shows the lowest strength value, because of the presence of at least four types of discontinuities, including intact bedding planes, incipient, stylolites and refilled (see Fig. 5a, c). Limestones, fresh to slightly altered and altered volcanics show different stress-strain patterns as well as different failure modes (Fig. 5a, b, c). In general terms, the failure mode of low porosity limestones and fresh to slightly altered volcanics is brittle, while hydrothermally altered samples tend to be more ductile due to an increase in porosity. As graphically described in Fig. 5 a and b, sudden stress decreases in the stress-strain curves could be associated with small displacement into the plane of discontinuities and to the coalescence of macropores, for limestones and altered volcanic samples, respectively. Particularly, the hydrothermally altered volcanic samples, including Ac31 and Ac66, after the initial failure, do not completely break apart (Fig. 5b).

Fig. 5
figure 5

Stress–strain relationship for each cylindrical specimen for (a) limestones and (b) hydrothermal altered volcanic samples. c Pictures of representative specimens of each group. The curves of each specimen are identified with dash lines. Specific feature of each cylindrical rock specimen is marked. The scale of the compressive stress is not the same in a and b: the top in b is represented by a black dash line. Note: stress-strain relationship of fresh to slightly altered volcanic samples is not included in Fig. 3b because of the large differences in stress magnitude with altered samples

Full size image

Fracture influence on water permeability of rocks

A total of 60 specimens (26-mm diameter) were fractured by a point load test and tested for fracture permeability (Kf). The effective porosity after fracturing (ηef) was calculated using Eq. (5). Table 2 shows these two values and the increment of effective porosity after fracture induction (∆ηe=ηef - ηe). In general, all the tested specimens showed an increase in the effective porosity due to the fracture. A maximum increase of 2.24% and a minimum of 0.19% were calculated for volcanic samples. For limestones, a maximum increase of 1.85% and a minimum of 0.02% were registered. For all the specimens, fracture permeability showed higher values than the initial matrix permeability. For volcanic specimens, a maximum increase value of 1.61×10−13 m2 and a minimum of 4.14×10−15 m2 were measured. For limestone, a maximum increase value of 2.98×10−14 m2 and a minimum of 1.61x10-16 m2 were measured (Table 2). Figure 6 shows the exponential relationship between the increment of effective porosity after fracturing (Δηe) and fracture permeability (KL) for volcanic (Fig. 6a) and limestone (Fig. 6b) rocks. Previous investigations on fracture permeability using a similar methodology (e.g., Lamur et al. 2017; Kushnir et al. 2018) found the same tendency of increase. The low resulting R2 in the equations can be explained by the generated asperities during the fracturing. The higher increases in permeability values in volcanic samples are linked not only to the grain size as established by Lamur et al. (2017) but also to the pore size. The higher the pore size the higher the fracture permeability.

Table 2 Summary of the effective porosity and permeability values of the induced fracture specimens
Full size table
Fig. 6
figure 6

The relationships between fracture permeability (Kf) and increased porosity after the fracture (Δηe) for (a) volcanic and (b) limestones samples. Linear trend and equation are included

Full size image

To measure the relative effect of the measured petrophysical parameters in the fracture permeability, a multiple linear regression analysis was implemented. The model that better represents the phenomena includes the total porosity (ηT), effective porosity (ηe), and effective porosity after fracture (ηef) as independent variables. The dependent variable (fracture permeability) is converted by the Log10 function to obtain a normal distribution. The resulting model is represented by Eq. (6). The model has a corrected R2 factor of 0.60 and a p-value of 3.3×10−4. In other words, 60% of the variations of the model are very well explained by the independent variables (p-value ≤ 0.001). The model is statistically significant.

$${K}_{Lf}\ \left({m}^2\right)=0.6242{\eta}_{ef}-0.1610{\eta}_T-1.2904{\eta}_e-14.92$$
(6)

The model can be used to predict the fracture permeability in similar rocks with mechanically induced fractures. The use of Eq. (5) to calculate the increase of effective porosity after fracturing is an easy alternative to quantify the fracture permeability. During the fracture induction process, small rock fragments were removed from the ridges of the specimen. These fragments, which do not belong to the fracture, make no contribution to the fracture permeability. Excluding this material from Eq. (5) can enhance the model accuracy.

Tiab and Donaldson (2016) highlighted the importance of grain size in the relationships between porosity and permeability, as observed in the distribution of the measured values (Fig. 4a). Specimens with a visibly finer and homogeneous grain size (limestones and fresh volcanic units) tend to be grouped in one zone of the graph. On the other hand, altered volcanic samples with a clearly coarser grain size and a non-homogeneous distribution tend to spread in a wider area. This tendency is not exclusively related to grain size, as defined by the previous authors. It can be observed in the pore size distribution results (Fig. 3a, b) that specimens with homogeneous pore systems (limestone units and the Ac66 unit) show fewer variations during permeability measurements than specimens with a wider pore size distribution (volcanic altered samples). This tendency was observed not only during matrix permeability measurements but also in fracture permeability.

As mentioned, one of the limitations of using mercury intrusion is the coverage range of the method. Other investigations in the characterization of grain size and pore systems have included micro-CT scans (Fusi and Martinez-Martinez 2013; Reedy 2022) and fracture surface scans (Blöcher et al. 2019; Chuyen et al. 2023). One of the main limitations of micro-CT scans is the size of the samples. To obtain high-resolution images, the size of the plugs is limited to a few centimeters and inducing fractures can be a challenging task. Fracture scanning includes important features of the fracture walls (rugosity, tortuosity). Nevertheless, the analysis requires more sophisticated data manipulation and interpretation.

Since the proposed methodology includes a basic petrophysical characterization of rocks, a wide range of experiments can be conducted in the area to achieve a better characterization of all the rock units. The experiments used for this work can be applied to other zones; however, it is essential to consider the singularities of each zone and design the experiments accordingly. The presented results can serve as a first approximation to predict the evolution of permeability and can be included in extensive databases to feed numerical models in the area.

Fracture influence on gas permeability of rocks

The different properties, including microstructure (e.g., effective porosity, pore type, and pore throats), together with textural properties (e.g., particle size, shape, spatial orientation), and grain-size parameters, greatly control certain mechanisms of fluid transport through the rock matrix and the fracture network (e.g., diffusion, dispersion). Diffusion is referred to as random movements of the molecules and is not controlled by fluid flow. It is barely related to flow over long distances or with fluid-flow velocities. In porous media, three distinct diffusion mechanisms exist, including Knudsen diffusion, which refers to the collision between gas molecules and pore walls (Pan et al. 2010). Besides, dispersion mechanisms result from variations in fluid flow velocity in the rock system, caused mainly by variations in trace lengths, geometry (size, aperture, aspect ratio), orientation, and roughness of boundaries of the interconnected pores and fractures (Zhao et al. 2010).

Observations indicate that the factors influencing diffusion and dispersion mechanisms during permeability measurements resemble those governing gas slippage phenomena in laboratory gas permeability tests. Thus, the intrinsic characteristics of each rock type and the specific attributes of each specimen play a crucial role in determining permeability values. Figure 7 illustrates the gas permeability obtained for each specimen, taking into account the reciprocal mean pressures. For graph interpretation, the following points must be considered:

  1. 1)

    Specimens with the five reciprocal mean pressure points closely positioned and distributed to the right of the graph: it means that the pore system of the specimen is efficient for permeability (an ideal horizontal laminar flow of gas under steady-state isothermal conditions is fulfilled).

  2. 2)

    Specimens with measurement points spaced apart: contain macro pores (cross-linked, vuggy; see pictures of the specimens included in Figs. 5 and 7) and result in wide permeability variation. Completely altered volcanic samples, including Ac31 and Ac50, typically present this pattern.

Fig. 7
figure 7

Gas permeability (Kg) versus reciprocal mean pressure (1/Pmean [Abs Atm-1]). Rectangles indicate the range of permeability of samples, while the solid red lines indicate the permeability classification according to those discussed in bibliography (e.g., Schön 2015)

Full size image

  • According to permeability patterns shown in Fig. 7, and following the permeability classification proposed by Schön (2015), studied rocks are classified as:

  • Rock with poor permeability: fresh and intact specimens of both volcanic and limestones. According to Table 1 and Fig. 3b, their percentage of effective porosity is less than 1.5%, and the average throat pore size diameter obtained by the mercury porosimeter in a range of 0.001 to 100 μm is 35 μm.

  • Rocks with poor to fair permeability: slightly altered specimens. Values of effective porosity are about 50%. Part of it (<10%) is concentrated in two different groups ranging from 0.010 to 2 and from 60 to 80 μm in minor proportions, respectively (Table 1 and Fig. 3b).

  • Rocks with fair to moderate permeability: induced fracture specimens of both volcanic and limestones, where the values of permeability increased by at least 0.5%. This increase is observed in Fig. 7, particularly the values of both permeability and reciprocal mean pressure are positioned to the right of the graph.

  • Rocks with good to very good permeability: completely altered volcanic specimens, particularly Ac31. According to Table 1, their percentage of effective porosity is about 50%, part of it concentrated on a centimeter scale.

Conclusions

The main objective of the study was to analyze the physical, mechanical, and hydric properties, of both volcanics, including those altered, and limestones from the Acoculco Caldera Complex, paying special attention to the influence of the degree of hydrothermal alteration and fractures on strength and permeability:

Limestones and fresh to slightly altered volcanic samples show similar mechanical and hydraulic behavior, being the volcanics slightly weaker and more permeable than limestone ones. Differences between both lithotypes are mainly related to the porous system of each one. The total and effective porosity values of limestone are homogeneous and the variations in both gas permeability and mechanical strength rely on the fractures and microfractures in each specimen and their characteristics as orientation with respect to the load axis, thickness, and fracture fills.

The variations and standard deviations in the permeability values of volcanic rocks suggest that not only the effective porosity values play a key role but also the architecture of the connected passages of pores (the pore size and geometry have a dominant influence) and the grain size. Moreover, the increase in macro porosity of each specimen associated with cross-linked and vuggy pore types, results in a wide variation of permeability values. On the contrary, in limestone specimens, in which there is almost no connectivity between pores, and all of them are in the same range of pore size, the permeability value relies completely on the presence of fracture whether natural or induced. In addition, values of permeability of a fractured specimen are long related to other physical characteristics, such as the total porosity and the increase in the effective porosity after the fracture: the resulting equation from the multiple linear regression has good representability of this phenomena (R2 = 0.6).

The alteration degree of the volcanic samples is key in the mechanical and hydric behavior of rocks. Alteration on volcanic samples causes an increment of both total and effective porosity. Consequently, altered volcanic samples show the weakest strength as well as a marked ductile behavior in the mechanical failure mode. Moreover, the higher porosity and the more connected porous system generate a significant increase in the permeability, reaching up kg values from 8·10−17 m2 (fresh samples) to 2·10−14 m2 (slightly altered specimens) and 1·10−11 m2 (completely hydrothermally altered).

Finally, the experiments used for this work can be applied to other zones; however, it is essential to consider the singularities of each zone and design the experiments accordingly. The presented results can serve as a first approximation to predict the evolution of permeability and can be included in extensive databases to feed numerical models in the area.