Introduction

Lower structure of a construction involves the condition of compacted soil. Compaction is the process whereby soil and other construction materials are mechanically compressed through a reduction in the air voids (Williams 1949; Holtz et al. 2010; Razouki et al. 2012). Although impact compaction using Proctor tests is commonly used to assess soil and granular unbound materials compaction, many of DOTs are interested in implementing deformation and strength-based specifications for compaction control of unbound materials. This action can help in assessing the bearing capacity of the selected material simply and quickly using the recent developed techniques instead of the conventional techniques which have been considered as time-consuming methods.

Note that compaction control based on only an index of strength/stiffness of compacted soil has such a drawback that, for a fixed value of dry density (ρd), the index may increase significantly as the degree of saturation, Sr, of compacted soil becomes lower than the optimum degree of saturation (Sr) defined as Sr when (ρd) max is obtained for a given compaction energy level (Tatsuoka and Correia 2018).

To address this problem and to speed up the construction process and reduce costly construction oversight, the Swedish transport administration has supported many projects under two decades to verify the adequacy of using the light-weight deflectometer (LWD) in compaction control of local Swedish unbound roads materials (Enkell et al. 1999; Kuttah 2020a, 2020b, Kuttah 2021 and Kuttah 2022). This technology has been used internationally as a quality control/quality assurance (QC/QA) device for earthwork construction and in many pavements condition assessment for maintenance and rehabilitation (Nazzal 2003; Adam and Kopf 2004; Fleming et al 2007; Tompai 2008; Siekmeier et al. 2009; Senseney and Mooney 2010; Volovski et al 2018; Elhakim et al 2014; Umashankar et al 2016; Schwartz et al 2017; Kumar et al 2017; Singh et al 2018; Akey et al 2022). Nevertheless, there are various types of commercially available LWD designs that yield different deformation and elastic modulus values (Thom and Fleming 2002; Hildebrand 2003 and Schwartz and Afsharikia 2018).

Vennapusa and White (2009) studied the factors influencing the measured moduli with several different LWD manufacturers, including Zorn and Dynatest. They found that major factors that affect surface modulus included the size of the loading plate, plate contact stress and rigidity, and the type and location of deflection transducer. They further noticed that the LWDs that use accelerometers to measure the deflection of the plate measured larger deflections than devices making use of geophones to measure ground deflection.

This proves problematic because transportation agencies are beginning to prescribe target deformations and/or elastic modulus values measured by LWD during earthwork construction.

According to Nazarian et al. (2015) target modulus should be set in conjunction with establishing the design modulus considering the moisture content at the time of compaction and moisture content and density at the time of testing.

Research efforts have been undertaken to develop experimental correlations between LWD measurements and other performance characteristics of the pavement structures; however, a detailed evaluation of various LWD devices and their effect on the QC process is still needed. (Tirado et al 2015).

In Sweden, the move toward specifying magnitudes of deformation and/or modulus suggests a need for standardization and investigation of the effect of LWD sensing and testing configurations on the differences in measured parameters for Swedish local materials used in the construction of roads. Such an investigation is important for the potential use of LWD in the quality control during road constructions in Sweden.

Stamp and Mooney (2013) have investigated the influences of the deflection sensor type (accelerometer versus geophone), sensing configuration (plate response versus ground response), plate rigidity, and nature (shape) of the applied load pulse on the measured deflection. However, a systematic investigation of the interaction between the effect of sensing configuration and other influence factors such as testing moisture content, load repeatability, and load magnitude (not the load pulse shape) on the measured deformation has not been studied yet.

Also, LWDs built to ASTM E2583-07 (2020) and ASTM E2835-21 (2021) specifications will always produce different results (because they are based on different LWD’s sensing configurations, ground vs. plate deformations), and the relationship between these results will be difficult to predict according to Stamp and Mooney (2013). Actually, such relationships have not been established yet, and such an investigation is important for the potential standardization of the LWD. Therefore, a comprehensive investigation has been undertaken in the current study to contribute to solving this challenge. The ground deformations could be predicted from the measured plate deformations considering the influence of different testing factors, namely, the moisture content, the applied load magnitude, and the number of the applied load pulses for two types of tested materials. The proposed relationship between the plate deformations and ground deformations will help in overcoming the standardization problem of various LWD devices and their effect on the QC process.

To reach the goal of the study, many in situ LWD and in situ moisture contents tests in addition to various laboratory tests have been carried out on two selected construction materials, namely, sandy subgrade soil and local unbound granular material usually used in Sweden as base course. A new multifunctional LWD has been developed solely to fulfil the requirement of the current study. Fruitful results and correlations between sensing configuration of LWD and testing conditions have been obtained as discussed in detail in the following paragraphs.

The used LWD working features

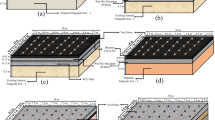
The light-weight deflectometer (LWD) is a device that measures the vertical deformation caused by a falling mass impacting a plate resting on the ground (Fig. 1).

Fig. 1
figure 1

Configuration of the LWD developed for the current study

Full size image

The measured peak deformation may be employed either directly as a measure of a soil’s stiffness or degree of compaction or together with the peak force in the calculation of an estimated dynamic modulus Evd of the tested material. The estimation of Evd is based on the well-known Boussinesq solution relating the static deformation of an elastic half-space subjected to an axisymmetric surface loading as given by Eq. 1. The Evd is calculated using the elastic half-space theory. The LWD theory and the measured modulus have been discussed in several studies (Fleming et al 2002; White et al 2007 and Mooney and Miller 2009) and are not included in this paper. This equation assumes the test media to be a linearly elastic, isotropic, homogeneous semi-infinite continuum. Two of the parameters required for determining the modulus, the shape factor for the distribution of the contact stress between the plate and the soil (A) and Poisson’s ratio (ν), are assumed.

$${E}_{vd}=\frac{2k{\left(1-v\right)}^{2}}{A{r}_{o}}$$
(1)

where

k :

soil stiffness = load (peak)/deformation (peak)

r o :

the plate radius

A :

stress distribution factor

Ν :

Poisson’s ratio

Note that

A:

3 π/4 = 2.35 for parabolic stress distribution (Granular material)

A:

4 for inverse-parabolic stress distribution (Cohesive soil)

A variety of design configurations were considered when manufacturing the new LWD to enable a thorough investigation of the influences of the sensing configuration (plate response versus ground response) and magnitude of the applied load on the measured deformation.

The used LWD has been supplied with a two-buffer configuration to increase the dampening of the impact (dynamic) load and to limit the movement of the LWD during testing. The drop height can be easily and quickly adjusted by a movable release handle and hereby changing the maximum impact force. The peak value of the impact force is registered based on the actual measurements from a load cell. The vertical surface deformation is measured by using a geophone in direct contact with the ground through three holes in the plate. In addition, three geophones are directly mounted on the plate to measure the deformations, symmetrically around the hole (see Fig. 1). All the used geophones are of the same type and properties. A 300 mm diameter load plate has been used in this study. The mass of the load plate is 10 kg, and the magnitude of the applied load can be varied by changing the drop height through a movable release handle. The peak value of the impact force is based on actual measurements from the load cell. The LWD software integrates the velocity geophone data to displacement and uses flexible values (can be adjust by the user for specific soil types) for the stress distribution factor A and Poisson’s ratio used to estimate Evd. The data collection software is installed in a PC coupled to the LWD. The deformation modulus of the surface and/or plate (Evd) in addition to the time history graph from both the deformation sensors and the load sensor can be displayed in the PC screen in real time. Relevant information such as name, place, weather, and comments can be added to the data file for each measuring point. The collected test data can be printed as a report or can be exported to other software like MS Excel for further processing.

More figures displaying the LWD components in another aligned positions are given in Kuttah (2020b) and Kuttah (2021). Also, more information about the pulse load time and collision time of the tested materials are available in Kuttah (2020a) and Kuttah (2021).

Materials used

Two types of commonly available materials have been chosen, namely, sandy subgrade soil and local unbound granular material usually used in Sweden as a base course. The chosen base course material fulfilled the Swedish standard requirements on unbound materials used for road constructions in Sweden according to TRVKB 10 (2011).

The particle size distribution of the tested sandy subgrade soil and the unbound granular material (0/32) are illustrated in Fig. 2.

Fig. 2
figure 2

Particle size distribution of the tested materials

Full size image

According to VVTK Väg (2008), the tested sandy soil is material type 2 (frost hazard class 1). The specific gravity of the selected sandy soil was tested according to SS-EN 1097–6 (2013), and it was found to be 2.664.

The specific gravity of the selected base material was tested according to SS-EN 1097–6 (2013), and it was found to be 2.72.

The compaction properties of the chosen materials were determined by a modified Proctor test as per ASTM D1557 (2012). The test was performed by compacting several CBR soil samples using a cylindrical mold of 152.4 mm diameter. The CBR soil samples were compacted at different molding water contents to determine the water-density relationship. The results of the compaction tests revealed that the compaction curve of the tested sandy soil is a one-and-one-half-peak curve with two optimum water contents and two maximum dry densities. One of the maximum dry densities lies on the dry side (at W = 0%) and the other one lies at the wet side (at around W = 12%). The maximum dry densities are 1.8 and 1.72 g.cm−3 at 0 and 12% water content, respectively (see Fig. 3a).

Fig. 3
figure 3

Compaction curve of the tested a sandy soil and b granular base material, using modified Proctor compaction

Full size image

The results of the compaction tests on the selected base material revealed that the compaction curve of the tested material is also a one-and-one-half-peak curve with two optimum water contents and two maximum dry densities. One of the maximum dry densities lies on the dry side (at W = 0%) and the other one lies at the wet side (at around W = 6%), as shown in Fig. 3b. The maximum dry densities are 2.2 g.cm−3 and 2.3 g.cm−3 at 0% and 5.7% water content, respectively.

In situ testing procedure

The testing program consisted of carrying out in situ tests at a large test pit for the material compaction under controlled conditions. Correspondingly, a test pit at the backyard of the Swedish Road and Transport Research Institute (VTI) was constructed to carry out the in situ LWD, densities and moister contents measurements using Nuclear Density Gauge (NDG). The test pit was instrumented with an electric drive motor roof panel. The roof panel can be opened and closed with the help of an electric motor to control as much as possible the testing conditions in the test pit, specially, controlling the weather effect.

The test pit was approximately 10 m long × 5 m width × 1.5 m depth. Figure 4 shows the test pit boundaries before filling with the tested material. During construction, the full depth of the test pit was filled with the material selected for testing (i.e., filed with sand for stage 1 testing, and then the sand was removed, and the test pit was filled with the selected base material for testing in stage 2 of the project). The test pit was also equipped with a concrete well with a water discharging motor that was used to control the ground water level during testing.

Fig. 4
figure 4

The test pit filled with the compacted granular base material

Full size image

The test pit was filled by the tested material with the help of an excavator and then compacted with a small vibrator (Fig. 4). When the compaction was completed, the final layer surfaces (for the case of sand and then for the granular base material) were marked with circles representing the selected places of the points to be tested, as shown in Fig. 4.

The testing program includes in situ LWD testing on two types of construction materials, namely, sandy soil and granular base course material. In parallel with in situ LWD testing, densities and moister contents measurements were carried out using Nuclear Density Gauge. The in situ LWD tests were carried out at three different applied load magnitudes, namely, 3 kN, 5 kN, and 7 kN under different testing moisture contents and for many load applications as discussed in detail in the next paragraphs. This research is part of a wide LWD research carried out at VTI to standardize the used LWD and start a new usage of LWD to measure the stiffness of the compacted material after bringing the soil to the near elastic behavior by applying many weight drops as discussed in detail by Kuttah (2021). Therefore, the current study includes LWD measurements of up to 55 weight drops. In addition, it has been noticed that the correlation between measured G0 and PA is affected by the number of LWD weight drops; therefore, this influencing factor has been adopted in this analysis and correlations.

In situ LWD tests on the sandy soil

After compacting the sandy soil, LWD tests and the corresponding NDG tests were performed at various points under relatively low moisture contents (between 3 and 4%). At this range of low moisture content, the LWD tests were performed at three different applied load magnitudes, namely, 3 kN, 5 kN, and 7 kN. After completing these tests at relatively low moisture content, the compacted soil was watered, and the moisture content increased to about 9% (after watering). The water was sprinkled by a sprinkler, and after watering, the material was left for a couple of hours before testing to ensure, as much as possible, that the water content has been distributed thoroughly along the depth of the test pit. Then, the field LWD tests were carried out at only 7 kN for few points. For each similar combination of moisture content and applied load magnitude, the average values of the deformations of at least two points were considered for all load applications (up to 55 load drops per tested point).

In situ LWD tests on the base material

Similarly, after compacting the base material, LWD tests and the corresponding NDG tests were performed at various points under relatively low moisture contents (about 3 to 4%). At this range of low moisture content, the LWD tests were performed at three different applied load magnitudes, namely, 3 kN, 5 kN, and 7 kN. After completing these tests at relatively low moisture content, the compacted soil was watered, and the moisture content increased to about 6.6% (after watering). Similarly, as for the case of sandy soil, after sprinkling water, the material was left for a couple of hours before testing to ensure uniform distribution of water along the test pit depth.

Then, the field LWD tests were carried out at only 7 kN for few points. For each similar combination of moisture content and applied load magnitude, the average values of the deformations of at least two points were considered for all many load applications (up to 55 load drops per tested point).

Results and discussions

Interactions among factors affecting the measured deformations and Evd of the sandy soil

The influence of sensing configuration (ground versus plate) on the measured deformation was explored in relation with other testing factors such as the moisture content (W), applied load magnitude (P), and the number of load applications (N). Figure 5 illustrates the influence of the sensing configuration on the measured deformations (i.e., ground versus plate deformations) at different applied load magnitudes and load applications for the sandy soil.

Fig. 5
figure 5

Effect of sensing configuration and applied load magnitude on the measured deformations at W between 3 and 4% for the sandy soil

Full size image

It can be seen from Fig. 5 that the mean plate-based deformations are greater than ground-based deformations across all tests carried out at different applied load magnitudes and for a wide range of load applications. One can also notice that with increasing the number of load applications, the differences between plate-based deformations and ground-based deformations decreased for the three adopted applied load magnitudes (namely, 7 kN, 5 kN, and 3 kN).

For the same applied load, the most significant contributor to this difference is the sensing configuration; peak ground-based deformations were lower than the peak plate-based deformations by between 55 and 86% on average. The repetition of the load applications from the first drop to the 25th drop can contribute between 14 and 27% to the difference between ground and plate deformations. The respective influences of the load magnitudes are between 6 and 18%.

Also, it can be seen from Fig. 5 that, generally, the deformation differs greatly in the initial stage of loading as the load increases. This is a usual observed phenomenon with repeated loading since as the number of applied loads increases, the material is subjected to additional compaction (post-compaction effect) and becomes denser; hence, the deformation is reduced with the successive loading.

Furthermore, the deformations increased slightly with increasing the moisture content, but the differences between the ground and plate deformations were almost the same for the two moisture contents under similar other testing conditions (i.e., the number of loads applications and applied load magnitude). The effect of moisture content for the same applied load of 7 kN ranged between 1 and 6% which is minor in comparison to that of the sensing configuration (see Fig. 6). Generally, the nature of the difference is linked to a time delay in the experimental plate and ground surface deformation response registered during testing, something which was discussed by Stamp and Mooney (2013).

Fig. 6
figure 6

Effect of moisture content and sensing configuration on the measured deformations for the sandy soil

Full size image

As mentioned previously, for each similar combination of moisture content and applied load magnitude, the average values of the deformations of at least two points were considered for all load applications.

In terms of the effect of the sensing configuration on the dynamic deformation moduli of the sandy soil Evd, Eq. 1 has been used to calculate the Evd moduli by considering Poisson’s ratio (ν) = 0.35 and A = 2.35.

For the sandy soil, Fig. 7 shows the effect of consecutive dropping of the falling weight on the average Evd for tested points at low moister content testing conditions (between 3 and 4) and under 7 kN, 5 kN, and 3 kN falling weight, respectively. Similarly, Fig. 8 shows the effect of consecutive dropping of the falling weight on the average Evd of two identical tested points at moist condition (W = 9.1%) and under the effect of 7 kN drop weight.

Fig. 7
figure 7

Effect of sensing configuration and applied load magnitude on the measured Evd moduli at W between 3 and 4% for the sandy soil

Full size image
Fig. 8
figure 8

Effect of moisture content and sensing configuration on the measured Evd at P = 7 kN for the sandy soil

Full size image

It can be seen from Figs. 7 and 8 that the Evd of ground and plates increase with increasing the number of falling weight drops in all cases. This can be attributed to the decrease of plastic deformation with increasing the number of drops.

In addition, it can be noticed from Figs. 7 and 8 that, in all cases, the Evd moduli calculated based on ground deformation measurement were higher than the corresponding Evd moduli calculated based on plate deformations measurements. This obvious is due to the fact that the registered ground deformations were lower than the corresponding plate deformations captured simultaneously. This finding can be attributed to the fact that the soil under the plate is loaded more than the soil under the holes existing around the center of the plate where a geophone passes through these holes, as described previously.

Also, it can be seen from Fig. 8 that increasing the moisture content led to a slight reduction in Evd moduli something which goes well with the deformations given in Fig. 6.

Interactions among factors affecting the measured deformations and Evd of the granular base

For the granular base material, a number of factors contributing to the difference in measured peak deformation values have been studied as for the case of the sandy soil including sensing configuration (ground surface versus plate), load pulse magnitude, the moisture content of the tested material, and the number of loads applications. For the same applied load, the most significant contributor to this difference is the sensing configuration, as for the case of sand, peak ground-based deformations were lower than the peak plate-based deformations by between 50 and 70% on average (see Fig. 9). The load magnitudes have also an influence on the magnitude of measured ground and plate deformations as these deformations increased considerably with increasing the applied load magnitude, but the influence of the load magnitude on the difference between the ground and plate deformations ranged between 1 and 7%, and hence, it is minor in comparison to that of the sensing configuration. The repeatability of the load applications from the first drop to the 40th drop can contribute between 9 and 14% to the difference between ground and plate deformations. It has been noticed that the ground and plate deformations decrease with increasing the number of load applications, and the differences between the ground and plate deformations decrease also with increasing the number of load applications under similar testing conditions (i.e., for the same moisture content and applied load magnitude) (see Fig. 9).

Fig. 9
figure 9

Effect of sensing configuration and applied load magnitude on the measured deformations at about 3% water content for the base course

Full size image

Furthermore, the moisture content showed also a very slight influence on the deformations of the granular base material as in the case of the sandy soil. The reported influences of the moisture content on the ground and plate deformations for the same applied load of 7 kN ranged between 1 and 11% which is also lower than the effect of the sensing configuration (see Fig. 10).

Fig. 10
figure 10

Effect of moisture content and sensing configuration on the measured deformations for the base course

Full size image

Figure 11 shows the changes of the measured dynamic deformation moduli with increasing the number of falling weight drops on points tested at about 3 to 4% moisture content under 3 kN, 5 kN, and 7 kN applied loads, respectively. Similarly, Fig. 12 represents the effect of the number of drops of 7 kN load on the Evd moduli measured on points at moist conditions (about 6.5% moisture content).

Fig. 11
figure 11

Effect of sensing configuration, applied load magnitude, and the number of load applications on the measured Evd at W between 3 and 4% for the granular base material

Full size image
Fig. 12
figure 12

Effect of the moisture content, number of load applications, and sensing configuration on the measured Evd at P = 7 kN for the granular base material

Full size image

It can be seen from Figs. 11 and 12 that a general increasing trend of ground and plate Evd with increasing the number of falling weight drops has been observed in all cases. As in the case of the tested sandy soil, this can be attributed to the influence of the decreasing plastic deformation of the tested unbound granular material after successive weight drops.

In addition to the above, it can be noticed from Figs. 11 and 12 that, in all cases, the Evd moduli calculated based on surface deformation measurement were higher than the corresponding Evd moduli calculated based on plate deformations measurements. This is obvious since the registered surface deformations were lower than the corresponding plate deformations captured simultaneously. This behavior coincides with that of the sandy subgrade soil, which was previously explained.

Correlation between the ground and plate deformations as a function of other influencing factors

Multiple regression analysis has been used to correlate the ground deformation to the corresponding plate deformation measurements considering the effect of the applied load magnitudes, the number of loads applications, and the moisture contents for the sandy soil and granular base material.

Very strong linear correlations have been found for both types of materials tested as described below.

Equation 2 represents a model to estimate the ground deformation (G0, in µm) from the plate deformation (PA, in µm), the load magnitude (P, in kN), the moisture content (W, in %), and the number of applied loads (N) for the sandy soil.

$$\mathrm{G}0=0.57\mathrm{ PA}+17.4 P+3.85 W+0.75 N-62.7$$
(2)

It can be seen from Fig. 13a and b that the ground deformations, predicted using Eq. 2, are close to the measured ground deformations almost for all given testing conditions.

Fig. 13
figure 13

Prediction of the ground deformation from the plate deformation under different testing conditions for the sandy soil, a at W = 3.5% and b at W = 9.1%

Full size image

The fitting is best for the cases of W = 3.5% at P = 3 kN and at W = 9.1% at P = 7 kN. The multiple coefficient of correlation (R = 0.98) indicates a very strong correlation after Anderson and Sclove (1978) or a very high correlation after Asuero et al. (2006).

Likewise, Eq. 3 shows a correlation between the ground deformation (G0, in µm) and the plate deformation (PA, in µm), the load magnitude (P, in kN), the moisture content (W, in %), and the number of applied loads (N) and for the granular base material.

$$\mathrm{G}0=0.35\mathrm{ PA}+25.3 P+5 W+0.24 N-49.8$$
(3)

It can be seen from Fig. 14a and b that the ground deformations, predicted using Eq. 3, are very close to the measured ground deformations for all given testing conditions.

Fig. 14
figure 14

Prediction of the ground deformation from the plate deformation under different testing conditions for the granular base, a at W = 3.2% and b at W = 6.6%

Full size image

The fitting is best for the cases of W = 3.5% at P = 3 kN and at W = 9.1% at P = 7 kN. The multiple coefficient of correlation (R = 0.99) indicates a very strong correlation after Anderson and Sclove (1978).

In addition, a more general equation could be developed using multiple regression analysis to correlate the ground deformation to the corresponding plate deformation measurements for both tested materials. The general function (referred to as Eq. 4) can predict the ground-based deformation with multiple coefficient of correlation (R = 0.988) indicating a very strong correlation after Anderson and Sclove (1978) or a very high correlation after Asuero et al. (2006).

$$\mathrm{G}0=0.54\mathrm{ PA}+15.56 P+5.34 M+0.63 N-0.56 S-102$$
(4)

In this equation, the percent material passing 4 mm sieve (S) has been included as an additional dependent factor in the equation to reflect the influence of the material type.

Figure 15 shows a scatter plot with a line of equality comparing G0, measured with LWD, and estimated with Eq. 4 for sandy soil and base course material. The line of equality between measured and predicted G0 from Eq. 4 is very strong with R = 0.996.

Fig. 15
figure 15

Scatter plot with line of equality comparing G0, measured with LWD, and estimated with Eq. 4 for sandy soil and base course material. The values of G0 were very strong correlated (R = 0.996)

Full size image

Correspondingly, Eqs. 2, 3, and 4 allow the transportation agencies to specify target deformation using LWD of different sensing configurations during earthwork construction. This will facilitate the standardization and adaptation of LWD in quality control of unbound materials during construction using single specification.

Conclusions and recommendations

Based on this study carried out on sandy subgrade soil and granular base material, to assess the effect of LWD sensing configuration, applied load pulse magnitude, moisture content (W) during testing, and the number of load applications (N) on the LWD deformation measurements, the following conclusions can be obtained:

  1. 1-

    The influence of sensing configuration, applied load pulse magnitude, moisture content (W) during testing, and the number of load applications (N) on the LWD deformation measurements revealed that the sensing configuration (measurement of plate versus ground surface) is the main contributor to the LWD deformation differences among other influencing factors.

  2. 2-

    The peak ground-based deformations were lower than the ground surface deformations by 55 to 86% on sandy soil and by 50 to 70% on granular base material.

  3. 3-

    The respective influences of the load magnitude, load repeatability, and moisture content on deformation measurements led to relatively small differences for the case of sandy soil and the granular base material.

  4. 4-

    With respect to modulus of deformation (Evd), a general increasing trend of the ground and plate Evd moduli with an increasing number of falling weight drops has been observed in all cases for both types of tested materials. In addition, the Evd moduli calculated based on the surface deformation measurement were higher than the corresponding Evd moduli calculated based on plate deformations measurements.

  5. 5-

    Considering the multiple factors involved in this study and the material dependency, the differences between plate-based and ground-based deformations could be predicted as given in Eq. 2 for the sandy soil, Eq. 3 for the granular base, and Eq. 4 for both tested materials.

All the equations developed in this study are recommended to be used. Nevertheless, it is important to keep in mind that they have been developed for specific materials and testing conditions (i.e., tested water contents and applied stress levels). When using the equations for different testing materials and conditions than what they were developed for, a combination of previous experience and engineering judgement should be considered.