Introduction

Permeability affects many geotechnical characteristics of soils. The importance of knowing the permeability is indisputable for drainage applications in hydrogeology and civil engineering, in which the medium is characterised by the absence of clays. The degree of compaction of granular drainages is also an important characteristic, but the authors consider that the influence on permeability must be studied in two different stages, in its initial conditions (loose packing) and after any natural compaction process. This second stage does not mean a single second condition, as the compaction process can have occurred over time, by different settlements produced by rainwater flow, adding weight, or any other (as typical consolidation processes considered in triaxial tests), reducing the permeability values.

Estimating the permeability of porous granular media includes, in a generic way, any measurable properties that allow this parameter to be predicted, the most accepted ones starting with granulometric data, and later adding the porosity value. The last substantially improved the quality of estimations because the porosity reflects the degree of compaction of the medium. Relationships to estimate permeability without considering porosity are particularly useful for the initial conditions of drainages, as a specific case of granular media, but when changes of compaction occur, the porosity values — easily measurable — must be added to modify the initial estimation.

In regards to relationships only with granulometric data, the more used relationships provide permeability values increasing with a given size grain (dGR, d10, d50… etc.), where dGR is the average grain size (in mm) and d50 and d10 are the mesh sizes of the sieve through which 50% and 10% of the sample pass, respectively. In these relationships, the inclusion of the grading coefficient is unintuitive and provides very different results. This led to consider defining a new, easily obtainable size that implicitly includes the grading coefficient, which is one of the aims of this paper. To achieve this goal, first the main relationships to estimate permeability values on the average grain size of each medium and on the grading coefficient of grain size were selected. Starting from a series of natural sands with specific characteristics of grain size, laboratory tests with specific deposition conditions that emulate those of the drainages were carried out. Then, a single parameter has been defined: a new effective diameter related to grain size and grading coefficient that can be used as a single variable in a new relationship also developed in this work for estimating permeability. The differences with published equations are showed in the “Results and discussion” section.

Related to inclusion of the porosity value, in practice, structural changes may occur with respect to initial conditions due to, for example, natural settlement or humidity changes, modifying the compaction of the sample, and hence its porosity. Given that the widely accepted Kozeny-Carman Eq. (1927–1939) was developed for mono-size grains, in the last decades the grading coefficient was added to new relationships (they will be detailed in the “Background” section). However, the permeability values provided by existing relationships increase with the grading coefficient, so an exhaustive analysis was necessary.

Over time, the authors have carried out a series of investigations with the objective of developing new expressions to estimate permeability in different media. Among other conclusions, Díaz-Curiel et al. (2016) found that the permeability acquired by natural detrital media is not as unambiguously related to porosity as previously thought for cemented media in the oil field. Their work reaffirmed the negative correlation between porosity and permeability of unconsolidated media, used in hydrogeology. In addition, it was concluded that the relationship between permeability and porosity depends on the variation of the permeability exponent, m, given by the petrophysical Archie’s 1st law (Archie 1942), F = 1/Øm (where F, known as the formation factor, is the ratio between the resistivity of the medium and that of the formation fluid, and Ø is the porosity). As a result, the permeability–porosity relation shows quasi-parallel convex curves with different position along the Ø-axis for different permeability exponents, which conversion into grading coefficient terms is the other objective of this work. Continuing with this line, the next goal of this study is to meet a relationship showing a similar behaviour but depending on grading coefficient. To achieve this goal, widely accepted data (Beard and Weyl 1973) on permeability versus grain size and grading coefficient, and data specifically measured for this study, were used to determine a fitting function for estimating the permeability values. The synthetic samples have similar characteristics than Beard and Weyl data to allow for the comparison of the results.

In addition to a new specific relationship k(dGR, SC) for drainages (shown in the “Specific relationship k(dGR,SC) for drainages” section), the main difference of the current proposal with respect to previous work on relationship k(dGR, SC, Ø) is that the permeability values decrease with the grain size grading (higher grading coefficient), as shown in the “General relationship to estimate permeability” section. The advantage of this new relationship is that all terms related to grain characteristics are directly extracted from the grain size distribution itself without the need for additional calculations.

Background

Estimate permeability from granulometric data

The first studies on the indirect estimation of the permeability of unconsolidated sedimentary formations were based on a certain grain size. These studies built on the work of Hazen (1892) for media with a porosity of around 36%, whose expression for estimating the permeability at 20 °C (after converting m/day to Darcys) is:

$$k\left({d}_{10}\right)\approx 0.89\cdot {d}_{10}^{2},$$
(1)

Numerous relationships have been developed (Fair and Hatch 1933; Fraser 1935; Rose and Smith 1957; Morrow et al. 1969; Shepherd 1989; Song et al. 2009), and all agree that permeability has a positive correlation with grain size.

The relationships between permeability and grain parameters are formulated in terms of the average grain size, a granulometric grading coefficient, and grain shape factors; for unconsolidated media, the first two are the most critical. The influence of the grain shape on the permeability values, considering the two differentiated characteristics of sphericity and angularity, was addressed almost a century ago (Fair and Hatch 1933). Classical values of the shape factor α are 1.1 for rounded sands, 1.25 for medium angularity sands, and 1.4 for angular sands (Loudon 1952), but new values and analytical solutions are being proposed (Silvestri et al. 2011; Nomura et al. 2018; Nguyen and Indraratna 2020). Although this factor should be considered in drainage calculations for crushing quarry waste, as a function of the obvious differences in grain shape with regard to aggregates from gravel pits, the shape factor is not addressed in this study.

As with the utilisation of d10 by Hazen, using a single datum of the grain size distribution (GSD) curve may, in practice, be influenced by local variations in that curve. Hence, it was considered more appropriate to use a parameter that better depicts the whole distribution. The inclusion of grading in the expression for permeability is supported by the results of Beard and Weyl (1973) using artificial sand samples: for each average grain size, the measured permeability values increased with gradation, at a ratio ranging from ~ 25 for larger grain sizes to ~ 500 for smaller grain sizes. The influence of this distribution has been considered in the literature in different ways (Wang et al. 2017), with the grading entropy being the most widely used in recent decades (Boadu 2000; Lörincz et al. 2008; McDougall et al. 2013; Feng et al. 2018; Arshad et al. 2019). To analyse the particular case of drainage packing, the expressions derived by Krumbein and Monk (1942) and Alyamani and Sen (1993) are considered in this study. The “Beyer relationship” referred to by Wang et al. (2017), written as k = 6·10−4·981·log(500/CU)·d102 (CU being the coefficient of granulometric uniformity established by Hazen) is not considered in this study because, for a normal range of CU (between 1 and 10), the range of permeability variations is very low (lesser than 60%).

The relationship developed by Krumbein and Monk is applied under the assumption that the grain size curve fits a lognormal distribution, which becomes a normal distribution when the abscissa is φ = log2(d), where d is the grain size diameter. The permeability values (in Darcys) are given by the following expression:

$$k\left({d}_{GR}, {\sigma }_{\mathrm{\varphi }}\right)=0.73\cdot {d}_{GR}^{2}\cdot \mathrm{exp}\left(-1.31\cdot {\sigma }_{\mathrm{\varphi }}\right),$$
(2)

where σφ is the standard deviation of the grain size curve in units of φ.

In Alyamani and Sen’s work, the sum of the grain size and grading was used as an effective diameter through the expression (after converting m/day to Darcys):

$$k\left({d}_{0}, {d}_{10},{d}_{50}\right)\approx 1.5\cdot {\left\{{d}_{0}+0.025\cdot \left({d}_{50}-{d}_{10}\right)\right\}}^{2},$$
(3)

where d0 is the grain size (in mm) intercepted by a straight line approaching the steepest part of a truncated GSD.

Including porosity in permeability estimation

Estimating permeability from only granulometric data lacks a consideration of the degree of compaction or grain packing, which is generally included through the porosity value. In terms of estimating the permeability from granulometric characteristics and porosity, Slichter (1899) developed a function of the effective grain diameter dEF, written as k = 1009·dEF2/PC, where PC is a porosity-dependent coefficient given in his Table II. Those PC values fit to the function 1.023/Ø3.3 with a mean deviation of less than 0.4%, resulting k≈1000·dEF2·Ø3.3.

Subsequently, Kozeny (1927) and Carman (1939) established a permeability relationship as a function of the specific surface area of the pores SPOR, given by k = CK·Ø3/SPOR2, where CK is a constant that has an initial value CK≈g/5, g being the gravitational acceleration. Relating SPOR with the specific grain surface SGR (surface of the grains per unit volume) by the expression SPOR2 = SGR2·(1-Ø)2, and considering that for spherical grains SGR = 6/dGR (dGR being the average grain size), the previous relationship takes the form:

$$k={\mathrm{C}}_{KC}\cdot {d}_{GR}^{2}\cdot {\varnothing }^{3}/{(1-\varnothing )}^{2},$$
(4)

where CKC is a new constant that takes a value of 5.45 under the above considerations. Later studies replaced the average diameter by different effective diameters (Panda and Lake 1994; Carrier 2003; Trani and Indraratna 2010; Indraratna et al. 2012; Erguler 2016; Zheng and Tannant 2017; Maroof et al. 2020).

The generality of the Kozeny–Carman equation comes from the ability to use different specific surfaces of the pores of a medium, which can be estimated from the specific grain surface obtained by measurements per mass unit (e.g. methylene blue, nitrogen adsorption). One of the existing analysis of the Kozeny equation starts from the equivalence used in Kozeny’s publication between the specific surface area SS and the grain size deff, which for spherical particles is deff = 6/SS. Specific surface can be also estimated from the grain size distribution of soil by Chapuis and Légaré (1992): SS = 6/ρS·Σ((Pd+ − Pd)/d) where ρS is density (kg/m3) of grains, and (Pd+ − Pd) is the percentage of solid mass smaller than size d + and larger than size d (Trani and Indraratna 2010; Nguyen and Indraratna 2020). In the work of Nguyen and Indraratna (2020) (with diameters d50 between 0.1 and 0.9 mm, CU between 1.4 and 2.1, porosity Ø between 0.34 and 0.46), shape factor α between 1.02 for glass beads and 1.52 for natural sands is obtained by the ratio between specific surface area of irregular particles and the specific surface area of spherical particles.

It is important to note that this study does not continue with the inclusion of the specific surface area of the grains in the Kozeny-Carman equation, initiated with the work of Chapuis and Légaré (1992) and continued with Chapuis and Aubertin (2003) and other later works. In contrast, this part of the current study consists of a proposal to include the grading coefficient in the Kozeny-Carman equation in a very different way to that existing in the literature. Nor is it intended to show a review of all modifications of the Kozeny-Carman equation as it is shown in some of the comparative studies that will be referred below. Therefore, this study starts from the limitation of the Kozeny-Carman equation as it was established for homometric grains; and only the problems of all existing modifications in the literature on the Kozeny-Carman equation that include grading coefficients are presented.

Although the Kozeny–Carman equation is the most widely used expression, its re-examination remains an objective of interest (Costa 2006; Xu and Yu 2008; Nooruddin and Hossain 2011; Khabbazi et al. 2013; Nomura et al. 2018). Different equations for k(dGR,Ø) can be found in many comparative studies published in the past decade (Vienken and Dietrich 2011; Chapuis 2012; Lu et al. 2012; Oh et al. 2013; Rosas et al. 2015; Devlin 2015; Cabalar and Akbulut 2016; Riha et al. 2018; Arshad et al. 2019). Some studies have analysed media comprising aggregates with an average coarse or large grain size (Bao et al. 2021; Koohmishi and Azarhoosh 2021). Most of the relationships analysed in these works were developed before 2000. Limitations of the different relationships for permeability estimations can be found in these and other works (Gao et al. 2019; Toumpanou et al. 2021). Kozeny-Carman equation has gone far beyond the theoretical condition that it was supposed to be (see Costa 2006; Nguyen and Indraratna 2017).

Despite the high degree of application of the Kozeny–Carman equation, it only quantifies the influence of grain characteristics in terms of average size, without considering the gradation of the GSD. In this study, it is demonstrated that the inclusion of the granulometric grading improves the indirect estimation of permeability. This highlights the importance of grading in the geotechnics field, as its effect on the geomechanical behaviour of soils is long-established in the literature (Iwasaki and Tatsuoka 1977; Wood and Maeda 2008; Wichtmann and Triantafyllidis 2013; Aziz 2020).

The importance of grain size grading was stressed by Masch and Denny (1966), and led to proposals such as that from Berg (1970), in which a deviation coefficient was related to the granulometric curve, and Van Baaren (1979), which included a variable grading coefficient ranging from 0.7 to 1.0. Both of these studies use f(Ø) functions different to that of Kozeny–Carman: f(Ø) = Ø3/(1 − Ø)2 (which, it should be noted, approximates other algebraic functions, for example, to the power function 2.7·Ø3.3). Other researchers included the grain size grading in the estimation of permeability, such as k = 0.1·CU1/3·Ø5/(1 − Ø)4·d102 proposed by Mbonimpa et al. (2002); the “Shahabi correlation” k = 1.2·CU0.735·d100.89· Ø3/(1 − Ø)2 referred to by Chapuis (2012), the “Pavchich relation” k = 0.455·CU1/6·Ø/(1 − Ø)·d17 referred to by Riha et al. (2018); and the “Amer and Awad model” к = 3.5·10−6/ν·CU0.6·Ø3/(1 − Ø)2·d102.32 referred to by Arshad et al. (2019). These relationships are not considered in this study, because the permeability values increase with the grain grading in these expressions, and the authors disagree with this positive correlation.

Materials and methods

To develop fitting functions for empirical data in order to improve the specific estimation of drainage permeability, the results presented in Beard and Weyl (1973) were analysed. This work was selected because it is widely accepted by the specialised community. The porosity and permeability values presented therein were measured on synthetic samples of sands with no clay content. The samples were elaborated with eight average grain sizes (between 0.044 and 1 mm), six different grading levels (from extremely graded — lower values of SC- to very poor grading – higher values of SC — as defined by Beard and Weyl, see Fig. 1), and were synthesised in two specific ways, dry-loose and wet-packed. In that work, they detail that “the sand was allowed to settle in air and then wetted with distilled water and compacted by tamping with a wooden rod”. The groups of different granulometric gradations in that work were created by means of a sorting or grading coefficient SC, which is given by the relationship (Trask 1932):

$${S}_{C}=\sqrt{{d}_{75}/{d}_{25}},$$
(5)

where d75 and d25 are the mesh sizes of the sieve through which 75% and 25% of the sample pass, respectively. This coefficient provides an estimation of the granulometric gradation in which the influence of the grains greater and smaller than the average size is similar, as opposed to the coefficients that use d10. To facilitate the comparison with the coefficient of uniformity, a relation between both coefficients has been developed for the analysed natural sands, meeting that CU≈SC2.5.

Fig. 1
figure 1

(Ø,k) data from Beard and Weyl (1973) for different grading coefficients and k(Ø) fitting curves

Full size image

As for the coefficient of granulometric uniformity, the grading coefficient is computed based on two diameters, hence they do not fully describe the grain size distribution (limitations on fully describing such a curve is addressed in the “Results and discussion” section). However, the use of grading coefficients is very common in relationships to estimate permeability (see references cited in “Background” section), even in the studies starting from micro-computed tomography (Taylor et al. 2019).

Although in the last two decades, techniques such as Laser scanning (Eshel et al. 2004; Ryżak and Bieganowski 2011) are being used, in this study it is considered that the substitution in the empirical relationships of certain mesh diameters by the more accurate laser diameters does not necessarily lead to a drastic change, if the sieves used for granulometric test are gradual as the ones shown in Table 1.

Table 1 Sieves used for granulometric tests
Full size table

The porosity values obtained in both modes exhibit a tendency to increase as the grain size decreases, producing a smaller variation in the more graded samples (this tendency matches the variation presented by Rogers and Head (1961)). The difference produced by the two methods of synthesising the samples has an average variation of ΔØ ~ 13% for dry-loose samples and ΔØ ~ 5% for wet-packed samples.

The permeability values reported in Beard and Weyl’s work were only measured for wet-packed samples (see Table 7 of their paper). For each granulometric grading coefficient, they verified that the permeability decreases as the porosity increases, at a ratio ranging from ~ 100 for extreme gradation to ~ 250 for very poor gradation (according to their definition). Figure 1 shows these (Ø,k) values and, assuming a gradual behaviour of k(Ø), the fitted curves for a family of power functions of porosity are included. These power functions are used in order to only show the general tendency of data and are supported by Slichter equation.

Figure 1 reflects a reality that contrasts with the generalised application of the Kozeny–Carman equation for two distinct reasons. The Kozeny–Carman equation does not include any dependence on granulometric gradation, which, as shown in Fig. 1, produces differences in the permeability value of the same order as those due to porosity differences. It has conventionally been considered that permeability presents a positive correlation with porosity, as it does not consider dependence on grain size. Nevertheless, in Fig. 1, this correlation is negative. The new view of Beard and Weyl’s results, presented in Fig. 1, supports the need to include the granulometric gradation when estimating permeability, which is developed in this study.

To achieve the objective of the present study, the results obtained for natural soils were used to establish a new effective size, and a series of porosity and permeability measurements were carried out on synthesised sand samples. The natural soils consisted of ten samples (M1–M10) analysed by the authors in a previous study (unpublished). A general relationship was then sought to estimate the permeability of the synthetic sands, considering that the results of this study should reflect the behaviour reported in Beard and Weyl (1973).

Although granulometric data are available, in many cases, the porosity value of the future drainage is not known. Therefore, a relationship was developed to estimate the permeability specifically for drainages depending only on the average grain size and the grading coefficient.

Establishing a new effective diameter

In estimating the permeability, the authors considered it useful to search for a new effective diameter that includes the granulometric gradation. The sieves used to obtain the granulometric curves have various mesh sizes, allowing five points per logarithmic cycle to be obtained (Table 1).

The set of sieves in Table 1 is that described in standard UNE 103,101:1995 (“grain size analysis of soil by screening”). Of these, the authors do not recommend the group of sieves that appears as “of common use” for estimating permeability. The curves obtained for the analysed samples are presented in Fig. 2.

Fig. 2
figure 2

Granulometric curves of 10 natural soil samples

Full size image

As can be seen in Fig. 2, these are unimodal curves corresponding to sands with an average diameter between ~ 0.5 and ~ 1.5 mm, and with very low (< 1%) amounts of fines (< 0.08 mm). The particular characteristic of these curves is not so much that they are very smooth (without discontinuities), but rather their grading coefficients are very homogeneous (with values varying between 1.44 and 2.15 mm). There is no significant correlation between the average diameter and the grading coefficient.

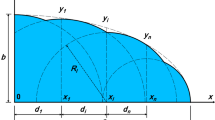
To establish the new effective diameter, it was assumed that the cutting point in the abscissa of a straight line that represents the granulometric curve includes information about both the average grain size and the granulometric gradation. Therefore, it was decided that, as a new effective diameter for estimating permeability, a value obtained directly from the granulometric curve would be used. Given the extensive use of the grading coefficient defined by Trask (1932), which uses the values d25 and d75, and after a detailed analysis of the obtained granulometric curves, the authors took the cutting diameter dC to be the intersection with the abscissa of the straight line passing through the two quartiles d25 and d75 (see Fig. 3).

Fig. 3
figure 3

Granulometric curves with lines Pd75 − Pd25 for the analysed natural soil samples

Full size image

To determine a mathematical expression for the cutting diameter dC, a fitting relationship was developed using the values d50, d25 and d75. The correlation between the cutting diameter and d50 was directly appreciated on results of Fig. 3, and different expression with d25 and d75 were correlated with the graphical cut-off diameter, obtaining the maximum correlation coefficient for d25/d75. The resulting relationship for the cutting diameter dC is given by the Eq. (6):

$${d}_{C}={d}_{50}/({d}_{75}/{d}_{25})={d}_{50}/{S}_{C}^{2},$$
(6)

the results from which show an average deviation of 3.2% with respect to the intersection with the abscissa of the straight line passing through the two quartiles d25 and d75. Figure 4 shows the cutting diameter values together with the curve given by Eq. (6).

Fig. 4
figure 4

Cutting diameter estimated by Eq. (6) versus graphical cutting diameter for the analysed natural soil samples

Full size image

Note that dC does not correspond to any diameter that characterizes the grains, although it has dimension of a length. The inclusion of the grading coefficient in this diameter gives it a more general character, although it cannot be overtly extended to any media because the analysed samples were obtained from a specific sedimentary environment.

Measurements

To measure porosity and permeability, 16 synthetic sand samples (S-1–S-16) were formed in order to have four mean grain size values (0.15, 0.35, 0.65, and 0.85 mm) and four grain grading coefficients (1.1, 1.5, 2.1, and 2.7). These values were selected to achieve results close to the data reported by Beard and Weyl. The soil specimens were formed using dry-loose synthesis because, of the two modes used in Beard and Weyl’s work, this is more suited to the backfilling conditions of drainages. Table 2 shows the resulting grain size and grading coefficient values.

Table 2 Average values of porosity and permeability obtained for different values of average grain size and grading coefficient
Full size table

Porosity values were calculated using the relationship given by Krumbein and Monk: Ø = (VT − VGR)/VT, where VT and VGR are the volume of the sample (two heights were taken from each sample and averaged to obtain the VT) and the volume of grains, respectively; in this study, a grain density of 2.65 g/cm3 was used. The permeability values were measured using a rigid permeameter of 74-mm diameter developed in the Prospecting Laboratory of the Universidad Politécnica de Madrid and trying to minimise the common errors described by Chapuis (2012). Permeability values were calculated using Darcy’s equation, for varying intervals to obtain water volumes of ~ 2.0 × 10−4 m3 (subsequently measured in detail), and using pressure differences of ~ 3 × 104 Pa, from which the corresponding pressure gradients were obtained as a function of sample heights. A correction of the water viscosity for temperature was applied, using the expression \(\nu \left(T\right)=1.8\cdot {e}^{-0.044\cdot {T}^{0.85}} \left(in cP\right)\) (Díaz-Curiel et al. 1997). To minimise the settlement effect of the different parts of the sample, water filling was performed from below to make its advance as slow as possible. After the first two control repetitions, high variability was observed between the porosity (approx. 15%) and permeability values, although with more variability between the porosity values. Therefore, three different tests were repeated for each synthesised sample to obtain the mean results. However, Nomura et al. (2018) found that this influence can produce changes in the specific surface of up to 1:3. Table 2 shows the average porosity and permeability values obtained (Fig. 5).

Fig. 5
figure 5

Granulometric curves of the synthetic samples

Full size image

Given the different nature of the samples, the mean grain sizes and grading coefficients are not exactly what were predicted, although the average for each of the groups of samples coincides with the expected value.

Specific relationship k(d GR,S C) for drainages

Unlike the work of Beard and Weyl, in which no mathematical expression was derived for the results, a permeability fitting relationship as a function of the average grain size, dGR, and the grading coefficient, SC, was sought. Note that this search was carried out using a selective process of simple functions that present the minimum error with respect to the data. The expression developed for dGR in mm is:

$$k\left({d}_{GR},{S}_{C}\right)=1.0\cdot {({d}_{GR}/{S}_{C}^{2})}^{1.43},$$
(7)

where the permeability results are in Darcys.

Taking into account the expression for the grading coefficient and Eq. (6), Eq. (7) yields:

$$k\left({d}_{C}\right)=1.0\cdot {{d}_{C}}^{1.43},$$
(8)

With this new expression, the objective of expressing the permeability of drainages as a function of a single size parameter is achieved, with the effective diameter dC being easily obtained from the grain size curve.

To check the adjustment accuracy of Eqs. (7) and (8), permeability values were calculated following Eq. (7) using dGR and SC data from the synthetic samples. These are plotted against the measured permeability data in Fig. 6; the R-squared value or determination coefficient, R2, is very high (R2 = 0.99), reflecting the adjustment accuracy.

Fig. 6
figure 6

Estimated permeability given by Eq. (7) versus measured permeability values for the synthetic samples

Full size image

As Eq. (7) was obtained for dry-loose samples, it cannot be generalised a priori for media with different degrees of compaction, such as the wet compacted samples analysed by Beard and Weyl or those corresponding to natural media.

General relationship to estimate permeability

The values presented in Table 2 allow the generality of the Kozeny–Carman equation to be reviewed from a different perspective with regard to its independence from granulometric gradation. Unlike the suggestion in the introduction about the use of specific deposition characteristics that imply a certain degree of compaction and which have been applied for the development of the specific k(dGR,SC) relationship for drainages, this process will account for the variation of porosity. The idea was to use a modified Kozeny–Carman equation that reflects the variation of permeability values with respect to porosity (see Fig. 7), considering a variable factor CS that depends on the grading coefficient, instead of the CKC constant value of the original Kozeny-Carman equation:

$$k={C}_{S}\cdot {d}_{GR}^{2}\cdot {\varnothing }^{3}/{(1-\varnothing )}^{2},$$
(9)

where CS takes values of 133–816 for the given dataset. Cs is not a new variable, but a variable factor that is expected to include a constant coefficient (the constant coefficient in the modified Kozeny-Carman equation), which in this study is differentiated from the original Kozeny-Carman constant CKC. Thus, the comparison with Kozeny-Carman constant will allow to evaluate whether the new modification of the Kozeny-Carman equation should be considered as the result obtained for specific data or whether the developed expression is equally generalisable as the Kozeny-Carman equation.

Fig. 7
figure 7

Measured permeability versus porosity values of the synthetic samples together with the results from Eq. (11) for the corresponding grain size, porosity, and grading coefficient values

Full size image

Some authors (Xu and Yu 2008; Ozgumus et al. 2014) consider that including other parameters in Kozeny-Carman equation means a change of the constant coefficient in that equation. For example, considering the shape factor CKC → CKC/α. However, in the current study replacing the Kozeny-Carman constant by different other it is considered as a slight modification of Kozeny-Carman equation for fit to specific data or media. Instead, the current proposal tries not to be a simple change of the constant coefficient in the modified Kozeny-Carman equation, but a new relationship in which the inclusion of the grading coefficient is clearly differentiated.

To determine CS as a function of SC, different functions were tested to determine the smallest deviation between the permeability values resulting from Eq. (7) and the measured data. The result, which has a fitting accuracy of R2 = 0.99, is given by:

$${C}_{S}=4.3/{S}_{C}^{2},$$
(10)

Substituting Eq. (10) into Eq. (9) yields:

$$k=4.3\frac{{d}_{GR}^{2}\cdot {\varnothing }^{3}}{{S}_{C}^{2}\cdot {(1-\varnothing )}^{2}},$$
(11)

where the permeability results are in Darcys for dGR in mm. The mean geometric deviation between the measured data and permeability results from Eq. (11) is ×  ÷ 1.17 (where ×  ÷ denotes multiplied or divided by).

Results and discussion

The main results of the current methodological study would be:

  1. (a)

    The cutting diameter of straight line defined by (Pd25, Pd75) with the abscissa’s axis on GSD has been considered as a new effective diameter dC for natural sands, because this is comprising the average grain size and the central slope of the GSD.

  2. (b)

    The cutting diameter dC has been fitted to a mathematical relationship as a function on d50, d25, and d75, allowing to include the grading coefficient by Eq. (6): \({d}_{\mathrm{C}}={d}_{50}/\left({d}_{75}/{d}_{25}\right)= {d}_{50}/{S}_{\mathrm{C}}^{2}\).

  3. (c)

    Using the loose packing data from Beard and Weil, permeability values versus grain size and grading has been fitted to a new relationship, resulting in Eqs. (7) and (8)

    $$k\left({d}_{\mathrm{GR}}, {S}_{\mathrm{C}}\right)=1.0\cdot {\left({d}_{\mathrm{GR}}/{S}_{\mathrm{C}}^{2}\right)}^{1.43}=1.0\cdot {d}_{\mathrm{C}}^{1.43}$$

    A comparative study of the results from Eq. (8) with respect to the previous selected relationships that involved a single diameter.

  4. (d)

    Measurements of porosity and permeability on loosing synthetic samples composed of grains from natural sands have been carried out.

  5. (e)

    Starting from Eqs. (7) and (8), a modifying of Kozeny equation was developed, given by k = CS·dGR2·Ø3/(1 − Ø)2 (Eq. (9)), where CS = 4.3/SC2 (Eq. (10)), resulting in a final expression, Eq. (11):

    $$k=4.3\frac{{d}_{\mathrm{GR}}^{2}\cdot {\varnothing }^{3}}{{S}_{\mathrm{C}}^{2}\cdot \left(1-{\varnothing }^{2}\right)}$$

To validate Eq. (11) for sands with compaction degrees other than loose packing, it will be below applied to the wet packed sand data given by Beard and Weyl.

Concerning the grading coefficient, it is worth mentioning that it presents an inconvenience when adopting the d75 and d25 values given by the granulometric curves, as these may have occasional discontinuities with respect to a gradual behaviour. This effect was not reflected in the samples analysed in this study, which were highly homogeneous sands with little presence of fines. In the same way, the granulometric curves associated with Beard and Weyl’s work were not presented, but analysis of the grain size of the samples by microphotographs indicates a smooth GSD. Although certain discontinuities in unimodal curves are, in some cases, due to an inappropriate selection of sieves, these discontinuities could require the GSD to be smoothed before Eqs. (7) and (8) can be used.

Regarding the previous models that include the granulometric gradation considered in this study, some limitations of each are worth mentioning. Krumbein and Monk’s model has the disadvantage that the use of non-conventional φ units for the mesh size necessitates the adjustment of its constants for sieves from the standardised series (e.g. ISO, ASTM, DIN). Moreover, the main objection is that the starting hypothesis, i.e. that a lognormal distribution of grain sizes fits a Gaussian distribution, can introduce errors in estimating the width and symmetry. This fact can be seen in samples M-7 and M-9, shown in Fig. 8 together with the Gauss curves of minimum deviation.

Fig. 8
figure 8

Granulometric histograms and RMS Gauss curves of a M-7 sample and b M-9 sample

Full size image

Figure 8a shows that when the relative width (kurtosis) is reduced (and the same would occur for curves with very high relative widths), the points corresponding to 25% and 75% retained mass are quite similar for both curves (~ 0.06). However, in cases where the GSD is asymmetric, which may occur with some probability, the Gaussian curve adjusted to give the minimum error can produce very different values. In sample M-9 (Fig. 8b), the values for 25% and 75% are ~ 0.05 and ~ 0.08. The symmetry of the Gaussian distribution is precisely one of its characteristics. This fact causes the slope of the accumulated granulometric curve to be very different from the corresponding Gaussian adjustment, something that is considered a critical factor for this permeability estimation.

It also seems appropriate to make a comparison between the results obtained with Eq. (8) and those of the granulometric methods cited for estimating permeability, i.e. Hazen, Krumbein and Monk, and Alyamani and Sen, the results of Mbonimpa et al. (2002) have also been included. For this comparison, samples M-1–M-10 were chosen because they are independent of samples S-1–S-16 used to obtain Eq. (8). Figure 9 shows the results obtained for the samples in increasing order of permeability values.

Fig. 9
figure 9

Permeability values from different sources for the analysed natural soil samples

Full size image

Although the method of considering the granulometric gradation is different in each model, the first observation is that they all present a high correlation. Averaging the values provided by Krumbein and Monk’s model gives a value that is 6.6 times higher than that of Hazen’s model, 5.1 times higher than Alyamani and Sen’s model, and 2.7 times higher than Eq. (11). In our opinion, the first two models give very high values, up to ~ 1 Darcy for sample M-9, which has an average grain size of 1.6 mm and a grading coefficient of 1.8. For aggregates selected from gravel pits, which typically have higher grain sizes, this difference can produce a clear overestimation in drainage performance. There is a particular similarity between the results from Eq. (11) and those from Hazen’s model due to the high correlation coefficient between d10 and dC (with dC ~ 1.1·d10). This is probably because the standard deviation of the grading coefficient with respect to its average value (1.76) is very low. The fact that, on average, the values obtained with the methodologies from these three studies are similar to those obtained with the proposed method indicates that the samples had a similar degree of compaction to the dry-loose samples considered in this study. The results from Mbonimpa et al. (2002) equation, show a negative correlation with Krumbein and Monk and with Alyamani and Sen due to, as already cited, in the first the permeability values increase with the uniformity coefficient.

The major drawback of Alyamani and Sen’s model is its way of obtaining the grain size d0, corresponding to the intercepted diameter, because the fitting line is obtained on a truncated granulometric curve. To obtain the final expression developed in that work, the slope of the curve was included. A narrow granulometric curve will correspond to a highly graded medium with more permeability than a wider curve with the same d10 (less graded). At the same time, the cut-off point of the approximation line of the highly graded medium will be greater than that of the poorest graded medium, for which this value will be clearly lower than d10.

To check that Eq. (11) is valid for sands with compaction degrees other than dry-loose, it was applied to the wet-packed sand data given by Beard and Weyl. Figure 10 shows these porosity–permeability data together with the results of applying Eq. (11). The R2 coefficient is sufficiently high (0.98), and the average geometric deviation between Beard and Weyl’s data and Eq. (11) is ×  ÷ 1.11. Although the average deviation with respect to Beard and Weyl’s data is very small, it must be pointed out that the lower permeability values in their data were estimated rather than being measured.

Fig. 10
figure 10

Permeability versus porosity values from Beard and Weyl (1973) together with the results from Eq. (11) for the grain size, porosity, and grading coefficient values

Full size image

For the more graded data (lower SC values), the results from Eq. (11) are, on average, 1.27 times lower than those predicted by the Kozeny–Carman equation. As in all expressions for estimating permeability, the value of the constant factor has a great influence on the results—changing the value of 4.3 used in Eq. (11) to 5.45 produces values that match the Kozeny–Carman results. The main difference is that, for the less graded data (higher SC values), the Kozeny–Carman equation produces values that are more than seven times those obtained by Eq. (11). This is to be expected, because the former considers the same constant for any grading coefficient.

Finally, the permeability values obtained from Eq. (11) are compared with the results from the Kozeny–Carman equation for Beard and Weyl’s wet-packed data in Fig. 11. In Fig. 11, it can be seen that the Kozeny–Carman estimation progressively moves away from the obtained values as the measured permeability decreases, despite the fact that, in the tests of Kozeny’s equation by Carman, the mean grain sizes of 10–100 μm were clearly lower than those analysed in this study. The distance of the Kozeny–Carman results from the diagonal (estimated permeability equal to measured permeability) suggests a very high deviation for low permeability values. In addition to the accuracy of the estimation obtained through Eq. (11), its dispersion is clearly lower (R2 = 0.98) than that resulting from the Kozeny–Carman equation (R2 = 0.92).

Fig. 11
figure 11

Comparing permeability results versus porosity between Kozeny–Carman equation and Eq. (11) for Beard and Weyl wet-packed data

Full size image

As it is said in the introduction, the addition of porosity substantially improves the quality of permeability estimations. However, in drainage engineering practice, this estimation from GSD is very usual, whose main limitation is, as it argued along this work, the differences occurring in many cases with respect to the initial loose packing conditions.

In this study, several grain shapes of samples are not examined, so we cannot comprehensively ascertain the influence of grain shape on the measured permeability. However, from the images of the samples (Fig. 12), it is observed that the grains show different shapes from rounded to angular so that an intermediate value of the shape factor of α = 1.26 can be adopted, between 1 (for spheroidal grains) and 1.52 (for natural sand, Nguyen and Indraratna 2020). Then, considering that 4.3 × 1.26–5.42, by including the shape factor, Eq. (11) would become:

Fig. 12
figure 12

Photogram of samples S-6 (a) and S-8 (b)

Full size image
$$k=\frac{5.42}{\alpha }\frac{{d}_{\mathrm{GR}}^{2}\cdot {\varnothing }^{3}}{{S}_{\mathrm{C}}^{2}\cdot {\left(1-\varnothing \right)}^{2}}$$
(12)

Note that the constant coefficient finally obtained practically coincides with the initial Kozeny-Carman constant CKC shown in Eq. (4). Thus, for spherical grains (α = 1) and homometric grain sizes (SC = 1), Eq. (12) matches with Kozeny-Carman equation at 99.4% of confidence.

Strength tests have also not been included in this study, but there are numerous studies that relate grading coefficient to mechanical strength (Monkul 2013; Hyodo et al. 2017; Sun et al. 2019; Xin et al. 2019; Aziz 2020), so the authors believe that in the case of drainages under load, it would be necessary to analyse this aspect.

Conclusions

As a conclusion, and with the described limitations, this study has established a new effective diameter dC which characterises drainages because it is directly related to permeability. This parameter can be obtained in two immediate ways: numerically using Eq. (6) or graphically. The established new effective diameter results in a very intuitive and practical size to indicate both size and grading of a soil. Although the developed relationship Eq. (6) to obtained dC: \({d}_{\mathrm{C}}={d}_{50}/({d}_{75}/{d}_{25})={d}_{50}/{S}_{\mathrm{C}}^{2}\) from GSD data has shown a very low deviation, it would be interesting to overtly verify to any soils. The relationships Eq. (7) and (8) developed in this study to estimate permeability values from dC for loose packing sands \(k\left({d}_{\mathrm{GR}}, {S}_{\mathrm{C}}\right)=1.0\cdot {\left({d}_{\mathrm{GR}}/{S}_{\mathrm{C}}^{2}\right)}^{1.43}=1.0\cdot {d}_{\mathrm{C}}^{1.43}\), show a high agreement with the measurements of existing data (Beard and Weil). Although comparative assessment on these relationships shows high relative differences from existing correlations, the new ones are more reasonable as they do not reach such high permeability values given the grain size characteristics of the samples. Equation (8) provides an estimation of the permeability of drainages in civil works using only this effective diameter, although it is not truly independent of the granulometric gradation.

Moreover, the new formula Eq. (11) developed for estimating the permeability for sands with any packing \(k=4.3\frac{{d}_{\mathrm{GR}}^{2}\cdot {\varnothing }^{3}}{{S}_{\mathrm{C}}^{2}\cdot \left(1-{\varnothing }^{2}\right)}\), shows a strong contrast to existing relationships in the literature that include gradation coefficients. Although several more advanced techniques are providing new equations to estimate the permeability values of aggregates, the relationships obtained with the conventional parameters represent a lower cost and accessible solution that includes the main factors affecting permeability. It represents a clear contribution to the permeability estimation of unconsolidated detritic surface media. Similar to the Kozeny–Carman equation, Eq. (11) takes into account the degree of compaction by including porosity, but also includes the grading, so that it can be considered of general application to any unconsolidated medium composed of natural sands. According to Eq. (11), the permeability decreases with the grain grading, presenting a clear difference with respect to the relationships in the literature that included this grading in the Kozeny–Carman equation.

The higher accuracy of the Eq. (11) proposed in the present study with respect to the Kozeny-Carman equation has been verified with widely recognised data on natural sands (see Fig. 11). Considering that this study focuses on granulometric expressions for estimating permeability of granular media for which the grain size distribution is available, the ease of use of Eq. (11) lies in the fact that all the terms related to grain characteristics are extracted directly from the GSD, without the need for any additional calculations.

With regard to the constant factor of equation to estimated permeability, it would not initially depend on the structural parameters of the medium. In the authors opinion it could present a small variability over the appropriate value due, among other reasons, to uncontrolled shortcomings in the measurements associated with the instrumentation itself and not with the methodology.

The proposed Eq. (11) is currently validated with soil samples having a grading coefficients SC in the range 1.06–2.77 (CU up to ~ 13), so further effort is needed to confirm the model performance onto the soils with wider gradation. Considering the grain sizes used in this study, it is not ascertainable that developed relationships can apply to samples comprising aggregates with an average grain size» 2 mm (as used in ballasted railway tracks). However, the nature of changes introduced in the Kozeny-Carman equation neither allows to reject the new relationships. To verify the application of the new relationships to these media, it would be necessary to develop new measurements with a design of experiments according to the characteristics of the samples, using the corresponding shape factor if they are formed with crushed aggregates. In this study, as mentioned in the “Estimate permeability from granulometric data” section, the influence of the grain shape of the samples is not examined. In order to comprehensively determine the influence of grain shape on the measured permeability, a study with a wide variety of sample origins would be necessary. However, considering the little range of this factor, the use of a mean value from the ranges of variation given in the literature can be considered as a good enough approximation. In short, Eq. (11) without considering the shape factor and Eq. (12) including it, complete the influence of the main factors affecting the permeability value of granular media.