Introduction

Groundwater heat pump (GWHP) systems utilize groundwater as a heat source and/or a heat sink for temperature regulation purposes in buildings. GWHPs usually comprise pumping up groundwater from a production well to a heat exchanger, and re-injecting the heat exchanged water into the aquifer through an injection well; see Fig. 1. This technology can reduce the electricity demand by ~ 60–70% compared to conventional electric heating. However, the economic and environmental benefits of GWHPs are hampered by various clogging mechanisms which obstruct the groundwater flow in well filters, groundwater pumps, heat exchangers, pipes, etc. (Jenne et al. 1992; Bakema 2001; Possemiers et al. 2016; Snijders and Drijver 2016; Gjengedal et al. 2020).

Fig. 1
figure 1

Sketch of a typical groundwater heat pump system (GWHP) design in Melhus, Norway (Gjengedal et al. 2021)

Full size image

A groundwater heat pump system resembles a siphon; an inverted U-shaped tube that moves liquid up from one reservoir and down to another one under the influence of gravity and cohesive forces (Çengel and Cimbala 2010). This creates vacuum pressures on the top side of the GWHP, which initially lowers the required pumping head from the submersible pump in the production well. However, the vacuum pressures induce gas formation which will clog the system and increase the required pumping head through the pipeline. The siphon effect thus leads to unstable operating conditions for the submersible pump. Designers of GWHPs and other systems containing injection wells are therefore advised to keep the pipes pressurized (i.e., with pressure higher than the atmospheric) (Sniegocki and Reed 1963; Olsthoorn 1982; Andersson 1988; Jenne et al. 1992; Banks 2012; Snijders and Drijver 2016; Guttman et al. 2017; Gjengedal et al. 2019).

Limited literature exists on the cost–benefit of pressurizing versus gas clogging and how to design and dimension gas control measures. This knowledge gap is sought tightened in this article by presenting analytical tools from hydraulic engineering applied to gas clogging problems in GWHP systems. Additionally, practical advice on how to mitigate gas clogging is presented and discussed.

The case study focuses on the Lena terrasse GWHP plant in Melhus, Norway, which currently operates without dedicated measures to pressurize its groundwater pipes. This work is a continuation of a theoretical analysis of gas clogging in GWHP systems (Gjengedal et al. 2019) and an article concerning the instrumentation and monitoring of the same GWHP system as in this study (Gjengedal et al. 2021). Two years of monitoring have provided data for testing and modifying the conclusions in Gjengedal et al. (2019, 2021) and facilitated new insights into troubleshooting and solving gas clogging problems.

Gas in water pipes

Gas can form in pipes either by degassing of dissolved gases in the water or in-leakage through improperly sealed pipes. For dilute solutions, Henry’s law states that the solubility cA of gas A is proportional to the gas’ partial pressure pA in contact with the solvent liquid (Stumm and Morgan 1996):

$${p}_{A}={K}_{H, A}{c}_{A}$$
(1)

where the solubility constant KH,A typically increases with temperature. Since Eq. 1 is valid for all gases, the total amount of gas dissolved in water cgas is proportional to the total gas pressure pgas. Thus, if the liquid pressure p falls below pgas, or the temperature increases, gas will escape the liquid phase (i.e., degas). In a review of gas-phase formation during thermal energy storage in near-surface aquifers by Lüders et al. (2016), 95% of the groundwaters were found to be in contact with pgas ≤ 1.41 atm, with a median pgas = 1.02 atm. Pressure drops below atmospheric pressure (patm = 1 atm) creates a pressure gradient from outside towards the interior of the pipe. This may facilitate air in-leakage through improperly sealed parts of the pipeline (Bakema 2001). Vacuum pressures thus expose the pipeline to risk of gas formation both from in situ degassing and air in-leakage.

Flowing water is exposed to pressure drops when the elevation and/or the velocity increases and due to frictional losses to its surroundings (Çengel and Cimbala 2010). Thus, if groundwater is extracted from an aquifer near gas saturation pressures, the pressure drop resulting from locally elevated water flow around the well filter may lead to degassing. Surface tension between the gas bubbles and porous media then may obstruct (i.e., clog) the water flow and increase the pressure drawdown in the extraction well. Water flow through the GWHP system will result in pressure drops from frictional losses and higher elevations (i.e., the siphon effect). This makes the injection well prone to vacuum pressures. Thus, gas bubbles moving with the flow can also clog the injection well filter and the surrounding aquifer formation, before eventually becoming dissolved if sufficient overpressure (p > pgas) is applied to the bubbles in the aquifer. According to Bakema (2001), gas clogging is a bigger problem in injection well filters than in extraction well filters. Furthermore, degassing and air in-leakage may indirectly increase the precipitation potential for typical incrustation minerals such as oxides and carbonates; oxygen in-leakage will trigger oxidation of iron, while CO2 degassing decreases oxide/carbonate solubility by increasing the pH.

Gas does not necessarily accumulate where it first forms but tends to rise to the highest point in the pipes due to buoyancy forces. The drag exerted by the flow on a gas bubble opposes this effect by pushing the bubble in the flow direction. The balance between these two effects can be expressed by the Froude number Fr (Çengel and Cimbala 2010)

$$Fr=\frac{q}{\sqrt{g{L}_{c}}}$$
(2)

where q is the flow rate Q divided by flow cross section A, g is gravitational acceleration, and Lc is a characteristic length (i.e., the pipe diameter in a circular pipe). Extensive theoretical and experimental research has been conducted to find a critical Froude number Frc; the minimum Froude number which causes gas bubbles to be carried with the liquid flow. Some of the relevant results for this case study are listed in Table 1. The results show that Frc depends on the pipe inclination. For upward oriented pipes, the gas will move in the flow direction. For horizontal and downward facing pipes, experimental results indicate that Frc is lowest in vertical, higher in horizontal, and highest in inclined pipes (30–45°).

Table 1 Review of critical Froude numbers Frc for air bubble transport in water pipes of different inclinations and diameters
Full size table

The actual Froude number Fr must therefore exceed the maximum Frc for inclined pipes to remove gas from downward bends between horizontal and vertical pipe sections. If not, gas will accumulate in pockets at local high points and on the downward side of bends, where the flow velocity is unable to exceed the critical Frc number; see Fig. 2. This also means that an initially empty (i.e., a gas-filled GWHP system) must start operation at Fr > Frc to remove the gas and become water-filled. Conversely, a system where Fr < Frc will remain at least partly gas-filled during operation.

Fig. 2
figure 2

Gas pocket entrapped around a local high point of a pipe. The extra head loss caused by the gas pocket hgas is shown

Full size image

Gas pockets will lead to higher head losses in the pipeline (i.e., clogging) by inducing open channel or gravity driven flow. This is known as waterfall flow among pipe engineers. The gas phase has lower density than water, meaning that the pipe pressure at the top and bottom of a gas pocket will be approximately the same. The gas pocket then causes a head loss hgas equal to the elevation drop from top to bottom of the gas pocket (Corcos 2003); see Fig. 2. Thus, vacuum pressures and subcritical Froude numbers are sought avoided in pipe networks.

Site description

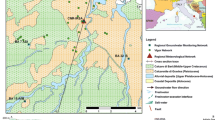
Ten groundwater heat pump systems operate within a radius of 500 m in the town center of Melhus, Norway (Fig. 3). All systems extract groundwater from the Melhus aquifer: a coarse unconsolidated ice marginal deposit from Younger Dryas, with the Melhus Ridge as its most prominent feature. The aquifer is hydraulically connected with River Gaula which controls the water table, some ~ 10–20 m below terrain level (Hellestveit 2018). A marine clay layer on top of the ice marginal deposit has left the aquifer with semi-confined characteristics and a saline, reducing water quality (Riise 2015).

Fig. 3
figure 3

Map of Melhus town center with the Lena terrasse GWHP location (Case study) indicated. Location of study area is also shown in the map inset in the upper right corner, where the highlighted area is Norway

Full size image

The Lena terrasse GWHP supplies 350 kW heating to 119 apartments; see the area marked with “Case study” in Fig. 3. The groundwater part of the system comprises a production well with a submersible pump, water pipes, a heat exchanger, and an injection well; see Fig. 4. The production well is 36.4 m deep, with a screen of 6 m, and a 1-m sump pipe below the screen. A Grundfos SP 60–5 pump is installed right above the well screen, operating at variable speed drive between 6 and 16 l/s. The injection well is 36.5 m deep, with 10 m of screen, and 3 m of sump pipe in the bottom. Both wells are made up of 158/168 mm ID/OD stainless steel casing and 150/161 mm ID/OD screens with 1 mm continuous slots. The gasket plate heat exchanger conducts heat from the groundwater to a secondary circuit of ethylene glycol with a capacity of 260 kW. The temperature of the produced groundwater is reduced 3–5 K in the heat exchanger. For an in-depth description of the system and heating operation at Lena terrasse, see Gjengedal et al. (2021).

Fig. 4
figure 4

Modified from Gjengedal et al. (2021)

Conceptual model and monitoring scheme of the Lena terrasse groundwater heat pump system (GWHP), including monitoring of p = pressure, T = temperature, Q = groundwater flow rate, and P = power demand of the pump.

Full size image

The Lena terrasse GWHP system has suffered from major incrustation problems caused by iron oxides and sediments, especially in the heat exchanger and the injection well (Riise 2015; Gjengedal et al. 2020). This has motivated the authors to examine measures to improve the GWHP’s operational conditions. The piping part of the GWHP (Table 2), from the submersible pump inlet in the production well to the end of the injection pipe inside the injection well, has been the focus during the present work.

Table 2 Pipeline structure from submersible pump to the end of the injection line. Data partly from Gjengedal et al. (2021)
Full size table

Methods and materials

Pressure, temperature, flow rate, and pump power demand have been continuously monitored at Lena terrasse since April 2019; see Table 3. Two years of monitoring data, from May 2019 to May 2021, are presented in this article. The pressure sensors p1 and p4 are located inside the wells, but outside the submersible pump inlet and injection pipe outlet, respectively. Step–discharge tests of the system have been performed semi-monthly according to a procedure developed by Gjengedal et al. (2020). One test carried out on 11 March 2021 is analyzed in this article. The test comprised operating the pump stepwise at four different frequencies (ω), 60, 70, 80, and 90% of the maximum, which yielded flow rates Q of 5.7, 8.5, 11.1, and 13.6 l/s, respectively. Meanwhile, pressures (p1–p4) and pump power consumption (P) were continuously measured. Each step lasted until the pressure measurements stabilized (i.e., 5–10 min). Additionally, a manual manometer (p*) was temporarily installed at the top of the injection well (see Fig. 4) and read off during each of the four steps. This location was expected to represent the minimum pressure in the groundwater circuit (Gjengedal et al. 2019) and thus of special interest with regard to gas clogging. Additionally, gas-related field observations were noted during visits to the GWHP plant.

Table 3 Monitoring equipment and accuracy. Data partly from Gjengedal et al. (2021). See Fig. 4 for location of instruments
Full size table

Pressures and pump power measurements during the step–discharge test of 11 March 2021 were used to produce four hydraulic grade lines (HGL), one for each step. A HGL visualizes the sum of pressure and elevation head of a fluid versus the pipe profile. Intersection between the hydraulic grade lines and the pipe profile indicates atmospheric pressure conditions (p = 1 atm). Hydraulic grade lines below or above the pipe profile indicate p < 1 atm and p > 1 atm, respectively (Çengel and Cimbala 2010). The hydraulic grade lines were drawn as straight lines between six points; five based on pressure measurements (p1–p4, p*); and one from calculation of the pumping head (hp) (Çengel and Cimbala 2010):

$${h}_{p}=\frac{P\eta }{\rho gQ}$$
(3)

where P is pump power consumption, η is the pump efficiency including the motor and frequency converter, ρ is water density, g is gravitational acceleration, and Q is volumetric flow rate. Grundfos (n.d.) provided η values of 43.1, 51.2, 55.6, and 57.5% for pump frequencies 60, 70, 80, and 90%, respectively. GPS measured elevation data of the wells were retrieved from Riise (2015). No internal pipe friction loss calculations were conducted. Lines where p = 1.41 atm and p = 0 atm were also drawn, representing the 95-percentile of groundwater gas pressures (Lüders et al. 2016) and the absolute vapor pressure, respectively.

Equation 2 was modified by using the definition of flow velocity q = Q/A for a water-filled circular pipe with cross-sectional area A = π d2/4. Based on critical Froude numbers Frc from Table 1 and diameters d from Table 2, critical flow rate Qc ranges could be calculated for each pipe segment:

$${Q}_{c, i}=\frac{\uppi \sqrt{g}}{4}F{r}_{c,i} \ {d}^{5/2}$$
(4)

where i = min, max corresponding to the minimum and maximum empirical Frc values in Table 1. Measured Q was plotted versus the critical flow rates along the pipeline. This was used to assess the likelihood of gas entrapment: Q ≥ Qc, max was interpreted as unlikely, Qc, min ≤ Q < Qc, max was interpreted as possible, while Q < Qc, min was interpreted as likely.

Results

Figure 5 displays 2 years of monitoring data from the Lena terrasse GWHP system. The pressure right after the heat exchanger (p3), pump power consumption (P), and pumping rate (Q) remains relatively stable during large portions of this period, despite the injection pressure (p4) increasing 10–15 m; see Fig. 5. The pressure build-up is due to well filter incrustations. This is evident from p4 which is lower after injection well rehabilitations. Thus, the increase in incrustation resistance in the injection well filter does not impact the head loss or pump power consumption between the heat exchanger and the end of the injection pipeline.

Fig. 5
figure 5

Two years of monitoring data (daily median) of groundwater flow rate (Q) pressure after heat exchanger (p3), pressure inside injection well (p4), and power consumption of the submersible groundwater pump (P). HE rehab. = heat exchanger rehabilitation, Inj. rehab. = injection well rehabilitation. 11.03.21 (purple star) indicates the time when the analyzed step–discharge test was conducted

Full size image

The P and Q is not perfectly correlated, as would be expected for a pump operating with a fixed resistance. For instance, in May–July 2020 Q first increases and later decreases, while P remains stable. This can be explained by the yearly snowmelt flood which leads to a peak discharge in River Gaula and a corresponding increase in recharge to the Melhus aquifer. This has been confirmed by water table fluctuations in nearby observation wells (Geological Survey of Norway (NGU) 2021).

Some gas-related field observations have also been noted. Large amounts of gas have released from the pipeline through a water tap located after the heat exchanger (Fig. 4) during water chemical sampling with a flow-through cell. Trickling or stream sounds have been heard from the groundwater pipes in the machinery room and the injection well drain, especially at low pumping rates.

Data from the step–discharge test of 11 March 2021 (purple star in Fig. 5) are presented in Fig. 6, in a format suitable to assess risk of gas formation (a) and gas entrapment (b) in the pipeline from the production well via heat exchanger to the injection well. Figure 6a displays hydraulic grade lines for pumping frequencies 60–90%. The plot shows that vacuum pressures occur at ω = 60–80%. At ω = 90%, the flow is pressurized (p > 1 atm) throughout the entire pipe circuit, but partly below the p = 1.41 atm-line. The lowest pressures are found on the injection side of the GWHP system. This is due to frictional losses as the water flows through the pipeline. It is evident from the HGLs’ inclinations that the frictional losses increase with pumping rate in the production pipe. Meanwhile, the head losses decrease as the pumping rate increases in the injection pipe. This indicates different flow regimes in the production and injection pipeline. The pressure in the injection well (p4) increases considerably, while the production well pressure (p1) stays relatively stable, as the flow rate increases. This indicates that clogging is more intense in the injection than in the production well filter.

Fig. 6
figure 6

Plots used to assess risk of gas formation (a) and gas entrapment (b) in the pipeline from the production well via heat exchanger to the injection well. Results from a step discharge test at the Lena terrasse GWHP plotted as (a) hydraulic grade lines (HGLs) based on pressure measurements (p1-4, p*) and pumping head (hp; see Eq. 3) at pump frequencies (ω) between 60 and 90% vs. pipe profile, p = 1.41 atm, and absolute vapor pressure (p = 0 atm) lines and (b) critical flow rates (Qc, min, Qc, max) for gas entrapment plotted versus measured flow rates (Q) in horizontal and downward inclined pipes. Stars represent downward bends (i.e., where Qc values are highest)

Full size image

Figure 6b shows measured and critical flow rates plotted versus length along the pipeline at different pump frequencies, ω. The Qc values vary little throughout the system. Exceptions are found in the downward bends (stars), downward vertical pipe segments, and the injection well where pipe diameter is smaller; see Table 2. Q < Qc, min at ω = 60–80% and Qc, min < Q < Qc, max at ω = 90% in the surface part of the pipeline (i.e., between the top of the production and the top of the injection well). However, the Qc, min is higher than all measured Q values in the downward bends. The measured pumping rates exceed the critical flow rates in the injection well.

Discussion

The results presented in Fig. 5 indicate a waterfall flow between the heat exchanger and the injection well during typical operating conditions (i.e., ω = 60–80%). This is evident from the parameters p3, Q, and P being independent of pressure in the injection well p4. This indicates that the submersible pump only lifts the water to the heat exchanger. The water then discharges by gravity down through the injection well (i.e., “waterfall flow”). The inverse correlation between head loss from p* to p4 and pumping rate Q at ω = 60–80% (Fig. 6a) further supports the assumption of a gravity-driven flow in the injection well. The opposite would be expected for a pressurized pipe flow (Çengel and Cimbala 2010), as observed between the groundwater pump in the production well (p1 + hp) and the heat exchanger (p2).

Vacuum pressures occur between the heat exchanger (p3) and the top of the injection well (p*) at pumping speeds between 60 and 80% (see Fig. 6a). This involves risk of gas formation in this part of the system. At the same pumping speeds, Q < Qc, min indicates risk of gas entrapment (i.e., pipes will remain partly gas-filled). This is confirmed by observation of gas release from the water tap in Fig. 4. The entrapped gas causes the gravity-driven waterfall flow down through the injection pipe. This is probably what is causing the trickling stream sounds heard in the machinery room and the injection well drain. The head loss then equals the elevation difference between the heat exchanger and the water table in the injection well, as shown in Fig. 2.

At 90% pumping frequency, the frictional losses in the pipeline and the injection well filter are high enough to keep the flow pressurized throughout the entire groundwater circuit. This means there is less risk of gas formation, although at high gas pressures (pgas > 1.1 atm) degassing could occur. It should be noted that the HGL in Fig. 6a represents intense injection well filter clogging conditions (i.e., elevated p4 values), which adds backpressure to the flow. As the head difference p1-p4 increases, the flow situation progressively resembles pumping from a lower to a higher reservoir rather than a siphon. Consequently, the potential for vacuum conditions and gravity-driven waterfall flow down through the injection well decreases. However, vacuum conditions could occur at higher pumping frequencies than shown in this study after injection well rehabilitation. This illustrates that vacuum conditions and waterfall flow are dynamic phenomena.

The flow rate is in the range Qc, min < Q < Qc, max when ω = 90%, meaning gas entrapment is possible but not definitely occurring. This indicates that flushing the system at 90% could be enough to push out some of the stagnant gas pockets, but not from the local high points. Particularly, gas entrapment risk is associated with downward bends marked with stars in Fig. 6b. At these points, the submersible pump will not be able to remove the gas (i.e., fill the pipeline with water) even at max pumping. This implies that if the GWHP system is filled with air upon start-up, the system will never become completely water-filled, but remain partly gas-filled.

There is a risk that gas bubbles are carried with the flow and clog the injection well filter and aquifer formation, because the flow rates are higher than the critical one in the injection pipe (Fig. 6b). Gas clogging would lead to a rapid pressure build-up (i.e., within seconds–minutes) in the injection well (Bakema 2001). The injection well clogging at Lena terrasse is a much slower process (i.e., on the scale of weeks-months) and is attributed to sediments and iron oxide incrustations. The negligible injection well filter gas clogging could be explained by sufficient overpressure at the end of the injection pipe (p > 2 atm (Fig. 6a)) to dissolve the gas before injection into the aquifer.

The risk of gas formation and entrapment at all pumping rates, although lower at ω ≥ 90%, suggests that measures against gas clogging should be considered for the Lena terrasse GWHP.

How to avoid gas clogging

The easiest way to keep the Lena terrasse GWHP pressurized and to hinder gas entrapment would be to run the system continuously at larger pumping rates; see Fig. 6. However, this would also involve numerous disadvantages. Firstly, it would mean larger pumping costs and less flexibility to adjust pumping rate to the heating demand during part load conditions. Secondly, higher flow rates also mean more turbulence, which is known to trigger erosion in the well filter and consequently sand production (Bakema 2001; Snijders and Drijver 2016). Lastly, laboratory experiments have shown that reaction kinetics of calcite (Zeppenfeld 2005) and iron hydroxides (Du et al. 2018) precipitation increase with increasing turbulence. Thus, increasing the pumping rate does not seem to be an appropriate solution to gas clogging in GWHP systems.

Alternatively, the pressure in the groundwater circuit could be increased without increasing the pumping rate. To achieve this, the pipe network must be modified to increase the frictional losses on the injection side of the system. This can be done either by installing a narrower injection pipe (Olsthoorn 1982; Corcos 2003) or a constant or adjustable orifice at the end of the injection line (Sniegocki and Reed 1963; Olsthoorn 1982; Andersson 1988; Guttman et al. 2017). Solutions which allow adjusting the frictional losses are preferred since the groundwater pumping rate in GWHP systems typically is regulated by the heat demand. An automated backpressure valve offers the desired flexibility (Snijders and Drijver 2016). The valve should be installed at the end of the injection pipe: (1) below the natural groundwater table to avoid water cascading and (2) above the well screen to allow gas bubbles to rise to the top of the injection well instead of clogging the well filter (Guttman et al. 2017). However, the technical complexity of these valves makes them expensive. A simpler, but still adjustable measure to pressurize the injection flow was chosen at Arlanda airport’s aquifer thermal energy storage (ATES, i.e., a GWHP also comprising seasonal storage of heat) system in Stockholm, Sweden. Multiple narrow injection pipes were installed inside the same injection well with on/off valves in the top part. This facilitates stepwise adjustment to the frictional flow resistance by adjusting the number of open injection pipes (O. Andersson, personal communication, 13 January 2022). On the downside, this solution may necessitate larger well diameters (i.e., higher drilling costs).

Figure 7 displays two suggested system designs and instrumentations to avoid gas clogging. The designs include the following:

  • A backpressure valve at the end of the injection pipe (a) or multiple narrow injection pipes (b)

  • Pressure monitoring on top of the injection well

  • Air release valve(s) at the local high point(s) where gas tends to get trapped

Fig. 7
figure 7

Two proposed injection well designs and instrumentations to mitigate gas clogging. Red color indicates components which are currently not custom to the GWHP design in Melhus, Norway. The hL’s correspond to flow head losses through various components: hL, valve through the backpressure valve, hL, pipe through the injection pipe, and hL, filter through the well screen and filter. hwt represents the head difference from top of the injection well to the natural water table, and hc is the chosen critical head at the top of the injection well. The p’s represent pressure measurements

Full size image

The frictional resistance that must be added by the backpressure valve hvalve and injection pipe hpipe must obey the equation:

$${h}_{valve}+{h}_{pipe}={h}_{c}+{h}_{wt}-{h}_{filter}$$
(5)

where hc is the critical overpressure necessary to avoid degassing, hwt is the height from the top of the injection well down to the natural water table, and hfilter are the frictional losses in the injection well filter; see Fig. 7. hwt and hfilter can be measured in the field when the system is turned off and on, respectively, while hpipe can be estimated from typical friction coefficients for internal flow (Çengel and Cimbala 2010). Conversely, if hvalve + hpipe < hwt − hfilter, then the injection pipe will not be pressurized. This was observed at the Lena terrasse GWHP when an insufficiently narrow constriction was installed at the end of the injection pipe in Spring 2020. As a result, the system remained unpressurized.

The hc must be chosen, either based on direct gas measurements of the aquifer or typical values with some factor of safety. Since direct gas measurements are expensive and therefore seldom carried out, the 95-percentile for gas pressures at 1.41 atm from Lüders et al. (2016) could be used as a design baseline. A hc = 0.5 bar \(\approx\) 5 m of water column was chosen for the Fladie GWHP in Sweden (Andersson 1988). This corresponds with Lüders et al. (2016) pgas value multiplied by a ~ 1.25 overpressure safety factor, and thus seems like a resonable hc value.

The extra pumping head required (\(\Delta\) hp) at the Lena terrasse GWHP would approximately equal the hc value. This is due to the present waterfall flow which comprises injection well head losses equal to hwt; see Fig. 7. Using Eq. 3 and assuming an average yearly pumping rate Q = 10 l/s (i.e., ω ~ 75%) at Lena terrasse, \(\Delta\) hp = 5 m, g = 9,81 m/s2, ρ = 1000 kg/m3, η = 50%, yields an extra pump power consumption ~ 8600 kWh/year. This introduces relatively small extra operational costs to the system, which had and average power input ~ 300 000 kWh/year to the heat pump and submersible pump in 2019–2020. Still, it discourages supplying more backpressure hvalve than needed to satisfy Eq. 5, as this would increase the pumping costs. A pressure sensor is recommended at the top of the injection well to make sure the right resistance \({h}_{valve}+{h}_{pipe}\) is supplied to maintain p = hc at the top of the injection well. Both the hpipe and hfilter head losses depend on the flow rate, while the latter is also strongly dependent on well filter incrustation extent. Accordingly, \({h}_{valve}+{h}_{pipe}\) must be regulated, with less constriction of the flow at higher flow rates and as the injection well filter clogs.

Independent of the pressure being pumped up to a level above hc, the flow rate will still not be sufficient to remove entrapped gas. The system would then benefit from air release valves at the local high points to release entrapped gas from the pipes (Corcos 2003; Pozos et al. 2010). Double orifice air valves are typically used for this purpose (Chadwick et al. 2013). The designer should make sure that p > 1 atm where the air release valves are located, to avoid gas in-leakage through the valves. The need for air release on local high points also stipulates that the number of bends and local high points should be kept to a minimum. During startup of an initially gas-filled system, the air release valves will let out entrapped gas and make sure the system gets filled with water. At Lena terrasse, four local high points where air release valves should be installed are identified: at the top of the production, at the top of the injection well, and before and after the heat exchanger; see Fig. 6b.

Backpressure valve or multiple injection pipes, pressure sensors, and air release valve(s) introduce extra investment costs for GWHP systems, but cause relatively modest extra operational costs. The potential benefits from pressure control, although not quantified here, justifies considering these measures for the Lena terrasse GWHP and during the design phase of new systems.

Conclusions

Monitoring data and field observations show that the groundwater pipes at the Lena terrasse groundwater heat pump (GWHP) system are partly gas-filled during operation. This is caused by vacuum pressures and the associated risk of gas formation, and groundwater flow rates which are insufficient to remove gas from the pipeline. The risk of both gas formation and gas entrapment is higher at lower pumping rates and on the injection side of the heat exchanger. The gas leads to a gravity-driven waterfall flow from the heat exchanger down through the injection well, where the head loss equals the elevation drop.

Attention should be directed towards pressurizing (p > 1 atm) the system to mitigate gas clogging. The overpressure should be adjustable, to accommodate changing pumping rates and injection well clogging conditions. This can be achieved either by (1) installing a backpressure valve at the end of the injection pipe or (2) multiple injection pipes regulated by on/off vales inside the same injection well. The valve or pipes should be designed and regulated to maintain an overpressure hc ≥ 5 m water column. The pressure minimum is typically found at the top of the injection well. A pressure sensor should be installed at this point to document that the system is kept sufficiently pressurized. Local high points are especially prone to gas entrapment. Air release valves should be installed at these locations to release entrapped gas and make sure the system is kept water-filled.

The extra required pumping head from the backpressure valve or multiple injection pipes would approximately equal the chosen critical overpressure hc. This introduces quite modest extra operational costs to the GWHP.