Introduction

Mass movements on slopes, both at regional and detailed scales, are probably the most frequently researched topic by engineering geologists. According to Hungr et al. (2014), of the earliest mass movement classifications was published by Baltzer (1875), who was probably the first to define three basic types of movement: fall, slide and flow. The first classification system published in English and accepted by experts and scientists in many countries was published by Varnes (1978). According to Varnes, there are five basic types of movements: fall, topple, slide, lateral spread and flow; a complex mass movement on a slope is a combination of two or three of these basic movement types. In terms of the type of displaced material, movements can be divided into those that occurred in rock masses, coarse-grained soils and fine-grained soils, amounting to a total of 29 types of mass movements on slopes (Varnes 1978). Varnes’ classification scheme has been supplemented over time (e.g.Cruden and Varnes 1996; Highland and Bobrowsky 2008; Hungr et al. 2014), but the basic principle according to which movements are classified in terms of the type of movement and type of displaced material has remained unchanged to date. According to Varnes (1978), in falls, a “mass of any size is detached from a steep slope or cliff, along a surface on which little or no shear displacement takes place, and descends mostly through the air by free fall, leaping, bounding, or rolling, movements are very rapid to extremely rapid and may or may not be preceded by minor movements leading to progressive separation of the mass from its source.” According to the same author, a topple is a “kind of movement consists of the forward rotation of unit or units about some pivot point, below or low in the unit, under the action of gravity and forces exerted by adjacent units or by fluids in cracks, it is tilting without collapse.” Although these movement types differ, for the needs of this research, rockfall and rock topple slope movements are treated as a single process: rockfall. If the described process occurs in a rock mass at the toe of a steep slope or cliff, it generates sediment body made of rock fragments called talus (Bates and Jackson 1984). The sizes of these fragments range from a few centimeters to blocks with volumes as large as 100 m3 or more, representing a risk for both people and structures regardless of whether they are located within the source area, talus slope or rock-fall shadow (Parise 2002). To define locations for further or more detailed research, the studied terrain must be evaluated to define areas where this process is most likely to occur. This type of approach disregards the volume of the detached blocks and their trajectories, two important variables that can be important when deciding which parts of a slope should have priority in remediation. In the literature, Frattini et al. (2008) systematized the main factors that determine whether a rockfall will occur, including the rock mass strength (Hoek and Brown 1988), discontinuity condition and its spatial orientation relative to the slope (Hoek and Bray 1981), rock mass weathering degree (Matsouka and Sakai 1999; Jaboyedoff et al. 2004), and local static or dynamic loading conditions (Kobayashi et al. 1990). In that paper, the authors gave a brief presentation of the current rockfall hazard assessment approaches. Examples of zoning research in which rockfall-prone areas were identified have been presented, for instance, by Loye et al. (2009), Shirzadi et al. (2012), Marquínez et al. (2003), Bostjančić (2016), Bostjančić and Pollak (2020), and Depountis et al. (2020). In this research, to prepare a high-quality inventory of locations where rockfalls have occurred, the seed cell concept introduced by Süzen and Doyuran (2004) was applied and tested on talus polygons in the Dubračina River basin. This basin is located approximately 15 km (air distance) southeast of the city of Rijeka, which is, from a geological point of view, a carbonate-flysch overthrust zone. The basic input data used in this research were a geological map with a scale of 1:5000 prepared by the Croatian Geological Survey (2007a, 2007b, 2007c) and a bare-earth 1-m DTM obtained by airborne LIDAR at the end of March 2012. In addition to the above products, topographic maps with scales of 1:5000 and 1:25,000 as well as a digital orthophoto at a scale of 1:5000 were used. The main objective of this research was to prepare a reliable rockfall susceptibility map that emphasized rockfall-prone areas using the bivariate statistical technique based on a talus deposit inventory map and available causative factor maps in the GIS environment. All presented maps in the paper were prepared with the grid of official Croatian geodetic coordinate system HTRS96/TM. Talus mapping was performed with a 1-m DTM and its topographic derivatives. The spatial impact of contributing factors on the rockfall process was tested by chi-squared statistics; then, the frequency ratio method (Lee and Talib 2005) was used to calculate the weight that determined the relative contribution of each factor class to the process occurrence. During this research, two susceptibility maps were produced: one using all available factors and another using only the four most significant factors. The quality of these two maps was compared, and the results are presented in this paper.

Study area

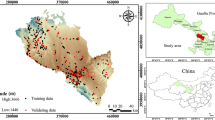
The Dubračina River basin, located in Primorje-Gorski Kotar County, covers a surface area of 43.57 km2. The river basin outline, taken from Ožanić et al. (2011), is shown in Fig. 1. Figure 2 shows the topographic map of the river basin at the 1:100,000 scale.

Fig. 1
figure 1

The location of the Dubračina River basin (white polygon) on Google Earth

Full size image
Fig. 2
figure 2

Topographic map of the Dubračina River basin (black outline) at the original scale of 1:100,000

Full size image

The river basin is bordered by limestone cliffs striking NW–SE (Dinaric striking) and formed by Neogene (Grimani et al. 1973; Blašković 1999) and Quaternary tectonics (Blašković and Tišljar 1983). A valley sits between the cliffs (Fig. 3) with underlying flysch deposits.

Fig. 3
figure 3

A slope map of the Dubračina River basin with hillshade as the basemap

Full size image

The basic geological map of the Dubračina River basin (1:100,000 scale) shown in Fig. 4 was published by Šušnjar et al. (1970). According to the authors, carbonate deposits of Cretaceous age, flysch deposits of Eocene age and Quaternary soils of diluvial and alluvial genesis can be mapped at the surface.

Fig. 4
figure 4

The basic geological map of the Dubračina River basin at the original scale of 1:100,000 (Šušnjar et al. 1970)

Full size image

Elevations above sea level within the study area, according to the DTM, range between -2 m and 923 m.

For the purpose of engineering-geological zoning research, the Croatian Meteorological and Hydrological Service (2011 unpublished) prepared a mean annual precipitation map of the Dubračina River basin for the 1981–2010 climatic period that shows that the precipitation in the river basin ranged between 1260 and 2260 mm. The minimum air temperatures ranged between − 10 and − 15 °C, and the maximum air temperatures ranged between 35 and 40 °C (Zaninović et al. 2008). These values were calculated based on data recorded over the 1971–2000 climatic period with a 50-year return period.

According to the Croatian Environmental Agency (2012), at a scale of 1:100,000, the river basin contains 11 level-3 CORINE land cover classes, among which broad-leaved forests and sclerophyllous vegetation account for 59.86% of the surface area.

This study area was selected for airborne LIDAR scanning because it contains abundant superficial processes that can be mapped on the surface. In addition to rockfalls, slides, creeps and erosional processes are also clearly visible. The final scanning result was a bare-earth 1-m DTM that, together with a geological map with a scale of 1:5000 prepared in 2007, caused this basin to be selected for the research presented in this paper.

Zonation methodology

According to the generally accepted zonation definition provided by Varnes (1984), the study area was divided into segments that differed according to the slope mass movement hazard degree. Aleotti and Chowdhury (1999) divided zonation methods into qualitative and quantitative. Qualitative methods are entirely based on the knowledge and experience of the expert preparing the zonation, whereas the purpose of quantitative methods is to minimize the impact of the subjectivity of an expert’s personal knowledge and experience on the final layout of the map. In this research, the weight of each factor class that affects surface process was calculated by applying the quantitative bivariate statistical zonation frequency ratio method (Lee and Talib 2005). The first and most important step in terrain zonation according to the susceptibility of an area to a certain type of slope mass movement is preparing the inventory. In this research, two inventories were prepared at the scale of 1:5000 to zone the terrain according to rockfall susceptibility. The first of these was an inventory of talus fans located at the toes of carbonate cliffs; the other inventory, derived from the first, contained rockfall source areas above the talus fans.

The talus inventory was prepared by visual analyses of the digital orthophoto and the hillshade map, slope map and contour map obtained from the bare-earth 1-m DTM. Figure 5 shows a characteristic location and a manually defined talus outline resulting from this visual analysis. Figure 5 also clearly shows the possibilities of the high-resolution DTM in terms of talus mapping. Without this model, the talus fan outlines would be much less precisely spatially defined.

Fig. 5
figure 5

Digital orthophoto and topographic derivatives of a 1-m high-resolution DTM enabling the remote mapping of talus outlines. a Digital orthophoto showing a talus fan. b Hillshade map generated by simulating the position of sunlight at an azimuth of 315° and an inclination of 45°. c Slope map. d Contour map with 1-m equidistance. e, f Talus outlines on the hillshade map (e) and on the digital orthophoto (f) resulting from visual analyses of the maps under a, b, c, and d

Full size image

According to the seed cell concept introduced by Süzen and Doyuran (2004), the terrain buffer zone around the crown and flanks of a slide should be used to define the pre-sliding conditions rather than the relief within the slide outline. Although sliding is not the same type of process, this concept is applied to define the conditions that enable the formation of talus as a consequence of a rockfall process. A graphical presentation of the seed cell concept is shown in Fig. 6.

Fig. 6
figure 6

Graphical presentation of the seed cell concept according to Süzen and Doyuran (2004) for the sliding process. a Slide block diagram. b Outline of the slide, contour lines, and catchment boundaries. c Valid seed cell buffer zone (gray colored) excluding cells that crossed the catchment boundary. The gray-colored cells are used for the spatial analyses

Full size image

In the first step, the seed cell talus inventory is prepared; around each talus polygon, a 25-m buffer zone is defined. A part of the automatically obtained zone around each talus fan is located at the rockfall source area, and another part is located on the slope under the talus fan and cannot represent the rockfall source area. Therefore, the part of the seed cell located under the talus fan is excluded from further analysis so that the surface of the resulting polygon is located only above the talus representing the rockfall source area. The exclusion of the areas that do not represent the source areas is defined manually in the GIS environment using the digital terrain model (Fig. 7).

Fig. 7
figure 7

Preparing the seed cell talus inventory. a Digital orthophoto showing the talus. b Talus polygon generated by visual analysis of the digital orthophoto and DTM. c Twenty-five-meter buffer zone around the talus polygon. d Seed cell talus polygon representing the rockfall source area

Full size image

The spatial distributions of superficial mass movements can be affected by various factors (the lithology, slope, aspect, etc.), and an overview of the factors used in susceptibility assessments was provided by Van Western et al. (2008). Each factor used in the assessments must be statistically demonstrated to affect the spatial distribution of the process; to do this, the chi-squared test was applied in this research. This test is based on comparing the observed and expected frequencies of the studied phenomenon (Davis 1986). An example of its application can be found in a paper published by Komac (2012). To be able to perform the test, each polygon in the inventory must be replaced with a centroid automatically in the GIS environment. However, due to the arched shape of the rockfall source area, 57% of the centroids are located outside the corresponding polygon. Therefore, the assessment was conducted on talus polygons for which 95% of the centroids were located within the polygon. It logically follows that the same factors affected both the spatial distribution of the talus polygons and the rockfall source areas since these landforms are always spatially associated. The chi-squared test begins with the hypothesis that the factor does not affect the occurrence of the superficial process. The chi-squared statistic values resulting from the test are then compared with the critical values listed in Table 1. The critical value depends on the degree of freedom and the required significance level.

Table 1 The critical values of the chi-squared test for 12 degrees of freedom (df) and significance level (p) 0.05
Full size table

The significance level represents the probability of rejecting a hypothesis when it is true. In other words, it represents an acceptable error probability, meaning that an impact on a process was indicated when this impact actually did not exist. In this research, a value of 5%, that is, 0.05, was taken as the acceptable error probability. The degree of freedom (df) was calculated according to the equation \(df=(m-1)\times (n-1)\), where “m” is the number of factor classes (number of rows) and “n” is the number of columns with frequencies.

Since, in this research, the number of columns with frequencies is always 2 (one column with observed frequencies and one column with expected frequencies), the number of degrees of freedom is one fewer than the number of factor classes.

If the value obtained using the chi-squared test is higher than the critical value, the hypothesis is rejected, meaning the factor affects the occurrence of the superficial process; if the value was lower than the critical value, the hypothesis is accepted, meaning the factor does not affect the occurrence of the superficial process. If we compare the observed and expected frequencies, the factor classes with positive and negative effects on the occurrence of superficial processes can be discerned.

To calculate the weight \(\left({W}_{i}\right)\) that determines the relative contribution of each factor class to the occurrence of the superficial process, the frequency ratio method (Lee and Talib 2005) was used in this research. It defines the weight as follows: \({W}_{i}=[A/B]/[C/D]\), where A is the area of the process within the factor class, B is the total area of the process, C is the area of the factor class, and D is the total area of all the classes. Both quotients from this equation must be expressed as percentages. Since this research aims to establish which areas have the greatest spatial probability of rockfall occurrence, the area of the process is represented by the rockfall source area.

After calculations, the weights must be normalized (Win), for which purpose the min–max scaling was used:\({W}_{in}=\left[{W}_{i}-{W}_{i-min}\right]/[{W}_{i-max}-{W}_{i-min}]\), where Wi is the weight before normalization, Wi-min is the minimum weight within the specific contributing factor, and Wi-max is the maximum. The normalized values obtained in this manner range between 0 and 1, and normalization must be conducted separately for each contributing factor.

In addition to the class weights, susceptibility mapping also requires the calculation of predictor (contributing factor) weights. The first step is to calculate the predictor rating (PR) defined by Ghosh et al. (2011) as follows:\(\mathrm{PR}=({W}_{imax}-{W}_{imin})/{({W}_{imax}-{W}_{imin})}_{min}\), where Wimax is the maximum class weight within each individual factor map, Wimin represents the minimum class weight, and \({{(W}_{imax}-{W}_{imin})}_{min}\) represents the minimum difference between the maximum and minimum weights determined among all the differences in the selected factor maps affecting the process. After the PR value has been calculated, a nine-point pairwise rating scale matrix for AHP analysis is usually formed (Saaty 1977). In this research, instead of the nine-point procedure, the PR values were used to form the matrix as described in the paper published by Althuwaynee et al. (2014). An illustrative example of a pairwise comparison square matrix with three factor maps is shown in Table 2.

Table 2 An illustrative example of a pairwise comparison square matrix wherein the input data are the predictor ratings (PR) obtained from three factor maps
Full size table

After the square matrix was solved, the eigenvector was estimated according to Ghosh et al. (2011) by normalizing the values in each column. Normalization was conducted by dividing each value in the matrix column by the sum of the columns, as indicated in Table 3. The sum of each row from the matrix represents the predictor weight. Finally, the values were multiplied by 10 to allow an easier comparison with the original PR values. Afterward, the shares of each factor map’s impact on the final susceptibility map were determined.

Table 3 An illustrative example of the eigenvector and predictor weight calculations for the causative factor maps
Full size table

Each factor map with normalized class weights must be multiplied by the predictor weights and then summed to obtain the raster susceptibility map (Voogd 1982). The predictor weights can also be determined based on the researcher’s experience (heuristic method). However, the described scheme based on statistical processing (AHP; Saaty 1977) is more objective.

The resulting map was reclassified into five classes (zones) that differed according to the terrain’s susceptibility to the occurrence of the studied process: extremely low, low, moderate, high, and very high susceptibility classes. Reclassification was performed automatically in the GIS environment by applying the Jenks (1967) method, which was also used by Komac (2012) in his research.

Each susceptibility map must be validated. For this purpose, the inventory was divided into the training set and the validation set. According to Chung and Fabri (2003), there are three ways to separate training data. This paper applied the random partition method to provide a generally even spatial distribution of the data in the validation set.

In this paper, the susceptibility map validation was performed using the calculation of the area under the (ROC) curve, where the x-axis represents the cumulative share of susceptibility class areas in relation to the total studied area and the y axis represents the cumulative share of the process area by susceptibility classes in relation to the total process area used for the susceptibility map validation. The input data used for the analysis included the susceptibility map reclassified into 100 classes arranged from raster cells (pixels) with higher susceptibility values to lower values and the binary map of the study area. In the binary map, all the cells with a value of 1 represented the rockfall source area used for the validation, whereas the rest of the study area had cell values of 0. The combination of the indicated maps in the GIS environment resulted in a diagram indicating the prediction level in the resulting susceptibility map.

Results

As mentioned before, the most important step in the mass movement susceptibility zonation is preparing the quality inventory of the studied process. A total of 94 talus polygons were mapped in the Dubračina River basin, covering an area of 1425.143 m2, which accounts for 3.27% of the total river basin area. Đomlija (2018) also worked on talus mapping of the Dubračina River basin. For each talus polygon, the pertaining rockfall source area was created as described above, after which the rockfall source area polygons were manually divided into the training set and the validation set. Their spatial distributions within the river basin are shown in Fig. 8. The total rockfall source area was 724,726 m2, of which the training set accounted for 63.88% and the validation set accounted for 36.12%.

Fig. 8
figure 8

Spatial distributions of talus (blue polygons), the rockfall source area training set (yellow polygons), and the rockfall source area validation set (white polygons)

Full size image

Using the chi-squared test and centroids of the talus polygons, the statistically significant factors that affect the spatial distribution of the talus were determined, presuming that the spatial distribution of the rockfall source areas was affected by the same factors. The results of the statistical analysis for each individual factor map are shown in Table 4. The only factor that was not used to prepare the susceptibility zonation map was the mean annual precipitation, as the test showed that this factor did not affect the spatial distribution of talus, that is, the rockfall source area. The factor maps used in the statistical analyses are shown in Fig. 9a, b. Notably, the slope map is shown in three classes for the clarity of presentation, while the 13-class map indicated in Table 4 was used in the analyses.

Fig. 9
figure 9

a Factor (predictor) maps (CORINE land cover, lithology, slope, aspect, distance from spring, distance from road) used in the chi-squared tests with rockfall source area polygons. b Factor (predictor) maps (distance from fault, distance from stream, distance from rock-soil geological boundary, and mean annual precipitation) used in the chi-squared tests with rockfall source area polygons.

Full size image
Table 4 Application of the chi-squared test on the talus inventory using available factor (predictor) maps
Full size table

For each factor class, the weight representing the relative contribution of the class to the occurrence of the studied process was calculated. In this research, the frequency ratio method (Lee and Talib 2005) was used to calculate weights as described in the “Zonation methodology” section using the training data set. Table 5 shows the input data and the calculation results of the class weight of each causative factor, i.e., the factor map.

Table 5 Weights of the causative factor classes obtained from the frequency ratio method (Lee and Talib 2005)
Full size table

The class weights were applied to calculate the predictor ratings (Table 6) used in the matrix pairwise comparison (Table 7); Table 8 shows the eigenvectors and predictor weights. If the value of the matrix cell in Table 7 is higher than 1, the predictor in the column has a greater impact on process occurrence in relation to the predictor shown in the row, and vice versa.

Table 6 Predictor rating calculations for the utilized factor (predictor) maps
Full size table
Table 7 Matrix pairwise comparison of predictor ratings for each causative factor (predictor) map listed in Table 6
Full size table
Table 8 Eigenvectors and predictor weights of the causative factor (predictor) maps used in this research
Full size table

The rockfall susceptibility map prepared by applying all nine factors whose impacts were proven through the chi-squared test is shown in Fig. 10. Table 9 shows the distribution of the rockfall susceptibility class areas.

Fig. 10
figure 10

Rockfall susceptibility map of the Dubračina River basin prepared with nine causative factors

Full size image
Table 9 Distribution of the areas of rockfall susceptibility classes from the map prepared with nine causative factors
Full size table

The quality of the rockfall susceptibility map was verified by overlapping the rockfall source area polygons used for the validation with the susceptibility map, after which the ROC curve was constructed, as shown in Fig. 11, dubbed the prediction rate curve by Chung and Fabbri (2003). The map quality was measured according to the area under the curve (AUC): a larger area signifies a better map quality, i.e., that the location of a future rockfall can be predicted with greater precision. Any map with an area under the curve smaller than 50 is considered a poor susceptibility map and should not be taken into consideration as relevant. The area under the ROC curve of the map prepared using nine factors was 89.72, indicating that the susceptibility map can be described as a good map according to the classification from Table 10.

Fig. 11
figure 11

Prediction rate curve for the rockfall susceptibility map of the Dubračina River basin arranged in classes with decreasing modelled susceptibility values. The map was prepared using nine causative factors

Full size image
Table 10 Descriptive ratings of susceptibility maps based on the area under the prediction rate curve
Full size table
Table 11 Distribution of rockfall susceptibility class areas in the map prepared with four causative factors (CORINE land cover, lithology, slope and distance from the rock-soil geological boundary)
Full size table

Table 8 shows that the susceptibility map is dominantly affected by four factors (CORINE land cover, lithology, slope and distance from the rock-soil geological boundary) at 86.3%. Therefore, for the purpose of comparison, a susceptibility map using only these four causative factors was prepared and is shown in Fig. 12.

Fig. 12
figure 12

Rockfall susceptibility map of the Dubračina River basin prepared with four causative factors (CORINE land cover, lithology, slope, and distance from the rock-soil geological boundary)

Full size image

The distribution of rockfall susceptibility class areas obtained by applying only the four most significant factors is shown in Table 11, and the ROC curve for this map shown in Fig. 13, in which the area under the curve is 88.91, is practically the same as that in the map prepared based on nine factors. However, significant differences can be observed by comparing the data in Tables 9 and 11.

Fig. 13
figure 13

Prediction rate curve for the rockfall susceptibility map of the Dubračina River basin arranged in classes with decreasing modelled susceptibility values. The map was prepared using four causative factors (CORINE land cover, lithology, slope, and distance from the rock-soil geological boundary)

Full size image

Discussion

A 1-m DTM was used in this research for the purpose of mapping talus naturally located at the toes of steep cliffs, as these areas are sometimes difficult to reach in the course of field work. Sometimes digital orthophoto does not allow vegetation-free talus and the steep cliffs above the talus, which is also free of vegetation, to be differentiated, and this significantly affects the precision of talus outline mapping. When talus is covered with vegetation, it is almost impossible to recognize it by visual analysis of a digital orthophoto. The use of a bare-earth high-resolution DTM for the purpose of talus mapping of the Dubračina River basin as an example generated very good results because, in this region, talus bodies are clearly visible in the model. These talus bodies are characterized by smooth terrain surfaces and fan-like shapes (Fig. 5). Talus recognition is also facilitated by its spatial-geomorphological position, as talus fans are located at the toes of steep cliffs that can easily be discerned using a DTM.

By applying the seed cell concept to the talus polygons, a rockfall source area inventory could be created in a standardised manner and used with applied susceptibility zonation methods to predict the future spatial occurrence of rockfall-prone/source areas. In this research, the rockfall source area used for the spatial analysis was defined as a 25-m buffer zone on the steep cliff above each talus polygon (Fig. 14). The width of the zone could vary as long as it was located on the cliff and not on the carbonate plateau, which was not the source area. The distance of 25 m was accepted after visual and manual analyses of the bare-earth high-resolution DTM of the study area.

Fig. 14
figure 14

Hillshade ground plan of a talus body, steep cliff and carbonate plateau with a 25-m buffer zone on the cliff above the talus polygon; this zone is the rockfall source area used in the spatial analysis to prepare the rockfall susceptibility map

Full size image

To enable a quality comparison, two rockfall susceptibility maps were prepared in this research. One of these maps was prepared with all nine factors established based on how they affect the surface process as established using the chi-squared test, while the other map was prepared with the four most significant causative factors whose aggregate-share impact on the nine-factor susceptibility map was 86.3%: the slope (61.6%), lithology (13.4%), land cover (6.2%), and distance from the geological rock-soil geological boundary (5.1%). According to the proposed descriptive susceptibility map quality ratings, both maps can be considered good, with practically identical areas under their ROC curves (Figs. 11 and 13). However, the map prepared by applying only four dominant causative factors (CORINE land cover, lithology, slope, and distance from the rock-soil geological boundary) can be considered better than the map considering nine factors. The high and very high susceptibility areas were much smaller in the map considering four factors, covering 5.25% of the river basin area, whereas in the nine-factor susceptibility map, the same area accounted for 12.41% of the river basin area, meaning the most critical locations rockfall-wise were defined much more precisely in the map prepared with four factors. The same can be said of the area of very low susceptibility, which was more than double in the map prepared based on four factors than in the nine-factor map, representing a much more realistic presentation of the condition of the study area. The four-factor susceptibility map is better because it rejects the factors whose impacts on the studied process were statistically proven by the chi-squared test but that actually had no impact on the occurrence of rockfalls in the Dubračina River basin. These factors included the distance from a spring, distance from a road and distance from a stream. This corresponds to the insights obtained from the scaled factor weights (Table 5), as the class that was spatially closest to the rockfall source area did not have the highest weight, which it should have had in an actual impact case.

The slope class with the highest weight was the 85° to 90° class, followed by the 80° to 85° and 75° to 80° classes. The stratigraphic unit designated Qs, which represented talus, had the highest weight. This is talus area that was mapped for the purpose of preparing a lithology map with a scale of 1:5000 when the high-resolution DTM of the study area was not available. It is clear that these talus polygons overlapped, to a certain extent, with the rockfall source area inventory prepared by virtue of a high-resolution DTM as part of this research. After the stratigraphic unit designated Qs, the highest weights pertained to units E1,2 and K2, consisting of carbonate rock masses, delimiting the river basin and largely representing areas where rockfalls are sourced. The Dubračina River basin is a carbonate-flysch overthrust zone. The central part of the river basin is a valley with underlying flysch that is largely covered with Quaternary soil of diluvial and alluvial genesis with very few bedrock outcrops surrounded by steep carbonate rock mass cliffs. It was therefore logical to prepare a factor map of the distances from the rock-soil geological boundary because this boundary is largely located in the interface zone between the Quaternary soils and steep cliffs that represent rockfall source areas; within this factor, the highest weight pertained to the 0-to-100-m distance class. Figure 15 shows an excerpt from the rockfall susceptibility map of the Dubračina River basin with an area of approximately 83,000 m2; in this map, red signifies a very high susceptibility degree. As expected, the area with the highest rockfall susceptibility degree is located on a steep cliff. However, some high-susceptibility areas can also be found at the toes of cliffs where talus polygons are located, which was not expected. This is because lithology was established through analyses to represent the second-most contributing factor on the susceptibility map immediately after the slope. Figure 15 shows the talus polygon from the lithology map with a 1:5000 scale used as a factor map in the susceptibility assessment; in this figure, it is evident that talus partially encompassed the cliff and also partially covered the talus at the toe of the cliff that was mapped by applying the 1-m digital terrain model. Because of the spatial overlap of the training rockfall source areas with the talus polygons from the lithology map (Fig. 15), talus (Qs) was found to have the highest weight in relation to the other units from the lithological map. This leads to the conclusion that talus (Qs) as a lithological unit must be excluded from rockfall susceptibility assessments in cases when talus inventories are prepared independently of existing lithology maps, as overlaps can occur between the training rockfall source areas and the talus polygons in the lithology map. This is particularly prominent in this research because the talus and rockfall source area inventories were prepared by applying the 1-m DTM, while, on the other hand, the lithology map used was prepared at a scale of 1:5000. In cases where talus (Qs) as a lithological unit is used to obtain a talus inventory in rockfall susceptibility assessments, it is understood that this unit must be excluded from the lithology map when spatial analyses are performed.

Fig. 15
figure 15

Spatial overlap of the very-high-susceptibility degree areas, talus polygons from lithology map, talus polygons from the inventory prepared using a 1-m DTM and the training rockfall source areas with the hillshade map as the background

Full size image

According to Wieczorek (1996), the most common natural mass movement triggers are intense rainfall, rapid snowmelt, water level change, volcanic eruption, and earthquake shaking. Scientific research of rockfall hazard triggers in Dubračina River basin is not conducted, but it can be assumed that intense rainfall and earthquake are playing the major role. The rapid infiltration of rainfall, causing rock saturation and a temporary rise in pore-water pressure, can be mechanism by which rockfalls are generated. Data from Croatian earthquake catalogue (Herak et al. 1996) clearly indicate the wider research area as very active seismic zone. According to Herak et al. (2011) PGA is 0.24 g for 475-year return period and maximum expected MCS earthquake intensity is 8° for 500-year return period (Kuk 1987) which along with data from catalogue consequently may indicate earthquake shaking as a potential trigger of rockfall hazard.

The results of the research presented here have shown that the factor maps used in this study can provide a quality rockfall-susceptibility map containing rockfall-prone areas at a scale 1:5000. The spatial orientation and condition of the rock mass joint sets, rock mass weathering degree, in addition to slope and lithology, are the most significant contributing factors defining the spatial probability of a rockfall occurrence. However, this research contributes to the preparation of susceptibility maps covering large and inaccessible areas with limited existing geological data, which is still a major challenge for researchers (Komac 2012).

Conclusions

Based on the results of research conducted in the Dubračina River basin, with frequent rockfall occurrences, the following conclusion can be drawn:

  • The 1-m DTM used in this study represents a very useful tool that can facilitate the preparation of high-quality talus inventories; talus fans are often located on very hard-to-reach terrain areas where remote sensing is the only data source.

  • If talus mapping is conducted based on the bare-earth high-resolution DTM, the seed cell concept can be used to prepare a high-quality inventory of rockfall occurrence locations. This means that the obtained inventory comprises the preconditions of rockfall initiation, which are then applied in the mapping process to define the rockfall source (prone) areas.

  • Bearing in mind that this research was conducted in the carbonate-flysch overthrust zone using the available factor maps, the four most significant factors that mutually affected the layout of the susceptibility map with a share of 86.3% were the slope (61.6%), lithology (13.4%), CORINE land cover (6.2%), and distance from the rock-soil geological boundary (5.1%).

  • The application of the bivariate statistical zonation method called the “frequency ratio method” was justified and enabled the production of a good-quality rockfall susceptibility map.

  • The quality of the rockfall susceptibility map prepared based on the four most significant contributing factors according to the “area under the curve” criterion did not differ from the quality of the susceptibility map prepared based on all nine factor maps available in this research and whose impact on the process was proven by the chi-squared test.

  • The areas of high and very high rockfall susceptibility degrees were smaller in the susceptibility map based on the four most significant factors than in the map based on nine factors, meaning that the spatial definition of critical areas was more precise in the four-factor map.

  • This research shows that reliable rockfall susceptibility maps can be prepared even for areas in which data on important causative factors of rockfall occurrences, such as spatial orientation and condition of the rock mass joint sets, and rock mass weathering degree, are not available. Collecting these data on very steep slopes where rockfalls occur is often very demanding and time-consuming field work and is also very expensive. It can therefore be said that where the terrain zonation scale is 1: 5000 or lower, a quality geological map and high-resolution DTM (plus a digital orthophoto) are sufficient to prepare a rockfall susceptibility map over a large research area. The procedure described in this study can generate satisfactory and reliable results. Mapping rockfall susceptibility on a more detailed scale requires the collection of additional data, as mentioned above.