Outside options in neutral allocation of discrete resources

Abstract

Serial dictatorships have emerged as the canonical simple mechanisms in the literature on the allocation of indivisible goods without transfers. They are the only neutral and group-strategy-proof mechanisms in environments in which agents have no outside options and hence no individual rationality constraints (Svensson in Soc Choice Welfare 16:557–567, 1999). Accounting for outside options and individual rationality constraints, our main result constructs the class of group-strategy-proof, neutral, and non-wasteful mechanisms. These mechanisms are also Pareto efficient and we call them binary serial dictatorships. The abundance of the outside option—anybody who wants can opt out to get it—is crucial for our result.

1 Introduction

Serial dictatorships have often emerged as the canonical simple mechanisms in the literature on the allocation of indivisible objects without transfers and with single-unit demands (i.e., the Hylland and Zeckhauser 1979 model). A serial dictatorship mechanism allocates objects by ordering agents, and then letting the first agent choose her most preferred object, thereafter letting the second agent choose his most preferred object among those still available, etc. Svensson (1999) explains the attractiveness of serial dictatorships by showing that they are the only neutral and group strategy-proof mechanisms. A mechanism is neutral if its outcome does not depend on the labelling of objects.¹ A mechanism is group strategy-proof if there is no group of agents that can misstate their preferences and obtain a weakly better house, and such that at least one agent in the group gets a strictly better house. Svensson restricts attention to environments in which agents have no outside options and hence no individual rationality constraints.

We allow for the outside options: each agent can remain unmatched if she chooses to, i.e., participation is voluntary. Our main result establishes that the class of group strategy-proof, neutral, non-wasteful and individually-rational mechanisms consists of mechanisms we call binary serial dictatorships. Individual rationality ensures voluntary participation: no agent is assigned a house worse than her outside option. Non-wastefulness is a weak efficiency property: a mechanism is non-wasteful if there is no unassigned house that an agent prefers to be matched with rather than her assignment. The class of binary serial dictatorships generalizes serial dictatorships to the setting with outside options. A binary serial dictatorship first assigns a selected agent her most preferred outcome among all houses and her outside option; we also refer to being assigned the outside option as being unmatched. A second agent is then assigned his most preferred outcome among all not-yet-assigned houses and his outside option. In contrast to serial dictatorships, the identity of the second agent can depend on whether the first agent is matched with a house or with an outside option. The mechanism then repeats the procedure, selecting a third agent whose identity depends on whether the first and second agent were matched with houses or outside options, etc.²

Our characterization has two corollaries. First, because binary serial dictatorships are Pareto efficient, we can conclude that binary serial dictatorships are also the class of group strategy-proof, neutral, Pareto efficient and individually-rational mechanisms. Second, in the subdomain of our preference domain in which the outside option is always ranked last by all agents—the domain that most previous axiomatic studies on house allocation used—our result implies that a mechanism is group strategy-proof, neutral, and non-wasteful if and only if it is a serial dictatorship.

Serial dictatorships were introduced by Satterthwaite and Sonnenschein (1981) in private good economies and studied by Svensson (1994) in the house allocation context as a strategy-proof mechanism in absence of outside options (also see Roth 1982). In addition to Svensson (1999), Ergin (2000) characterized serial dictatorships by maintaining the neutrality requirement and replacing group strategy-proofness with monotonicity and consistency axioms. Abdulkadiroğlu and Sönmez (1998) showed that, given a fixed preference profile, each Pareto efficient outcome can be obtained by running a serial dictatorship.³ Sönmez and Ünver (2010) studied neutrality and strategy-proofness, together with additional axioms, and allow agents to have property rights over some of the goods (see also Abdulkadiroğlu and Sönmez 1999 for this model). Pycia and Ünver (2021) showed that Arrovian efficient and strategy-proof mechanisms resemble sequential dictatorships except that in the last step of the algorithm, when there are only two goods left, two agents might be endowed with these goods and allowed to trade them; Pycia (2016) showed that a similar class of sequential-dictatorship-like mechanisms characterizes strong obvious strategy-proofness and Pareto efficiency. These papers focus on environments without outside options.

The present paper contributes to the analysis of the voluntary participation in allocation of indivisible goods without transfers in the presence of outside options. The previous analyses of this issue focused on population monotonicity (Ehlers et al. 2002) and resource monotonicity (Ehlers and Klaus 2003); assumptions we do not impose. Following the initial draft of our work, others have examined outside options in related environments. Nanyang (2014) used neutrality and additional axioms to characterize sequential dictatorships. Erdil (2014) showed in a domain without transfers that non-wasteful and strategy-proof deterministic mechanisms are not dominated by strategy-proof deterministic mechanisms. In school-choice domain, Kesten and Kurino (2019) showed that with outside options there is no mechanism that Pareto-dominates the student-optimal stable school-choice mechanism. They also study maximal subdomains of preferences where such result no longer holds. In a more general setting with or without transfers, Alva and Manjunath (2019) showed that if a pair of individual rational and strategy-proof mechanisms are participation equivalent (i.e., if at every problem every agent either receives her outside option under both mechanisms or is assigned a non-outside-option outcome under both) then they should be welfare equivalent.⁴ Calsamiglia et al. (2020) showed that the presence of outside options has an even bigger impact on individually-rational but non-strategy-proof mechanisms as it enables agents with better outside option to choose more risky equilibrium strategies. Some of the conceptual modeling and market design for kidney exchange hinges on the outside-option-like protections for patients and the incompatible donors they bring to the exchange: the donor brought by a patient can only be matched with other patients if the patient is matched with a compatible donor (e.g., Roth et al. 2005, 2007). The donor a patient brought to the exchange can thus be seen as the patient’s outside option.⁵

While we show that Svensson’s serial dictatorship insight can be modified so as to make it valid when agents have outside options, there are many other standard mechanism design problems in which whether agents have the ability to take an outside option crucially affects the standard results. For instance, in the setting with monetary transfers and quasi-linear utilities, the impossibility of ex-post Pareto efficient and Bayesian incentive compatible bilateral trade shown by Myerson and Satterthwaite (1983) crucially depends on individual rationality. The Coasian dynamics of Gul et al. (1986) hinges on the inability of buyers to take an outside option, as shown by Board and Pycia (2014).

2 House allocation problem with outside options

Let I be a finite set of agents. Let H be a finite set of indivisible goods that we refer to as houses (following the terminology of Shapley and Scarf 1974). Each agent i has a strict preference relation over H and her outside option denoted by $x_{\varnothing }$; we assume $x_{\varnothing }\not \in H$. The strict preference relation is denoted by $\succ _{i}$. Let $\succeq _{i}$ be the induced weak preference relation from $\succ _{i}$,⁶ that is for any $x,y\in H\cup \{x_{\varnothing }\}$,

$$\begin{aligned} x\succeq _{i}y\qquad \iff \qquad x=y\hbox { or }x\succ _{i}y. \end{aligned}$$

We denote the preference relation of agent i by the induced weak preference relation $\succeq _{i}$. Let ${\mathcal {R}}$ be the set of preference relations. Let $\succeq$ $=$ $(\succeq _{i})_{i\in I}\in {\mathcal {R}}^{\left| I\right| }$ be a preference profile. Each agent has not only right to hold on to her own house, but also have rights on the vacant houses, which are social endowments. Triple $\left\langle I,H,\succeq \right\rangle$ is a house allocation problem with outside options.

An outcome of a problem is a matching. Following Pycia and Ünver (2017), we define the auxiliary concept of a submatching first. A submatching is an assignment that assigns to some agents a house or the outside option (in either case we write that the agents are matched), and no two agents are assigned the same house. Formally, for any given $J\subseteq I$, a submatching is a function $\sigma :J\longrightarrow H\cup \{x_{\varnothing }\}$ such that for every $\,i,j\in J$, $\sigma (i)=\sigma (j)\Rightarrow i=j$ or $\sigma (i)=x_{\varnothing }$. We will occasionally use the set interpretation of functions to denote the submatching $\sigma$ as well, i.e., $\sigma =\left\{ \left( i,\sigma (i)\right) \right\} _{i\in J}$. Let ${\mathcal {S}}$ be the set of submatchings, which includes also the empty submatching $\emptyset$. We denote the set of agents over which the submatching $\sigma$ is defined as $I^{\sigma }=J$; moreover, let $H^{\sigma }$ be the houses matched in the submatching $\sigma$: $H^{\sigma }=\sigma (I^{\sigma }){\setminus }\{x_{\varnothing }\}$. A matching is a submatching $\sigma$ such that $I^{\sigma }=I$. Let ${\mathcal {M}}$ denote the set of matchings. Let ${\overline{{\mathcal {M}}}}={\mathcal {S}}{\setminus }{\mathcal {M}}$ denote the set of submatchings that are not matchings.

A mechanism assigns a matching for each problem. Throughout the paper, we fix I and H, and thus, a problem is given by the preference profile $\succeq$. Therefore, formally a mechanism is a function $\varphi :{\mathcal {R}}^{\left| I\right| }\longrightarrow {\mathcal {M}}$.

2.1 Axioms

A matching is individually rational, if no agent receives a house worse than the outside option: $\mu \in {\mathcal {M}}$ is individually rational if for every $i\in I$, $\mu (i)\succeq _{i}x_{\varnothing }$. A mechanism is individually rational, if it finds an individually-rational matching for each problem.

A matching is non-wasteful, if no agent receives an option that is worse than a house that is unassigned: $\mu \in {\mathcal {M}}$ is non-wasteful if for every $i\in I$, $\mu (i)\succeq _{i}h$ for every $h\in H{\setminus } H^{\mu }$. Non-wastefulness would imply individual rationality if $x_{\varnothing }$ were (equivalently) considered as a house with $\left| I\right|$ copies. Thus, one can think of individual rationality as a special instance of non-wastefulness. A mechanism is non-wasteful, if it finds a non-wasteful matching for each problem.

A matching is Pareto efficient, if there is no matching that makes everybody weakly better off, and at least one agent strictly better off. That is, a matching $\mu \in {\mathcal {M}}$ is Pareto efficient if there exists no matching $\nu \in {\mathcal {M}}$ such that for every $i\in I$, $\nu (i)\succeq _{i}\mu (i),$ and for some $i\in I$, $\nu (i)\succ _{i}\mu (i)$. A mechanism is Pareto efficient, if it finds a Pareto–efficient matching for each problem.

Individual rationality, non-wastefulness and Pareto efficiency are related concepts.

Lemma 1

If a matching is Pareto efficient then it is individually rational and non-wasteful.

Proof

[Proof of Lemma 1] Let $\mu$ be an individually irrational or wasteful matching. Then there exists some agent $i\in I$, with $g\succ _{i}\mu (i)$ such that either $g=x_{\varnothing }$ or $g\in H$ is not assigned to any agent. Consider the following matching $\nu$: for every $j\in I{\setminus }\{i\}$, $\nu (j)=\mu (j)$ and $\nu (i)=g$. Clearly $\nu$ Pareto-dominates $\mu$; hence, $\mu$ is not Pareto efficient. $\square$

A mechanism is non-bossy if whenever an agent misreports her preferences and cannot change her house assigned by the mechanism, then she cannot change the matching assigned by the mechanism, either (Satterthwaite and Sonnenschein 1981). Formally, a mechanism $\varphi$ is non-bossy if for every $\succeq \in {\mathcal {R}}^{\left| I\right| },$ $i\in I$, and $\succeq _{i}^{\prime }\in {\mathcal {R}}$,

$$\begin{aligned} \varphi \left[ \succeq _{i}^{\prime },\succeq _{-i}\right] (i)=\varphi \left[ \succeq \right] (i)\quad \Rightarrow \quad \varphi \left[ \succeq _{i}^{\prime },\succeq _{-i}\right] =\varphi \left[ \succeq \right] . \end{aligned}$$

A mechanism is strategy-proof if an agent cannot receive a better house by misreporting her preferences. Formally, a mechanism $\varphi$ is strategy-proof if for every $\succeq \in {\mathcal {R}}^{\left| I\right| },$ $i\in I$, and $\succeq _{i}^{\prime }\in {\mathcal {R}}$,

$$\begin{aligned} \varphi \left[ \succeq \right] (i)\mathrel {\succeq _{i}}\varphi \left[ \succeq _{i}^{\prime },\succeq _{-i}\right] (i). \end{aligned}$$

A mechanism is group strategy-proof if there is no group of agents that can misstate their preferences so that they all obtain a weakly better house and at least one agent in the group gets a strictly better house. Formally, a mechanism $\varphi$ is group strategy-proof if there are no $\succeq \in {\mathcal {R}}^{\left| I\right| }$, $J\subseteq I$, and $\succeq _{J}^{\prime }\in {\mathcal {R}}^{\left| J\right| }$ such that

$$\begin{aligned}{} & {} \varphi \left[ \succeq _{J}^{\prime },\succeq _{-J}\right] (i)\mathrel {\succeq _{i}}\varphi \left[ \succeq \right] (i)\qquad \forall i\in J,\hbox { and} \\{} & {} \quad \varphi \left[ \succeq _{J}^{\prime },\succeq _{-J}\right] (j)\mathrel {\succ _{j}}\varphi \left[ \succeq \right] (j)\qquad \exists j\in J. \end{aligned}$$

A mechanism is Maskin monotonic if whenever the preferences of agents change in a way such that the lower contour set at the assigned option under the original preferences is a subset of the lower contour set at the same option under the new preferences, then the matching assigned by the mechanism does not change (Maskin 1999). Formally, a mechanism $\varphi$ is monotonic if for every $\succeq ,\succeq ^{\prime }\in {\mathcal {R}}^{\left| I\right| }$ and $i\in I$,

$$\begin{aligned} \left\{ x\in H\cup \{x_{\varnothing }\}:\varphi \left[ \succeq \right] (i)\mathrel {\succeq _{i}}x\right\}{} & {} \subseteq \left\{ x\in H\cup \{x_{\varnothing }\}:\varphi \left[ \succeq \right] (i)\mathrel {\succeq _{i}^{\prime }}x\right\} \\ {}{} & {} \quad \Rightarrow \quad \varphi \left[ \succeq ^{\prime }\right] =\varphi \left[ \succeq \right] . \end{aligned}$$

In this case, we say that $\succeq '$ is a monotonic transformation of $\succeq$ under $\varphi$.

Axioms of strategy-proofness, non-bossiness, group strategy-proofness and monotonicity are very related concepts, and the following lemmata show their relationships:

Lemma 2

(Pápai 2000) A mechanism is group strategy-proof if and only if it is strategy-proof and non-bossy.

Lemma 3

(Takemiya 2001) A mechanism is monotonic if and only if it is group strategy-proof.

These lemmata were previously proven in a domain without outside options but the proofs carry over to our setting. For a general treatment of these and similar equivalences, see Pycia and Ünver (2021).

The last concept we use is neutrality. In order to introduce it, we first define two auxiliary concepts. A relabeling is a one-to-one and onto function $\pi :H\cup \{x_{\varnothing }\}\rightarrow H\cup \{x_{\varnothing }\}$ such that $\pi (x_{\varnothing })=x_{\varnothing }$. That is, under a relabeling, the names of houses are exchanged. Let $\Pi$ be the set of relabeling functions. For example, under relabeling $\pi \in \Pi$, for house $h\in H$, $\pi (h)$ is house h’s new name. For any $\succeq \in {\mathcal {R}}^{\left| I\right| }$, and $\pi \in \Pi$, the relabeled preference profile $\succeq ^{\pi }\in {\mathcal {R}}^{\left| I\right| }$ is such that for every $i\in I$,

$$\begin{aligned} x\mathrel {\succeq _{i}^{\pi }}y\quad \Longleftrightarrow \quad \pi ^{-1}(x)\mathrel {\succeq _{i}}\pi ^{-1}(y)\hbox {\qquad }\forall \;x,\;y\in H\cup \{x_{\varnothing }\}. \end{aligned}$$

That is, under the relabeled preference profile, the original names of the houses are replaced by their new names.

A mechanism is neutral if renaming of houses results with everybody receiving the house which is the renamed version of her old assignment. Formally a mechanism $\varphi$ is neutral if for any $\succeq \in {\mathcal {R}}^{\left| I\right| }$ and $\pi \in \Pi$,

$$\begin{aligned} \varphi \left[ \succeq ^{\pi }\right] (i)=\pi \left( \varphi \left[ \succeq \right] (i)\right) \qquad \forall i\in I. \end{aligned}$$

3 Binary serial dictatorships

We now construct the class of mechanisms that characterize the axioms group strategy-proofness, neutrality, individual rationality, and non-wastefulness. We start with the definition of a standard sequential dictatorship. A sequential order is a function $f:{\overline{{\mathcal {M}}}}\rightarrow I$ such that $f(\sigma )\in I{\setminus } I^{\sigma }$ for every $\sigma \in {\overline{{\mathcal {M}}}}$. A sequential dictatorship is a mechanism $\phi ^{f}$, which is induced by a sequential order f, and its outcome is found by the following iterative algorithm given a preference profile $\succeq$:

Step 1: Agent $i_{1}=f(\emptyset )$ is assigned her favorite option in $H\cup \{x_{\varnothing }\}$; let this option be denoted as $x_{1}$.

$\quad \vdots$

Step $\ell$: Let $\sigma _{\ell -1}=\left\{ (i_{1},x_{1}),(i_{2},x_{2}),...,(i_{\ell -1},x_{\ell -1})\right\}$. Agent $i_{\ell }=f(\sigma _{\ell -1})$ is assigned her favorite option in $(H{\setminus } H^{\sigma _{\ell -1}})\cup \{x_{\varnothing }\}$; let this option be denoted as $x_{\ell }$.

Sequential dictatorships are strategy-proof, non-bossy, and Pareto efficient. But they are not neutral in general. We need to restrict the set of sequential dictatorships considerably to obtain a neutral mechanism.

A binary serial order is a sequential order f such that $f(\sigma )=f(\sigma ')$ for $\sigma ,\sigma '\in {\overline{{\mathcal {M}}}}$ that satisfy $I^{\sigma }=I^{\sigma '}$ and $\sigma ^{-1}(x_{\varnothing })=\left. \sigma ^{\prime }\right. ^{-1}(x_{\varnothing })$. We refer to a sequential dictatorship induced by a binary serial order as a binary serial dictatorship. In binary serial dictatorships, the agent with the priority to choose is determined by who among the previous agents are assigned the outside option. We can hence simplify our notation as follows. Let ${\mathcal {B}}=\left\{ \beta :J\rightarrow \{0,1\}:J\subsetneq I\right\}$. An element $\beta \in {\mathcal {B}}$ is referred to as a binary submatching. Moreover, let (i, 0) refer to “i is assigned the outside option” and (i, 1) refer to “i is assigned a house.” Let $I^{\beta }=J$ be the set of agents matched under $\beta$. Each binary serial order is determined by a function $f:{\mathcal {B}}\rightarrow I$ such that for every $\beta \in {\mathcal {B}}$, $f(\beta )\in I{{\setminus }}I^{\beta }$. We say a submatching $\sigma \in {\overline{{\mathcal {M}}}}$ is consistent with a binary submatching $\beta \in {\mathcal {B}}$ if $I^{\sigma }=I^{\beta }$ and $\beta (i)={\mathbb {I}}\{\sigma (i)\in H\}$ for every $i\in I^{\beta }$.⁷

Serial dictatorships are a subclass of binary serial dictatorships (and hence of sequential dictatorships): a serial dictatorship is a sequential dictatorship $\phi ^{f}$ such that $f(\sigma )=f(\sigma ')$ for every $\sigma ,\sigma '\in {\overline{{\mathcal {M}}}}$ with $I^{\sigma }=I^{\sigma '}$. We refer to such a sequential order f as a linear order.

4 The characterization

Our main result is as follows:

Theorem 1

A mechanism is group strategy-proof, neutral, individually rational, and non-wasteful if and only if it is a binary serial dictatorship.

Proof of Theorem 1

Let $\phi ^{f}$ be a binary serial dictatorship. Then, $\phi ^{f}$ is a hierarchical exchange mechanism; this class of mechanisms was introduced by Pápai (2000) for settings without outside options and extended to the setting with outside options by Pycia and Ünver (2011). Pápai (2000) showed that in her setting hierarchical exchange mechanisms are group strategy-proof and Pareto efficient, and this insight as well as Pápai’s proof extend to our setting; see Pycia and Ünver (2011) for details. Thus, $\phi ^{f}$ is group strategy-proof and Pareto efficient; Pareto efficiency implies non-wastefulness and individual rationality. Because the definition of $\phi ^{f}$ does not depend on the names of houses assigned, $\phi ^{f}$ is also neutral.

$\implies$Let $\varphi$ be a group strategy-proof, neutral, non-wasteful, and individually rational mechanism. By Lemma 2, $\varphi$ is strategy-proof and non-bossy. By Lemma 3, $\varphi$ is monotonic.

We introduce some definitions for the proof.

An ordered submatching is defined as an ordered list $\left( (j_{1},y_{1}),\ldots ,(j_{\ell },y_{\ell })\right)$ such that $\left\{ (j_{1},y_{1}),\ldots ,(j_{\ell },y_{\ell })\right\} \in {\mathcal {S}}$; we say that the submatching and the ordered submatching are associated. With a slight abuse of notation, we occasionally use $\sigma$ to refer to both an ordered submatching and its associated submatching.

Given a sequential order f, a relevant ordered submatching of f is an ordered submatching $\left( (j_{1},y_{1}),\ldots ,(j_{\ell },y_{\ell })\right)$ such that $j_{1}=f(\emptyset )$ and $j_{k}=f\left( \left\{ (j_{1},y_{1}),...,\right. \right. \left. \left. (j_{k-1},y_{k-1})\right\} \right)$ for all integers k such that $2\le k<\ell$. We say that $\sigma =\left\{ (j_{1},y_{1}),\ldots ,(j_{\ell },y_{\ell })\right\}$ is a relevant submatching of f if there is an ordering of the pairs in $\sigma$ such that $\left( (j_{1},y_{1}),\ldots ,(j_{\ell },y_{\ell })\right)$ is a relevant ordered submatching of f. In particular, the relevant submatchings include the empty submatching $\emptyset$, the singleton submatchings $\{\left( f(\emptyset ),y_{1}\right) \}$ for any option $y_{1}$, the two-agent submatchings $\left\{ \left( f(\emptyset ),y_{1}\right) ,\left( f\left( \left\{ \left( f(\emptyset ),y_{1}\right) \right\} \right) ,y_{2}\right) \right\}$, etc. Note that if $\sigma =\left\{ (j_{1},y_{1}),\ldots ,(j_{\ell },y_{\ell })\right\}$ is a relevant submatching of f then there is a unique relevant ordered submatching associated with it; furthermore, for each $k=1,...,\left| \sigma \right| -1$, there is a unique subset of $\sigma$ that is a relevant submatching for f and has length k. Let ${\mathcal {S}}^{f}$ be the set of all relevant submatchings of f.

We analogously define the set ${\mathcal {B}}^{f}$ of relevant binary submatchings of a binary serial order f. If $\beta =\left\{ (j_{1},\varepsilon _{1}),\ldots ,(j_{\ell },\varepsilon _{\ell })\right\}$, where $\varepsilon _{1},...,\varepsilon _{\ell }\in \left\{ 0,1\right\}$, is a relevant binary submatching for f then, for any $k=1,...,\left| \beta \right| -1$, there is a unique subset of $\beta$ that is a relevant submatching for f and has length k.

Given an ordered submatching $\sigma =\left( (j_{1},y_{1}),\ldots ,(j_{\ell },y_{\ell })\right)$ and distinct options $x_{1},\ldots ,x_{m}\in \left( H{\setminus } H^{\sigma }\right) \cup \{x_{\varnothing }\}$, let ${\mathcal {R}}^{\sigma ;x_{1},\ldots ,x_{m}}$ be the domain of the preference profiles $\succeq \in {\mathcal {R}}^{|I|}$ such that:

• for every $j_{k}\in I^{\sigma }$, $\succeq _{j_{k}}$ ranks the houses $\{y_{1},y_{2},...,y_{k-1}\}\cap H$ in order of their indices, then $y_{k}$, and then houses $\{y_{k+1},y_{k+2},...,y_{\ell }\}\cap H$ in order of their indices, and then $\{x_{1},x_{2},...,x_{m}\}{\setminus }\{y_{k}\}$ in order of their indices, and finally other options in arbitrary order.

• for every $i\in I{\setminus } I^{\sigma }$, $\succeq _{i}$ ranks houses $\{y_{1},y_{2},...,y_{\ell }\}\cap H$ in order of indices, then $x_{1},\ldots ,x_{m}$, in this order and then other options in arbitrary order.

We are ready to continue with the proof. We iteratively construct a binary serial order f: $\square$

Step 1: Let $\beta =\emptyset$ be the initial binary submatching. Fix a house $h_{\emptyset }\in H$. Fix a profile $\succeq ^{\emptyset }\in {\mathcal {R}}^{\emptyset ;h_{\emptyset },x_{\varnothing }}$; then $\varphi ^{-1}\left[ \succeq ^{\emptyset }\right] (h_{\emptyset })\in I$ by non-wastefulness of $\varphi$. Let $f(\emptyset )=\varphi ^{-1}\left[ \succeq ^{\emptyset }\right] (h_{\emptyset })$ and $\sigma _{\emptyset }=\left( \left( f\left( \emptyset \right) ,h_{\emptyset }\right) \right)$.

$\quad \quad \vdots$

Step $\ell +1$ for $\ell \in \{1,2,\ldots ,|I|-1\}$: For every $\beta \in {\mathcal {B}}$ with $\big |I^{\beta }\big |=\ell$ we do the following:

• 1. If $\beta$ is not relevant with respect to the part of the binary ordering f constructed till now, then pick $f(\beta )\in I{\setminus } I^{\beta }$ arbitrarily.

• 2. Otherwise, let $\beta '\subsetneq \beta$ be the unique relevant binary submatching of $\beta$ with $|I^{\beta '}|=\ell -1$. Fix an ordered submatching $\sigma _{\beta }=\left( \sigma _{\beta '}\;,\;(j_{\ell },y_{\ell })\right)$ where $j_{\ell }=f(\beta ')$ as constructed in Step $\ell$ and let $y_{\ell }$ be such that its choice makes $\sigma _{\beta }$ consistent with $\beta$, i.e., $y_{\ell }=h_{\beta '}$ if $\beta (j_{\ell })=1$ and $y_{\ell }=x_{\varnothing }$ if $\beta (j_{\ell })=0$.

  • (a) If $H{\setminus } H^{\sigma _{\beta }}=\emptyset$, then pick $f(\beta )\in I{\setminus } I^{\beta }$ arbitrarily.

  • (b) Otherwise, fix a house $h_{\beta }\in H{\setminus } H^{\sigma _{\beta }}$ ensuring that $h_{\beta }=h_{\beta '}$ in case $H{\setminus } H^{\sigma _{\beta }}=H{\setminus } H^{\sigma _{\beta '}}$. Fix a preference profile $\succeq ^{\beta }\in {\mathcal {R}}^{\sigma _{\beta };h_{\beta },x_{\varnothing }}$. By non-wastefulness of $\varphi$, ${\varphi ^{-1}\left[ \succeq ^{\beta }\right] (h_{\beta })\in I}$. Let $f(\beta )=\varphi ^{-1}\left[ \succeq ^{\beta }\right] (h_{\beta })$.

Notice that in Step $\ell +1.2$(b) there is no conflict between assuming that $h_{\beta }$ is a house and requiring that $h_{\beta }=h_{\beta '}$ in case $H{\setminus } H^{\sigma _{\beta }}=H{\setminus } H^{\sigma _{\beta '}}$ as we start with $h_{\emptyset }$ which is a house in Step 1.

The following claim is the crucial step in our proof.

Claim. Binary serial order f is well defined. Moreover, suppose $\beta \in {\mathcal {B}}^{f}$, its ordered submatching used in the above construction is given as $\sigma _{\beta }$, and $\succeq \in {\mathcal {R}}^{\sigma _{\beta }}$ is such that if $H^{\sigma _{\beta }}\subsetneq H$, then for each $i\in I{\setminus } I^{\beta }$ and each $h\in H{\setminus }\left( H^{\sigma _{\beta }}\cup \{h_{\beta }\}\right)$, $x_{\varnothing }\mathrel {\succ _{i}}h$, where $h_{\beta }$ is defined in the above construction. Then, we have

$$\begin{aligned} \varphi \left[ \succeq \right] (i)&=\sigma _{\beta }(i)=\phi ^{f}\left[ \succeq \right] (i)\qquad \forall \;i\in I^{\beta }. \end{aligned}$$

(1)

Proof of Claim. We prove the claim by induction on $\ell =\big |I^{\beta }\big |\in \{0,1,...,\left| I\right| -1\}$ showing that Eq. (1) is satisfied, and thus, $f(\beta )$ is well defined by establishing that $f(\beta )\in I{\setminus } I^{\beta }$.⁸

Step 1: We have $\beta =\emptyset$ and the statement trivially holds. Agent $f(\emptyset )$ is well defined by non-wastefulness of $\varphi$.

Step $\ell +1$ for $\ell \in \{1,2,\ldots ,|I|-1\}$: As our inductive assumption, suppose the claim holds for any $\beta \in {\mathcal {B}}^{f}$ with $\big |I^{\beta }\big |<\ell$ and f is well defined for all relevant binary submatchings $\beta '\subseteq \beta$. Fix $\beta \in {\mathcal {B}}^{f}$ with $\big |I^{\beta }\big |=\ell$. If $\Big |\beta ^{-1}(1)\Big |=\Big |\left\{ i\in I^{\beta }:\beta (i)=1\right\} \Big |\ge |H|$, then the claim follows from the previous steps and individual rationality; hence we assume $\Big |\beta ^{-1}(1)\Big |<|H|$.

Let $\beta =\left( \left( j_{1},\beta (j_{1}),\ldots ,j_{\ell },\beta (j_{\ell })\right) \right)$ be such that its consistent ordered submatching $\sigma _{\beta }=\left( (j_{1},y_{1}),\ldots ,(j_{\ell },y_{\ell })\right)$ and preference profile $\succeq ^{\beta }$ are as defined in the construction of f above. Let $H^{\sigma _{\beta }}=\{h_{1},\ldots ,h_{q}\}$ for some $q\le \ell$ such that houses $h_{1},\ldots ,h_{q}$ are assigned to agents in $\beta ^{-1}(1)$ according to their indices, respectively. Thus, for each $y_{m}\in \{y_{1},y_{2},\ldots ,y_{\ell }\}\cap H=H^{\sigma _{\beta }}$ there exists some $h_{r}\in H^{\sigma _{\beta }}$ such that $y_{m}=h_{r}$. Also note that $y_{m}\in \{y_{1},y_{2},\ldots ,y_{\ell }\}{\setminus } H^{\sigma _{\beta }}$ implies $y_{m}=x_{\varnothing }$.

Let ${\tilde{\beta }}\subsetneq \beta$ be the relevant ordered binary submatching of $\beta$ such that $\sigma _{{\tilde{\beta }}}=\left( (j_{1},y_{1}),\ldots ,(j_{{\tilde{\ell }}-1},y_{{\tilde{\ell }}-1})\right)$ where ${{\tilde{\ell }}}$ is defined as $y_{{\tilde{\ell }}}=h_{q}$ if $q>1$ (thus, we have $\beta (j_{{\tilde{\ell }}})=1$ and $\beta (j_{{\tilde{\ell }}+1})=\ldots =\beta (j_{\ell })=0$) and $\sigma _{{\tilde{\beta }}}=\emptyset$ otherwise. Thus, $h_{{\tilde{\beta }}}=y_{{\tilde{\ell }}}=h_{q}$.

We show that for every $J\subseteq I{\setminus } I^{\beta }$ and $k\le \ell$,

$$\begin{aligned} \varphi \left[ \succeq _{I^{\beta }\cup J}^{\beta }\;,\;\succeq _{-I^{\beta }\cup J}^{{\tilde{\beta }}}\right] (j_{k})&=y_{k}=\phi ^{f}\left[ \succeq _{I^{\beta }\cup J}^{\beta }\;,\;\succeq _{-I^{\beta }\cup J}^{{\tilde{\beta }}}\right] (j_{k}) \end{aligned}$$

(2)

where $\succeq ^{\beta }$ and $\succeq ^{{\tilde{\beta }}}$ are defined in the construction of f above, which in turn proves Eq. (1) holds for Step $\ell +1$. The second equality follows by definition of $\phi ^{f}$ and the inductive assumption that f is well defined until the end of Step $\ell$. We prove the first equality by induction on $t=\left| J\right|$:

Step $\ell +1.0$: For $J=\emptyset$, monotonicity of $\varphi$ and the outer inductive assumption for Step $\ell$ together imply Eq. (2).

Step $\ell +1.t$ for $t\in \{1,2,\ldots ,|I|-\ell \}$: Fix $J\subseteq I{\setminus } I^{\beta }$ such that $|J|=t$. Suppose as the inner inductive assumption for every $J'\subsetneq I{\setminus } I^{\beta }$ with $|J'|<t$, Eq. (2) holds. Denote:

$$\begin{aligned} {\hat{\succeq }}=\left( \succeq _{I^{\beta }\cup J}^{\beta }\;,\;\succeq _{-I^{\beta }\cup J}^{{\tilde{\beta }}}\right) , \end{aligned}$$

and fix

$$\begin{aligned} i\in J. \end{aligned}$$

By inner inductive assumption for Step $\ell +1.t-1$ and individual rationality of $\varphi$ for i, we have ${\varphi \left[ \succeq _{i}^{{\tilde{\beta }}},{\hat{\succeq }}_{-i}\right] (i)=x_{\varnothing }}$. By strategy-proofness of $\varphi$, $\varphi \left[ {\hat{\succeq }}\right] (i)\in \{h_{\beta },x_{\varnothing }\}$, as i makes only $h_{\beta }$ acceptable as her last choice in changing $\succeq _{i}^{{\tilde{\beta }}}$ to $\succeq _{i}^{\beta }$.

If $\varphi \left[ {\hat{\succeq }}\right] (i)=x_{\varnothing }$, then by non-bossiness of $\varphi$ for i, $\varphi \left[ {\hat{\succeq }}\right] =\varphi \left[ \succeq _{i}^{{\tilde{\beta }}},{\hat{\succeq }}_{-i}\right]$. Eq. (2) for J follows from the inner inductive assumption for Step $\ell +1$ $.t-1$.

Suppose $\varphi \left[ {\hat{\succeq }}\right] (i)=h_{\beta }$, which is the sole remaining possibility. To reach a contradiction suppose Eq. (2) does not hold. We have two main cases, either there is no $j_{n}\in I^{\beta }$ such that $y_{n}=x_{\varnothing }$ and $\varphi \left[ {\hat{\succeq }}\right] (j_{n})\not =x_{\varnothing }$ or there is some $j_{n}\in I^{\beta }$ such that $y_{n}=x_{\varnothing }$ and $\varphi \left[ {\hat{\succeq }}\right] (j_{n})\not =x_{\varnothing }$.

$\underline{{\hbox {Case 1.}}}$ There is no $j_{n}\in I^{\beta }$ such that $y_{n}=x_{\varnothing }$ and $\varphi \left[ {\hat{\succeq }}\right] (j_{n})\not =x_{\varnothing }$. Let $j_{k}\in I^{\beta }$ be the agent with the highest index $k\in \{1,2,\ldots ,\ell \}$ such that $y_{k}\in H$ and it is not assigned to $j_{k}$ under $\varphi \left[ {\hat{\succeq }}\right]$. Let

$$\begin{aligned} y_{k}=h_{p}\quad \exists \;h_{p}\in H^{\sigma _{\beta }}=\{y_{1},y_{2},\ldots ,y_{\ell }\}\cap H=\{h_{1},h_{2},\ldots ,h_{q}\}. \end{aligned}$$

By non-wastefulness of $\varphi$, there exists some $j\in I$ such that

$$\begin{aligned} \varphi \left[ {\hat{\succeq }}\right] (j)=y_{k}=h_{p}. \end{aligned}$$

Observe that, for each $i^{*}\in J{\setminus }\{i\}$, ${\hat{\succeq }}=\left( \succeq _{I^{\beta }\cup J}^{\beta }\text {\;},\text {\;}\succeq _{-I^{\beta }\cup J}^{{\tilde{\beta }}}\right)$ can be obtained from $\left( \succeq _{I^{\beta }\cup (J{\setminus }\{i^{*}\})}^{\beta }\text {\;},\text {\;}\succeq _{-I^{\beta }\cup (J{\setminus }\{i^{*}\})}^{\beta }\right)$ by $i^{*}$ flipping her preference from $\succeq _{i^{*}}^{{\tilde{\beta }}}$ to $\succeq _{i^{*}}^{\beta }$ then with the same argument for i and the induction assumption for Step $\ell +1.t-1$ we have that $\varphi \left[ {\hat{\succeq }}\right] (i^{*})\in \{h_{\beta },x_{\varnothing }\}$. Since $\varphi \left[ {\hat{\succeq }}\right] (i)=h_{\beta }$, $\varphi \left[ {\hat{\succeq }}\right] (i^{*})=x_{\varnothing }$. Thus, $j\not \in J$.

Also observe that as we are in Case 1, an important implication of choosing k as large as possible with the property $\varphi \left[ {\hat{\succeq }}\right] (j_{k})\not =y_{k}\in H$ is that if $j=j_{m}\in I^{\beta }$ for some index m then $m\in \{1,\ldots ,k-1\}$ and $y_{m}\mathrel {{\hat{\succ }}_{j_{m}}}y_{k}=h_{p}$, implying $m<k$, and Case 1 further implies $y_{m}\in H$.

We will use these observations later, so we formalize last two paragraphs’ conclusions as follows:

Observation 1. If $j=j_{m}\in I^{\beta }$ for some m, then $y_{m}\in H$ and $m<k$. Moreover, for each $i^{*}\in J{\setminus }\{i\},$ $\varphi \left[ {\hat{\succeq }}\right] (i^{*})=x_{\varnothing }$ and thus, $j\not \in J$.

Thus, so far, for each $i^{*}\in I$,⁹

(3)

where $\varphi \left[ {\hat{\succeq }}\right] (j)=h_{p}$ is in boldface and $\varphi \left[ {\hat{\succeq }}\right] (i)=h_{\beta }$ is underlined; $\varphi \left[ {\hat{\succeq }}\right] (i^{*})$ is boxed for each agent $i^{*}$ if it can be determined, and otherwise, the options that this assignment cannot be are indicated with an underbrace notation. In addition to this, $\varphi \left[ {\hat{\succeq }}\right] (i^{*})$ cannot be any house ranked below $x_{\varnothing }$ by individual rationality of $\varphi$.¹⁰

We define a new preference profile ${\tilde{\succeq }}$ that is obtained from ${\hat{\succeq }}$ by demoting $h_{p}$ just below $h_{q}$ for agent j, while still keeping $h_{p}$ acceptable, and demoting $h_{p}$ to be unacceptable for all other agents if it is not already unacceptable (i.e., for each $j_{m}\in \{j_{1},j_{2},\ldots ,j_{k-1}\}$ with $y_{m}=x_{\varnothing }$ , house $h_{p}=y_{k}$ is already unacceptable, and for everybody else it is an acceptable house as denoted in Eq. (3)). Therefore, $\left( {\hat{\succeq }}_{j},{\tilde{\succeq }}_{-j}\right)$ is a monotonic transformation of ${\hat{\succeq }}$ under $\varphi$ because $\varphi \left[ {\hat{\succeq }}\right] (j)=h_{p}$ and it is demoted in all agents’ preferences in ${\tilde{\succeq }}_{-j}$ but only j’s. By monotonicity of $\varphi$, we have

$$\begin{aligned} \varphi \left[ {\hat{\succeq }}_{j},{\tilde{\succeq }}_{-j}\right] =\varphi \left[ {\hat{\succeq }}\right] . \end{aligned}$$

(4)

By strategy-proofness of $\varphi$ for j, as $\varphi \left[ {\hat{\succeq }}\right] (j)=h_{p}$ is demoted just below $h_{q}$ under ${\tilde{\succeq }}_{j}$, j can only receive the houses ranked in the interval $h_{p},h_{p+1},\ldots ,h_{q}$ under ${\hat{\succeq }}_{j}$ (and thus, ranked in the ranking interval $h_{p+1},h_{p+2},\ldots ,h_{q},h_{p}$ under ${\tilde{\succeq }}_{j}$), i.e,

$$\begin{aligned} \varphi \left[ {\tilde{\succeq }}\right] (j)\in \{h_{p},h_{p+1},\ldots ,h_{q}\}. \end{aligned}$$

In the proof of Case 1, we use a relabeling $\pi$ defined as

• $\pi (h_{p})=h_{\beta }$,

• $\pi (h_{r})=h_{r-1}$ for each $r\in \{p+1,\ldots ,q\}$,

• $\pi (h_{\beta })=h_{q}$, and

• $\pi (h)=h$ for each $h\in H{\setminus }\{h_{p},h_{p+1}\ldots ,h_{q},h_{\beta }\}$.

We have two further cases:

$\underline{{\hbox {Case 1.1.}}}$ $\varphi \left[ {\tilde{\succeq }}\right] (j)=h_{s}\in \{h_{p+1},h_{p+2},\ldots ,h_{q}\}=\{y_{k+1},y_{k+2},\ldots ,y_{\ell }\}\cap H$.¹¹ Now, $h_{s}=y_{n}$ for some $n\in \{k+1,k+2,\ldots ,\ell \}$. By choice of j and Observation 1, $j_{n}\not =j$.

Modify ${\tilde{\succeq }}_{j}$ further so that $h_{p}$ is ranked below $x_{\varnothing }$ for j as well and otherwise the rankings of options are unchanged. With slight abuse of notation, we continue calling this preference relation ${\tilde{\succeq }}_{j}$. Observe that this change does not change $\varphi \left[ {\tilde{\succeq }}\right]$ by $\varphi$’s strategy-proofness and non-bossiness.

By neutrality of $\varphi$, we have

$$\begin{aligned} \varphi \left[ {\tilde{\succeq }}^{\pi }\right] (j)=\pi (h_{s})=h_{s-1}. \end{aligned}$$

(5)

Recall (i) the largest index house in $H^{\sigma _{\beta }}=\{y_{1},\ldots ,y_{\ell }\}\cap H=\{h_{1},\ldots ,h_{q}\}$, which is $h_{q}$, is assigned under $\sigma _{\beta }$ to $j_{{\tilde{\ell }}}\in I^{\beta }=\{j_{1},\ldots ,j_{\ell }\}$ (so that $h_{q}=y_{{\tilde{\ell }}}$ and if ${\tilde{\ell }}<\ell$ then $y_{{\tilde{\ell }}+1}=y_{{\tilde{\ell }}+2}=\ldots =y_{\ell }=x_{\varnothing }$), (ii) the relevant binary submatching ${\tilde{\beta }}\subsetneq \beta$ was defined so that it has the consistent ordered submatching $\sigma _{{\tilde{\beta }}}=\left( (j_{1},y_{1}),\ldots ,(j_{{\tilde{\ell }}-1},y_{{\tilde{\ell }}-1})\right)$, and (iii) that $f({\tilde{\beta }})=j_{{\tilde{\ell }}}$ and $h_{{\tilde{\beta }}}=h_{q}=y_{{\tilde{\ell }}}$ (all defined at the beginning of the outer inductive proof for Step $\ell +1$).

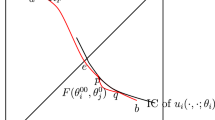
The last preference profile in Fig. 1 shows $\succeq ^{{\tilde{\beta }}}$ . Recall that ${\tilde{\beta }}$ was processed in Step ${\tilde{\ell }}<\ell +1$ of the construction of f. The assignments of agents are determined by the outer inductive assumption for Step ${\tilde{\ell }}$ and individual rationality of $\varphi$ . The other preference profiles used in Case 1.1 are also shown in Fig. 1. In particular, the inductive assumption and what we have so far imply that

• if $j=j_{m}\in I^{\beta }$ for some $j_{m}$, then $m<k<n\le {\tilde{\ell }}$ and $y_{m}\in H$ (by Observation 1, $y_{k}=h_{p}$, $y_{n}=h_{s}$, and $y_{{\tilde{\ell }}}=h_{q}$, and the definition of these houses); therefore, $\succeq _{j}^{{\tilde{\beta }}}$ and ${\tilde{\succeq }}_{j}^{\pi }$ have identical rankings of houses from top to $y_{m}$, and we have $\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] (j)=y_{m}$;

• if $j\notin I^{\beta }$ then ${\tilde{\succeq }}_{j}^{\pi }$ has a subset of acceptable houses of what $\succeq _{j}^{{\tilde{\beta }}}$ has, and we have $\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] (j)=x_{\varnothing }$ by the inductive assumption for Step ${\tilde{\ell }}$;

• both $\succeq ^{{\tilde{\beta }}}$ and ${\tilde{\succeq }}^{\pi }$ have identical rankings for acceptable houses for all agents in J (including i, as $i\in J$), all agents $j_{m}\in I^{\beta }{\setminus }\{j\}$ such that $y_{m}\in H$ (including $j_{{\tilde{\ell }}}$ and $j_{n}$), all agents $j_{m}\in \{j_{1},\ldots ,j_{n-1}\}$ such that $y_{m}=x_{\varnothing }$, and all agents in $\{j_{{\tilde{\ell }}+1},\ldots ,j_{\ell }\}$;

• for each agent $j_{m}\in \{j_{n+1},\ldots ,j_{{\tilde{\ell }}-1}\}$ such that $y_{m}=x_{\varnothing }$, ${\tilde{\succeq }}_{j_{m}}^{\pi }$ has a subset of acceptable houses of what $\succeq _{j_{m}}^{{\tilde{\beta }}}$ has, and we have $\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] (j_{m})=y_{m}=x_{\varnothing }$ by the inductive assumption for Step ${\tilde{\ell }}$; and

• for each agent $i^{*}\in I{\setminus }\left( I^{\beta }\cup J\cup \{j\}\right)$, ${\tilde{\succeq }}_{i^{*}}^{\pi }$ deems house $h_{q}$ unacceptable but otherwise keeps the same rankings for acceptable houses as $\succeq _{i^{*}}^{{\tilde{\beta }}}$, and we have $\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] (i^{*})=x_{\varnothing }$ by the inductive assumption for Step ${\tilde{\ell }}$.

Therefore, ${\tilde{\succeq }}^{\pi }$ is a monotonic transformation of $\succeq ^{{\tilde{\beta }}}$ under $\varphi$ (also see Fig. 1). Hence, by monotonicity of $\varphi$, $\varphi \left[ {\tilde{\succeq }}^{\pi }\right] =\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] .$

By the outer inductive assumption for Step ${\tilde{\ell }}$, $\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] (j)\not =h_{s-1}$ as house $h_{s-1}$ is a house assigned to one of the agents $j_{k},....,j_{{\tilde{\ell }}},$ and either (i) $j\not \in I^{\beta }$ so that $\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] (j)=x_{\varnothing }$ or (ii) $j=j_{m}\in \{j_{1},\ldots ,j_{k-1}\}$ and $\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] (j)=y_{m}$ is a house indexed smaller than $h_{s-1}$ as mentioned in the first two points above. However, we established that $\varphi \left[ {\tilde{\succeq }}^{\pi }\right] (j)=h_{s-1}$ in Eq. (5). This contradicts $\varphi \left[ {\tilde{\succeq }}^{\pi }\right] =\varphi \left[ \succeq ^{{\tilde{\beta }}}\right]$, and thus, Case 1.1. cannot hold.

Fig. 1

The preference profiles in Case 1.1 assuming that agent $i^{*}\in I{\setminus }\{i,j\}$ and she denotes a generic agent. Agent j’s assignment is in boldface and i’s assignment is underlined under each preference profile under $\varphi$. Assignments of all agents under $\varphi$ are boxed whenever they can be determined. Ranking ${\tilde{\succeq }}_{j}$ refers to the version of this ranking introduced in Case 1.1; in particular, $h_{\beta }$ is unacceptable under this ranking. Recall that $I^{{\tilde{\beta }}}=\{j_{1},\ldots ,j_{{\tilde{\ell }}-1}\}$, $I^{\beta }=I^{{\tilde{\beta }}}\cup \{j_{{\tilde{\ell }}},\ldots ,j_{\ell }\}$, and $y_{{\tilde{\ell }}}=h_{q}=h_{{\tilde{\beta }}}\in H$, $y_{n}=h_{s}\in H$, $y_{k}=h_{p}\in H$ with $k<n\le {\tilde{\ell }}$

$\underline{{\hbox {Case 1.2.}}}$ $\varphi \left[ {\tilde{\succeq }}\right] (j)=h_{p}$: By non-bossiness of $\varphi$ involving agent j, $\varphi \left[ {\tilde{\succeq }}\right] =\varphi \left[ {\hat{\succeq }}_{j},{\tilde{\succeq }}_{-j}\right]$. Thus, $\varphi \left[ {\tilde{\succeq }}\right] =\varphi \left[ {\hat{\succeq }}\right]$ by Eq. (4). By neutrality of $\varphi$, we have

$$\begin{aligned} \varphi \left[ {\tilde{\succeq }}^{\pi }\right] (j)=\pi (h_{p})=h_{\beta }\,\,\;\text {and}\;\,\,\varphi \left[ {\tilde{\succeq }}^{\pi }\right] (i)=\pi (h_{\beta })=h_{q}. \end{aligned}$$

(6)

We summarize the preference profiles used in Case 1.2 in Fig. 2. To see its accuracy observe the following:

• For all $i^{*}\in I{\setminus }\{j\}$, we shifted up all acceptable houses in order starting with $h_{p+1}$ and ending with the last acceptable house (if $h_{p+1}$ is acceptable), as $h_{p}$ is demoted under ${\hat{\succeq }}_{i^{*}}$ to be unacceptable and we obtained ${\tilde{\succeq }}_{i^{*}}$. Then by using the relabeling $\pi$, these houses were effectively shifted back down under ${\tilde{\succeq }}_{i^{*}}^{\pi }$ with the exception that $\pi (h_{p})=h_{\beta }$ remained unacceptable.

• For agent j, we shifted up all houses $h_{p+1},h_{p+2},\ldots ,h_{q}$ in order as $h_{p}$ is demoted with respect to ${\hat{\succeq }}_{j}$ but is kept acceptable just below $h_{q}$ and we obtained ${\tilde{\succeq }}_{j}$ (while $h_{\beta }$ may or may not be acceptable depending on $j\in I^{\beta }$ or $j\not \in I^{\beta }$, respectively). Then by using the relabeling $\pi$, these houses were effectively shifted back down under ${\tilde{\succeq }}_{j}^{\pi }$ and $\pi (h_{p})=h_{\beta }$ remained acceptable (while $\pi (h_{\beta })=h_{q}$ may or may not be acceptable depending on $j\in I^{\beta }$ or $j\not \in I^{\beta }$, respectively, as just noted in the previous statement).

Consider the following change in j’s preference ${\tilde{\succeq }}_{j}^{\pi }$ such that $h_{q}$ is ranked as the second to last acceptable option just above $h_{\beta }$ (if it is not already so) so that we get

$$\begin{aligned} \succeq _{j}^{\beta }=h_{1},\ldots ,h_{q-1},h_{q},h_{\beta },x_{\varnothing },\ldots \end{aligned}$$

There is a slight abuse of notation here, as the preference $\succeq _{j}^{\beta }$ used in construction of $f(\beta )$ and the above preference relation may differ how they rank options below $x_{\emptyset }$. Since $\varphi$ is individually rational, strategy-proof, and non-bossy, the outcome of the mechanism does not depend on this part of preferences. Thus, we keep the same name for the preference relation $\succeq _{j}^{\beta }$ (we use the same slight abuse of notation for $\succeq _{i}^{\beta }$ below in Case 1.2.1). Then by strategy-proofness of $\varphi$ for j and by Eq. (6), we have $\varphi \left[ \succeq _{j}^{\beta },{\tilde{\succeq }}_{-j}^{\pi }\right] (j)\in \{h_{q},h_{\beta }\}$. There are two further subcases:

Fig. 2

The preference profiles in Case 1.2 (see Caption of Fig. 1 for further information)

$\underline{{\hbox {Case 1.2.1.}}}$ $\varphi \left[ \succeq _{j}^{\beta },{\tilde{\succeq }}_{-j}^{\pi }\right] (j)=h_{\beta }$ : Then by Eq. (6) and by non-bossiness of $\varphi$ for j we have $\varphi \left[ \succeq _{j}^{\beta },{\tilde{\succeq }}_{-j}^{\pi }\right] =\varphi \left[ {\tilde{\succeq }}^{\pi }\right]$ and hence, $\varphi \left[ \succeq _{j}^{\beta },{\tilde{\succeq }}_{-j}^{\pi }\right] (i)=h_{q}$ (by Eq. (6)). Consider the preference change for i from ${\tilde{\succeq }}_{i}^{\pi }$ by ranking $h_{\beta }$ just below $h_{q}$ as the last acceptable option so that we obtain

$$\begin{aligned} \succeq _{i}^{\beta }=h_{1},\ldots ,h_{q-1},h_{q},h_{\beta },x_{\varnothing },\ldots \end{aligned}$$

By strategy-proofness of $\varphi$ involving i, we have $\varphi \left[ \succeq _{\{i,j\}}^{\beta },{\tilde{\succeq }}_{-\{i,j\}}^{\pi }\right] (i)=\varphi \left[ \succeq _{j}^{\beta },{\tilde{\succeq }}_{-j}^{\pi }\right] (i)=h_{q}$. Also observe that $\left( \succeq _{\{i,j\}}^{\beta },{\tilde{\succeq }}_{-\{i,j\}}^{\pi }\right)$ is a monotonic transformation of ${\hat{\succeq }}$ (see Fig. 2). By monotonicity of $\varphi$, $\varphi \left[ \succeq _{\{i,j\}}^{\beta },{\tilde{\succeq }}_{-\{i,j\}}^{\pi }\right] =\varphi \left[ {\hat{\succeq }}\right]$. However, the facts that $\varphi \left[ {\hat{\succeq }}\right] (i)=h_{\beta }$ and $\varphi \left[ \succeq _{\{i,j\}}^{\beta },{\tilde{\succeq }}_{-\{i,j\}}^{\pi }\right] (i)=h_{q}$ contradict the previous statement.

$\underline{{\hbox {Case 1.2.2.}}}$ $\varphi \left[ \succeq _{j}^{\beta },{\tilde{\succeq }}_{-j}^{\pi }\right] (j)=h_{q}$: Consider the relevant binary submatching ${\tilde{\beta }}\subsetneq \beta$ with $\big |I^{{\tilde{\beta }}}\big |={\tilde{\ell }}-1$, $h_{q}=h_{{\tilde{\beta }}}$, and ${\tilde{\beta }}$ is the smallest relevant submatching of $\beta$ with this last property as defined at the beginning of the outer inductive proof for Step $\ell +1$. Recall that $\succeq _{j}^{\beta }$ ranks $h_{\beta }$ as acceptable below $h_{q}=h_{{\tilde{\beta }}}$ but otherwise the acceptable options and their ranking are identical with $\succeq _{j}^{{\tilde{\beta }}}$. Thus, by strategy-proofness and non-bossiness of $\varphi$ for j we have $\varphi \left[ \succeq _{j}^{{\tilde{\beta }}},{\tilde{\succeq }}_{-j}^{\pi }\right] =\varphi \left[ \succeq _{j}^{\beta },{\tilde{\succeq }}_{-j}^{\pi }\right]$. Then from Fig. 2 observe that, $\left( \succeq _{j}^{{\tilde{\beta }}},{\tilde{\succeq }}_{-j}^{\pi }\right)$ is a monotonic transformation of $\succeq ^{{\tilde{\beta }}}$, and hence by monotonicity of $\varphi$, we have $\varphi \left[ \succeq _{j}^{{\tilde{\beta }}},{\tilde{\succeq }}_{-j}^{\pi }\right] =\varphi \left[ \succeq ^{{\tilde{\beta }}}\right]$. In the outer inductive assumption of Step ${\tilde{\ell }}<\ell +1$ for the outer induction we assumed that $\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] (j_{m})=y_{m}$ for all $m=1,\ldots ,{\tilde{\ell }}-1$, and $\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] (f({\tilde{\beta }}))=h_{q}=h_{{\tilde{\beta }}}$ (actually exactly $f({\tilde{\beta }})=j_{{\tilde{\ell }}}$, that is how she is defined). Now if $j\not \in I^{\beta }$ then $j\not =j_{{\tilde{\ell }}}$. If $j=j_{m}\in I^{\beta }$ for some m then by Observation 1 as $m<k$ and $k\le \ell$ such that $y_{k}=h_{p}$ is a house, then $k\le {\tilde{\ell }}$ as well, as $j_{{\tilde{\ell }}}$ is the last agent in $\beta$ who is matched; these imply $m\not ={\tilde{\ell }}$ and thus $j\not =j_{{\tilde{\ell }}}$. Therefore, $\varphi \left[ \succeq ^{{\tilde{\beta }}}\right] (j_{{\tilde{\ell }}})=h_{{\tilde{\beta }}}=h_{q}$ contradicts $\varphi \left[ \succeq _{j}^{{\tilde{\beta }}},{\tilde{\succeq }}_{-j}^{\pi }\right] (j)=h_{q}$ as the two assignments should be the same.

In either case, we found that such an agent j cannot exist proving the inductive statement Eq. (2) for J. This completes Case 1.2 (and in turn Case 1).

$\underline{{\hbox {Case 2.}}}$ There is some agent $j_{n}\in I^{\beta }$ such that $y_{n}=x_{\varnothing }$ and $\varphi \left[ {\hat{\succeq }}\right] (j_{n})\not =x_{\varnothing }$. Without loss of generality, we assume that n is the largest index of an agent in $I^{\beta }$ with this property. Therefore, for each $j_{m}\in I^{\beta }$ with $m>n$ and $y_{m}=x_{\varnothing }$ we have $\varphi \left[ {\hat{\succeq }}\right] (j_{m})=y_{m}=x_{\varnothing }$. Then by individual rationality of $\varphi$, we have

$$\begin{aligned} \varphi \left[ {\hat{\succeq }}\right] (j_{n})=y_{k}=h_{p}\in H^{\sigma _{\beta }}=\{y_{1},\ldots ,y_{\ell }\}\cap H=\{h_{1},\ldots ,h_{q}\} \end{aligned}$$

for some k and p such that $1\le k<n\le \ell$ and $1\le p\le q$.

We construct a new preference profile ${\tilde{\succeq }}$ such that

• ${\tilde{\succeq }}_{j_{n}}=h_{1},\ldots ,h_{p},\ldots ,h_{q},h_{\beta },x_{\varnothing },\ldots$,

• ${\tilde{\succeq }}_{i}={\hat{\succeq }}_{i}$,

• ${\tilde{\succeq }}_{j_{m}}=x_{\varnothing },\ldots \quad$ for each m with $\ell \ge m>n$ and $\varphi \left[ {\hat{\succeq }}\right] (j_{m})=y_{m}=x_{\varnothing }$, and

• ${\tilde{\succeq }}_{i^{*}}=h_{1},\ldots ,h_{q},x_{\varnothing },\ldots \quad$ for each agent $i^{*}$ who is not considered above.

Profile ${\tilde{\succeq }}$ is a monotonic transformation of ${\hat{\succeq }}$ under $\varphi$: To see this observe that to construct ${\tilde{\succeq }}$ from ${\hat{\succeq }}$, we changed worse options than $h_{p}$ for $j_{n}$, we made $x_{\varnothing }$ the first choice of some of the agents who are assigned $x_{\varnothing }$ in $\varphi \left[ {\hat{\succeq }}\right]$, and we made $h_{\beta }$, which is the assignment of i under $\varphi \left[ {\hat{\succeq }}\right]$, unacceptable for some agents. Since $\varphi$ is monotonic, $\varphi \left[ {\tilde{\succeq }}\right] =\varphi \left[ {\hat{\succeq }}\right] .$

We define a new relevant binary submatching ${\hat{\beta }}$ of f of some size less than $\ell$ by iteratively constructing a series of relevant binary submatchings $\beta _{0}\subseteq \beta _{1}\subseteq \ldots \subseteq {\hat{\beta }}$ so that $H^{\sigma _{{\hat{\beta }}}}=H^{\sigma _{\beta }}=\{h_{1},\ldots ,h_{q}\}$.

Step 0. We start with $\beta _{0}=\left( \left( j,\beta (j_{1})\right) ,\ldots ,\left( j_{n-1},\beta (j_{n-1})\right) ,(j_{n},1)\right)$, and hence, we assign $j_{n}$ 1 in $\beta _{0}$, which is different from her 0 assignment in $\beta$.

$\quad \quad \vdots$

Step ${\hat{m}}$ for ${\hat{m}}\in \{1,2,\ldots ,\ell -n\}$. Suppose the relevant binary submatching $\beta _{{\hat{m}}-1}\supsetneq \beta _{0}$ of size ${\hat{m}}+n$ is defined in Step ${\hat{m}}-1$. Since f is well defined for binary submatchings of size ${\hat{m}}+n<\ell$ by the outer inductive assumption, $f(\beta _{{\hat{m}}-1})$ is also well defined. Let $i^{*}=f(\beta _{{\hat{m}}-1})$. We have two cases:

• 1. If $i^{*}\in I^{\beta }{\setminus } I^{\beta _{{\hat{m}}-1}}$ then let

  $$\begin{aligned} \beta _{{\hat{m}}}=\left( \beta _{{\hat{m}}-1},\left( i^{*},\beta (i^{*})\right) \right) \end{aligned}$$

  and

• 2. If $i^{*}\in I{\setminus } I^{\beta }$ then let

  $$\begin{aligned} \beta _{{\hat{m}}}=\left( \beta _{{\hat{m}}-1},(i^{*},1)\right) . \end{aligned}$$

If $\Big |\beta _{{\hat{m}}}^{-1}(1)\Big |=q$, i.e., the number of agents who are matched under $\beta _{{\hat{m}}}$ is equal to the number of houses in $\sigma _{\beta }$, which is q (and in turn, this is the number of agents matched under $\beta$), then we stop the construction and set ${\hat{\beta }}=\beta _{{\hat{m}}}$. Otherwise we continue with Step ${\hat{m}}+1$.

This construction ends at some step by finiteness. By the outer inductive assumption, the resulting ${\hat{\beta }}$ is relevant for the part of the binary serial order f constructed till Step $\big |I^{{\hat{\beta }}}\big |+1<\ell +1$. To see why $\big |I^{{\hat{\beta }}}\big |<\ell =|I^{\beta }|$ holds, observe that (i) except $j_{n}$, we keep the 0 assignments of agents in $\beta$ also in ${\hat{\beta }}$, (ii) although $j_{n}$ has 0 assignment in $\beta$, we assigned her 1 in ${\hat{\beta }}$, (iii) we do not include any additional pair with a 0 assignment to ${\hat{\beta }}$ that is not included in $\beta$, and (iv) exactly q agents are assigned 1 in both$\beta$ and ${\hat{\beta }}$.

In the construction we have $H^{\sigma _{{\hat{\beta }}}}=H^{\sigma _{\beta }}=\{h_{1},\ldots ,h_{q}\}$, and hence

$$\begin{aligned} h_{{\hat{\beta }}}&=h_{\beta }. \end{aligned}$$

(7)

Consider a preference profile $\succeq '\in {\mathcal {R}}^{\sigma _{{\hat{\beta }}}}$ defined for the relevant binary submatching ${\hat{\beta }}$ of f in Step $\big |I^{{\hat{\beta }}}\big |+1$ of the outer inductive step such that for each $i^{*}\in I{\setminus } I^{{\hat{\beta }}}$

$$\begin{aligned} \succeq _{i^{*}}'&=\left\{ \begin{array}{ll} h_{1},\ldots ,h_{q},h_{{\hat{\beta }}},x_{\varnothing },\ldots &{} \text {if }i^{*}=i\\ h_{1},\ldots ,h_{q},x_{\varnothing },\ldots &{} \text {otherwise} \end{array}\right. . \end{aligned}$$

The preference profile ${\tilde{\succeq }}$ is a monotonic transformation of $\succeq '$ under $\varphi$ because of the outer inductive assumption for Step $\big |I^{{\hat{\beta }}}\big |+1<\ell +1$ and because we have $\varphi [\succeq '](i)=h_{\beta }=h_{{\hat{\beta }}}$ by non-wastefulness of $\varphi$ (see Fig. 3). In particular, the same assumption implies $\varphi \left[ \succeq '\right] (j_{k})=y_{k}(=h_{p})$. By monotonicity of $\varphi$, we have $\varphi \left[ {\tilde{\succeq }}\right] =\varphi \left[ \succeq '\right]$. We reach a contradiction because $\varphi \left[ {\tilde{\succeq }}\right] (j_{n})=y_{k}.$ Thus, such an agent $j_{n}$ cannot exist, and Case 2 cannot hold.

Fig. 3

The preference profiles in Case 2 assuming that agent $i^{*}\in I{\setminus }\{i,j_{n}\}$ and she denotes a generic agent. Note that $h_{{\hat{\beta }}}=h_{\beta }$ (by Eq. (7)). Agent $j_{n}$’s assignment is in boldface and i’s assignment is underlined, if it can be determined, under each preference profile under $\varphi$. Assignments of all agents under $\varphi$ are boxed whenever they can be determined. If $j_{\ell }=j_{n}$ then we have the minor abuse of notation that $h_{r(n)+1}=h_{\beta }$

In all cases, we showed that the failure of Eq. (1) leads to a contradiction. We thus showed that Eq. (1) holds for Step $\ell +1$. Moreover, agent $f(\beta )\in I{\setminus } I^{\beta }$ is well defined as when $J=I{\setminus } I^{\beta }$, $f(\beta )=\varphi ^{-1}[\succeq ^{\beta }](h_{\beta })\in I{\setminus } I^{\beta }$ by Eq. (2) and non-wastefulness of $\varphi$, completing the proof of the Claim. $\diamondsuit$

To finish the proof of the theorem, take an arbitrary $\succeq \in {\mathcal {R}}^{|I|}$. Let $\mu =\phi ^{f}\left[ \succeq \right]$. Let $\beta \in {\mathcal {B}}^{f}$ be such that $\big |I^{\beta }\big |=|I|-1$ and $\beta$ is consistent with submatching

$$\begin{aligned} \sigma =\left( \left( j_{1},\mu (j_{1})\right) ,\ldots ,\left( j_{|I|-1},\mu (j_{|I|-1})\right) \right) \end{aligned}$$

and

$$\begin{aligned} \left( \left( j_{1},\mu (j_{1})\right) ,\ldots ,\left( j_{k},\mu (j_{k})\right) \right) \in {\mathcal {S}}^{f}\qquad \forall \;k\le |I|-1. \end{aligned}$$

Let $j_{|I|}=f(\beta )$, be the last remaining person in I. If $\mu (j_{|I|})\in H$, then let $\succeq '\in {\mathcal {R}}^{\sigma ;\mu (j_{|I|}),x_{\varnothing }}$ and otherwise, let $\succeq '\in {\mathcal {R}}^{\sigma ;x_{\varnothing }}$. Suppose $h_{1},\ldots ,h_{q}$ is the ordering of acceptable houses in the relevant ordered consistent submatching $\sigma _{\beta }$ used in construction of $f(\beta )$ in Step |I|. We define a relabeling $\pi$ which relabels houses $h_{1},\ldots ,h_{q}$ in this order with the names of the houses among the assignments $\mu (j_{1}),\ldots ,\mu (j_{|I|-1})$ in the same order. Let ${\hat{\succeq }}\in {\mathcal {R}}^{\sigma _{\beta };\mu (j_{|I|}),x_{\varnothing }}$if $\mu (j_{|I|})\in H$, and ${\hat{\succeq }}\in {\mathcal {R}}^{\sigma _{\beta };x_{\varnothing }}$, otherwise. We obtain

$$\begin{aligned} \varphi \left[ \succeq '\right] =\varphi \left[ {\hat{\succeq }}^{\pi }\right] =\phi ^{f}\left[ {\hat{\succeq }}^{\pi }\right] =\phi ^{f}\left[ \succeq '\right] \end{aligned}$$

where the first and last equalities follow from neutrality of $\varphi$ and $\phi ^{f}$ (and the fact that the ranking of unacceptable options do not affect the outcome under monotonic and individually rational mechanisms, which both $\varphi$ and $\phi ^{f}$ are), and the middle equality follows (i) from the Claim for all agents in $I^{\beta }$ and (ii) from non-wastefulness of $\varphi$ if $\mu (j_{|I|})\in H$ and individual rationality of $\varphi$ if $\mu (j_{|I|})=x_{\varnothing }$ for agent $j_{|I|}$. Moreover, $\succeq$ is a monotonic transformation of $\succeq '$ under both $\varphi$ and $\phi ^{f}$, which are both monotonic, and this implies the first and last equalities below (where the middle equality was established in the displayed equality above):

$$\begin{aligned} \varphi \left[ \succeq \right] =\varphi \left[ \succeq '\right] =\phi ^{f}\left[ \succeq '\right] =\phi ^{f}\left[ \succeq \right] . \end{aligned}$$

This completes the proof. $\square$

5 Independence of the axioms

By relaxing each axiom one at a time, we now show that there exists a mechanism which is not a binary serial dictatorship and yet satisfies the remaining axioms. We also show that the axioms remain independent if we substitute strategy-proofness and non-bossiness for group strategy-proofness (see Lemma 1 for this two-axiom reformulation of grup strategy-proofness).

Example 1

A mechanism that is non-strategy-proof, non-bossy, neutral, non-wasteful, and individually rational: Take a binary serial order. Run the associated binary serial dictatorship with the following modification: Reverse the preference order of each agent for all houses that she ranked higher than the outside option and keep the relative order of other options the same.

Example 2

A mechanism that is strategy-proof, bossy, neutral, non-wasteful, and individually rational: Let $f,f'$ be two binary serial orders such that $f(\emptyset )=f'(\emptyset )$, but otherwise the orders do not match in general, i.e., $f\not =f'$. Let $\varphi$ be a mechanism such that for $i=f(\emptyset )=f'(\emptyset )$

$$\begin{aligned} \varphi \left[ \succeq \right] =\left\{ \begin{array}{ll} \phi ^{f}\left[ \succeq \right] &{} \hbox {if }h\succ _{i}x_{\varnothing }\quad \forall h\in H\\ \phi ^{f'}\left[ \succeq \right] &{} \hbox {otherwise} \end{array}\right. , \end{aligned}$$

i.e., the binary serial order that will be used in the binary serial dictatorship is determined by the preferences of the initial dictator (but not necessarily by her assigned option), depending on whether she prefers all houses to the outside option or not.

Example 3

A mechanism that is strategy-proof, non-bossy, non-neutral, non-wasteful, and individually rational: A top-trading-cycles mechanism (a la Pápai 2000) that gives the ownership rights of objects to at least two different agents at the beginning.

Example 4

A mechanism that is strategy-proof, non-bossy, neutral, wasteful, and individually rational: A mechanism that leaves every agent always unmatched.

Example 5

A mechanism that is strategy-proof, non-bossy, neutral, non-wasteful, and individually irrational: Take a binary serial order. Run the associated binary serial dictatorship with the following modification: During her turn each agent is assigned the best available house according to her preferences if there are still available houses (even if the outside option is preferred to that house) and the outside option otherwise.

6 Serial dictatorships with outside options

Svensson’s serial dictatorship characterization also obtains in the subdomain of our preference domain in which the outside option is always ranked at the bottom of preferences. This is the preference domain analyzed in Pápai (2000) and in the following literature. Let this restricted set of preferences be denoted by ${\hat{{\mathcal {R}}}}$.

Theorem 2

A mechanism defined over ${{\hat{{\mathcal {R}}}}}^{|I|}$ is group strategy-proof, neutral, and non-wasteful if and only if it is a serial dictatorship.

This result is a corollary of Pycia and Ünver (2017): they characterize group strategy-proof and Pareto efficient mechanisms as Trading Cycle mechanisms introduced in their paper. As the conjunction of group strategy-proof and Pareto efficient is equivalent to the conjunction of group strategy-proof and non-wasteful, to prove the above theorem it is sufficient to check that TC mechanisms different from serial dictatorships are not neutral, which is straightforward.¹² Note that—unlike in Svensson’s original characterization—non-wastefulness is not a redundant axiom: a mechanism that leaves all agents unmatched satisfies all axioms but non-wastefulness.

7 Conclusion: scarcity vs abundance

A natural reading of our result is that in the presence of incentive and efficiency assumptions, neutral mechanisms belong to the class of sequential dictatorships. How general is this insight? How different is our version of it from Svensson’s (1999) characterization of serial dictatorships without outside options? To get a sense of the difference between our result and Svensson’s, consider a setting with houses and cars, with no outside options. We can embed Svensson’s setting in this environment by assuming that there are no cars and we can embed our setting in this environment by assuming that cars are abundant. In this general environment, let us consider mechanisms that are neutral with respect to houses. This concept reduces to neutrality in both Svensson’s and our setting. In this environment, the following mechanisms are neutral: any top-trading-cycles mechanisms (TTC, hierarchical exchange) of Pápai (2000) in which in each round one agent controls houses and a different agent controls cars. Each of these two agents would get her top available choice if it is controlled by her, and they would trade with each other if they like each other’s objects the most. However, whenever there is a conflict in their top choices, the agent holding the property right for the object they both want would receive the object. With three or more types of objects (e.g. houses, cars, and boats), we can even have trading-cycles mechanisms (TC) of Pycia and Ünver (2017) that are neutral among houses. Similar mechanism classes arise in settings when some objects have copies as long as the number of copies is strictly less than |I|. Neutrality among houses leads to sequential dictatorships when the goods are very scarce or when they are abundant, but in general, subclasses of sequential dictatorships cannot characterize neutral, group-strategy-proof, non-wasteful, and individually-rational mechanisms. Instead, the environment we study and the one studied by Svensson are two extreme cases of the general environment in which the connection between sequential dictatorships and neutrality is true.¹³

On the other hand, analogues of our results can be derived for domains with multiple abundant goods. Suppose for instance that we have multiple types of outside options that can each be attained by any agent, and agents value such outside options differently. In this case, a variant of our characterization would continue to hold: In this case, instead of a binary serial dictatorship, we will obtain a $(\ell +1)$—sequential dictatorship where $\ell$ is the number of different outside options, and recursively define its sequential order f as follows: for each relevant ordered submatching $\sigma =\left( (i_{1},x_{1}),(i_{2},x_{2}),\ldots ,(i_{n-1},x_{n-1})\right)$, once agent $f(\sigma )$ is defined as the next agent who owns all available houses, for any ordered submatching $\sigma '=\left( \sigma ,(f(\sigma ),x_{n})\right)$ agent $f(\sigma ')$ can be $\ell +1$ different agents depending on $x_{n}$ being one the $\ell$ outside options or a real house. Our proof can be extended to this case.