And the first runner-up is...: comparing winner selection procedures in multi-winner Tullock contests

Abstract

We characterise the strategic equivalence among k-winner contests using simultaneous and sequential winner selection. We test this prediction of strategic equivalence using a series of laboratory experiments, contrasting 1-winner contests with 2-winner contests, varying in the latter whether the outcome is revealed sequentially or in a single stage. We find that in the long run, average bidding levels are similar across strategically-equivalent contests. However, adaptation in 2-winner contests is slower and less systematic, which is consistent with the property that simultaneous winner selection results in outcomes that are more random than in the 1-winner case.

1 Introduction

Many contests result naturally in more than one contestant “winning.” Universities admit a subset of the students who apply each year; only some athletes trying out for a sports team will “make the cut”; and many academic conferences accept only some of the papers submitted.¹ In most of these cases the final outcome is stochastic instead of deterministic, and therefore the framework initiated by Tullock (1980) is appropriate. However, although in these settings each contestant chooses an “effort” level once, the same effort can be used for multiple selection draws (e.g., Clark and Riis 1996; Fu et al. 2014), and unlike Tullock’s original model, more than one of them are successful.

For the case of a single-winner contest, Tullock (1980)’s model sets the ratio of the probabilities that any two contestants i and j win the contest to be the ratio of their respective effort levels. Several different approaches have been proposed which extend this contest success function to the case in which there are $k\ge 1$ of prizes with equal value. Berry (1993) was the first to propose such an extension. Berry (1993)’s approach can be thought of as a contest among all subsets of contestants of size k. Specifically, for each subset of k players, the effort of that subset is given by summing the efforts of the players comprising the subset. These group efforts are then the inputs into Tullock’s contest success function. The “contestants” in Berry’s model are thus not the individual players, but the possible subgroups of winners, and the winners are determined as a joint selection as a group. In the case of $k=1$ it is immediate that Berry’s mechanism reduces to Tullock’s.

Berry (1993)’s description of this extension to the Tullock contest success function therefore has an unusual feature: contestants are ultimately successful as a group, but each chooses their efforts individually and independently. Loosely speaking, in an n-contestant contest, their efforts contribute to the chances of winning of $n-1 \atopwithdelims ()k-1$ “teams” with different compositions. Chowdhury and Kim (2014) proposed an alternative mechanism which does not express the chances of success in terms of groups: their survivor selection mechanism ranks players from last up to first, eliminating one player at each stage using a Tullock-style contest failure function, and so unfolds over (up to) $n-1$ stages.

There are a few experimental studies looking at the relative optimality of different types of multi-winner contests vis-á-vis the single-winner contest. For example, Herbring and Irlenbusch (2003) and Muller and Schotter (2010) report that multiple prizes generate higher effort than a single prize in perfectly discriminating all-pay contests, whereas, Chen et al. (2011), Sheremeta (2011), and Shupp et al. (2014) study multiple prizes in imperfectly discriminating contests. In particular, Chen et al. (2011) study the provision of an additional prize in a rank-order tournament with heterogeneous players, and Sheremeta (2011) and Shupp et al. (2014) compare a single-winner contest with multi-winner contests where the multiple winners are selected via a sequence of single-winner draws as in Clark and Riis (1996).

In this paper, we provide a first experimental study in contest design in multi-winner Tullock-style contests.² We generalise the analysis of Chowdhury and Kim (2014) to show that, in the case in which there are k winners who each receive a prize of the same value, the survivor selection mechanism produces the same distribution over prize allocations as Berry (1993)’s joint selection, for all configurations of contestants’ efforts. This result proposes a null hypothesis that these mechanisms should be equivalent in principle, and will elicit comparable levels of efforts from the participants. This equivalence is important to note. As shown in Fu and Lu (2009), under a sequential winner selection process, a grand contest provides higher level of effort than a set of small contests. However, Chowdhury and Kim (2017) show that this result is reversed when a sequential loser elimination process is employed. Hence, the equivalence noted above also means that a simultaneous winner selection should be accompanied with a set of small contests.

Another attractive feature of survivor selection is that, as noted by Fu et al. (2014), it mirrors the way that contest outcomes are sometimes revealed, with the announcement of the elimination of unsuccessful candidates first.³ Because Berry (1993)’s rule requires consideration of the chances of winning across $n-1 \atopwithdelims ()k-1$ teams while survivor selection takes only up to $n-1$ stages to resolve the prizes, a possible benefit of survivor selection is that it might be more learnable. Contestants might find it easier to follow the logic of how their efforts map into chances of winning a prize because the process of determining the successful contestants is not expressed across many possible teams.⁴

However, survivor selection breaks a symmetry in Berry (1993)’s expression of the contest success function, in which not only the k winning places are indistinguishable from each other, but the $n-k$ unsuccessful places are likewise indistinguishable.⁵ The equivalence between joint selection and survivor selection would fail if contestants distinguished among the unsuccessful places due to behavioural reasons such as joy of winning (Sheremeta 2010) or, conversely, preferences over the sequence of losing out.

We develop the concept of the effective prize value of a Tullock-style contest using the survivor selection mechanism for any arbitrary set of prize values. The effective prize value is defined as the value of the prize of a single-winner Tullock contest which would generate the same best response function for a risk-neutral contestant. This allows us to calibrate our comparisons of the performance of both multi-winner mechanisms against the familiar and well-studied single-winner case. We show that efforts in the survivor selection mechanism would be lower if participants valued finishing as the “first runner-up”.

We investigate, for the first time in the literature, the contest design questions of equivalence and learnability of these mechanisms in a laboratory experiment in which we extend the ticket-based implementation of Tullock contests developed in Chowdhury et al. (2019) to the Berry (1993) and Chowdhury and Kim (2014) mechanisms. Our results are broadly supportive of both equivalence and learnability. In the long run average bids are similar in 1-winner and 2-winner contests, and in the sequential and simultaneous implementations of 2-winner contests. However, we observe somewhat slower adaptation in the 2-winner contests, which would be consistent with the link between effort and success being more random in these 2-winner contests than the 1-winner counterpart.

Section 2 provides a self-contained analysis of the mechanisms of Berry (1993) and Chowdhury and Kim (2014), generalising the results from both and introducing the concept of the effective prize value as a sufficient statistic measuring the incentives to give effort in these mechanisms. Section 3 outlines the experimental design we developed for evaluating the performance of contests which are strategically equivalent under standard assumptions. We report our data and results in Sect. 4, and conclude with a brief discussion in Sect. 5.

2 Theoretical framework

2.1 A Tullock contest with discriminated prizes

There are $n\ge 2$ players, indexed by $i=1,2,\ldots ,n$ who compete in a contest for a set of prizes $\{v_r\}_{r=1}^n$.⁶ Each player i chooses a bid $b_i\in \left[ 0,\infty \right)$, which is irrevocably sunk, irrespective of the outcome of the contest. The outcome of the contest is a rank ordering of the players $(p_r)_{r=1}^n$, where $p_r$ is the index of the player assigned rank r. Any given profile $\textbf{b}=\left( b_i\right) _{i=1}^n$ of bids results in a probability distribution over the set of possible rank orderings. Let $\rho _{ir}(\textbf{b})$ denote the probability that player i is assigned to rank r given bid profile $\textbf{b}$. The payoff to player i given profile $\textbf{b}$ is then $u_i(\textbf{b})=\sum _{r=1}^n \rho _{ir}(\textbf{b})v_r - b_i$.

A special case of this is the single-winner (or 1-winner) contest, in which $v_1=w$ and $v_r=0$ for $2\le r \le n$. In the model of Tullock (1980), the probability player i wins the prize w is given by the contest success function

$$\begin{aligned} \rho _{i1}(\textbf{b}) = {\left\{ \begin{array}{ll} \frac{b_i}{\sum _{j=1}^n b_j} &{} \quad \textrm{if } \sum _{j=1}^n b_j > 0 \\ \frac{1}{n} &{} \quad \textrm{if } \sum _{j=1}^n b_j = 0 \\ \end{array}\right. } \end{aligned}$$

Player i’s utility function is $u_i(\textbf{b})=\rho _{i1}(\textbf{b})w - b_i$. Assuming $v_1>0$, that is, that winning the single prize is a good thing, his best-response function if $\sum _{j\not =i} b_j>0$ is

$$\begin{aligned} b_i^\star (\textbf{b}_{-i}) = \max \left( \sqrt{w\sum _{j\ne i}b_j} - \sum _{j\ne i} b_j, 0 \right) . \end{aligned}$$

(1)

In the contingency where $\sum _{j\not =i} b_j=0$, the best response is not well-defined because of the discontinuity in the payoff function at $\textbf{b}=\textbf{0}$. Importantly, $b_i=0$ is not a best response to $\textbf{b}_{-i}=\textbf{0}$, and therefore $\textbf{b}=\textbf{0}$ is not an equilibrium. The unique Nash equilibrium profile is symmetric, with $b_i^{1W}=\frac{n-1}{n^2}w$ for all bidders.⁷ To embed Tullock (1980)’s model in our setting, any distribution over ranks for the remaining $n-1$ players can be chosen, insofar as prizes 2 to n are payoff-equivalent.

Turning to the general case where prizes are distinguished, one method for determining the rank ordering is the survivor selection mechanism proposed by Chowdhury and Kim (2014), in which ranks are determined from the lowest rank (n) upwards in sequence. We extend their analysis to allow for asymmetric bid profiles, and for any sequence of prize values. There are $n-1$ stages, which we number $n,n-1,\ldots ,2$ for convenience; at stage r, the identity of the player assigned to rank r and receiving prize $v_r$ is determined. The final stage, stage 2, determines the player receiving prize $v_2$, with the last unassigned player receiving prize $v_1$. Let $M_r$ be the set of players still active at the start of stage r. In this mechanism, the conditional probability of a player $i\in M_r$ being eliminated at stage r is a Tullock-type contest failure function,

$$\begin{aligned} \rho _{ir}(\textbf{b}|i\in M_r) = {\left\{ \begin{array}{ll} \frac{\sum _{j\in M_r\setminus \{p_r\}} b_j}{(r-1)\sum _{j\in M_r} b_j} &{} \quad \textrm{if } \sum _{j=1}^n b_j > 0 \\ \frac{1}{n} &{} \quad \textrm{if } \sum _{j=1}^n b_j = 0 \\ \end{array}\right. } \end{aligned}$$

(2)

Proposition 1

A risk-neutral player’s best response function in a contest with prizes $\{v_r\}_{r=1}^n$ conducted using the survivor selection mechanism is the same as their best response function in a single-winner Tullock contest in which the value of the single nonzero prize is $\tilde{v}\equiv v_1-\frac{\sum _{r=2}^n v_r}{n-1}$. In particular, a risk-neutral player i’s best response to any $\textbf{b}$ with $\sum _{j\not = i}b_j>0$ is

$$\begin{aligned} b_i^\star (\textbf{b}_{-i}) = \max \left( \sqrt{\tilde{v}\sum _{j\ne i}b_j} - \sum _{j\ne i} b_j, 0 \right) \end{aligned}$$

(3)

and the unique Nash equilibrium profile if all bidders are risk-neutral is

$$\begin{aligned} b_i^{NE}= {\left\{ \begin{array}{ll} \frac{n-1}{n^2} \tilde{v} &{} \quad \mathrm {if~} \tilde{v}>0 \\ 0 &{} \quad \mathrm {if~} \tilde{v}\le 0 \end{array}\right. } \end{aligned}$$

(4)

for all bidders i.

Proof

See Appendix A. $\square$

We refer to the quantity $\tilde{v}$ as the effective prize value for a given prize structure.⁸

2.2 Multiple winners with identical prizes

Distinguishing among the winners of different prizes is only essential when prizes are distinct. In this section, we consider the case of a k-winner contest, in which the top k prizes are identical to each other, $v_1=\cdots =v_k\equiv w$, and all other prizes $v_{k+1}=\cdots = v_n=0$. It is natural to refer to the players receiving the top k prizes as the winners. In this setting the effective prize value is $\tilde{v}=\frac{n-k}{n-1}w$.

Berry (1993) proposed a joint selection mechanism, in which a subset of k players is selected directly in one step to receive the top k prizes. Let $\mathcal {N}_k$ denote the set of all subsets consisting of exactly k players. The probability a given subset $\textbf{K}\in \mathcal {N}_k$ of players is selected to be the winners of the k prizes is

$$\begin{aligned} f_{\textbf{K}}(\textbf{e}) = \frac{\sum _{j\in \textbf{K}} b_j}{\sum _{\kappa \in \mathcal {N}_k} \sum _{j\in \kappa } b_j}. \end{aligned}$$

(5)

Proposition 2

Fix $k\ge 1$, and let $v_r=w$ for $r\le k$ and $v_r=0$ for $r>k$. For each profile $\textbf{b}$ of bids, the joint selection mechanism of Berry (1993) and the survivor selection mechanism of Chowdhury and Kim (2014) produce identical distributions of allocations of the prizes.

Proof

See Appendix A. $\square$

2.3 Behavioural extensions

In the model as analysed so far, the utility function assumes that each prize has a value which is measured in units of the cost of bids.⁹ The specific subjective values players assign to prizes are not directly observable. In a laboratory setting, prizes are usually set to be cash amounts, and the cash values of the prizes and the cost per unit effort can be used to generate a predicted equilibrium effort level for risk-neutral players using (4).

In laboratory experiments with 1-winner Tullock contests, bids frequently exceed the (risk-neutral) Nash equilibrium. One factor which has been proposed to contribute to high bids is that the value of receiving the prize is more than its cash value, for example, due to a joy of winning (Sheremeta 2010; Astor et al. 2013; Herbst 2016; Boosey et al. 2017). In the 1-winner case, one of the reasons a prize may be more highly valued is that it is unique; there is only one prize and only one player receives it. In the k-winner contest, winning may still bring some joy, but the prize is no longer unique. The absence of uniqueness would decrease the non-monetary component of the value of the prize.

Hypothesis 1

Fix $1<k<n$, and consider a 1-winner and a k-winner contest which have the same effective prize value $\tilde{v}$ when measured in monetary terms. Because the prize is unique in the 1-winner contest, efforts will be higher in the 1-winner than the k-winner when using the joint selection mechanism.

Justification  If both contests have the same effective prize value in monetary terms, then the uniqueness of the prize in the 1-winner contest implies it has a higher effective prize value when taking into account non-monetary considerations. The best-response function (3) shows that the effort level will therefore be higher for each given $\textbf{b}_{-i}$ in the 1-winner contest than the k-winner contest. $\square$

In the k-winner contest setting, there is no need to distinguish among the ranks $k-1$ to n, insofar as all of those prizes are identical. Nevertheless, the survivor selection mechanism could be useful in this setting for practical reasons; it might be easier for players to understand, and echoes mechanisms for revealing results that are used in real life, such as naming a “runner up” (and sometimes a “second runner up” and so on). Suppose, as envisaged by Chowdhury and Kim (2014), we implement a k-winner contest in which the survivor selection continues until the point where k players remain, and then terminates with the remaining players awarded the k winning prizes without distinction among them. The information about the ordering of elimination of the unsuccessful players is irrelevant in terms of the material outcomes of the mechanism, in that all eliminated players receive identical prizes. Nevertheless, players might attach additional significance to the rank ordering; for example, valuing being the runner up by finishing in $(k+1)$st place. This would be captured in the game by assigning a value $v_{k+1}>0$ to the $(k+1)$st prize.

Hypothesis 2

Fix $1<k<n$, and consider a k-winner contest with the same prize value w, implemented in one case using survivor selection and in another using joint selection. Because being named a runner up (e.g. for the $(k+1)$st place) may be valued, efforts will be higher for each given $\textbf{b}_{-i}$ in the joint selection mechanism than the survivor selection mechanism.

Justification   In terms of the model, valuing being named a runner up in the survivor selection mechanism would set $v_{k+1}>0$ (and possibly other prizes between $k+2$ and $n-1$) while retaining $v_n=0$. The best-response function (3) shows that the resulting effort level would be lower for each given $\textbf{b}_{-i}$ in the survivor selection mechanism than in the joint selection mechanism. $\square$

We note that the comparative statics which generate Hypotheses 1 and 2 are based on inspection of the best-response function, and require neither equilibrium nor symmetry in the idiosyncratic prize valuations across players.

We turn now to a consideration of how the dynamics of bidding across the experiment might differ between 1-winner and k-winner contests. The potential learnability of the k-winner contests is relevant to assessing their suitability for practical implementation. On the surface, the description of both implementations of k-winner contests is more complex than for the 1-winner counterpart. Berry’s formula for the simultaneous selection of winners involves more terms, while eliminating contestants sequentially means there are multiple stages that a contestant might need to reason through. This assessment of the apparent complexity of the k-winner contest is based heuristically on the description of the two k-winner mechanisms. In contrast, the two k-winner mechanisms generate the exact same distributions over outcomes. This would suggest that players who experience the mechanisms, reflecting on and reacting to the expected payoffs associated with their bids, should find the mechanisms equally easy (or difficult) to learn how to play.

There is, however, evidence that people respond more to the realised outcome of the contest than to the expected outcome. Chowdhury et al. (2014) demonstrated the dynamics of play converge more tightly around the Nash equilibrium when the expected payoffs are realised using the share rule, and Lim et al. (2014), among others, find that participants adjust their bids differently after winning a contest than after losing one.

Hypothesis 3

Fix $1<k<n$, and consider a 1-winner and a k-winner contest which have the same effective prize value. Bidders will adapt their bids less systematically in the k-winner contest.

Justification   The expression for the effective prize value shows that the k-winner contests we consider are equivalent, in expected earnings terms, to conducting a 1-winner contest for one prize, and then allocating the remaining $k-1$ prizes at random. Even when the 1-winner and k-winner contests result in the same expected earnings, the realised payoff from the k-winner contest is therefore more noisy. If participants condition changes in their bid on the realised outcome of the contest, the changes they make will be less systematic in the k-winner contest than in the 1-winner. $\square$

3 Experiment

3.1 Parametric design

We implement three contest environments in which the effective prize size is held constant. In our experiments we choose $n=4$, the most common number of players in the literature of experiments with Tullock contests. We described the task as “bidding for a reward.”¹⁰ We set the monetary value of the effective prize value to be 160,¹¹ which means in the 1-winner (1W) treatment, the reward is 160. If prize uniqueness is indeed relevant, we expect the maximum contrast would be between the 1-winner and 2-winner cases. Therefore, we implement 2-winner contests using both joint selection (2J) and survivor selection (2S) mechanisms; to generate the same monetary effective prize value, in these settings the two winners each received rewards of 240. We follow the most common convention in the literature and give each participant at the start of each contest an endowment equal to the value of the reward.¹² A participant’s monetary payoff from a single contest game was equal to their endowment minus their bid, plus the value of the reward if they were selected to receive one.

3.2 Implementation of the contests

In each given session, participants played 30 contest periods in one of the environments. The number of periods was announced in the instructions. The groups of participants were randomly assigned at the start of a session, then held fixed throughout the session. Within a group, members were referred to anonymously by ID numbers 1, 2, 3, and 4; these ID numbers were randomised after each period. All interaction was mediated through computer terminals, using zTree. Fischbacher (2007) A participant’s complete history of their own bids and their earnings in each period was provided throughout the experiment. Formally, therefore, the 4 participants in a group play a repeated game of 30 periods, with a common public history. By standard arguments, the unique subgame-perfect equilibrium of this supergame interaction is to play the Nash equilibrium of 30 in all periods.

A practical challenge in a controlled implementation of survivor selection and joint selection is the translation of the selection probabilities (2) and (5), respectively, into an accessible format. Our behavioural hypotheses are on the potential non-monetary valuations associated with rankings that participants may have, which could be confounded by the more complex calculation that is inherent in determining those selection probabilities in the 2-winner case.

We therefore implemented the contests using an extension of the ticket protocol as described and tested for the 1-winner contest in Chowdhury et al. (2019). At the start of each period, each participant selected a bid, which could be any integer number of pence from 0 up to $v_1$, inclusive. These bids were translated into tickets of different types.

Each virtual ticket was given a number from 1 up to the total number of tickets created. The computer drew one of those ticket numbers at random, displayed the ticket number drawn, and indicated the type of the ticket with that number.¹³ The type of ticket determined which players received, or were eliminated from receiving, a reward.

In the 1-winner (1W) treatment, for each player i there was a corresponding ticket type Type i. The number of tickets of Type i was given by player i’s bid $b_i$, resulting in $b_1+b_2+b_3+b_4$ tickets. The recipient of the reward was determined by a single draw from the pool of tickets; if a Type i ticket was drawn, player i received the reward.

In the joint selection (2J) treatment, for each pair of players (i, j) there was a corresponding ticket type Type i &j. The number of tickets of Type i &j was given by $b_i+b_j$, resulting in $3(b_1+b_2+b_3+b_4)$ tickets. The recipients of the rewards were determined by a single draw from the pool of tickets; if a Type i &j ticket was drawn, players i and j received the rewards.

In the survivor selection (2S) treatment, the outcome was realised in two stages. In the first stage, for each triad of players (i, j, k) there was a corresponding ticket type Type i &j &k. The number of tickets of Type i &j &k was given by $b_i+b_j+b_k$, resulting in $6(b_1+b_2+b_3+b_4)$ tickets. The survivors of the first stage were determined by a draw from this pool of tickets; if a Type i &j &k ticket was drawn, players i, j, and k survived to the second stage.¹⁴ The second stage is procedurally identical to joint selection, except restricted to the three surviving players. A new pool of tickets was then created. If players i, j, and k were the surviving players, then there would be $b_i+b_j$ tickets of Type i &j, $b_i+b_k$ tickets of Type i &k, and $b_j+b_k$ tickets of Type j &k, for a total of $2(b_i+b_j+b_k)$ tickets. The recipients of the rewards were determined by a single draw from this pool of tickets.

3.3 Procedures

We report on four sessions for each treatment.¹⁵ There were 12 participants in each session, who were randomly allocated into the fixed groups of four, in which they remained for the entire experiment. There are therefore 12 independent groups in each treatment. Sessions were conducted at the Centre for Behavioural and Experimental Social Science (CBESS) at the University of East Anglia, using the participant pool of student subjects maintained by hRoot. Bock et al. (2014) At the end of each session, 5 of the 30 periods were selected at random to determine earnings. Sessions lasted between 60 and 90 min, with 2S sessions naturally lasting slightly longer due to the two-stage realisation of the outcomes. Participants earned in 1W between £4.92 and £12.76 (mean £8.64, SD £1.55); in 2J between £10.16 and £22.83 (mean £16.29, SD £3.36); and in 2S between £9.73 and £24.05 (mean £16.15, SD £3.20).

Fig. 1

All bids by period, grouped by treatment. Each dot represents the bid of one participant in one period. The solid line plots the evolution of the overall mean bid, and the shaded areas the interquartile range. The horizontal dashed line indicates the Nash equilibrium bid of 30

4 Results

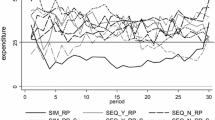
We begin with an overview of all of the bids in our sample. Figure 1 provides dotplots for all bids made in each period. Overlaid are solid lines indicating the mean bid in the period, and a shaded area which covers the interquartile range of bids for the period. Broadly speaking, the dynamics of play over time are similar to those which are typically found in Tullock contest experiments. Bids in the initial period are above the Nash equilibrium. Over time the measures of central tendency of the bids move towards the equilibrium, while dispersion around the mean or median persists.

Fig. 2

Distribution of group mean bids by treatment. For each period, the vertical boxes plot the interquartile range of average bids across groups. The black diamonds indicate the median of the group averages

Recalling that participants played in fixed groups for all 30 periods, we turn to looking at the group as the unit of independent observation. For each group in each period we compute the mean bid of the group, and, in Fig. 2, we present boxplots capturing the distribution of these group mean bids across periods. This view of the data tells a similar story to that of Fig. 1, while pointing out that for some periods late in the 2-winner treatment, the median group actually bids slightly less on average than the equilibrium prediction. Figures 1 and 2 also illustrate that there is one outlier, a participant in 2S who consistently bid 150, resulting in the mean bid of their group being consistently around 90. From this it can be seen that the other participants in that outlier group bid on average about 20, which qualitatively is in the direction recommended by the reaction function in the presence of a persistently high bidder.

Table 1 Descriptive statistics on average bids by group

Fig. 3

Distribution of average group bids, all periods. Each dot represents the average bid in one group. The horizontal box indicates the interquartile range of each distribution

Table 1 reports summary statistics of average bids across groups, using the group as the unit of observation. When looking across the entire 30-period supergame, bids are slightly higher in the 2-winner contests. Closer inspection reveals this is a game of two halves. Higher bids in 2-winner contests are driven by behaviour in the first half of the supergame; in the second half, the average across groups is similar across all treatments, and the median group bids are actually lower in 2-winner contests. Groups in 2-winner contests, however, are more heterogeneous. Figure 3 plots the distribution of group mean bids over the full supergame; more extreme groups, both with higher and lower bids, tend to be observed in 2-winner treatments.

Table 2 Descriptive statistics for first-period bids. The unit of observation is the individual bidder

Result 1

First-period bids are higher in 2-winner contests.

Proof

(Support) When looking at the first period, we are able to treat all bids as independent as participants have had as yet no interaction. Table 2 provides summary statistics of the distribution of first-period bids. A Mann–Whitney–Wilcoxon (MWW) test comparing bids in 1W against those in 2-winner contests (2J and 2S pooled) rejects the null hypothesis of equal distributions ($p=0.05$, $r=0.40$).¹⁶ If we are willing also to attach significance to the magnitudes of the bids instead of only their relative ranking, a two-sample t-test with unequal variances rejects the null hypothesis of equal mean bids between 1W and 2-winner contests ($p=0.005$). $\square$

Because this result goes so strongly in the opposite direction from the prediction of Hypothesis 1, it deserves further comment. As an ex-post explanation, we propose this result is driven by a naïve response of participants to the description of the environment. In the first period, participants do not yet have experience with the mechanisms, and, in particular, the strategic importance of the fact that two participants receive the reward in the 2-winner contests. Our theoretical development in 2 shows how to integrate the number of winners and the value of the reward to determine the effective prize value, which is sufficient to determine strategic responses. Participants only see the raw information in the instructions, and, in particular, that the value of the prize is 240. As a rough calculation, recall that the equilibrium effort is proportional to the effective prize size. If participants neglected the fact of multiple winners in the 2-winner contest and looked only at the headline prize value of 240, we might expect bids to be 50% higher than in 1W, in which the prize value is 160. The grand average of first-period bids across both 2-winner contests is 84.3, compared to 60.1 in 1W, an increase of approximately 40%.

Our experiment was not designed to identify potential causes of this pattern of first-period bids. However, these initial conditions are transient; experience with the mechanism in all cases leads to similar average bidding behaviour.

Result 2

Mean bids across groups are not different across treatments in the second half of the supergame.

Proof

(Support) A Kruskal-Wallis test comparing the three treatments does not reject the null hypothesis of equal distributions ($p=0.87$). Pairwise comparisons of treatments using MWW likewise show small effect sizes when comparing 1W to 2J ($p=0.82$, $r=0.53$), 1W to 2S ($p=0.49$, $r=0.58$), and 2J to 2S ($p=0.86$, $r=0.48$), as does comparing 1W to the pooled 2-winner contests ($p=0.59$, $r=0.56$). $\square$

The ranking of 1W against the 2-winner contests is in the direction of Hypothesis 1, but the effect sizes are negligible; we find no evidence in support of a hypothesis that uniqueness of the prize is an important driver of behaviour after repeated experience with the mechanism. We also find no evidence that revealing outcomes simultaneously or sequentially affects long-run behaviour, in contrast to Hypothesis 2.¹⁷

To address our hypotheses about the learnability of 2-winner contests, we follow Chowdhury et al. (2019) by looking at the payoff space. Consider a group g in session s of treatment m, and let $b_{it}$ be the bid submitted by bidder i in period t. This bid had an expected payoff to i of¹⁸

$$\begin{aligned} \pi _{it} = \frac{b_{it}}{\sum _{j\in g} b_{jt}} \times 160 - b_{it} + K_m. \end{aligned}$$

Let $B_{it}=\sum _{j\in g:j\not =i} b_{jt}$ be the sum of the bids of others in the group, the ex-post best response for bidder i, $\tilde{b}_{it}$, would be given by (3) if bids were permitted to be continuous. Bids are required to be discrete in our experiment; the quasiconcavity of the expected payoff function ensures that the discretised best response $b_{it}^\star \in \{\lceil \tilde{b}_{it}^\star \rceil ,\lfloor \tilde{b}_{it}^\star \rfloor \}$ This discretised best response generates an expected payoff to i of

$$\begin{aligned} \pi _{it}^\star = \frac{b_{it}^\star }{b_{it}^\star + B_{it}} \times 160 - b_{it}^\star + K_m. \end{aligned}$$

We then define the measure of disequilibrium for the group as $\varepsilon _{msgt}=\textrm{median}_{i\in g}\{\pi _{it}^\star - \pi _{it}\}$. By construction $\varepsilon _{msgt}\ge 0$ with $\varepsilon _{msgt}=0$ only at the Nash equilibrium.

Fig. 4

Ex-post measure of disequilibrium within groups ($\varepsilon _{csgt}$), by period. Each dot indicates the value of the measure for one group in the corresponding period. The solid line plots the evolution of the mean across groups, and the shaded areas the interquartile range. The two arrows in 2S indicate one group in each of periods 1 and 2 with $\varepsilon _{msgt}>120$

In Fig. 4 we show the evolution of the distribution of the disequilibrium measure $\varepsilon$ across groups over the experiment. Graphically this supports the assertion of Hypothesis 3, insofar as in both 2-winner treatments we observe some groups playing strategy profiles with large $\varepsilon$ even in the periods at the end of the experiment. This plot however does not take into account across-group heterogeneity, and so to assess whether adaptation is indeed systematically different across treatments a panel approach is required.

Fig. 5

Average value of disequilibrium measure $\varepsilon$ in period $t+1$, as a function of a group’s realised $\varepsilon$ in current period t

To provide a view of the data which respects this panel structure, in Fig. 5 we plot the average value of $\varepsilon _{msg(t+1)}$ as a function of $\varepsilon _{msgt}$, where we round the latter value to the nearest multiple of 10 for aggregation. In this graph, the 45-degree line indicates no systematic adaptation in the sense defined by this measure; the farther below the 45-degree line, the more rapid the adaptation towards bids which leave less money on the table. We observe that the 2-winner treatments are comparable to each other, but lie not too far below the 45-degree line, indicating relatively slow adaptation, while in the 1-winner treatment we observe adaptation which reduces $\varepsilon$ more systematically.

Table 3 Parameter estimates for model (6) of evolution of $\varepsilon _{msgt}$ over time

Result 3

Learning, as measured by ex-post amounts of money left on the table, is generally more systematic in 1-winner than 2-winner treatments. The long run disequilibrium level is higher in 2-winner treatments.

Proof

(Support) For each treatment m, and for the 2-winner treatments pooled, we estimate the dynamic panel model

$$\begin{aligned} \varepsilon _{msg(t+1)} = \alpha _m + \beta _m \varepsilon _{msgt}, \end{aligned}$$

(6)

using the method of Arellano and Bond (1991), and report the results in Table 3. Comparing 1-winner and 2-winner treatments in aggregate, we reject the hypothesis that $\varepsilon _{\text {1W},sgt}=\varepsilon _{\text {2J+2S},sgt}$ at the 10% level ($p=.056$ against two-sided alternative). The evidence is more clear when comparing 1W to 2J ($p=.013$) than 1W to 2S ($p=.122$).

We can use the point estimates of $\alpha$ and $\beta$ to compute the implied fixed-point of (6). This would be the prediction for the long-run value of the amount of money left on the table ex-post. All the fixed points are above zero. $\square$

The analysis above indicates that, to the extent we can say play is converging over time, it is a convergence not to the point prediction of the Nash equilibrium, but towards a distribution of play in some neighbourhood of the equilibrium in which the ex-post suboptimality of bids in expected-payoff terms is small but persistent.¹⁹

5 Discussion

We provide one of the first experimental studies on selecting multiple winners in Tullock-style imperfectly discriminating contests. We extend to the case of multiple winners a lottery ticket paradigm to implement the random realisation of the outcome of the contest. Our results provide some guidance for the practical implementation of Berry’s extension of the Tullock contest to the selection of multiple winners. Theoretical analysis, combined with previous behavioural results on how people adapt their play over time in contests, suggested that the 2-winner contests would be more difficult for people to “learn”. Indeed we find evidence to support this hypothesis; adaptation is indeed less systematic in the more noisy 2-winner contests, but nevertheless in the long run bids on average in the 2-winner contests are similar to the strategically equivalent 1-winner contest.

Empirically studying the learnability of a mechanism is important because previous experiments have reported that people do react to the ex-post outcome of the contest. In the context of our controlled laboratory experiment, a heuristic of taking the contest outcome into account for formulating strategy is not optimal for maximising payoffs. We provide the full profile of bids in each period, and this is enough, in principle at least, for a contestant to determine their best response, whether they wished to maximise expected earnings, or if they wanted to take into account risk or explicitly target probabilities of winning. The outcome of the contest contains no additional information. Although reacting to the contest outcome is therefore not optimal in our experiment, it would not at all naïve for someone playing a contest “in the wild”, in which other’s bids may not be observed, or, in the case of contests where the bid is, for example, an effort choice, even meaningfully observable. In that setting, one’s own previous choices and the outcome of the contests may be all a contestant has to go on. Therefore, the observation that adaptation is slower in the 2-winner contests could be a relevant consideration for implementation.

There is a sense in which the 2-winner contests are more complex to implement and, presumably, to understand solely from their description. In the 1-winner Tullock contest, the probability of winning a prize is straightforward to operationalise, for example using the instantiation of (virtual) tickets as in our experiment. It is less straightforward to understand immediately from the description of the Berry CSF how one’s chances of winning a prize in the 2-winner contest change as a function of one’s own bid, given some arbitrary conjecture of bids by the other participants in the group. As a crude counting-based measure of complexity, there are simply more types of tickets in both of the the 2-winner contests than in the 1-winner contest, and further there are two layers of ticket types in our exposition of the survivor selection mechanism.

Although our analysis in Sect. 2 establishes strategic equivalence for contests with the same effective prize value, the algebra in that section does not directly inform how either of the 2-winner contests are implemented. To clarify this point, consider a famous example of strategically equivalent mechanisms in the setting of auctions for a single indivisible good when bidders have private values. It is well-known that there is an equivalence in theory between the second-price sealed-bid auction, and an ascending “clock” auction. In both cases it is a weakly dominant strategy to “bid one’s own value.” Experimentally, it is routinely found that many participants do not bid their value in the second-price auction, while after a small amount of experience most bidders do drop out at their value in the clock version. One reason for this is that the clock auction takes the bidder through the chain of strategic reasoning that we use in the game-theoretic analysis, making it transparent that the sensible thing to do is to stay in the auction as long as the price is below their value, and exit as soon as it is above; in effect it helps bidders reason contingency-by-contingency, which is exactly how game theory says they ought to. Viewed this way, the ascending clock auction translates game-theoretic reasoning into a procedure people find it easy to follow.

The parallel in imperfectly-discriminating contests using Berry’s success function would be to transform to a 1-winner contest with the equivalent prize value, and allocate the remaining prizes/payoffs randomly. As noted, this is not natural, or even feasible in many situations in which prizes are not (only) amounts of money.²⁰ It is therefore an empirical question, whether people compete differently in multi-winner contests when the procedure for realising the winner is described and implemented differently. The mechanism in survivor selection is used in practice to communicate the outcome of contests. This makes it a natural candidate for consideration; on the one hand participants might find this implementation easier to understand, but survivor selection necessarily creates a distinction among otherwise identical “non-winner” places which could trigger idiosyncratic preferences for valuing, e.g., being the “first runner-up.” We do not find significant differences between joint and survivor selection, indicating that a contest designer is indeed free to choose either to suit their needs.²¹

Appendices

Proofs

1.1 Proposition 1

Before stating the proof of Proposition 1, we first establish two lemmas.

Lemma 1

Fix a profile of bids $\textbf{b}$ with $b_i>0$ for at least one player i, and any stage $2\le r \le n$. The probability that a given sequence $(p_n,p_{n-1},\ldots ,p_{r+1})$ is the sequence of players eliminated prior to stage r is

$$\begin{aligned} \frac{(r-1)! \sum _{j\in M_r} b_j}{(n-1)! \sum _{j\in M_n} b_j} \end{aligned}$$

(7)

Proof

We prove the claim by induction. For the base case of $r+1=n$, Eq. (7) simplifies to $\frac{(n-2)! \sum _{j\in M_n \setminus \{p_n\}} b_j}{(n-1)! \sum _{j\in M_n} b_j}= \frac{\sum _{j\in M_n \setminus \{p_n\}} b_j}{(n-1) \sum _{j\in M_n} b_j}$, which is (2) for $s=n$ as desired.

Now, fix a stage r and a sequence $(p_n,p_{n-1},\ldots ,p_{r+1},p_r)$, and assume the induction claim is true for $(p_n,p_{n-1},\ldots ,p_{r+1})$. The probability that $p_r$ is eliminated in stage r, conditional on $p_n,p_{n-1},\ldots ,p_{r+1}$ being previously eliminated, is

$$\begin{aligned}{} & {} \frac{(r-1)! \sum _{j\in M_r} b_j}{(n-1)! \sum _{j\in M_n} b_j} \times \frac{\sum _{j\in M_r \setminus \{p_r\}} b_j}{(r-1)\sum _{j\in M_r} b_j} \\ {}{} & {} \quad = \frac{(r-2)! \sum _{j\in M_r \setminus \{p_r\}} b_j}{(n-1)! \sum _{j\in M_n} b_j} = \frac{(r-2)! \sum _{j\in M_{r-1}} b_j}{(n-1)! \sum _{j\in M_n} b_j}, \end{aligned}$$

which is exactly the induction hypothesis with $r-1$ replacing r. $\square$

Lemma 2

Fix a profile of bids $\textbf{b}$ with $b_i>0$ for at least one player i. The probability that a given player i is eliminated at a given stage $2\le r\le n$, and therefore receives prize $v_r$, is

$$\begin{aligned} \rho _{ir}(\textbf{b}) = \frac{\sum _{j\ne i} b_j}{(n-1)\sum _{j\in N}b_j}, \end{aligned}$$

(8)

which is independent of r.

Proof

Fix a stage r, and let $\mathcal {M}^i_r$ be the set of subsets of players, which consist of exactly r players, one of whom is player i. Fix one such subset $M_r\in \mathcal {M}^i_r$. There are $(n-r)!$ sequences of prior eliminations of the players in $M_n\setminus M_r$ that result in $M_r$ being the remaining set at the start of stage r. Lemma 1 shows that the probability of each one of these sequences is identical, as the expression (7) does not depend on the order of elimination. By a counting argument, the probability that the set $M_r$ is the set of players to survive elimination rounds $n,n-1,\ldots ,r+1$ is therefore

$$\begin{aligned} (n-r)! \frac{(r-1)! \sum _{j\in M_r} b_j}{(n-1)! \sum _{j\in M_n} b_j} = \frac{\sum _{j\in M_r} b_j}{\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) \sum _{j\in M_n} b_j}. \end{aligned}$$

The joint probability that $M_r$ have survived to stage r and then i is eliminated in stage r is

$$\begin{aligned}{} & {} \frac{\sum _{j\in M_r} b_j}{\left( {\begin{array}{c}n-1\\ r-1\end{array}}\right) \sum _{j\in M_n} b_j} \times \frac{\sum _{j\in M_r\setminus \{i\}} b_j}{(r-1)\sum _{j\in M_r} b_j}= \frac{\sum _{j\in M_r\setminus \{i\}}b_j}{\frac{(n-1)!}{(r-2)!(n-r)!}\sum _{j\in M_n}b_j} \nonumber \\ {}{} & {} \quad = \frac{\sum _{j\in M_r\setminus \{i\}}b_j}{(n-1)\left( {\begin{array}{c}n-2\\ r-2\end{array}}\right) \sum _{j\in M_n}b_j}. \end{aligned}$$

(9)

Only the numerator of (9) depends on $M_r$. Consider $\sum _{M_r\in \mathcal {M}^i_r} \sum _{j\in M_r\setminus \{i\}}b_j$. For each other player $j\not = i$, there are $\left( {\begin{array}{c}n-2\\ r-2\end{array}}\right)$ sets in $\mathcal {M}^i_r$ which also contain player j, and therefore $b_j$ appears $\left( {\begin{array}{c}n-2\\ r-2\end{array}}\right)$ times in the double sum. Therefore, the total probability of player i being eliminated at stage r is

$$\begin{aligned} \sum _{M_r\in \mathcal {M}_r} \frac{\sum _{j\in M_r\setminus \{i\}}b_j}{(n-1)\left( {\begin{array}{c}n-2\\ r-2\end{array}}\right) \sum _{j\in M_n}b_j} = \frac{\left( {\begin{array}{c}n-2\\ r-2\end{array}}\right) \sum _{j\ne i} b_j}{(n-1)\left( {\begin{array}{c}n-2\\ r-2\end{array}}\right) \sum _{j\in M_n}b_j} = \frac{\sum _{j\not = i} b_j}{(n-1) \sum _{j\in M_n} b_j}. \end{aligned}$$

$\square$

Proof of Proposition 1

Fix a profile of bids $\textbf{b}$ with $b_i>0$ for at least one i. Lemma 2 shows that the conditional Tullock-type failure function (2) results in all prizes other than the first being awarded uniformly according to the unconditional Tullock-type failure function (8). The probability of receiving the first prize $v_1$ is therefore

$$\begin{aligned} 1 - (n-1)\frac{\sum _{j\ne i} b_j}{(n-1)\sum _{j\in N}b_j} = \frac{b_i}{\sum _{j\in N}b_j}, \end{aligned}$$

which is exactly the standard Tullock-type success function. If, on the other hand, $\textbf{b}=\textbf{0}$, the probability of receiving $v-1$ is $\frac{1}{n}$, just as in the single-winner Tullock game. Therefore the expected payoff to player i is

$$\begin{aligned} u_i(\textbf{b}) = {\left\{ \begin{array}{ll} \frac{b_i}{\sum _{j\in N}b_j}v_1 + \frac{\sum _{j\ne i}b_j}{\sum _{j\in N}b_j} \cdot \frac{\sum _{r=2}^n v_r}{n-1} - b_i &{} \quad \textrm{if } \sum _{j=1}^n b_j > 0 \\ \frac{1}{n} v_1 + \frac{1}{n} \sum _{r=2}^n v_r &{} \quad \textrm{if } \sum _{j=1}^n b_j = 0. \end{array}\right. } \end{aligned}$$

This is exactly equivalent to a single-winner Tullock contest in which all non-winners receive a payoff of $\frac{\sum _{r=2}^n v_r}{n-1}$, and is therefore strategically equivalent to a single-winner Tullock contest with $w=v_1-\frac{\sum _{r=2}^n v_r}{n-1}$ as the prize. In particular, player i’s best response to any $\textbf{b}$ with $\sum _{j\not = i}b_j>0$ is

$$\begin{aligned} b_i^\star (\textbf{b}_{-i}) = \max \left( \sqrt{\left( v_1-\frac{\sum _{r=2}^n v_r}{n-1}\right) \sum _{j\ne i}b_j} - \sum _{j\ne i} b_j, 0 \right) \end{aligned}$$

and the unique Nash equilibrium is

$$\begin{aligned} b^{SS}= {\left\{ \begin{array}{ll} \frac{n-1}{n^2} \left( v_1-\frac{\sum _{r=2}^n v_r}{n-1}\right) &{} \quad \mathrm {if~} v_1-\frac{\sum _{r=2}^n v_r}{n-1}>0 \\ 0 &{} \quad \mathrm {if~} v_1-\frac{\sum _{r=2}^n v_r}{n-1} \le 0. \end{array}\right. } \end{aligned}$$

Defining $\tilde{v}\equiv v_1-\frac{\sum _{r=2}^n v_r}{n-1}$ completes the result. $\square$

1.2 Proposition 2

Proof of Proposition 2

There are $\left( {\begin{array}{c}n\\ k\end{array}}\right)$ sets in $\mathcal {N}_k$. Each player j appears in exactly $\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right)$ of those sets. Therefore

$$\begin{aligned} \sum _{\kappa \in \mathcal {N}_k} \sum _{j\in \kappa } b_j = \sum _{j=1}^n \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) b_j. \end{aligned}$$

Let $\mathcal {N}^i_k$ denote the set of all subsets consisting of exactly k players, one of which is player i. There are $\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right)$ sets in $\mathcal {N}^i_k$. Observe that each player $j\not =i$ appears in exactly $\left( {\begin{array}{c}n-2\\ k-2\end{array}}\right)$ of those sets. Therefore

$$\begin{aligned} \sum _{\textbf{K}\in \mathcal {N}^i_k} \sum _{j\in \textbf{K}} b_j = \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) b_i + \sum _{j\not =i} \left( {\begin{array}{c}n-2\\ k-2\end{array}}\right) b_j. \end{aligned}$$

Player i receives one of the prizes valued at w if one of the sets in $\mathcal {N}^i_k$ is selected, which occurs with probability

$$\begin{aligned} \sum _{\textbf{K}\in \mathcal {N}^i_k} p_{\textbf{K}}(\textbf{b})= & {} \frac{\sum _{\textbf{K}\in \mathcal {N}^i_k} \sum _{j\in \textbf{K}} b_j}{\sum _{\kappa \in \mathcal {N}_k} \sum _{j\in \kappa } b_j} \nonumber \\= & {} \frac{\left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) b_i + \sum _{j\not =i} \left( {\begin{array}{c}n-2\\ k-2\end{array}}\right) b_j}{\sum _{j=1}^n \left( {\begin{array}{c}n-1\\ k-1\end{array}}\right) b_j} \nonumber \\= & {} \frac{b_i}{\sum _{j=1}^n b_j} + \frac{k-1}{n-1} \cdot \frac{\sum _{j\not =i} b_j}{\sum _{j=1}^n b_j}. \end{aligned}$$

(10)

We see immediately that (10) is exactly the probability of winning the first prize in survivor selection, plus $k-1$ times the probability (8) of winning any of the other prizes. Therefore, for each contingency $\textbf{b}$, the probability of player i winning one of the k prizes valued v is the same as in the survivor selection mechanism. $\square$

Instructions

1.1 Introduction (common to all treatments)

Welcome! You are about to participate in an experiment in the economics of decision-making.

If you follow the instructions and make appropriate decisions, you can earn an appreciable amount of money. At the end of today’s session you will be paid in private and in cash.

It is important that you remain silent and do not look at other people’s work. If you have any questions, or need assistance of any kind, please raise your hand and an experimenter will come to you. If you talk, laugh, exclaim out loud, etc., you will be asked to leave and you will not be paid. We expect and appreciate your cooperation.

Today’s session consists of two parts. The decisions you make in the two parts are completely unrelated to each other. Your earnings for the session will be the total of your earnings from the two parts.

1.2 Treatment-specific instructions for 1W

Part 2 of the session consists of 30 decision-making periods. At the conclusion of Part 2, any 5 of the 30 periods will be chosen at random, and your earnings from this part of the experiment will be calculated as the sum of your earnings from those 5 selected periods.

At the beginning of Part 2, you will be randomly and anonymously placed into a group of 4 participants. Within each group, one participant will have ID number 1, one ID number 2, one ID number 3, and one ID number 4. The composition of your group remains the same for all 30 periods but the individual ID numbers within a group are randomly reassigned in every period.

In each period, you may bid for a reward worth 160 pence. In your group, one of the four participants will receive a reward. You begin each period with an endowment of 160 pence. You may bid any whole number of pence from 0 to 160; fractions or decimals may not be used.

If you receive a reward in a period, your earnings will be calculated as:

Your payoff in pence = your endowment − your bid + the reward.

That is,

Your payoff in pence = 160 − your bid + 160.

If you do not receive a reward in a period, your earnings will be calculated as:

Your payoff in pence = your endowment − your bid

That is,

Your payoff in pence = your endowment − your bid

The chance that you receive a reward in a period depends on how much you bid, and also how much the other participants in your group bid. At the start of each period, all four participants of each group will decide how much to bid. Once the bids are determined, a computerised lottery will be conducted to determine which participant in the group will receive the reward. In this lottery draw, there are four types of tickets: Type 1, Type 2, Type 3 and Type 4. Each type of ticket corresponds to the participant who will receive the reward if a ticket of that type is drawn. So, if a Type 1 ticket is drawn, then participant 1 will receive the reward; if a Type 2 ticket is drawn, then participant 2 will receive the reward; and so on.

The number of each type of ticket depends on the bids of the corresponding participant:

• Number of Type 1 tickets = Bid of participant 1

• Number of Type 2 tickets = Bid of participant 2

• Number of Type 3 tickets = Bid of participant 3

• Number of Type 4 tickets = Bid of participant 4

Each ticket is equally likely to be drawn by the computer. If the ticket type that is drawn has your ID number, then you will receive a reward for that period.

We will now work through an example of how the numbers of lottery tickets are computed, and what you will see during a typical period of the session.

An example. Suppose participant 1 bids 80 pence, participant 2 bids 6 pence, participant 3 bids 124 pence, and participant 4 bids 45 pence. Then:

• Number of Type 1 tickets = Bid of participant 1 = 80

• Number of Type 2 tickets = Bid of participant 2 = 6

• Number of Type 3 tickets = Bid of participant 3 = 124

• Number of Type 4 tickets = Bid of participant 4 = 45

There will therefore be a total of 80 + 6 + 124 + 45 = 255 tickets in the lottery. Each ticket is equally likely to be selected. In each period, the calculations above will be summarised for you on your screen, using a table like the one in this screenshot:

Interpretation of the table: The horizontal rows in the above table contain the ID numbers of the four participants in every period. The vertical columns list the participants’ bids, the corresponding ticket types, the total number of each type of ticket (second column from right) and the range of ticket numbers for each type of ticket (last column). Note that the total number of each ticket type is exactly same as the corresponding participant’s bid. For example, the total number of Type 1 tickets is equal to Participant 1’s bid.

The last column gives the range of ticket numbers for each ticket type. Any ticket number that lies within that range is a ticket of the corresponding type. That is, all the ticket numbers from 81 to 86 are tickets of Type 2, which implies a total of 6 tickets of Type 2, as appears in the ‘Total Tickets’ column. In case a participant bids zero, there will be no ticket that contains his or her ID number. In such a case, the last column will show ‘No tickets’ for that particular ticket type.

The computer then selects one ticket at random. The number and the type of the drawn ticket will appear below the table. The ID number on the ticket type indicate the participant receiving the reward.

At the end of 30 periods, the experimenter will approach a random participant and will ask him/her to pick up five balls from a sack containing 30 balls numbered from 1 to 30. The numbers on those five balls will indicate the 5 periods, for which you will be paid in Part 2. Your earnings from all the preceding periods will be throughout present on your screen.

1.3 Treatment-specific instructions for 2J

Part 2 of the session consists of 30 decision-making periods. At the conclusion of Part 2, any 5 of the 30 periods will be chosen at random, and your earnings from this part of the experiment will be calculated as the sum of your earnings from those 5 selected periods.

At the beginning of Part 2, you will be randomly and anonymously placed into a group of 4 participants. Within each group, one participant will have ID number 1, one ID number 2, one ID number 3, and one ID number 4. The composition of your group remains the same for all 30 periods but the individual ID numbers within a group are randomly reassigned in every period.

In each period, you may bid for a reward worth 240 pence. In your group, two of the four participants will receive a reward. You begin each period with an endowment of 240 pence. You may bid any whole number of pence from 0 to 240; fractions or decimals may not be used.

If you receive a reward in a period, your earnings will be calculated as:

Your payoff in pence = your endowment − your bid + the reward.

That is,

Your payoff in pence = 240 − your bid + 240.

If you do not receive a reward in a period, your earnings will be calculated as:

Your payoff in pence = your endowment − your bid

That is,

Your payoff in pence = your endowment − your bid

The chance that you receive a reward in a period depends on how much you bid, and also how much the other participants in your group bid. At the start of each period, all four participants of each group will decide how much to bid. Once the bids are determined, a computerised lottery will be conducted to determine which two participants in the group will receive the rewards.

In this lottery draw, there are six types of tickets: Type 1 &2, Type 1 &3, Type 1 &4, Type 2 &3, Type 2 &4, and Type 3 &4. Each type of ticket corresponds to the two participants who will receive the rewards if a ticket of that type is drawn. So, if a Type 1 &2 ticket is drawn, then participants 1 and 2 will receive the rewards; if a Type 1 &3 ticket is drawn, then participants 1 and 3 will receive the rewards; and so on.

The number of tickets of each type depends on the bids of the corresponding two participants:

• Number of Type 1 &2 tickets = Bid of participant 1 + Bid of participant 2

• Number of Type 1 &3 tickets = Bid of participant 1 + Bid of participant 3

• Number of Type 1 &4 tickets = Bid of participant 1 + Bid of participant 4

• Number of Type 2 &3 tickets = Bid of participant 2 + Bid of participant 3

• Number of Type 2 &4 tickets = Bid of participant 2 + Bid of participant 4

• Number of Type 3 &4 tickets = Bid of participant 3 + Bid of participant 4

Each ticket is equally likely to be drawn by the computer. If the ticket type that is drawn includes your ID number, then you will receive a reward for that period.

We will now work through an example of how the numbers of lottery tickets are computed, and what you will see during a typical period of the session.

An example. Suppose participant 1 bids 80 pence, participant 2 bids 6 pence, participant 3 bids 124 pence, and participant 4 bids 45 pence. Then:

• Number of Type 1 &2 tickets = Bid of participant 1 + Bid of participant 2 = 80 + 6 = 86

• Number of Type 1 &3 tickets = Bid of participant 1 + Bid of participant 3 = 80 + 124 = 204

• Number of Type 1 &4 tickets = Bid of participant 1 + Bid of participant 4 = 80 + 45 = 125

• Number of Type 2 &3 tickets = Bid of participant 2 + Bid of participant 3 = 6 + 124 = 130

• Number of Type 2 &4 tickets = Bid of participant 2 + Bid of participant 4 = 6 + 45 = 51

• Number of Type 3 &4 tickets = Bid of participant 3 + Bid of participant 4 = 124 + 45 = 169

There will therefore be a total of 86 + 204 + 125 + 130 + 51 + 169 = 765 tickets in the lottery. Each ticket is equally likely to be selected. In each period, the calculations above will be summarised for you on your screen, using a table like the one in the following screenshot.

Interpretation of the table: The horizontal rows in the above table show the different types of lottery tickets that are generated by the computer in every period. The vertical columns list the participants’ bids, the total number of each type of ticket (second column from right) and the range of ticket numbers for each type of ticket (last column). Note that the total number of each ticket type is the sum of the two corresponding participants’ bids. For example, total number of Type 1 &2 tickets is the sum total of Participant 1’s bid and participant 2’s bid. Therefore, the table cell corresponding to Type 1 &2 and Participant 4’s bid is kept blank, and so is the table cell corresponding to Type 1 &2 and Participant 3’s bid. Similarly, the table cell corresponding to Type 2 &3 and Participant 1’s bid is kept blank, and so is the one corresponding to Type 2 &3 and Participant 4’s bid.

The last column gives the range of ticket numbers for each ticket type. Any ticket number that lies within that range is a ticket of the corresponding type. That is, all the ticket numbers from 87 to 290 are tickets of Type 1 &3, which implies a total of 204 tickets of Type 1 &3, as appears in the ‘Total Tickets’ column. In case any three participants all bid zero, there will be no ticket that contains those three ID numbers together. In such a case, the last column will show ‘No tickets’ for that particular ticket type.

The computer then selects one ticket at random. The number and the type of the drawn ticket will appear below the table. The two ID numbers on the ticket type indicate the two participants receiving the rewards.

At the end of 30 periods, the experimenter will approach a random participant and will ask him/her to pick up five balls from a sack containing 30 balls numbered from 1 to 30. The numbers on those five balls will indicate the 5 periods, for which you will be paid in Part 2. Your earnings from all the preceding periods will be throughout present on your screen.

1.4 Treatment-specific instructions for 2S

Part 2 of the session consists of 30 decision-making periods. At the conclusion of Part 2, any 5 of the 30 periods will be chosen at random, and your earnings from this part of the experiment will be calculated as the sum of your earnings from those 5 selected periods.

At the beginning of Part 2, you will be randomly and anonymously placed into a group of 4 participants. Within each group, one participant will have ID number 1, one ID number 2, one ID number 3, and one ID number 4. The composition of your group remains the same for all 30 periods but the individual ID numbers within a group are randomly reassigned in every period.

In each period, you may bid for a reward worth 240 pence. In your group, two of the four participants will receive a reward. You begin each period with an endowment of 240 pence. You may bid any whole number of pence from 0 to 240; fractions or decimals may not be used.

If you receive a reward in a period, your earnings will be calculated as:

Your payoff in pence = your endowment − your bid + the reward.

That is,

Your payoff in pence = 240 − your bid + 240.

If you do not receive a reward in a period, your earnings will be calculated as:

Your payoff in pence = your endowment − your bid

That is,

Your payoff in pence = your endowment − your bid

The chance that you receive a reward in a period depends on how much you bid, and also how much the other participants in your group bid. At the start of each period, all four participants of each group will decide how much to bid. Once the bids are determined, a computerised lottery will be conducted to determine which two participants in the group will receive the rewards.

This lottery will be conducted in two phases. In the first phase, there are four types of tickets: Type 1 &2 &3, Type 1 &2 &4, Type 1 &3 &4, and Type 2 &3 &4. Each type of ticket corresponds to the three participants who will continue on to the second phase if a ticket of that type is drawn. So, if a Type 1 &2 &3 ticket is drawn, then participants 1, 2, and 3 will continue to the second phase; if a Type 1 &3 &4 ticket is drawn, then participants 1, 3, and 4 will continue to the second phase; and so on.

The number of tickets of each type depends on the bids of the corresponding three participants:

• Number of Type 1 &2 &3 tickets = Bid of participant 1 + Bid of participant 2 + Bid of participant 3

• Number of Type 1 &2 &4 tickets = Bid of participant 1 + Bid of participant 2 + Bid of participant 4

• Number of Type 1 &3 &4 tickets = Bid of participant 1 + Bid of participant 3 + Bid of participant 4

• Number of Type 2 &3 &4 tickets = Bid of participant 2 + Bid of participant 3 + Bid of participant 4

Each ticket is equally likely to be drawn by the computer. If the ticket type that is drawn includes your ID number, then you will continue to the second phase.

In the second phase, there are three types of tickets. The types of tickets depend on which three participants have continued on to the second phase:

• If Participants 1, 2, and 3 have continued, then the types will be Type 1 &2, Type 1 &3, and Type 2 &3;

• If Participants 1, 2, and 4 have continued, then the types will be Type 1 &2, Type 1 &4, and Type 2 &4;

• If Participants 1, 3, and 4 have continued, then the types will be Type 1 &3, Type 1 &4, and Type 3 &4;

• If Participants 2, 3, and 4 have continued, then the types will be Type 2 &3, Type 2 &4, and Type 3 &4.

Each type of ticket corresponds to the two participants who will receive the two rewards if a ticket of that type is drawn. So, if a Type 1 &2 ticket is drawn, then participants 1 and 2 will receive the rewards; if a Type 1 &3 ticket is drawn, then participants 1 and 3 will receive the rewards; and so on. The number of each type of tickets will be computed using a formula similar to the one used in the first phase. Suppose, for example, that in the first phase a Type 1 &2 &3 ticket was chosen, and Participants 1, 2, and 3 have continued to the second phase. Then, the number of tickets of each type depends on the bids of the corresponding participants as follows:

• Number of Type 1 &2 tickets = Bid of participant 1 + Bid of participant 2

• Number of Type 1 &3 tickets = Bid of participant 1 + Bid of participant 3

• Number of Type 2 &3 tickets = Bid of participant 2 + Bid of participant 3.

The formulas for the cases when a Type 1 &2 &4, Type 1 &3 &4, or Type 2 &3 &4 ticket is chosen in the first phase are similar. We will now work through an example of how the numbers of lottery tickets are computed, and what you will see during a typical period of the session.

An example. Suppose participant 1 bids 80 pence, participant 2 bids 6 pence, participant 3 bids 124 pence, and participant 4 bids 45 pence. Then, in the first phase:

• Number of Type 1 &2 &3 tickets = Bid of participant 1 + Bid of participant 2 + Bid of participant 3 = 80 + 6 + 124 = 210

• Number of Type 1 &2 &4 tickets = Bid of participant 1 + Bid of participant 2 + Bid of participant 4 = 80 + 6 + 45 = 131

• Number of Type 1 &3 &4 tickets = Bid of participant 1 + Bid of participant 3 + Bid of participant 4 = 80 + 124 + 45 = 249

• Number of Type 2 &3 &4 tickets = Bid of participant 2 + Bid of participant 3 + Bid of participant 4 = 6 + 124 + 45 = 175

There will therefore be a total of 210 + 131 + 249 + 175 = 765 tickets in the first phase lottery. Each ticket is equally likely to be selected. In each period, the calculations above will be summarised for you on your screen, using a table like the one in this screenshot:

Interpretation of the table: The horizontal rows in the above table shows the different types of lottery tickets that are generated by the computer in every period. The vertical columns lists the participants’ bids, the total number of each type of ticket (second column from right) and the range of ticket numbers for each type of ticket (last column). Note that the total number of each ticket type is the sum of the three corresponding participants’ bids. For example, total number of Type 1 &2 &3 tickets is the sum total of Participant 1’s bid, Participant 2’s bid and participant 3’s bid. Therefore, the table cell corresponding to Type 1 &2 &3 and Participant 4’s bid is kept blank. Similarly, the table cell corresponding to Type 2 &3 &4 and Participant 1’s bid is blank. The last column gives the range of ticket numbers for each ticket type. Any ticket number that lies within that range is a ticket of the corresponding type. That is, all the ticket numbers from 211 to 341 are tickets of Type 1 &2 &4, which implies a total of 131 tickets of Type 1 &2 &4, as appears in the ‘Total Tickets’ column. In case any three participants all bid zero, there will be no ticket that contains those three ID numbers together. In such a case, the last column will show ‘No numbers’ for that particular ticket type.

The computer then selects one ticket at random. The number and the type of the drawn ticket will appear below the table. The three ID numbers on the ticket type indicate the three participants continuing to Phase 2.

Suppose a ticket of Type 1 &2 &3 is selected in the first phase. Then, in the second phase, there will be Type 1 &2, Type 1 &3, and Type 2 &3 tickets. The number of tickets of each type will be:

• Number of Type 1 &2 tickets = Bid of participant 1 + Bid of participant 2 = 80 + 6 = 86

• Number of Type 1 &3 tickets = Bid of participant 1 + Bid of participant 3 = 80 + 124 = 204

• Number of Type 2 &3 tickets = Bid of participant 2 + Bid of participant 3 = 6 + 124 = 130.

There will therefore be a total of 86 + 204 + 130 = 420 tickets in the second phase lottery. Each ticket is equally likely to be selected.

In each period, the calculations above will be summarised for you on your screen, using a table like the one in the following screenshot.

The interpretation of this table is same as the table shown in phase 1. Since only three participants survive for phase 2, this table contains three rows for the ticket types. The columns and the interpretation of the cells are the same. Again the computer selects one ticket at random. The number and the type of the drawn ticket will appear below the table. The two ID numbers on the ticket type indicate the two participants receiving the rewards.

At the end of 30 periods, the experimenter will approach a random participant and will ask him/her to pick up five balls from a sack containing 30 balls numbered from 1 to 30. The numbers on those five balls will indicate the 5 periods, for which you will be paid in Part 2. Your earnings from all the preceding periods will be throughout present on your screen.

Feedback screen

Below is the screenshot of a typical feedback table for Treatment 2J. Similar screens were used for 1W and 2S; in 2S, there were two such tables, one for each draw.