Resource allocations with guaranteed awards in claims problems

Abstract

The notion of lower bound on awards has been introduced in the literature to analyze the establishment of guarantees that ensure a minimum award to each agent involved in situations of conflicting claims, such as the rationing of a resource or the distribution of the assets of a bankrupt firm. Indeed, this concept has a core role in many approaches related to the problem of fair allocation (Thomson in Math Soc Sci 74:41–59, 2015) and a range of such lower bounds have been proposed: the minimal right (Curiel et al. in Z Oper Res 31:A143–A159, 1987), the fair bound (Moulin in Handb Soc Choice Welf 1:289–357, 2002), securement (Moreno-Ternero and Villar in Math Soc Sci 47(2):245–257, 2004) and the $\min$ bound (Dominguez in mimeo, 2006). In this context, the key contribution of the current paper is to show that there is a correspondence between lower bounds and rules; i.e., associated to each particular lower bound, we find a specific way of distributing the resources. In doing so, we provide new characterizations for two well known rules, the constrained equal awards and Ibn Ezra’s rules. A dual analysis, by using upper bounds on awards will provide characterizations of the dual of the previously mentioned rules: the constrained equal losses rule and the dual of Ibn Ezra’s rule.

1 Introduction

The so-called claims problem reflects a situation where the agents’ claims cannot be totally honored when a resource must be distributed among them. The way of rationing this resource among the agents, taking into account their claims, is prescribed by a rule. In this context, we analyze how to distribute any increase of the endowment in terms of two general concepts: first, establishing that each agent should be guaranteed a minimum award, which is determined by a particular lower bound (respect of the lower bound); and, then, requiring that agents with equal guarantees, should be treated equally (equal treatment of equals).

It is noteworthy that the concern of ensuring some minimum individual rights has figured in a large number of contexts. Specifically, the Universal Basic Income is a classical issue that has attracted much attention in the social policy literature and the political agenda during the last two decades (Noguera 2010). Additionally, the establishment of a minimum wage in the labor market, the debate about ensuring a universal minimum health coverage in the U.S. Senate, the European Structural and Investment Funds, ensuring minimum quantities in heritage laws, fishing quotas (Iñarra and Prellezo 2008; Kampas 2015), or, the negotiations of $CO^2$ emissions, a relevant issue nowadays (Giménez-Gómez et al. 2016), are further real-life examples.

From a theoretical point of view, the idea of establishing minimum guarantees on awards underlies the analysis of claims problems from its beginning (O’Neill 1982) up to the present day (Giménez-Gómez and Marco-Gil 2014). Indeed, for each problem, the formal definition of a rule already includes the requirement that awards be non-negative, which represents a lower bound on awards. In fact, there are some solutions that always ensure a strictly positive quantity to each agent (with positive claim): this is the case of the constrained equal awards rule (Maimonides 2000), the $\alpha _{\min }$ solution (Giménez-Gómez and Peris 2014), or solutions that are defined by positive eigenvectors (Subiza et al. 2015).

The impact of requiring that a rule fulfills a lower bound was first analyzed by Dominguez and Thomson (2006) and Yeh (2008). Afterwards, the recursive application of a lower bound has been analyzed in the literature, showing that (under some mild conditions) this process provides a unique rule. In particular, Dominguez (2013) and Giménez-Gómez and Marco-Gil (2014), among others, find out that some well known rules are retrieved by recursively applying lower bounds and, consequently, they provide new axiomatic characterizations of classical rules.

Our present approach elaborates on these previous works but, instead of applying a lower bound recursively, we require that rules should fulfill the lower bound and some additional conditions on the distribution of the resources, which also depend on the lower bound being used. Specifically, we require that a rule (i) guarantees to each individual at least the amount determined by the particular lower bound being used (respect of the lower bound); and, (ii) fulfills axioms related to equal treatment of equals (conditional equal treatment), or related to some monotonicity behaviour (conditional resource monotonicity, conditional equal bound monotonicity, or priority). The idea behind these axioms is to compare the guaranteed awards among the agents and, on this basis, to determine the way of distributing the endowment whenever it increases.

A key point in our study is the selection of a specific lower bound on which the aforementioned axioms are based. Hence, we need to choose a meaningful lower bound in the sense that it should be different from zero, whenever the claim is different from zero (quoting Dominguez 2013, words, “these lower bounds satisfy positivity"). In this regard, by focusing on three lower bounds (the fair bound Moulin 2002), securement (Moreno-Ternero and Villar 2004), and the $\min$ bound (Dominguez 2006), our main results show how these axioms provide new characterizations of the constrained equal awards and Ibn Ezra’s rules.

As we obtain new characterizations of the constrained equal awards and Ibn Ezra’s rules, we present some previous results to better understand our contribution.

• (1) Regarding the CEA rule, it is the only rule satisfying:

  • (a) equal treatment of equals, invariance under claims truncation, and composition up (Dagan 1996).

  • (b) conditional full compensation and composition down (Villar and Herrero 2002).

  • (c) conditional full compensation and claims monotonicity (Yeh (2001), mimeo, cited in Thomson (2003)).

  • (d) respect of the securement bound, null claims consistency and composition up (Yeh 2008).

  • (e) respect of the fair bound, composition down and zero-consistency (Moulin 2002).

• (2) As far as we know, the first characterization result of Ibn Ezra’s rule is due to (Bergantiños and Méndez-Naya 2001)

  • (f) the Ibn Ezra rule is the unique rule satisfying equal treatment of equals and additivity.

  These authors extend and characterize the solution for general claims problems. In Alcalde et al. (2005) this solution is also extended and its characterization uses cooperative game conditions

  • (g) the generalized Ibn Ezra value is the unique bankruptcy value satisfying anonymity, transitional dummy and worth-generators composition.

  They show that this extension fulfills order preservation, continuity, claims and estate monotonicity, supermodularity, and homogeneity.

Finally, note that when facing a claims problem, each individual has a claim on the endowment that represents the maximum amount she can receive and, at the same time, the maximum amount she can lose. The agent’s loss is equal to the difference between her claim and her award. By focusing on losses (the so-called dual approach), a lower bound on awards provides the maximum amount that individual can lose; that is, we are considering upper bounds on losses. Analogously, a lower bound on losses provides an upper bound on awards. By analyzing the implications of the existence of lower bounds on losses, we straightforwardly obtain from the previous results characterizations of their dual rules: the constrained equal losses and the dual Ibn Ezra’s rule.

The paper is organized as follows. Section 2 presents the main definitions. Section 3 introduces the axioms and Sect. 4 provides our main results. In Sect. 5 we present some comments dealing with the dual approach: upper bounds. Finally, Sect. 6 comments on the dual approach and mentions some possible future research.

2 Preliminaries

2.1 Claims problems and rules

Throughout the paper we consider a set of agents $N=\left\{ 1,2,\ldots ,n\right\}$, each one having a claim $c_i\in {\mathbb {R}}_{+}$ on a divisible resource, the endowment, $E \in {\mathbb {R}}_{+}$. Let $c \equiv (c_i)_{i\in N}$ be the claims vector. A claims problem appears whenever the endowment is not enough to satisfy the aggregate claim. Without loss of generality, we assume that the agents are indexed according to their claims, $c_{1}\le c_{2}\le \cdots \le c_{n}.$ The pair $(E,c)\in {\mathbb {R}}_{+}\times {\mathbb {R}}^n_+$ represents the claims problem, and ${\mathcal {C}}$ denotes the set of all claims problems.

A rule is a single-valued function $\varphi :{\mathcal {C}} \rightarrow {\mathbb {R}}_{+}^{n}$ such that for each problem $(E,c) \in {\mathcal {C}},$ and each $i \in N$, $0\le \varphi _{i}(E,c)\le c_{i}$ (non-negativity and claim-boundedness), and $\sum _{i=1}^{n}\varphi _{i}(E,c)=E$ (efficiency).

An important rule in the literature is the constrained equal awards (Maimonides, 12th century). This rule proposes an egalitarian distribution of the awards among the claimants, given some constraints.¹

For each $(E,c) \in {\mathcal {C}}$ and each $i\in N,$ the constrained equal awards rule, CEA, recommends $CEA_{i}(E,c)= \min \left\{ c_{i},\lambda \right\} ,$ where $\lambda$ is chosen so that $\sum _{i=1}^{n}\min \left\{ c_{i},\lambda \right\}$ $=E.$

Ibn Ezra’s rule is another classical proposal for solving claims problems.² This rule is only defined whenever the endowment is lower than the greatest claim; so it requires a restriction on the domain of claims problems: ${\mathcal {C}}_{IE} = \left\{ (E, c) \in {\mathcal {C}}: E\le c_n \right\}$.

For each $(E,c) \in {\mathcal {C}}_{IE}$ and each $i\in N$, Ibn Ezra’s rule, IE, assigns the awards

$$\begin{aligned} IE_{i} (E,c) = \sum _{k=1}^{i}\frac{ \min \left\{ c_{k},E \right\} - \min \left\{ c_{k-1}, E\right\} }{n - k + 1 }, \end{aligned}$$

where, for notational convenience, we set $c_0 = 0$.

2.2 Lower bounds on awards

For each claims problem, a lower bound on awards is a function that associates to each agent a guaranteed amount that she should receive, fulfilling three compulsory conditions:

• (i) Rationality: the guaranteed award is non-negative and lower than the agent’s claim.

• (ii) Feasibility: the endowment allows the allocation of these guaranteed awards to the agents.

• (iii) Order preservation: the larger the claim, the larger the guaranteed award (ie, the guaranteed award does not reverse the order of the claims).

Formally, we define a lower bound as a function $b:{\mathcal {C}} \rightarrow {\mathbb {R}}_{+}^{n}$, which maps each claims problem $(E,c)\in {\mathcal {C}}$ to a vector b(E, c) such that for each $i\in N,$ $0\le b_{i}(E,c)\le c_{i}$ and $\sum _{i=1}^{n} b_{i}(E,c) \le E.$

2.3 An inventory of lower bounds

The first lower bound formally defined was proposed by Curiel et al. (1987), under the name of minimal right. It requires that each agent receives what is available whenever the other agents have already received their claim in full, or zero if this is not possible.

Minimal right, mr: for each $(E,c)\in {\mathcal {C}}$ and each $i\in N,$ $mr_{i}(E,c)=\max \left\{ 0,E-\sum _{j\in N \smallsetminus \left\{ i\right\} } c_j \right\}$.

Remark 1

As mentioned in Thomson (2015), it follows directly from the definition that any rule proposes an allocation above mr.

Afterwards, Moulin (2002) introduces the fair bound, which establishes that agents should receive at least the minimum of equal division and their claim.

Fair bound, f: for each $(E,c)\in {\mathcal {C}}$ and each $i\in N,$ $f_{i}(E,c)=\min \left\{ c_{i},\frac{E}{n}\right\}$.

Furthermore, Moreno-Ternero and Villar (2004) propose the securement bound, that guarantees (if possible) the n-th part of each agent’s claim or the n-th part of the endowment (the minimum of these amounts).

Securement, s: for each $(E,c)\in {\mathcal {C}}$ and each $i\in N,$ $s_{i}(E,c)= \frac{1}{n} \min \left\{ c_{i}, E\right\}$.

Finally, Dominguez (2006) introduces the $\min$ bound, that proposes that each agent receives (if possible) the n-th part of the smallest claim (otherwise, this bound guarantees an equal division of the endowment).

Min bound, m: for each $(E,c)\in {\mathcal {C}}$ and each $i\in N,$ $m_{i}(E,c)= \frac{1}{n} \min \left\{ c_1, E\right\}$.

Remark 2

For each $(E,c) \in {\mathcal {C}}$ and each individual $i \in N$,

    $0 \le m_i(E,c) = \frac{1}{n} \min \left\{ c_{1}, E\right\} \le s_i(E,c) = \frac{1}{n} \min \left\{ c_{i}, E\right\} \le f_i(E,c) = \frac{1}{n} \min \left\{ n c_{i}, E\right\} \le c_i$.

That is, the fair bound guarantees the highest awards to all agents, while the min bound provides the lowest guarantees. Note that whenever $E \le c_1$, then $m_i(E,c) = s_i(E,c) = f_i(E,c) = \frac{E}{n}$.

3 Axiomatic analysis

As aforementioned, our main contribution is based on the study of those rules that fulfill an arbitrary fixed lower bound b and some additional conditions on the allocation of the endowment. In doing so, we refer to this bound b some of the main axioms that are considered as a minimum requirement of fairness in claims problems (Thomson 2003).

3.1 Respect of the lower bound

Our basic requirement establishes that the lower bound is satisfied in any claims problem.

Respect of the lower bound: For each $(E,c)\in {\mathcal {C}}$ and each $i \in N,$ $\varphi _{i}(E,c) \ge b_{i}(E,c).$

This axiom requires that each agent has a guaranteed minimum level on awards. It is clear that if a rule satisfies this axiom with respect to a lower bound, it also respects any smaller lower bound. By Remark 2, the $\min$ bound provides the smallest guarantees, so a larger number of rules fulfill respect of the $\min$ bound. Furthermore, it is noteworthy the following relationships among the lower bounds:

Respect of fair bound $\Rightarrow$ Respect of securement $\Rightarrow$ Respect of $\min$ bound

When using the minimal right bound, if $\sum _{i=1}^{n-1} c_i \ge E$ we obtain that $mr_i = 0$ for all agents. So, in this kind of problems, respect of the minimal right is fulfilled by any rule and the axiom has no effect. Nevertheless, when using the fair bound, this axiom seems to induce the CEA rule (although, as we show below, this is not true and additional axioms are needed to characterize this rule). Finally, the CEA and Ibn Ezra’s rules fulfills this condition when applying the securement bound.

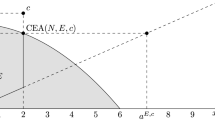
In this regard, Fig. 1 shows the fulfillment of this axiom in the two-agent case (with $c_1 \le c_2$). A rule fulfills respect of the lower bound if it provides efficient allocations $\left( x_1 + x_2 = E\right)$ that lie between the black dashed lines. When these lines coincide they appear as a solid black line, so a unique allocation is determined. Note that in the two-agent case, respect of the fair bound determines the CEA rule. In any case, if the endowment is below $c_1$, $E \le c_1$, the rules should divide this endowment equally between the two agents. If $E > c_1$ then, there is some room for different rules (the region between the dashed lines) that varies from one lower bound to another.

Fig. 1

Respect of the lower bound for $b=f$ (A), for $b=s$, with $c_1 < c_2/2$ (B), for $b=s$, with $c_1 \ge c_2/2$ (C), and for $b=m$ (D). We consider a two-agent claims problem $(E,(c_1,c_2))$, with $c_1 \le c_2$. A rule $\varphi$ fulfills respect of the lower bound if the allocations it provides lie between the black dashed lines. When these lines coincide they appear depicted as a solid black line. For instance, in case (A) the CEA rule is completely characterized by this axiom in the two-agent case. In case (B), respect of the securement bound only establishes the awards (equals for both agents) when $E \le c_1$. If $E > c_1$ all sharing of E that lie between black dashed lines fulfill respect of the securement bound

3.2 Constrained equal treatment of equals

Why should agents with equal bounds receive different awards? The next axiom is based on the idea that equal claimants should be equally treated.

Constrained equal treatment of equals: For each $(E,c)\in {\mathcal {C}}$ and each $i,j\in N$ such that $c_i \le c_j$, $b_{i}(E,c) = b_{j}(E,c)$ implies $\varphi _{i}(E,c) = \varphi _{j}(E,c),$ or $\varphi _{i}(E,c) = c_{i} \le \varphi _{j}(E,c).$

The above axiom demands equal treatment for equal agents (regarding their lower bounds), unless one of them has her demand met in full. Note that, if the lower bound is order preserving (all considered lower bounds satisfy this condition), the above axiom implies that agents with the same claim receive the same award.

When using the minimal right, a rule fulfilling constrained equal treatment of equals coincides with CEA in problems such that $\sum _{i=1}^{n-1} c_i \ge E$. So this axiom is very strong when applied with this lower bound. This is not the case when the axiom is applied with other lower bounds (for instance, CEA and Ibn Ezra’s rules fulfill this axiom when using securement).

Note that this axiom tries to equalize awards of agents with the same bound (not with the same claim). So, by depending on the lower bound it is more or less demanding. In particular, it is highly demanding when using the $\min$ bound, since this bound proposes the same awards for each agent (indeed, as shown below, this axiom with the $\min$ bound completely characterizes the CEA rule). Finally, it is noteworthy that whenever the bound is very sensitive to agents’ claims, only the agents with the same claim have the same guarantee (this is the case, for instance, of the securement bound in claims problems such that $c_i \le E$, for each $i \in N$).

3.3 Changes in the endowment

The following axioms analyze the effects of an increase in the endowment, while claims remain unchanged. We propose that changes in the final allocation should depend on the changes in the guarantees of the agents.

Constrained resource monotonicity: If $(E,c),(E^{\prime },c)\in {\mathcal {C}}$ are two claims problems such that $E>E^{\prime }$, then for each $i\in N$, $\varphi _{i}(E,c) - \varphi _{i}(E',c) \ge b_{i}(E,c) - b_{i}(E',c), \text { or } \varphi _{i}(E,c) = c_{i}.$

This axiom requires that any change in the awards received by an agent due to a change in the endowment E should be at least equal to the change in her bound. As before, we need to restrict this idea so that no one receives more than her claim.

When applied to the $\min$ bound, and $c_1 \le E'$, it simply says that the rule is resource monotonic (and all rules fulfill it in this kind of claims problems). A similar comment can be made with the minimal right bound in claims problems such that $\sum _{i=1}^{n-1} c_i \ge E$.

Constrained equal bound monotonicity: If $(E,c),(E^{\prime },c)\in {\mathcal {C}}$ are two claims problems such that $E>E^{\prime }$, then for each $i,j\in N$ with $c_i \le c_j$,

$b_{i}(E,c) -b_{i}(E',c) = b_{j}(E,c)-b_{j}(E',c)$ implies

$\varphi _{i}(E,c) - \varphi _{i}(E',c) = \varphi _{j}(E,c) - \varphi _{j}(E',c), \text { or } \varphi _{i}(E,c) = c_{i} \le \varphi _{j}(E,c).$

This axiom demands that the increase in the endowment should be shared equally among agents who experience an equal change in their lower bound, restricted to no one receives more than her claim. When applied with the $\min$ or fair bounds, the axiom is strongly linked to the CEA rule.

Priority in allocation:³ If $(E,c),(E^{\prime },c)\in {\mathcal {C}}$ are two claims problems such that $E>E^{\prime }$, then for each $i\in N$, $\varphi _{i}(E,c) - \varphi _{i}(E^{\prime },c) >0$ if and only if $b_{i}(E,c) -b_{i}(E^{\prime },c) >0.$

Priority in allocation states that the agents whose lower bound increases, and only those agents, should benefit from an increase in the endowment.

When using the $\min$ bound, and $c_1 \le E'$, this axiom requires nothing since the guarantees on both claims problems coincide and all rules fulfill this condition. The same occurs with securement bound in problems such that $c_i \le E'$, for each $i \in N$. If we consider the fair bound, this axiom is sensitive for relatively larger claimants $c_i \ge E'/n$, but it does not affect smaller claimants, since their fair bound does not change.

Giménez-Gómez and Peris (2015) analyze, in the framework of redistribution problems, the effect of ensuring to each individual her minimal right. Then, under some premises, the minimal right based egalitarian rule, which is somewhat related to the constrained equal losses, appears linked to priority. The results obtained can be easily adapted to claims problems. Henceforth, the current paper focuses on the remaining lower bounds: the fair bound, securement and the $\min$ bound. Hereinafter, let ${\mathcal {L}}$ denote the family of these lower bounds: ${\mathcal {L}} = \left\{ f, \, s, \, m \right\}$. The following results show some relationships among the introduced axioms.

Lemma 1

For each lower bound $b \in {\mathcal {L}}$,

• 1. Constrained resource monotonicity implies respect of the lower bound.

• 2. Constrained equal bound monotonicity implies constrained equal treatment of equals.

Proof

The proof comes straighfowardly by just applying both axioms to the claims problem (E, c) and (0, c). $\square$

Lemma 2

When using the $\min$ bound,

• 1. Constrained equal treatment of equals implies respect of the lower bound.

• 2. Constrained equal bound monotonicity implies constrained resource monotonicity.

Proof

Note that the guaranteed award provided by the $\min$ bound coincides for each agent:

$(1) m_i(E,c) = \frac{c_1}{n} \le \frac{E}{n} \,, \quad \text {or} \quad (2) m_i(E,c) = \frac{E}{n} \le \frac{c_1}{n}.$

Consider a rule $\varphi$ satisfying constrained equal treatment of equals. As the lower bound coincides for each agent, this axiom implies that agents receive the same award, or receive their claim in full. In both cases, $\varphi _i(E,c) \ge m_i(E,c)$ and then respect of the lower bound holds. Analogously, it is straightforward to prove that constrained equal bound monotonicity implies constrained resource monotonicity. $\square$

4 Main results

We analyze how some combinations of the aforementioned axioms with respect one of the proposed lower bounds uniquely determine a rule. In particular, we provide characterizations of the constrained equal awards and Ibn Ezra’s rules.

4.1 Summarizing results and discussion

Table 1 summarizes the results obtained in the present paper. It shows the fulfillment of the introduced axioms with respect to the lower bounds in ${\mathcal {L}}$ by the CEA and Ibn Ezra’s rules.

As this table depicts, the fair and $\min$ bounds are closely linked to the CEA rule, whereas securement is also linked to Ibn Ezra’s rule. The result in Moulin (2002), that characterizes CEA by means of respect of the fair bound, composition up, and null claims consistency, also shows the link between CEA and the fair bound.⁴

Regarding the axioms, it is noteworthy that constrained equal treatment of equals and constrained equal bound monotonicity appear clearly linked to the CEA rule, although they are no useful to characterize this rule when the securement bound is used, whereas priority is linked to Ibn Ezra’s rule. Next sub-sections formally present our results.

Table 1 Axiom fulfillment

4.2 Constrained equal awards rule

By analyzing the effect of the introduced axioms with the fair and $\min$ bounds, the CEA rule is characterized. In doing so, our first result shows that the CEA rule fulfills respect of the lower bound and constrained equal treatment of equals for each lower bound in ${\mathcal {L}}$.

Proposition 1

For each lower bound $b \in {\mathcal {L}}$,

• 1) The constrained equal awards rule fulfills respect of the lower bound.

• 2) The constrained equal awards rule fulfills constrained equal treatment of equals.

Proof

The first part comes from Remark 2 and Moulin (2002). To prove the second part, let $b \in {\mathcal {L}}$, (E, c) $\in {\mathcal {C}}$ and $i,j \in N$ such that $c_i \le c_j$ and $b_i(E,c) = b_j(E,c).$ Then,

$$\begin{aligned} CEA_i(E,c) =\min \left\{ c_i,\lambda \right\} \le \min \left\{ c_j,\lambda \right\} = CEA_j(E,c), \end{aligned}$$

which implies $CEA_i(E,c) = CEA_j(E,c)$, if the minimum is $\lambda$ in both cases or, whenever the first minimum is $c_i$, $CEA_i(E,c) = c_i \le CEA_j(E,c).$ $\square$

By considering the fair bound, we obtain the following characterization results.

Theorem 1

When using the fair bound, the constrained equal awards rule is the only rule satisfying respect of the lower bound and constrained equal treatment of equals.

Proof

From Proposition 1CEA satisfies respect of the fair bound and constrained equal treatment of equals.

Let $\varphi$ satisfy respect of the fair bound and constrained equal treatment of equals. For each $(E,c) \in {\mathcal {C}}$, as $E < \sum _{i=1}^{n} c_{i} \le nc_{n},$ there is some $k \in N$ such that $E < nc_{k}.$ Note that, by definition, the fair bound is the same for each agent whenever $E \le n c_{1}$ ($c_1$ is the lowest claim). Furthermore, this lower bound changes as $\frac{E}{n}$ increases. Henceforth, we use this fact to divide all the possible cases that cause variation in the agents’ fair bound.

If $E < nc_{1},$ then $f_i(E,c) = \frac{E}{n} \le c_i$, for each $i \in N$. By respect of the lower bound, $\varphi _i(E,c) = \frac{E}{n} = CEA_i(E,c)$ for each $i \in N$ (given that any rule satisfies efficiency).

Otherwise, there is some $k \in N$ such that $n c_{k-1} \le E < nc_{k}.$ For each $i \le k-1$, $f_{i}(E,c) = c_{i}$, and for each $i \ge k$, $f_{i}(E,c) = \frac{E}{n}.$ By respect of the lower bound, for each $i \le k-1$, $\varphi _{i}(E,c) = c_{i}$ (given that any rule satisfies claim-boundedness). Constrained equal treatment of equals and efficiency imply an equal sharing of $E' = E-(c_1+c_2+\cdots +c_{k-1}),$ among agents $i=k,\ldots ,n$, unless some of those agents get more than her claim.

If $\frac{E'}{n-(k-1)} > c_{k},$ then constrained equal treatment of equals imply $\varphi _{k}(E,c) = c_{k}$ (since any rule satisfies claim-boundedness). Now, constrained equal treatment of equals, $\varphi _{i}(E,c) = \varphi _{j}(E,c),$ for each $i,j > k,$ implies $\varphi _{i}(E,c) = \frac{E-\sum _{i=1}^{k} c_{i}}{n-k}$ for each $i > k$ (since any rule satisfies efficiency), unless this amount is greater than some claims.

If $\frac{E''}{n-k} > c_{k+1},$ $E'' = E-(c_1+c_2+\cdots +c_{k}),$ constrained equal treatment of equals implies $\varphi _{k+1}(E,c) = c_{k+1}$ and the remainder must be distributed equally by constrained equal treatment of equals, unless this amount is greater than some claims (given that any rule satisfies claim-boundedness and efficiency). This argument is repeated until no one gets more than their claim, and we observe that the result is $\varphi (E,c) = CEA(E,c)$. $\square$

The following example shows the independence of the axioms used in Theorem 1.

Example 1

For any claims problem (E, c), let $F= \sum _{i=1}^n f_i(E,c)$, where $f_i(E,c)$ is the fair bound of individual $i \in N$ in problem (E, c). Let Pr denote the proportional rule

$$\begin{aligned} Pr_i(E,c) = \frac{c_i}{\sum _{k=1}^n c_k} E \end{aligned}$$

Then, the rule ${\varphi }^{a}$ defined by:

$$\begin{aligned} {\varphi }^{a}(E,c) = f(E,c) + Pr(E-F,c-f(E,c)) \end{aligned}$$

obviously satisfies respect of the fair bound, since the proportional rule assigns non-negative awards. But it does not satisfy constrained equal treatment of equals: let the claims problem $(E,c) = \left( 80,(10,20,40,50)\right)$, $f(E,c)=(10,20,20,20)$, so agents 3 and 4 have the same fair bound. Nevertheless, these agents receive different awards, ${\varphi }^{a}(E,c) = (10,20, 24,26)$.

Given a claims problem (E, c), let $N_+$ be the subset of agents such that $c_i \ge \frac{E}{n}$ and split the claims vector $c =\left( c_-,c_+\right)$, so that $c_-$ corresponds to the agents not in $N_+$, and $c_+$ to the agents in $N_+$. Let ${\widetilde{C}} = \sum _{i\in N_+} c_i$, ${\widetilde{E}} = \min \left\{ E, {\widetilde{C}}\right\}$ and let the rule $\varphi ^b$ defined by:

$$\begin{aligned} \varphi _i^b(E,c) = \left\{ \begin{array}{ll} CEA_i\left( {\widetilde{E}} ,c_+\right) &{}\quad if i \in N_+ \\ CEA_i\left( E- {\widetilde{E}} ,c_-\right) &{}\quad otherwise \\ \end{array} \right. \end{aligned}$$

If $f_i(E,c) = f_j(E,c)$, $c_i \le c_j$, we have two possibilities: $f_i(E,c) = f_j(E,c) = \frac{E}{n}$, or $c_i = c_j < \frac{E}{n}$. In the first case, $i,j \in N_+$ and then $\varphi _i^b(E,c) = \varphi _j^b(E,c)$, or $\varphi _i^b(E,c) = c_i$. In the second case, $i,j \in N_-$ and both claims are equal, so $\varphi _i^b(E,c) = \varphi _j^b(E,c)$. Then, this rule satisfies constrained equal treatment of equals. To show that is does not satisfy respect of the fair bound let the claims problem $(E,c) = \left( 300,(10,100,200,500)\right)$, so that $\varphi ^b(E,c) = (0,100,100,100)$ and $\varphi _1^b(E,c) =0 < f_1(E,c) = 10$.

Remark 3

The above result shows that respect of the fair bound almost provides the constrained equal awards rule. A mild axiom ensuring equal treatment of agents with the same claim, or agents with claims larger than the equal allocation of the endowment, $c_i >E/n$, leads to the constrained equal awards rule. Moreover, as Example 2 shows, that fair bound is the smallest bound so that Theorem 1 remains valid; i.e., for any other bound $b \ne f$ with $b \le f$ the result does not hold.⁵

Example 2

Let us consider the claims problem (E, c), with $E=100$, $c = (10,20,50,70)$. Then,

$$\begin{aligned} f(E,c) = (10,20,25,25) \qquad CEA(E,c) = (10,20,35,35) \end{aligned}$$

If we now use a lower bound $b \ne f$ with $b \le f$ the CEA is not uniquely obtained. For instance, if $b=(b_1,20,25,25)$, $b_1 < 10$, then the reasoning in Theorem 1 yields to the family of solutions satisfying:

$$\begin{aligned} \varphi _1(E,c) \ge b_1, \quad \varphi _2(E,c) =20, \quad \varphi _3(E,c) = \varphi _4(E,c) = 25 + \frac{10-b_1}{2} \end{aligned}$$

If, instead of requiring respect of the fair bound, we ask for constrained resource monotonicity again the CEA rule is obtained. Note that, when requiring this axiom, the increase in the endowment is allocated in terms of the increase in the fair bound. So, only agents with claims larger than the equal allocation of the endowment are guaranteed an increase in their awards.

Theorem 2

When using the fair bound, the constrained equal awards rule is the only rule satisfying constrained resource monotonicity and constrained equal treatment of equals.

Proof

By Proposition 1, CEA satisfies constrained equal treatment of equals. To prove that it also fulfills constrained resource monotonicity, let (E, c) and $(E',c)$ $\in {\mathcal {C}}$ be such that $E' < E$. If for some $i \in N$ $CEA_i(E,c) < c_i$, then $\min \left\{ c_i,\lambda \right\} = \lambda < c_i$, so $CEA_{i}(E',c) = \min \left\{ c_i,\lambda ' \right\} = \lambda ' < c_i$, since $E' < E.$ Therefore,

From the definition of CEA,

As $E' < E$, $s \le r$ and

$$\begin{aligned} \lambda '\le & {} \frac{E'- \left( c_1+c_2+\cdots +c_r\right) }{n-r} \qquad \Rightarrow \qquad \lambda - \lambda ' \ge \frac{E-E'}{n-r} \ge \frac{E-E'}{n} \\&= f_{i}(E,c) - f_{i}(E',c). \end{aligned}$$

Hence, constrained resource monotonicity is fulfilled in this case. On the other hand, whenever ${CEA}_{i}(E,c) = {c}_{i}$ the axiom is obviously fulfilled.

Conversely, let $\varphi$ be a rule satisfying constrained equal treatment of equals and constrained resource monotonicity. From Lemma 1, $\varphi$ fulfills respect of the fair bound, and Theorem 1 implies $\varphi = CEA.$ $\square$

The following example shows the independence of the axioms used in Theorem 2.

Example 3

Since constrained resource monotonicity implies respect of the fair bound, rule $\varphi ^b$ in Example 1 satisfies constrained equal treatment of equals and does not satisfy constrained resource monotonicity.

Given a claims problem (E, c), we divide the set of agents in subgroups of agents with the same claim: $N = S_1 \cup S_2 \cup \cdots \cup S_k$, such that for each $i,j \in S_r$, $c_i = c_j$. Let $c_r$ be the claim of agents in $S_r$, $f_r$ the fair bound of these agents, and $s_r$ the cardinal of this set, $s_r = |S_r|$. Then we define the rule $\varphi ^{c}$ in the following way:

a):

First, each agent receives her fair bound $f_i(E,c)$. Let $F = \sum _{i \in N} f_i(E,c)$, the part of the endowment that has been allocated.

b):

Define $G_k =\min \left\{ E-F, s_k(c_k - f_k)\right\}$ and assign equally $G_k$ among agents in $S_k$, so each one receives an additional amount of $\frac{G_k}{s_k}$.

c):

If $E - F - G_k > 0$, define $G_{k-1} =\min \left\{ E-F-G_k, s_{k-1}(c_{k-1} - f_{k-1})\right\}$ and assign equally $G_{k-1}$ among agents in $S_{k-1}$, so each one receives an additional amount of $\frac{G_{k-1}}{s_{k-1}}$.

d):

Repeat the process until the assets are exhausted.

This rule satisfies constrained resource monotonicity but it does not fulfill constrained equal treatment of equals, as shows the following claims problem: let $(E,c) = \left( 60, (10,20,50,80)\right)$; then, $f(E,c) = (10,15,15,15)$ and $\varphi ^{c}(E,c) = (10,15,15,20)$, so agents with the same fair bound receive different awards.

As a consequence of the relationships among axioms, we obtain two additional characterization results.

Corollary 1

When using the fair bound, the constrained equal awards rule is the only rule satisfying respect of the lower bound and constrained equal bound monotonicity.

Proof

By Proposition 1, CEA satisfies respect of the lower bound. In order to prove that it also fulfills constrained equal bound monotonicity, let (E, c) and $(E',c)$ $\in {\mathcal {C}}$ be such that $E' < E$, and two agents $i,j \in N$ with $c_{i} \le c_{j}.$ We suppose that $f_{i}(E,c)-f_{i}(E',c) = f_{j}(E,c)-f_{j}(E',c).$ We distinguish several possible cases:

• a) If $f_{i}(E,c)=\frac{E}{n}$, then $f_{i}(E',c)=\frac{E'}{n}$. In this case, either

  • (i) $CEA_{i}(E,c)= CEA_{j}(E,c) = \lambda < c_i$, in which case $CEA_{i}(E',c)= CEA_{j}(E',c) = \lambda ' < c_i$, since $E' < E$, and

    $$\begin{aligned} CEA_{i}(E,c)- CEA_{i}(E',c) = CEA_{j}(E,c)- CEA_{j}(E',c) = \lambda - \lambda ' \text {; or } \end{aligned}$$

  • (ii) $CEA_{i}(E,c)=c_{i} \le CEA_{j}(E,c)$.

• b) If $f_{i}(E,c)=c_{i}$, then $CEA_{i}(E,c)=c_{i} \le CEA_{j}(E,c)$.

Hence CEA satisfies constrained equal bound monotonicity.

Consider now a rule $\varphi$ satisfying respect of the lower bound and constrained equal bound monotonicity. From Lemma 1, $\varphi$ fulfills constrained equal treatment of equals, so that Theorem 1 implies $\varphi = CEA.$ $\square$

Corollary 2

When using the fair bound, the constrained equal awards rule is the only rule satisfying constrained resource monotonicity and constrained equal bound monotonicity.

Proof

From Lemma 1, constrained resource monotonicity implies respect of the lower bound, and constrained equal bound monotonicity implies constrained equal treatment of equals. Moreover, by Theorem 1, Theorem 2 and Corollary 1, CEA fulfills the four axioms. So, this result comes straightforwardly. $\square$

Now, by choosing the $\min$ bound the CEA rule is characterized by a single axiom. It is noteworthy that the $\min$ bound only depends on the endowment, E, and on the minimum claim, $c_1$. So, it guarantees the same amount to all agents.

Theorem 3

When using the $\min$ bound,

• 1) The CEA rule is the only rule satisfying constrained equal treatment of equals.

• 2) The CEA rule is the only rule satisfying constrained equal bound monotonicity.

Proof

1) From Proposition 1CEA fulfills constrained equal treatment of equals.

Now, consider a rule $\varphi$ satisfying constrained equal treatment of equals and a claims problem $(E,c) \in {\mathcal {C}}$. As agents are ordered according to their claims, $m_{i}(E,c)= \min \left\{ \frac{c_1}{n},\frac{E}{n} \right\} ,$ the same for each $i \in N$. There are two possibilities:

• a) If $E \le c_{1}$, then $m_{i}(E,c)= \frac{E}{n}$. By constrained equal treatment of equals and efficiency, $\varphi _i(E,c) = \frac{E}{n} = CEA_{i}(E,c).$

• b) If $E > c_{1}$, then $m_{i}(E,c)= \frac{c_1}{n}$. By constrained equal treatment of equals, all individuals receive the same amount $\lambda$ unless they receive $c_i \le \lambda$, and this coincides with CEA(E, c).

Hence, $\varphi = CEA.$

2) First, we prove that CEA fulfills constrained equal bound monotonicity. Let $(E,c), (E',c) \in {\mathcal {C}},$ $E' < E$ and two agents $i,j \in N$, with $c_i \le c_j.$ As $CEA_{i}(E,c) = \min \left\{ \lambda , c_i \right\}$, we have the following two possibilities:

• a) If $CEA_{i}(E,c) = c_i$, the condition is fulfilled.

• b) If $CEA_{i}(E,c) = \lambda$, then $CEA_{j}(E,c) = \lambda$ and, as $E' < E$, $CEA_{i}(E',c) = CEA_{j}(E',c) = \lambda ' < \lambda$. Then,

  $$\begin{aligned} CEA_{i}(E,c) - CEA_{i}(E',c) = CEA_{j}(E,c) - CEA_{j}(E',c) = \lambda - \lambda '. \end{aligned}$$

Hence, CEA fulfills constrained equal bound monotonicity.

Now, let $\varphi$ be a rule satisfying constrained equal bound monotonicity. From Lemma 1 constrained equal treatment of equals is fulfilled and then, as we have just proved, $\varphi = CEA.$ $\square$

Finally, by selecting the securement bound, the CEA rule is not characterized, althoug it fulfills constrained resource monotonicity and constrained equal bound monotonicity.

Proposition 2

When using the securement bound, the constrained equal awards rule satisfies constrained resource monotonicity and constrained equal bound monotonicity.

Proof

Let (E, c), $(E',c)$ be two claims problems such that $E'<E$. As CEA satisfies composition up⁶

$$\begin{aligned} CEA_i(E,c) - CEA_i(E',c) = CEA_i\left( E-E',{\widetilde{c}}\right) \ge \min \left\{ \frac{1}{n} (E-E'),{\widetilde{c}}_i \right\} \end{aligned}$$

where ${\widetilde{c}} = c- CEA(E',c)$. On the other hand

$$\begin{aligned} s_i(E,c) - s_i(E',c) = \left\{ \begin{array}{llll} (a) &{} 0 &{} if &{} c_i \le E'< E \\ (b) &{} \frac{1}{n}(c_i - E') &{} if &{} E'< c_i< E \\ (c) &{} \frac{1}{n}(E-E') &{} if &{} E'< E < c_i \\ \end{array} \right. \end{aligned}$$

In case (a) the required inequality is obviously fulfilled. In case (b), $E -E' \ge c_i - E'$, and ${\widetilde{c}}_i = c_i - CEA_i(E',c) \ge c_i - E'$, so the axiom holds. Finally, in case (c), the minimum is $\frac{1}{n}(E-E')$ and both expressions coincide. Therefore, CEA satisfies constrained resource monotonicity.

Let (E, c), $(E',c)$ be two claims problems such that $E'<E$, and let $i,j\in N$ be such that $c_i \le c_j$, $s_{i}(E,c) -s_{i}(E',c) = s_{j}(E,c)-s_{j}(E',c)$. There are only two possible cases compatible with the mentioned conditions:

• 1. $c_i \le c_j \le E' < E$, when $s_i(E,c) = s_i(E'c)=\frac{1}{n}c_i$, $s_j(E,c) = s_j(E'c)=\frac{1}{n}c_i$. Then, $CEA_i(E,c) = CEA_j(E,c)$, unless $CEA_i(E,c) = c_i$ and $CEA_i(E',c) = CEA_j(E',c)$, unless $CEA_i(E',c) = c_i$ which implies $CEA_i(E,c) = c_i$. In any case, $CEA_i(E,c) - CEA_i(E',c) = CEA_j(E,c) - CEA_j(E',c)$, or $CEA_i(E,c) = c_i$.

• 2. $c_j \ge c_i \ge E > E'$, when $s_i(E,c) = s_i(E'c)=\frac{1}{n}c_i$, $s_j(E,c) = s_j(E'c)=\frac{1}{n}c_i$. Then, $CEA_i(E,c) = CEA_j(E,c) = \frac{1}{n}E$, $CEA_i(E',c) = CEA_j(E',c) = \frac{1}{n}E'$, so $CEA_i(E,c) - CEA_i(E',c) = CEA_j(E,c) = CEA_j(E',c) = \frac{1}{n}(E-E')$.

So, in both cases, CEA fulfills the required condition and constrained equal bound monotonicity is satisfied. $\square$

4.3 Ibn Ezra’s rule

By using the securement bound we obtain a characterization of Ibn Ezra’s rule.

Theorem 4

When using securement bound, Ibn Ezra’s rule is the only rule in the class of claims problems ${\mathcal {C}}_{IE}$ satisfying constrained equal bound monotonicity and priority in allocation.

Proof

To prove that IE satisfies the required axioms, let $(E,c),(E',c) \in {\mathcal {C}}_{IE}$ be such that $E' < E.$

• (1) Constrained equal bound monotonicity. Let $i,j \in N$ be such that $c_i \le c_j$ and $s_i(E,c) - s_i(E',c) = s_j(E,c) - s_j(E',c).$ Only the following possibilities are compatible:

  • a) $s_i(E,c) = s_j(E,c) = \frac{E}{n}$, $s_i(E',c) = s_j(E',c) = \frac{E'}{n}$. This case corresponds to $E' < E \le c_i \le c_j$, which implies that $IE_{i}(E,c) = IE_{j}(E,c)$ and $IE_{i}(E',c) = IE_{j}(E',c)$. Then, constrained equal bound monotonicity is satisfied.

  • b) $s_i(E,c) = s_i(E',c) = \frac{c_i}{n}$, $s_j(E,c) = s_j(E',c) = \frac{c_j}{n}$. This case corresponds to $c_i \le c_j \le E' < E$, which implies that $IE_{i}(E,c) = IE_{j}(E,c) = \frac{E}{n}$ and $IE_{i}(E',c) = IE_{j}(E',c) = \frac{E'}{n}$. Then, constrained equal bound monotonicity is also satisfied.

• (2) Priority in allocation. First note that $s_i(E,c) > s_i(E',c)$ implies $c_i > E'$ and then $IE_{i}(E,c) > IE_{i}(E',c).$ Conversely, if $IE_{i}(E,c) > IE_{i}(E',c),$ necessarily $E' < c_i,$ and $s_i(E,c) = \min \left\{ \frac{E}{n}, \frac{c_i}{n} \right\} > \frac{E'}{n} = s_i(E',c)$.

To prove the uniqueness let $\varphi$ be a rule fulfilling the axioms and $(E,c) \in {\mathcal {C}}_{IE}.$ Then:

• (a) Let us suppose $E \le c_{1}$ and set $E'=0.$ Then, $s_{i}(E,c) = \frac{E}{n}$, $s_{i}(E',c) =0$, for each $i \in N.$ Priority entails that all agents awards increase from $E'=0$. Constrained equal bound monotonicity implies that all awards equally increase, so efficiency implies $\varphi _{i}(E,c) = \frac{E}{n} = IE_{i}(E,c).$

• (b) If $c_{1} < E \le c_{2}$, $s_{1}(E,c) = \frac{c_1}{n}$ and, for each $j \ge 2$, $s_{j}(E,c) = \frac{E}{n}$. If we set $E'= c_1$, $s_{i}(E',c) = \frac{c_1}{n}$ for each $i \in N$. Priority entails that only agents $i \ge 2$ increase their awards, so by constrained equal bound monotonicity and efficiency $\varphi _{1}(E,c) = \frac{c_{1}}{n}$, and $\varphi _{j}(E,c) =\frac{c_{1}}{n}+ \frac{E^{\prime } - c_{1}}{n-1}$, that coincides with IE(E, c).

• (c) If $c_{i} < E \le c_{i+1}$, we repeat the previous argument by comparing (E, c) with the problem $(E',c),$ such that $E' = c_i$.

Hence, $\varphi (E,c) = IE(E,c)$. $\square$

The following example shows the independence of the axioms used in Theorem 4.

Example 4

We know that CEA satisfies constrained equal bound monotonicity (Proposition 2). Let the claims problems $(E,c) = \left( 300,(200,400)\right)$ and $(E',c) = \left( 200,(200,400)\right)$. Then,

$$\begin{aligned} s(E,c)= & {} (100,200), \, s(E',c) = (100,100), \, \\ CEA(E,c)= & {} (150,150), \, CEA(E',c) = (100,100) \end{aligned}$$

so agent 1 increases her awards without increasing her lower bound contradicting priority in allocation.

Let $N^1 = \left\{ i \in N : c_i > E\right\} ,$ $n^1$ its cardinal and $N^2 = N \setminus N^1.$ Let $\varphi$ be the rule defined for any problem (E, c) as:

$$\begin{aligned} \varphi (E,c) = s(E,c) + \delta (E,c), \end{aligned}$$

where $\delta _i(E,c) = 0$, for $i \in N^2$ and $\delta _i(E,c)= \frac{1}{n^1}(E-S)$, for $i \in N^1$, $S= \sum _{i\in N} s_i(E,c)$. It is clear that this rule satisfies priority in allocation. Let the claims problems $(E,c) = \left( 120,(30,120,150)\right)$ and $(E',c) = \left( 90,(30,120,150)\right)$. Then,

$$\begin{aligned} s(E,c)= & {} (10,40,40), \, s(E',c) = (10,30,30), \,\\ \varphi (E,c)= & {} (10,40,70), \, \varphi (E',c) = (10,30,50) \end{aligned}$$

so agent 3 increases her awards more than agent 2 does, contradicting constrained equal bound monotonicity.

Finally, our last result shows additional axioms that Ibn Ezra’s rule holds.

Proposition 3

When using the securement bound, Ibn Ezra’s rule satisfies respect of the lower bound and constrained resource monotonicity in the class of claims problems ${\mathcal {C}}_{IE}$.

Proof

As constrained resource monotonicity implies respect of the lower bound, we only need to prove the fulfilment of the former axiom.

Let $(E,c),(E',c) \in {\mathcal {C}}_{IE}$ be such that $E' < E.$ Constrained resource monotonicity is written in this case as:

$$\begin{aligned} IE_i(E,c) - IE_i(E'c) \ge \frac{1}{n} \left( \min \left\{ c_i,E\right\} - \min \left\{ c_i,E'\right\} \right) \end{aligned}$$

(1)

For $i \in N$, the following cases are possible:

• a) $c_i \le E' < E$

• b) $c_{i-1} \le E' < c_i \le E$

• c) $E' < c_{i-1} \le c_i \le E$

• d) $c_{i-1} \le E'< E < c_i$

• e) $E'< c_{i-1} \le E < c_i$

• f) $E'< E < c_{i-1} \le c_i$

In any case, it is easy to check that Equation (1) holds. $\square$

4.4 Extending Ibn Ezra’s rule

Bergantiños and Méndez-Naya (2001) and Alcalde et al. (2005) propose alternative ways to extend Ibn Ezra’s rule to the entire set of claims problems ${\mathcal {C}}$. We will use the former one, that we represent by ${IE}^{*}$ and that can be stated as follows: for each (E, c) in ${\mathcal {C}}$

$$\begin{aligned} {IE}^{*}(E,c) = \left\{ \begin{array}{lll} IE(E,c) &{} &{} {\hbox {if}} {c}_{n} \ge E\\ &{} \\ IE(c_{n},c) + {IE}^{*}\left( E-{c}_{n}, c - {IE}({c}_{n},c)\right) &{} &{} \hbox {otherwise} \\ \end{array} \right. \end{aligned}$$

(2)

Note that this is a recursive definition: if we are in the second case, we may need to apply the recursive process several times.

5 Upper bounds: the dual approach

An important tool in the analysis of claims problems is the notion of duality: we focus on losses incurred by the agents (what they do not receive with respect to their claims) instead of focusing on awards. The total loss in a claims problem $(E,c) \in {\mathcal {C}}$ is defined as the difference between the aggregate claim and the endowment; that is, $L = \sum _{i=1}^{n} c_i - E.$ Hence, (L, c) is also a claims problem, which is known as the dual problem. Then, given a claims rule $\varphi$, its dual rule, $\varphi ^{d},$ assigns losses in the same way as $\varphi$ assigns gains (Aumann and Maschler 1985). Formally, for all $i=1,2,\ldots ,n$

$$\begin{aligned} \varphi _{i}^{d}(E,c)=c_{i}-\varphi _{i}(L,c). \end{aligned}$$

(3)

The dual of the CEA rule is the constrained equal losses rule (Herrero 2003), which is defined as: for each (E, c) in ${\mathcal {C}}$ and each $i\in N,$ $CEL_{i}(E,c)\equiv \max \left\{ 0,c_{i}-\mu \right\} ,$ where $\mu$ is chosen so that $\sum _{i\in N}\max \left\{ 0,c_{i}-\mu \right\} =E$.

Following the duality notion given by (3), the dual of Ibn Ezra’s rule must fulfill:

$$\begin{aligned} IE_i^d(E,c) = c_i - IE_i(L,c) \qquad \qquad i=1,2, \ldots ,n. \end{aligned}$$

but the problem (L, c) does not necessarily belong to the class ${\mathcal {C}}_{IE}$ and Ibn Ezra’s classical rule cannot be applied and we need to apply the recursive method given by expression (2). For instance, if we consider the claims problem (E, c), with $E=50$, $c = (10,20,50,70)$, then

$$\begin{aligned} IE(E,c) = \left( \frac{5}{2}, \frac{35}{6}, \frac{125}{6}, \frac{125}{6}\right) \qquad L = 100 \qquad IE^*(L,c) = \left( \frac{23}{5}, \frac{71}{7}, \frac{98}{3}, \frac{158}{3} \right) \end{aligned}$$

so

$$\begin{aligned} IE^d(E,c) = \left( \frac{27}{5}, \frac{69}{7}, \frac{52}{3}, \frac{52}{3} \right) . \end{aligned}$$

Our final discussion is devoted to the analysis of the existence of upper bounds. The idea of an upper bound on awards is to establish the maximum amount that an individual i should obtain in a particular claims problem by taking into account her claim $c_i$, the endowment E and other individuals’ claims. In fact, the definition of a claims rule already requires an upper bound on awards: no one can get more than her respective claim. Formally, an upper bound is a function $B:{\mathcal {C}} \rightarrow {\mathbb {R}}_{+}^{n}$ which maps each claims problem $(E,c)\in {\mathcal {C}}$ to a vector B(E, c), such that for each $i \in N$, $0\le B_{i}(E,c)\le c_{i}$ and $\sum _{i=1}^{n} B_{i}(E,c) \ge E$.

Moulin (2002) introduces the fair upper bound u: for each (E, c) $\in {\mathcal {C}}$ and each $i\in N,$ $u_{i}(E,c)= \max \left\{ 0,c_{i}-\frac{L}{n}\right\} , \text {where} \ L = \sum _{i=1}^n c_i - E.$

If we observe this definition,

$$\begin{aligned} u_{i}(E,c)= - \min \left\{ 0,-c_{i}+\frac{L}{n}\right\} = c_i - \min \left\{ c_i,\frac{L}{n}\right\} = c_i - f_i(L,c). \end{aligned}$$

That is, the fair upper bound can be defined by using the fair lower bound on the dual claims problem (L, c); and vice versa: the fair upper bound defines a lower bound on the dual problem that coincides with the fair lower bound.

The same occurs with any upper bound: $c_i - B_i(E,c)$ defines a lower bound of the dual claims problem (L, c), since

• (i) $0\le c_i - B_{i}(E,c)\le c_{i}$

• (ii) $\sum _{i=1}^{n}\left( c_i - B_{i}(E,c) \right) = C - \sum _{i=1}^{n} B_i(E,c) \le C - E = L$

We use this duality approach to introduce the upper bounds associated to the securement and $\min$ lower bounds.

Upper-securement, us: for each (E, c) $\in {\mathcal {C}}$ and each $i\in N,$

$$\begin{aligned} {us}_{i}(E,c)= {c}_{i} - {s}_{i}(L,c)= {c}_i - \frac{1}{n} \min \left\{ {c}_{i}, L\right\} = \max \left\{ {c}_{i}-\frac{{c}_{i}}{n},{c}_{i}-\frac{L}{n}\right\} . \end{aligned}$$

Upper-min, um: for each (E, c) $\in {\mathcal {C}}$ and each $i\in N,$

$$\begin{aligned} {um}_{i}(E,c)= & {} {c}_i - {m}_i(L,c) = {c}_i - \frac{1}{n} \min \left\{ {\min }_{j\in {N}} { {c}_{j}}, L\right\} \\= & {} \max \left\{ {c}_{i}-\frac{{\min }_{j\in {N}} { {c}_{j}}}{n},{c}_{i}-\frac{L}{n}\right\} . \end{aligned}$$

Remark 4

The dual of minimal right (maximal right), Mr, would be analogously defined by

$$\begin{aligned} Mr_{i}(E,c)= & {} c_i - mr_i(L,c) = c_i - \max \left\{ 0,L-\sum _{j\in N\text { } \smallsetminus \left\{ i\right\} } c_j \right\} \\= & {} \min \left\{ c_{i},C-L \right\} = \min \left\{ c_{i},E \right\} \end{aligned}$$

that corresponds with the notion of truncated claims introduced in Curiel et al. (1987).

On the part of the axioms, two properties are dual if whenever a rule satisfies one of the properties, its dual rule satisfies the other. Then, when a rule $\varphi$ fulfills some axiom with respect to a given lower bound, its dual rule $\varphi ^d$ fulfills the dual axiom with respect to the dual upper bound. Regarding the properties we have used, the dual of constrained equal treatment of equals coincides with itself and the same occurs with constrained resource monotonicity and priority in allocation. The dual of the axioms respect of the lower bound (that we call respect of the upper bound) and constrained resource monotonicity (that we call constrained resource upper monotonicity) are obtained by reversing the inequality in the original properties.

The following results are an immediate consequence of the corresponding ones obtained in Sect. 4.

Corollary 3

Considering the upper bound $B = u$, CEL is the only rule satisfying either:

• 1. respect of the upper bound and constrained equal treatment of equals; or

• 2. constrained resource monotonicity and constrained equal treatment of equals.

Corollary 4

Considering the upper bound $B = um$, CEL is the only rule satisfying either:

• 1. constrained equal treatment of equals; or

• 2. constrained equal bound monotonicity.

Corollary 5

Considering the upper bound $B = us$, $IE^{d}$ is the only rule satisfying constrained equal bound monotonicity and priority in allocation.

6 Final remarks

Throughout this paper, we have shown how lower bounds can be associated with a particular rule: the fair and $\min$ bounds are linked to the constrained equal awards rule, and the securement bound is associated to Ibn Ezra’s rule.

Related research, analyzing lower/upper bound in claims problems may be found in Thomson and Yeh (2008) use the minimal right lower bound to define an operator (minimal rights first) and analyze the properties that are preserved under this operator. As they mention, the mr lower bound may guarantee a null amount to all agents. Furthermore, in terms of characterizing the claims rules, it should be mentioned that any claims rule fulfills respect of the minimal rights lower bound. Hougaard et al. (2012) introduce the notion of baseline in a claims problem that includes both lower and upper bounds (and other possibilities). Like in Thomson and Yeh (2008) they analyze the properties that are preserved under this operator. The main feature in this work is to unify three apparently unrelated approaches to the problem of adjudicating conflicting claims: baseline rationing, composition properties, and lower bounds. Finally, Hougaard et al. (2013) use the baselines as reference points (additionally to the claims vector) to define an operator (baselines first) that generalizes the minimal rights first operator defined in Thomson and Yeh (2008).

This correspondence between lower bounds and rules makes us wonder about bounds that may be linked to other important rules such as the proportional rule, the Talmudian rule, etc., a question that remains open. Furthermore, we put forward for discussion the converse question: if we propose a reasonable lower bound on awards for each agent, is it possible to define a unique rule satisfying the required axioms? There are conditions that allow to associate a unique rule satisfying the recursive extension of a lower bound (see, for instance, the positivity condition used in Dominguez 2006), so we speculate whether it would be possible to combine respect of the lower bound with some other condition to define a unique rule.