Coalition-proof stable networks

Abstract

We propose the notion of coalition-proof stability for predicting the networks that could emerge when group deviations are allowed. A network is coalition-proof stable if there exists no coalition which has a credible group deviation. A coalition is said to have a credible group deviation if there is a profitable group deviation to some network and there is no subcoalition of the deviating players which has a subsequent credible group deviation. Coalition-proof stability is a coarsening of strong stability. We emphasize the importance of coalition-proof stability by considering four models where a strongly stable network fails to exist while a coalition-proof stable network does exist. We provide an easy to verify condition for the existence of a coalition-proof stable network while a strongly stable network may not exist. There is no relationship between the set of coalition-proof stable networks and the set of networks induced by a coalition-proof Nash equilibrium of Myerson’s linking game.

1 Introduction

The organization of players into networks plays an important role in the determination of the outcome of many social and economic interactions. Moreover, in many situations (R&D networks, trade networks, buyers-sellers networks, criminal networks, ...) networks are neither fixed nor randomly determined but rather emerge through the decisions taken by the players.¹

Jackson and Wolinsky (1996) propose the notion of pairwise stability to determine the networks that one might expect to emerge in the long run. A network is pairwise stable if no player benefits from severing one of her links and no two players benefit from adding a link between them. Pairwise stability only considers deviations involving a single link at a time. That is, link addition is bilateral (two players that would be involved in the link must agree to adding the link), link deletion is unilateral (at least one player involved in the link must agree to deleting the link), and network changes take place one link at a time. But, it might be that some group of players could all be made better off by some complicated reorganization of their links, which is not accounted for under pairwise stability. Hence, Jackson and van den Nouweland (2005) propose the notion of strong stability that allows for group deviations involving several links within some group of players at a time. Link addition is bilateral, link deletion is unilateral, and multiple link changes can take place at a time. Whether a pairwise deviation or a group deviation makes more sense depend on the setting within which network formation takes place.

However, strongly stable networks often fail to exist because networks can be classified as not stable while they rely on group deviations that are not credible. A network can be considered unstable because some coalition of players has a profitable group deviation leading to some network even though a subcoalition of the deviating players would have incentives to deviate subsequently to another network. That is, the credibility of some group deviations can be questioned.

We propose the notion of coalition-proof stability for predicting the networks that could emerge in the long run. A network is said to be coalition-proof stable if there exists no coalition which has a credible group deviation. A coalition is said to have a credible group deviation if there is a profitable group deviation to some network and there is no subcoalition of the deviating players which has a subsequent credible group deviation. Coalition-proof stability is a coarsening of strong stability.

We emphasize the importance of coalition-proof stability by providing three network models where a strongly stable network fails to exist while a coalition-proof stable network does exist. In Belleflamme and Bloch (2004) model of market-sharing agreements, there is no strongly stable network while the empty network is the unique coalition-proof stable network. In Jackson and Watts (2002) model of exchange networks, coalition-proof stability leads to networks consisting of separate pairs. Finally, in a simplified version of Calvo-Armengol and Zenou (2004) model of criminal networks, coalition-proof stability predicts the emergence of a network with a minimally winning component.

Since a coalition-proof stable network may also fail to exist, we look for conditions such that the existence of a coalition-proof stable network is guaranteed while a strongly stable network may not exist. We provide easy to verify conditions that are satisfied by the coalition-proof stable networks in the market sharing model and in the exchange model. We next show that under a componentwise egalitarian utility function where players belonging to the same component get the same utility and there are no externalities across components, there always exists a coalition-proof stable network and coalition-proof stability coincides with strong stability. If, in addition, the utility function is top convex then both strong stability and coalition-proof stability single out the strongly efficient networks.

We show that there is no relationship between the set of coalition-proof stable networks and the set of networks induced by a coalition-proof Nash equilibrium of Myerson’s (1991) noncooperative linking game. In Myerson’s linking game, players choose simultaneously the links they wish to form and the formation of a link requires the consent of both players. Dutta and Mutuswami (1997) propose the concepts of strong stability and weak stability: a network is strongly (weakly) stable if it corresponds to a strong (coalition-proof) Nash equilibrium of Myerson’s (1991) linking game.² We argue that coalition-proof stability often tends to predict the most plausible networks while some coalition-proof Nash equilibria of Myerson’s linking game support overconnected networks. For instance, in the criminal networks model where network components compete for a loot, coalition-proof stability predicts the emergence of a network with a minimally winning component, while there is no strongly stable network and coalition-proof Nash equilibria of Myerson’s linking game sustain many more networks. The reason why coalition-proof Nash equilibria of Myerson’s linking game support overconnected networks has to do with the following drawback. If the deviation by a coalition involves the deletion of links with players outside the coalition, then a single deviating player who has just deleted a link with some player not in the deviating coalition can form again this link in a subsequent deviation without requiring the mutual consent of the other player. Coalition-proof stability overcomes such a drawback by requiring that this player belongs to the deviating coalition in the subsequent deviation.

Up to now we consider (strict) group deviations where a group of players deviate only if each of its members can be made (strictly) better off. Alternatively, we can look at weak group deviations where a group of players deviate only if at least one of its members is (strictly) better off while all other members are at least as well off. Although strong stability with weak group deviations refines strong stability with strict group deviations, we show that there is no relationship between coalition-proof stability with strict group deviations and coalition-proof stability with weak group deviations. However, if the network utility function is link-responsive (i.e. no player is indifferent to a change in her set of links), then both notions coincide. We next consider an upper limit to the size of a deviating group and we find that the set of coalition-proof stable networks weakly decreases with this upper limit.

Finally, there are situations where only pairwise deviations are feasible. In such situations farsighted players may look beyond the immediate consequence of adding or deleting a link and anticipate the subsequent changes that will occur afterwards. Is coalition-proof stability with farsighted players but restricted to pairwise deviations equivalent to coalition-proof stability with group deviations? In general, the answer is no. Nevertheless, the set of coalition-proof farsightedly stable networks and the set of farsightedly stable networks coincide under the componentwise egalitarian utility function.

The paper is organized as follows. In Sect. 2 we introduce networks, pairwise stability, strong stability, and we define the new notion of coalition-proof stability. In Sect. 3 we provide three examples in which a strongly stable network fails to exist while a coalition-proof stable network does exist. In Sect. 4 we study the existence and efficiency of coalition-proof stable networks. In Sect. 5 we compare coalition-proof stability with coalition-proof Nash equilibrium of Myerson’s linking game. In Sect. 6 we discuss some extensions. We first look at strict versus weak group deviations. We next study coalition-proof stability under limited size group deviations. We finally extend our notion of coalition-proof stability to farsighted players. In Sect. 7 we conclude.

2 Coalition-proof stability

Let $N=\{1,...,n\}$ be the finite set of players who are connected in some network relationship. The network relationships are reciprocal and the network is thus modeled as a non-directed graph. A network g is a list of players who are linked to each other. We write $ij\in g$ to indicate that i and j are linked in the network g. Let $g^{S}$ be the set of all subsets of $S\subseteq N$ of size 2, so $g^{N}$ is the complete network. The set of all possible networks on N is denoted by ${\mathcal {G}}$ and consists of all subsets of $g^{N}$. The network obtained by adding link ij to an existing network g is denoted $g+ij$ and the network obtained by cutting link ij from an existing network g is denoted $g-ij$. For any network g , we denote by $N(g)=\{i\mid \exists$ j such that $ij\in g\}$ the set of players who have at least one link in the network g. Let $N_{i}(g)=\{j\in N\mid ij\in g\}$ be the set of neighbors of player i in g. The degree of player i in network g, denoted $d_{i}(g)$, is the cardinality of i’s set of neighbors, $d_{i}(g)=\#N_{i}(g)$. A path in a network g between i and j is a sequence of players $i_{1},\ldots ,i_{K}$ such that $i_{k}i_{k+1}\in g$ for each $k\in \{1,\ldots ,K-1\}$ with $i_{1}=i$ and $i_{K}=j$. A non-empty network $h\subseteq g$ is a component of g, if for all $i\in N(h)$ and $j\in N(h)\setminus \{i\}$, there exists a path in h connecting i and j, and for any $i\in N(h)$ and $j\in N(g)$, $ij\in g$ implies $ij\in h$.³ We denote by C(g) the set of components of g. A component h of g is minimally connected if h has $\#N(h)-1$ links (i.e. every pair of players in the component is connected by exactly one path). The partition of N induced by g is denoted by $\Pi (g)$, where $S\in \Pi (g)$ if and only if either there exists $h\in C(g)$ such that $S=N(h)$ or there exists $i\notin N(g)$ such that $S=\{i\}$. A network utility function (or payoff function) is a mapping $u:{\mathcal {G}}\rightarrow {\mathbb {R}}^{N}$ that assigns to each network g a utility $u_{i}(g)$ for each player $i\in N$. A network $g\in {\mathcal {G}}$ is strongly efficient relative to u if it maximizes $\sum _{i\in N}u_{i}(g)$.

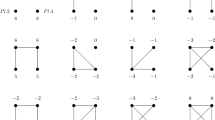
One way to analyze the networks that one might expect to emerge in the long run is to examine a sort of equilibrium requirement that players not benefit from altering the structure of the network. Jackson and Wolinsky (1996) define the notion of pairwise stability. A network is pairwise stable if no player benefits from severing one of their links and no other two players benefit from adding a link between them. Formally, a network g is pairwise stable with respect to u if and only if (i) for all $ij\in g$, $u_{i}(g)\ge u_{i}(g-ij)$ and $u_{j}(g)\ge u_{j}(g-ij)$, and (ii) for all $ij\notin g$, if $u_{i}(g)<u_{i}(g+ij)$ then $u_{j}(g)\ge u_{j}(g+ij)$.⁴ Two networks g and $g^{\prime }$ are adjacent if they differ by one link. That is, $g^{\prime }$ is adjacent to g if $g^{\prime }=g+ij$ or $g^{\prime }=g-ij$ for some ij. A network $g^{\prime }$ defeats g if either $g^{\prime }=g-ij$ with $u_{i}(g^{\prime })>u_{i}(g)$ or $u_{j}(g^{\prime })>u_{j}(g)$, or if $g^{\prime }=g+ij$ with $u_{i}(g^{\prime })>u_{i}(g)$ and $u_{j}(g^{\prime })>u_{j}(g)$. Hence, a network is pairwise stable if and only if it is not defeated by another (necessarily adjacent) network. Consider the example where three players can form links and where the payoffs are given in Fig. 1. Only the partial networks $g_{1}$, $g_{2}$ and $g_{3}$ are pairwise stable. The empty network $g_{0}$ is not pairwise stable because two players have incentives to link to each other; the star networks $g_{4}$ , $g_{5}$ and $g_{6}$ are not pairwise stable since the player in the center has an incentive to delete one of her links to form a partial network; and the complete network $g_{7}$ is not pairwise stable since each player has an incentive to delete one of her links to form a star network.

Fig. 1

The networks that can be formed among three players with their utilities

The notion of pairwise stability only considers deviations by at most a pair of players at a time. It might be that some group of players could all be made better off by some complicated reorganization of their links, which is not accounted for under pairwise stability. Group deviations make sense in situations where players have substantial information about the overall structure and potential payoffs and can coordinate their actions. Dutta and Mutuswami (1997) and Jackson and van den Nouweland (2005) propose alternative definitions of stability that allow for group deviations. The definition of strong stability of Dutta and Mutuswami (1997) considers a deviation to be valid only if all members of a deviating coalition are strictly better off, while the definition of Jackson and van den Nouweland (2005) is slightly stronger by allowing for a deviation to be valid if some members are strictly better off and others are weakly better off. Under the definition of Dutta and Mutuswami (1997), a network is strongly stable if it corresponds to a strong Nash equilibrium of Myerson’s linking game.

We consider here a strict version of Jackson and van den Nouweland (2005) notion of strong stability that refines the set of pairwise stable networks.

Definition 1

Coalition $S\subseteq N$ is said to have a group deviation from g to $g^{\prime }$ if

(i):

$ij\in g^{\prime }$ and $ij\notin g$ $\Rightarrow \{i,j\}\subseteq S$,

(ii):

$ij\in g$ and $ij\notin g^{\prime }$ $\Rightarrow \{i,j\}\cap S\ne \emptyset$,

(iii):

$u_{i}(g^{\prime })>u_{i}(g)$ for all $i\in S$.

A coalition S is said to have a group deviation from the network g to the network $g^{\prime }$ if three conditions are satisfied. Condition (i) requires that any new links that are added can only be between players inside S. Condition (ii) requires that there must be at least one player belonging to S for the deletion of a link. Condition (iii) requires that all members of S are better off. This definition identifies possible profitable changes in a network that can be made by a coalition S.

Definition 2

A network g is strongly stable if there exists no coalition $S\subseteq N$ which has a group deviation from g.

Let $\mathbf {SS}$ be the set of strongly stable networks. In the example of Fig. 1, the partial networks $g_{1}$, $g_{2}$ and $g_{3}$ are not strongly stable since the three players have incentives to deviate together to form the complete network (and hence, a strongly stable network fails to exist).

Under the notion of strong stability, some networks are declared not stable meanwhile they rely on group deviations that are not credible. Hence, we now introduce the notion of coalition-proof stability (CPS) that checks for the credibility of group deviations.

Definition 3

Coalition $S\subseteq N$ is said to have a credible group deviation from g if

(i):

$g^{\prime }$ is a group deviation from g by S, and

(ii):

there exists no subcoalition $T\varsubsetneq S$ which has a credible group deviation from $g^{\prime }$.

Notice the recursion in the definition of a credible group deviation. Each singleton coalition has a credible deviation if it has a deviation; each two-player coalition has a credible group deviation if it has a group deviation at which no player of the two has a credible deviation; each three-player coalition has a credible group deviation if it has a group deviation at which no player of the three and no two-player coalition among them have a credible group deviation; and so on.

Definition 4

A network g is coalition-proof stable (CPS) if there exists no coalition $S\subseteq N$ which has a credible group deviation from g.

The concept of coalition-proof stability is weaker than that of strong stability: fewer group deviations are allowed, since some are declared not credible because of their lack of internal consistency. Let $\mathbf {CPS}$ be the set of coalition-proof stable networks. In the example of Fig. 1, there is no strongly stable network. But, for instance, the profitable group deviation from the partial network $g_{2}$ to the complete network $g_{7}$ by players 1, 2 and 3 is not credible because at $g_{7}$ one of the deviating player has a profitable deviation to some star network ($g_{4}$ or $g_{5}$ or $g_{6}$) that do not involve other players. Hence, $\{12\}$ (and $\{13\}$, $\{23\}$) is a coalition-proof stable network.

3 Examples

We now provide three examples in which a strongly stable network fails to exist while a coalition-proof stable network does exist.

3.1 Market sharing agreements

We reconsider Belleflamme and Bloch (2004) model of market sharing agreements with $n\ge 3$ firms. Players are referred to as firms. Each player i has a home market and can be active on the foreign markets. For any market i, let $n_{i}$ be the number of active players on the market. Let $\pi _{i}^{j}(n_{i})$ be the profit of player j on market i. Players can sign bilateral market sharing agreements that refrains them from entering on the other player’s market. Let g be a network of market sharing agreements: $ij\in g$ means that players i and j are linked by a market sharing agreement and are not active on each other’s market, while $ij\notin g$ means that player i is present on market j and player j on market i. On each market, active players compete à la Cournot with zero marginal cost and a linear inverse demand given by $p=10-q$. Then, profits on markets are simply given by $\pi _{i}^{j}(n_{i})=100/(n_{i}+1)^{2}$. The payoff of player i is given by the sum of the profits player i gets on her home market and on all foreign markets for which she has not formed market sharing agreements:

$$\begin{aligned} u_{i}(g)=\pi _{i}^{i}(n_{i})+\sum _{j:ij\notin g}\pi _{j}^{i}(n_{j})\text {.} \end{aligned}$$

Proposition 1

In the market sharing networks model, there is no strongly stable network, $\mathbf {SS}=\emptyset$, while the empty network $g^{\emptyset }$ is the unique coalition-proof stable network, $\mathbf {CPS}=\{g^{\emptyset }\}$.

Proof

(i) We first show that all networks $g\ne g^{\emptyset }$ are neither strongly stable nor coalition-proof stable. Take any $g\ne g^{\emptyset }$. We have that any player i such that $n>n_{i}\ge n_{j}$ for all $j\in N$ has incentives to delete all her links.⁵ Indeed, $u_{i}(g)=100/(n_{i}+1)^{2}+\sum _{j:ij\notin g}100/(n_{j}+1)^{2}$ and $u_{i}(g^{\prime })=100/(n+1)^{2}+\sum _{j:ij\notin g}100/(n_{j}+1)^{2}+\sum _{k:ik\notin g^{\prime },ik\in g}100/(n_{k}+1)^{2}$ with $g^{\prime }=g\setminus \{jk\in g\mid j=i$ or $k=i\}$. Since $n>n_{i}\ge n_{j}$ for all $j\in N$, we have that $100(n-n_{i})/(n_{i}+2)^{2}\le \sum _{k:ik\notin g^{\prime },ik\in g}100/(n_{k}+1)^{2}$ and $100/(n_{i}+1)^{2}<100/(n+1)^{2}+100(n-n_{i})/(n_{i}+2)^{2}$. Hence, $u_{i}(g)<u_{i}(g^{\prime })$. In other words, players having the less number of market sharing agreements among players that do have market sharing agreements have incentives to cancel all their market sharing agreements. Since this deviation involves only a single player, it is a credible one. Thus, all networks $g\ne g^{\emptyset }$ are not coalition-proof stable.

(ii) We next show that the empty network $g^{\emptyset }$ is not strongly stable. From $g^{\emptyset }$, the grand coalition N has a group deviation to the complete network $g^{N}$. Indeed, $u_{i}(g^{\emptyset })=100n/(n+1)^{2}<u_{i}(g^{N})=100/4$ for all $i\in N$. However, any group deviation from $g^{\emptyset }$ to some g is not credible since there is some $\{i\}$ who has a credible group deviation from g as shown in (i). Thus, the empty network $g^{\emptyset }$ is the unique coalition-proof stable network. $\square$

3.2 Exchange networks

In Jackson and Watts (2002) model of exchange networks, four players get value from trading goods with each other. There are two goods, x and y. The payoff of each player i is given by $u_{i}(x,y)=x\cdot y-cd_{i}$ where c is the cost for maintaining a link. Players form first a network. Players then receive a random endowment which is independently and identically distributed: $x=1,y=0$ with probability 1/2 and $x=0,y=1$ with probability 1/2. Finally, trade flows without friction along any path and each connected component trades to a Walrasian equilibrium. Thus, the networks $\{12,23\}$ and $\{12,23,13\}$ lead to the same expected trades, but lead to different costs of links. Ignoring the costs of links, the player’s expected payoff is increasing and strictly concave in the number of other players that she is connected to: (i) the payoff of being alone is 0 ; (ii) the expected payoff of being connected to one player is 1/8; (iii) the expected payoff of being connected to two players is 1/6; (iv) the expected payoff of being connected to three players is 3/16. Let $c=5/96$ be the cost of maintaining a link.

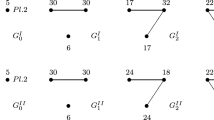
There is no pairwise (hence, no strongly) stable network in Jackson and Watts exchange networks model with four players. The network $\{12,34\}$ is defeated by $\{12,23,34\}$ which is defeated by $\{12,23\}$ which is defeated by $\{12\}$ which is defeated by $\{12,34\}$. See Fig. 2.

Fig. 2

Exchange networks

Proposition 2

In the exchange networks model with four players, there is no strongly stable network while the networks $\{12,34\}$, $\{13,24\}$ and $\{14,23\}$ are the coalition-proof stable networks.

Proof

(i) Notice first that the minimally connected networks⁶ connecting four players (like $\{12,23,34\}$) are not coalition-proof stable since a player who has two links has incentives to delete her link to a loose end player. It is a unilateral profitable deviation that does not require the consent of another player. Similarly, the minimally connected networks connecting three players (like $\{12,23\}$) are not coalition-proof stable since the player who has two links has incentives to delete one of her links. Finally, the networks connecting only two players (like $\{12\}$) are not coalition-proof stable since the other two players have incentives to link to each other to form a network with two components (like $\{12,34\}$). This deviation is credible since both deviating players have no unilateral profitable deviation afterwards.

(ii) We now argue that $\{12,34\}$ (hence, $\{13,24\}$ and $\{14,23\}$) is a coalition-proof stable network. Notice that the deviation by players 2 and 3 from $\{12,34\}$ to $\{12,23,34\}$ might be questionable since at $\{12,23,34\}$ one of the two players has incentives to delete one of her links. For instance, player 3 has incentives to cut the link 34 to reach the network $\{12,23\}$ where she gets a payoff of 11/96 instead of 8/96. Hence, the profitable group deviation from $\{12,34\}$ to $\{12,23,34\}$ by players 2 and 3 is not credible because at $\{12,23,34\}$ one of the deviating players has a profitable deviation to $\{12,23\}$ that do not involve other players. Thus, $\{12,34\}$, $\{13,24\}$ and $\{14,23\}$ are the coalition-proof stable networks. $\square$

3.3 Criminal networks

We consider a simplified version of Calvo-Armengol and Zenou (2004) model where criminals compete with each other in criminal activities but benefit from having criminal friends. Players are referred to as criminals. If two players are connected, then they are part of the same criminal group. Criminal groups compete for winning the loot. The loot is divided among the winning criminal group based on the network architecture. A criminal group is winning only if the majority of players belong to the team. Within the winning criminal group, the loot is divided equally among the players who have the highest number of links. Criminals who end up with the loot can be caught with some positive probability. The higher the number of links player i has, the lower i’s probability of being caught. In the case player i is caught, i’s rewards are punished at a rate $\phi >0$ with $\phi <n^{2}c/B$. For any group $S\in \Pi (g)$ of connected players, let ${\overline{d}}(S)=\max _{i\in S}d_{i}$. Formally, the payoff of player $i\in S$ , $S\in \Pi (g)$, is given by⁷

$$\begin{aligned} u_{i}(g)= & {} \frac{B}{\#\{j\in S\mid d_{j}={\overline{d}}(S)\}}\\&\left( 1-\frac{ \#S-1-d_{i}}{\#S}\phi \right) -cd_{i}\text { if }\#S>n/2\text { and }d_{i}= {\overline{d}}(S)\text {,} \end{aligned}$$

and $u_{i}(g)=-cd_{i}$ otherwise.

In Fig. 3 we depict the networks and the payoffs in the case of three players. In the empty network, there is no criminal winner and all players get 0; in the partial networks, the criminal group composed of the two linked players wins the loot and they share it equally (B/2); in the star networks, there is a single criminal group and the player in the center gets the whole loot (B); in the complete network, the three players share equally the loot (B/3).

Fig. 3

Criminal networks among three players with their utilities

Proposition 3

In the criminal networks model with $B>n(n-1)c$, $\mathbf {SS}=\emptyset$ while $\mathbf {CPS}=\{g^{S^{*}}\mid (n+2)/2\ge \#S^{*}>n/2\}$.

Proof

(i) Take any g such that there is some $i\in N(g)$ with $u_{i}(g)<0$. In g, either i belongs to a loosing component or i belongs to the winning component but she has less links than some other member(s) of the winning component. Then, player i has incentives to cut all her links and the deviation from g to $g {\setminus } \{jk\in g\mid j=i$ or $k=i\}$ is credible. Thus, the only candidates for being strongly stable or coalition-proof stable are networks such that players who have links belong to the winning component and have the same number of links: g such that $\#C(g)=1$, $d_{i}(g)=d_{j}(g)$ for all $i,j\in S\in \Pi (g)$, and $\#S>n/2$.

(ii) Take any g such that $\#C(g)=1$ and $d_{i}(g)=d_{j}(g)<\#S-1$ for all $i,j\in S\in \Pi (g)$, $\#S>(n+2)/2\ge \#S^{*}>n/2$. Two players $i,j\in S$ such that $ij\notin g$ have incentives to add this link to form $g+ij$ and sharing together the entire loot B. This is a credible group deviation for $S=\{i,j\}$. Hence, $g\notin \mathbf {SS}$ and $g\notin \mathbf {CPS}$.

(iii) Take any $g^{S}$ such that $\#S>(n+2)/2\ge \#S^{*}>n/2$. The members of any coalition $S^{*}\varsubsetneq S$ have incentives to deviate from $g^{S}$ to $g^{S^{*}}$ since $u_{i}(g^{S})=B/\#S-c( \#S-1)<u_{i}(g^{S^{*}})=B/\#S^{*}-c(\#S^{*}-1)$. Moreover, this deviation is credible since $g^{S^{*}}\in \mathbf {CPS}$ as shown in (vi). Hence, $g^{S}\notin \mathbf {SS}$ and $g^{S}\notin \mathbf {CPS}$.

(iv) Take the empty network $g^{\emptyset }$. The members of any coalition $S^{*}\varsubsetneq S$ (with $(n+2)/2\ge \#S^{*}>n/2$) have incentives to deviate from $g^{\emptyset }$ to $g^{S^{*}}$. Moreover, this deviation is credible since $g^{S^{*}}\in \mathbf {CPS}$ as shown below in (vi). Hence, $g^{\emptyset }\notin \mathbf {SS}$ and $g^{\emptyset }\notin \mathbf {CPS}$.

Thus, the only candidates for being strongly stable or coalition-proof stable are networks g such that $g\subseteq g^{S^{*}}$, $\#C(g)=1$ and $d_{i}(g)=d_{j}(g)$ for all $i,j\in S^{*}\in \Pi (g)$ with $(n+2)/2\ge \#S^{*}>n/2$.

(v) Any network g such that $g\varsubsetneq g^{S^{*}}$, $\#C(g)=1$ and $d_{i}(g)=d_{j}(g)$ for all $i,j\in S^{*}\in \Pi (g)$ are not strongly stable nor coalition-proof stable since two players i and j such that $i,j\in S^{*}$ and $ij\notin g$ have incentives to add this link to form $g+ij$ and to obtain $B\left( 1-\frac{\#S^{*}-1-(d_{i}(g)+1) }{\#S^{*}}\phi \right) /2-c(d_{i}(g)+1)$ by sharing together the entire loot B instead of getting $B\left( 1-\frac{\#S^{*}-1-d_{i}(g)}{ \#S^{*}}\phi \right) /\#S^{*}-cd_{i}(g)$. Moreover, this is a credible group deviation for $S=\{i,j\}$. Hence, $g\notin \mathbf {SS}$ and $g\notin \mathbf {CPS}$.

(vi) The network $g^{S^{*}}\notin \mathbf {SS}$ since the members of coalition $S^{*}$ have a group deviation to the circle network among the members of $S^{*}$ ($g^{\prime }$ such that $g^{\prime }\varsubsetneq g^{S^{*}}$, $\#C(g^{\prime })=1$ and $d_{i}(g^{\prime })=d_{j}(g^{\prime })=2$ for all $i,j\in S^{*}\in \Pi (g)$) where they get $B\left( 1-\frac{\#S^{*}-3}{\#S^{*}}\phi \right) /\#S^{*}-2c$ instead of $B/\#S^{*}-c(\#S^{*}-1)$. Since $\phi <n^{2}c/B$ it is profitable for them to deviate. However, this group deviation from $g^{S^{*}}$ to the circle network $g^{\prime }$ is not credible since there is a subcoalition $\{i,j\}\varsubsetneq S^{*}$ such that $ij\notin g^{\prime }$ who has a credible deviation by adding the link ij to $g^{\prime }$ to form $g^{\prime }+ij$ and sharing together the entire loot B. Similarly, any group deviation from $g^{S^{*}}$ to $g^{\prime \prime }$ such that $g^{\prime \prime }\varsubsetneq g^{S^{*}}$, $\#C(g^{\prime \prime })=1$ and $d_{i}(g^{\prime \prime })=d_{j}(g^{\prime \prime })=k$ for all $i,j\in S^{*}\in \Pi (g)$ with $2<k<\#S^{*}-1$ is not credible. Hence, $g^{S^{*}}\in \mathbf {CPS}$.

Thus, we have $\mathbf {SS}=\emptyset$ and $\mathbf {CPS}=\{g^{S^{*}}\mid (n+2)/2\ge \#S^{*}>n/2\}$. $\square$

4 Existence and efficiency

Similarly to SS, a CPS network may fail to exist. Take Jackson and Wolinsky (1996) coauthor model with three players. Payoffs for each possible network are given in Fig. 4. The complete network $g_{7}$ is the unique pairwise stable network⁸ but is not strongly stable since a coalition of players $\{i,j\}$ have a group deviation to the network $\{ij\}$ where they both get a payoff of 3 instead of 2.5. Moreover, this group deviation is credible since none of the deviating players has an incentive to cut the link afterwards. Consider now the group deviation by $\{i,j\}$ from $\{ik,kj\}$ to $\{ij,ik,kj\}$. This deviation is credible since nor $\{i\}$ nor $\{j\}$ has a deviation at $\{ij,ik,kj\}$. A similar reasoning holds for the group deviation by $\{i,j\}$ from $\{ik\}$ to $\{ij,ik\}$ and from $g^{\emptyset }$ to $\{ij\}$. Hence, there is no CPS network in the coauthor model with three players.

Fig. 4

The co-author model with three players

We now provide easy to verify conditions for the existence of a CPS network while a SS network might not exist.

Remark 1

The network g is a coalition-proof stable network if

(i):

no coalition $S\subseteq N$ of size one $(\#S=1)$ has a group deviation from g, and

(ii):

for any coalition $S\subseteq N$ of size two or more $(\#S\ge 2)$ that has a group deviation from g to some $g^{\prime }$ there is a subcoalition $S^{\prime }\varsubsetneq S$ of size one $(\#S^{\prime }=1)$ that has a group deviation from $g^{\prime }$.

Thus, if there is a network in which (i) no player has a unilateral profitable deviation and (ii) for any profitable group deviation, one of the deviating players has a subsequent unilateral profitable deviation, then this network is coalition-proof stable. The empty network in the market sharing model and the separate pairs in the exchange model do satisfy the conditions of the above corollary.

We next look for conditions on the utility function such that the existence of CPS and SS is guaranteed. Let

$$\begin{aligned} g(S)=\left\{ g\subseteq g^{S}\left| \frac{\sum _{i\in N(g)}u_{i}(g)}{ \#N(g)}\ge \frac{\sum _{i\in N(g^{\prime })}u_{i}(g^{\prime })}{ \#N(g^{\prime })}\text { }\forall g^{\prime }\subseteq g^{S}\text {, } g^{\prime }\ne \emptyset \right. \right\} \end{aligned}$$

be the set of networks with the highest average payoff out of those that can be formed by players in $S\subseteq N$. Suppose that u is a componentwise egalitarian utility function such that (i) players belonging to the same component get the same utility and (ii) there are no externalities across components (i.e. payoffs of players belonging to a component in a given network do not depend on the structure of other components). Given a componentwise egalitarian utility function u such that (i) $u_{i}(g)=u_{j}(g)$ for all $i,j\in S\in \Pi (g)$ and (ii) $u_{i}(g)=u_{i}(h)$ with $h\in C(g)$ and $i\in N(h)$, find a network ${\widehat{g}}$ through the following algorithm due to Banerjee (1999). Pick some $h_{1}\in g(N)$. Next, pick some $h_{2}\in g(N\setminus N(h_{1}))$. At stage k pick some $h_{k}\in g(N\setminus \cup _{l\le k-1}N(h_{l}))$. Since N is finite this process stops after a finite number K of stages. The union of the components picked in this way defines a network ${\widehat{g}}$. We denote by ${\widehat{G}}$ the set of all networks that can be found through this algorithm. We also look for conditions on the utility function such that both CPS and SS sustain efficiency. The network utility function u is top convex if some strongly efficient network maximizes the per-capita sum of utilities among players. Let $\rho (u,S)=\max _{g\subseteq g^{S}}\sum _{i\in S}u_{i}(g)/\#S$. The network utility function u is top convex if $\rho (u,N)\ge \rho (u,S)$ for all $S\subseteq N$.

Suppose that u is such that (i) players belonging to the same component get the same utility and (ii) there are no externalities across components. Proposition 4 shows that both strong stability and coalition-proof stability coincide. In addition, if u is top convex then both strong stability and coalition-proof stability single out the strongly efficient networks, independently of strict or weak group deviations. All the proofs not in the main text can be found in the appendix.

Proposition 4

Take any componentwise egalitarian utility function u such that (i) $u_{i}(g)=u_{j}(g)$ for all $i,j\in S\in \Pi (g)$ and (ii) $u_{i}(g)=u_{i}(h)$ with $h\in C(g)$ and $i\in N(h)$. We have $\mathbf {CPS}=\mathbf {SS}={\widehat{G}}$. Moreover, if u is top convex, then $\mathbf {CPS}=\mathbf {SS}=E$.

Grandjean et al. (2011) show that, when players are farsighted, the set of strongly efficient networks is the unique pairwise farsightedly stable set if and only if u is top convex. So, strong stability or coalition-proof stability selects the networks that are stable when players are farsighted if u is top convex.

5 Myerson’s linking game

An alternative way to model network formation is Myerson’s (1991) linking game $G=\left\langle N,(\Sigma _{i})_{i\in N},(U_{i})_{i\in N}\right\rangle$ where players choose simultaneously the links they wish to form and where the formation of a link requires the consent of both players.⁹ A strategy of player $i\in N$ is a vector $\sigma _{i}=(\sigma _{i1},...,\sigma _{ii-1},\sigma _{ii+1},...,\sigma _{in})$ where $\sigma _{ij}\in \{0,1\}$ for each $j\in N\setminus \{i\}$. If $\sigma _{ij}=1$, player i wishes to form a link with player j. Let $\Sigma _{i}$ be the strategy set of player i and $\Sigma$ be the set of strategy profiles. Given the strategy profile $\sigma =(\sigma _{1},...,\sigma _{n})$, the network $g(\sigma )$ is formed where $ij\in g(\sigma )$ if and only if $\sigma _{ij}=1$ and $\sigma _{ji}=1$. The payoff function of player i is given by $U_{i}(\sigma )=u_{i}(g(\sigma ))$ for all $\sigma \in \Sigma$, with $g(\sigma )=\{ij\mid \sigma _{ij}=1$ and $\sigma _{ji}=1\}$.¹⁰

Definition 5

(Aumann 1959) A strategy profile $\sigma ^{*}\in \Sigma$ is a strong Nash equilibrium of Myerson’s linking game $\left\langle N,(\Sigma _{i})_{i\in N},(U_{i})_{i\in N}\right\rangle$ if there is no $S\subseteq N$ and $\sigma \in \Sigma$ such that (i) $\sigma _{i}=\sigma _{i}^{*}$ for all $i\notin S$ and (ii) $U_{i}(\sigma )>U_{i}(\sigma ^{*})$ for all $i\in S$.

Let $\mathbf {SNE}\equiv \{g(\sigma )\in {\mathcal {G}}\mid \sigma$ is a strong Nash equilibrium of Myerson’s linking game $\left\langle N,(\Sigma _{i})_{i\in N},(U_{i})_{i\in N}\right\rangle \}$ be the networks induced by a strong Nash equilibrium of Myerson’s linking game. It corresponds to Dutta and Mutuswami (1997) set of strongly stable networks.

Proposition 5

$\mathbf {SS}=\mathbf {SNE}$

For Myerson’s linking game $G=\left\langle N,(\Sigma _{i})_{i\in N},(U_{i})_{i\in N}\right\rangle$ and any fixed strategy profile $\sigma$, let $G_{\sigma }^{S}=\left\langle S,(\Sigma _{i})_{i\in S},({\widetilde{U}} _{i})_{i\in S}\right\rangle$ be the reduced Myerson’s linking game for coalition S given $\sigma$ where ${\widetilde{U}}_{i}(\sigma ^{\prime })=U_{i}(\sigma _{S}^{\prime },\sigma _{N\setminus S})$. The reduced game is obtained by fixing the strategies of all the players outside S and defining the utility of every player given this fixed strategy choices.

Definition 6

(Bernheim et al. 1987) A coalition-proof Nash equilibrium (CPNE) of Myerson’s linking game $G=\left\langle N,(\Sigma _{i})_{i\in N},(U_{i})_{i\in N}\right\rangle$ is defined recursively. For $n=1$, $\sigma _{i}^{*}$ is a coalition-proof Nash equilibrium (CPNE) if and only if $U_{i}(\sigma _{i}^{*})\ge U_{i}(\sigma _{i})$ for any $\sigma _{i}\in \Sigma _{i}$. Let $n>1$ and assume that CPNE have been defined for all $m<n$. Then,

• (i) $\sigma ^{*}$ is self-enforcing for G if and only if, for all $S\varsubsetneq N$, $\sigma _{S}^{*}$ is a CPNE of $G_{\sigma ^{*}}^{S}$.

• (ii) $\sigma ^{*}$ is a CPNE if and only if it is self-enforcing and there does not exist another self-enforcing strategy $\sigma$ such that $U_{i}(\sigma )>U_{i}(\sigma ^{*})$ for all $i\in N$.

Let $\mathbf {CPNE}\equiv \{g(\sigma )\in {\mathcal {G}}\mid \sigma$ is a coalition-proof Nash equilibrium of Myerson’s linking game $\left\langle N,(\Sigma _{i})_{i\in N},(U_{i})_{i\in N}\right\rangle \}$ be the networks induced by a coalition-proof Nash equilibrium of Myerson’s linking game. It corresponds to Dutta and Mutuswami (1997) set of weakly stable networks.

Next example shows that there is no relationship between $\mathbf {CPNE}$ and $\mathbf {CPS}$. In Fig. 5 we depict some networks and their payoffs for an example with four players. For all other network configurations, the four players get a payoff of $-10$. Solving this example we get that $g_{1}\in \mathbf {CPNE}$ and $g_{0}\notin \mathbf {CPNE}$ while $g_{1}\notin \mathbf {CPS}$ and $g_{0}\in \mathbf {CPS}$. Intuitively, the group deviation by $\{1,3\}$ from $\sigma ^{*}$ where $\sigma _{12}^{*}=0,\sigma _{13}^{*}=1,\sigma _{14}^{*}=1$, $\sigma _{2k}^{*}=0,k=1,3,4$, $\sigma _{31}^{*}=1,\sigma _{32}^{*}=0,\sigma _{34}^{*}=1$, $\sigma _{41}^{*}=1,\sigma _{42}^{*}=0,\sigma _{43}^{*}=1$ (with $g(\sigma ^{*})=g_{1}$) to $\sigma ^{\prime }$ where $\sigma _{12}^{\prime }=0,\sigma _{13}^{\prime }=1,\sigma _{14}^{\prime }=0$, $\sigma _{2k}^{\prime }=0,k=1,3,4$, $\sigma _{31}^{\prime }=1,\sigma _{32}^{\prime }=0,\sigma _{34}^{\prime }=0$, $\sigma _{41}^{\prime }=1,\sigma _{42}^{\prime }=0,\sigma _{43}^{\prime }=1$ (with $g(\sigma ^{\prime })=g_{2}$) is not self-enforcing. Given $\sigma ^{\prime }$, player 3 has incentives to switch from $\sigma _{31}^{\prime }=1,\sigma _{32}^{\prime }=0,\sigma _{34}^{\prime }=0$ to $\sigma _{31}^{\prime \prime }=0,\sigma _{32}^{\prime \prime }=0,\sigma _{34}^{\prime \prime }=1$ with $g(\sigma ^{\prime \prime })=g_{3}$. Hence, the group deviation from $\sigma$ where $\sigma _{12}=1,\sigma _{13}=0,\sigma _{14}=0$, $\sigma _{21}=1,\sigma _{23}=0,\sigma _{24}=1$, $\sigma _{3k}=0,k=1,2,4$, $\sigma _{41}=0,\sigma _{42}=1,\sigma _{43}=0$ (with $g(\sigma )=g_{0}$) to $\sigma ^{*}$ where $\sigma _{12}^{*}=0,\sigma _{13}^{*}=1,\sigma _{14}^{*}=1$, $\sigma _{2k}^{*}=0,k=1,3,4$, $\sigma _{31}^{*}=1,\sigma _{32}^{*}=0,\sigma _{34}^{*}=1$, $\sigma _{41}^{*}=1,\sigma _{42}^{*}=0,\sigma _{43}^{*}=1$ (with $g(\sigma ^{*})=g_{1}$) becomes self-enforcing and so $g_{0}\notin \mathbf {CPNE}$ while $g_{1}\in \mathbf {CPNE}$. But, the group deviation by $\{1,3\}$ from $g_{1}$ to $g_{2}$ is credible. At $g_{2}$ nor $\{1\}$ nor $\{3\}$ has a deviation alone. Thus, the group deviation by $\{1,3,4\}$ from $g_{0}$ to $g_{1}$ is not credible since $\{1,3\}\varsubsetneq \{1,3,4\}$ has a credible group deviation from $g_{1}$ to $g_{2}$. Hence, $g_{0}\in \mathbf {CPS}$ while $g_{1}\notin \mathbf {CPS}$.

Fig. 5

No relationship between CPS and CPNE

Nevertheless, in some interesting examples, CPS is more realistic. For instance, in the criminal networks model, coalition-proof stability predicts the emergence of a network with a minimally winning component, while there is no strongly stable network and coalition-proof Nash equilibria of Myerson’s linking game sustain many networks that are overconnected.

Proposition 6

In the criminal networks model with $B>n(n-1)c$, $\mathbf {CPNE}=\{g^{S}\mid \#S>n/2\}$.

The criminal networks model highlights a drawback of CPNE in Myerson’s linking game. If the deviation by a coalition involves the deletion of links with players outside the coalition, then a single deviating player who has just deleted a link with some player not in the deviating coalition can form again this link in a subsequent deviation without requiring the mutual consent of the other player. CPS overcomes such a drawback by requiring that this player belongs to the deviating coalition in the subsequent deviation. This drawback is the reason why coalition-proof Nash equilibria of Myerson’s linking game sustain many overconnected networks.

6 Discussion

6.1 Strict versus weak group deviations

Two different notions of a group deviation or move can be found in the game-theoretic literature. Up to now we have considered (strict) group deviations where a group of players deviate only if each of its members can be made (strictly) better off. Alternatively, we could look at weak group deviations where a group of players deviate only if at least one of its members is (strictly) better off while all other members are at least as well off. Weak group deviations make sense when very small transfers among the deviating group of players are allowed.

Definition 7

Coalition $S\subseteq N$ is said to have a weak group deviation from g to $g^{\prime }$ if

(i):

$ij\in g^{\prime }$ and $ij\notin g$ $\Rightarrow \{i,j\}\subseteq S$,

(ii):

$ij\in g$ and $ij\notin g^{\prime }$ $\Rightarrow \{i,j\}\cap S\ne \emptyset$,

(iii):

$u_{i}(g^{\prime })\ge u_{i}(g)$ for all $i\in S$ and there is $j\in S$ such that $u_{j}(g^{\prime })>u_{j}(g)$.

A coalition S is said to have a weak group deviation from the network g to the network $g^{\prime }$ if three conditions are satisfied. Condition (i) requires that any new links that are added can only be between players inside S. Condition (ii) requires that there must be at least one player belonging to S for the deletion of a link. Condition (iii) requires that some members of S are better off and other members of S are at least as well off.

Definition 8

(Jackson and van den Nouweland 2005) A network g is w-strongly stable if there exists no coalition $S\subseteq N$ which has a weak group deviation from g.

Let $\mathbf {wSS}$ be the set of w-strongly stable networks. It corresponds to Jackson and van den Nouweland (2005) set of strongly stable networks. Obviously, $\mathbf {wSS}\subseteq \mathbf {SS}$.

Definition 9

Coalition $S\subseteq N$ is said to have a credible weak group deviation from g if

(i):

$g^{\prime }$ is a weak group deviation from g by S, and

(ii):

there exists no subcoalition $T\varsubsetneq S$ which has a weak credible group deviation from $g^{\prime }$.

Definition 10

A network g is w-coalition-proof stable if there exists no coalition $S\subseteq N$ which has a weak credible group deviation from g.

Let $\mathbf {wCPS}$ be the set of w-coalition-proof stable networks. The next two examples show that there is no relationship between wCPS and CPS whereas wSS is a refinement of SS. Take $N=\{1,2\}$ with $u_{1}(g^{\emptyset })=u_{2}(g^{\emptyset })=0$, $u_{1}(\{12\})=0$ and $u_{2}(\{12\})=1$. Then, $\mathbf {wCPS}=\{\{12\}\}$ while $\mathbf {CPS}=\{g^{\emptyset },\{12\}\}$. In the example of Fig. 6, we get $\mathbf {wCPS} =\{g_{0},g_{7}\}$ while $\mathbf {CPS}=\{g_{4},g_{7}\}$. The network $g_{0}$ is coalition-proof stable under weak group deviations but not under (strict) group deviations. The only profitable deviation from $g_{0}$ is to $g_{4}$ and it involves all players. But, under weak group deviations, this deviation is not credible since at $g_{4}$ players 2 and 3 have incentives to move to $g_{7}$. Hence, $g_{0}$ is coalition-proof stable under weak group deviations. However, at $g_{4}$ player 3 would block the deviation to $g_{7}$ under (strict) group deviations. Hence, the deviation from $g_{0}$ to $g_{4}$ is credible and $g_{0}$ is not coalition-proof stable under (strict) group deviations.

Fig. 6

No relationship between wCPS and CPS

We now provide a condition on the utility function such that $\mathbf {wCPS}= \mathbf {CPS}$. Let $L_{i}(g)=\{jk\in g\mid j=i$ or $k=i\}$ be the set of player i’s links in g and $L_{i}(g^{N}\setminus g)=\{ij\in g^{N}\mid j\ne i$ and $ij\notin g\}$ be the set of player i’s links not in g. So, $ij\notin g$ is equivalent to $ij\in L_{i}(g^{N}\setminus g)$. Ilkiliç and Ikizler (2019) introduce the property of link-responsiveness. Under link-responsiveness, no player is indifferent to a change in her set of links. Formally, the network utility function u is link-responsive on g if and only if we have $u_{i}(g+l^{\prime }-l)\ne u_{i}(g)$, for all $i\in N$, and for all $l\subseteq L_{i}(g)$ and $l^{\prime }\in L_{i}(g^{N}\setminus g)$ such that $g+l^{\prime }-l\ne g$.

Proposition 7

Take any link-responsive u. We have $\mathbf {wSS}= \mathbf {SS}$ and $\mathbf {wCPS}=\mathbf {CPS}$.

6.2 Limited size group deviations

Up to now it has been assumed that groups of any size can possibly deviate. But deviations by larger groups are usually more demanding in terms of coordination than smaller group deviations.¹¹ What would happen if there is an upper limit to the size of a deviating group?

Definition 11

A network g is k-coalition-proof stable (CPS(k)) if there exists no coalition $S\subseteq N$ of size $\#S\le k$ which has a credible group deviation from g.

Let $\mathbf {CPS(k)}$ be the set of k-coalition-proof stable networks. It is the set of networks that are coalition-proof stable when there is an upper limit k ($2\le k\le n$) to the size of the groups that can deviate. If $g\notin \mathbf {CPS(k)}$ then $g\notin \mathbf {CPS(k+1)}$ since there exists a credible group deviation by some group S with $\#S\le k$ to some $g^{\prime }$. Allowing for larger groups to deviate cannot render this deviation non-credible since the credibility is only judged with respect to subsequent deviations by subgroups of S.

Proposition 8

$\mathbf {CPS(k+1)\subseteq CPS(k)}$ for $k=2,...,n-1$.

Proposition 8 implies that the set of k-coalition-proof stable networks weakly decreases with the upper limit to the size of a deviating group.

6.3 Coalition-proof farsightedly stable networks

There are situations where only pairwise deviations are feasible. Pairwise deviations involve a single link at a time: link addition is bilateral, link deletion is unilateral and network changes take place one link at a time. In such situations farsighted players may look beyond the immediate consequence of adding or deleting a link and anticipate the subsequent changes that will occur afterwards.¹² One raising question is whether or when coalition-proof stability with farsighted players but restricted to pairwise deviations is equivalent to coalition-proof stability with group deviations.

Definition 12

A farsighted improving path from a network g to a network $g^{\prime }$ for a coalition $S\subseteq N$ is a finite sequence of networks $g_{1},\ldots ,g_{K}$ with $g_{1}=g$ and $g_{K}=g^{\prime }$ such that for any $k\in \{1,\ldots ,K-1\}$ either

(i):

$g_{k+1}=g_{k}-ij$ for some ij such that $U_{i}(g_{K})>U_{i}(g_{k})$ and $i\in S$ or $U_{j}(g_{K})>U_{j}(g_{k})$ and $j\in S$; or

(ii):

$g_{k+1}=g_{k}+ij$ for some ij such that $U_{i}(g_{K})>U_{i}(g_{k})$, $U_{j}(g_{K})>U_{j}(g_{k})$ and $i,j\in S$.

If there exists a farsighted improving path from a network g to a network $g^{\prime }$ for a given coalition $S\subseteq N$, then we write $g\rightarrow _{S}g^{\prime }$. The set of all networks that can be reached from a network $g\in {\mathcal {G}}$ for a given coalition $S\subseteq N$ by a farsighted improving path is denoted by $\phi _{S}(g)$, $\phi _{S}(g)=\left\{ g^{\prime }\in {\mathcal {G}}\mid g\rightarrow _{S}g^{\prime }\right\}$.

Definition 13

Coalition $S\subseteq N$ is said to have a farsighted deviation from g to $g^{\prime }$ if $g^{\prime }\in \phi _{S}(g)$.

Definition 14

A network g is farsightedly stable if there exists no coalition $S\subseteq N$ which has a farsighted deviation from g.

Definition 15

Coalition $S\subseteq N$ is said to have a credible farsighted deviation from g if

(i):

$g^{\prime }$ is a farsighted deviation from g by S (i.e. $g^{\prime }\in \phi _{S}(g)$), and

(ii):

there exists no subcoalition $T\varsubsetneq S$ which has a credible farsighted deviation from $g^{\prime }$.

Definition 16

A network g is coalition-proof farsightedly stable if there exists no coalition $S\subseteq N$ which has a credible farsighted deviation from g.

Let $\mathbf {CPFS}$ be the set of coalition-proof farsightedly stable networks and let $\mathbf {FS}$ be the set of farsightedly stable networks. We now show that $\mathbf {CPFS}$ and $\mathbf {FS}$ coincide under the componentwise egalitarian utility function.

Proposition 9

Take any componentwise egalitarian utility function u such that $\mathbf {(i)}$ $u_{i}(g)=u_{j}(g)$ for all $i,j\in S\in \Pi (g)$ and $\mathbf {(ii)}$ $u_{i}(g)=u_{i}(h)$ with $h\in C(g)$ and $i\in N(h)$. We have $\mathbf {CPFS}=\mathbf {FS}={\widehat{G}}$.

Combining Proposition 4 with Proposition 9 we have that $\mathbf {CPFS}=\mathbf {CPS}$ under any componentwise egalitarian utility function.

Corollary 1

Take any componentwise egalitarian utility function u such that $\mathbf { (i)}$ $u_{i}(g)=u_{j}(g)$ for all $i,j\in S\in \Pi (g)$ and $\mathbf {(ii)}$ $u_{i}(g)=u_{i}(h)$ with $h\in C(g)$ and $i\in N(h)$. We have $\mathbf {CPFS}= \mathbf {CPS}$.

Moreover, under any componentwise egalitarian utility function, $\mathbf {CPFS }$ not only coincides with $\mathbf {CPS}$ and $\mathbf {FS}$ but it also coincides with alternative farsighted concepts like the vNM farsighted stable set or the pairwise farsightedly stable set (see Herings et al. 2009; or Mauleon and Vannetelbosch 2016; among others).

However, in general, $\mathbf {CPFS}$ can lead to different outcomes than $\mathbf {CPS}$ and other farsighted concepts. For instance, in the example of Fig. 5, $\mathbf {CPS}=$ $\{g_{0},g_{2},g_{3}\}$ while $\mathbf {CPFS}=\emptyset$ and both the vNM farsighted stable set and the pairwise farsightedly stable set single out the network $g_{2}$. None of the networks are coalition-proof farsightedly stable because (i) from $g_{0}$ there is a credible farsighted deviation by $S=\{1,2,3\}$ to $g_{2}$;¹³ (ii) from $g_{2}$ there is a credible farsighted deviation by $S=\{3,4\}$ to $g_{3}$; (iii) from $g_{3}$ there is a credible farsighted deviation by $S=\{1,2,4\}$ to $g_{0}$; and (iv) from $g_{1}$ there is a credible farsighted deviation by $S=\{1,3\}$ to $g_{2}$. In the example of Fig. 1, $\mathbf {CPFS}=$ $\{g_{1},g_{2},g_{3}\}=\mathbf {CPS}$ while the vNM farsighted stable set is $\{g_{1},g_{2},g_{3},g_{7}\}$.

7 Conclusion

We have proposed the notion of coalition-proof stability for predicting the networks that could emerge when group deviations are allowed. A network is coalition-proof stable if there exists no coalition which has a credible group deviation. A coalition is said to have a credible group deviation if there is a profitable group deviation to some network and there is no subcoalition of the deviating players which has a subsequent credible group deviation. Obviously, coalition-proof stability is a coarsening of strong stability. We have emphasized the importance of coalition-proof stability by considering three network models where a strongly stable network fails to exist while a coalition-proof stable network does exist. We have provided an easy to verify condition for the existence of a coalition-proof stable network while a strongly stable network may not exist. We have shown that there is no relationship between the set of coalition-proof stable networks and the set of networks induced by a coalition-proof Nash equilibrium of Myerson’s linking game.

The concept of coalition-proof stability could be useful in the study of the formation of a network of bilateral free trade agreements. Goyal and Joshi (2006) show that global free trade, represented by the complete network, is pairwise stable, implying that global free trade, if reached, will prevail. However, the complete network is not the unique pairwise stable network. Is global free trade strongly stable or coalition-proof stable? Can global free trade be obtained from the empty network or any preexisting free trade network through coordination among some group of countries?¹⁴

Appendix

Proof of Proposition 4

(i) Take any $g\in {\widehat{G}}$ where $g=\cup _{k=1}^{K}h_{k}$ with $h_{k}\in g(N{\setminus } \cup _{l\le k-1}N(h_{l}))$. Players belonging to $N(h_{1})$ in g will never engage in a group deviation since they can never be (strictly) better off than in g. Players belonging to $N(h_{2})$ in g will only engage in a group deviation if they can end up in some h such that $u_{i}(h)>u_{i}(h_{2})$. Suppose there exists some h such that $u_{i}(h)>u_{i}(h_{2})$. Since $h_{2}\in g(N\setminus N(h_{1}))$ it follows that $N(h)\cap N(h_{1})\ne \emptyset$. Given that players in $N(h_{1})$ will never engage in a group deviation, players belonging to $N(h_{2})$ can never end up (strictly) better off than in g. So, players belonging to $N(h_{2})$ in g will never engage in a group deviation. Players belonging to $N(h_{k})$ in g will only engage in a group deviation if they can end up in some h such that $u_{i}(h)>u_{i}(h_{k})$. Suppose there exists some h such that $u_{i}(h)>u_{i}(h_{k})$. Since $h_{k}\in g(N\setminus \cup _{l\le k-1}N(h_{l}))$ it follows that $N(h)\cap \{\cup _{l\le k-1}N(h_{l})\}\ne \emptyset$. Given that players in $\cup _{l\le k-1}N(h_{l})$ will never engage in a group deviation, players belonging to $N(h_{k})$ can never end up (strictly) better off than in g. So, players belonging to $N(h_{k})$ in g will never engage in a group deviation; and so on. Thus, $\mathbf {SS}\supseteq {\widehat{G}}$ and $\mathbf {CPS}\supseteq {\widehat{G}}$.

(ii) Take any $g^{\prime }\notin {\widehat{G}}$. We show that there always exist a credible group deviation from $g^{\prime }$.

(Step 1.) If there exists some $h_{1}\in g(N)$ such that $h_{1}\in C(g^{\prime })$ then go to Step 2. Otherwise, pick some $h_{1}\in g(N)$. In $g^{\prime }$ all players are strictly worse off than the players belonging to $N(h_{1})$. Then, we have that all members of $N(h_{1})$ have a group deviation from $g^{\prime }$ to $g^{\prime \prime }=g^{\prime }|_{N\setminus N(h_{1})}\cup h_{1}$. Indeed, players who belong to $N(h_{1})$ delete their links in $g^{\prime }$ with players not in $N(h_{1})$ and build the missing links of $h_{1}$. So, $g^{\prime }\notin \mathbf {SS}$. Since $h_{1}\in g(N)$, it is a credible group deviation. Indeed, there is no $S\varsubsetneq N(h_{1})$ that has a group deviation at $g^{\prime \prime }=g^{\prime }|_{N\setminus N(h_{1})}\cup h_{1}$. So, $g^{\prime }\notin \mathbf {CPS}$.

(Step 2.) If there exists some $h_{2}\in g(N\setminus N(h_{1}))$ such that $h_{2}\in C(g^{\prime })$ then go to Step 3. Otherwise, pick some $h_{2}\in g(N\setminus N(h_{1}))$. In $g^{\prime }$ all the remaining players who are belonging to $N\setminus N(h_{1})$ are strictly worse off than the players belonging to $N(h_{2})$. Then, we have that all members of $N(h_{2})$ have a group deviation from $g^{\prime }$ to $g^{\prime \prime }=g^{\prime }|_{N\setminus N(h_{2})}\cup h_{2}$. Indeed, players who belong to $N(h_{2})$ delete their links in $g^{\prime }$ with players not in $N(h_{2})$ and build the missing links of $h_{2}$. So, $g^{\prime }\notin \mathbf {SS}$. Since $h_{2}\in g(N\setminus N(h_{1}))$, it is a credible group deviation. Indeed, there is no $S\varsubsetneq N(h_{2})$ that has a group deviation at $g^{\prime \prime }=g^{\prime }|_{N\setminus N(h_{2})}\cup h_{2}$. So, $g^{\prime }\notin \mathbf {CPS}$.

(Step k.) If there exists some $h_{k}\in g(N\setminus \{N(h_{1})\cup ...\cup N(k-1)\})$ such that $h_{k}\in C(g^{\prime })$ then go to Step $k+1$. Otherwise, pick some $h_{k}\in g(N\setminus \{N(h_{1})\cup ...\cup N(k-1)\})$. In $g^{\prime }$ all the remaining players who are belonging to $N\setminus \{N(h_{1})\cup ...\cup N(k-1)\}$ are strictly worse off than the players belonging to $N(h_{k})$. Then, we have that all members of $N(h_{k})$ have a group deviation from $g^{\prime }$ to $g^{\prime \prime }=g^{\prime }|_{N\setminus N(h_{k})}\cup h_{k}$. Indeed, players who belong to $N(h_{k})$ delete their links in $g^{\prime }$ with players not in $N(h_{k})$ and build the missing links of $h_{k}$. So, $g^{\prime }\notin \mathbf {SS}$. Since $h_{k}\in g(N{\setminus } \{N(h_{1})\cup ...\cup N(k-1)\}$, it is a credible group deviation. Indeed, there is no $S\varsubsetneq N(h_{k})$ that has a group deviation at $g^{\prime \prime }=g^{\prime }|_{N\setminus N(h_{k})}\cup h_{k}$. So, $g^{\prime }\notin \mathbf {CPS}$.

(Step K.) Pick some $h_{K}\in g(N\setminus \{N(h_{1})\cup ...\cup N(K-1)\})$. In $g^{\prime }$ all the remaining players who are belonging to $N\setminus \{N(h_{1})\cup ...\cup N(K-1)\}$ are strictly worse off than the players belonging to $N(h_{K})$. Then, we have that all members of $N(h_{K})$ have a group deviation from $g^{\prime }$ to $g^{\prime \prime }=g^{\prime }|_{N\setminus N(h_{K})}\cup h_{K}$. Indeed, players who belong to $N(h_{K})$ delete their links in $g^{\prime }$ with players not in $N(h_{K})$ and build the missing links of $h_{K}$. So, $g^{\prime }\notin \mathbf {SS}$. Since $h_{K}\in g(N\setminus \{N(h_{1})\cup ...\cup N(K-1)\}$, it is a credible group deviation. Indeed, there is no $S\varsubsetneq N(h_{K})$ that has a group deviation at $g^{\prime \prime }=g^{\prime }|_{N\setminus N(h_{K})}\cup h_{K}$. So, $g^{\prime }\notin \mathbf {CPS}$.

Thus, $g^{\prime }\notin {\widehat{G}}\Rightarrow g^{\prime }\notin \mathbf {CPS }$ and $g^{\prime }\notin {\widehat{G}}\Rightarrow g^{\prime }\notin \mathbf {SS }$. It then follows from (i) that $\mathbf {SS}={\widehat{G}}$ and $\mathbf {CPS}={\widehat{G}}$.

Top convexity of u implies that all components of a strongly efficient network must lead to the same per-capita sum of utilities (if some component led to a lower per-capita sum of utilities than the average, then another component would have to lead to a higher per-capita sum of utilities than the average which would contradict top convexity). Top convexity also implies that under a componentwise egalitarian utility function any $g\in E$ Pareto dominates all $g^{\prime }\notin E$. Then, it is immediate that $E\subseteq \mathbf {SS}$ and $E\subseteq \mathbf {CPS}$, and $\{g^{\prime }\}\cap \mathbf {SS}=\emptyset$ and $\{g^{\prime }\}\cap \mathbf {CPS} =\emptyset$ for all $g^{\prime }\in {\mathcal {G}}\setminus E$. Hence, $\mathbf {CPS}=\mathbf {SS}=E$. $\square$

Proof of Proposition 5

($\Leftarrow$) Suppose that $\sigma$ with $g(\sigma )=g$ is a strong Nash equilibrium of Myerson’s linking game. Suppose on the contrary that g is not strongly stable. That is, there is a group deviation by $S\subseteq N$ to $g^{\prime }$ such that (i) $ij\in g^{\prime }$ and $ij\notin g$ $\Rightarrow \{i,j\}\subseteq S$, (ii) $ij\in g$ and $ij\notin g^{\prime }$ $\Rightarrow \{i,j\}\cap S\ne \emptyset$, (iii) $u_{i}(g^{\prime })>u_{i}(g)$ for all $i\in S$. We now show that there is a group deviation by S from $\sigma$ with $g(\sigma )=g$ to $\sigma ^{\prime }$ with $g(\sigma ^{\prime })=g^{\prime }$. Take (a) for all $j\notin S$, $\sigma _{j}^{\prime }=\sigma _{j}$, (b) for all $i,j\in S$, $\sigma _{ij}^{\prime }=\sigma _{ji}^{\prime }=1$ if and only if $ij\in g^{\prime }$, (c) for all $i\in S$, for all $j\notin S$, $\sigma _{ij}^{\prime }=0$ if and only if $ij\notin g^{\prime }$. Since $U_{i}(\sigma ^{\prime })=u_{i}(g(\sigma ^{\prime }))=u_{i}(g^{\prime })>U_{i}(\sigma )=u_{i}(g(\sigma ))=u_{i}(g)$ for all $i\in S$, it then contradicts that $\sigma$ is a strong Nash equilibrium of Myerson’s linking game. Thus, g is strongly stable.

($\Rightarrow$) Suppose that g is strongly stable. Take $\sigma$ such that, for all $i,j\in N$, $\sigma _{ij}=1$ if and only if $ij\in g$. Suppose that $\sigma$ is not a strong Nash equilibrium of Myerson’s linking game. That is, there is $S\subseteq N$ and $\sigma ^{\prime }$ with $g(\sigma ^{\prime })=g^{\prime }$ such that (i) $\sigma _{i}^{\prime }=\sigma _{i}$ for all $i\notin S$ and (ii) $U_{i}(\sigma ^{\prime })>U_{i}(\sigma )$ for all $i\in S$. Since $\sigma _{ij}=\sigma _{ji}=0$ and $\sigma _{ij}^{\prime }=\sigma _{ji}^{\prime }=1$ we have that $ij\in g^{\prime }$ and $ij\notin g$ implies that $\{i,j\}\subseteq S$. Since $\sigma _{ij}=\sigma _{ji}=1$ and $\sigma _{ij}^{\prime }=0$ or $\sigma _{ji}^{\prime }=0$ we have that $ij\in g$ and $ij\notin g^{\prime }$ $\Rightarrow \{i,j\}\cap S\ne \emptyset$. Since $U_{i}(\sigma ^{\prime })>U_{i}(\sigma )$ for all $i\in S$ we have that $u_{i}(g(\sigma ^{\prime }))=u_{i}(g^{\prime })>u_{i}(g(\sigma ))=u_{i}(g)$ for all $i\in S$. So, there is a group deviation by S from g to $g^{\prime }$. It then contradicts that g is strongly stable. Thus, $\sigma$ with $g(\sigma )=g$ is a strong Nash equilibrium of Myerson’s linking game. $\square$

Proof of Proposition 6

We now show that $\mathbf {CPNE}=\{g^{S}\mid \#S>n/2\}$.

(i) Take any $\sigma$ such that there is some $i\in N(g(\sigma ))$ with $U_{i}(\sigma )=u_{i}(g(\sigma ))<0$. Then, $\sigma$ is not a strong Nash equilibrium nor a coalition-proof Nash equilibrium of the Myerson’s linking game since there is $\{i\}$ and $\sigma ^{\prime }$ with $\sigma _{j}^{\prime }=\sigma _{j}$ for all $j\ne i$ and $\sigma _{i}^{\prime }=(0,0,...,0,0)$ such that $U_{i}(\sigma )=u_{i}(g(\sigma ))<U_{i}(\sigma ^{\prime })=u_{i}(g(\sigma ^{\prime }))$. The deviation from $\sigma$ to $\sigma ^{\prime }$ is self-enforcing since $\{i\}$ is a singleton.

(ii) Take any $\sigma$ such that $\#C(g(\sigma ))=1$, $d_{i}(g(\sigma ))=d_{j}(g(\sigma ))\ne \#S-1$ for all $i,j\in S\in \Pi (g)$ , $\#S>n/2$, and $\sigma _{l}=(0,0,...,0,0)$ for all $l\notin S$. Then, $\sigma$ is not a strong Nash equilibrium nor a coalition-proof Nash equilibrium of the Myerson’s linking game since there is $\{i,j\}\varsubsetneq S$ and $\sigma ^{\prime }$ with $\sigma _{k}^{\prime }=\sigma _{k}$ for all $k\ne i,j$, $\sigma _{i}^{\prime }=\sigma _{i}$ except that $\sigma _{ij}=0$ while $\sigma _{ij}^{\prime }=1$, $\sigma _{j}^{\prime }=\sigma _{j}$ except that $\sigma _{ji}=0$ while $\sigma _{ji}^{\prime }=1$ such that $U_{i}(\sigma )=u_{i}(g(\sigma ))<U_{i}(\sigma ^{\prime })=u_{i}(g(\sigma ^{\prime }))$ and $U_{j}(\sigma )=u_{j}(g(\sigma ))<U_{j}(\sigma ^{\prime })=u_{j}(g(\sigma ^{\prime }))$. This deviation from $\sigma$ to $\sigma ^{\prime }$ is self-enforcing since no player belonging to $\{i,j\}$ has an incentive to deviate from $\sigma ^{\prime }$ by cutting one of her links.

(iii) Take any $\sigma$ such that $g(\sigma )=g^{S}$, $\#S>n/2$ and $\sigma _{l}=(0,0,...,0,0)$ for all $l\notin S$. Then, $\sigma$ is not a strong Nash equilibrium of the Myerson’s linking game. In $\sigma$, we have $\sigma _{ij}=1$ and $\sigma _{ji}=1$ for all $i,j\in S$. There are profitable deviations from $\sigma$ to $\sigma ^{\prime }$ by coalition $S^{\prime }$, $S^{\prime }\cap S\ne \emptyset$, such that $g(\sigma ^{\prime })\subseteq g^{S^{\prime }}$, $\#C(g(\sigma ^{\prime }))=1$, $d_{i}(g(\sigma ^{\prime }))=d_{j}(g(\sigma ^{\prime }))<\#S-1$ for all $i,j\in S^{\prime }$, and $\#S^{\prime }>n/2$. (a) If $S^{\prime }=S$ then there is $\{i,j\}\varsubsetneq S^{\prime }$ and $\sigma ^{\prime \prime }$ with $\sigma _{k}^{\prime \prime }=\sigma _{k}^{\prime }$ for all $k\ne i,j$ , $\sigma _{i}^{\prime \prime }=\sigma _{i}^{\prime }$ except that $\sigma _{ij}^{\prime }=0$ while $\sigma _{ij}^{\prime \prime }=1$, $\sigma _{j}^{\prime \prime }=\sigma _{j}^{\prime }$ except that $\sigma _{ji}^{\prime }=0$ while $\sigma _{ji}^{\prime \prime }=1$ such that $U_{i}(\sigma ^{\prime })=u_{i}(g(\sigma ^{\prime }))<U_{i}(\sigma ^{\prime \prime })=u_{i}(g(\sigma ^{\prime \prime }))$ and $U_{j}(\sigma ^{\prime })=u_{j}(g(\sigma ^{\prime }))<U_{j}(\sigma ^{\prime \prime })=u_{j}(g(\sigma ^{\prime \prime }))$. The deviation from $\sigma ^{\prime }$ to $\sigma ^{\prime \prime }$ is self-enforcing since no player belonging to $\{i,j\}$ has an incentive to deviate from $\sigma ^{\prime \prime }$ by cutting one of her links. Hence, the first deviation by $S^{\prime }$ from $\sigma$ to $\sigma ^{\prime }$ is not self-enforcing and $\sigma$ is a coalition-proof Nash equilibrium of the Myerson’s linking game. (b) If $S^{\prime }\ne S$ then there is $i\in S^{\prime }\cap S$ and $j\in S\setminus S^{\prime }$ and $\sigma ^{\prime \prime }$ with $\sigma _{k}^{\prime \prime }=\sigma _{k}^{\prime }$ for all $k\ne i,j$, $\sigma _{i}^{\prime \prime }=\sigma _{i}^{\prime }$ except that $\sigma _{ij}^{\prime }=0$ while $\sigma _{ij}^{\prime \prime }=1$, $\sigma _{j}^{\prime \prime }=\sigma _{j}^{\prime }=\sigma _{j}$ with $\sigma _{ji}=1$ such that $U_{i}(\sigma ^{\prime })=u_{i}(g(\sigma ^{\prime }))<U_{i}(\sigma ^{\prime \prime })=u_{i}(g(\sigma ^{\prime \prime }))$. The deviation from $\sigma ^{\prime }$ to $\sigma ^{\prime \prime }$ is self-enforcing since it involves only player i and she has an incentive to deviate from $\sigma ^{\prime }$ by linking to player j. Hence, the first deviation by $S^{\prime }$ from $\sigma$ to $\sigma ^{\prime }$ is not self-enforcing and $\sigma$ is a coalition-proof Nash equilibrium of the Myerson’s linking game. So, any $\sigma$ such that $g(\sigma )=g^{S}$, $\#S>n/2$ and $\sigma _{l}=(0,0,...,0,0)$ for all $l\notin S$ is a coalition-proof Nash equilibrium of the Myerson’s linking game.

(iv) Take $\sigma$ such $g(\sigma )=g^{\emptyset }$. There is a deviation from $\sigma$ to $\sigma ^{\prime }$ such that $g(\sigma ^{\prime })=g^{N}$ by the grand coalition. Hence, $\sigma$ is not a strong Nash equilibrium of the Myerson’s linking game. Moreover, this deviation is self-enforcing since any deviation from $\sigma ^{\prime }$ by any coalition $S\varsubsetneq N$ is not self-enforcing as shown in (iii). Hence, $\sigma$ such $g(\sigma )=g^{\emptyset }$ is not a coalition-proof Nash equilibrium of the Myerson’s linking game.

So, $\sigma$ is a coalition-proof Nash equilibrium of the Myerson’s linking game if and only if $g(\sigma )=g^{S}$, $\#S>n/2$ and $\sigma _{l}=(0,0,...,0,0)$ for all $l\notin S$. $\square$

Proof of Proposition 7

We first show that $S\subseteq N$ has a weak group deviation from g to $g^{\prime }$ if and only if $S\subseteq N$ has a (strict) group deviation from g to $g^{\prime }$. ($\Leftarrow$) If $S\subseteq N$ has a (strict) group deviation from g to $g^{\prime }$, $S\subseteq N$ has obviously a weak group deviation from g to $g^{\prime }$ (independently of link-responsiveness). ($\Rightarrow$) Suppose that $S\subseteq N$ has a weak group deviation from g to $g^{\prime }$. We have that (i) $ij\in g^{\prime }$ and $ij\notin g$ $\Rightarrow \{i,j\}\subseteq S$, (ii) $ij\in g$ and $ij\notin g^{\prime }$ $\Rightarrow \{i,j\}\cap S\ne \emptyset$, (iii) $u_{i}(g^{\prime })\ge u_{i}(g)$ for all $i\in S$ and there is $j\in S$ such that $u_{j}(g^{\prime })>u_{j}(g)$. (i) and (ii) implies that $L_{i}(g)\ne L_{i}(g^{\prime })$ for all $i\in S$. By link-responsiveness, we have $u_{i}(g^{\prime })\ne u_{i}(g)$ for all $i\in S$. Thus, $u_{i}(g^{\prime })>u_{i}(g)$ for all $i\in S$ and $S\subseteq N$ has a (strict) group deviation from g to $g^{\prime }$. Hence, $\mathbf {wSS}= \mathbf {SS}$. From Definition 3 and Definition 9 it follows that $S\subseteq N$ has a credible weak group deviation from g to $g^{\prime }$ if and only if $S\subseteq N$ has a credible (strict) group deviation from g to $g^{\prime }$. Hence, $\mathbf { wCPS}=\mathbf {CPS}$. $\square$

Proof of Proposition 9

(i) Take any $g\in {\widehat{G}}$ where $g=\cup _{k=1}^{K}h_{k}$ with $h_{k}\in g(N\setminus \cup _{l\le k-1}N(h_{l}))$. Players belonging to $N(h_{1})$ in g who are looking forward will never engage in a move since they can never be strictly better off than in g given the componentwise egalitarian utility function u. Players belonging to $N(h_{2})$ in g who are forward looking will only engage in a move if they can end up in some h such that $u_{i}(h)>u_{i}(h_{2})$. Suppose there exists some h such that $u_{i}(h)>u_{i}(h_{2})$. Since $h_{2}\in g\left( N\setminus N(h_{1})\right)$ it follows that $N(h)\cap N(h_{1})\ne \emptyset$. Given that players in $N(h_{1})$ will never engage in a move, players belonging to $N(h_{2})$ can never end up strictly better off than in g under the componentwise egalitarian utility function u. So, players belonging to $N(h_{2})$ in g will never engage in a move. Players belonging to $N(h_{k})$ in g who are forward looking will only engage in a move if they can end up in some h such that $u_{i}(h)>u_{i}(h_{k})$. Suppose there exists some h such that $u_{i}(h)>u_{i}(h_{k})$. Since $h_{k}\in g\left( N\setminus \cup _{l\le k-1}N(h_{l})\right)$ it follows that $N(h)\cap \left\{ \cup _{l\le k-1}N(h_{l})\right\} \ne \emptyset$. Given that players in $\cup _{l\le k-1}N(h_{l})$ will never engage in a move, players belonging to $N(h_{k})$ can never end up strictly better off than in g under the componentwise egalitarian utility function u. So, players belonging to $N(h_{k})$ in g will never engage in a move; and so on. Thus, $\phi _{S}(g)=\emptyset$ for all $S\subseteq N$. Hence, $\mathbf {FS}\supseteq {\widehat{G}}$ and $\mathbf { CPFS}\supseteq {\widehat{G}}$.

(ii) Take any $g^{\prime }\notin {\widehat{G}}$. We show that there always exist a credible farsighted deviation from $g^{\prime }$ to some $g\in {\widehat{G}}$.

(Step 1.) If there exists some $h_{1}\in g(N)$ such that $h_{1}\in C(g^{\prime })$ then go to Step 2 with $g_{1}=g^{\prime }$. Otherwise, two cases have to be considered. (A) There exists $h\in C(g^{\prime })$ such that $h_{1}\varsubsetneq h$ for some $h_{1}\in g(N)$. Then, take $h_{1}\in g(N)$ such that there does not exist $h_{1}^{\prime }\in g(N)$ with $h_{1}\varsubsetneq h_{1}^{\prime }\varsubsetneq h$. From $g^{\prime }$, let the players who belong to $N(h_{1})$ and who look forward to $g\in {\widehat{G}}$ delete successively their links that are not in $h_{1}$ to reach $g_{1}=g^{\prime }-\{ij\mid i\in N(h_{1})$ and $ij\notin h_{1}\}$. Along the sequence from $g^{\prime }$ to $g_{1}$ all players who are moving always prefer the end network g to the current network. (B) There does not exist $h\in C(g^{\prime })$ such that $h_{1}\varsubsetneq h$ with $h_{1}\in g(N)$. Pick $h_{1}\in g(N)$ such that there does not exist $h_{1}^{\prime }\in g(N)$ with $h_{1}^{\prime }\varsubsetneq h_{1}$. From $g^{\prime }$, let the players who belong to $N(h_{1})$ and who are looking forward to $g\in {\widehat{G}}$ such that $h_{1}\in C(g)$ first delete successively their links not in $h_{1}$ and then build successively the links in $h_{1}$ that are not in $g^{\prime }$ leading to $g_{1}=g^{\prime }-\{ij\mid i\in N(h_{1})$ and $ij\notin h_{1}\}+\{ij\mid i\in N(h_{1})$, $ij\in h_{1}$ and $ij\notin g^{\prime }\}$. Along the sequence from $g^{\prime }$ to $g_{1}$ all players who are moving always prefer the end network g to the current network. Once $g_{1}$ and $h_{1}$ are formed, we move to Step 2.

(Step 2.) If there exists some $h_{2}\in g(N\setminus N(h_{1}))$ such that $h_{2}\in C(g_{1})$ then go to Step 3 with $g_{2}=g_{1}$. Otherwise, two cases have to be considered. (A) There exists $h\in C(g^{\prime })$ such that $h_{2}\varsubsetneq h$ for some $h_{2}\in g(N\setminus N(h_{1}))$. Then, take $h_{2}\in g(N\setminus N(h_{1}))$ such that there does not exist $h_{2}^{\prime }\in g(N\setminus N(h_{1}))$ with $h_{2}\varsubsetneq h_{2}^{\prime }\varsubsetneq h$. From $g_{1}$ let the players who belong to $N(h_{2})$ and who look forward to $g\in {\widehat{G}}$ such that $h_{1}\in C(g)$ and $h_{2}\in C(g)$ delete successively all their links that are not in $h_{2}$ to reach $g_{2}=g_{1}-\{ij\mid i\in N(h_{2})$ and $ij\notin h_{2}\}$. Along the sequence from $g_{1}$ to $g_{2}$ all players who are moving always prefer the end network g to the current network. (B) There does not exist $h\in C(g^{\prime })$ such that $h_{2}\varsubsetneq h$ with $h_{2}\in g(N\setminus N(h_{1}))$. Pick $h_{2}\in g(N\setminus N(h_{1}))$ such that there does not exist $h_{2}^{\prime }\in g(N\setminus N(h_{1}))$ with $h_{2}^{\prime }\varsubsetneq h_{2}$. From $g_{1}$ let the players who belong to $N(h_{2})$ and who are looking forward to $g\in {\widehat{G}}$ such that $h_{1}\in C(g)$ and $h_{2}\in C(g)$ first delete successively their links not in $h_{2}$ and then build successively the links in $h_{2}$ that are not in $g_{1}$ leading to $g_{2}=g_{1}-\{ij\mid i\in N(h_{2})$ and $ij\notin h_{2}\}+\{ij\mid i\in N(h_{2})$, $ij\in h_{2}$ and $ij\notin g_{1}\}$. Along the sequence from $g_{1}$ to $g_{2}$ all players who are moving always prefer the end network g to the current network. Once $g_{2}$ and $h_{2}$ are formed, we move to Step 3.

(Step k.) If there exists some $h_{k}\in g(N\setminus \{N(h_{1})\cup ...\cup N(k-1)\})$ such that $h_{k}\in C(g_{k-1})$ then go to Step $k+1$ with $g_{k}=g_{k-1}$. Otherwise, two cases have to be considered. (A) There exists $h\in C(g^{\prime })$ such that $h_{k}\varsubsetneq h$ for some $h_{k}\in g(N\setminus \{N(h_{1})\cup ...\cup N(k-1)\})$. Then, take $h_{k}\in g(N\setminus \{N(h_{1})\cup ...\cup N(k-1)\})$ such that there does not exist $h_{k}^{\prime }\in g(N\setminus \{N(h_{1})\cup ...\cup N(k-1)\})$ with $h_{k}\varsubsetneq h_{k}^{\prime }\varsubsetneq h$. From $g_{k-1}$ let the players who belong to $N(h_{k})$ and who look forward to $g\in {\widehat{G}}$ such that $h_{1}\in C(g)$, $h_{2}\in C(g)$, ..., $h_{k}\in C(g)$ delete successively their links not in $h_{k}$ to reach $g_{k}=g_{k-1}-\{ij\mid i\in N(h_{k})$ and $ij\notin h_{k}\}$ . Along the sequence from $g_{k-1}$ to $g_{k}$ all players who are moving always prefer the end network g to the current network. (B) There does not exist $h\in C(g^{\prime })$ such that $h_{k}\varsubsetneq h$ with $h_{k}\in g(N\setminus \{N(h_{1})\cup ...\cup N(k-1)\})$. Pick $h_{k}\in g(N\setminus \{N(h_{1})\cup ...\cup N(k-1)\})$ such that there does not exist $h_{k}^{\prime }\in g(N\setminus \{N(h_{1})\cup ...\cup N(k-1)\})$ with $h_{k}^{\prime }\varsubsetneq h_{k}$. From $g_{k-1}$ let the players who belong to $N(h_{k})$ and who are looking forward to $g\in {\widehat{G}}$ such that $h_{1}\in C(g)$, $h_{2}\in C(g)$, ..., $h_{k}\in C(g)$ first delete successively their links not in $h_{k}$ and then build successively the links in $h_{k}$ that are not in $g_{k-1}$ leading to $g_{k}=g_{k-1}-\{ij\mid i\in N(h_{k})$ and $ij\notin h_{k}\}+\{ij\mid i\in N(h_{k})$, $ij\in h_{k}$ and $ij\notin g_{k-1}\}$. Along the sequence from $g_{k-1}$ to $g_{k}$ all players who are moving always prefer the end network g to the current network. Once $g_{k}$ and $h_{k}$ are formed, we move to Step $k+1$; and so on until we reach the network $g=\bigcup _{k=1}^{K}h_{k}$ with $h_{k}\in g(N\setminus \cup _{i\le k-1}N(h_{i}))$.

Thus, we have build a farsightedly improving path from $g^{\prime }$ to g. That is, $g\in \phi _{S}(g^{\prime })$ for some $S\subseteq N$. Since $\phi _{S}(g)=\emptyset$ for all $S\subseteq N$, for all $g\in {\widehat{G}}$, there is no farsighted deviation from g. Hence, the farsighted deviation from $g^{\prime }\notin {\widehat{G}}$ to $g\in {\widehat{G}}$ is credible. Thus, $g^{\prime }\notin {\widehat{G}}\Rightarrow g^{\prime }\notin \mathbf { CPFS}$ and $g^{\prime }\notin {\widehat{G}}\Rightarrow g^{\prime }\notin \mathbf {FS}$. It then follows from (i) that $\mathbf {FS}={\widehat{G}}$ and $\mathbf {CPFS}={\widehat{G}}$ under any componentwise egalitarian utility function. $\square$