Abstract
This paper considers an exchange economy with no individual endowment where agents have classical quasi-linear preferences and the total available resources are to be distributed amongst a set of agents according to their reported preferences over the resources. We show that there is no social choice function (SCF) that is compatible with equal treatment of the equals, strategy-proofness and Pareto-efficiency. As a consequence, we explore an alternative notion of efficiency, the “Pareto-efficient in the range,” and observe that fairness and strategy-proofness are consistent with this notion of efficiency. A characterization of such SCFs for economies with two goods and two agents is established.
Similar content being viewed by others
Notes
An SCF is non-bossy, if a change in an agent’s reported preference does not lead to a change in her allocation, then allocations of other agents also do not change.
\((x_{i}^{1},y_{i}^{1})\ge (x_{i}^{2},y_{i}^{2})\) means \(x_{ij}^{1}\ge x_{ij}^{2}\) for \(j=1,\ldots ,m\) and \(y_{i}^{1}\ge y_{i}^{2}\) where one of the inequalities holds strictly. The following are defined for positive consumption bundles, i.e. bundles in which quantities of all goods are positive. Strict convexity: if \((x_{i}^{1},y_{i}^{1})\ne (x_{i}^{2},y_{i}^{2})\in UC((x_{i},y_{i}),u_{i}(\cdot ;\theta _{i}))\) then \(u_{i}(\lambda (x_{i}^{1},y_{i}^{1})+(1-\lambda )(x_{i}^{2},y_{i}^{2});\theta _{i})>u_{i}((x_{i},y_{i});\theta _{i})\), \(0<\lambda <1\). Strict monotonicity: for \((x_{i}^{1},y_{i}^{1})\ge (x_{i}^{2},y_{i}^{2})\) \(u_{i}((x_{i}^{1},y_{i}^{1});\theta _{i})>u_{i}((x_{i}^{2},y_{i}^{2});\theta _{i})\).
For instance in \(Top(\theta _{i}, A)=((x_{i},y_{i}),(x_{j},y_{j}))\) agent i’s utility is maximized at \((x_{i},y_{i})\).
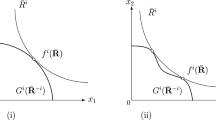
A circle in \(\mathbb {R}^{2}\) is connected but not simply connected.
If there is a subset of the interior of the region encompassed by the four curves which is a part of the complement of \(R_{F}\), then all the allocations outside the region will have to be in the range of F since the complement of \(R_{F}\) is connected because \(R_{F}\) is simply connected.
Let \(\theta _{1}<\theta _{2}\), \(x_{1}<x_{2}, y_{2}<y_{1}\). If \(\theta _{1}\sqrt{x_{2}}+y_{2}>\theta _{1}\sqrt{x_{1}}+y_{1}\), then \(\theta _{2}\sqrt{x_{2}}+y_{2}>\theta _{2}\sqrt{x_{1}}+y_{1}\). Note \(\theta _{1}\sqrt{x_{2}}+y_{2}>\theta _{1}\sqrt{x_{1}}+y_{1}\implies y_{2}-y_{1}>\theta _{1}[\sqrt{x_{1}}-\sqrt{x_{2}}]\). Then \(\theta _{2}\sqrt{x_{2}}+y_{2}-\theta _{2}\sqrt{x_{1}}-y_{1}=\theta _{2}[\sqrt{x_{2}}-\sqrt{x_{1}}]+[y_{2}-y_{1}]>\theta _{2}[\sqrt{x_{2}}-\sqrt{x_{1}}]+\theta _{1}[\sqrt{x_{1}}-\sqrt{x_{2}}]=[\theta _{2}-\theta _{1}][\sqrt{x_{2}}-\sqrt{x_{1}}]>0\).
In order to see the construction of large \(\theta _{i}\) observe that indifference curves, expressed as functions of \(y_{i}\), of the sequence of preferences \(n\sqrt{x_{i}}+y_{i}\) through \((x_{i}(v_{i},v_{j}),y_{i}(v_{i},v_{j}))\) converges uniformly to the line segment, that passes through \((x_{i}(v_{i},v_{j}),y_{i}(v_{i},v_{j}))\), with 0 slope in \([y_{i}(v_{i},v_{j}),\Omega _{y}]\). The relevant sequence of functions is given by \(f^{n}(y_{i})=\frac{1}{n^{2}}[n\sqrt{x_{i}(v_{i},v_{j})}+y_{i}(v_{i},v_{j})-y_{i}]^{2}\) and the limiting function is \(f(y_{i})=x_{i}(v_{i},v_{j})\) for all \(y_{i}\in [y_{i}(v_{i},v_{j}),\Omega _{y}]\). For uniform convergence we apply Theorem 7.13 in Rudin (1976). Fix \(0<y_{i}^{*}\), then \(f^{n}\) converges uniformly to f in \([y_{i}^{*},y_{i}(v_{i},v_{j})]\) by Theorem 7.13 in Rudin (1976). Therefore for \(\theta _{i}\) larger the indifference curve of \(\theta _{i}\) will lie above the one of \(v_{i}\) in \([y_{i}(v_{i},v_{j}),\Omega _{y}]\).
References
Barberà S, Jackson MO (1995) Strategy-proof exchange. Econometrica 63:51–87
Goswami MP (2015) Non fixed-price trading rules in single-crossing classical exchange economies. Soc Choice Welfare 44:389–422
Goswami MP, Mitra M, Sen A (2014) Strategy-proofness and Pareto-efficiency in quasi-linear exchange economies. Theo Econ 9:361–381
Hurwicz L (1972) On informationally decentralized systems, McGuire. B and Radner, R (eds), Decision and Organization, Amstredam: North-Holland, 297-336
Hurwicz L, Walker M (1990) On the generic nonmanipulability of dominant strategy allocation mechanisms: a general theorem that includes pure exchange economies. Econometrica 58:683–704
Momi T (2020) Efficient and strategy-proof allocation mechanisms in many-agent economies. Social Choice and Welfare (forthcoming)
Nicolò A (2004) Efficiency and truthfulness with Leontief preferences. A note on two-agent two-good economies. Rev Econ Design 8:373–382
Rudin W (1976) Principles of Mathematical Analysis, 3rd edn. McGraw-Hill, Inc, New York
Serizawa S, Weymark JA (2003) Efficient strategy-proof exchange and minimum consumption guarantees. J Econ Theo 109:246–263
Weymark JA (2011) A unified approach to strategy-proofness for single-peaked preferences. SERIEs 2:529–550
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
I express my gratitude to Arunava Sen, two anonymous referees, the editor-in-chief and an associate editor of the journal for their invaluable suggestions. I am extremely thankful to Kalpajyoti Hazarika, Mousumi Kalita and Ramya Lakshmanan.
Appendix
Appendix
Proof: of Proposition 6
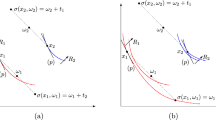
By Proposition 5\(R_{F}\) is ordered. Since \(R_{F}\) is closed, let b denote the end point on \(R_{F}\) below the ray that connects origin of the agents in \(\Delta \) and d denote the end point on \(R_{F}\) above the ray from the origin. Let [eb] part of \(R_{F}\) below the ray; and [de] denote the part of \(R_{F}\) above the ray. This scenario is graphically depicted in Figure 1.
Claim 3
Preferences restricted to \(R_{F}\) are single peaked on both sides of the ray that connects the origins of the agents.
Proofof Claim 3
Without loss of generality consider [eb]. Let \(F\left( \theta _{i}^{0},\theta _{j}^{0}\right) =b\). By strong equal treatment of the equals \(F\left( \theta _{j}^{0}, \theta _{j}^{0}\right) =e\). By strategy-proofness of i, \(\theta _{j}^{0}<\theta _{i}^{0}\).
By continuity of F each allocation in [eb] is obtained by \(F\left( \theta _{i},\theta _{j}^{0}\right) \) for some preference in \(\theta _{i}\in \left[ \theta _{j}^{0},\theta _{i}^{0}\right] \). By strategy-proofness of i, \(F_{i}(\theta _{i},\theta _{j}^{0})\in Top([eb], \theta _{i})\). We show \(F_{i}\left( \theta _{i},\theta _{j}^{0})= Top([eb], \theta _{i}\right) \).
Suppose by the way of contradiction \(p_{i}\ne q_{i}\in Top([eb],\theta _{i})\). Let for \(\theta _{i}^{00}\in \left[ \theta _{j}^{0},\theta _{i}^{0}\right] \), \(F_{i}\left( \theta _{i}^{00},\theta _{j}^{0}\right) \in [pq]\subseteq [eb]\), \(F_{i}\left( \theta _{i}^{00},\theta _{j}^{0}\right) \notin \{p_{i},q_{i}\}\). By strategy-proofness of i, \(F_{i}(\theta _{i}^{00},\theta _{j}^{0})\in Top([pq],\theta _{i}^{00})\). But then there is an indifference curve of \(\theta _{i}^{00}\) which is tangential to the indifference curve of \(\theta _{i}\) that joins p and q, which is a contradiction because \(\frac{\theta _{i}^{'}}{2\sqrt{x_{i}}}=\frac{\theta _{i}^{''}}{2\sqrt{x_{i}}}\) implies \(\theta _{i}^{'}=\theta _{i}^{''}\). Figure 1 illustrates this point.
A similar argument shows that the allocations further away from \(F_{i}(\theta _{i}, \theta _{j}^{00})\) are worse elements according to \(\theta _{i}\). To see this we note that if an allocation further away from \(F_{i}\left( \theta _{i},\theta _{j}^{0}\right) \) is preferred, say p, over an allocation which is closer to \(F_{i}\left( \theta _{i},\theta _{j}^{0}\right) \), say q; then by continuity of preferences the indifference curve through p will intersect [eb] twice, because \(F_{i}\left( \theta _{i},\theta _{j}^{0}\right) = Top([eb], \theta _{i})\). Thereafter arguments are similar to the ones that were used to show \(F_{i}\left( \theta _{i},\theta _{j}^{0}\right) = Top([eb], \theta _{i})\) to reach a contradiction that indifference curves of two different preferences are tangential.
We have shown that each allocation in [eb] is obtained as peak of some preference \(\theta _{i}\) of agent i. Now consider any preference of agent i. Since [eb] is compact any preference of agent i restricted [eb] obtains a maximum on [eb]. By similar arguments as above these restrictions to [eb] are single-peaked.
Claim 4
There is an agent i whose preferences restricted to \(R_{F}\) are single-peaked.
Proof: of Claim 4
Suppose \(\theta _{j}^{*}\) has two peaks, \(\tilde{p}\) above the ray and \(\tilde{q}\) below the ray that connects origins of the agents. Let \(F(\theta _{i}^{\#},\theta _{j}^{\#})=d\). By strategy-proofness of i \(F(\theta _{i}^{1},\theta _{j}^{\#})=d\) for all \(\theta _{i}^{1}<\theta _{i}^{\#}\). By strategy-proofness of j \(F(\theta _{i}^{1},\theta _{j}^{1})=d\) for all \(\theta _{j}^{1}>\theta _{j}^{\#}\). Choose \(\theta _{i}^{1}\) small and \(\theta _{j}^{1}\) large so that \(\theta _{i}^{1}<\theta _{j}^{*}<\theta _{j}^{1}\). By strong equal treatment of the equals \(F(\theta _{i}^{1},\theta _{i}^{1})=e\). Then \(F(\theta _{i}^{1},\theta _{j}^{*})=\tilde{p}\), by strategy-proofness of j and continuity of F.
Similarly, there is \(\theta _{i}^{2}\), such that \(\theta _{i}^{2}>\theta _{j}^{*}\) such that \(F(\theta _{i}^{2},\theta _{j}^{*})=\tilde{q}\). Now \(F(\theta _{j}^{*},\theta _{j}^{*})=e\). Consider \(F(\theta _{j}^{*},\theta _{j}^{*} )=e\) and \(F(\theta _{i}^{1},\theta _{j}^{*})=\tilde{p}\). By strategy-proofness of i, \(e_{i}=F_{i}(\theta _{j}^{*},\theta _{j}^{*} )\in Top([pe],\theta _{i}=\theta _{j}^{*})\). By Claim 3, the preference \(\theta _{j}^{*}\) restricted to [de] is single-peaked; hence \(e_{i}=Top([de],\theta _{i}=\theta _{j}^{*})\). A similar argument yields \(e_{i}=Top([eb],\theta _{i}=\theta _{j}^{*})\). Therefore, \(e_{i}=Top(R_{F},\theta _{i}=\theta _{j}^{*})\). This means \(e_{i}=Top([de],\theta _{i})\) if \(\theta _{i}>\theta _{j}^{*}\), hence \(Top(R_{F},\theta _{i})\in [eb]\) if \(\theta _{i}>\theta _{j}^{*}\).Footnote 6 Similarly, \(Top(R_{F},\theta _{i})\in [de]\) if \(\theta _{i}<\theta _{j}^{*}\). By Claim 3 agent i’s preference restricted to \(R_{F}\) are single-peaked.
Now we define an order on \(R_{F}\). Let \(p^{0}=((x_{i}^{0},y_{i}^{0}),(x_{j}^{0},y_{j}^{0})) ,q^{00}=((x_{i}^{00},y_{i}^{00}),(x_{j}^{00},y_{j}^{00}))\in R_{F}\). Let \(p^{0}\prec q^{00}\) if and only if \(x_{i}^{0}<x_{i}^{00}\). Let agent i’s preferences be single peaked on \(R_{F}\). Let \(A=\{(\theta _{i},\theta _{j})\mid Top(\theta _{i}, R_{F})\in [eb]\}\), \(B=\{(\theta _{i},\theta _{j})\mid Top(\theta _{i}, R_{F})\in [de]\}\).
Claim 5
\(F(\theta _{i},\theta _{j})\in [eb]\) if \(\theta _{i}\in A\); and \(F(\theta _{i},\theta _{j})\in [de]\) if \(\theta _{i}\in B\).
Proof: of Claim 5
Suppose \(\theta _{i}\in A\). Suppose by the way of contradiction \(q=Top(\theta _{i}, [eb])\) and \(q\ne e\), and \(F(\theta _{i},\theta _{j})=p\in [de]\) and \(p\ne e\). Since agent i’s preferences are single-peaked in \(R_{F}\) \(e_{i}P_{\theta _{i}}p_{i}\). By strong equal treatment of the equals \(F(\theta _{j},\theta _{j})=e\). Hence agent i can manipulate at \((\theta _{i},\theta _{j})\) via \(\theta _{j}\).
Consider [eb], let \(F|_{[eb]}\) denote F restricted to [eb]. Since preferences of both agents are single-peaked in [eb], and F is Pareto-efficient in the range, then due to the tops-only property of single-peaked domains for strategy-proof SCFs, Theorem 3 in Weymark (2011) for \(\gamma _{i}\in [eb]\) \(i=1,2\) entails,
\(F|_{[eb]}(\theta _{i},\theta _{j})=\)
\(\text {min}\{b,\text {max}\{Top(\theta _{i},[eb]),\gamma _{i}\}, \text {max}\{Top(\theta _{j},[eb]),\gamma _{j}\}, \text {max}\{Top(\theta _{i},[eb]),Top(\theta _{j},[eb]),e\}\}\).
Min and Max are according to \(\prec \). Choose \(\theta ^{*}\) small so that \(F|_{[eb]}(\theta ^{*},\theta ^{*})=\)
\(\text {min}\{b,\text {max}\{e,\gamma _{i}\}, \text {max}\{b,\gamma _{j}\}, \text {max}\{e,b,e\}\}=\text {min}\{b,\text {max}\{e,\gamma _{i}\}, \text {max}\{b,\gamma _{j}\}, b\}\).
By strong equal treatment of the equals, \(F(\theta ^{*},\theta ^{*})=e\). Hence \(\gamma _{i}=e\). Similarly for \(\theta ^{**}\) large we obtain \(\gamma _{j}=e\).
Then \(F|_{[eb]}(\theta _{i},\theta _{j})=\)
\(\text {min}\{Top(\theta _{i},[eb]), Top(\theta _{j},[eb]), \text {max}\{Top(\theta _{i},[eb]),Top(\theta _{j},[eb]),e\}\}\).
When \(F|_{[eb]}(\theta _{i},\theta _{j})\ne e \) then \(e\prec F|_{[eb]}(\theta _{i},\theta _{j})=\min \{Top(\theta _{i},[eb]),Top(\theta _{j},[eb])\}\). When \(F|_{[eb]}(\theta _{i},\theta _{j})= e \) then either \(e=Top(\theta _{i},[eb])\) or \(e= Top(\theta _{j},[eb])\). Hence, \(F|_{[eb]}(\theta _{i},\theta _{j})= \text {median}\{Top(\theta _{i},[eb]), Top(\theta _{j},[eb]), e\}\). Analogously, \(F|_{[de]}(\theta _{i},\theta _{j}) = \text {median}\{Top(\theta _{i},[de]), Top(\theta _{j},[de]), e\}\).
Now we show the converse of Proposition 6. From Definition 13 it is immediate that F is strategy-proof and Pareto-efficient in the range. We show that that F satisfies strong equal treatment of the equals. If \(\theta _{i}=\theta _{j}\) then e is a Pareto-efficient allocation for the profile \((\theta _{i},\theta _{j})\).
Suppose by the way of contradiction \(F(\theta ^{*}, \theta ^{*})\in [eb]\setminus \{e\}\). By definition of F either \(F_{i}(\theta ^{*}, \theta ^{*})=Top(\theta _{i},[eb])\) or \(F_{j}(\theta ^{*}, \theta ^{*})=Top(\theta _{i},[eb])\). Let \(F_{i}(\theta ^{*}, \theta ^{*})=Top(\theta _{i}=\theta ^{*},[eb])\). Note that e is a Pareto-efficient allocation at the profile \((\theta ^{*},\theta ^{*})\). Since agent i’s preferences restricted to [eb] are single-peaked all allocations between e, i.e. not including e, and \(F(\theta ^{*},\theta ^{*})\) are strictly preferred to e by i under \(\theta ^{*}\). Since e is Pareto-efficient and preferences are strictly convex e is strictly preferred to all allocations between e, i.e. not including e, and \(F(\theta ^{*},\theta ^{*})\) by j under \(\theta ^{*}\). Therefore for any \(a\in [eb]\) to be at least as good e for j under \(\theta ^{*}\) it must that there is \(c\in [eb]\) such that j is indifferent to e and c and [ec] is the in lower contour set of \(\theta ^{*}\) for j. But then this cannot happen as indifference curves of two different preference are not tangential. Hence \(e_{j}=Top(\theta _{j}=\theta ^{*},[eb])\). Then \(F(\theta ^{*},\theta ^{*})=e\) by definition of F, hence we arrive at a contradiction. A similar argument follows if \(F_{j}(\theta ^{*}, \theta ^{*})=Top(\theta _{j}=\theta ^{*},[eb])\). \(\square \)
Details of Example 2. This example gives a median rule which is anonymous. Suppose, \(\Omega _{x}=2,\Omega _{y}=2\). Here, \(e=((1,1),(1,1))\). Let \(i=1\) and \(j=2\). We first define a subset in the interior of \(\Delta \) and then define a median rule for which the subset is the range of that rule. The plot of the subset in \(\Delta \) describes a curve, and the curve is symmetric around the \(45^{0}\) ray emanating from the origins of the agents and passing through \(e=((1,1)(1,1))\). We show that agent-preferences restricted to this curve are single-peaked. The median rule then obtained is anonymous because the curve is symmetric around the \(45^{0}\) ray. Now we proceed to show the construction of this curve. For \(((x_{1},y_{1}),(x_{2},y_{2}))\) in the interior of \(\Delta \) with \(x_{1}>y_{1}\) consider the curve described by the equation \(x_{1}^{\frac{2}{3}}+y_{1}=2\). Symmetrically, consider the curve described by the equation \(x_{2}^{\frac{2}{3}}+y_{2}=2\) for the allocations with \(x_{2}>y_{2}\). This gives us the subset that we wish to support as the range of a median rule for the preferences of the agents drawn from \(\mathbb {D}\).
Note that (1, 1) satisfies \(x_{1}^{\frac{2}{3}}+y_{1}=2\). Now maximize \(\theta _{1}\sqrt{x_{1}}+y_{1}\) subject to \(x_{1}^{\frac{2}{3}}+y_{1}=2\). By replacing for \(y_{1}\), the maximization problem becomes maximize \(\theta _{1}\sqrt{x_{1}}+2-x_{1}^{\frac{2}{3}}\). The first order condition is \(\frac{\theta _{1}}{2\sqrt{x_{1}}}=\frac{2}{3}x_{1}^{-\frac{1}{3}}\). Then, \(x_{1}^{\frac{1}{6}}=\frac{3\theta _{1}}{4}\). Hence \(x_{1}=(\frac{3\theta _{1}}{4})^{6}\). The second order derivative of \(\theta _{1}\sqrt{x_{1}}+2-x_{1}^{\frac{2}{3}}\) is \(\frac{-\theta _{1}}{4}x_{1}^{-\frac{3}{2}}+\frac{2}{9}x_{1}^{-\frac{4}{3}}\). For \(x_{1}=(\frac{3\theta _{1}}{4})^{6}\) the second order condition is \(\frac{-\theta _{1}}{4}(\frac{3\theta _{1}}{4})^{-9}+\frac{2}{9}(\frac{3\theta _{1}}{4})^{-8}= (\frac{3\theta _{1}}{4})^{-8}[-\frac{1}{3}+\frac{2}{9}]<0\). The bundle (1, 1) is attained as maximum for \(\theta _{1}=\frac{4}{3}\) i.e. \(x_{1}=(\frac{3\theta _{1}}{4})^{6}=1\) for \(\theta _{1}=\frac{4}{3}\). In order to define a range consider \(x_{1}^{\frac{2}{3}}+y_{1}=2\) up to \(x_{1}^{*}<2\) such that \(y_{1}^{*}=2-(x_{1}^{*})^{\frac{2}{3}}<2\). This ensures the part of range that lies below the \(45^{0}\) line from the origin of agent 1 is in the interior of \(\Delta \). Since we want F to be anonymous, consider \(x_{2}^{\frac{2}{3}}+y_{2}=2\) to be the part of the range on the other side of the \(45^{0}\) ray from 2’s origin up to \((x_{2}^{*},y_{2}^{*})\) such that \(x_{2}^{*}=x_{1}^{*}\) and \(y_{2}^{*}=y_{1}^{*}\). From agent 1’s origin \(x_{2}^{\frac{2}{3}}+y_{2}=2\) is concave hence agent 1 will have a unique maximum on \(x_{2}^{\frac{2}{3}}+y_{2}=2\). For \(\theta _{1}=\frac{4}{3}\) the solution to Maximize \(\frac{4}{3}\sqrt{x_{1}}+y_{1}\) subject to \(x_{2}^{\frac{2}{3}}+y_{2}=2\) is (1, 1). To see this consider Maximize \(\theta _{1}\sqrt{x_{1}}+y_{1}\) subject to \((2-x_{1})^{\frac{2}{3}}+2-y_{1}=2\). The first order condition after substituting for \(y_{1}\) is \(\theta _{1}\frac{1}{2\sqrt{x_{1}}}-\frac{2}{3}(2-x_{1})^{\frac{2}{3}-1}=0\). Therefore if \(\theta _{1}=\frac{4}{3}\), then \(x_{1}=1\). Since (1, 1) is the unique maximum for agent 1 for the preference \(\frac{4}{3}\sqrt{x_{1}}+y_{1}\) subject to \(x_{1}^{\frac{2}{3}}+y_{1}=2\) and \(x_{2}^{\frac{2}{3}}+y_{2}=2\) and indifference curves of two distinct preference in \(\mathbb {D}\) are not tangential in the interior of \(\Delta \) agent 1’s preferences are single-peaked on the entire set \(x_{1}^{\frac{2}{3}}+y_{1}=2\) union \(x_{2}^{\frac{2}{3}}+y_{2}=2\). Similarly agent 2’s preferences are single-peaked on \(x_{1}^{\frac{2}{3}}+y_{1}=2\) union \(x_{2}^{\frac{2}{3}}+y_{2}=2\). Then median rule with \(e=((1,1),(1,1))\) and the union of \(x_{1}^{\frac{2}{3}}+y_{1}=2\) and \(x_{2}^{\frac{2}{3}}+y_{2}=2\) as its range is continuous, strategy-proof, anonymous, and Pareto-efficient in the range which is closed and simply-connected. \(\square \)
Proof: of Proposition 7
The fact that \(R_{F}\) is a median rule follows from Proposition 6. We show that that \(R_{F}\) is a line segment.
First we show that the range of \(F:\mathbb {D}^{ql}\times \mathbb {D}^{ql}\rightarrow \Delta \) is the same as the range of F restricted to \(\mathbb {D}\times \mathbb {D}\). That is \(\{((x_{1},y_{1}),(x_{2},y_{2}))\in \Delta \mid F(u_{1},u_{2});~\text {for some}~ (u_{1},u_{2})\in \mathbb {D}\times \mathbb {D}\}=R_{F}\). This is proved in Lemma 4. Then in Lemma 5 we show that the range of \(F:\mathbb {D}^{ql}\times \mathbb {D}^{ql}\rightarrow \Delta \) is a line segment. \(\square \)
Lemma 4
Range of F is ordered and same as the range of F restricted to \(\mathbb {D}\times \mathbb {D}\).
Proof
We prove the lemma in various steps.
Step 1: We show that the range of F restricted to \(\mathbb {D}\times \mathbb {D}\) is an ordered set.
Suppose by the way of contradiction the range of F restricted to \(\mathbb {D}\times \mathbb {D}\) is not ordered. In that case we obtain four curves as described in Proposition 5. Since \(R_{F}\) is simply connected and \(((0,0),(\Omega _{x},\Omega _{y})\) is not in the range as \(R_{F}\) is a subset of the interior of \(\Delta \), all the allocations encompassed by the four curves are in the range of F. Let \((v_{i},v_{j})\in \mathbb {D}^{ql}\times \mathbb {D}^{ql}\) be such that \(F(v_{i},v_{j})=(x_{i}(v_{i},v_{j}),y_{i}(v_{i},v_{j}))\) is in the interior of the region encompassed by the four curves. We obtain these curves in a manner analogous to the ones obtained in the proof of Proposition 5 because \(\mathbb {D}\) is connected as a subspace of \(\mathbb {D}^{ql}\) and F is continuous. Let \((\theta _{i},\theta _{j})\in \mathbb {D}\times \mathbb {D}\) be such that \(x_{i}(v_{i},v_{j})=x_{i}(\theta _{i},\theta _{j})\) and \(y_{i}(v_{i},v_{j})>y_{i}(\theta _{i},\theta _{j})\).
Choose \(w_{i}\in \mathbb {D}^{ql}\) such that, \(w_{i}\) is a common MMT of \(u_{i}(\cdot ;\theta _{i})\) in \(\Delta \) through \(F_{i}(\theta _{i},\theta _{j})\); and of \(v_{i}\) through \(F(v_{i},v_{j})\). By strategy-proofness of i, \(F(\theta _{i},\theta _{j})=F(w_{i},\theta _{j})\) and \(F(v_{i},v_{j})=F(w_{i},v_{j})\). Then agent j can manipulate at \((w_{i},v_{j})\) via \(\theta _{j}\). In Step 1a we describe the construction of the common MMT in \(\Delta \).
Step 1a: Choose \(\theta _{i}^{'}\) large enough such that the upper contour set of \(u_{i}(\cdot ,\cdot ;\theta _{i}^{'})\) is a proper subset of the upper contour sets of both \(v_{i}\) and \(u_{i}(\cdot ,\cdot ;\theta _{i})\) for \(x_{i}<x_{i}(v_{i},v_{j})=x_{i}(\theta _{i},\theta _{j})\) in \(\Delta \). Also choose \(\theta _{i}^{''}\) small enough so that the upper contour set of \(u_{i}(\cdot ,\cdot ;\theta _{i}^{'})\) is a proper subset of the upper contour sets of both \(v_{i}\) and \(u_{i}(\cdot ,\cdot ;\theta _{i})\) for \(x_{i}>x_{i}(v_{i},v_{j})=x_{i}(\theta _{i},\theta _{j})\) in \(\Delta \). Let \(w_{i}\) be a preference such that its indifference curves are given by the ones of \(u_{i}(\cdot ;\theta _{i}^{'})\) for all \((x_{i},y_{i})\) with \(x_{i}\le x_{i}(\theta _{i},\theta _{j})=x_{i}(v_{i},v_{j})\); and that its indifference curves are given by the ones of \(u_{i}(\cdot ;\theta _{i}^{'})\) for all \((x_{i},y_{i})\) with \(x_{i}\ge x_{i}(\theta _{i},\theta _{j})=x_{i}(v_{i},v_{j})\). Since \(u_{i}(\cdot ,\cdot ;\theta _{i}^{'})\) and \(u_{i}(\cdot ,\cdot ;\theta _{i}^{''})\) are quasi-linear, \(w_{i}\) is quasi-linear i.e. \((x_{i}^{'},y_{i}^{'}) I_{w_{i}}(x_{i}^{''},y_{i}^{''})\implies (x_{i}^{'},y_{i}^{'}+t) I_{w_{i}}(x_{i}^{''},y_{i}^{''}+t)\) for \(t\in \mathbb {R}\).
Step 2: By Step 1, \(R_{F}\) restricted to \(\mathbb {D}\times \mathbb {D}\) is an ordered set. Since F restricted to \(\mathbb {D}\times \mathbb {D}\) is continuous and \(\mathbb {D}\times \mathbb {D}\) is connected the range of F restricted to \(\mathbb {D}\times \mathbb {D}\) is connected. We show that this connected ordered set is the range of \(F:\mathbb {D}^{ql}\times \mathbb {D}^{ql}\rightarrow \Delta \) as well.
Suppose by the way of contradiction consider \(F(v_{i},v_{j})\) such that there is no \((\theta _{i},\theta _{j})\) for which \(F(v_{i},v_{j})=F(\theta _{i},\theta _{j})\); and \(x_{i}(v_{i},v_{j})=x_{i}(\theta _{i},\theta _{j})\) for some \((\theta _{i},\theta _{j})\). By using MMT in \(\Delta \) and by an argument similar to the one used in Step 1 we reach a contradiction.
Now by the way of contradiction consider \(F(v_{i},v_{j})\) such that \(x_{i}(v_{i},v_{j})>x_{i}(\theta _{i},\theta _{j})\) for all \((\theta _{i},\theta _{j})\). Then choose \(\theta _{i}\) large enough so that the indifference curve of \(u_{i}(\cdot ;\theta _{i})\) passing through \(F_{i}(v_{i},v_{j})\) lies above the indifference one of \(v_{i}\) passing through \(F_{i}(v_{i},v_{j})\) in the interval \([0,x_{i}(v_{i},v_{j}))\). By strategy-proofness of i, \(x_{i}(\theta _{i},v_{j})\ge x_{i}(v_{i},v_{j})\).Footnote 7
After this choose \(\theta _{j}\) small so that the indifference curve of \(u_{j}(\cdot ;\theta _{j})\) passing through \(F_{j}(\theta _{i},v_{j})\) lies above the one of \(v_{j}\) passing through \(F_{j}(\theta _{i},v_{j})\) in the interval \((x_{j}(\theta _{i},v_{j}),\Omega _{x})]\). By strategy-proofness of j, \(x_{j}(\theta _{i},\theta _{j})\le x_{j}(\theta _{i},v_{j})\). But then \(F(\theta _{i},\theta _{j})\) does not lie in the range of F obtained by restricting the domain of F to \(\mathbb {D}\times \mathbb {D}\) which is a contradiction.
The argument for the case \(F(v_{i},v_{j})\) such that \(x_{i}(v_{i},v_{j})<x_{i}(\theta _{i},\theta _{j})\) for all \((\theta _{i},\theta _{j})\) is similar. This completes the proof of Lemma 4. \(\square \)
In the next lemma we show that the range of F is a line segment, which completes the proof of Proposition 7.
Lemma 5
\(R_{F}\) is a straight line segment through e.
Proof
Since the proof only requires one agent, say i, in order to make the exposition less cumbersome consumption bundles of agent i are denoted by \((x_{1},y_{1}), (x_{2},y_{2})\) etc. instead of \((x_{i1},y_{i1}), (x_{i2},y_{i2})\).
Let \(e_{i}=(x_{1},y_{1})\) and \(b_{i}=(x_{2},y_{2})\). Suppose by the way of contradiction e, p, b are not collinear and let \(p_{i}=(x_{3},y_{3})\) lies below the line that joins e and b from agent i’s origin. Observe that for any fix \(\alpha \) with \(0<\alpha <1\), \(\theta _{i} x_{i}^{\alpha }+y_{i}\), \(\theta >0\) is a set of classical quasi-linear preferences.
We show that there is a preference \(\theta _{i} x_{i}^{\alpha }+y_{i}\), \(0<\alpha <1\) and \(\theta _{i}>0\) such that an indifference curve of this preference passes through \(e_{i}\) and \(b_{i}\) and they are preferred to \(p_{i}\) by agent i. We first illustrate how the proof follows after we show the existence of such a preference.
Let the parameters of this preference be denoted by \((\theta _{i}^{*},\alpha ^{*})\). For \(\alpha ^{*}\) let \(\mathbb {D}^{\alpha ^{*}}=\{\theta _{i} x_{i}^{\alpha ^{*}}+y_{i};\theta _{i}>0\}\). We note that \(\mathbb {D}^{\alpha ^{*}}\) is a set of quasi-linear preferences where indifference curves of two distinct preference from \(\mathbb {D}^{\alpha ^{*}}\) cannot be tangential in the interior of \(\Delta \).
Now let \(F(u_{i},u_{j})=b\). Then by arguments that are similar to the ones in Step 2 of Lemma 4 we obtain \(\theta _{j} x^{\alpha ^{*}}+y_{j}\) and \(\theta _{i} x^{\alpha ^{*}}+y_{i}\) such that \(F(\theta _{i},\theta _{j} )=F(u_{i},u_{j})\), where \(\theta _{i}\) is large and \(\theta _{j}\) is small. By anonymity \(F(\theta _{j},\theta _{j})=e\). By continuity of F every allocation in [eb] is an image of a profile in \(\mathbb {D}^{\alpha *}\times \mathbb {D}^{\alpha *}\). Now we can repeat the arguments in Claim 3 to show that the preferences from \(\mathbb {D}^{\alpha ^{*}}\) restricted to [eb] are single-peaked. This is a contradiction because p is a peak for some preference in \(\mathbb {D}^{\alpha ^{*}}\) for agent i and hence indifference curves of two distinct preference in \(\mathbb {D}^{\alpha ^{*}}\) are tangential in the interior of \(\Delta \) as e and b are on the same indifference curve of the preference \(\theta _{i}^{*}x_{i}^{\alpha ^{*}}+y_{i}\).
We have \(x_{2}-x_{1}>0\) and \(y_{1}-y_{2}>0\). For any given \(\alpha \), the preference \(\frac{y_{1}-y_{2}}{x_{2}^{\alpha }-x_{1}^{\alpha }}x^{\alpha }+y\) has an indifference curve that passes through \(e_{i}=(x_{1},y_{1})\) and \(b_{i}=(x_{2},y_{2})\). That is, \(\frac{y_{1}-y_{2}}{x_{2}^{\alpha }-x_{1}^{\alpha }}x_{1}^{\alpha }+y_{1}=\frac{y_{1}-y_{2}}{x_{2}^{\alpha }-x_{1}^{\alpha }}x_{2}^{\alpha }+y_{2}\). We show that there is \(\alpha ^{*}\) such that \(e_{i}\) and \(b_{i}\) are preferred to \(p_{i}\) by \(\frac{y_{1}-y_{2}}{x_{2}^{\alpha ^{*}}-x_{1}^{\alpha ^{*}}}x^{\alpha ^{*}}+y\); where \(\theta ^{*}=\frac{y_{1}-y_{2}}{x_{2}^{\alpha ^{*}}-x_{1}^{\alpha ^{*}}}\). Now we show the existence of \(\alpha ^{*}\).
Consider the following sequence of such functions for \(\alpha ^{n}=1-\frac{1}{n},n\ge 2\):
The sequence \(\{f^{n}\}_{n=2}^{\infty }\) converges point wise to \(f(x)=\Big [\frac{y_{1}-y_{2}}{x_{2}-x_{1}} x_{2} +y_{2} \Big ] -\frac{y_{1}-y_{2}}{ x_{2} - x_{1}} x\) for \(x\in [x_{1},x_{2}]\), where f is the equation of the straight line passing through \((x_{1},y_{1})\) and \((x_{2},y_{2})\) with slope \(-\frac{y_{1}-y_{2}}{ x_{2} - x_{1}}\) and intercept \(\Big [\frac{y_{1}-y_{2}}{x_{2}-x_{1}} x_{2} +y_{2} \Big ]\). Let \(p_{i}=(x_{3},y_{3})\). By point wise convergence to the line segment through \(e_{i}\) and \(b_{i}\), there is \(n^{*}\) such that \(f^{n^{*}}(x_{3})>y_{3}\); then set \(\alpha ^{*}=1-\frac{1}{n^{*}}\). \(\square \)
Rights and permissions
About this article
Cite this article
Goswami, M.P. Non-dictatorial public distribution rules. Rev Econ Design 26, 165–183 (2022). https://doi.org/10.1007/s10058-021-00262-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10058-021-00262-7
Keywords
- Strategy-proofness
- Pareto-efficiency
- Pareto-efficiency in the range
- Equal treatment of the equals
- Quasi-linear preferences
- Public distribution