Assignment of heterogeneous agents in trees under the permission value

Abstract

We investigate assignment of heterogeneous agents in trees where the payoff is given by the permission value. We focus on optimal hierarchies, namely those, for which the payoff of the top agent is maximized. For additive games, such hierarchies are always cogent, namely, more productive agents occupy higher positions. The result can be extended to non-additive games with appropriate restrictions on the value function. Next, we consider auctions where agents bid for positions in a vertical hierarchy of depth 2 . Under standard auctions, usually this results in a non-cogent hierarchy.

1 Introduction

The paper addresses the issue of allocation of positions in a fixed hierarchical firm where the payoffs are determined by a certain cooperative game theoretic solution concept—the permission value seminally introduced by van den Brink and Gilles (1996). Previous literature on allocation of positions in a hierarchical firm has used non-cooperative game theory. For instance, Lazear and Rosen (1981) use rank order tournaments to allocate positions in a vertical hierarchy. Using cooperative game theory to address the assignment problem is a new and novel approach. It forms part of the growing literature aimed at bringing cooperative game theory to address issues with regard to the firm (see below for the other papers in this direction). In particular, we address the issue of how positions in a hierarchical firm should be allocated to workers with varying levels of productivity. In particular, we address the question that if productivity of a worker is unambigously defined, do more productive workers occupy higher positions? The issue is important in itself because if this holds, the allocation can be regarded as “fair” or “meritocratic” in a certain sense.

Myerson’s (1977) seminal paper introduced graph restricted cooperative games. The basic idea was that not all coalitions were formable/feasible as in cooperative games. The restrictions on coalition formation are represented by an undirected graph. A component is a maximally connected subgraph of the network. The network induces a partition of a coalition to sub-coalitions based on components. The value of a coalition then is basically the sum of the values of its components in the subgraph induced by this coalition. Such games are referred to as communication graph restricted games. The Shapley value (Shapley 1953) of the restricted game is called the Myerson value.

Gilles et al. (1992) have introduced games with permission structures in which in addition to the graph, there is a dominance structure where agents are in a superior-subordinate relationship with each other. So, agents whose superiors are outside the coalition are rendered unproductive, and in the restricted game (which we call the conjunctively restricted game), the value of the coalition is reduced to that of the sovereign part of the coalition which involves only those agents whose superiors are part of the coalition. van den Brink and Gilles (1996) further define an allocation rule for such games which they call the (conjunctive) permission value, which is the Shapley value of the restricted game.

We consider a fixed hierarchy whose topology is a tree. We also restrict ourselves only to the linear technology. All levels of the hierarchy are productive and the workers are heterogeneous in the sense that they have different levels of productivity reflecting their innate abilities. Payoffs of all workers and the top agent/entrepreneur is decided by the permission value. We are primarily interested in how agents should be allocated with regard to positions in this fixed hierarchy. Each allocation yields a different payoff to the agent occupying the top position or root of the tree. This agent is the top agent/entrepreneur and decides the allocation to maximize his payoff. We find for additive games, that the allocation which maximizes the payoff of the top agent (which we call an optimal allocation) has more productive agents occupying higher positions in the tree. We call the latter a cogent allocation. The result can be extended to non-additive games albeit with severe restrictions on the value function.

The second part of our paper links the allocation of positions to auction theory. We study a vertical hierarchy of depth 3 where positions are auctioned. If the entrepreneur is not aware of the productivities of the workers, he might like to assign them using some auction procedure. We derive the result that under standard auctions, in an equilibrium, a non-cogent allocation usually results. We provide some insight behind this result. In all previous papers, there is positional rent in the sense that homogeneous workers at higher levels earn more. In our paper, this feature is preserved even among heterogeneous workers. In fact workers with low productivity have more to gain by rising through the ranks compared to high productivity workers. Consequently, while allocating positions using a standard auction mechanism, they bid more and the resulting hierarchy is non-cogent in case of vertical hierarchies of depth 2. We also provide insights with regard to why these results cannot necessarily be extended to deeper hierarchies.

Other papers that have used cooperative game theory to analyze the hierarchical firm are van den Brink and Ruys (2008) and van den Brink (2008). van den Brink and Ruys (2008) also apply the permission value to a hierarchical firm but their focus is on firm size/structure. In addition to linear technology, they also analyze other CES production technologies such as the Cobb-Douglas technology.¹ The lowest level of the hierarchy is productive and payoffs are determined by the permission value. In their model, workers are homogeneous and only regular hierarchies are analyzed which are basically trees with fixed span of control. The top agent/ entrepreneur decides the structure of the hierarchy. Intermediate levels are filled by managers who are not themselves productive but play the role of coordinating the activities with the firm. Thus, as the depth of the hierarchy increases, the exploitation of the lowest level of workers is greater reducing their wages. They first analyze the structure of the firm under linear and Cobb-Douglas production technology under fixed reservation wage and profit. In the former, the wages are reduced to the level of reservation wages under reasonable assumptions and thus the depth of the hierarchy is endogenously determined. In the latter, a flat structure with only two levels emerge. They extend this model to a general equilibrium framework where the reservation wages and are replaced by competitively determined wages and competitively determined prices are used. They show the existence of such an equilibrium. They conclude by showing the existence of a finite firm under general production functions that follow supermodularity.

van den Brink (2008) also study a similar hierarchical firm where the lowest level is productive but focus on differences of wages among the different levels of the firm. The hierarchy is given by a tree and wages are based on weighted marginal contribution of workers which is a generalization of the permission value. The weights are determined by the sizes of the coalitions, and include Shapley weights, in which case, the wage based on weighted marginal contributions coincides with the permission value. He finds that under reasonable assumptions (monotonicity and supermodularity) about the value function, the wage of a manager is always as high as the wage of her subordinates, but never exceeds the sum of wages of direct subordinates. These two facts present bounds on the wage function and he subsequently demonstrates cases in which these bounds are achieved. He also discusses specific production functions in the class of CES functions with homogeneous workers in regular hierarchies, and specifies those production functions for which these bounds are reached.

We highlight some of the differences between van den Brink and Ruys (2008) and our paper, since it is most closely related to our paper. In their paper, the workers are homogeneous so assignment of positions is not a strategic variable. Instead, the number of levels (endogenously determined by the profit maximizing firm) is the strategic variable. In our paper, the number of levels are fixed but the workers are heterogeneous and all levels (not just the lowest level) are productive. Hence, the assignment of positions is the strategic variable.

The application of cooperative game theory to analyze issues in the hierarchical firm is quite recent. There is a significant amount of literature that uses non-cooperative game theory to analyze the hierarchical firm. Perhaps the earliest paper dealing with the hierarchical firm and optimal firm size is Williamson (1967). He analyzes a model of a hierarchical firm with linear technology where with each additional level, there is some loss of control and fall in productivity by a fixed proportion. Only the lowest level is productive. With a fixed span of control (number of subordinates per superior), deeper hierarchies have more workers but also more loss of control. He shows that a profit maximizing firm will chose an optimal level of depth and hence an optimal firm size.²

Rajan and Zingales (2001) analyze a hierarchical firm in an overlapping generations framework with linear technology where each worker bargains with a unified coalition of his direct and indirect superiors. The bargaining takes place sequentially from the bottom to the top. The outside option is provided by the possibility of expropriation, as each worker can leave the firm at any point with his subordinates and compete with the top agent/entrepreneur. He can take part of the firm resources with him. They show that firm structure is determined by industry characteristics.

In our paper the focus is not so much as what firm structure would emerge (which we assume is fixed exogenously), but how positions in the fixed hierarchy are allocated. Such allocation issues have previously been studied using a non-cooperative game theoretic framework by Lazear and Rosen (1981). They use rank order tournaments to allocate positions in a vertical hierarchy of depth 2 to workers whose productivity is a function of his/her investment plus a random component. They explore the efficiency of such a compensation scheme in terms of investment as a function of spread between the prizes of the contest. They also compare it to other compensation schemes such as piece rates with regard to allocation of resources.

We note that the permission value is not the only allocation rule in the literature for games with a permission structure. van den Brink et al. (2017) describe other allocation rules. Most prominent among these is the hierarchical outcome based on Demange (2004). The hierarchical outcome is calculated using backward induction starting with the agents at the bottom of the hierarchy and then proceeding to higher levels. The coalition of each player along with his/her subordinates is called the team headed by the player in question. In our framework,³ each player earns the value of the team he heads minus the value of the teams headed by his direct successors.⁴

Other allocation rules are the top value and the Myerson value. The top value assigns the entire value of the grand coalition to the agent occupying the root of the tree and zero to all other players. While this may appear extreme, it is precisely the hierarchical outcome of the conjunctively restricted game described above. Finally, the Myerson value is the Myerson value of the communication graph restricted game when the directed links of a hierarchy are turned into undirected links.⁵

Faigle and Kern (1992) take a different approach. While the conjunctively restricted games is well defined for all possible coalitions, they consider cooperative games that are defined only with regard to feasible coalitions. Feasible coalitions are those where if a player is included in a coalition, all its superiors must be included as well. So, while the conjunctively restricted game considers any coalition but only evaluates it differently compared to a standard cooperative game, in Faigle and Kern (1992), a coalition in which all superiors of a player in the coalition are not included will not form at all. The difference of approach leads to different outcomes. The Shapley value of games considered by Faigle and Kern (1992) differs from the permission value.

It is an interesting question whether the results of this paper can be extended to the other allocation rules on games with a permission structure.

The rest of the paper proceeds as follows. Section 2 discusses the notation and terminology. Section 3 shows the equivalence of optimal and cogent allocations for additive games. Section 4 discusses auctioning of positions. Section 5 concludes. Some of the more esoteric proofs are relegated to the Appendix.

2 Games with permission structures

A transferable utility game or TU-game is a pair (N, v), such that $N=\{1, \ldots ,n\}$ is a finite set of n agents and $v:2^{N}\longrightarrow \mathbb {R}$ satisfies $v(\emptyset )=0$. Typical agents in N are referred to as i, j and t and typical coalitions in $2^{N}$ are referred to as A and B. For any coalition $A\in 2^{N}$, v(A) is the worth of A and $a=|A|$. The set of all characteristic functions v on the player set N is denoted by $\mathcal {G}^{N}$. A TU-game is additive if $v(A)=\underset{i\in A }{\sum }v(\{i\})$ for all $A\in 2^{N}\backslash \{\emptyset \}$.

An allocation rule for TU-games is a function f, which assigns to each TU-game (N, v) and to each $i\in N$ a value $f_{i}(N,v)\in \mathbb {R}$. A well-known allocation rule for TU-games is the Shapley valueSh such that

$$\begin{aligned} \forall (N,v),\forall i\in N,\quad Sh_{i}(N,v)=\sum _{A\in 2^{N}:i\in A}\frac{ (n-a)!(a-1)!}{n!}\left[ v(A)-v(A\backslash \{i\})\right] . \end{aligned}$$

The unanimity basis of $\mathcal {G}^{N}$ consists of games (called unanimity games) $\{u_{A}|A\subseteq N,A\ne \emptyset \}$ given by

$$\begin{aligned} u_{A}(B)=\left\{ \begin{array}{c} 1 \hbox { if } A\subseteq B \\ \ \ 0\hbox { otherwise}. \end{array} \right. \end{aligned}$$

Furthermore, $v\in \mathcal {G}^{N}$ can be expressed as

$$\begin{aligned} v=\underset{A\subseteq N,A\ne \emptyset }{\mathop {\displaystyle \sum }}\Delta _{v}(A)u_{A} \end{aligned}$$

(1)

where $\Delta _{v}(A)={\sum _{B\subseteq A} }(-1)^{\left| A\right| -\left| B\right| }v(B)$ is referred to as Harsanyi dividend of the coalition A. The Shapley value divides the Harsanyi dividends of the coalition equally among all its members. Hence, it can be shown that

$$\begin{aligned} Sh_{i}(N,v)=\underset{A\subseteq N,i\in A}{\mathop {\displaystyle \sum }}\frac{\Delta _{v}(A)}{ \left| A\right| }. \end{aligned}$$

(2)

A hierarchy is a pair $(M,\,S)$ consisting of a finite set of m positions $M=\{1,\,\ldots ,\,m\}$ and a permission structure determined by an asymmetric map⁶$S:M\rightarrow 2^{M}$ which assigns to each position $k\in M$ a set of successors S(k) where $k\notin S(k)$. The set $S^{-1}(k)=\{r\in M\,|\,k\in S(r)\}$ is the set of predecessors of k. The collection of all hierarchies on M is denoted by $\mathcal {S}^{M}$. Positions will be indexed by k, r and $\tau$.

The transitive closure of a permission structure S is given by the map $\widehat{S}:M\rightarrow 2^{M}$. For every $k\in M$, $r\in \widehat{S}(k)$ if there exists a sequence of positions $(h_{1},\,h_{2},\,\ldots ,\,h_{z})$ such that $h_{1}=k$, $h_{z}=r$ and $h_{x+1}\in S(h_{x})$ for all $1\le x\le z-1$. The positions $r\in \widehat{S}(k)$ are the subordinates of k. The positions in $\widehat{S}^{-1}(k)=\{r\in M\,|\,k\in \widehat{S}(r)\}$ are the superiors of k. Let $B_{S}=\{k\in M\,|\,S^{-1}(k)=\emptyset \}$ be the set of top positions and $W_{S}=\{k\in M\,|\,S(k)=\emptyset \}$ the set of front positions in the hierarchy (M, S).

We can extend these definitions to sets of positions rather than single positions. Hence, denote for all $E\subseteq M$,

$$\begin{aligned} \widehat{S}\left( E\right) =\underset{k\in E}{\mathop {\displaystyle \bigcup }}\widehat{S}\left( k\right) . \end{aligned}$$

Similarly,

$$\begin{aligned} \widehat{S}^{-1}\left( E\right) =\underset{k\in E}{\mathop {\displaystyle \bigcup }}\widehat{S} ^{-1}\left( k\right) . \end{aligned}$$

A hierarchy is a forest if $B_{S}\ne \emptyset$ and $\left| S^{-1}(k)\right| =1$ for all $k\in M{\setminus } B_{S}$. It is a tree if it is a forest and $|B_{S}|=1$.

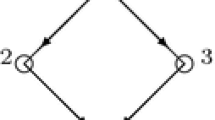
Let $(M,\,S)$ be a tree. The level of position $k\in M$, denoted by $l_{k}$, where k is a non-negative integer is the cardinality of the set of its superior positions: $l_{k}=|\widehat{S}^{-1}(k)|$. Levels in a tree will be denoted by l and $\eta$ (Fig. 1).

We will be dealing exclusively with trees. Hence, we employ some special notation for trees. For a tree, the positions at the lth level are members of a set $M_{l}$ for $l=0,1,\ldots ,\mu (M,S)$ where $\mu (M,S)={Max}_{ k\in W_{S}}\left| \widehat{S}^{-1}(k)\right|$, called the depth of the tree. $\mu (M,S)+1$ indicates the total number of levels in the tree (M, S). Note that $M_{\mu (M,S)}\subseteq W_{S}$. Positions at a certain level have the same relational distance to the top level.

To denote a certain position in a tree, we will occasionally use a double-index notation. The members of the set $M_{l}$ are given by $\{p_{l,1},\ldots ,p_{l,\left| M_{l}\right| }\}$ for $l=1,\ldots ,\mu (M,S)$ where $p_{l,1}$ indicates the position at level l to the extreme left, $p_{l,2}$ indicates the position next to $p_{l,1}$, and so forth with $p_{l,\left| M_{l}\right| }$ being the position at level l to the extreme right.

Finally, we denote by $\widehat{S}_{l}(k)$ the set of subordinate positions of k at level l,  namely, $\widehat{S}_{l}(k)=\widehat{S}(k)\cap M_{l}.$

A special kind of tree is an $(\mu ,s)$-hierarchy, if there exists $\mu ,s\in \mathbb {N}$, such that $\left| S\left( k\right) \right| =s$ for all $k\in M\backslash W_{S}$ and $\mu (M,S)=\mu$ where s is called the span of control. If $s=1$, we refer to the $(\mu ,s)$-hierarchy as a vertical hierarchy.

Fig. 1

Levels in a tree

An allocation problem is a four tuple (N, v, M, S) where (N, v) is a TU-game and (M, S) is a tree in which the objective is to assign positions in the tree (M, S) to the agents in N, taking the possibilities created by v into account. We focus on the case where $n=m$. An allocation can be thus described as a bijection $\pi :N\rightarrow M$ such that for each $i\in N$, $\pi (i)\in M$ is the position which is assigned to the agent $i\in N$. Let $\Pi$ be the (finite) set of all allocations.

An allocation $\pi$ creates a game with a permission structure⁷ given by $(N,v,S_{\pi })$ where $S_{\pi }$ is the relational structure among players induced by allocation $\pi$. The set of all possible relational structures among players in N is given by $\mathcal {S}^{N}$ and hence $S_{\pi }\in \mathcal {S}^{N}$. For all $i\in N$, $S_{\pi }(i)=\left\{ j\in N|\pi (j)\in S(\pi (i))\right\}$ and $S_{\pi }^{-1}(i)=\left\{ j\in N|\pi (j)\in S^{-1}(\pi (i))\right\}$. Likewise, $\widehat{S}_{\pi }(i)=\left\{ j\in N|\pi (j)\in \widehat{S}(\pi (i))\right\}$ and $\widehat{S}_{\pi }^{-1}(i)=\left\{ j\in N|\pi (j)\in \widehat{S}^{-1}(\pi (i))\right\}$. These relations can be generalized to sets of players rather than individual players. Hence, for $A\subseteq N$, $S_{\pi }(A)={\bigcup }_{i\in A} S_{\pi }(i)$ and $S_{\pi }^{-1}(A)={\bigcup }_{i\in A}S_{\pi }^{-1}(i)$. Similarly, $\widehat{S}_{\pi }(A)={\bigcup }_{i\in A} \widehat{S}_{\pi }(i)$ and $\widehat{S}_{\pi }^{-1}(A)={\mathop {\bigcup }_{i\in A}} \widehat{S}_{\pi }^{-1}(i)$.

Players occupying superior positions “dominate” players occupying subordinate positions in the sense that the latter need the former’s permission in order to become productive. Under the “conjunctive approach” due to to Gilles et al. (1992), members of a coalition cannot act without the permission of all their superiors.⁸

Hence, in any coalition A, if any player $i\in A$ belongs to $\widehat{S} _{\pi }(N\backslash A)$, he is rendered unproductive. Define $\sigma _{S_{\pi }}(A)=A\backslash \widehat{S}_{\pi }(N\backslash A)$ as the sovereign part of $A\subseteq N$. It consists of those players in A whose superiors (or players occupying superior positions under $\pi$) are in A. Basically, it excludes those players who are subordinates (or players occupying subordinate positions under $\pi$) of players outside A.

We can define a linear projection mapping $\mathcal {R}_{S_{\pi }}:\mathcal {G} ^{N}\rightarrow \mathcal {G}^{N}$ where

$$\begin{aligned} \mathcal {R}_{S_{\pi }}(v)(A)=v(\sigma _{S_{\pi }}(A)). \end{aligned}$$

$\mathcal {R}_{S_{\pi }}$ is called the conjunctive restriction of v on $S_{\pi }$.

An allocation rule for games with a permission structure is a function that assigns to every game with a permission structure $(N,v,S_{\pi })$ a distribution of the value v(N) of the grand coalition N over all the players in N. Here we concentrate on the allocation rule referred to as the (conjunctive) permission value$\varphi :\mathcal {G}^{N}\times \mathcal {S}^{N}\rightarrow \mathbb {R}^{N}$ that is given by

$$\begin{aligned} \varphi _{i}(v,S_{\pi })=Sh_{i}(N,\mathcal {R}_{S_{\pi }}(v)). \end{aligned}$$

The authorizing set of $A\subseteq N$ is given by $A\cup \widehat{S}_{\pi }^{-1}(A)$ and denoted by $\alpha _{S_{\pi }}(A)$. It consists of A together with all its superiors (or players occupying superior positions under $\pi$). Gilles and van den Brink (1996) show that

$$\begin{aligned} \varphi _{i}(v,S_{\pi })=\underset{A\in \Gamma _{i}}{\sum }\dfrac{\Delta _{v}(A)}{\left| \alpha _{S_{\pi }}(A)\right| } \end{aligned}$$

(3)

where $\Gamma _{i}=\left\{ A\subseteq N|A\cap \left[ \widehat{S}_{\pi }(i)\cup \{i\}\right] \ne \emptyset \right\}$. Further, if $\pi (i)\in B_{S}$, $\Gamma _{i}=2^{N}$ and hence,

$$\begin{aligned} \varphi _{i}(v,S_{\pi })=\underset{A\subseteq N}{\sum }\dfrac{\Delta _{v}(A) }{\left| \alpha _{S_{\pi }}(A)\right| }. \end{aligned}$$

(4)

3 Cogent and optimal allocations

3.1 Additive games

In this subsection, we consider only additive games with weight vector $\lambda$ denoted by $v_{\lambda }\in \mathcal {G}^{N}$ and given by

$$\begin{aligned} v_{\lambda }(E)=\underset{i\in E}{\mathop {\displaystyle \sum }}\lambda _{i}\text {, }E\subseteq N \text {.} \end{aligned}$$

In a tree $(M,\,S)$, given that each agent has only one predecessor and $\left| B_{S}\right| =1$, we shall show that (3) takes the following form:

$$\begin{aligned} \varphi _{i}(v_{\lambda },S_{\pi })=\frac{\lambda _{i}}{l_{\pi (i)}+1}+ \overset{\mu (M,S)}{\underset{\eta =l_{\pi (i)+1}}{\mathop {\displaystyle \sum }}\text { }}\underset{ \pi (j)\in \widehat{S}_{\eta }(\pi (i))}{\mathop {\displaystyle \sum }}\frac{\lambda _{j}}{\eta +1}. \end{aligned}$$

(5)

For additive games

$$\begin{aligned} \Delta _{v}(A)=\left\{ \begin{array}{c} \lambda _{i}\qquad \text { if }A=\{i\}\text {;} \\ 0\qquad \text { otherwise.} \end{array} \right. \end{aligned}$$

Hence, from (3), we get that

$$\begin{aligned} \varphi _{i}(v_{\lambda },S_{\pi })= & {} \underset{\left\{ j\right\} \in \Gamma _{i}}{\sum }\dfrac{\Delta _{v}(\left\{ j\right\} )}{\left| \alpha _{S_{\pi }}(\left\{ j\right\} )\right| } \nonumber \\= & {} \underset{\left\{ j\right\} \in \Gamma _{i}}{\sum }\dfrac{\lambda _{j}}{ \left| \alpha _{S_{\pi }}(\left\{ j\right\} )\right| }. \end{aligned}$$

(6)

Now, the set of singletons belonging to $\Gamma _{i}$ includes the player i and all her subordinates $j\in \widehat{S}_{\pi }(i)$. Any agent j occupying a position k at a level $\eta$ has $\eta$ superiors, namely,

$$\begin{aligned} \widehat{S}^{-1}(k)=\widehat{S}^{-1}(\pi (j))=\eta \text {.} \end{aligned}$$

Therefore, $\left| \alpha _{S_{\pi }}(\left\{ j\right\} )\right| =\eta +1$. Furthermore, the set of subordinates of i at level $\eta$ (where $\eta =l_{\pi (i)+1},\ldots ,\mu (M,S)$) is given by $\widehat{S} _{\eta }(\pi (i))$. Hence, we get (5) from (6).

Let us impose the restriction that $\lambda _{i}>0$ for all $i\in N\backslash \{1\}$ and $\lambda _{i}\ne \lambda _{j}$ for all $i\ne j$. The space of additive games that satisfy these restrictions is referred to as $\mathcal {G}_{\lambda }^{N*}$.

We shall restrict ourselves to allocations in which agent 1 occupies the top position. Let $\Pi _{1}\subseteq \Pi$ denote the set of all allocations that satisfy this property.

Suppose agent 1 decides the allocation. He will obviously choose the allocation that maximizes his payoff. We refer to such an allocation as the optimal allocation.

Definition 1

Given a tree (M, S) and an additive game $v_{\lambda }\in \mathcal {G} _{\lambda }^{N*}$, an optimal allocation $\pi \in \Pi _{1}$ is one that maximizes $\varphi _{1}(v_{\lambda },S_{\pi })$ among all allocations $\pi \in \Pi _{1}$.

Next, we shall define a cogent allocation. A cogent allocation is one in which more productive agents occupy higher levels.

Definition 2

Given a tree (M, S) and an additive game $v_{\lambda }\in \mathcal {G} _{\lambda }^{N*}$, an allocation $\pi \in \Pi _{1}$ is cogent if for any two agents i,  $j\in N\backslash \{1\}$, $\lambda _{i}>\lambda _{j}\Leftrightarrow l_{\pi (i)}\leqslant l_{\pi (j)}.$

It takes a moment’s reflection to realize that an allocation is optimal if and only if it is cogent. The fact that the contribution of a player on some position k is distributed amongst this player and all its superiors immediately implies that an optimal assignment should be cogent, because when a player is moved to a higher level, then his contribution is distributed amongst fewer players, giving a bigger share to the top-player (who always belongs to the set of superiors). So, more productive players should be placed higher in the hierarchy than less productive players. We formally prove this in form of the proposition below.

Proposition 1

An allocation is optimal if and only if it is cogent.

Proof

First, we will prove that an optimal allocation is cogent. Towards a contradiction, consider an allocation $\pi \in \Pi _{1}$ that is optimal but not cogent. Then, there must be at least two agents i and j such that $l_{\pi (i)}>l_{\pi (j)}$ but $\lambda _{i}>\lambda _{j}$. Consider an alternative allocation $\pi ^{\prime }\in \Pi _{1}$ that swaps these two agents in these positions such that agent i is assigned to position $\pi (j)$ and agent j is assigned to position $\pi (i)$ and for all $t\in N\backslash \{i,j)$, $\pi ^{\prime }(t)=\pi (t)$. Then, the payoff of 1 changes by

$$\begin{aligned}&\dfrac{\lambda _{i}}{l_{\pi (j)}+1}+\dfrac{\lambda _{j}}{l_{\pi (i)}+1}- \dfrac{\lambda _{i}}{l_{\pi (i)}+1}-\dfrac{\lambda _{j}}{l_{\pi (j)}+1} \nonumber \\&\quad =\left( \lambda _{i}-\lambda _{j}\right) \left[ \dfrac{1}{l_{\pi (j)}+1}- \dfrac{1}{l_{\pi (i)}+1}\right] \nonumber \\&\quad =\dfrac{\left( \lambda _{i}-\lambda _{j}\right) \left( l_{\pi (i)}-l_{\pi (j)}\right) }{\left( l_{\pi (j)}+1\right) \left( l_{\pi (i)}+1\right) }>0 \text {.} \end{aligned}$$

(7)

This contradicts that $\pi$ is optimal.

Next, we will prove that any cogent assignment is optimal. Without loss of generality, let us rank the agents based on their productivity. In other words, let us re-label the agents such that $\lambda _{2}>\lambda _{3}>\lambda _{4}>\cdots >\lambda _{\left| N\right| }$. Based on this we can identify an agent with her productivity.

First note that, using the double index notation introduced above, in all cogent allocations, the set of agents $\{t+1,t+2,\ldots ,t+\left| M_{l}\right| \}$ occupy positions at level l given by $\{p_{l,1},\ldots ,p_{l,\left| M_{l}\right| }\}$ where $t={\mathop {\displaystyle \sum }}_{\eta =0}^{l-1}\left| M_{\eta }\right|$; in any particular order. In other words, the difference between two arbitrary cogent assignments only involves a re-assignment of agents among positions at the same level rather than between levels. Since such an re-assignment does not change the payoff of the top agent, all cogent assignments result in the same amount of payoff to the top agent. Given the fact that any optimal assignment is cogent, this completes the proof.⁹$\square$

3.2 Extension to non-additive games

Let us now consider the possibility of extending the above result to non-additive games. The first question is how do we define productivity in the case of non-additive games. If we simply denote it by the amount that an agent individually can produce, namely, $v\left( \left\{ i\right\} \right)$ , then it can be shown that in the general case, the result of Proposition 1 does not hold.

Example 1

¹⁰Let player 1 be a null player and consider the three player game below.

A	$\{2\}$	$\{3\}$	$\{4\}$	$\{2,3\}$	$\{2,4\}$	$\{3,4\}$	$\{2,3,4\}$
v(A)	12	6	0	30	42	54	114
$\Delta _{v}(A)$	12	6	0	12	30	48	6

The game is totally positive (all dividends are non-negative) which implies that it is convex and hence superadditive. Let the hierarchy in question is a vertical hierarchy with depth 4. Then, the cogent allocation $\pi _{1}$ is given by $\pi _{1}(j)=p_{j-1,1}$ for $j=2,3,4$. The payoff of 1 in this hierarchy is 33. However, consider the allocation $\pi _{2}$ such that $\pi _{2}(4)=p_{2,1};$$\pi _{2}(3)=p_{1,1}$ and $\pi _{2}(2)=p_{3,1}$. The payoff of 1 increases to 34.

The result of Proposition 1 does not necessary hold if we use another measure of productivity. For instance, suppose we rank agents according to their Shapley value. Defining productivity as being measured by the Shapley value, one can show that the newly defined cogent hierarchy does not maximize the top agent’s payoff. It is easy to check that $Sh_{2}(N,v)=35$, $Sh_{3}(N,v)=38$ and $Sh_{4}(N,v)=41$. Hence, the cogent allocation $\pi _{3}$ is given by $\pi _{3}(j)=p_{5-j,1}$ for each $j\in \{2,3,4\}$. In this allocation, player 1’s payoff is 33 which is less than that in $\pi _{2}$ .

The main hindrance to the result holding successfully is that an agent’s productivity may vary depending on what coalition he is part of. For instance, in Example 1, agent 3 by himself is less productive than agent 2 but he makes a far greater marginal contribution than agent 2 when in a coalition with agent 4.

Hence, we define a class of games where the notion of higher productivity remains consistent irrespective of the coalition the agent is part of. Namely, for any coalition $B\subseteq N\backslash \{i,j\}$, $v\left( \left\{ i\right\} \right) >v\left( \left\{ j\right\} \right)$ implies $v\left( B\cup \left\{ i\right\} \right) >v\left( B\cup \left\{ j\right\} \right)$. In fact, we introduce a stronger condition that implies the above.

Definition 3

A TU cooperative game $\left( N,v\right)$ belongs to the class $\Omega$ if $v\left( \left\{ i\right\} \right) >v\left( \left\{ j\right\} \right)$ implies $\Delta _{v}\left( B\cup \left\{ i\right\} \right) \geqslant \Delta _{v}\left( B\cup \left\{ j\right\} \right)$ for all $B\subseteq N\backslash \{i,j\}$.

The condition is trivially satisfied for additive games. It directly implies our condition of consistent productivities . However it is not satisfied by convex games or even totally positive games as Example 1 illustrates.

Proposition 2

For a TU cooperative game in $\left( N,v\right)$ in $\Omega$, for any coalition $B\subseteq N\backslash \{i,j\}$, $v\left( \left\{ i\right\} \right) >v\left( \left\{ j\right\} \right)$ implies $v\left( B\cup \left\{ i\right\} \right) >v\left( B\cup \left\{ j\right\} \right)$.

Proof

$$\begin{aligned} v\left( B\cup \left\{ i\right\} \right)= & {} \underset{C\subseteq B\cup \left\{ i\right\} \backslash \emptyset }{\mathop {\displaystyle \sum }}\Delta v\left( C\right) \\= & {} \Delta _{v}\left( \left\{ i\right\} \right) +\underset{C\subseteq B,C\ne \emptyset }{\mathop {\displaystyle \sum }}\Delta _{v}\left( C\cup \left\{ i\right\} \right) +\underset{C\subseteq B,C\ne \emptyset }{\mathop {\displaystyle \sum }}\Delta _{v}\left( C\right) \\= & {} v\left( \left\{ i\right\} \right) +\underset{C\subseteq B,C\ne \emptyset }{\mathop {\displaystyle \sum }}\Delta _{v}\left( C\cup \left\{ i\right\} \right) + \underset{C\subseteq B,C\ne \emptyset }{\mathop {\displaystyle \sum }}\Delta _{v}\left( C\right) . \end{aligned}$$

Also,

$$\begin{aligned} v\left( B\cup \left\{ j\right\} \right)= & {} \underset{C\subseteq B\cup \left\{ j\right\} \backslash \emptyset }{\mathop {\displaystyle \sum }}\Delta v\left( C\right) \\= & {} \Delta _{v}\left( \left\{ j\right\} \right) +\underset{C\subseteq B,C\ne \emptyset }{\mathop {\displaystyle \sum }}\Delta _{v}\left( C\cup \left\{ j\right\} \right) +\underset{C\subseteq B,C\ne \emptyset }{\mathop {\displaystyle \sum }}\Delta _{v}\left( C\right) \\= & {} v\left( \left\{ j\right\} \right) +\underset{C\subseteq B,C\ne \emptyset }{\mathop {\displaystyle \sum }}\Delta _{v}\left( C\cup \left\{ j\right\} \right) + \underset{C\subseteq B,C\ne \emptyset }{\mathop {\displaystyle \sum }}\Delta _{v}\left( C\right) . \end{aligned}$$

Given $v\left( \left\{ i\right\} \right) >v\left( \left\{ j\right\} \right)$ , and $\Delta _{v}\left( C\cup \left\{ i\right\} \right) \geqslant \Delta _{v}\left( C\cup \left\{ j\right\} \right)$ for all $C\subseteq B$, the result follows. $\square$

We claim the following result.

Proposition 3

If the TU cooperative game belongs to the class $\Omega$ and the hierarchy is vertical, an allocation is optimal if and only if it is cogent.

The proof of this proposition is given in the appendix.

4 Bidding for positions

For any game $v_{\lambda }\in \mathcal {G}_{\lambda }^{N*}$ and any tree (M, S), while agent 1 would like a cogent allocation, suppose player 1 lets players 2 and 3 bid for getting the best position. The question is, can we devise a simple auction mechanism by which a cogent allocation results? We show here that a simple all-pay auction mechanism with regard to a vertical hierarchy of depth 3 results in a non-cogent allocation under sequential bidding but the surplus extracted by 1 is greater than the loss of payoff due to a non-cogent hierarchy. The first price mechanism admits a multiplicity of equilibria also resulting in non-cogent hierarchies. Some of the multiple equilibria in a second price auction mechanism can result in cogent hierarchies but the focal ones result in a non-cogent hierarchy.

Consider a game $v_{\lambda }\in \mathcal {G}_{\lambda }^{N*}$ where $\left| N\right| =3$, $\lambda _{2}>\lambda _{3}$, and a vertical hierarchy (M, S) with depth 3. Assume $\lambda _{1}=0$. Agent 1 is not aware of the productivities of 2 and 3. But 2 and 3 know their own as well as each other’s productivity. Agents 2 and 3 submit bids $b_{2}$ and $b_{3}$ and the person with the higher bid gets the higher position. If the bids are identical, then the tie is broken by tossing a fair coin. We shall assume that bids take place in increments of $\varepsilon$ (where $\varepsilon \in \mathbb {R}_{++}$) starting from zero. Hence, $b_{i}\in \{b\varepsilon |b\in \mathbb {N\cup \{}0\mathbb {\}}\}$ for $i=2,3$.¹¹ The set of feasible allocations $\Pi _{1}=\{\pi _{1},\pi _{2}\}$; where $\pi _{1}(2)=p_{1,1}$ and $\pi _{1}(3)=p_{2,1}$; and $\pi _{2}(3)=p_{1,1}$ and $\pi _{2}(2)=p_{2,1}$. Allocation $\pi _{1}$ is cogent while $\pi _{2}$ is not. Given that the game and the tree are fixed, the permission value is the function of the allocation only, and we can employ the abbreviated notation $\varphi _{i}(v_{\lambda },S_{\pi })=\varphi _{i}(\pi )$. Note that

$$\begin{aligned} \varphi _{1}(\pi _{1})= & {} \dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}; \\ \varphi _{2}(\pi _{1})= & {} \dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}; \\ \varphi _{3}(\pi _{1})= & {} \dfrac{\lambda _{3}}{3}; \end{aligned}$$

and

$$\begin{aligned} \varphi _{1}(\pi _{2})= & {} \dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{2}; \\ \varphi _{2}(\pi _{2})= & {} \dfrac{\lambda _{2}}{3}; \\ \varphi _{3}(\pi _{2})= & {} \dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{2}. \end{aligned}$$

Of course, the allocation that will result is a function of the bids given by $\pi (b_{2},b_{3})$. Now,

$$\begin{aligned} \pi (b_{2},b_{3})=\left\{ \begin{array}{l} \pi _{1}\text { if }b_{2}>b_{3}; \\ \pi _{2}\text { if }b_{2}<b_{3}; \end{array} \right. . \end{aligned}$$

On the other hand, if $b_{2}=b_{3}$, then, either of the two allocations can result with a probability of $\dfrac{1}{2}.$

4.1 All pay auctions

Under all pay auctions, both bids have to be paid to 1 after the allocation of positions. Therefore, the payoff of agent i can be expressed as a function of bids as follows:

$$\begin{aligned} f_{i}\left( b_{2},b_{3}\right) =\varphi _{i}(\pi (b_{2},b_{3}))-b_{i} \end{aligned}$$

if $b_{2}\ne b_{3}$. On the other hand, if $b_{2}=b_{3}$,

$$\begin{aligned} f_{i}\left( b_{2},b_{3}\right) =\dfrac{1}{2}\varphi _{i}\left( \pi _{1}\right) +\dfrac{1}{2}\varphi _{i}\left( \pi _{2}\right) -b_{i} \text {.} \end{aligned}$$

Consider the bidding game where both players bid simultaneously. We claim that this game does not admit a Nash equilibrium in pure strategies.

Proposition 4

The simultaneous bidding game does not admit a Nash equilibrium in pure strategies.

We shall prove Proposition 4. We begin by showing that matching a bid is a “never best response” strategy.

Lemma 1

Let the best response correspondence of player i be given by $R_{i}\left( b_{-i}\right)$ given that the other player bids $b_{-i}$. Then,

$$\begin{aligned} b_{-i}\notin R_{i}\left( b_{-i}\right) \text {.} \end{aligned}$$

Proof

Suppose player i bids $b_{-i}$. Then, his payoff is given by

$$\begin{aligned} \dfrac{1}{2}\varphi _{i}\left( \pi _{1}\right) +\dfrac{1}{2} \varphi _{i}\left( \pi _{2}\right) -b_{-i}. \end{aligned}$$

(8)

If on the other hand, he bids $b_{-i}+\varepsilon$, his payoff is

$$\begin{aligned} \varphi _{i}\left( \pi _{1}\right) -b_{-i}-\varepsilon \end{aligned}$$

(9)

if $i=2$ and

$$\begin{aligned} \varphi _{i}\left( \pi _{2}\right) -b_{-i}-\varepsilon \end{aligned}$$

(10)

if $i=3$.

Start with $i=2$. $\varphi _{2}\left( \pi _{1}\right) -\varphi _{2}\left( \pi _{2}\right) =\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}>0$. Now, (9) is greater than (8) if

$$\begin{aligned} \dfrac{1}{2}\left[ \varphi _{2}\left( \pi _{1}\right) -\varphi _{2}\left( \pi _{2}\right) \right] -\varepsilon> & {} 0 \\ \text {or, }\dfrac{\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}> & {} \varepsilon \text {.} \end{aligned}$$

Assuming $\varepsilon$ is sufficiently small, this will be the case. The proof for $i=3$ is similar. $\square$

The best response bids will fall into two categories. Either a player will bid zero or a player will bid $\varepsilon$ higher than his rival. The next lemma proves this.

Lemma 2

For any arbitrary $b_{-i}$, $R_{i}\left( b_{-i}\right) \subseteq \{0,b_{-i}+\varepsilon \}$.

Proof

We prove the lemma for $i=2$. The proof for $i=3$ is similar. Given that player 2 will never bid $b_{3}$ by Lemma 1, there are two possibilities. Either $b_{2}>b_{3}$ or $b_{2}<b_{3}$. Consider the first case. In this case,

$$\begin{aligned} f_{2}(b_{2},b_{3})=\varphi _{2}\left( \pi _{1}\right) -b_{2}\text {. } \end{aligned}$$

The payoff is strictly decreasing in $b_{2}$ and hence is maximized by minimizing $b_{2}$ subject to the constraint that $b_{2}>b_{3}$. This is precisely $b_{3}+\varepsilon$.

Next, consider the case $b_{2}<b_{3}$. In this case,

$$\begin{aligned} f_{2}(b_{2},b_{3})=\varphi _{2}\left( \pi _{2}\right) -b_{2}\text {. } \end{aligned}$$

Again the payoff is decreasing in $b_{2}$ and so it is maximized by choosing the minimum feasible $b_{2}$ which is zero. $\square$

Next, we focus on which of the two bidding strategies will be chosen given a certain bid by the other player. This is shown by the next lemma.

Lemma 3

There exists a certain critical threshold $B_{i}$ for player i such that:

• (i) If $b_{-i}<B_{i}$, then $R_{i}\left( b_{-i}\right) =\left\{ b_{-i}+\varepsilon \right\} ,$

• (ii) If $b_{-i}>B_{i}$, then $R_{i}\left( b_{-i}\right) =\left\{ 0\right\} ,$

• (iii) If $b_{-i}=B_{i}$, then $R_{i}\left( b_{-i}\right) =\left\{ b_{-i}+\varepsilon ,0\right\}$.

Proof

We prove the lemma for $i=2$. The proof for $i=3$ is similar. From Lemma 2, player 2 will either bid $b_{3}+\varepsilon$ or, zero. The payoffs are respectively $\varphi _{2}\left( \pi _{1}\right) -b_{3}-\varepsilon$ and $\varphi _{2}\left( \pi _{2}\right)$. Hence,

$$\begin{aligned} \varphi _{2}\left( \pi _{1}\right) -b_{3}-\varepsilon> & {} \varphi _{2}\left( \pi _{2}\right) \\\Leftrightarrow & {} b_{3}<\varphi _{2}\left( \pi _{1}\right) -\varphi _{2}\left( \pi _{2}\right) -\varepsilon . \end{aligned}$$

Similarly,

$$\begin{aligned} \varphi _{2}\left( \pi _{1}\right) -b_{3}-\varepsilon< & {} \varphi _{2}\left( \pi _{2}\right) \\\Leftrightarrow & {} b_{3}>\varphi _{2}\left( \pi _{1}\right) -\varphi _{2}\left( \pi _{2}\right) -\varepsilon . \end{aligned}$$

Finally,

$$\begin{aligned} \varphi _{2}\left( \pi _{1}\right) -b_{3}-\varepsilon= & {} \varphi _{2}\left( \pi _{2}\right) \\\Longleftrightarrow & {} b_{3}=\varphi _{2}\left( \pi _{1}\right) -\varphi _{2}\left( \pi _{2}\right) -\varepsilon . \end{aligned}$$

Hence, assuming $B_{2}=\varphi _{2}\left( \pi _{1}\right) -\varphi _{2}\left( \pi _{2}\right) -\varepsilon$, the lemma is proven. Similarly, $B_{3}=\varphi _{3}\left( \pi _{2}\right) -\varphi _{3}\left( \pi _{1}\right) -\varepsilon$. $\square$

Note that

$$\begin{aligned} B_{2}= & {} \varphi _{2}\left( \pi _{1}\right) -\varphi _{2}\left( \pi _{2}\right) -\varepsilon \nonumber \\= & {} \dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}-\varepsilon \end{aligned}$$

(11)

and

$$\begin{aligned} B_{3}= & {} \varphi _{3}\left( \pi _{2}\right) -\varphi _{3}\left( \pi _{1}\right) -\varepsilon \nonumber \\= & {} \dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}-\varepsilon . \end{aligned}$$

(12)

Finally we prove Proposition 4.

Proof of Proposition 4

Towards a contradiction, suppose a Nash equilibrium $(b_{2}^{*},b_{3}^{*})$ exists. Then,

$$\begin{aligned} b_{2}^{*}\in & {} R_{2}\left( b_{3}^{*}\right) \text { and} \\ b_{3}^{*}\in & {} R_{3}\left( b_{2}^{*}\right) . \end{aligned}$$

We consider three separate cases.

Case 1: Suppose $b_{2}^{*}=0$. Then, $b_{3}^{*}\in R_{3}\left( b_{2}^{*}\right) =R_{3}\left( 0\right) =\left\{ \varepsilon \right\}$. But $R_{2}\left( b_{3}^{*}\right) =R_{2}\left( \varepsilon \right) =\left\{ 2\cdot \varepsilon \right\}$ and $0\notin R_{2}\left( \varepsilon \right)$ which is a contradiction.

Case 2: Next, suppose $b_{3}^{*}=0$. We can arrive at a contradiction by a method similar to Case 1.

Case 3: Suppose $b_{2}^{*}\ne 0$ and $b_{3}^{*}\ne 0$. By Lemma 2, $b_{2}^{*}=b_{3}^{*}+\varepsilon$ and $b_{3}^{*}=b_{2}^{*}+\varepsilon$ simultaneously which is an impossibility. $\square$

In Fig. 2 below, we plot the best response correspondences. There is no point of intersection between them.

Next, consider sequential bidding. Either 2 or 3 could be the first mover. We claim that both have unique Nash equilibria which result in a non-cogent allocation. We show this below.

Suppose 2 bids first followed by 3. First, 2’s profit function is given by

$$\begin{aligned} \begin{array}{ll} f_{2}\left( b_{2},b_{3}\right) = &{} \left\{ \begin{array}{l} \varphi _{2}\left( \pi _{1}\right) -b_{2} \\ \dfrac{1}{2}\varphi _{2}\left( \pi _{1}\right) +\dfrac{1}{2} \varphi _{2}\left( \pi _{2}\right) -b_{2} \\ \varphi _{2}\left( \pi _{2}\right) -b_{2} \end{array} \begin{array}{l} \hbox { if }~b_{2}>b_{3}; \\ \hbox { if }~b_{2}=b_{3}; \\ \hbox { if }~b_{2}<b_{3}. \end{array} \right. \end{array} \end{aligned}$$

Fig. 2

Best response functions under simultaneous bidding

Now, given that 2 is the first mover, he anticipates 3’s moves from her reaction function, and hence we can replace $b_{3}$ by elements of $R_{3}(b_{2})$ where $R_{3}(b_{2})$ derived earlier was given by:

$$\begin{aligned} R_{3}\left( b_{2}\right) =\left\{ \begin{array}{ll} \left\{ b_{2}+\varepsilon \right\} &{}\quad \hbox {if }~b_{2}<\dfrac{\lambda _{2}}{3}+ \dfrac{\lambda _{3}}{6}-\varepsilon ; \\ \left\{ b_{2}+\varepsilon ,0\right\} &{}\quad \hbox {if }~b_{2}=\dfrac{\lambda _{2}}{3}+ \dfrac{\lambda _{3}}{6}-\varepsilon ; \\ \left\{ 0\right\} &{}\quad \hbox {if }~b_{2}>\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6 }-\varepsilon . \end{array} \right. \end{aligned}$$

Therefore, 2’s profit function is given by

$$\begin{aligned} \widehat{f}_{2}\left( b_{2}\right)= & {} f_{2}\left( b_{2},R_{3}\left( b_{2}\right) \right) \nonumber \\= & {} \left\{ \begin{array}{l} \varphi _{2}\left( \pi _{1}\right) -b_{2} \\ \upsilon \left( \varphi _{2}\left( \pi _{1}\right) -b_{2}\right) +\left( 1-\upsilon \right) \left( \varphi _{2}\left( \pi _{2}\right) -b_{2}\right) \\ \varphi _{2}\left( \pi _{2}\right) -b_{2} \end{array} \begin{array}{l} \hbox { if }~ b_{2}>\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}-\varepsilon ;\\ \hbox { if }~ b_{2}=\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}-\varepsilon ;\\ \hbox { if }~ b_{2}<\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}-\varepsilon . \end{array} \right. \nonumber \\= & {} \left\{ \begin{array}{l} \dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{2} \\ \upsilon \left( \dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}\right) +\left( 1-\upsilon \right) \left( \dfrac{\lambda _{2}}{3}\right) -b_{2} \\ \dfrac{\lambda _{2}}{3}-b_{2} \end{array} \begin{array}{l} \hbox { if }~ b_{2}>\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}-\varepsilon ;\\ \hbox { if }~ b_{2}=\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}-\varepsilon ;\\ \hbox { if }~ b_{2}<\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}-\varepsilon . \end{array} \right. \end{aligned}$$

(13)

where $\upsilon$ is some real number such that $0\leqslant \upsilon \leqslant 1$ representing an arbitrary probability. Treating the three possibilities of (13) as three cases, in each case the payoffs are decreasing in $b_{2}$. So, we can restrict attention to only those possibilities where the value of $b_{2}$ is the minimum feasible number. This gives rise to the following payoff function.

$$\begin{aligned} \widehat{f}_{2}\left( b_{2}\right)= & {} \left\{ \begin{array}{l} \dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-\dfrac{\lambda _{2}}{3}- \dfrac{\lambda _{3}}{6} \\ \upsilon \left( \dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}\right) +\left( 1-\upsilon \right) \left( \dfrac{\lambda _{2}}{3}\right) -\dfrac{ \lambda _{2}}{3}-\dfrac{\lambda _{3}}{6}+\varepsilon \\ \dfrac{\lambda _{2}}{3} \end{array} \begin{array}{l} \hbox { if }~ b_{2}=\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}; \\ \hbox { if }~ b_{2}=\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}-\varepsilon ;\\ \hbox { if }~ b_{2}=0. \end{array} \right. \nonumber \\= & {} \left\{ \begin{array}{l} \dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{6} \\ \upsilon \left( \dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{6}\right) -\left( 1-\upsilon \right) \left( \dfrac{\lambda _{3}}{6}\right) +\varepsilon \\ \dfrac{\lambda _{2}}{3} \end{array} \begin{array}{l} \hbox { if }~ b_{2}=\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}; \\ \hbox { if }~ b_{2}=\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}-\varepsilon ;\\ \hbox { if }~ b_{2}=0. \end{array} \right. \end{aligned}$$

(14)

Two facts emerge from (14). First, 2 will be averse to bidding $b_{2}=\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}-\varepsilon$ because bidding $\varepsilon$ higher will almost always yield a higher (expected) payoff.¹² Second, given $\dfrac{\lambda _{2}}{ 6}+\dfrac{\lambda _{3}}{6}<\dfrac{\lambda _{2}}{3}$, in equilibrium he will bid zero. 3 will bid $\varepsilon$ . We summarize this result in the form of a proposition below.

Proposition 5

In the bidding game where 2 is the first mover and 3 bids second, there is an unique SPNE in which 2 bids zero and 3 bids $\varepsilon$ . The allocation that results is $\pi _{2}$. The surplus extracted is $\varepsilon$.

Finally, consider sequential bidding where 3 is the first mover. The reaction function of 2 derived earlier is given by:

$$\begin{aligned} R_{2}\left( b_{3}\right) =\left\{ \begin{array}{ll} \left\{ b_{3}+\varepsilon \right\} &{}\quad \hbox {if }~ b_{3}<\dfrac{\lambda _{2}}{6}+ \dfrac{\lambda _{3}}{3}-\varepsilon \\ \left\{ b_{3}+\varepsilon ,0\right\} &{}\quad \hbox {if }~ b_{3}=\dfrac{\lambda _{2}}{6}+ \dfrac{\lambda _{3}}{3}-\varepsilon \\ \left\{ 0\right\} &{}\quad \hbox {if }~ b_{3}>\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3 }-\varepsilon . \end{array} \right. . \end{aligned}$$

Therefore, 3’s profit function is given by ($\upsilon$ is a real number such that $0\leqslant \upsilon \leqslant 1$),

$$\begin{aligned} \widehat{f}_{3}\left( b_{3}\right)= & {} f_{3}\left( R_{2}\left( b_{3}\right) ,b_{3}\right) \\= & {} \left\{ \begin{array}{l} \varphi _{3}\left( \pi _{2}\right) -b_{3} \\ \upsilon \left( \varphi _{3}\left( \pi _{2}\right) -b_{3}\right) +\left( 1-\upsilon \right) \left( \varphi _{3}\left( \pi _{1}\right) -b_{3}\right) \\ \varphi _{3}\left( \pi _{1}\right) -b_{3} \end{array} \begin{array}{l} \hbox { if }~ b_{3}>\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}-\varepsilon ; \\ \hbox { if }~ b_{3}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}-\varepsilon ; \\ \hbox { if }~ b_{3}<\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}-\varepsilon . \end{array} \right. \\= & {} \left\{ \begin{array}{l} \dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{2}-b_{3} \\ \upsilon \left( \dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{2} -b_{3}\right) +\left( 1-\upsilon \right) \left( \dfrac{\lambda _{3}}{3} -b_{3}\right) \\ \dfrac{\lambda _{3}}{3}-b_{3} \end{array} \begin{array}{l} \hbox { if }~ b_{3}>\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}-\varepsilon ; \\ \hbox { if }~ b_{3}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}-\varepsilon ; \\ \hbox { if }~ b_{3}<\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}-\varepsilon . \end{array} \right. \end{aligned}$$

Since the payoffs are decreasing in $b_{3}$, we restrict ourselves to situations where $b_{3}$ is the minimum feasible number. Therefore,

$$\begin{aligned} \widehat{f}_{3}\left( b_{3}\right)= & {} \left\{ \begin{array}{l} \dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{2}-b_{3} \\ \upsilon \left( \dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{2} -b_{3}\right) +\left( 1-\upsilon \right) \left( \dfrac{\lambda _{3}}{3} -b_{3}\right) \\ \dfrac{\lambda _{3}}{3}-b_{3} \end{array} \begin{array}{l} \hbox { if }~ b_{3}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3};\\ \hbox { if }~ b_{3}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}-\varepsilon ;\\ \hbox { if }~ b_{3}=0. \end{array} \right. \\= & {} \left\{ \begin{array}{l} \dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{6} \\ \upsilon \left( \dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{6}\right) -\left( 1-\upsilon \right) \left( \dfrac{\lambda _{2}}{6}\right) +\varepsilon \\ \dfrac{\lambda _{3}}{3} \end{array} \begin{array}{l} \hbox { if }~ b_{3}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3};\\ \hbox { if }~ b_{3}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}-\varepsilon ;\\ \hbox { if }~ b_{3}=0. \end{array} \right. \end{aligned}$$

Since $\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{6}>\dfrac{\lambda _{3}}{3 }$, the optimal strategy for 3 is to bid $b_{3}=\dfrac{\lambda _{3}}{3}+ \dfrac{\lambda _{2}}{6}$.¹³ Player 2 bids zero again. We summarize this in form of the following proposition.

Proposition 6

In the bidding game where 3 is the first mover and 2 bids second, there is an unique SPNE in which 2 bids zero and 3 bids $\dfrac{\lambda _{2}}{6 }+\dfrac{\lambda _{3}}{3}$. The allocation that results is $\pi _{2}$. The surplus extracted is $\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3} }{3}$.

Sequential bidding always results in a non-cogent hierarchy.

4.2 First price auction

Under first price auctions, only the winner of the higher position pays his bid and the winner of the lower positions pays nothing. Furthermore, the bid paid is the bid of the winner of the higher position. We show below that there are multiple Nash equilibria all of which result in a non-cogent allocation.

There are again three possibilities which we delineate as three cases.

Case 1: $b_{2}>b_{3}$

The players’ payoffs are given by:

$$\begin{aligned} f_{2}(b_{2},b_{3})= & {} \varphi _{2}(\pi _{1})-b_{2}=\dfrac{\lambda _{2}}{2}+ \dfrac{\lambda _{3}}{3}-b_{2}; \\ f_{3}(b_{2},b_{3})= & {} \varphi _{3}(\pi _{1})=\dfrac{\lambda _{3}}{3}. \end{aligned}$$

Case 2: $b_{2}<b_{3}$

The players’ payoffs are given by:

$$\begin{aligned} f_{2}(b_{2},b_{3})= & {} \varphi _{2}(\pi _{2})=\dfrac{\lambda _{2}}{3}; \\ f_{3}(b_{2},b_{3})= & {} \varphi _{3}(\pi _{2})-b_{3}=\dfrac{\lambda _{2}}{3}+ \dfrac{\lambda _{3}}{2}-b_{3}. \end{aligned}$$

Case 3: $b_{2}=b_{3}=b$

The players’ payoffs are given by:

$$\begin{aligned} f_{i}(b_{2},b_{3})=\dfrac{1}{2}\varphi _{i}\left( \pi _{1}\right) + \dfrac{1}{2}\varphi _{i}\left( \pi _{2}\right) -\frac{b}{2}. \end{aligned}$$

for $i=1,2$.

Hence,

$$\begin{aligned} f_{2}(b_{2},b_{3})= & {} \frac{5\lambda _{2}}{12}+\frac{\lambda _{3}}{6}-\frac{b }{2}; \\ f_{3}(b_{2},b_{3})= & {} \frac{5\lambda _{3}}{12}+\frac{\lambda _{2}}{6}-\frac{b }{2}. \end{aligned}$$

We will start with some basic results. But first define

$$\begin{aligned} \widehat{B}_{2}= & {} \dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3} =B_{2}+\varepsilon ; \end{aligned}$$

(15)

$$\begin{aligned} \widehat{B}_{3}= & {} \dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6} =B_{3}+\varepsilon . \end{aligned}$$

(16)

Lemma 4

If a player i overbids, his optimal bid is given by $b_{-i}+\varepsilon$.

Proof

We prove the lemma for $i=2$. The proof for $i=3$ is similar.

Suppose a player overbids. Then, he gets $\varphi _{2}\left( \pi _{1}\right) -b_{2}$. The payoff is strictly decreasing in $b_{2}$ and hence is maximized by minimizing $b_{2}$ subject to the constraint that $b_{2}>b_{3}$. This is precisely $b_{3}+\varepsilon$. $\square$

Lemma 5

If a player i underbids, his optimal bid is given by $\{\tau \varepsilon \in [0,b_{-i}-\varepsilon ]$ where $\tau \in \mathbb {N}\}$.

Proof

Suppose a player i underbids. Then, his payoff is $\dfrac{\lambda _{i}}{3}$ and is independent of his bid. Thus all bids $\tau \varepsilon \in [0,b_{-i}-\varepsilon ]$ where $\tau \in \mathbb {N}$ constitute optimal bids. $\square$

We identify the best response functions.

Lemma 6

Let the best response function for player i be given by $R_{i}(b_{-i})$. Then,

• (i) if $0\leqslant b_{-i}<\widehat{B}_{i}-2\varepsilon$, then $R_{i}\left( b_{-i}\right) =\left\{ b_{-i}+\varepsilon \right\}$,

• (ii) if $b_{-i}=\widehat{B}_{i}-2\varepsilon$, then $R_{i}\left( b_{-i}\right) =\left\{ b_{-i},b_{-i}+\varepsilon \right\}$,

• (iii) if $b_{-i}=\widehat{B}_{i}-\varepsilon$, then $R_{i}\left( b_{-i}\right) =\left\{ b_{-i}\right\}$,

• (iv) if $b_{-i}=\widehat{B}_{i}$, then $R_{i}\left( b_{-i}\right) =\left\{ \tau \varepsilon \in [0,b_{-i}]\text { where }\tau \in \mathbb {N} \right\}$

• (v) if $b_{-i}>\widehat{B}_{i}$, then $R_{i}\left( b_{-i}\right) =\left\{ \tau \varepsilon \in [0,b_{-i}-\varepsilon ]\text { where }\tau \in \mathbb {N}\right\}$,

where $\widehat{B}_{i}$, $i=2,3$ are given by (11) and (12).

Proof

We prove the lemma for $i=2$. The proof for $i=3$ is similar. Suppose player 3 bids $b_{3}$. How would player 2 react to this? He can overbid, underbid or match 3’s bid.

If he overbids, he gets by $\varphi _{2}\left( \pi _{1}\right) -b_{2}$ which by Lemma 4 is $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}-\varepsilon$. If he matches, he gets $\dfrac{1}{2}\varphi _{2}\left( \pi _{1}\right) +\dfrac{1}{2}\varphi _{2}\left( \pi _{2}\right) -\dfrac{b_{2}}{2}=\dfrac{5\lambda _{2}}{12}+\dfrac{ \lambda _{3}}{6}-\dfrac{b_{3}}{2}$. If he underbids, he gets $\varphi _{2}\left( \pi _{2}\right) =\dfrac{\lambda _{2}}{3}$. Let us identify the best responses.

First, $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}-\varepsilon > \dfrac{\lambda _{2}}{3}\Leftrightarrow b_{3}<\dfrac{\lambda _{2}}{6}+\dfrac{ \lambda _{3}}{3}-\varepsilon$. Furthermore, $\dfrac{\lambda _{2}}{2}+\dfrac{ \lambda _{3}}{3}-b_{3}-\varepsilon >\dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}\Leftrightarrow b_{3}<\dfrac{\lambda _{2}}{6}+ \dfrac{\lambda _{3}}{3}-2\varepsilon$. Hence, if $b_{3}<\dfrac{\lambda _{2} }{6}+\dfrac{\lambda _{3}}{3}-2\varepsilon =\widehat{B}_{2}-2\varepsilon$, overbidding is the best response and $R_{2}\left( b_{3}\right) =\left\{ b_{3}+\varepsilon \right\}$.

Second, $\dfrac{\lambda _{2}}{3}>\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3} }{3}-b_{3}-\varepsilon \Leftrightarrow b_{3}>\dfrac{\lambda _{2}}{6}+\dfrac{ \lambda _{3}}{3}-\varepsilon$. Furthermore, $\dfrac{\lambda _{2}}{3}>\dfrac{ 5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}\Leftrightarrow b_{3}>\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$. Hence, if $b_{3}> \dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}=\widehat{B}_{2}$, underbidding is the best response.

Finally, $\dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}> \dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}-\varepsilon \Leftrightarrow b_{3}>\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3} -2\varepsilon$. Furthermore, $\dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3} }{6}-\dfrac{b_{3}}{2}>\dfrac{\lambda _{2}}{3}\Leftrightarrow b_{3}<\dfrac{ \lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$. Hence, if $\dfrac{\lambda _{2}}{6} +\dfrac{\lambda _{3}}{3}-2\varepsilon<b_{3}<\dfrac{\lambda _{2}}{6}+\dfrac{ \lambda _{3}}{3}\Rightarrow b_{3}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3} }{3}-\varepsilon =\widehat{B}_{2}-\varepsilon$, then matching is the best response.

Also, note that $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3} -b_{3}-\varepsilon =\dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{ b_{3}}{2}\Leftrightarrow b_{3}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3 }-2\varepsilon =\widehat{B}_{2}-2\varepsilon$. In this case, both matching and overbidding yield an equal payoff of $\dfrac{\lambda _{2}}{3} +\varepsilon$ which is greater than $\dfrac{\lambda _{2}}{3}$, the payoff from underbidding.

Further, $\dfrac{\lambda _{2}}{3}=\dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}\Leftrightarrow b_{3}=\dfrac{\lambda _{2}}{6}+ \dfrac{\lambda _{3}}{3}=\widehat{B}_{2}$. In this case, both matching and underbidding gives an equal payoff of $\dfrac{\lambda _{2}}{3}$, which is greater than $\dfrac{\lambda _{2}}{3}-\varepsilon$, the payoff from overbidding.

While not directly relevant, it is worth noting that $\dfrac{\lambda _{2}}{2} +\dfrac{\lambda _{3}}{3}-b_{3}-\varepsilon =\dfrac{\lambda _{2}}{3} \Leftrightarrow b_{3}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3} -\varepsilon =\widehat{B}_{2}-\varepsilon$ but in this case, neither overbidding nor underbidding is a best response though they give identical payoffs. This completes the proof. $\square$

We plot the best response correspondences of players 2 and 3. Then, we superimpose them on each other to identify the Nash equilibria (Figs. 3, 4, 5).

Fig. 3

Best response of player 2

Fig. 4

Best response of player 3

Fig. 5

Nash equilibria of first price auction

We summarize these results in form of the proposition below. While a proof is superfluous given the diagram, we also provide one for the sake of completeness.

Proposition 7

The set of Nash equilibria are given by $(b_{2}^{*},b_{3}^{*})$ where $b_{3}^{*}=b_{2}^{*}+\varepsilon$ and $\widehat{B} _{2}\leqslant b_{2}^{*}\leqslant \widehat{B}_{3}-2\varepsilon .$

Proof

We have to show that $b_{2}^{*}\in R_{2}(b_{3}^{*})$ and $b_{3}^{*}\in R_{3}(b_{2}^{*})$.

First, when $b_{2}^{*}=\widehat{B}_{3}-2\varepsilon$, $R_{3}\left( b_{2}^{*}\right) =\left\{ b_{2}^{*},b_{2}^{*}+\varepsilon \right\}$ and when $b_{2}^{*}<\widehat{B}_{3}-2\varepsilon$, $R_{3}\left( b_{2}^{*}\right) =\{b_{2}^{*}+\varepsilon \}$. So, in all cases, $b_{3}^{*}\in R_{3}(b_{2}^{*})$.

Next, $b_{2}^{*}\geqslant \widehat{B}_{2}$ and $b_{3}^{*}=b_{2}^{*}+\varepsilon$ imply $b_{3}^{*}\geqslant \widehat{B} _{2}+\varepsilon$. Hence, $b_{3}^{*}>\widehat{B}_{2}$, hence, $R_{2}(b_{3}^{*})=\left\{ \tau \varepsilon \in [0,b_{3}^{*}-\varepsilon ]\text { where }\tau \in \mathbb {N}\right\}$. Hence, $b_{2}^{*}=b_{3}^{*}-\varepsilon \in R_{2}(b_{3}^{*})$. $\square$

The interesting feature about the set of Nash equilibria is that they lie above the 45 degree line. So, in all these equilibria, 3 bids higher than 2, so all these equilibria result in a non-cogent allocation. We summarize this result in form of the proposition below.

Proposition 8

An equilibria of the first price auction always yields a non-cogent allocation.

4.3 Second price auction

Under second price auctions, only the winner of the higher position pays the bid and the winner of the lower positions pays nothing. Furthermore, the bid paid is the bid of the winner of the lower position. We show below that there are multiple Nash equilibria which may result in a cogent or non-cogent allocation.

There are again three possibilities which we delineate as three cases.

Case 1: $b_{2}>b_{3}$

The players’ payoffs are given by:

$$\begin{aligned} f_{2}(b_{2},b_{3})= & {} \varphi _{2}(\pi _{1})-b_{3}=\dfrac{\lambda _{2}}{2}+ \dfrac{\lambda _{3}}{3}-b_{3}; \\ f_{3}(b_{2},b_{3})= & {} \varphi _{3}(\pi _{1})=\dfrac{\lambda _{3}}{3}. \end{aligned}$$

Case 2: $b_{2}<b_{3}$

The players’ payoffs are given by:

$$\begin{aligned} f_{2}(b_{2},b_{3})= & {} \varphi _{2}(\pi _{2})=\dfrac{\lambda _{2}}{3}; \\ f_{3}(b_{2},b_{3})= & {} \varphi _{3}(\pi _{2})-b_{2}=\dfrac{\lambda _{2}}{3}+ \dfrac{\lambda _{3}}{2}-b_{2}. \end{aligned}$$

Case 3: $b_{2}=b_{3}=b$

The players’ payoffs are given by:

$$\begin{aligned} f_{i}(b_{2},b_{3})=\dfrac{1}{2}\varphi _{i}\left( \pi _{1}\right) + \dfrac{1}{2}\varphi _{i}\left( \pi _{2}\right) -\frac{b}{2}. \end{aligned}$$

for $i=1,2$.

Hence,

$$\begin{aligned} f_{2}(b_{2},b_{3})= & {} \frac{5\lambda _{2}}{12}+\frac{\lambda _{3}}{6}-\frac{b }{2}; \\ f_{3}(b_{2},b_{3})= & {} \frac{5\lambda _{3}}{12}+\frac{\lambda _{2}}{6}-\frac{b }{2}. \end{aligned}$$

We identify the best response functions.

Lemma 7

• (i) If $0\leqslant b_{-i}<\widehat{B}_{i}$, then $R_{i}\left( b_{-i}\right) =\{\tau \varepsilon \in [b_{-i}+\varepsilon ,\infty )$ where $\tau \in \mathbb {N}\}$,

• (ii) if $b_{-i}=\widehat{B}_{i}$, then $R_{i}\left( b_{-i}\right) =\{\tau \varepsilon \in [0,\infty )$ where $\tau \in \mathbb {N}\}$,

• (iii) if $b_{-i}>\widehat{B}_{i}$, then $R_{i}\left( b_{-i}\right) =\left\{ \tau \varepsilon \in [0,b_{-i}-\varepsilon ]\text { where }\tau \in \mathbb {N}\right\}$,

where $\widehat{B}_{i}$, $i=2,3$ are given by (15) and (16).

Proof

We prove the lemma for $i=2$. The proof for $i=3$ is similar. Suppose player 3 bids $b_{3}$. How would player 2 react to this? He can overbid, underbid or match 3’s bid.

If he overbids, he gets by $\varphi _{2}\left( \pi _{1}\right) -b_{3}=\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}$. If he matches, he gets $\dfrac{1}{2}\varphi _{2}\left( \pi _{1}\right) + \dfrac{1}{2}\varphi _{2}\left( \pi _{2}\right) -\dfrac{b_{3}}{2}= \dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}$. If he underbids, he gets $\varphi _{2}\left( \pi _{2}\right) =\dfrac{ \lambda _{2}}{3}$. Let us identify the best responses.

First, $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}>\dfrac{\lambda _{2}}{3}\Leftrightarrow b_{3}<\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$. Furthermore, $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}> \dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2} \Leftrightarrow \dfrac{b_{3}}{2}<\dfrac{\lambda _{2}}{12}+\dfrac{\lambda _{3} }{6}\Leftrightarrow b_{3}<\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$. Hence, if $b_{3}<\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}=\widehat{B} _{2}$, overbidding is the unique best response and $R_{2}\left( b_{3}\right) =\{\tau \varepsilon \in [b_{3}+\varepsilon ,\infty )$ where $\tau \in \mathbb {N}\}$ where $\mathbb {N}$ is the set of natural numbers.

Next, $\dfrac{\lambda _{2}}{3}>\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3 }-b_{3}\Leftrightarrow b_{3}>\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$ . Furthermore, $\dfrac{\lambda _{2}}{3}>\dfrac{5\lambda _{2}}{12}+\dfrac{ \lambda _{3}}{6}-\dfrac{b_{3}}{2}\Leftrightarrow \dfrac{b_{3}}{2}>\dfrac{ \lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}\Leftrightarrow b_{3}>\dfrac{ \lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$. Hence, if $b_{3}>\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}=\widehat{B}_{2}$, underbidding is the unique best response and $R_{2}(b_{3})=\{\tau \varepsilon \in [0,b_{3}-\varepsilon ]$ where $\tau \in \mathbb {N\}}$.

Finally, $\dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}> \dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}\Leftrightarrow \dfrac{ b_{3}}{2}>\dfrac{\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}\Leftrightarrow b_{3}>\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}=\widehat{B}_{2}$. Also, $\dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}> \dfrac{\lambda _{2}}{3}\Leftrightarrow \dfrac{b_{3}}{2}<\dfrac{\lambda _{2}}{ 12}+\dfrac{\lambda _{3}}{6}\Leftrightarrow b_{3}<\dfrac{\lambda _{2}}{6}+ \dfrac{\lambda _{3}}{3}=\widehat{B}_{2}$. Hence, matching a bid is never an unique best response.

The only remaining case to be studied is what happens when $b_{3}=\dfrac{ \lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}=\widehat{B}_{2}$. If 2 overbids, he gets $\dfrac{\lambda _{2}}{3}$. If he matches, he gets $\dfrac{\lambda _{2}}{3}$. If he underbids, he gets $\dfrac{\lambda _{2}}{3}$. So, $R_{2}(b_{3})=\{\tau \varepsilon \in [0,\infty ]$ where $\tau \in \mathbb {N\}}$. $\square$

We plot the best response correspondences of players 2 and 3. Note that the bids are in discrete multiples of $\varepsilon$ so the figure is not strictly accurate. The coloured areas highlight the zones such that all discrete bids in those zones constitute valid best response bids. Then, we superimpose them on each other to identify the Nash equilibria (highlighted in red) (Figs. 6, 7).

Fig. 6

Best response of player 2

Fig. 7

Best response of player 3

There is an infinite number of such equilibria. These equilibria come in two categories. First, player 2 bids high and player 3 bids low. Second player 3 bids high and player 2 bids low. A focal equilibrium among these large numbers of equilibria is the valuation equilibrium. Vickrey (1961) has shown that in a standard single object second price action, it is a weakly dominant strategy to bid one’s valuation. Because this is a somewhat different setting, we must first define what we would consider to be the valuation of the higher position. We define valuation of the higher position to be the payoff of the higher position minus the player of the lower position. We confirm that using this definition, the analogy of Vickrey’s theorem holds as well.

Lemma 8

For, player 2, bidding $\widehat{B}_{2}=\dfrac{\lambda _{2}}{6}+\dfrac{ \lambda _{3}}{3}$ is a weakly dominant strategy. For player 3, $\widehat{B} _{3}=\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}$ bidding is a weakly dominant strategy.

Proof

We shall prove this result for player 2. The result for player 3 follows analogously.

Suppose player 3 bids $b_{3}$. There are three possibilities which we delineate as three cases.

Case 1: $b_{3}>\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$

Currently by bidding $\widehat{B}_{2}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$, player 2 is getting $\dfrac{\lambda _{2}}{3}$. Can he do any better by bidding something else?

• If he bids $b_{2}>b_{3}$, he gets $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}<\dfrac{\lambda _{2}}{3}$.

• If he bids $b_{2}=b_{3}$, he gets $\dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}<\dfrac{\lambda _{2}}{3}$.

• If he bids $b_{2}$ such that $b_{3}>b_{2}>\dfrac{\lambda _{2}}{6}+\dfrac{ \lambda _{3}}{3}$, he gets $\dfrac{\lambda _{2}}{3}$.

• If he bids $b_{2}<\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$, he gets $\dfrac{\lambda _{2}}{3}$.

Clearly, bidding his valuation gives player 2 as great a payoff as bidding anything else.

Case 2: $b_{3}<\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$

Currently, by bidding $\widehat{B}_{2}=\dfrac{\lambda _{2}}{6}+\dfrac{ \lambda _{3}}{3}$, player 2 is getting $\dfrac{\lambda _{2}}{2}+\dfrac{ \lambda _{3}}{3}-b_{3}$. Can he do better by bidding anything else?

• If he bids $b_{2}>\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$, he gets $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}$.

• If he bids $b_{2}$ such that $b_{3}<b_{2}<\dfrac{\lambda _{2}}{6}+\dfrac{ \lambda _{3}}{3}$, he gets $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3} -b_{3}$.

• If he bids $b_{2}=b_{3}$, he gets $\dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}$. This is smaller than his current payoff since $\left( \dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}\right) -\left( \dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}\right)$$=$$\dfrac{1}{2}\left( \dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3} -b_{3}\right) >0$.

• If he bids $b_{2}<b_{3}$, he gets $\dfrac{\lambda _{2}}{3}<\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}$ given $\dfrac{\lambda _{2}}{2}+ \dfrac{\lambda _{3}}{3}-b_{3}$ > $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-\dfrac{\lambda _{2}}{6}-\dfrac{\lambda _{3}}{3}$$=$$\dfrac{ \lambda _{2}}{3}.$

Hence, bidding his valuation gives player 2 as great a payoff as bidding anything else.

Case 3: $b_{3}=\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$

Currently, player 2 is getting $\dfrac{5\lambda _{2}}{12}+\dfrac{\lambda _{3}}{6}-\dfrac{b_{3}}{2}=\dfrac{\lambda _{2}}{3}$. Can he do better by bidding anything else?

• If he bids $b_{2}>b_{3}$, he gets $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}-b_{3}=\dfrac{\lambda _{2}}{3}$.

• If he bids $b_{2}<b_{3}$, he gets $\dfrac{\lambda _{2}}{3}$.

Hence, bidding his valuation gives player 2 as great a payoff as bidding anything else. This completes the proof. $\square$

In this equilibrium, the resulting allocation is non-cogent just as in a all-pay auction, because 3’s valuation from the higher position is greater than 2’s valuation, so 3 will bid higher.

Equilibria exist that result in cogent allocations under second price auctions unlike first price and all pay auctions. We conclude this subsection by pointing out such an equilibria. For instance consider the equilibria represented by point A in Fig. 8. Here, $(b_{2}^{*},b_{3}^{*})=\left( \dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}, \dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}\right) =(\widehat{B}_{3}, \widehat{B}_{2})$. So 2 bids 3’s valuation and 3 bids 2’s valuation. This equilibrium is not very plausible however because each players best response correspondence includes all possible bids.

Fig. 8

Nash equilibria of second price auction

4.4 Intuition

We discuss the intuition behind these results as well as an extension to trees of arbitrary depth. The reason that the less productive player bids more (and consequently, we end up with a non-cogent hierarchy) is that he has more to gain because he gets a productive subordinate, while the productive player gets a less productive subordinate and therefore has less to gain from securing the higher level. The difference in gross payoffs (gross of the bids) for the less productive player between being allocated $p_{1,1}$ and $p_{2,1}$ is $\dfrac{\lambda _{2}}{3}+\dfrac{\lambda _{3}}{6}$ which is greater than the similar difference for the more productive player, namely, $\dfrac{\lambda _{2}}{6}+\dfrac{\lambda _{3}}{3}$, the difference of the two being $\dfrac{\lambda _{2}-\lambda _{3}}{6}$. Given that there is no budget constraint, it is in the interest of the less productive player to bid more.

In the case of trees of arbitrary depth, this feature is not necessarily preserved, and besides the fact that the bidding strategies are more complicated, it is not necessarily the case that less productive players will have a tendency to bid more than more productive players and so a non-cogent equilibrium hierarchy may not form. Consider a tree of depth $l_{1}+l_{2}+l_{3}$ where all positions have been allocated except for a position at level $l_{1}$ and a position at level $l_{1}+l_{2}$. Suppose 2 and 3 are bidding for those positions. The gain to 3 from moving up from level $l_{1}+l_{2}$ to $l_{1}$ exceeds the gain to 2 from moving up between these two levels by $\dfrac{(\lambda _{2}-\lambda _{3})(l_{1}-l_{2}+1)}{(l_{1}+l_{2}+1)(l_{1}+1)}$. If $l_{2}$ is sufficiently large, the expression is negative. The reason is that while 2 has an unproductive subordinate, while 3 has a productive one, 2’s loss due to exploitation of superiors is greater than 3 given his higher productivity to begin with. So, one cannot necessarily extend this result to trees of arbitrary size. Besides the intuition, in general, there are formidable difficulties in extending these results to hierarchies of depth 3 or more, as given the interdependence of valuations, the incentives of the players are far from clear, so it is difficult to derive the equilibria of the auctions in a straightforward way.

4.5 Optimal auction design

Let us now examine when is it optimal to organize such an auction. Given that second price and first price auctions result in multiple equilibria, we can only do this for sequential all pay auctions. Without an auction, the top agent’s expected payoff is $\dfrac{5}{12}(\lambda _{2}+\lambda _{3})$ given that he does not know productivities and assigns agents arbitrarily. With an auction, his payoff is $\left( \dfrac{5\lambda _{2}}{12}+\dfrac{ 2\lambda _{3}}{3}\right) +\dfrac{\varepsilon }{2}$ which includes both the payoff from the non-cogent hierarchy and the surplus extracted.¹⁴ So, it is always beneficial to assign agents using an auction, if the procedure is not too costly to organize because the surplus extracted is greater than the loss of payoff due to a non-cogent hierarchy.

There is yet another interesting issue that one may highlight. Suppose the top agent is aware of the productivities. Even then it is worthwhile to organize an auction. Without an auction, the payoff of the top agent is $\dfrac{\lambda _{2}}{2}+\dfrac{\lambda _{3}}{3}$. With an auction where 3 is the first mover, the payoff of the top agent is $\dfrac{\lambda _{2}}{2}+ \dfrac{5\lambda _{3}}{6}$ which is greater. Again the surplus extracted by this procedure is greater than the loss due to the resulting non-cogent allocation.

5 Conclusion

We have therefore shown that in hierarchical situations where payoff is determined by the permission value in trees under additive games, cogent and optimal allocations coincide. We have extended these results to non-additive games but with severe restrictions on the value function. We also study auctioning these positions using a bidding mechanism in a vertical hierarchy of depth 3 and this usually result in a non-cogent allocation.

Topics for further research include whether the results of Sect. 3 can be extended to non-additive games even further than we do now, what mechanism can result in a cogent allocation, if any, and whether the results of Sect. 4 can be extended to more complicated hierarchies. We can also move from allocation to positions in a fixed hierarchy to a framework of flexible hierarchies where both the hierarchy and the allocation are variable. We can also explore links between our approach and bidding mechanisms that implement the Shapley value or its variants, like, for instance, in Perez-Castrillo and Wettstein (2001).

Appendix

From (4), for all $\pi \in \Pi _{1}$

$$\begin{aligned} \varphi _{1}(v,S_{\pi })=\underset{A\subseteq N}{\sum }\frac{\Delta _{v}(A)}{ \left| \alpha _{S_{\pi }}(A)\right| }. \end{aligned}$$

(17)

We introduce some additional notation in this section. For a player set $A\subseteq N$, define the set of positions occupied by agents in A under an allocation $\pi$ by $A_{\pi }^{\prime }\subseteq M$. Obviously $N_{\pi }^{\prime }=M$ for all $\pi \in \Pi$.

Lemma 9

Consider two allocations $\pi _{1},\pi _{2}\in \Pi _{1}$. Let $\widehat{N}=\{i\in N|\pi _{1}(i)=\pi _{2}(i)\}$, hence $N\backslash \widehat{ N}=\{i\in N|\pi _{1}(i)\ne \pi _{2}(i)\}$. Then, (i) if $A\subseteq \widehat{N}$, then $\left| \alpha _{S_{\pi _{1}}}(A)\right| =\left| \alpha _{S_{\pi _{2}}}(A)\right|$. (ii) If $N\backslash \widehat{N}\subseteq A$, then $\left| \alpha _{S_{\pi _{1}}}(A)\right| =\left| \alpha _{S_{\pi _{2}}}(A)\right|$.

Proof

Let $A_{\pi }^{\prime }\subseteq M$ be defined by $\{k\in M|\pi (i)\in A\}$. Then, $\left| \alpha _{S_{\pi _{1}}}(A)\right| =\left| \alpha _{S}(A_{\pi _{1}}^{\prime })\right|$ and $\left| \alpha _{S_{\pi _{2}}}(A)\right| =\left| \alpha _{S}(A_{\pi _{2}}^{\prime })\right|$.

First consider (i). If $A\subseteq \widehat{N}$, then agents in A have not changed their position in going from $\pi _{1}$ to $\pi _{2}$. Hence, $A_{\pi _{1}}^{\prime }=A_{\pi _{2}}^{\prime }$. Consequently, $\alpha _{S}(A_{\pi _{1}}^{\prime })=\alpha _{S}(A_{\pi _{2}}^{\prime })$. Now, given that $\left| \alpha _{S_{\pi _{1}}}(A)\right| =\left| \alpha _{S}(A_{\pi _{1}}^{\prime })\right|$ and $\left| \alpha _{S_{\pi _{2}}}(A)\right| =\left| \alpha _{S}(A_{\pi _{2}}^{\prime })\right|$, the result follows.

Next, consider (ii). This time while some agents in A have changed their position in going from $\pi _{1}$ to $\pi _{2}$, the changes do not involve positions outside the positions occupied by agents in A. Hence, $A_{\pi _{1}}^{\prime }=A_{\pi _{2}}^{\prime }$. Consequently, $\alpha _{S}(A_{\pi _{1}}^{\prime })=\alpha _{S}(A_{\pi _{2}}^{\prime })$. Given that $\left| \alpha _{S_{\pi _{1}}}(A)\right| =\left| \alpha _{S}(A_{\pi _{1}}^{\prime })\right|$ and $\left| \alpha _{S_{\pi _{2}}}(A)\right| =\left| \alpha _{S}(A_{\pi _{2}}^{\prime })\right|$, the result follows. $\square$

Lemma 10

Consider two allocations $\pi _{1},\pi _{2}\in \Pi _{1}$ such that $\pi _{1}(i)=\pi _{2}(j)$ and $\pi _{1}(j)=\pi _{2}(i)$ and $\pi _{1}(t)=\pi _{2}(t)$ for all $t\ne i,j$. Then,

$$\begin{aligned}&\varphi _{1}(v,S_{\pi _{2}})-\varphi _{1}(v,S_{\pi _{1}}) \\&\quad =\underset{{B\subseteq N\backslash \{i,j\}}}{\sum }\left[ \Delta _{v}(B\cup \{i\})-\Delta _{v}(B\cup \{j\})\right] \left[ \frac{1}{\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| }-\frac{1}{\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| }\right] . \end{aligned}$$

Proof

From Lemma 9, for each $A\subseteq N$ such that $A\supseteq \{i,j\}$ , we have $\left| \alpha _{S_{\pi _{1}}}(A)\right| =\left| \alpha _{S_{\pi _{2}}}(A)\right|$. For each $A\subseteq N$ such that $A\cap \{i,j\}=\emptyset$, we obtain the same result $\left| \alpha _{S_{\pi _{1}}}(A)\right| =\left| \alpha _{S_{\pi _{2}}}(A)\right|$. Hence, combining this fact and (17),

$$\begin{aligned}&\varphi _{1}(v,S_{\pi _{2}})-\varphi _{1}(v,S_{\pi _{1}}) \\&\quad =\mathop {\mathop {\mathop {\sum }\limits _{A\subseteq N}}\limits _{i\in A}}\limits _{j\notin A} \frac{\Delta _{v}(A)}{\left| \alpha _{S_{\pi _{2}}}(A)\right| }+ \mathop {\mathop {\mathop {\sum }\limits _{A\subseteq N}}\limits _{{j\in A}, i\notin A}}\frac{\Delta _{v}(A) }{\left| \alpha _{S_{\pi _{2}}}(A)\right| } \\&\qquad -\mathop {\mathop {\mathop {\sum }\limits _{A\subseteq N}}\limits _{i\in A}}\limits _{j\notin A}\frac{ \Delta _{v}(A)}{\left| \alpha _{S_{\pi _{1}}}(A)\right| }- \mathop {\mathop {\mathop {\sum }\limits _{A\subseteq N}}\limits _{{j\in A}, i\notin A}}\frac{\Delta _{v}(A) }{\left| \alpha _{S_{\pi _{1}}}(A)\right| } \\&\quad =\mathop {\mathop {\mathop {\sum }\limits _{A\subseteq N}}\limits _{i\in A}}\limits _{j\notin A}\Delta _{v}(A)\left[ \frac{1}{\left| \alpha _{S_{\pi _{2}}}(A)\right| }- \frac{1}{\left| \alpha _{S_{\pi _{1}}}(A)\right| }\right] \\&\qquad -\mathop {\mathop {\mathop {\sum }\limits _{A\subseteq N}}\limits _{{j\in A}, i\notin A}}\Delta _{v}(A)\left[ -\frac{1}{\left| \alpha _{S_{\pi _{2}}}(A)\right| }+ \frac{1}{\left| \alpha _{S_{\pi _{1}}}(A)\right| }\right] \\&\quad =\underset{{B\subseteq N\backslash \{i,j\}}}{\sum }\Delta _{v}(B\cup \{i\}) \left[ \frac{1}{\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| }- \frac{1}{\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| }\right] \\&\qquad -\underset{{B\subseteq N\backslash \{i,j\}}}{\sum }\Delta _{v}(B\cup \{j\}) \left[ -\frac{1}{\left| \alpha _{S_{\pi _{2}}}(B\cup \{j\})\right| }+ \frac{1}{\left| \alpha _{S_{\pi _{1}}}(B\cup \{j\})\right| }\right] . \end{aligned}$$

While moving from $\pi _{1}$ to $\pi _{2}$, only i and j interchange positions. The rest of the agents keep their positions unchanged. So, for ${ B\subseteq N\backslash \{i,j\}}$, the set of superiors of $B\cup \{i\}$ under allocation $\pi _{1}$ is precisely set of superiors of $B\cup \{j\}$ under $\pi _{2}$. Likewise, the set of superiors of $B\cup \{i\}$ under allocation $\pi _{2}$ is precisely set of superiors of $B\cup \{j\}$ under $\pi _{1}$. We obtain $\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| =\left| \alpha _{S_{\pi _{2}}}(B\cup \{j\})\right|$ and $\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| =\left| \alpha _{S_{\pi _{1}}}(B\cup \{j\})\right|$, and we can conclude that

$$\begin{aligned}&\varphi _{1}(v,S_{\pi _{2}})-\varphi _{1}(v,S_{\pi _{1}}) \nonumber \\&\quad =\underset{{B\subseteq N\backslash \{i,j\}}}{\sum }\left[ \Delta _{v}(B\cup \{i\})-\Delta _{v}(B\cup \{j\})\right] \left[ \frac{1}{\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| }{-}\frac{1}{\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| }\right] \text {.}\nonumber \\ \end{aligned}$$

(18)

$\square$

The reader may verify that (18) morphs into (7), when we restrict ourselves to additive games since non-singleton coalitions have a Harsayni dividend of zero.

Now, consider a coalition $B\cup \{i\}$ in (18). Observe that if $v\left( \left\{ i\right\} \right) >v\left( \left\{ j\right\} \right)$, then the $\Delta _{v}(B\cup \{i\})-\Delta _{v}(B\cup \{j\})$ is strictly positive for singleton coalitions ($B=\emptyset$) and non-negative for non-singleton coalitions if the game belongs to the class $\Omega$. However, even if the level occupied by player i in allocation $\pi _{1}$ is greater than that occupied by player j, the expression $[ \frac{1}{ \left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| }-\frac{1}{ \left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| }]$ is not necessarily positive (or non-negative for that matter) precluding the straight forward generalization of Proposition 1 to non-additive games. Only for special trees, namely, vertical hierarchies, is the aforesaid expression always non-negative. This is proved in the next lemma.

Lemma 11

Consider a vertical hierarchy and an allocation $\pi _{1}\in \Pi _{1}$. Let $i\in N$ and $j\in N$ be such that $l_{\pi _{1}(i)}>l_{\pi _{1}(j)}$ . Consider an allocation $\pi _{2}$ such that $\pi _{2}(j)=\pi _{1}(i)$ and $\pi _{2}(i)=\pi _{1}(j)$ and $\pi _{2}(t)=\pi _{1}(t)$ for all $t\ne i,j$. Then, for all $B\subseteq N\backslash \{i,j\}$, we get

$$\begin{aligned} \frac{1}{\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| }-\frac{1 }{\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| }\geqslant 0. \end{aligned}$$

Furthermore, if $B=\emptyset$, then,

$$\begin{aligned} \frac{1}{\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| }-\frac{1 }{\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| }>0. \end{aligned}$$

Proof

Let us begin by considering non-empty B. Let the highest level among all members of B in the allocation $\pi _{1}$ be given by $l_{B}$. Namely,

$$\begin{aligned} l_{B}=\max \left\{ l_{\pi _{1}(t)}|t\in B\right\} . \end{aligned}$$

Note that since $\pi _{2}(i)=\pi _{1}(j)$, it follows that $l_{\pi _{2}(i)}=l_{\pi _{1}(j)}$. Hence, we shall replace $l_{\pi _{2}(i)}$ by $l_{\pi _{1}(j)}$ below.

Since in a vertical hierarchy, no two players have the same level, $l_{B}\ne l_{\pi _{1}(i)}\ne l_{\pi _{1}(j)}$. We can discern three cases:

Case 1: $l_{B}<l_{\pi _{1}(j)}<l_{\pi _{1}(i)}$

In this case, $\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| =l_{\pi _{1}(j)}+1$ and $\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| =l_{\pi _{1}(i)}+1$. Therefore,

$$\begin{aligned}&\frac{1}{\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| }-\frac{ 1}{\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| } \\&\quad =\frac{1}{l_{\pi _{1}(j)}+1}-\frac{1}{l_{\pi _{1}(i)}+1} \\&\quad =\dfrac{\left( l_{\pi _{1}(i)}-l_{\pi _{1}(j)}\right) }{\left( l_{\pi _{1}(j)}+1\right) \left( l_{\pi _{1}(i)}+1\right) }>0. \end{aligned}$$

Case 2: $l_{\pi _{1}(j)}<l_{B}<l_{\pi _{1}(i)}$

In this case, $\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| =l_{B}+1$ and $\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| =l_{\pi _{1}(i)}+1$. Therefore,

$$\begin{aligned}&\frac{1}{\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| }-\frac{ 1}{\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| } \\&\quad =\frac{1}{l_{B}+1}-\frac{1}{l_{\pi _{1}(i)}+1} \\&\quad =\dfrac{\left( l_{\pi _{1}(i)}-l_{B}\right) }{\left( l_{B}+1\right) \left( l_{\pi _{1}(i)}+1\right) }>0. \end{aligned}$$

Case 3: $l_{\pi _{1}(j)}<l_{\pi _{1}(i)}<l_{B}$

In this case, $\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| =l_{B}+1$ and $\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| =l_{B}+1$. Therefore,

$$\begin{aligned}&\frac{1}{\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| }-\frac{ 1}{\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| } \\&\quad =\frac{1}{l_{B}+1}-\frac{1}{l_{B}+1}=0. \end{aligned}$$

If finally, $B=\emptyset ,$$B\cup \{i\}=\{i\}$ and

$$\begin{aligned}&\frac{1}{\left| \alpha _{S_{\pi _{2}}}(B\cup \{i\})\right| }-\frac{ 1}{\left| \alpha _{S_{\pi _{1}}}(B\cup \{i\})\right| } \\&\quad =\frac{1}{l_{\pi _{1}(j)}+1}-\frac{1}{l_{\pi _{1}(i)}+1} \\&\quad =\dfrac{\left( l_{\pi _{1}(i)}-l_{\pi _{1}(j)}\right) }{\left( l_{\pi _{1}(j)}+1\right) \left( l_{\pi _{1}(i)}+1\right) }>0. \end{aligned}$$

This completes the proof. $\square$

Finally, we can use Lemma 10 and Lemma 11 to arrive at Proposition 3.

Proof of Proposition 3

Towards a contradiction, consider an allocation $\pi _{1}\in \Pi _{1}$ that is optimal but not cogent. Then, there must be at least two agents i and j such that $l_{\pi _{1}(i)}>l_{\pi _{1}(j)}$ but $v\left( \{i\}\right) >v\left( \{j\}\right)$. Consider an allocation $\pi _{2}\in \Pi _{1}$ that swaps these two agents in these positions, namely $\pi _{2}(j)=\pi _{1}(i)$ and $\pi _{2}(i)=\pi _{1}(j)$ and $\pi _{2}(t)=\pi _{1}(t)$ for all $t\ne i,j$. By Lemma 10 and 11, we obtain that $\varphi _{1}(v,S_{\pi _{2}})-\varphi _{1}(v,S_{\pi _{1}})>0$. Hence, $\pi _{1}$ cannot be optimal. Hence, an optimal hierarchy is cogent. The converse is obvious since a cogent hierarchy is uniquely defined. $\square$