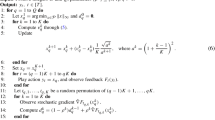Revenue comparison of discrete private-value auctions via weak dominance

Abstract

We employ weak dominance to analyze both first-price and second-price auctions under the discrete private-value setting. We provide a condition under which the expected revenue from second-price auction is higher than that of first-price auction. We also provide implications for large auctions, including the “virtual” revenue equivalence.

1 Introduction

The comparison of the expected revenues from private-value first-price and second-price auctions (FPA and SPA henceforth) has been extensively analyzed, including the revenue equivalence result by Riley and Samuelson (1981) and Myerson (1981). It also has been shown that once some underlying assumptions are relaxed, not only the revenue equivalence result does not necessarily hold, but the comparison results become ambiguous.¹ In addition, the analyses often have been limited to the two-player case, implying the lack of implications for large auctions. Although our main results are not specific to large auctions, the explicit analysis of large auctions is also important since (i) the understanding of large auctions has been of theoretical interest (e.g., Wilson 1977), and (ii) the emergence of online auctions, for example, has made large auctions empirically more relevant.

In this paper, we revisit the revenue comparison of FPA and SPA. There are two departures from the literature. One is the use of the maximal elimination of weakly dominated bids—all weakly dominated bids are eliminated—for both FPA and SPA.² It has been typically the case that while SPA is analyzed by the maximal elimination of weakly dominated bids, FPA is analyzed by Bayesian Nash equilibrium. It would be ideal to use the same solution concept to assess the differences purely stemming from the comparison of two distinct institutions.³ Another departure is that we follow a seminal work by Dekel and Wolinsky (2003), which analyze FPA via rationalizability, and adopt discrete sets for both bids and values.⁴ One advantage of the adoption of weak dominance and discrete setting is that we require minimal assumptions. In particular, our analysis allows asymmetry and an arbitrary number of players.

After providing technical details in Sect. 2, we compare the expected revenues of FPA and SPA from the auctioneer’s point of view in Sect. 3. Our main result provides a condition under which SPA generates a higher expected revenue compared to FPA. The key is the comparison of the winning bids in FPA and SPA. The result on the winning bids in FPA is due to Battigalli and Siniscalchi (2003) and Dekel and Wolinsky (2003) who provide upper bounds for bids via weak dominance. The maximal elimination of weakly dominated bids implies that the winning bids in SPA is higher than that of FPA. This leads to the comparison of the highest bid in FPA and the second highest bid in SPA. Our condition (on the auctioneer’s belief regarding players’ values) concerns the case where the highest and the second highest bids are the same in SPA, in which case the price the winner pays in SPA is higher than that of FPA.⁵ We also show that this result holds for large auctions. Under the assumptions of (i) independently distributed values and (ii) the same highest value (whose probability is bounded below by an arbitrary small number) for every player’s support, the expected revenue from SPA is higher than that of FPA in large auctions.

In Sect. 4, we employ the iterative maximal elimination of weakly dominates bids to further analyze players’ behavior. We provide a condition (on players’ beliefs regarding opponets’ values) for the uniqueness result à laDekel and Wolinsky (2003) and Robles and Shimoji (2012). Based on this result, with the additional assumption of (iii) players’ risk-aversion, we show that as the number of players increases, the difference in the expected revenues of FPA and SPA converges to the smallest monetary unit, which we denote d. This implies the virtual revenue equivalence in large auctions for small d.

For asymmetric auctions, Kirkegaard (2012) identified sufficient conditions under which FPA generates a higher expected revenue compared to SPA. Note that our result has a different implication. Both the use of weak dominance for FPA and the discrete setting lead to this difference. In Sect. 5, we use an example to demonstrate that the discretized version of the condition in Kirkegaard (2012) and ours are not mutually exclusive.

2 Preliminaries

The set of players is $N=\{1,\ldots , n\}$ with $n\ge 2$. We also deal with the auctioneer explicitly in Sect. 3. We assume that possible values and bids for each player are (non-negative) multiples of $d>0$, an increment. Before the auction starts, each player $i\in N$ observes her value, $v_{i}\in V_{i}=\{\underline{v}_{i}, \underline{v}_{i}+d, \ldots , \bar{v}_{i}-d, \bar{v}_{i} \}$ with $\underline{v}_{i}\ge 0$ for each $i\in N$. Let $\bar{v}=\max _{j\in N} \{\bar{v}_{j}\}$ and $\underline{v}=\max _{j\in N}\{\underline{v}_{j}\}$. Let v be a typical element of $V=\times _{j\in N} V_{j}$. We use the subscript “$-i$” to represent player i’s opponents. Player i’s utility function is $u_{i}: {\mathbb {R}} \rightarrow {\mathbb {R}}$ which is assumed to be strictly increasing.⁶ Player i’s utility is $u_{i}(v_{i}-s)$ if she wins the object while it is $u_{i}(0)$ otherwise.

We allow heterogeneous beliefs for players as well as the auctioneer. Let $p_{v_{i}}$ be player i’s belief regarding her opponents’ values when her value is $v_{i}\in V_{i}$. Let P represent the auctioneer’s belief over players’ values. We assume that each player $i\in N$ with any $v_{i}\in V_{i}$ assigns a strictly positive probability to every $v_{-i}\in V_{-i} = \times _{j\ne i} V_{j}$ and that the auctioneer assigns a strictly positive probability to every $v\in V$.

Each player i chooses her bid $b_{i}\in B_{i}=\{ 0,d,\ldots ,\bar{b}_{i}-d,\bar{b}_{i}\}$ where $\bar{v}_{i}\le \bar{b}_{i}$ for each $i\in N$ and hence $V_{i}\subseteq B_{i}$. A player wins only if her bid is the highest. If there are multiple players who chose the highest bid, each one of them has an equal chance of winning. If player $i\in N$ is the winner, the price she pays, s, is such that $s=b_{i}$ for FPA and $s=\max _{j\ne i} \{ b_{j} \}$ for SPA.

As stated in Sect. 1, we employ weak dominance as our solution concept. For each player $i\in N$, let ${\mathbf {b}}_{i}: V_{i}\rightarrow B_{i}$ be player i’s pure-strategy, and ${\mathbf {B}}_{i}$ be the set of player i’s strategies. A collection W includes a set $W_{i}(v_{i})\subseteq B_{i}$ for each $i\in N$ and $v_{i}\in V_{i}$. Given W, we say that ${\mathbf {b}}_{i}^{\prime }(v_{i})\in W_{i}(v_{i})$ weakly dominates ${\mathbf {b}}_{i}(v_{i})\in W_{i}(v_{i})$ in W for player i with $v_{i}$ if

$$\begin{aligned} \textstyle \sum \limits _{v_{-i}\in V_{-i}} \frac{ u_{i}({\mathbf {b}}_{i}^{\prime } (v_{i}), {\mathbf {b}}_{-i}(v_{-i})) }{ \eta ({\mathbf {b}}_{i}^{\prime }(v_{i}),{\mathbf {b}}_{-i}(v_{-i})) } p_{v_{i}} (v_{-i}) \ge \sum \limits _{v_{-i}\in V_{-i}} \frac{ u_{i}({\mathbf {b}}_{i} (v_{i}), {\mathbf {b}}_{-i}(v_{-i})) }{ \eta ({\mathbf {b}}_{i}(v_{i}), {\mathbf {b}}_{-i}(v_{-i})) } p_{v_{i}} (v_{-i}) \end{aligned}$$

for each ${\mathbf {b}}_{-i}$ with the strict inequality for some ${\mathbf {b}}^{\prime }_{-i}$ where (i) ${\mathbf {b}}_{-i}(v_{-i}), {\mathbf {b}}_{-i}^{\prime }(v_{-i})\in \times _{j\ne i} W_{j}(v_{j})$ for each $v_{-i}\in V_{-i}$ and (ii) for each $v\in V$ and $({\mathbf {b}}_{i}(v_{i}), {\mathbf {b}}_{-i}(v_{-i}))$,

$$\begin{aligned}&\eta ({\mathbf {b}}_{i}(v_{i}), {\mathbf {b}}_{-i}(v_{-i}))\\&\quad = \left\{ \begin{array}{c} 1 \\ \eta \end{array} \right\} \text { if } \left\{ \begin{array}{c} {\mathbf {b}}_{i}(v_{i}) \ne \bar{{\mathbf {b}}}_{i} \\ {\mathbf {b}}_{i}(v_{i}) = \bar{{\mathbf {b}}}_{i} \text { and } \# \{ j\ne i \text{ s.t. } {\mathbf {b}}_{j}(v_{j}) = \bar{{\mathbf {b}}}_{i} \} = \eta -1 \end{array} \right\} \end{aligned}$$

where $\bar{{\mathbf {b}}}_{i} = \max _{j\ne i} \{ {\mathbf {b}}_{j} (v_{j}) \}$.⁷ Regarding $\eta ({\mathbf {b}}_{i}(v_{i}), {\mathbf {b}}_{-i}(v_{-i}))$, while the former includes the cases where player i’s bid is either the unique highest or not the highest, the latter includes the cases where player i is one of the players with the highest bid.⁸ Given W, we say that ${\mathbf {b}}_{i}(v_{i})$ is weakly dominated in W if there exists ${\mathbf {b}}_{i}^{\prime }(v_{i})$ which weakly dominates ${\mathbf {b}}_{i}(v_{i})$ in W. Since we apply weak dominance conditional on a player’s realized value, it is interim weak dominance.

We now define the iterative maximal elimination of weakly dominated bids. For each $i\in N$ and $v_{i}\in V_{i}$, let $W_{i}^{0}(v_{i})= B_{i}$ and let $W^{0}$ be the corresponding collection. Given $W^{t}$, we define $W^{t+1}$ recursively for each $t=0,1,\ldots$:

$$\begin{aligned} W_{i}^{t+1}(v_{i}) = \left\{ b_{i} \in W_{i}^{t}(v_{i}) \mid b_{i} \text { is not weakly dominated in } W^{t}\right\} \end{aligned}$$

for each $i\in N$ and $v_{i}\in V_{i}$. Note that the expression above says that any weakly dominated bid is eliminated (i.e., “maximal elimination”). For each $i\in N$ and $v_{i}\in V_{i}$, $b_{i}\in B_{i}$ survives the iterative elimination of weakly dominated bids if $b_{i}\in W_{i}^{\infty }(v_{i})$. In Sect. 3, we refer to the case of $t=1$ while it is $t=\infty$ in Sect. 4.

3 Maximal elimination of weakly dominated bids

In this section, we solve both FPA and SPA via the maximal elimination of weakly dominated bids.

3.1 Winning bids in FPA and SPA

In SPA, for each $i\in N$ and $v_{i}\in V_{i}$, $b_{i}=v_{i}$ is the only bid surviving the maximal elimination of weakly dominated bids (i.e., weakly dominant bid). Given $v\in V$, the winning bid in SPA is hence $\max _{j\in N} \{v_{j}\}$.

For FPA, Battigalli and Siniscalchi (2003, p. 41) and Dekel and Wolinsky (2003, Sect. 4.3) show that for each $i\in N$ and $v_{i}\in V_{i}$, the highest bid which survives the maximal elimination of weakly dominated bids is strictly lower than $v_{i}$.⁹

Lemma 1

(Battigalli and Siniscalchi (2003) and Dekel and Wolinsky (2003)) For each $i\in N$ and $v_{i}\in V_{i}$, the highest bid which survives the maximal elimination of weakly dominated bids in FPA is $\max \{v_{i}-d, 0\}$.

We then have the following result.

Corollary 1

Given $v\in V$, the highest possible winning bid in FPA is $\max \{ \max _{j\in N} \{ v_{j}-d \}, 0 \}$.

Note that if $\underline{v}>0$, the expression is simply $\max _{j\in N}\{v_{j}-d\}$. Corollary 1 leads to the following result.

Lemma 2

Given $v\in V$, the winning bid in SPA is weakly higher than the winning bid in FPA. If $\max _{j\in N} \{v_{j}\}>0$, the winning bid in SPA is strictly higher than the winning bid in FPA.

If $\underline{v}>0$, the latter is indeed the case.

3.2 Revenue comparison

Lemma 2 implies that if two highest values are the same and strictly higher than 0, the revenue of SPA is strictly higher than that of FPA. The following result shows a condition under which this possibility of “ties” outweighs other possibilities, leading to our main result.

Proposition 1

The expected revenue from SPA is strictly higher than that of FPA if

$$\begin{aligned}&d \sum _{ v^{\prime }\in \{\max \{\underline{v}, d\}, \ldots , \bar{v} \} } P \left( \begin{array}{c} \exists i,j \in N \text{ such } \text{ that } v_{i}=v_{j}=v^{\prime } \\ v^{\prime }\ge v_{k} \forall k\in N\backslash \{i,j\} \end{array} \right) \\&\quad > \sum _{ v^{\prime }\in \{\max \{\underline{v}, 2d\}, \ldots , \bar{v} \} } \sum _{ v^{\prime \prime } \in \{ 0, \ldots , v^{\prime }-2d \} } [(v^{\prime }-d)-v^{\prime \prime }] P \left( \begin{array}{c} \exists i, j\in N \text{ such } \text{ that } v_{i}=v^{\prime } \\ v^{\prime }-2d\ge v_{j} = v^{\prime \prime } \ge v_{k} \forall k\in N \backslash \{i,j\} \end{array} \right) . \end{aligned}$$

The expression on the left-hand side of the condition concerns the cases in which the first and second highest values are equal, implying that the revenue from SPA is higher than that of FPA. The expression on the right-hand side concerns the cases where the difference between the first and second highest values are at least 2d, implying that the revenue from FPA can be higher than that of SPA.¹⁰ The condition thus implies the former dominates the latter, implying the result. In other words, if the chance that the highest and the second highest values are the same is sufficiently high, the expected revenue from SPA is higher than that of FPA.

Observation 1

Given that values are linear in d, the expressions on both sides are linear in d, implying that d’s in both sides offset each other. In other words, while the number of grids matters for the result, the size of d itself does not.

Fig. 1

Visualization of Proposition 1

To visualize the implication of Proposition 1, Fig. 1 plots the combination of two order statistics, the highest and the second highest values, $v^{\prime }$ and $v^{\prime \prime }$ respectively.

A : :

$v^{\prime }=v^{\prime \prime }$ corresponding to the left-hand side expression of Proposition 1. In this case, (i) SPA leads to a higher revenue than FPA, and (ii) the difference in the revenues is d.

B : :

$v^{\prime }= v^{\prime \prime }+d$ which does not appear in the expression. In this case, FPA and SPA generates the same revenue.

C : :

$v^{\prime }-v^{\prime \prime }\ge 2d$ corresponding to the expression on the right-hand side. They are the cases where (i) FPA generates a higher revenue than SPA and (ii) the difference of revenues is at most $(v^{\prime }-d) - v^{\prime \prime }\ge d$.

The expression in Proposition 1 says that if the realizations in A are likely, SPA generates a higher expected revenue than FPA.

3.3 Large auctions

We now provide a condition on the auctioneer’s belief under which Proposition 1 holds for sufficiently large n.¹¹ Given n, let

• $\bar{N}=\{i\in N \mid \bar{v}\in V_{i} \}$ and $\bar{n}=|\bar{N}|$,

• $q_{n}(\tilde{n})$ be the probability that $\bar{n}=\tilde{n}\in \{1, \ldots , n\}$, and

• $\rho _{i}(v_{i})$ be the probability that player i’s value is $v_{i}\in V_{i}$.

We need the following assumptions:

Assumption 1

Players’ values are independently distributed.

Assumption 2

There exists $\underline{\rho }\in (0,1)$ such that $\rho _{i}(\bar{v})\ge \underline{\rho }$ for each $i\in \bar{N}$.

The expression on the left-hand side in Proposition 1 contains the probabilities that the highest and second highest values are the same. The following result identifies a condition under which the expression in Proposition 1 holds as $n\rightarrow \infty$.¹²

Proposition 2

Given Assumptions 1 and 2, if

$$\begin{aligned} \lim _{n\rightarrow \infty } \left\{ \sum _{\bar{n}=2}^{n}q_{n}(\bar{n}) \left[ 1 - \bar{n} \underline{\rho }(1-\underline{\rho })^{\bar{n}-1} - (1-\underline{\rho })^{\bar{n}} \right] \right\} = 1, \end{aligned}$$

the condition in Proposition 1 holds for sufficiently large n.

The condition implies that as n becomes large, there are a sufficient number of players who has $\bar{v}$ in the support and the chance that there is at most one player whose value is $\bar{v}$ diminishes. Note that if $\bar{v}_{i}=\bar{v}$ for each $i\in N$, $\bar{n}=n$ and hence $q_{n}(n)=1$.

Corollary 2

Given Assumptions 1 and 2, if $\bar{v}_{i}=\bar{v}$ for each $i\in N$, Proposition 1 holds for sufficiently large n.

As an example, consider the case of $V_{i}=\{0, \ldots , \bar{v}\}$ for each $i\in N$ and each player’s value is independently and uniformly distributed. Let $|V|=m+1$ (i.e., $\bar{v}=md$) and hence the probability attached to each value is $\frac{1}{m+1}$. The expression in Proposition 1 becomes

$$\begin{aligned}&d \sum _{i = 2}^{ m+1} \left( \begin{array}{c} n \\ 2 \end{array} \right) \left( \frac{1}{m+1} \right) ^{2} \left( \frac{ i }{m+1} \right) ^{n-2} \\&\quad > \sum _{i = 3}^{m+1} \sum _{j=1}^{i-2} [(i-1)-j]d \left( \begin{array}{c} n \\ 1 \end{array} \right) \left( \frac{1}{m+1} \right) \left( \begin{array}{c} n-1 \\ 1 \end{array} \right) \left( \frac{1}{m+1} \right) \left( \frac{j}{m+1} \right) ^{n-2} \\ \end{aligned}$$

which can be simplified as:

$$\begin{aligned} \sum _{i= 2}^{ m +1} i^{n-2} - 2 \sum _{i = 3}^{ m+1 } \sum _{j = 1}^{i-2} (i-j-1) j^{n-2} >0. \end{aligned}$$

(1)

For large m, it is sufficient for the number of players, n, to be approximately 88.2% of m to maintain (1).

4 Iterative maximal elimination of weakly dominated bids

The result for FPA is not as sharp as that of SPA. This is because we have focused on (one round of) the maximal elimination of weakly dominated bids and strictly increasing utility functions. If we use the iterative maximal elimination of weakly dominated bids and weakly concave (still strictly increasing) utility functions, we obtain a condition under which the uniqueness result (i.e., for each $i\in N$ and $v_{i}\in V_{i}$, only one bid survives iterative weak dominance) is achieved for FPA. This is a variant of the results from Dekel and Wolinsky (2003) and Robles and Shimoji (2012) which use rationalizability.¹³ This result leads to the virtual revenue equivalence.

4.1 Uniqueness in FPA

In this subsection, we show a condition under which each player $i\in N$ with $v_{i}\in V_{i}$ has a unique bid surviving the iterative maximal elimination of weakly dominated bids. Let

• player $i^{\prime }\in N$ be such that $\bar{v}_{i^{\prime }} = \bar{v}$ and $\hat{v}=\max _{j\ne i^{\prime }} \{\bar{v}_{j}\}$ (i.e., the second highest upper bound).

We need the following assumption:

Assumption 3

For each $i\in N$, $u_{i}$ is weakly concave.

We then have the following result:

Proposition 3

Suppose Assumption 3 holds. For each $\alpha \in \{2, \ldots , \frac{\min \{\bar{v}-d, \hat{v}\}}{d} \}$, suppose that the following expression holds for each $i\in N$ with $v_{i}\ge (\alpha +1)d$:

$$\begin{aligned} \sum _{k=0}^{n-1} p_{v_{i}}\left( | \# \text { of } j\text {'s such that } v_{j}\ge \alpha d | = k \right) \frac{1}{k+1} \le \frac{v_{i}- \alpha d}{v_{i}-(\alpha -1)d}. \end{aligned}$$

Then,

• if $\bar{v}-\hat{v}\le d$, the only bid which survives iterative weak dominance is $b_{i}= \max \{ v_{i}-d,0\}$ for each $i\in N$ and $v_{i}\in V_{i}$, and

• if $\bar{v}-\hat{v}\ge 2d$, the only bid which survives iterative weak dominance is

  • 1. $b_{i}= \max \{ v_{i}-d,0\}$ for each i with $v_{i}\le \hat{v}+d$ and

  • 2. $b_{i^{\prime }}=\hat{v}$ for player $i^{\prime }$ with $v_{i^{\prime }} \ge \hat{v} +2d$.

Note that the right-hand side expression in the condition is at least $\frac{1}{2}$. The result is visualized in Fig. 2.

Fig. 2

Uniqueness in FPA

We already know that for $v_{i}\in \{0,d\}$, $b_{i}=0$ is the unique weakly dominant bid. With the assumption that $u_{i}$ is weakly concave, we can also show that for any $v_{i}\ge 2d$, $b_{i}=0$ is eliminated. Consider $v_{i}\ge 3 d$ and compare $b_{i}=d$ and $b_{i}=2d$:

• 1. $b_{i}=2d$ may win even if $b_{i}=d$ does not win (but not vice versa). In particular, if the opponents’ highest bid is 2d, the expected utility from $b_{i}=2d$ is strictly positive while it is zero for $b_{i}=d$.

• 2. If $b_{i}=d$ wins, the opponents’ highest bid is either d or 0. This is the only case where the expected utility from $b_{i}=2d$ may be lower than that of $b_{i}=d$. In this particular scenario, given the argument above,

  • $b_{j}=d$ for every $j\in N$ with $v_{j}\ge 2d$, and

  • $b_{j}=0$ (only surviving bid) for every $j\in N$ with $v_{j}\le d$.

  The corresponding utility is $u_{i}(v_{i}-d)$. The left-hand side expression in the condition corresponds to the probability that $b_{i}=d$ wins. Note that $b_{i}=2d$ wins in this case and the corresponding utility is $u_{i}(v_{i}-2d)$.

The condition in Proposition 3 rather states that the expected return from $b_{i}=2d$ is higher than that of $b_{i}=d$ if the opponents’ highest bid is either d or 0. This condition is sufficient as long as $u_{i}$ is weakly concave (Jensen’s inequality). The same argument is applied repeatedly to obtain the result.

We would like to emphasize two points. First, note that the condition in Proposition 3 is easier to be satisfied if, for player $i\in N$ with $v_{i}\ge (\alpha +1)d$, it is more likely that a large number of the opponents have values weakly higher than $\alpha d$. This can be seen in the example in the next subsection. Second, given that we allow heterogeneous beliefs, there are two reasons that neither of the conditions in Propositions 1 and 3 implies the other.¹⁴ One reason is that while the condition in Proposition 1 concerns the auctioneer’s belief regarding players’ values, the condition in Proposition 3 is related to players’ beliefs regarding opponents’ values. The other reason is a difference in their focuses. The condition in Proposition 1 looks at two order statistics, the highest and the second highest values. It thus has no implication about other lower values. The condition in Proposition 3, instead, concerns how many opponents have values above the threshold. It therefore does not say anything about how many of them have the highest and the second-highest values.

4.2 Example: condition of Proposition 3 and upper bounds in FPA

In this subsection, we provide a simple example for two reasons. First, the example demonstrates how the iterative elimination procedure works. This is, in particular, in relation to the condition in Proposition 3. Second, Lemma 1 identifies an upper bound of bid for each value in FPA. This becomes tight once we use the iterative maximal elimination of weakly dominated bids under the condition in Proposition 3. The example shows that if the condition in Proposition 3 does not hold, however, the application of the iterative maximal elimination of weakly dominated bids may lead to lower upper bounds in FPA.¹⁵

Consider two-player independent private-value FPA with $d=1$. The set of values for player $i=1,2$ is $V_{i}=\{0,1,2,3\}$ and let $B_{i}=V_{i}$. The chance of each $v_{i}$ is $\rho (0)=\alpha$, $\rho (1)=\beta$, $\rho (2)=\gamma$, and $\rho (3)=1-\alpha -\beta -\gamma$ where for each $v_{i}\in V_{i}$, $\rho (v_{i})\in (0,1)$.

First step Lemma 1 says that for each $i\in \{1,2\}$ and $v_{i}\in V_{i}$, any $b_{i}>\max \{ v_{i} -d , 0\}$ is weakly dominated. In addition, assuming that $u_{i}$ is weakly concave for each $i\in N$, $b_{i}=0$ is also weakly dominated for each $i\in \{1,2\}$ and $v_{i}\in \{2,3\}$ at the first step: For $v_{i}\in \{2,3\}$, the expected utility from $b_{i}=0$ is either (i) $\frac{1}{2}(u_{i}(v_{i})+u_{i}(0))$ if $b_{j}=0$ or (ii) $u_{i}(0)$ otherwise. The expected utility from $b_{i}=1$ is (i) $u_{i}(v_{i}-1)$ if $b_{j}=0$, (ii) $\frac{1}{2}(u_{i}(v_{i}-1)+u_{i}(0))$ if $b_{j}=1$ or (iii) $u_{i}(0)$ otherwise. Since

$$\begin{aligned} \textstyle u_{i}(v_{i}-1) \ge u_{i}(\frac{v_{i}}{2}) \ge \frac{1}{2} \left[ u_{i}(v_{i}) + u_{i}(0) \right] \end{aligned}$$

for each $v_{i}\in \{2,3\}$ where the second inequality comes from Jensen’s inequality, $b_{i}=1$ weakly dominates $b_{i}=0$ for each $i\in \{1,2\}$ and $v_{i}\in \{2,3\}$. For each $i\in \{1,2\}$, we have (i) $\{0\}$ for $v_{i}\in \{0,1\}$, (ii) $\{1\}$ for $v_{i}=2$, and (iii) $\{1,2\}$ for $v_{i}=3$ as remaining bids.

Second step Our focus is on $v_{i}=3$. The expected utility from $b_{i}=1$ is

$$\begin{aligned}&\textstyle (\alpha +\beta )u_{i}(2) + \gamma \left[ \frac{1}{2} (u_{i}(2)+u_{i}(0)) \right] \nonumber \\&\quad + (1-\alpha -\beta -\gamma ) \left[ \left\{ \begin{array}{c} \frac{1}{2}(u_{i}(2)+u_{i}(0)) \\ u_{i}(0) \end{array} \right\} \text { if } b_{j}(3) = \left\{ \begin{array}{c} 1 \\ 2 \end{array} \right\} \right] \end{aligned}$$

(2)

while the expected utility from $b_{i}=2$ is

$$\begin{aligned} (\alpha +\beta +\gamma )u_{i}(1) + (1-\alpha -\beta -\gamma ) \left[ \left\{ \begin{array}{c} u_{i}(1) \\ \frac{1}{2}(u_{i}(1)+u_{i}(0)) \end{array} \right\} \text{ if } b_{j}(3) = \left\{ \begin{array}{c} 1 \\ 2 \end{array} \right\} \right] .\nonumber \\ \end{aligned}$$

(3)

Then,

$$\begin{aligned}&(2)-(3) \\&\quad = \textstyle (\alpha +\beta )(u_{i}(2)-u_{i}(1)) + \gamma \left\{ \frac{1}{2}(u_{i}(2)+u_{i}(0)) - u_{i}(1) \right\} \\&\quad (1-\alpha -\beta -\gamma ) \left[ \left\{ \begin{array}{c} \frac{1}{2}(u_{i}(2)+u_{i}(0)) - u_{i}(1) \\ u_{i}(0) - \frac{1}{2}(u_{i}(1)+u_{i}(0)) \end{array} \right\} \text{ if } b_{j}(3) = \left\{ \begin{array}{c} 1 \\ 2 \end{array} \right\} \right] . \end{aligned}$$

Note (i) the first term is strictly positive, and (ii) the second term and the first expression of the third term ($b_{j}(3)=1$) are weakly positive since $u_{i}$ is weakly concave, and (iii) the second expression of the third term ($b_{j}(3)=2$) is strictly negative. First, if $\alpha +\beta$ is close to zero (i.e., the condition in Proposition 3 holds), $b_{i}=2$ weakly dominates $b_{i}=1$ for $v_{i}=3$, consistent with Proposition 3. Second, if $\alpha +\beta$ is close to one instead (i.e., the condition in Proposition 3 does not hold), $b_{i}=1$ strictly dominates $b_{i}=2$ for $v_{i}=3$. In other words, upper bounds of bids may be even lower than what Lemma 1 suggests.

4.3 Large auctions

Consider again the case of large auctions with independent distributions from the previous section. Remember the definition of $\hat{v}$ in the previous subsection: the second highest upper bound. Given n, let

• $\hat{N}_{i} = \{ j\in N\backslash \{i\} \mid \hat{v}\in V_{j} \}$ for each $i\in N$ and $\hat{n}_{i}=|\hat{N}_{i}|$,

• $r_{v_{i},n}(\tilde{n})$ be the probability from the view point of player i with $v_{i}\in V_{i}$ that $\hat{n}_{i}=\tilde{n}\in \{1, \ldots , n-1\}$, and

• $\tau _{i}(v_{i}\ge \tilde{v})$ be the probability that player i’s value $v_{i}\in V_{i}$ is weakly higher than $\tilde{v}$.

Instead of Assumption 2, we require the following:

Assumption 4

There exists $\underline{\tau }\in (0,1)$ such that $\tau _{i}(v_{i}\ge \hat{v})\ge \underline{\tau }$ for each $i\in \hat{N}$.

We then have the following result.

Proposition 4

Given Assumptions 1, 3 and 4, if

$$\begin{aligned} \lim _{n\rightarrow \infty } \left\{ \sum _{\hat{n}_{i}=1}^{n-1} r_{v_{i},n}(\hat{n}_{i}) \frac{1 - (1-\underline{\tau })^{\hat{n}_{i}}}{\hat{n}_{i}\underline{\tau }} \right\} \le \frac{1}{2}, \end{aligned}$$

for each $i\in N$ with $v_{i}\ge 3d$, the result of Proposition 3 holds for sufficiently large n.

For example, the condition holds if $r_{v_{i},n}(\hat{n})$ is lower for smaller $\hat{n}$’s. Again, if $\bar{v}_{i}=\bar{v}$ for each $i\in N$ (i.e., $r_{v_{i},n}(n-1)=1$), the result immediately holds.

Corollary 3

Given Assumptions 1, 3 and 4, if $\bar{v}_{i}=\bar{v}$ for each $i\in N$, Proposition 3 holds for sufficiently large n.

As an example, consider again the case where $V_{i}=\{0, \ldots , md\}$ for each $i\in N$ and the values are independently and uniformly distributed. Given $\alpha \in \{2, \ldots , m-1\}$, the left-hand side expression in Proposition 3 becomes

$$\begin{aligned}&\sum _{k=0}^{n-1}\left( \begin{array}{c} n-1 \\ k \end{array} \right) \left( \frac{m+1-\alpha }{m+1} \right) ^{k} \left( \frac{\alpha }{m+1} \right) ^{(n-1)-k} \left( \frac{1}{k+1} \right) \\&\quad = \frac{m+1}{(m+1-\alpha ) n} \left[ 1 - \left( \frac{\alpha }{m+1} \right) ^{n} \right] . \end{aligned}$$

Remember that the right-hand side expression in Proposition 3 is at least $\frac{1}{2}$. Thus, for any $\alpha \in \{ 2, \ldots , m-1\}$, $n\ge m+1$ suffices.

Given Corollaries 2 and 3 above, we have the following result.¹⁶

Proposition 5

Given Assumptions 1, 2, 3 and 4, if $\bar{v}_{i}=\bar{v}$ for each $i\in N$, the difference of the expected revenues from FPA and SPA via iterative weak dominance converges to d as $n\rightarrow \infty$.

This can be seen as the virtual revenue equivalence result for small d in large auctions.

5 Discussion

In this section, we discuss (i) the order dependence of weak dominance, and (ii) the comparison of our result to Kirkegaard (2012).

5.1 Order dependence

The emphasis on “maximal” elimination is due to the possibility of the order dependence of weak dominance.¹⁷ That is, different orders of elimination could lead to different predictions. As an example, consider the two-player SPA where the supports of their values, $V_{i}=\{ \underline{v}_{i}, \ldots , \bar{v}_{i}\}$ for each $i\in \{1,2\}$, is such that $\bar{v}_{2}<\underline{v}_{1}$. First, eliminate all bids except $b_{1}=v_{1}$ for player 1 with $v_{1}\in V_{1}$ at the first step. Then, for player 2, eliminate every $b_{2}\ge \underline{v}_{1}$ at the second step. No further elimination occurs. In this case, the second highest bid can be higher or lower than $v_{2}$, and the price the winner (player 1) pays cannot be uniquely identified for any $v_{2}\in V_{2}$. Note that this applies not only to our result, but also to previous studies which use weak dominance for SPA.

Despite this observation, to support our use of maximal elimination, we point out that Brandenburger et al. (2008) provide an epistemic foundation for the iterative maximal elimination of weakly dominated strategies.¹⁸

5.2 On Kirkegaard (2012)

Kirkegaard (2012) identifies two conditions under which FPA leads to a higher expected revenue than SPA. There are several reasons why our result is different from that of Kirkegaard (2012). One reason is that values and bids are discrete in our setting while they are continuous in Kirkegaard (2012)—a tie is not possible in Kirkegaard (2012). Another reason is that while our focus is on weak dominance, Kirkegaard (2012) uses Bayesian Nash Equilibrium for FPA. We now demonstrate that even if (a discretized version of) a condition in Kirkegaard (2012) is satisfied in our discrete setting, it is possible that our condition still hold.¹⁹

Kirkegaard (2012) considers the case of (i) two players and (ii) the bid and value spaces are continuous. Take $V_{i}^{\prime }$ as a closed interval for $i\in \{1, 2\}$, i.e,. $V_{i}^{\prime }={[}\underline{v}_{i}, \bar{v}_{i}{]}$. Kirkegaard (2012) assumes that the supports for values are such that $0\le \underline{v}_{2}\le \underline{v}_{1}$ and $\bar{v}_{2} {<} \bar{v}_{1}$ (player 1 is strong and player 2 is weak). Let $F_{i}(v)$ be the pdf for player i’s value. Kirkegaard (2012) assumes

$$\begin{aligned} \frac{ f_{1}(v) }{ F_{1}(v) } \ge \frac{ f_{2}(v) }{ F_{2}(v) } \text { and } \frac{ f_{1}(v) }{ 1- F_{1}(v) } \le \frac{ f_{2}(v) }{ 1 - F_{2}(v) } \text { for any } v\in V_{1}^{\prime }\cap V_{2}^{\prime }. \end{aligned}$$

(4)

That is, $F_{1}$ dominates $F_{2}$ in terms of not only the reverse hazard rate but also the hazard rate. Given $v_{2}$, let $r(v_{2})= F_{1}^{-1} (F_{2}(v_{2}))$ (or $F_{1}(r(v_{2})) = F_{2}(v_{2})$). The sufficient condition in Kirkegaard (2012, Expression (9)) is

$$\begin{aligned} f_{2}(v_{2}) \ge f_{1}(v_{1}) \text { for all } v_{2}\in V_{2}^{\prime } \text { and } v_{1}\in [v_{2}, r(v_{2})]. \end{aligned}$$

(5)

Note that in the discrete setting, there does not exist the corresponding $r(v_{2})$ for each $v_{2}\in V_{2}$ generically. Thus, we instead require (5) to hold for every $v_{1}\in \{ v_{2}, \ldots , \bar{v}_{1} \}$. We also look at the discretized version of (4).

We now turn to an example in the discrete setting. Consider the following example:

$$\begin{aligned} V_{1}= & {} \{ \underline{v}_{2}, \underbrace{ \underline{v}_{2}+d, \ldots , \bar{v}_{2}}_{\kappa }, \bar{v}_{2}+d \} \text{ and } \\ V_{2}= & {} \{ \underline{v}_{2}, \underbrace{ \underline{v}_{2}+d, \ldots , \bar{v}_{2} }_{\kappa } \} \end{aligned}$$

where (i) $\underline{v}_{2}>0$ and (ii) $\kappa$ is a positive integer. Note that $\bar{v}_{1}=\bar{v}_{2}+d$ and hence $V_{2}\subset V_{1}$. The players’ values are independently distributed. Let

• $\rho _{1}(v_{1})=\varepsilon$ for each $v_{1}\in V_{1}\backslash \{\underline{v}_{2}\}$ and $\rho _{2}(v_{2})=\varepsilon$ for each $v\in V_{2}\backslash \{\underline{v}_{2}\}$, and

• $\rho _{1}(\underline{v}_{2}) = 1- (\kappa +1)\varepsilon$ and $\rho _{2}(\underline{v}_{2})=1-\kappa \varepsilon$.

We also assume that $\varepsilon$ is sufficiently small.

The first inequality in (4) holds with the equality for $\underline{v}_{2}$ and with the strict inequality for every $v\in V_{2}\backslash \{\underline{v}_{2}\}$. The second inequality in (4) holds with strict inequality for every $v\in V_{2}$. The inequality in (5) holds with the strict inequality for $\underline{v}_{2}$ and with the equality for every $v_{1}\in V_{1}\backslash \{\underline{v}_{2}\}$ and $v_{2}\in V_{2}\backslash \{\underline{v}_{2}\}$. Consider the expression in Proposition 1. For sufficiently small $\varepsilon$, the sum of probabilities on the left-hand side is close to one, implying that the inequality is satisfied.²⁰

Appendices

Appendix A: Proof of Proposition 1

The highest possible revenue in FPA is $\max \{ \max _{i\in N} \{ v_{i}-d \},0 \}$. The revenue in SPA is the second highest value. Note that if there are multiple highest values which are strictly higher than 0, the revenue from SPA is strictly higher than that of FPA.

Let $v^{\prime }$ be the highest value and $v^{\prime \prime }$ be the second highest value. The expected revenue from SPA (left-hand side) is strictly higher than that of FPA (right-hand side) if

$$\begin{aligned}&\sum _{ v^{\prime }\in \{\max \{\underline{v}, d\}, \ldots , \bar{v} \} } \sum _{ v^{\prime \prime } \in \{ 0, \ldots , v^{\prime } \} } v^{\prime \prime } P \left( \begin{array}{c} \exists i, j\in N \text{ such } \text{ that } \\ v^{\prime } = v_{i} \ge v^{\prime \prime } = v_{j} \ge v_{k} \forall k\in N \backslash \{i,j\} \end{array} \right) \\&\quad> \sum _{ v^{\prime }\in \{\max \{\underline{v},d\}, \ldots , \bar{v} \} } (v^{\prime }-d) P \left( \begin{array}{c} \exists i\in N \text{ such } \text{ that } \\ v_{i}=v^{\prime }\ge v_{j} \forall j\in N\backslash \{i\} \end{array} \right) \\&\quad \Leftrightarrow \sum _{ v^{\prime }\in \{\max \{\underline{v},d\}, \ldots , \bar{v} \} } v^{\prime } P \left( \begin{array}{c} \exists i,j \in N \text{ such } \text{ that } v_{i}=v_{j}=v^{\prime } \\ v^{\prime }\ge v_{k} \forall k\in N\backslash \{i,j\} \end{array} \right) \\&\qquad + \sum _{ v^{\prime }\in \{\max \{\underline{v},d\}, \ldots , \bar{v} \} } (v^{\prime }-d) P \left( \begin{array}{c} \exists i,j \in N \text { such that } v_{i} = v^{\prime } \\ v_{j} = v^{\prime }-d \ge v_{k} \forall k\in N\backslash \{i,j\} \end{array} \right) \\&\qquad + \sum _{ v^{\prime }\in \{\max \{\underline{v},2d\}, \ldots , \bar{v} \} } \sum _{ v^{\prime \prime } \in \{ 0, \ldots , v^{\prime }-2d \} } v^{\prime \prime } P \left( \begin{array}{c} \exists i, j\in N \text{ such } \text{ that } v_{i}=v^{\prime } \\ v^{\prime }-2d\ge v_{j} = v^{\prime \prime } \ge v_{k} \forall k\in N \backslash \{i,j\} \end{array} \right) \\&\quad> \sum _{v^{\prime } \in \{\max \{\underline{v},d\}, \ldots , \bar{v}\}} (v^{\prime }-d) P \left( \begin{array}{c} \exists i, j\in N \text{ such } \text{ that } v_{i}= v_{j}=v^{\prime } \\ v^{\prime } \ge v_{k} \forall k\in N \backslash \{i,j\} \end{array} \right) \\&\qquad + \sum _{ v^{\prime }\in \{\max \{\underline{v},d\}, \ldots , \bar{v} \} } (v^{\prime }-d) P \left( \begin{array}{c} \exists i, j\in N \text { such that } v_{i}=v^{\prime } \\ v_{j} = v^{\prime }-d \ge v_{k} \forall k\in N \backslash \{i,j\} \end{array} \right) \\&\qquad + \sum _{ v^{\prime }\in \{\max \{\underline{v},2d\}, \ldots , \bar{v} \} } (v^{\prime }-d) \sum _{v^{\prime \prime } \in \{ 0, \ldots , v^{\prime }-2d \} } P \left( \begin{array}{c} \exists i, j\in N \text{ such } \text{ that } v_{i}=v^{\prime } \\ v^{\prime }-2d\ge v_{j} = v^{\prime \prime } \ge v_{k} \forall k\in N \backslash \{i,j\} \end{array} \right) \\&\quad \Leftrightarrow d \sum _{ v^{\prime }\in \{\max \{\underline{v},d\}, \ldots , \bar{v} \} } P \left( \begin{array}{c} \exists i,j \in N \text { such that } v_{i}=v_{j}=v^{\prime } \\ v^{\prime }\ge v_{k} \forall k\in N\backslash \{i,j\} \end{array} \right) \\&\quad > \sum _{ v^{\prime }\in \{\max \{\underline{v},2d\}, \ldots , \bar{v} \} } \sum _{ v^{\prime \prime } \in \{ 0, \ldots , v^{\prime }-2d \} } [(v^{\prime }-d)-v^{\prime \prime }] P \left( \begin{array}{c} \exists i, j\in N \text { such that } v_{i}=v^{\prime } \\ v^{\prime }-2d\ge v_{j} = v^{\prime \prime } \ge v_{k} \forall k\in N \backslash \{i,j\} \end{array} \right) . \end{aligned}$$

Appendix B: Proof for Proposition 2

Given n and $\bar{n}$ where $2\le \bar{n} \le n$, take the probability that the second highest value is $\bar{v}$:

$$\begin{aligned} \sum _{\eta =2}^{\bar{n}} \left[ \sum _{i_{1}\in \bar{N}} \sum _{i_{2}> i_{1}} \cdots \sum _{i_{\eta }>i_{\eta -1} } \rho _{i_{1}}(\bar{v})\rho _{i_{2}}(\bar{v}) \cdots \rho _{i_{\eta }}(\bar{v}) \prod _{k\ne i_{1},\ldots ,i_{\eta }} (1-\rho _{k}(\bar{v})) \right] \end{aligned}$$

(6)

where $\{i_{1}, \ldots , i_{\eta }\}\subseteq \bar{N}$. The lower bound of the expression above is

$$\begin{aligned}&\sum _{\eta =2}^{\bar{n}} \left( \begin{array}{c} \bar{n} \\ \eta \end{array} \right) \underline{\rho }^{\eta } (1-\underline{\rho })^{\bar{n}-\eta } \\&\quad = \sum _{\eta =0}^{\bar{n}} \left( \begin{array}{c} \bar{n} \\ \eta \end{array} \right) \underline{\rho }^{\eta } (1-\underline{\rho })^{\bar{n}-\eta } - \bar{n} \underline{\rho }(1-\underline{\rho })^{\bar{n}-1} - (1-\underline{\rho })^{\bar{n}} \\&\quad = 1 - \bar{n} \underline{\rho }(1-\underline{\rho })^{\bar{n}-1} - (1-\underline{\rho })^{\bar{n}}. \end{aligned}$$

Note that the last two expression converge to zero as $\bar{n}\rightarrow \infty$ (Corollary 2).

The lower bound for the left-hand expression in Proposition 1 (without d) is hence

$$\begin{aligned} \sum _{\bar{n}=2}^{n}q_{n}(\bar{n}) \left[ 1 - \bar{n} \underline{\rho }(1-\underline{\rho })^{\bar{n}-1} - (1-\underline{\rho })^{\bar{n}} \right] . \end{aligned}$$

Hence, if

$$\begin{aligned} \lim _{n\rightarrow \infty } \left\{ \sum _{\bar{n}=2}^{n}q_{n}(\bar{n}) \left[ 1 - \bar{n} \underline{\rho }(1-\underline{\rho })^{\bar{n}-1} - (1-\underline{\rho })^{\bar{n}} \right] \right\} = 1, \end{aligned}$$

the expression on the left-hand side of Proposition 1 converges to d while the one on the right-hand side converges to zero.

Appendix C: Revenue comparison: uniform example

Consider again (1):

$$\begin{aligned} \sum _{i= 2}^{ m+1} i^{n-2} - 2\sum _{i = 3}^{ m+1 } \sum _{j = 1}^{i-2} (i-j-1) j^{n-2}>0, \end{aligned}$$

or

$$\begin{aligned} 2^{n-2} + \sum _{i=3}^{m+1} \left[ i^{n-2} - 2 \sum _{j=1}^{i-2}(i-j-1)j^{n-2} \right] > 0. \end{aligned}$$

We compare the terms in the parentheses for each $i\in \{3, \ldots , m+1\}$.

Let

$$\begin{aligned} A(i,n)= & {} i^{n-2} - 2\sum _{j=1}^{i-2}(i-j-1)j^{n-2} \nonumber \\= & {} i^{n-2} - 2\sum _{j=1}^{i-2}j^{n-2} - 2\sum _{j=1}^{i-2}((i-1)-j-1)j^{n-2} \nonumber \\= & {} i^{n-2} - 2\sum _{j=1}^{i-2}j^{n-2} - 2\sum _{j=1}^{i-3}((i-1)-j-1)j^{n-2} \nonumber \\= & {} i^{n-2} -2 \sum _{j=1}^{i-2}j^{n-2} - (i-1)^{n-2} \nonumber \\&+ \left[ (i-1)^{n-2} - 2\sum _{j=1}^{i-3}((i-1)-j-1)j^{n-2} \right] \nonumber \\= & {} i^{n-2} -2 \sum _{j=1}^{i-2}j^{n-2} - (i-1)^{n-2} + A(i-1,n), \end{aligned}$$

(7)

and

$$\begin{aligned} D(i,n)= & {} A(i,n) - A(i-1,n) \nonumber \\= & {} i^{n-2} -2 \sum _{j=1}^{i-2}j^{n-2} - (i-1)^{n-2} \nonumber \\= & {} i^{n-2} -2 \sum _{j=1}^{i-2}j^{n-2} \nonumber \\&-\,(i-1)^{n-2} - \left[ (i-1)^{n-2} -2 \sum _{j=1}^{i-3}j^{n-2} - (i-2)^{n-2} \right] \nonumber \\&+ \left[ (i-1)^{n-2} -2 \sum _{j=1}^{i-3}j^{n-2} - (i-2)^{n-2} \right] \nonumber \\= & {} i^{n-2} - (i-2)^{n-2} -2(i-1)^{n-2} +D(i-1,n). \end{aligned}$$

(8)

For every $i\ge 3$, (i) A(i, n) is strictly increasing in n if $A(i,n)\ge 0$ and (ii) D(i, n) is strictly increasing in n if $D(i,n)\ge 0$:

$$\begin{aligned} \frac{\partial A(i,n)}{\partial n}= & {} i^{n-2} \ln (i) - 2 \sum _{j=1}^{i-2}(i-j-1)j^{n-2} \ln (j)> \ln (i) A(i,n) \\ \frac{\partial D(i,n)}{\partial n}= & {} i^{n-2} \ln (i) - 2 \sum _{j=1}^{i-2}j^{n-2} \ln (j) - (i-1)^{n-2}\ln (i-1) > \ln (i)D(i,n). \end{aligned}$$

Hence, for every $i\ge 3$, if $A(i,n^{\prime })\ge 0$ for some $n^{\prime }$, $A(i,n)>0$ for any $n>n^{\prime }$. Likewise, if $D(i,n^{\prime \prime })\ge 0$ for some $n^{\prime \prime }$, $D(i,n)>0$ for any $n>n^{\prime \prime }$.

We use induction to show that our claim holds. For the initial step, note that

$$\begin{aligned} A(3,n)= & {} 3^{n-2} - (2\times 1^{n-2})> 0 \\ D(3,n)= & {} 3^{n-2} -(2\times 1^{n-2}) - 2^{n-2} > 0 \end{aligned}$$

for any $n\ge 4$.

Suppose now that there exist $\tilde{i}\ge 3$ and $\tilde{n}\ge 4$ such that for each $i\in \{3, \ldots , \tilde{i}\}$, $A(i,\tilde{n})> 0$ and $D(i,\tilde{n})> 0$ (this is the case for $\tilde{i}=3$ and $\tilde{n}=4$). If $A(\tilde{i}+1,\tilde{n})>0$, choosing $n=\tilde{n}$ suffices. Suppose instead $A(\tilde{i}+1,\tilde{n})\le 0$. Given that $A(\tilde{i},\tilde{n})>0$ and $D(\tilde{i},\tilde{n})> 0$, it suffices to find $n^{*}>\tilde{n}$ such that,

$$\begin{aligned} (\tilde{i}+1)^{n^{*}-2} - (\tilde{i}-1)^{n^{*}-2} -2\tilde{i}^{n^{*}-2} \ge 0. \end{aligned}$$

This is because $A(\tilde{i},n^{*})>0$ and $D(\tilde{i}, n^{*})>0$. The inequality above implies $D(\tilde{i}+1,n^{*})>0$ and hence $A(\tilde{i}+1.n^{*})>0$.

Note that

$$\begin{aligned}&i^{n-2} - (i-2)^{n-2} - 2(i-1)^{n-2} \\&\quad = (i-1)^{n-2} \left\{ \left( \frac{i}{i-1} \right) ^{n-2} - \left( \frac{i-2}{i-1} \right) ^{n-2} - 2 \right\} \\&\quad = (i-1)^{n-2} \left\{ \left[ \left( 1 + \frac{1}{i-1} \right) ^{i-1} \right] ^{\frac{n-2}{i-1}} - \left[ \left( 1 - \frac{1}{i-1} \right) ^{i-1} \right] ^{\frac{n-2}{i-1}} -2 \right\} \end{aligned}$$

where (i) the expression in the parentheses is strictly increasing with respect to the power (i.e., $\frac{n-2}{i-1}$) and (ii) we have $\lim _{i\rightarrow \infty }(1+\frac{1}{i-1})^{i-1}=e$ and $\lim _{i\rightarrow \infty } (1-\frac{1}{i-1})^{i-1} = e^{-1}$. Let $\ln (y)=\frac{n-2}{i-1}$ and we have

$$\begin{aligned} e^{ ln(y) } - \frac{1}{ e^{ln(y)} } \ge 2\Leftrightarrow & {} y^{2} - 2y - 1 \ge 0 \end{aligned}$$

where (i) $y=1+\sqrt{2}$ if the expression is zero and (ii) the expression is strictly increasing if $y>1$. Note that $\ln {(1+\sqrt{2})}\approx 0.8813$.²¹

Appendix D: Proof for Proposition 3

First step

• For each $i\in N$ and $v_{i}\in V_{i}\backslash \{0\}$, every $b_{i}\ge v_{i}$ is weakly dominated. None of them leads to a utility strictly higher than $u_{i}(0)$ while $b_{i}<v_{i}$ secures $u_{i}(0)$ or higher (e.g., the opponents’ highest bid is equal to $b_{i}$).

• For each $i\in N$ with $v_{i}=0$, every $b_{i}\ge d$ is weakly dominated. Every $b_{i}\ge d$ leads to a utility of $u_{i}(0)$ or less (e.g., every opponent bids zero) and $b_{i}=0$ guarantees $u_{i}(0)$.

• For each $i\in N$ with $v_{i}\ge 2d$, $b_{i}=d$ weakly dominates $b_{i}=0$. The only way $b_{i}=0$ wins is that every opponent bids zero as well. In this case, the expected utility with $b_{i}=0$ is $\frac{1}{n}u_{i}(v_{i})+\frac{n-1}{n}u_{i}(0)$ while it is $u_{i}(v_{i}-d)$ with $b_{i}=d$. Since $n\ge 2$, we have

  $$\begin{aligned} \textstyle u_{i}(v_{i}-d)= & {} u_{i}\left( \frac{v_{i}-d}{v_{i}} v_{i} \right) \ge \left( \frac{v_{i}-d}{v_{i}}\right) u_{i}(v_{i}) + \left( \frac{d}{v_{i}} \right) u_{i}(0) \\\ge & {} \left( \frac{1}{n} \right) u_{i}(v_{i}) + \left( \frac{n-1}{n} \right) u_{i}(0) \end{aligned}$$

  for any weakly concave $u_{i}$.²² For the other possibilities, $b_{i}=d$ leads to a utility weakly higher than that of $b_{i}=0$ (i.e., $u_{i}(0)$). In particular, if the opponents’ highest bid is d, the inequality is strict.

The sets of bids surviving the maximal elimination of weakly dominated bids are (i) $\{ \max \{v_{i}-d,0\} \}$ for $v_{i}\in \{0,d,2d\}$—note that they are unique—and (ii) $\{ d, \ldots , v_{i}-d \}$ for $v_{i}>2d$. We need to check that for every $v_{i}>2d$, no other bid is eliminated. For each $v_{i}>2d$, take any $b_{i}, \check{b}_{i} \in \{ d, \ldots , v_{i}-d \}$ where $\check{b}_{i}<b_{i}$.

• 1. $\check{b}_{i}$ does not weakly dominate $b_{i}$; if the opponents’ highest bid is $b_{i}$, the expected utility from $b_{i}$ is strictly higher than $u_{i}(0)$ while $\check{b}_{i}$ only leads to $u_{i}(0)$.

• 2. $b_{i}$ does not weakly dominate $\check{b}_{i}$; if the opponents bid zero, the utility from $\check{b}_{i}$ is strictly higher than that of $b_{i}$.

This completes the first step.²³

As in the main text, let $i^{\prime }\in N$ be such that $\bar{v}_{i^{\prime }}=\bar{v}$ and $\hat{v}=\max _{j\ne i^{\prime }} \{\bar{v}_{j} \}$. The next part is included if $\bar{v}-\hat{v}\ge 2d$.

Second step For player $i^{\prime }\in N$ with $v_{i^{\prime }}\ge \hat{v}+2d$, every $b_{i^{\prime }}\ge \hat{v}+d$ is weakly dominated since the highest possible bid of the opponents is $\hat{v}-d$.

In effect, we treat player $i^{\prime }$ with $v_{i^{\prime }}\ge \hat{v}+2d$ as $\hat{v}+d$ from the third step. The repetition of the next step leads to the result.

$\mathbf {\alpha }$-th step ($\alpha \ge 2$) Suppose that there exists $\alpha \ge 2$ such that for each $i\in N$, the set of remaining bids are

• $\{\max \{v_{i}-d, 0\}\}$ for $v_{i}\le \alpha d$, and

• $\{(\alpha -1)d, \ldots , v_{i}-d\}$ for $v_{i}\ge (\alpha +1)d$.²⁴

Take player $i\in N$ with $v_{i}\ge (\alpha +1)d$. We compare $b_{i}=(\alpha -1)d$ and $b_{i}=\alpha d$. Note that $b_{i}=(\alpha -1)d$ wins only if $b_{j}\le (\alpha -1)d$ for each $j\in N\backslash \{i\}$. In this scenario, the expected utility from $b_{i}=(\alpha -1)d$ is

$$\begin{aligned}&\sum _{k=0}^{n-1} p_{v_{i}}( | \# \text { of }j\text {'s such that } v_{j}\ge \alpha d | = k ) \left[ \left( \frac{1}{k+1} \right) u_{i}(v_{i}-(\alpha -1)d) \right. \nonumber \\&\quad \left. + \left( \frac{k}{k+1} \right) u_{i}(0) \right] \end{aligned}$$

(9)

while the utility from $b_{i}=\alpha d$ is $u_{i}(v_{i}-\alpha d)$.²⁵ Jensen’s inequality implies

$$\begin{aligned}&(9) \\\le & {} \sum _{k=0}^{n-1} p_{v_{i}} ( | \# \text { of }j\text { 's such that } v_{j}\ge \alpha d | = k ) u_{i} \left( \frac{v_{i}-(\alpha -1)d}{k+1} \right) \\\le & {} u_{i} \left( \sum _{k=0}^{n-1}p_{v_{i}} ( | \# \text { of }j\text {'s such that } v_{j}\ge \alpha d | = k ) \frac{v_{i}-(\alpha -1)d}{k+1} \right) . \end{aligned}$$

Since $u_{i}$ is strictly increasing, the inequality below is equivalent to $u_{i}(v_{i}-\alpha d) \ge$ (9):

$$\begin{aligned} v_{i}-\alpha d \ge \sum _{k=0}^{n-1} p_{v_{i}} ( | \# \text { of } j\text {'s such that } v_{j}\ge \alpha d | = k ) \frac{v_{i}-(\alpha -1)d}{k+1} \end{aligned}$$

or

$$\begin{aligned} \frac{ v_{i}-\alpha d }{ v_{i}-(\alpha -1)d } \ge \sum _{k=0}^{n-1} p_{v_{i}} ( | \# \text { of }j\text {'s such that } v_{j}\ge \alpha d | = k ) \frac{1}{k+1}. \end{aligned}$$

For the other profiles of the opponents’ bids, $b_{i}=\alpha d$ leads to a utility weakly higher than that of $b_{i}=(\alpha -1)d$. In particular, if the opponents’ highest bid is $\alpha d$, the inequality is strict. Hence, under the condition above, $b_{i}=\alpha d$ weakly dominates $b_{i}=(\alpha -1)d$ for each $i\in N$ with $v_{i}\ge (\alpha +1)d$.

Then, the remanning bids are

• $\{ \max \{v_{i}-d, 0\} \}$ for $v_{i}\le (\alpha +1)d$, and

• $\{ \alpha d, \ldots , \min \{v_{i}-d, \hat{v}\} \}$ for $v_{i}\ge (\alpha +2)d$.

We need to check that for each $i\in N$ with $v_{i}\ge (\alpha +2)d$, no other bid is eliminated. For each $v_{i}\ge (\alpha +2)d$, take any $b_{i}, \check{b}_{i}\in \{ \alpha d, \ldots , \min \{v_{i}-d, \hat{v}\} \}$ where $\check{b}_{i}<b_{i}$.

• 1. $\check{b}_{i}$ does not weakly dominate $b_{i}$; if the opponents’ highest bid is $b_{i}$, the expected utility from $b_{i}$ is strictly higher than $u_{i}(0)$ while $\check{b}_{i}$ only leads to $u_{i}(0)$.

• 2. $b_{i}$ does not weakly dominate $\check{b}_{i}$; if the opponent’s highest bid is $(\alpha -1)d$ or less, the utility from $\check{b}_{i}$ is strictly higher than that of $b_{i}$.

This completes the $\alpha$-th step. The repetition of the same argument leads to our claim.

Appendix E: Proof of Proposition 4

Given $\hat{N}$, when players’ values are independently distributed, the upper bound for the left-hand side of the condition in Proposition 3 (i.e., the chance that $b_{i}=(\alpha -1)d$ wins) is

$$\begin{aligned}&\sum _{k=0}^{\hat{n}-1} \left( \begin{array}{c} \hat{n}-1 \\ k \end{array} \right) \underline{\tau }^{k} (1-\underline{\tau })^{(\hat{n}-1)-k} \left( \frac{1}{k+1} \right) \\&\quad = \sum _{k=0}^{\hat{n}-1} \frac{(\hat{n}-1)!}{(k+1)!((\hat{n}-1)-k)!} \underline{\tau }^{k} (1-\underline{\tau })^{(\hat{n}-1)-k} \\&\quad = \frac{1}{\hat{n} \underline{\tau }} \sum _{k=0}^{\hat{n}-1} \frac{\hat{n}!}{(k+1)!(\hat{n}-(k+1))!} \underline{\tau }^{k+1} (1-\underline{\tau })^{\hat{n}-(k+1)} \\&\quad = \frac{1}{\hat{n} \underline{\tau }} \sum _{l=1}^{\hat{n}} \frac{\hat{n}!}{l!(\hat{n}-l)!} \underline{\tau }^{l} (1-\underline{\tau })^{\hat{n}-l} \\&\quad = \frac{1 - (1-\underline{\tau })^{\hat{n}}}{\hat{n}\underline{\tau }}. \end{aligned}$$

Note that there are at least two players who can have the values weakly higher than $\hat{v}$. Hence, given the definition of $\hat{v}$, $\hat{n}_{i}\ge 1$ for each $i\in N$.²⁶ Therefore, if

$$\begin{aligned} \lim _{n\rightarrow \infty } \left\{ \sum _{\hat{n}_{i}=1}^{n-1} r_{v_{i},n}(\hat{n}_{i}) \frac{ 1 - (1-\underline{\tau })^{\hat{n}_{i}}}{\hat{n}_{i}\underline{\tau }} \right\} \le \frac{1}{2} \end{aligned}$$

for each $i\in N$ with $v_{i}\ge 3d$, the condition in Proposition 3 holds. Remember that the expression on the right-hand expression in the condition of Proposition 3 is weakly higher than $\frac{1}{2}$.

Appendix F: Virtual revenue equivalence: uniform example

Given $\alpha$, we have

$$\begin{aligned}&\sum _{k=0}^{n-1}\left( \begin{array}{c} n-1 \\ k \end{array} \right) \left( \frac{m+1-\alpha }{m+1} \right) ^{k} \left( \frac{\alpha }{m+1} \right) ^{(n-1)-k} \left( \frac{1}{k+1} \right) \\&\quad = \left( \frac{1}{m+1} \right) ^{n-1} \sum _{k=0}^{n-1} \frac{ (n-1)! }{ k! [(n-1)-k]! } (m+1-\alpha )^{k} \alpha ^{(n-1)-k} \left( \frac{1}{k+1} \right) \\&\quad = \left( \frac{1}{m+1} \right) ^{n-1} \sum _{k=0}^{n-1} \frac{(n-1)!}{(k+1)!(n-(k+1))!} (m+1-\alpha )^{k} \alpha ^{(n-1)-k} \\&\quad = \frac{1}{(m+1-\alpha ) n} \left( \frac{1}{m+1} \right) ^{n-1} \sum _{k=0}^{n-1} \frac{n!}{(k+1)!(n-(k+1))!}\\&\qquad (m+1-\alpha )^{k+1} \alpha ^{(n-1)-k} \\&\quad = \frac{1}{(m+1-\alpha ) n} \left( \frac{1}{m+1} \right) ^{n-1} \sum _{k=0}^{n-1} \left( \begin{array}{c} n \\ k+1 \end{array} \right) (m+1-\alpha )^{k+1} \alpha ^{(n-1)-k} \\&\quad = \frac{1}{(m+1-\alpha ) n} \left( \frac{1}{m+1} \right) ^{n-1} \sum _{l=1}^{n} \left( \begin{array}{c} n \\ l \end{array} \right) (m+1-\alpha )^{l} \alpha ^{n-l} \\&\quad = \frac{1}{(m+1-\alpha ) n} \left( \frac{1}{m+1} \right) ^{n-1} \left[ \sum _{l=0}^{n} \left( \begin{array}{c} n \\ l \end{array} \right) (m+1-\alpha )^{l} \alpha ^{n-l} - \alpha ^{n} \right] \\&\quad = \frac{1}{(m+1-\alpha ) n} \left( \frac{1}{m+1} \right) ^{n-1} \left[ (m+1)^{n} - \alpha ^{n} \right] \\&\quad = \frac{m+1}{(m+1-\alpha ) n} \left[ 1 - \left( \frac{\alpha }{m+1} \right) ^{n} \right] . \end{aligned}$$