Skip to main content
SpringerLink
Log in

Stable and efficient coalitional networks

  • Original Paper
  • Published:
Review of Economic Design Aims and scope Submit manuscript

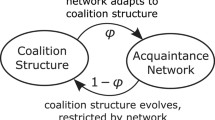
Abstract

We develop a theoretical framework that allows us to study which bilateral links and coalition structures are going to emerge at equilibrium. We define the notion of coalitional network to represent a network and a coalition structure, where the network specifies the nature of the relationship each individual has with her coalition members and with individuals outside her coalition. To predict the coalitional networks that are going to emerge at equilibrium we propose the concepts of strong stability and of contractual stability. Contractual stability imposes that any change made to the coalitional network needs the consent of both the deviating players and their original coalition partners. Requiring the consent of coalition members under the simple majority or unanimity decision rule may help to reconcile stability and efficiency. Moreover, this new framework can provide insights that one cannot obtain if coalition formation and network formation are tackled separately and independently.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. See Jackson (2008) for a comprehensive introduction to the theory of social and economic networks. Kranton and Minehart (2000) have analyzed the endogenous formation of networks between input suppliers and manufacturers while Mauleon et al. (2011) have studied the formation of networks between manufacturers and retailers. Wang and Watts (2006) have examined the formation of buyer-seller networks when sellers can form an association of sellers to pool their customers. Bloch et al. (2008) have studied bilateral insurance schemes across networks of individuals.

  2. Bloch and Dutta (2009) have analyzed the formation of communication networks when agents choose how much to invest in each link. See also Jackson and Rogers (2005) and Johnson and Gilles (2000).

  3. Basque Y is the name given to the Spanish high-speed rail network being built since 2006 between the three cities of the Basque Country Autonomous Community (Bilbao, Vitoria and San Sebastian). Since the Basque Y will connect Spain with the European high-speed network, the decision of linking the three cities and of the Y-shaped layout required the consent of the Basque Parliament and the Spanish authorities. In addition, The Spanish government manages the construction of the stretches in the provinces of Alava and Bizkaia while the Basque government takes care of the stretches in the province Gipuzkoa. See http://www.euskalyvasca.com/en/home.html.

  4. Colombian-Sicilian networks brought together Colombian cocaine suppliers with Sicilian groups possessing local knowledge, well-established heroin distribution networks, extensive bribery and corruption networks, and a full-fledged capability for money laundering. Italian and Russian criminal networks have also forged cooperative relationships. See Williams (2001).

  5. Rules of exit in alliances (R&D joint ventures, partnerships) are either exit at the will of the larger party subject to forewarning (simple majority rule) or exit without breach via a deadlock implemented by the contractual board where only unanimous decisions are taken (unanimity rule). See Smith (2005).

  6. All individuals who are part of a criminal organization like the Hells Angels are sponsored by an official member and have to gain the approval of 100 percent of members in order to climb the hierarchy. See Morselli (2009). Rules governing entry and exit in labor cooperatives may require the consent of partners. A new partner will enter the cooperative only if (i) she wishes to come in; (ii) her new partners wish to accept her; and (iii) she obtains from her former partners permission to withdraw (only if she was before member of another cooperative). See Drèze and Greenberg (1980).

  7. Notice that strongly stable coalitional networks are not strongly efficient in general.

  8. Caulier et al. (2012) have also considered situations where players are part of a network and belong to coalitions. However, each player’s payoff only depends on the network, and so, each player’s coalition only constrains her ability to add or delete links in the network.

  9. Modeling club structures as bipartite directed networks, Page and Wooders (2010) have formulated the problem of club formation with multiple memberships as a noncooperative game of network formation. See also Bloch and Dutta (2011) for a discussion of some recent literature on the endogenous formation of coalitions and networks.

  10. Throughout the paper we use the notation \(\subseteq \) for weak inclusion and \(\not \subseteq \) for strict inclusion. Finally, \(\#\) will refer to the notion of cardinality.

  11. A nonempty sub-coalitional network consisting of only one coalition is connected since by definition of nonemptyness there is at least one link among players in that coalition.

  12. These first two conditions have been introduced by Jackson and van den Nouweland (2005) to define the networks obtainable from a given network by a coalition \(S\).

  13. Notice that this definition allows the deviating coalition \(S\) to modify either the network structure (moving from \((g,P)\) to \((g^{\prime },P)\) according to conditions (i)-(ii)), or the coalition structure (moving from \( (g,P)\) to \((g,P^{\prime })\) according to conditions (iii)-(iv)), or both of them (moving from \((g,P)\) to \((g^{\prime },P^{\prime })\) according to conditions (i)-(iv)).

  14. Notice that Jackson and van den Nouweland’s (2005) version of strongly stability implies pairwise stability from Jackson and Wolinsky (1996). A network is pairwise stable if no player benefits from severing one of her links and no two players benefit from adding a link between them, with one benefiting strictly and the other at least weakly. However, Dutta and Mutuswami’s (1997) version of strongly stability only implies the strict version of pairwise stability when no two players strictly benefit from adding a link between them.

  15. The relationship between contractual stability under any decision rule embodied by a proportion \(q\) is obvious: a proportion \(q^{\prime }<q\) refines stability. That is, the set of contractually stable coalitional networks under \(q^{\prime }\) is (weakly) included in the set of contractually stable coalitional networks under \(q\). Indeed, the probability to block a deviation is greater the higher the proportion \(q\). When the proportion approaches zero \((q\rightarrow 0)\), coalitional membership has no matter in terms of consent.

  16. Notice that, from \((\{12,13,23\},\{\{1,2,3\}\})\), the most profitable deviation of coalition \(S=\left\{ i,j\right\} \) to a partial network \( g^{\prime }=\left\{ ij\right\} \) is the one in which the coalition structure is the grand coalition; i.e., the deviation to \((\{ij\},\{\{1,2,3\}\})\). Hence, the condition \(c\le 3\delta /4\) is enough to prevent deviations to this partial network with any coalition structure.

  17. As is standard in the IO literature, firms take the knowledge spillovers effect on the other firms’ costs into account when computing their optimal research investment. See Amir (2000), d’Aspremont and Jacquemin (1988), Goyal and Moraga-González (2001) and Mauleon et al. (2008), among others.

  18. All equilibrium expressions and proofs are available from the authors upon request.

  19. This result also holds in general for \(n\ge 3\).

  20. Notice that the results in this section hold because the definitions of contractual stability require for a deviation to be valid that all deviators (and all partners or a majority of them) are strictly better off as in Dutta and Mutuswami (1997).

  21. Jackson (2005b) has proposed a similar algorithm for finding a network that is pairwise stable and Pareto efficient under the classic component-wise egalitarian rule.

  22. See for instance Jackson (2008) or Wasserman and Fraust (1994). Research on community structures mainly deals with the detection of these communities in network data.

References

  • Amir R (2000) Modelling imperfectly appropriable R&D via spillovers. Int J Ind Organ 18:1013–1032

    Article  Google Scholar 

  • Bloch F (1995) Endogenous structures of association in oligopolies. Rand J Econ 26:537–556

    Article  Google Scholar 

  • Bloch F, Dutta B (2009) Communication networks with endogenous link strength. Games Econ Behav 66:39–56

    Article  Google Scholar 

  • Bloch F, Dutta B (2011) Formation of networks and coalitions. In: Benhabib J, Bisin A, Jackson MO (eds) Handbook of social economics. North Holland, Amsterdam

    Google Scholar 

  • Bloch F, Genicot G, Ray D (2008) Informal insurance in social networks. J Econ Theory 143:36–58

    Article  Google Scholar 

  • Bramoullé Y, Kranton R (2007) Public goods in networks. J Econ Theory 135:478–494

    Article  Google Scholar 

  • Caulier JF, Mauleon A, Vannetelbosch V (2012) Contractually stable networks. Forthcoming in Int J Game Theory

  • Caulier JF, Mauleon A, Vannetelbosch V (2011) Allocation rules for coalitional network games. CORE discussion paper, Université catholique de Louvain

  • d’Aspremont C, Jacquemin A (1988) Cooperative and noncooperative R&D in duopoly with spillovers. Am Econ Rev 78:1133–1137

    Google Scholar 

  • Drèze JH, Greenberg J (1980) Hedonic coalitions: optimality and stability. Econometrica 48:987–1003

    Article  Google Scholar 

  • Dutta B, Mutuswami S (1997) Stable networks. J Econ Theory 76:322–344

    Article  Google Scholar 

  • Goyal S, Joshi S (2003) Networks of collaboration in oligopoly. Games Econ Behav 43:57–85

    Article  Google Scholar 

  • Goyal S, Moraga-González JL (2001) R&D networks. Rand J Econ 32:686–707

    Article  Google Scholar 

  • Jackson MO (2005a) Allocation rules for network games. Games Econ Behav 51:128–154

    Article  Google Scholar 

  • Jackson MO (2005b) A survey of models of network formation: stability and efficiency. In: Demange G, Wooders M (eds) Group formation in economics: networks, clubs and coalitions. Cambridge University Press, Cambridge

    Google Scholar 

  • Jackson MO (2008) Social and economic networks. Princeton University Press, Princeton

    Google Scholar 

  • Jackson MO, Rogers BW (2005) The economics of small worlds. J Eur Econ Assoc 3:617–627

    Google Scholar 

  • Jackson MO, van den Nouweland A (2005) Strongly stable networks. Games Econ Behav 51:420–444

    Article  Google Scholar 

  • Jackson MO, Wolinsky A (1996) A strategic model of social and economic networks. J Econ Theory 71:44–74

    Article  Google Scholar 

  • Johnson C, Gilles RP (2000) Spatial social networks. Rev Econ Design 5:273–300

    Article  Google Scholar 

  • Kranton R, Minehart D (2000) Networks versus vertical integration. Rand J Econ 31:570–601

    Article  Google Scholar 

  • Mauleon A, Sempere-Monerris JJ, Vannetelbosch V (2008) Networks of knowledge among unionized firms. Can J Econ 41:971–997

    Article  Google Scholar 

  • Mauleon A, Sempere-Monerris JJ, Vannetelbosch V (2011) Networks of manufacturers and retailers. J Econ Behav Organ 77:351–367

    Article  Google Scholar 

  • Morselli C (2009) Inside criminal networks. Springer, New York

    Book  Google Scholar 

  • Myerson RB (1980) Conference structures and fair allocation rules. Int J Game Theory 9:169–182

    Article  Google Scholar 

  • Page FH Jr, Wooders M (2010) Club networks with multiple memberships and noncooperative stability. Games Econ Behav 70:12–20

    Article  Google Scholar 

  • Ray D, Vohra R (2001) Coalitional power and public goods. J Polit Econom 109:1355–1384

    Article  Google Scholar 

  • Smith DG (2005) The exit structure of strategic alliances. Univ Ill Law Rev 1:303–318

    Google Scholar 

  • Wang P, Watts A (2006) Formation of buyer-seller trade networks in a quality-differentiated product market. Can J Econ 39:971–1004

    Article  Google Scholar 

  • Wasserman S, Fraust K (1994) Social network analysis: methods and applications. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Williams P (2001) Transnational criminal networks. In: Arquilla J, Ronfeldt D (eds) Networks and netwars: the future of terror, crime, and militancy. RAND Corporation, Santa Monica

    Google Scholar 

Download references

Acknowledgments

We wish to thank the Associate Editor and an anonymous referee for helpful comments and suggestions. Vincent Vannetelbosch and Ana Mauleon are, respectively, Senior Research Associate and Research Associate of the National Fund for Scientific Research (FNRS). Financial support from Spanish Ministry of Sciences and Innovation under the project ECO2009-09120, support from Ministerio de Educación y Ciencia, Generalitat Valenciana and FEDER under the projects 2007-66581/ECON, ECO2010-20584 and PROMETEO/2009/068, and support of a SSTC grant from the Belgian State—Belgian Science Policy under the IAP contract P6/09 are gratefully acknowledged.

Author information

Authors and Affiliations

  1. CES, Université Paris 1 Panthéon-Sorbonne, Boulevard de l’Hôpital 106-112, 75647, Paris Cedex 13, France

    Jean-François Caulier

  2. CORE, Université catholique de Louvain, 34 voie du Roman Pays, 1348, Louvain-la-Neuve, Belgium

    Ana Mauleon, Jose J. Sempere-Monerris & Vincent Vannetelbosch

  3. CEREC, Facultés universitaires Saint-Louis, Boulevard du Jardin Botanique 43, 1000, Brussels, Belgium

    Ana Mauleon & Vincent Vannetelbosch

  4. Department of Economic Analysis and ERI-CES, Universidad de Valencia, Campus dels Tarongers, Avda. dels Tarongers s/n, 46022, Valencia, Spain

    Jose J. Sempere-Monerris

Authors
  1. Jean-François Caulier
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ana Mauleon
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jose J. Sempere-Monerris
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Vincent Vannetelbosch
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vincent Vannetelbosch.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Caulier, JF., Mauleon, A., Sempere-Monerris, J.J. et al. Stable and efficient coalitional networks. Rev Econ Design 17, 249–271 (2013). https://doi.org/10.1007/s10058-012-0132-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10058-012-0132-8

Keywords

JEL Classification

Search

Navigation