1 Introduction

Weather forecasting refers to the scientific process of predicting the state of the atmosphere based on specific time frames and locations [1]. Numerical weather prediction (NWP) utilises computer algorithms to provide a forecast based on current weather conditions by solving a large system of nonlinear mathematical equations, which are based on specific mathematical models. More specifically, these models define a coordinate system, which divides the earth into a 3-dimensional grid. The weather parameters such as winds, solar radiation, the phase change of water, heat transfer, relative humidity, and surface hydrology are measured within each grid and their interaction with neighbouring grids to predict atmospheric properties for the future [2].

Meteorology adopted a more quantitative approach with the advancement of technology and computer science, and forecast models became more accessible to researchers, forecasters, and other stakeholders. Many NWP systems were developed in recent years, such as Weather Research and Forecasting (WRF) model, where increasing high-performance computing power has facilitated the enhancement and the introduction of regional or limited area models [3]. As a consequence, the WRF model became the world’s most-used atmospheric NWP model due to its higher resolution rate, accuracy, open-source nature, community support, and a wide variety of usability within different domains [4, 5].

According to [1], data-driven computer modelling systems can be utilised to reduce the computational power of NWPs. In particular, artificial neural network (ANN) can be used for this purpose due to their adaptive nature and learning capabilities based on prior knowledge. This feature makes the ANN techniques very appealing in application domains for solving highly nonlinear phenomena. Deep models for multivariate time-series forecasting often use Recurrent Neural Networks (RNN) and Temporal Convolutional Networks (TCN). Recently, a variant of RNN called Long Short-Term Memory (LSTM) has attached considerable attention due to its superior performance. Such models have attracted considerable attention due to their superior performance [6,7,8]. Deep networks often use stacked neural networks and include several layers as part of the overall composition known as nodes. The computation takes place at the node level since it allows the combination of data input through a set of coefficients. Subsequently, the activation function gets established on the basis of input-weight products while signal progresses through the network [9]. Regression technique is often employed to develop and evaluate neural network models for accurate weather prediction as the weather information is captured by time-series data consisting of real numbers [10].

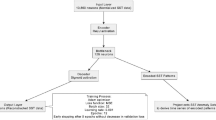
This article presents developing and evaluating a lightweight and novel weather forecasting system using modern neural networks. Figure 1 depicts a general overview of the research discussed in this article. More specifically, a suitable machine learning model is proposed by exploring temporal modelling approaches of LSTM and TCN, and compare its performance with classical machine learning approaches, statistical forecasting models, and a dynamic ensemble method. Secondly, we use the proposed model for short-term weather prediction and compare the model accuracy with the well-established WRF model. Finally, we reform the model for long-term weather forecasting, and analyse the model accuracy and compared the performance to the state-of-art WRF model.

Fig. 1
figure 1

Overview of the research

Full size image

In this study, we investigate LSTM and TCN over RNN since there is an inherent issue of the vanishing gradient problem with the RNN [6]. The LSTM and TCN can overcome this vanishing gradient issue, but it can easily use up the high capacity of memory [8, 11]. The rest of the article is organised as follows: Sect. 2 focuses on related work, and Sect. 3 discusses the research aims and objectives. In Sect. 4, we present the WRF model and its challenges, and Sect. 5 discusses the sequence modelling and prediction. In Sects. 6 and 7, we discuss the methodology and results. Finally, Sect. 8 concludes the article.

2 Related work

Numerical weather prediction (NWP) concept was proposed by Lewis Fry Richardson in 1922, and practical use of NWP began in 1955 after the development of programmable computers [1]. Neural networks-based weather forecasting has been evolved significantly in the last three decades. Before the year 2000, the model output statistics (MOS) was the most widely used approach to improve the numerical models’ ability to forecast by relating model outputs to observational data [12,13,14]. A mixed statistical or dynamic technique for the weather forecasting was introduced by [15] in 1983. The work in [16] added a new perception to dynamic modelling in 1991. These approaches have limitations and challenges such as massive computational requirements, lack of design methodologies for selecting the model architecture and parameters, and time-consuming to prediction resulting less reliability as the difference between the current time and the forecast time increases [13, 16, 17].

Artificial neural network-based minimum temperature prediction system was introduced in 1991 using the backpropagation algorithms [18, 19]. This concept considerably reduced the computational requirements of MOS directing an effective forecast [16]. A snowfall and rainfall forecasting model was introduced in 1995 from weather radar images with ANN [20]. The results show that the ANN is more effective than the traditional cross-correlation method, and the persistence prediction method is producing a substantial reduction in prediction error. In 1998, Oishi et al. developed a severe rainfall prediction method using AI [21]. The development method was unique as it is introduced inference (i.e. knowledge-based) rather than using numerical simulations. A multi-polynomial high order neural network (M-PHONN)-based rainfall prediction model was developed by Hui Qi and Ming Zhang in 2001 [22]. This new model has features such as increasing the speed, accuracy, and the robustness of the rainfall estimate. Therefore, this model could be used to complement the already established auto-estimator algorithms.

A multilayer perceptron network was trained with the backpropagation algorithm with momentum for temperature forecasting in 2002 [23]. The results were very encouraging and clearly demonstrated the potential for future weather forecasting applications. In the same year, a comparative was carried out analysing different neural network models for daily maximum and minimum temperature, and wind speed [24]. The results show that the radial basis function network (RBFN) produced the most accurate forecast compared to the Elman recurrent neural network (ELNN) and multi-layered perceptron (MLP) networks. In 2005, a rough set of fuzzy neural network was introduced to forecast weather parameters; dew temperature, wind speed, temperature, and visibility [25]. This model has several fuzzy rules, and their initial weights were estimated with a deeper network for weather forecasting. Moreover, Hayati and Mohebi proposed a successful model for temperature forecasting based on MLP.

A feature-based neural network model was introduced in 2008 to predict maximum temperature, minimum temperature, and relative humidity [26]. Neural network features are extracted over different periods as well as from the time-series weather parameter itself. In particular, feedforward ANN is utilised in this approach with backpropagation for supervised learning. The prediction results have a high degree of accuracy, and this modelling is recommended as an alternative to traditional meteorological approaches by [27,28,29]. In 2012, a backpropagation neural network (BPN) was implemented for temperature forecasting [27, 30]. This network has successfully identified the nonlinear structural relationship between various input weather parameters. Furthermore, a new hybrid model was introduced in 2014 to forecast the temperature which is based on an ensemble of neural networks (ENN) [31], and the results suggested that including image data would improve the prediction results. In the same year, a deep neural network-based feature representation for weather perdition model was developed for the temperature and dew point prediction [32].

In 2015, eight different novel regression tree structures were applied to short-term wind speed prediction [33]. The author also compared the best regression tree approach against other AI approaches such as support vector regression (SVR), MLP, extreme learning machines, and multi-linear regression approach. The best regression tree yields the best results for wind speed prediction. In the same year, a deep neural network was introduced for ultra-short-term wind forecasting with success [34]. Deep learning with LSTM layers has been introduced to precipitation nowcasting by Shi et al. [11]. The experimental results show that the LSTM network has the ability to capture spatiotemporal correlations and can be used to precipitation nowcasting. In the same year, a model was developed to predict the temperate in Nevada using a deep neural network with stacked denoising auto-encoders with higher accuracy of 97.97% compared to traditional neural networks (94.92%) [35]. In 2016, the multi-stacked deep learning LSTM approach was utilised to forecasting weather parameters temperature, humidity, and wind speed [36]. The author suggested that the model could be used to predict other weather parameters based on the effectiveness and accuracy of the results.

Traditional machine learning methods were analysed for radiation forecasting in 2017 [37]. The author concluded that the SVR, regression trees, and forests have produced a promising outcome for radiation forecasting. In 2018, the backpropagation neural (BPN) network’s performance compared with linear regression and regression tree for temperature forecasting [38]. As a result, a significant better temperature yields the BPN. In 2018, a short-term local rain and temperature forecasting model was developed using deep neural network [39]. The author concluded that the deep neural networks yield the highest accuracy for rain prediction among several machine learning methods. In the same year, the neural network approach is utilised to create models to predict sea surface temperature and soil moisture [40, 41].

The selected state-of-the-art deep learning approaches for weather forecasting and their contributions and differences with the previous approaches are discussed in Table 1.

Table 1 Existing deep learning approaches and their contributions
Full size table

The above existing weather forecasting models are able to predict up to maximum three weather parameters. Besides, weather forecasting is an entirely nonlinear process, and each parameter often depends upon one more other parameters [13, 42, 43]. These larger numbers of interrelated parameters work together, aiming for an accurate weather forecast in a more reliable NWP such as met office and WRF models [4, 44]. A maximum of up to four input weather parameters is considered in the existing AI-based forecasting models.

Based on the related work, it is evident that:

  • There is no identified attempt to compare an AI-based weather prediction with a well-established and existing weather forecasting model such as WRF;

  • There has been little or no attempt to compare traditional machine learning approaches with cutting-edge deep learning technologies for weather forecasting;

  • Most of the existing approaches use less than four interrelated input parameters for neural network-based weather forecasting model;

  • A complete AI-based weather forecasting model with up to 10 input/output weather parameters is yet to be explored.

3 Research aim and objectives

The work presented in this article aimed to develop a weather forecasting model to address the above-mentioned drawbacks using state-of-the-art deep models by establishing the following objectives.

  1. 1.

    To propose an efficient neural network-based weather forecasting model by exploring temporal modelling approaches of LSTM and TCN, and compare its performance with the existing approaches;

  2. 2.

    Use the proposed neural network model for short-term weather prediction and compare the results with WRF model prediction;

  3. 3.

    Fine-tune the proposed model for long-term weather forecasting;

  4. 4.

    Compare the model performances for long-term forecasting with the WRF model prediction.

Our approach is targeted to develop deep neural networks to solve the regression problem of weather forecasting. We propose two different regression models to assess proposed deep learning models, namely multi-input multi-output (MIMO) and multi-input single-output (MISO). In this article, we addressed the above objectives in detail in various sections. Objective 1, an effective neural network-based weather forecasting model is proposed and compared its performance with existing approaches in Sect. 7.1. Objective 2, the proposed model is used to short-term weather forecasting and compared its performance with the WRF model predictions in Sect. 7.2. For Objective 3 and Objective 4, the proposed model is fine-tuned for long-term forecasting and compared the results with the WRF model predictions in Sect. 7.3.

4 Weather research and forecasting (WRF) model

The WRF model was developed by Norwegian physicist Vilhelm Bjerknes in the latter part of the 1990s as part of a collaborative partnership with many environmental and meteorology organisations. The model involves solving of various thermodynamic equations so that numerical weather-based predictions can be made mainly through different vertical levels [45, 46]. The primary role of the WRF is to carry out analysis focusing on climate time scale via linking physics data between land, atmosphere and ocean. The WRF model is currently the world’s most-used atmospheric model since its initial public release in the year 2000 [5].

In order to investigate the model for real cases, it is necessary to install and configure WPS (WRF pre-processing system), WRF ARW (advanced research WRF model), and post-processing software. The WRF post-processing is not described in this article, as the main objective is to collect historical weather data for prediction and analyses. Interested researchers can refer to [47] for further details. The WRF ARW and the WPS share common routines, like WRF I/O API. Therefore, the successful compilation of the WPS depends upon the successful compilation of the WRF ARW model [4].

The WRF model needs to run in two different modes to extract time-series data. Firstly, historical weather data are collected and subsequently, predicted weather data is identified for evaluation purposes. For each instance, the model runs in a single domain mode and utilises different “namelist.wps” and “namelist.input” files to configure the WPS and WRF-ARW components [17]. GRIdded binary or general regularly distributed information in binary, often use as GRIB data, which is a concise data format commonly used in meteorology to store historical and forecast weather data [17, 48]. According to [49], Global Forecast System (GFS) GRIB data provides 0.25 degrees resolution and available to download every 3 h freely. Therefore, the GFS 3-hourly data are selected for this project, with a horizontal resolution set to 10 km.

One of the primary challenges in the WRF is its requirement for massive computational power to solve the equations that describe the atmosphere. Furthermore, atmospheric processes are associated with highly chaotic dynamical systems, which cause a limited model’s accuracy. As a consequence, the model forecast capabilities are less reliable as the difference between the current time and the forecast time increases [1, 50]. In addition, the WRF is a large and complex model with different versions and applications, which lead to the need for greater understanding of the model, its implementation and the different option associated with its execution [5]. The GFS 0.25 degrees dataset is the freely available highest resolution dataset for the WRF model. This allows the user to forecast weather data at a horizontal resolution about 27 km [48, 49]. This implies that the user can predict data with increased accuracy up to 27 km. The model calculates the lesser resolution data based on results obtained. Thus, the model obtains better results for long-range forecast and not for a selected geographical region, such as a farm, school, places of interest, and so on [5, 17, 51].

Based on the above discussion, we propose a novel lightweight weather prediction model that could run on a standalone PC for accurate weather prediction and could easily be deployed in a selected geographical region.

5 Sequence modelling and prediction

The modelling task has been highlighted before defining a network structure which involves time-series weather data sequence \( x_{0} , \ldots , x_{T} \) and wish to predict some corresponding outputs \( y_{0} , \ldots , y_{T} \) at each time. As presented in Table 2, there are 10 different weather parameters in data at a given time \( t, x_{t} = \left[ {p_{1} , \ldots , p_{10} } \right] \). The aim is to predict the value \( y_{t} \) at time \( t \), which is constrained to only previously observed inputs: \( x_{0} , \ldots ,x_{t - 1} \). Therefore, the sequence modelling network can be defined as a function \( {\mathcal{F} }:{ \mathcal{X}}^{{{\text{T}} + 1}} \to {\mathcal{Y}}^{T + 1} \) that produces the mapping \( \hat{y}_{0} , \ldots ,\hat{y}_{T} = { \mathcal{F}}\left( {x_{0} , \ldots , x_{T} } \right) \), if it satisfies the causal constraints, i.e. \( y_{t} \) only depends on \( x_{0} , \ldots ,x_{t} \) and not on any future inputs \( x_{t + 1} , \ldots ,x_{T} \). The main idea of learning in the sequence modelling is to find a network \( {\mathcal{F} } \) which minimises the loss (\( \ell ) \) between the actual outputs and the predictions, \( \ell \left( {y_{0} , \ldots ,y_{T} ,{ \mathcal{F}}\left( {x_{0} , \ldots ,x_{T} } \right)} \right) \) in which the sequences and predictions are drawn according to some distribution.

Table 2 Surface weather parameters (10 identified parameters used by our model)
Full size table

The WRF model with GFS-GRIB data can produce a large amount of historical weather data. Recurrent neural networks (RNN), LSTM, and TCN are extremely expressive models which are appropriate in such a scenario. These networks have attracted considerable attention due to their superior performance based on ability to learn highly complex vector-to-vector mapping [52, 53]. The LSTM is a specialised form of RNN that is designed for sequence modelling [52, 54]. Highly dimensional hidden states \( \varvec{H} \) are the basic building blocks of RNN which are updated with nonlinear activation function \( {\mathcal{F}} \). At a given time \( t \), the hidden state \( \varvec{H}_{t} \) is updated by \( \varvec{H}_{t} = { \mathcal{F}}\left( {\varvec{H}_{t - 1} , x_{t} } \right) \). The structure of \( \varvec{H} \) works as the memory of the network.

The state of the hidden layer at a given time is conditioned on its previous state. The RNN is extremely deep as they are maintained a vector activation through time at each timestep. This will result in high training time-consuming due to the exploding and the vanishing gradient problems [6]. The development of LSTM and TCN architectures have been addressed the gradient vanishing issue with RNN [55]. Therefore, we use state-of-art LSTM and TCN architecture to minimise the loss \( \ell (y_{0} , \ldots ,y_{T} ,{ \mathcal{F}}\left( {x_{0} , \ldots ,x_{T} )} \right) \) for effective modelling and prediction of time-series weather data.

5.1 Proposed deep model with long short-term memory (LSTM) layers

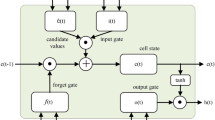
The proposed model is based on LSTM networks and uses temporal weather data to identify the patterns and produces weather predictions. As discussed in Sect. 5, we experiment with the state-of-the-art LSTM, which is a specialised form of RNN, and it is widely applied to handle temporal data. The key concepts of the LSTM have the ability to learn long-term dependencies by incorporating memory units. These memory units allow the network to learn, forget previously hidden states, and update hidden states [6, 9, 56]. Figure 2a shows the deep learning model consisting of stacked LSTM layers for weather forecasting using surface weather parameters. Table 2 describes the surface weather parameters, which are used as the input parameters. The model provides outputs, which are the predicted weather parameters.

Fig. 2
figure 2

a Proposed layered LSTM and b LSTM memory cell used for this research

Full size image

Figure 2b shows the LSTM memory architecture used in our model. More specifically, the proposed model has the input vector \( X_{t} = \left[ {p_{1} , p_{2} , \ldots , p_{9} ,p_{10} } \right] \) at a given time step \( t \), which consists of 10 different \( \left( {p_{1} \ldots p_{10} } \right) \) weather parameters. In a given time \( t \), the model updates the memory cells for long-term \( C_{t - 1} \) and short-term \( H_{t - 1} \) recall from the previous timestep \( t - 1 \) via:

$$ I_{t} = \tanh \left( {w_{xi} X_{t} + w_{hi} H_{t - 1} + b_{i} } \right) $$
$$ J_{t} = {\text{sigm}}\left( {w_{xj} X_{t} + w_{hi} H_{t - 1} + b_{j} } \right) $$
$$ F_{t} = {\text{sigm}}\left( {w_{xf} X_{t} + w_{hf} H_{t - 1} + b_{f} } \right) $$
$$ O_{t} = \tanh \left( {w_{xo} X_{t} + w_{ho} H_{t - 1} + b_{o} } \right) $$
$$ C_{t} = C_{t - 1} \odot F_{t} + I_{t} \odot J_{t} $$
$$ H_{t} = \tanh \left( {C_{t} } \right) \odot O_{t} $$
(1)

The notations of Eq. (1) are: \( w_{*} \)—weight matrices, \( b_{*} \)—biases, \( \odot \)—element-wise vector product, \( I_{t} \)—input gate and \( J_{t} \)—input moderation gate contributing to memory, \( F_{t} \)—forget gate, and \( O_{t} \)—output gate as a multiplier between memory gates. To allow the LSTM to make complex decisions over a short period of time, there are two types of hidden states, namely \( C_{t} \) and \( H_{t} \) [6, 57]. The LSTM has the ability to selectively consider its current inputs or forgets its previous memory by switching the gates \( I_{t} \) and \( F_{t} \). Similarly, the output gate \( O_{t} \) learns how much memory cell \( C_{t} \) needs to be transferred to the hidden state \( H_{t} \). Compared to the RNN, these additional memory cells give the ability to learn enormously complex and long-term temporal dynamics with the LSTM.

In this work, we propose two types of deep models to solve the regression problem involving weather forecasting, namely multi-input multi-output (MIMO) and multi-input single-output (MISO).

5.1.1 MIMO-LSTM

In the MIMO, all the weather parameters (i.e. 10 surface weather parameters in this study) are fed into the network, which is expected to predict the same number of parameters (i.e. 10 parameters in this study) as the output. Therefore, only one model is required for weather forecasting. Figure 3a depicts the basic arrangement of the MIMO.

Fig. 3
figure 3

The proposed MIMO and MISO deep architecture for weather forecasting

Full size image

5.1.2 MISO-LSTM

In MISO approach, all of the weather parameters (i.e. 10 surface weather parameters in this study) are fed into the network, which is expected to predict a single parameter. 10 different models are required as each of them is trained to predict a particular weather parameter. Figure 3b depicts the basic arrangement of the MIMO and the MISO.

5.2 Proposed deep model with temporal convolutional network (TCN) layers

The main characteristic of the TCN is that the network can take a sequence of any length as inputs and map it to an output sequence of the same length, just similar to the RNN categories. These networks involve causal convolutions and initially developed to examine long-range patterns using a hierarchy of temporal convolutional filters [8, 58, 59]. TCN architecture is quite simple and is informed by recent generic convolutional architectures for sequential data. This architecture has no skip connections across layers, conditioning, context stacking or gated activations, and autoregressive prediction and a very long memory.

The TCNs use dilated convolutions that enable an exponentially large receptive field, allowing very deep networks and very long effective history [60]. For instance, the dilation convolution operation \( F \) for a 1-D sequence of a given weather parameter \( p^{1} \), i.e. \( p = \left( {p_{0}^{1} , \ldots , p_{t}^{1} } \right) \) and a filter \( f :\left\{ {0, \ldots , k - 1} \right\} \), on element \( s = p_{{\hat{t}}}^{1} \) (where \( \hat{t} = 0, \ldots ,t \)) of the sequence is defined as:

$$ F\left( s \right) = \left( {p*_{d} f} \right)\left( s \right) = \mathop \sum \limits_{i = 0}^{k - 1} f\left( i \right) . p_{s - d.i} $$
(2)

The notations of Eq. (2) are: \( d \)—dilation factor, \( k \)—filter size, and \( s - d.i \) accounts for the direction of the past. The TCN consists of stacked units of one dimensional convolution with activation functions [7]. The architectural elements in a TCN with configurations dilations dilation factors \( d = 1, 2,\; {\text{and}} \;4 \) are shown in Fig. 4. The main purpose of the dilation to introduce a fixed step between every adjacent filter taps, and larger dilations and larger filter sizes k enable effectively expanding the receptive filed [8, 59]. The increment of \( d \) exponentially increase the depth of the network in these convolutions and this guarantees that there is some filters that hits each input within the effective history [59].

Fig. 4
figure 4

Architectural elements in a TCN with causal convolution and different dilation factors. The input to the TCN is \( x_{t} \) and output \( y_{t} \). The \( x_{t} \) contains 10-dimensional weather parameter

Full size image

5.2.1 MIMO-TCN and MISO-TCN

Similar to LSTM in Sects. 5.1.1 and 5.1.2, we also use the TCN in our proposed MIMO and MISO models.

5.3 Proposed model for weather forecasting

As discussed in Sects. 5.1 and 5.2, the LSTM and TCN deep learning approaches are proposed for weather forecasting. The MIMO and MISO are the two types of deep models to solve the regression problem. Therefore, proposed models for weather forecasting are MIMO-LSTM, MISO-LSTM, MIMO-TCN, and MISO-TCN. Deep learning models are discussed in [11, 34, 39, 61, 62] are single input single output models. The MISO are experimented in [35, 36] and a MIMO is discussed in [63]. All these models can be accepted up to four input parameters at a given time. Increased number of input parameters will increase the forecasting accuracy of an NWP model by distinguishing interrelationships among parameters [17, 47]. Our proposed model uses ten input parameters which has not been explored in the past for neural network-based weather forecasting. Subsequently, the research discusses in this article is explored for both MIMO and MISO.

Moreover, [62] uses the bidirectional recurrent network with weather-related input parameters successfully to predict the wind power up to 6 h. Therefore, bidirectional LSTM experiments in long-term forecasting and compare with the proposed model. Most of the researches discussed in Table 1 are attempted to forecasting a single or few parameters for a specific purpose rather developing a complete weather forecasting model. Our proposed model explores to complete AI-based fine-grained weather forecasting model.

We use Keras as a tool to implement both LSTM and TCN deep learning networks [56, 64,65,66].

6 Methodology

This is an empirical-based study and is focused on analysing the quantitative temporal weather data. There are 10 surface weather parameters utilised in this research for weather prediction. These weather parameters are identified by considering their usefulness in precision farming. Moreover, these surface parameters can be captured at a chosen location using various sensors using a local weather station.

6.1 Surface weather parameters

The surface weather parameters are observed and reported in for monitoring and forecasting purposes [67]. In our previous study, we defined 10 surface weather parameters for the forecasting, which can be extruded from GRIB data using the WRF model [66]. Those 10 surface parameters, as shown in Table 2.

The surface parameters of wind direction and wind speed can be calculated from the WRF surface variables \( U_{10} \) and \( V_{10} \) [4]. Table 2 shows the surface weather parameters which are utilised in this research. The XLAT—reference latitude and XLONG—reference longitude parameters are used with each data point for the location identification.

6.2 Data collection and preparation

As described in Sect. 4, the GRIB data is used to run the WRF model. A total of 12 weather parameters is extracted from the period of January 2018 to May 2018. This is used as the training dataset to train the proposed models. Similarly, the parameters in June 2018 data are used to test the network. This is to test different trained deep models to identify the best model for forecasting. The parameters in July 2018 are considered as the validation dataset, which is used as the ground truth to compare perdition from the best model. The WRF model is being run in forecast mode using the same format GRIB data for the month of July 2018 to evaluate the overall prediction performance of the WRF model.

The training data set has been normalised to keep each value in between − 1 and 1, and the same maximum and minimum variable values are used to normalise the testing and the evaluation data set. We apply a sliding window of 7 days temporal resolution on each dataset as input to the model and the temporal resolution of next 3 h data as the model’s output. By using this sliding window method, the size of our training dataset is ~ 6.5 GB with a sample size of 675,924, and the testing dataset is ~ 1.19 GB with a sample size of 114,450.

6.3 Model details

As shown in Table 3, six different configurations are considered for both MIMO-LSTM and MISO-LSTM models. Figure 2a depicts the general architecture of the proposed model. Each configuration has a different number of layers, and each layer consists of a different number of nodes. Each configuration is experimented with:

Table 3 Different LSTM layer configurations for MIMO-LSTM and MISO-LSTM
Full size table

  • Fixed learning rate (LR) and adaptive learning rate [68]. In the fixed learning rate, we set LR = 0.01. In the adaptive learning rate method, the LR (initial LR = 0.1) is reduced to half of the current LR in every 20 epochs to find the optimal model with best LR.

  • Adam [69] and SGD [70] optimizers to minimise a given cost function [56, 64].

The MIMO-TCN and MISO-TCN approaches have experimented with different configurations and controls, such as;

  • Filter sizes: 32, 64, 128, 256, and 512

  • Stacked TCN layers: 1, 2, 3, and 4 and

  • With different activation functions such as ‘linear’ and ‘tanh’

According to [8, 59, 71], the following controls are kept constant within these experiments as these do not impact on final results significantly in the regression model for time-series data; kernel size: 2, dilations: 7, where dilation values are: 1, 2, 4, 8, 16, 32, 64, batch size-64, and dropout rate-0, learning rate-0.01.

6.4 Evaluation metric

The proposed deep regression models are evaluated using the most common metrics of mean squared error (MSE), which is calculated as:

$$ {\text{MSE}}\, = \,\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {y_{\text{a}} - y_{\text{b}} } \right)^{2} $$
(3)

where \( y_{\text{a}} \) is the actual expected output, \( y_{\text{b}} \) is the model’s prediction, and \( n \) is number of samples.

6.5 Baseline approaches

Performances of the proposed LSTM and TCN models are compared with the following three types of baseline approaches. These approaches do not consider the temporal information rather count as another dimension in multivariate weather data.

  • Classic machine learning approaches

Standard regression (SR), support vector regression (SVR), and random forest (RF).

  • Statistical machine learning approaches

Autoregressive integrated moving average (ARIMA), vector auto regression (VAR), and vector error correction model (VECM).

  • A dynamic ensemble method

Arbitrage of forecasting expert (AFE).

We use both linear and RBF (radial basis function) kernels for SVR in our experiments and use the grid search algorithm technique to optimise both C and γ parameters. In linear kernel, the parameter C is selected among the range [0.01–10,000] with multiples of 10. In RGB kernel, the parameters C is selected as above but γ is selected among the range [0.0001, 0.001, 0.01, 0.1, 0.2, 0.5, 0.6, 0.9]. For RF [71], we select number of trees as [100, 250, 500]. For ARIMA model, we use the parameters p = 2, d = 0, and q = 1 [72]. For VAR and VECM, the auto option is selected for weather forecasting [73, 74]. The given software package is used for the AFE [75].

The baseline performances are compared with the proposed LSTM and TCN networks. These models are evaluated using the testing dataset to select the optimal model or a model with the least MSE, which can be used as a tool for future forecasting. The selected optimal is used to forecast the weather parameters for the validation dataset (model prediction), and the model predicted values are evaluated with respect to the ground truth. Similarly, the WRF model has been run in forecast mode using the same format GRIB data for the month of July 2018 (WRF Prediction). These WRF predicted values are evaluated with respect to the ground truth. Then, we compare the model prediction and WRF perdition to determine the possibility to use the proposed model for short-term weather forecasting (i.e. 3-h prediction). Then, the optimal model is re-tuned for long-term weather forecasting, such as 6, 9, 12, 24, and 48 h. Similar to the short-term forecasting, we compare the model predictions and WRF predictions to determine up to what extent the proposed model can be used for weather forecasting.

7 Results and discussion

There are three types of results, namely: (1) a comparison of various machine learning techniques, statistical forecasting approaches, and a dynamic ensemble method with the proposed approach for weather forecasting, (2) performance of short-term weather forecasting, and (3) performance of long-term weather forecasting using the proposed model. More specifically, the short-term weather forecasting refers to 3-h weather prediction, and long-term weather forecasting refers to 6-h, 9-h, 12-h, 24-h, and 48-h weather predictions.

7.1 Comparison of machine learning techniques for short-term weather forecasting

As described in Sect. 6.5, we examine the classic machine learning approaches (i.e. SR, SVR, RF), statistical forecasting approaches (i.e. ARIMA, VAR, and VECM), and a dynamic ensemble method (i.e. AFE). Finally, we compare these performances with the proposed deep models (i.e. MISO-LSTM, MISO-TCN, MIMO-LSTM, MIMO-TCN) consisting of cutting-edge networks such as LSTM and TCN layers. As described in Sects. 5.1 and 5.2, these models are evaluated using two different regression types, namely MISO and MIMO.

We evaluate the MISO models to determine the MISO-optimal with the least MSE for weather prediction. Table 4 and Fig. 5 represent the comparison of machine learning approaches for MISO. As per Table 4 and Fig. 5, the MISO-LSTM provides better performance with the least MSE for 6 parameters out of 10. Thus, the LSTM combined model with 10 parameters (i.e. MISO-LSTM) has been selected as the MISO proposed model.

Table 4 Comparison of machine learning approaches for MISO
Full size table
Fig. 5
figure 5

MISO analysis of different approaches to predicting different weather parameters (SR standard regression, ARIMA autoregressive integrated moving average, VAR vector autoregression, SVR support vector regression, VECM vector error correction model, AFE arbitrage of forecasting experts, RF random forest, LSTM long short-term memory, TCN temporal convolutional network)

Full size image

Similarly, we evaluate the MIMO models to determine the MIMO-optimal with the least MSE for weather prediction. Table 5 and Fig. 6 represent the comparison of machine learning approaches for MISO. We do not consider the approaches ARIMA, VAR, VECM, and AFE in MIMO. Therefore, we compare SR, multi-output SVR [76], and RF with the proposed deep models MIMO-LSTM and MIMO-TCN. The results are subsequently evaluated via the mean squared error. This is used to assess the best model (i.e. least MSE) after comparing the performance of all models.

Table 5 Comparison of machine learning approaches for MIMO
Full size table
Fig. 6
figure 6

MIMO analysis of different approaches to predicting different weather parameters (SR standard regression, SVR support vector regression, RM random forest, LSTM long short-term memory, and TCN temporal convolutional network)

Full size image

As per Table 5 and Fig. 6, the MIMO-LSTM provides high accuracy output with least MSE for 6 parameters out of 10. Therefore, the MIMO-LSTM has been selected as the proposed model (i.e. MIMO-optimal).

In both MIMO and MISO, the LSTM and the TCN produce high performance with smaller errors compared to the classic machine learning approaches and statistical forecasting approaches as presented in Figs. 5 and 6. The reason is that the selected parameters do not follow a linear path within selected sequential timeslots [77, 78] and there is a nonlinear interrelationship among parameters [6, 53, 79]. Besides, the sequential information is not encoded by the classic machine learning approaches and statistical forecasting models. The LSTM and TCN encode both multivariate and sequential information by taking them into another dimension in the input data [6, 59, 80].

7.2 Proposed models for short-term weather prediction

The least MSE for the MIMO is identified in the configuration with three LSTM layers, with 128, 512, and 256 number of nodes, respectively (i.e. MIMO-optimal model). We use the SGD optimiser with a fixed learning rate of 0.01 to optimise the MSE regression loss function. The model is trained for 230 epochs. In MISO, all these 10 models have different configurations with a different number of LSTM layers and nodes, activation functions, and optimisers (i.e. MISO-optimal). Table 6 and Fig. 7 graphically represent the comparison of MSE in each variable for both MIMO-optimal and MISO-optimal.

Table 6 MSE comparison
Full size table
Fig. 7
figure 7

Comparison of MIMO and MISO

Full size image

Table 6 shows the comparison of MSE in each variable for both MIMO and MISO. Figure 7 graphically represents these values to get an idea of whether to use the MIMO model or the MISO combined model to use as the best model for future predictions.

According to Fig. 7, there is no major gap between MSE values for each variable when compare the MIMO-optimal and MISO-optimal. These differences are less than 0.04 for each variable. These error figures are significantly smaller. Moreover, the MISO-optimal requires 10 different models for the prediction of 10 different weather parameters. Therefore, we consider the MIMO-optimal (i.e. MIMO-LSTM) model as a tool for future forecasting since it is easier to handle and less time and power consumption (only one model to run) than running 10 different models of MISO-optimal.

As described in Sect. 6.5, the validation dataset is utilised to get weather prediction using the proposed model. Similarly, the WRF model is run in forecast mode using the July 2018 data to compare results. Both WRF and model predicted values are compared with respect to the ground truth and calculated the MSE. Table 7 and Fig. 8 represent the MSE comparison values for each variable.

Table 7 Comparison of the proposed deep model with the WRF forecasting model for 3-h prediction
Full size table
Fig. 8
figure 8

Analysis of weather prediction of the WRF model and proposed deep learning LSTM model

Full size image

When comparing Table 7 and Fig. 8, the proposed deep model (i.e. MIMO-LSTM) provides comparatively best results (bolded in the table) on eight occasions out of 10. The WRF model provides the best results for the snow and soil moisture (SMOIS) variables. On both occasions, these error figures are quite small. For example, MSE for the variable snow is 0.0168574 kg/m2. This is quite a small and therefore, negligible. Similarly, the SMOIS has got a minimal and negligible error value. Figure 8k shows an overall comparison of both models.

As there are 125,373 samples in the July 2018 evaluation data, the proposed deep model and the WRF model will produce a similar number of samples as the predicted data. It is difficult to visualise all of these predictions because of the large sample size and therefore, a random sample of the 100 samples has been taken from the test set to compare with the respective ground truth. Figure 9 shows a comparison of the proposed deep model’s predictions verses the WRF model predictions. For each graph, the ground truth, WRF prediction, and the proposed deep model’s predictions are represented by each line with blue, green, and red colours, respectively.

As per Fig. 9, the red line-chart (deep model prediction) follows closely to the blue line-chart (ground truth) compared to the green-chart (WRF prediction). The WRF prediction is widely diverted in the parameters Rainc and Rainnc compared to the actual values. The deep model prediction is diverted in the parameter snow compared to the actual values. According to Fig. 7h, the highest snow prediction is 0.24 kg/m2. This is quite a small figure and can be negligible. Overall, the deep learning model provides a better short-term (up to 3 h) prediction compared to the WRF model.

Fig. 9
figure 9

Comparison of WRF prediction versus the MIMO-LSTM model prediction for 100 random data samples with respect to the ground truth (colour figure online)

Full size image

7.3 Proposed model for long-term weather forecasting

As described in Sect. 7.2, the proposed model (i.e. MIMO-LSTM) can be utilised for short-term weather forecasting, and it yields more accurate results compare to the well-known WRF model. In this section, our study is focused on exploring long-term weather prediction using the same historical weather data with 10 surface weather parameters.

7.3.1 Selection of an appropriate technique

As discussed in Sect. 7.1, the proposed model provides better performance compared to other machine learning techniques. Therefore, we use the same deep learning model with the LSTM layers for the long-term weather forecasting with the following variations. All these three variants use the same configuration and controls, which are comparable to the proposed MIMO-LSTM model.

  1. (a)

    Load the MIMO-LSTM optimal model weights (3-h) and fine-tune models for the long-term forecasting (shortened form: LSTM LW)

  2. (b)

    Train models for each time frame without loading the optimal model weights (shortened form: LSTM WL). That is train the model at the beginning of the training dataset and new labels.

  3. (c)

    We have also experimented with Bidirectional LSTM (Bi-LSTM). Compared to the LSTM, the Bi-LSTM has used two layers; one layer performs the operations following the forward direction (time-series data) of the data sequence, and the other layer applies its operations on in the reverse direction of the data sequence [81].

The following Table 8 shows the comparison of these three variations for each timeslot. As shown in Table 8, the Bi-LSTM provides slightly better results compared to the LSTM LW except for the timeslot 3-h. The LSTM WL produces weaker results compared to the both LSTM LW. The reason is that the LSTM LW used its optimal weight, which is already configured to re-train and yield a prediction. Moreover, this is re-tune the model which is matched to the new dataset [55]. The Bi-LSTM is also trained the model at the beginning similar to the LSTM WL. However, the Bi-LSTM provides more accurate results due to the ability to preserve the past and future values [81].

Table 8 Comparison of LSTM LW, LSTM WL, and Bi-LSTM
Full size table

The only drawback of the Bi-LSTM is that time taken to training, testing, and predicting data [82]. This is less efficient compared to the LSTM LW. Moreover, as can be observed in Table 8, there is a slight gap in the overall figures of MSE in both LSTM LW and Bi-LSTM. Therefore, we have selected the LSTM LW method for long-term forecasting for an effective and efficient outcome.

7.3.2 Long-term weather forecasting

The proposed model (i.e. MIMO-LSTM) consists of three LSTM layers with other controls. As described in Sect. 7.3.1 the LSTM with loading the optimal weight method is used for the long-term weather prediction. Therefore, the optimal model is re-tuned (i.e. load optimal model weight and re-train models) for timeslots 3-h, 6-h, 9-h, 12-h, 24-h, and 48-h. While re-tuning, the optimal models are found in different epochs such as 80, 10, 10, 10, and 10 for timeslots 6, 9, 12, 24, and 48 h, respectively.

Similar to the short-term weather forecasting, the optimal model for each timeslot is used to forecast the weather parameters for the July 2018 data (model prediction), and the model predicted values are evaluated with respect to the ground truth. The WRF model has been run in forecast mode using the same format GRIB data for the month of July 2018 (WRF prediction) based on the same conditions as model prediction (i.e. input 7 days data and predict weather parameters for timeslot 6, 9, 12, 24 and 48). The WRF predicted values are evaluated with respect to the ground truth. Finally, compare the model prediction and WRF prediction to determine what extent the deep learning model can be used for weather forecasting. Figure 10 shows a comparison of MSE values related to the proposed model and the WRF model for each time slot.

Fig. 10
figure 10

Compare proposed MIMO-LSTM model prediction with WRF prediction for long-term forecasting. The MSE values are calculated with respect to the ground truth in both WRF and LSTM models

Full size image

According to the results presented in Fig. 10, it is obvious that the WRF model produces better forecasting results for the very long-term compared to the deep learning model. The reason is that the WRF model is combined with many other climate models [4, 83, 84] and data is coming to the system globally [4, 49]. The deep learning model has predicted these outputs based on 5 months of training data. We could receive better results if we increase the size of the training dataset [56]. The Rainc and Rainnc parameters show much better results in the deep learning model compared to the WRF model for long-term forecasting. The experiments of [39] already proved that the deep learning neural networks yield the highest accuracy for rain prediction.

Contrarily, the SMOIS and snow parameters show weak results in deep learning compared to the WRF model at all timeslots. Simply, these error patterns are rather low (maximum error: Snow—0.016 kg/m2, SMOIS—0.00035 m3/m3) and can be negligible. This could be resolved by increasing the size of the sample data. All other occasions, the deep learning model provide more accurate prediction compared to the WRF model up to some extent, than the WRF model produces better prediction compared to the deep learning model. Figure 11 shows the comparison of overall error values of the WRF model and proposed deep learning model.

Fig. 11
figure 11

Comparison of overall MSE for each timeslot

Full size image

As indicated in Fig. 11, the deep learning model produces better predictions compared to the WRF model prediction up to 12 h overall. Therefore, we can use deep learning with LSTM model up to 12 h of weather forecasting much accurately compared to the well-recognised WRF model. The comparison of WRF prediction versus the LSTM model prediction for 50 random data samples with respect to the ground truth is shown in Fig. 12. For each graph, the ground truth, WRF prediction, and the proposed deep model’s predictions are represented by each line with blue, green, and red colours, respectively.

Fig. 12
figure 12figure 12figure 12

Comparison of WRF prediction versus the LSTM model prediction for 50 random data samples with respect to the ground truth (colour figure online)

Full size image

As per Fig. 12, the red line-chart (deep model prediction) followed closely to the blue line-chart (ground truth) up to some extent and diverted when time increases in many parameters. The green line-chart (WRF model prediction) also diverted from the blue line-chart when time increased, but this diversion is relatively small compared with the red line-chart. As shown in Fig. 12vi, vii, the rainc and rainnc values are accurate in the deep learning model compared to the WRF model for up to 48 h. As discussed earlier, the WRF model produces a better prediction for the Snow and SMOIS parameters. As shown in Fig. 12x, the difference is negligible for the parameter SMOIS. As shown in Fig. 12viii, the maximum snow values are shown in the 3 h line-chart. This value is equal to 0.24 kg/m2, and this is a relatively negligible figure. Overall, the deep learning model delivers a better forecasting prediction compared to the WRF model for up to 12 h.

7.4 Applicability of the new model

As described in Sect. 7.3, the proposed model can be used for weather prediction. Even, this model generates more accurate predictions compared to the well-recognised WRF model for up to 12 h. We use historical weather data to evaluate and validate these models. The only issue is we still use the WRF model to extract GRIB data to use as input for the new model (we use GFS GRIB data). On the other hand, it requires a minimum of 3 h of access GFS data after taking the atmospheric measurements. This includes the time taken to upload data to the website [4, 85]. In addition, the WRF model also taken the time to extract the GFS data depends on the computer system. Hence, the input data which are used in the new model are not the current atmospheric measurement data (i.e. older more than 3 h). Therefore, it is not practicable to use WRF data with the new model, and it will be highly beneficial to consider the use of local weather station data for weather forecasting.

8 Conclusion and future work

In this article, we demonstrate that the proposed lightweight deep model can be utilised for weather forecasting up to 12 h for 10 surface weather parameters. The model outperformed the state-of-the-art WRF model for up to 12 h. The proposed model could run on a standalone computer, and it could easily be deployed in a selected geographical region for fine-grained short to medium-term weather prediction. Furthermore, the proposed model is able to overcome some challenges within the WRF model, such as the understanding of the model and its installation, as well as its execution and portability. In particular, the deep model is portable and can be easily installed into a Python environment for effective results [17, 56]. This process is highly efficient compared to the WRF model.

This research is carried out using ten different surface weather parameters, and an increased number of inputs would probably lead to enhanced results. For example, there are 36 different pressure levels defined in the WRF model [17]. Only the pressure at two meters is considered within this research. There is a possibility to increase the accuracy of the results if we introduce all 36 possible pressure levels to the proposed model. However, it will increase the model complexity requiring a large number of parameters to estimate. Furthermore, January to May weather data is utilised for training the deep model, and the increase in the size of training dataset could help towards improved results in a deep learning network [56, 86].

Besides, we used the MIMO approach within this research to predict weather data. Table 5 and Fig. 7 show that the MISO approach produces better MSE values compared to the MIMO. Therefore, there is a huge potential that the MIMO approach will increase the accuracy of the results; even this method is less efficient compared to the MIMO. Besides, the Bi-LSTM yields high accuracy long-term prediction compared to the LSTM, as presented in Table 7. Therefore, we could get more accurate results if we use Bi-LSTM; even this method is not efficient due to high time-consumption.

These experiments show that we can apply the neural network approach for weather prediction. Based on the geographical appearance of location (such as the top of a mountain, land covered by several mountains, the slope of the land, etc.) the regional weather forecasting may not be accurate. As a solution, we could develop a lightweight (neural network-based) short-term weather forecasting system for the community of users utilising weather station data. These are our future experimentation.