Abstract
We propose a superimposing interferogram method to enhance the sensitivity and interference definition of spatial-phase-shift interferometers. The proposed method uses a multi-slit array as a redesigned field stop for the spatial-phase-shift interferometer. The widths of the apertural and blocked areas correspond to half the wavelength of the fringe pattern on the imaging plane and determine the wavelength that improves the interference definition while eliminating those wavelengths that worsen it, thus improving the interference definition of the interferogram. Additionally, to improve the interferometer’s sensitivity, several apertural areas were aligned to increase the amount of incident light. We performed spectroscopic measurements and confirmed improvements in both the sensitivity and the interference definition using a prototype of a bean-sized mid-infrared spectroscopic imager based on a one-shot Fourier spectroscope and a prototype multi-slit array. Although mid-infrared light is absorbed well by water and its intensity is thus weak for detection using the array sensors of cameras, mid-infrared spectroscopic imagers that incorporate our proposed method can be used for biomedical measurements of samples containing water.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We propose a method to improve the sensitivity and definition of a spatial-phase-shift interferometer using a field stop that has more than one aperture area running periodically along the horizontal axis. Our intention is to improve these parameters in our proposed spectrometer to enable the development of a small and low-cost mid-infrared spectroscopic imager that can be introduced into regular everyday applications as a non-invasive health-care sensor (e.g., for blood glucose monitoring). The mid-infrared region (wavelength 6–15 µm, wavenumber 1500–650 cm−1) is called the fingerprint region because components are easily identified by their spectroscopic absorbance in this region. However, it is difficult to obtain data that have a high signal-to-noise ratio using mid-infrared spectroscopic imagers because the photons of mid-infrared light are absorbed readily by water and the light intensities are thus very weak. There are two types of spectroscopy, wavelength dispersive [1,2,3] and Fourier, which have different optical systems. In principle, wavelength dispersive spectroscopy uses a slit to separate the weak light into individual wavelengths and then detects their intensities. Application of wavelength dispersive spectroscopy to mid-infrared spectra is difficult because the light intensities are low. Conversely, Fourier spectroscopy has high sensitivity and is well suited to mid-infrared measurement applications because it uses white light containing multiple wavelengths over a broadband. Fourier spectroscopy uses one of two types of instruments. The first is the temporal phase-shift interferometer [4,5,6,7], which registers optical path differences by moving a mirror, as used in the Fourier-transform infrared spectrometer based on the Michelson interferometer. The second is the spatial-phase-shift interferometer [8,9,10,11,12,13,14,15], which registers optical path differences using a Wollaston prism to remove the need for moving parts, as used in the static imaging Fourier transform spectrometer. To measure living structures, instruments require not only high sensitivity but also high time resolution because the light from living samples such as tissue containing blood vessels must be registered quantitatively and continuously. Spatial-phase-shift interferometers are, therefore, suitable for use in spectral measurements of living structures; however, the light intensity per pixel of the array device is too low because, in principle, over the objective plane of the interferometer, the beam will spread out from the bright point. Additionally, the interferometer has a field stop located at the objective plane to maintain light coherence.
In this paper, we propose a superimposing interferogram method that uses a multi-slit array to improve the sensitivity and the interference definition of a spatial-phase-shift interferometer. The multi-slit array is the field stop of the interferometer and has been designed to fit the aperture. The blocked area on the objective plane corresponds to one half-wavelength of the interferogram on the imaging plane. To improve the interference definition of the interferogram using this method, we selected the wavelength that improves the interference definition and removed those wavelengths that worsen it. Furthermore, several aperture areas are aligned to increase the amount of incident light and thus improve the sensitivity of the device. With increasing aperture area, both the sensitivity and the interference definition are enhanced.
Using our proposed multi-slit array, we were able to improve the sensitivity and the interference definition of a spatial-phase-shift interferometer for white light (from a metal halide lamp) and laser light (from a He–Ne laser). Using a prototype bean-sized mid-infrared spectrometer made from a spatial-phase-shift interferometer and white light (from a heater), we confirmed these improvements and demonstrated the feasibility of our proposed method for use in biomedical measurements.
2 Principle of the superimposing interferogram method and multi-slit array design
2.1 Dependence of the conversion factor on the optical system and relationship with the width of the aperture area of the field stop for the interferometer
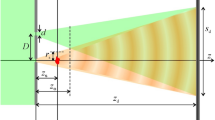
For our superimposing interferogram method, a multi-slit-array was designed based on a conventional field stop to have more than one aperture area running periodically along the horizontal axis. The conventional field stop of a spatial-phase-shift interferometer uses only the incident coherent light. However, these field stops yield low sensitivities because the aperture area of the incident light is small. As shown in Fig. 1, using one-shot Fourier spectroscopy [15], which uses one type of spatial-phase-shift interferometer, we tried to extend the width of the aperture area horizontally to increase the amount of incident light. We do not have to consider the height of the field stop because the height is determined by the optical superposition method [16]. As shown in Eqs. (1) and (2), the sensitivity (\(I_{{\text{s}}}\)) represents the median detected light intensity and the interference definition (\(I_{{\text{d}}}\)) is expressed expediently using the difference between the maximum (\(I_{{\max}}\)) and minimum (\(I_{{\min}}\)) values of the interferogram intensity because we wish to consider this definition separately from that of the detected light intensity.
The field stop width is L and the detected light intensity is 1 before the width is broadened. When the aperture area increases from 1 to 5L, the sensitivity increases in tandem from 1 to 5. However, we simultaneously discovered a phenomenon where the interference definition alternately improves and worsens. Because we developed an expression for the most appropriate width of the aperture area (L) and lined up the aperture area and the shielded area periodically by analyzing this phenomenon, the sensitivity and the definition can be increased at the same time by increasing the number of aperture areas. To explain this phenomenon and illustrate the principle of our proposed method, we present the schematic image shown in Fig. 2. Note that in Figs. 1 and 2 fringe patterns of white light are shown because their waveforms are easily viewable when they are superimposed on each other. First, as shown in Fig. 2a, the aperture area can be regarded as a bright point group on the field stop. The interference definition of the black interferogram formed by the light of the zero-point (center) bright point degrades when the blue interferograms, in which the phase is half the wavelength (\(\lambda /2\)) in the horizontal direction, are superimposed on it. Conversely, the interference definition of the red interferogram formed when the phase is one whole wavelength (\(\lambda\)) in the horizontal direction improves. As shown in Fig. 2b, the multi-slit array removes the bright points that form the blue interferogram (fringe pattern (b) in Fig. 2) by the shielded area when the phase is half the wavelength and uses the bright points to form the red interferogram (fringe pattern (a) in Fig. 2) when the phase is one whole wavelength to improve the sensitivity and the interference definition simultaneously (Fig. 1, right panel and Fig. 2, bottom panel). When the width of the bright point in Fig. 2 is equal to L, which is the width of the aperture area in Fig. 1, the total width of the aperture area in Fig. 2b is 3L. Therefore, if the aperture areas are lined up periodically and the number of aperture areas is \(n\), the sensitivity and the interference definition are both improved \(n\)-fold with use of monochromatic light. We call this method the multi-slit superimposing interferogram method.
We now describe how to calculate the width of the aperture and the blocked area on the multi-slit using the interference condition of the phase-shift operation. First, we introduce the optical path difference per pixel \(\Delta \lambda\). When using monochromatic light of wavelength \(\lambda\), the image width of the aperture area (\(L^{\prime}\)) on the imaging plane is set to
to stop the interferogram from cancelling the zero-point interferogram through the blocked area of the multi-slit array. The image width (\(L^{\prime}\)) on the imaging plane is then converted into a pixel count (\(L^{\prime\prime}\)) using
Next, we calculate the projection ratio of the grating, which is dependent on the positions of the objective plane and the imaging plane. We introduce the pitch \(P\) of a camera pixel, the focal length \(f_{1}\) of the objective lens, the focal length \(f_{2}\) of the imaging lens, the altitude \(x\) of the object, and the altitude \(x^{\prime}\) of the image. As shown in Fig. 3, the incident light of the zero-point on the objective plane forms an interferogram at the same phase position as the interferogram of the incident light that passes through the principal point of the objective lens. Therefore, when using a one-shot Fourier spectrometer, which projects the collimated light beam onto the imaging plane, the projection ratio of the grating is
Then, the width of the aperture area on the multi-slit array (\(L\)) at the objective plane is
2.2 Principle underlying the interferograms obtained using our multi-slit array
Figure 4a presents a fringe pattern of monochromatic light on the imaging plane. The width of the aperture area on the imaging plane is denoted by \(\Delta \theta\) and the amplitude of the fringe pattern is denoted by \(A\). The intensity \(I\left( \theta \right)\) of the interferogram formed by adding all interferograms of the bright points from \(\theta_{{\text{a}}}\) to \(\theta_{{\text{a}}} + \Delta \theta\) in the horizontal direction is calculated from
As shown in Fig. 4b, (1) is the amplitude of the interferogram (Fig. 5), (2) is the phase difference and (3) is the offset. Therefore, we can demonstrate the phenomena shown in Figs. 1 and 2 via simulations with calculations based on Eq. (7) and Fig. 4. For example, when \(\Delta \theta\) is 180°, the amplitude is at a maximum of \(2A\). When \(\Delta \theta\) is 360°, the amplitude is at a minimum of \(0\). The amplitude changes periodically from \(0\) to \(2A\) (from \(0\) to \(2\pi\)) and the offset increases as the width of the aperture area increases. We evaluate the sensitivity based on the intensity of the central interferogram on the vertical axis and the interference definition, i.e., the difference between \(I_{{\max}}\) and \(I_{{\min}}\).
When \(n\) aperture areas for which the phases are the same are aligned to form a multi-slit array, the amplitude and offset increase \(n\)-fold, as shown by:
That is, the sensitivity and the interference definition are improved by the multi-slit array.
When white light is also used, the width of the aperture can be calculated using its central wavelength \(\lambda_{{\text{c}}}\). The sensitivity increases \(n\)-fold with the aperture area. However, the intensity of the interference does not conform because the negative part, which is out of phase with the base interferogram by \(\frac{{\lambda_{{\text{m}}} }}{2}\), degrades the interference definition because the bright point that made the interferogram cannot be removed accurately (m is assigned a counting number). When the amplitude of the fringe pattern for the central wavelength is 1, the amplitude of the fringe pattern for each wavelength can then be calculated using (see Fig. 5).
When a bright point (i.e., an aperture area) on the side forms a fringe pattern, a stretched fringe pattern is then formed by the field angle of the incident light on the imaging plane. Consequently, the spectral peak is shifted to longer wavelengths. This shift can be corrected using Fig. 3 (plane view) and
where the length of the real fringe pattern is denoted by \(d\) and the length of the stretched fringe pattern on the imaging plane is denoted by D. We can calculate the required value for correction of the spectral peak using Eq. (10), which gives the magnification of the expansion. For example, the width L of the aperture area, which is calculated using \(\lambda_{{\text{c}}} = 10 \;{\mu m}\), is 43 µm, the number of aperture areas is 5, and we use an objective lens (focal length 3 mm). The spectral peak then shifts by 0.1% of the wavelength.
3 Demonstrating the proposed field stop and multi-slit array installed in a one-shot Fourier spectroscopic imager in visible and mid-infrared wavelength regions
3.1 Confirmation of phase shifts in the visible regime for each apertural area of the array
We performed experiments to verify our superimposing interferogram method using the multi-slit array and a one-shot Fourier spectroscopic imager. One-shot Fourier spectroscopy is based around the spatial-phase-shift interferometer and a simple optical system that includes only three lenses (an objective lens, a wedge and cuboid prism, and a cylindrical lens). The incident light emitted from the bright point on the field stop is collimated by the objective lens. A relatively inclined phase shifter, which is configured using the wedge glass and the cuboid glass, gives a continuous spatial phase difference between the upper and lower halves of the objective beams. The interferogram, which is focused along one direction (i.e., the horizontal direction) of the imaging plane by the cylindrical lens, can then be obtained spatially.
Figure 6 shows the optical system used for this verification experiment. A HeNe laser (GLG5360, NEC Corporation) was used as the light source and a complementary metal–oxide–semiconductor (CMOS) camera (STU-MBCM200U3V-NIR, OMRON Sentech Co., Ltd.) was used as a light-receiving device in the visible wavelength region. The pixel pitch was 5.5 µm and the number of pixels was 2048 × 1088 pixels. The focal length of the illumination lens was 60 mm, while that of the objective and imaging lenses was 50 mm. Using Eq. (6), the width of the field stop was calculated to be 15 µm when the optical magnification was the same size. In this experiment, the pinhole with a hole size of 15 µm was moved in 15 µm steps and the interferogram was sampled at each step to analyze the effect of the multi-slit array artificially. Figure 7 shows the results obtained using same optical system that was shown in Fig. 6 with a metal halide lamp (IMH-250, Sigma Koki Co., Ltd.) as a light source. At the corresponding blocked areas of the multi-slit array, the interferogram (gray graph) for which the phase is out by half a wavelength was compared with the interferogram (black graph) formed by the zero-point bright point, as shown in Figs. 6a and 7a. Additionally, the interferograms at the corresponding aperture areas of the multi-slit array were formed at the same phase with the interferogram formed by the zero-point bright point, as shown in Figs. 6b and 7b. The orange graphs were calculated by adding two interferograms at the corresponding aperture areas of the multi-slit array and the interferogram of the zero-point bright point. The green graphs were calculated by adding the interferogram at the corresponding aperture areas of the multi-slit array and the interferogram of the zero-point bright point. The blue graphs were formed using only the interferograms of the zero-point bright point. The interferograms of the green and orange graphs were obtained using the neutral density filter to cut the light intensity by 50%. With increasing numbers of superimposed interferograms, sensitivities of 117, 243, and 324 and interference definitions of 128, 265, and 346 were obtained in Fig. 6. As shown in Fig. 7, with increasing numbers of superimposed interferograms, sensitivities of 81, 159, and 234 and interference definitions of 27, 48, and 60 were obtained. The dark current noise of the camera was present in these interferograms. The errors of the interference definition and the sensitivity between the predicted value and the measured value should be less than 100 when calculated using the mean squared error (MSE) method because the maximum amplitude of the dark current was 10. We then confirmed that every error in the sensitivity and the interference definition in the green graphs and the orange graphs in Figs. 6 and 7 was less than 100. These errors were thus within the scope of the assumption. Therefore, for the added interferograms for which the phase differences are \(m\lambda\) (where \(\lambda\) is the wavelength of the light source used; in the case of a white light source, \(\lambda\) is equal to \(\lambda_{{\text{c}}}\)), we confirmed increases in the sensitivity and the interference definition in Figs. 6b and 7b in accordance with the number of interferograms added at the corresponding aperture area of the multi-slit array, thereby verifying the multi-slit principle for both monochromatic and white light.
3.2 Experimental results for the field stop used in the multi-slit array for visible and mid-infrared light
Using a prototype of the multi-slit array, we performed verification experiments for the superimposing interferogram method in the visible and mis-infrared regions.
In the experiment using visible wavelengths, the focal length of the illumination lens was 60 mm, whereas that of the objective and imaging lenses were 50 mm. The same CMOS camera and light source (the metal halide lamp) used in experiments to obtain Figs. 6 and 7 were used in the optical system to obtain Fig. 8. The width of the multi-slit array along the horizontal direction was 15 µm and the number of aperture areas along each line were set at one slit (blue plot), three slits (green plot), and five slits (orange plot); see center right diagrams of Fig. 8. The interferograms of the green and orange plots were obtained using the neutral density filter to reduce the light intensity by 50%. The width of each of the multi-slits in the vertical direction was calculated to be 5.5 µm using the optical superposition method. A multi-slit array was made from a Si wafer with a thickness of 300 µm. The apertures (15 × 5.5 µm) were fabricated by dry etching. From the expanded graph (see Fig. 8, center left), we obtained the coherent waveforms from the interferograms detected from the one-, three-, and five-aperture multi-slit arrays. Furthermore, when more apertures were used, greater improvements were obtained in the spectroscopic characteristics, the sensitivity, and the interference definition. With increasing number of apertures, sensitivities of 95, 142, and 184 and interference definitions of 17, 37, and 50 were obtained.
Additionally, we compared the full-width at half-maximum values in the spectroscopic characteristics of the one-shot Fourier spectroscopic imager and those of the wavelength-dispersive spectrometer (PMA-11, Hamamatsu Photonics K.K.). The spectroscopic characteristics of the light source were obtained using the wavelength-dispersive spectrometer (Fig. 8, top image). The spectral peaks of the metal halide lamp within the 400–500 nm range were not detected using the one-shot Fourier spectroscopic imager because of axial chromatic aberration. The full-width at half-maximum values at approximately 550 and 580 nm were 10.4 and 11.5 nm for the one-shot Fourier spectrometer and 5.27 and 9.02 nm for the dispersive spectrometer, respectively. The full-width at half-maximum values for the one-shot Fourier spectrometer were broader than those of the dispersive spectrometer because the wavelength resolution of the one-shot Fourier spectrometer was 8.3 nm. Increasing the angle of the inclined wedge prism improves the wavelength resolution.
In considering the error, processing the accuracy of the multi-slit arrays enables a quantitative evaluation of the experimental results. However, the aperture width has an error of approximately + 1 µm, based on the Si etching rate when the multi-slits are produced. For example, when we used a multi-slit with an aperture width of 43 µm that was calculated assuming a central wavelength of 10 µm and a multi-slit having an error of + 1 µm in its width from processing, light with a wavelength that was 2.3% longer than 10 µm passed through the aperture and formed the interferogram, which was then superimposed on the other interferogram formed by the 10-µm wavelength light. Therefore, the interference definition and the sensitivity deteriorated by 2.3% per slit (aperture). Because we used 15 µm widths for the five slits, the sensitivity and the interference definition were assumed to deteriorate by a maximum of 33.5% given an error in processing accuracy of approximately + 1 µm. The errors in sensitivity and interference definition between the predicted and measured values (Fig. 8) were 23 and 15%, respectively. We confirmed that these errors were less than 33.5% and were, therefore, within the scope of the assumption. We also confirmed the proposed principle and demonstrated the effect of the multi-slit array when applying the superimposing interferogram method. Because the slit holder had some misalignments in terms of angle \({\theta }_{y}\) and the \(x\) axis with respect to the optical axis, the center aperture of the multi-slit array was not on the zero-point of the optical axis. Therefore, the sensitivity and interference definition did not improve by exactly threefold and fivefold, respectively, following increases in the number of aperture areas.
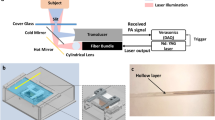
In experiments using mid-infrared wavelengths, we performed spectroscopic measurements using a prototype of a bean-sized mid-infrared spectroscopic imager based on the one-shot Fourier spectroscope, a prototype multi-slit array evaporated with Au to remove mid-infrared light in the blocked area, a microbolometer camera (Quark2, FLIR Systems, Inc.), a Kanthal filament light source (EK3430, Helioworks Inc.), and a band-pass filter (BP-10500-780, Spectrogon). The number of pixels was 336 × 256 pixels and the pixel pitch was 17 µm. The focal length of the two illumination lenses was 25 mm whereas that of the objective and imaging lenses was 3.32 mm. We compared the sensitivity and the interference definition for the different aperture numbers for the multi-slit array. Figure. 9 shows the optical system, the prototype mid-infrared spectroscopic imager, and the results of the experiments obtained by surveying a number of the 30 data points. We obtained the coherent waveform from the interferograms obtained with the three multi-slit arrays (Fig. 9). With increasing number of apertures, sensitivities of 98, 127, and 151 and interference definitions of 8, 21, and 23 were obtained. That is, we also confirmed improvements in both for the spatial-phase-shift interferometer when using our method for mid-infrared wavelengths.
Additionally, we compared the full-width at half-maximum values of the spectroscopic characteristics of the one-shot Fourier spectroscopic imager with those given in the specification sheet of the band-pass filter. The values obtained from the three- and five-slits spectrometer were 1262 and 1193 nm, respectively, whereas that from the band-pass filter’s specification sheet was 780 nm. The wavelength resolution of the prototype one-shot Fourier spectrometer was 511 nm. The full-width at half-maximum value of our spectrometer was broader than the value from the band-pass filter’s specification sheet because the spectroscopic characteristics include camera noise arising from a lack in sensitivity. We obtained the same full-width at half-maximum value as that on the band-pass filter’s specification sheet by installing a 17-slit multi-slit array in the spectrometer.
Thus, there is a need to consider not only every type of error caused by camera noise but also spherical aberrations and the processing accuracy of the multi-slit arrays to enable a quantitative evaluation of the experimental results. As described previously, if the five-slit multi-slit array had a processing accuracy error of approximately + 1 µm, the errors in the sensitivity and interference definition would be 11.5% (see Fig. 9). This would be the case if we had used a five-slit multi-slit array with an aperture width of 43 µm and the objective lens had a guaranteed condensing property on a 1 × 0.3 mm area of the objective plane, corresponding to the multi-slit pattern area. However, the three- and five-slit patterns were located outside this guaranteed area. Therefore, the sensitivity and the interference definition did not attain the three- and five-fold increases in these interferograms because of spherical aberration effects. In addition, because the spectroscopic imager had six degrees of freedom and was set by hand, the plane of the pattern area on the multi-slit array and the plane of the light-receiving device were not parallel. Moreover, because both the pattern axis of the multi-slit array and the optical axis were not vertical, the distribution of the light intensity was not equal on the light-receiving device. Therefore, we did not attain the n-fold increases in sensitivity and interference intensity when we used the n-aperture multi-slit array.
From the spectroscopic characteristics (Fig. 9), the spectral peaks appeared to shift toward longer wavelengths as the number of apertures increased. The spectral band becomes narrower with increasing aperture number because the central wavelength, which determines the aperture width of the multi-slit array, is extracted more strongly from the incident light. In viewing the interferograms (Figs. 8, 9), the interferogram from the five-slit array has a long waveform comprising light and dark variations similar for monochromatic light. Therefore, a strong spectrum peak at 10 µm (Fig. 9) was detected and the full-width at half-maximum value was narrower because the multi-slit array was designed based on the central wavelength of 10 µm. The full-width at half-maximum value of white light thus narrows and reaches the same value as that for monochromatic light. In future work, we intend to study this band narrowing using our method and then propose an optimal design method for the multi-slit arrays required for each interferometer, considering their different optical systems, to mitigate band narrowing and also to enhance the sensitivity and interference intensities of the spatial-phase-shift interferometers with broadband wavelengths.
4 Summary
We proposed a superimposing interferogram method that features a redesign of the conventional field stop of a spatial-phase-shift interferometer, specifically involving the use of a multi-slit array with more than one aperture area periodically spaced along the horizontal axis. Using monochromatic and white light, a pinhole, and a prototype multi-slit array, we obtained proof of the principle of our method in the visible light regime. Furthermore, using a bean-sized mid-infrared spectroscopic imager that incorporated the multi-slit array as a spatial-phase-shift interferometer and a band-pass filter, we confirmed improvements in sensitivity, interference intensity, and the spectroscopic characteristics in the mid-infrared regime.
In future work, we aim to develop an optimal design method to enhance the sensitivities and the interference definitions of spatial-phase-shift interferometers with broadband wavelengths. Subsequently, we plan to prototype another mid-infrared spectroscopic imager that has more aperture areas in the multi-slit array to improve the imager’s sensitivity and interferogram definition even further and then attach this imager to a light-receiving device to correct the optical axis of an imager or sensor. We hope to trial the imager in in vivo tests and to evaluate blood glucose concentrations quantitatively to realize our goal of non-invasive sensing of physiological biomarkers.
References
Shaw, G.A., Burke, H.K.: Spectral imaging for remote sensing. Linc. Lab. J. 14, 3–28 (2003)
Lu, G., Fei, B.: Medical hyperspectral imaging: a review. J. Biomed. Opt. 19, 10901 (2014)
Willoughby, C.T., Folkman, M.A., Figueroa, M.A.: Application of hyperspectral-imaging spectrometer systems to industrial inspection. In: Three-Dimensional and Unconventional Imaging for Industrial Inspection and Metrology 2599, 264–272 (1996)
Inoue, Y., Ishimaru, I., Yasokawa, T., Ishizaki, K., Yoshida, M., Kondo, M., Kuriyama, S., Masaki, T., Nakai, S., Takegawa, K., Tanaka, N.: Variable phase-contrast fluorescence spectrometry for fluorescently stained cells. Appl. Phys. Lett. 89, 121103 (2006)
Yamamoto, N., Kawashima, N., Kitazaki, T., Mori, K., Kang, H., Nishiyama, A., Wada, K., Ishimaru, I.: Ultrasonic standing wave preparation of a liquid cell for glucose measurements in urine by midinfrared spectroscopy and potential application to smart toilets. J. Biomed. Opt. 23, 050503 (2018)
Khalil, D., Sabry, Y., Omran, H., Medhat, M., Hafez, A., Saadany, B.: Characterization of MEMS FTIR spectrometer. In: Proceedings of the SPIE 7930, MOEMS and Miniaturized Systems X, 79300J (2011)
Ni, M., Feller, G., Irwin, J.W., Mason, J., Mudge, J.: High spectral resolution Fourier transform imaging spectroscopy in a Michelson interferometer with homodyne laser metrology control. In: Shen, S.S., Lewis, P.E. (eds.) Proceedings of the SPIE 7457, Imaging Spectrometry XIV, 74570L (2009)
Zhang, C, Bin, X., Zhao, B.: Static polarization interference imaging spectrometer (SPIIS). In: Proceedings of the SPIE 4087, Applications of Photonic Technology 4, 957–961 (2000)
Barnes, T.H.: Photodiode array Fourier transform spectrometer with improved dynamic range. Appl. Opt. 24, 3702–3706 (1985)
Padgett, M.J., Harvey, A.R.: A static Fourier-transform spectrometer based on Wollaston prisms. Rev. Sci. Instrum. 66, 2807–2811 (1995)
Schardt, M., Murr, P.J., Rauscher, M.S., Tremmel, A.J., Wiesent, B.R., Koch, A.W.: Static Fourier transform infrared spectrometer. Opt. Express 24, 7767–7776 (2016)
Köhler, M.H., Naßl, S.S., Kienle, P., Dong, X.-c, Koch, A.W.: Broadband static Fourier transform midinfrared spectrometer. Appl. Opt. 58, 3393–3400 (2019)
Köhler, M.H., et al.: Hyperspectral imager for the midinfrared spectral range using a single-mirror interferometer and a windowing method. OSA Contin. 2, 3212–3222 (2019)
Ferrec, Y., Primot, J.: Spaceborne hyperspectral imaging with a static Fourier transform spectrometer. SPIE Newsroom (2013). https://doi.org/10.1117/2.1201301.004601
Sato, S., Qi, W., Kawashima, N., Nogo, K., Hosono, S., Nishiyama, A., Wada, K., Ishimaru, I.: Ultraminiature one-shot Fourier-spectroscopic tomography. Opt. Eng. 55, 025106 (2016)
Qi, W., Suzuki, Y., Sato, S., Fujiwara, M., Kawashima, N., Suzuki, S., Abeygunawardhana, P., Wada, K., Nishiyama, A., Ishimaru, I.: Enhanced interference-pattern visibility using multislit optical superposition method for imaging-type two-dimensional Fourier spectroscopy. Appl. Opt. 54, 6254–6259 (2015)
Acknowledgments
We thank Richard Haase, Ph.D., and David MacDonald, MSc, from Edanz Group (www.edanzediting.com/ac) for editing drafts of this manuscript.
Funding
This study was supported by Japan Keirin Autorace (JKA) foundation (2019 M-163), by a Grant-in-Aid for Japan Society for the Promotion of Science (JSPS) Fellows (18J22468), and by a Grant-in-Aid for Scientific Research (B) (18H01452).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kawashima, N., Kitazaki, T., Nogo, K. et al. Superimposing interferogram method using a multi-slit array to enhance sensitivity and interference definition of spatial-phase-shift interferometers. Opt Rev 27, 530–541 (2020). https://doi.org/10.1007/s10043-020-00626-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10043-020-00626-4