Abstract
Because of its simple optical system setup and robust noise tolerance, non-interferometric phase retrieval is an important technique for phase-modulated holographic data storage. Usually, the iterative algorithm of non-interferometry needs hundreds of iteration numbers to retrieve phase accurately, the data transfer rate decreases severely. Strong constraints such as adding embedded data into the phase data page can reduce the iteration numbers, but this method decreases the code rate severely. In this paper, we proposed the advanced non-interferometric phase retrieval method based on the collinear system. By encoding the reference beam of the collinear optical holographic storage system with embedded data, the storage space of the signal beam data page is completely released and the encoding rate is doubled. The embedded data can provide more modulation index including phase and amplitude to shorten iterations, so the data transfer rate is also increased. In the simulation, we recorded a four-level phase pattern and retrieved the phase correctly.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With the development of the information age and the arrival of the big data era, the information storage demand has increased dramatically. The current storage technologies have been becoming unable to meet the human needs for data storage. In recent years, holographic optical storage technology has gradually become one of the most promising storage technology because of its high storage density, fast data transfer rate, and low cost and stable storage [1,2,3,4]. Optical holographic storage can encode and store data information in two ways: amplitude modulation and phase modulation. Because of its signal-to-noise ratio and encoding rate are relatively low, the amplitude-modulated holography storage technology has been unable to meet the current explosive data storage requirements gradually [5, 6].
Phase-modulated holography storage technology has attracted more and more attention because of its higher signal–noise-radio and storage density compared with the amplitude-modulated method. Since phase information cannot be detected directly by detectors such as CMOS or CCD, people use interferometry or non-interferometry method to retrieve the phase. There is a phase ambiguity problem in interferometry because of the cosine relationship between the interference intensity and the phase difference. Meanwhile, the interference intensity is unstable due to environmental disturbance. Multi-step phase-shifting interferometry can be used to solve the phase ambiguity problem and get the accurate phase information [7,8,9]. But multiple operations will reduce the data transfer rate and increase the error possibility. Using coding pairs can realize single-shot interferometry [10], but this method loses half of the code rate.
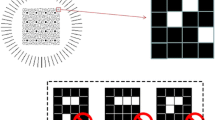
Non-interferometric methods for phase retrieval can not only solve the phase ambiguity issue but also have higher vibration tolerance. The iterative Fourier transform algorithm (IFTA) is one of the easiest non-interferometric iterative methods. It is originated from R.W. Gerchberg and W. O. Saxton in the 1970s and modified by James R. Fienup in the 1980s [11,12,13]. In our previous work, phase retrieval was achieved within 10 iterations using embedded data as a strong constraint for IFTA [14]. This work is applied to off-axis holographic systems and the illustration of the system is shown in Fig. 1. Because 50% of the storage capacity is used to store embedded data, the code rate is low.
In this paper, we propose the advanced non-interferometric phase retrieval method based on the collinear system to increase the code rate and storage density and accelerate phase retrieval further. Since the collinear system allows the signal beam and the reference beam in the same plane, the embedded data can be added to the reference beam only. Since the embedded data does not use signal light coding, the system coding rate is increased 2 times.
2 Methods
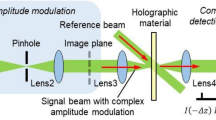
Collinear holography storage system [15, 16] was first proposed in 2005. It uses one spatial light modulator (SLM) to modulate the reference beam and signal beam, which are bundled on the same axis. In the recording process, the reference and signal beam irradiate on the recording medium through a single objective lens and a two-dimensional page data is recorded as a volumetric hologram in the material. In the reading process, only the outer ring reference beam is loaded on the SLM and irradiates the hologram. The reconstructed beam will be diffracted in the central area, and the zero-order diffraction of the reference beam will transmit to the corresponding positions with incident plane. Reconstructed light can be filtered separately using an aperture to get the signal part. The recording and reading process is shown in Fig. 2.
Since the reference beam and the signal beam of the collinear system are in the same plane, we propose to modulate the reference beam by known embedded data only. The encoding method of collinear and off-axis system are shown in Fig. 3. Compared with the off-axis method, since the reference beam has been known, there is no extra cost in the encoding, so that about 2 times the code rate is increased compared with the off-axis system.
So, our whole collinear non-interferometric phase retrieval system is illustrated in Fig. 4. Original phase data is the signal beam in the central part of the SLM, and embedded data is the reference beam in the outer part of the SLM. In the writing process, the signal beam and reference beam are both illuminated to record a hologram in the media. In the reading process, only the reference beam is illuminated and the reconstruction beam is diffracted. We designed to add an attenuator on the position of reference beam, because the diffractive signal part is too weak compared with the reference part. The Fourier intensity of the data page includes the reference and the signal part is captured by CMOS. Then, the fast iterative Fourier transform algorithm is used to recover the phase of the data page.
The calculation method of IFTA is as follows. At the beginning, we set an initial guess distribution \( \varphi_{0} \), includes embedded phase data in and random unknown phase data. Assign \( \varphi_{0} \) to \( \varphi_{k} \), where k = 1, 2,… denotes iteration number. Then we get a complex amplitude distribution \( U_{k} \) in the object domain as shown in Eq. (1):
We can get a complex amplitude distribution \( V_{k} \) on the Fourier domain after Fourier transform as shown in Eq. (2):
where F denotes Fourier transform operator, \( \left| {A_{k} } \right| \) and \( \phi_{k} \) denote amplitude and phase, respectively. Then we use the root square of intensity \( I \) captured by the CMOS to replace the amplitude \( \left| {A_{k} } \right| \), thus a new distribution \( {\text{V}}_{k}^{'} \) can be obtained, as shown in Eq. (3):
where I denote the intensity distribution image captured by CMOS.
After the inverse Fourier transform, a complex amplitude distribution \( U_{k}^{'} \) in the object domain is got, as shown in Eq. (4):
where \( \left| {A_{k}^{'} } \right| \) and \( \varphi_{k}^{'} \) denote new amplitude and phase values, respectively, in the object domain.
We use the constraints of phase-only and embedded phase data to correct the complex amplitude distribution. Therefore, amplitude \( \left| {A_{k}^{'} } \right| \) set to 1. The phase of the unknown data position is kept and the data in the embedded position is replaced by embedded phase data. Then we get a new distribution \( \left| {U_{k}^{''} } \right| \) shown in Eq. (5):
where \( \varphi_{k}^{''} \) is the new phase distribution and \( \varphi_{k}^{''} \) will be the new guess \( \varphi_{{\left( {k + 1} \right)}} \) for the next iteration. Then, we compute the new Fourier intensity distribution \( I_{k} \) by Eqs. (6) and (7):
where \( {\text{V}}_{k}^{''*} \) is the conjugation of \( {\text{V}}_{k}^{''} \).
We compute the intensity error rate \( E_{k} \) as shown in Eq. (8), and the difference between two adjacent intensity error rate \( \Delta E \) as shown in Eq. (9). Both I and \( I_{k} \) are normalized to 0–255. Set a threshold ɛ = 10−4 as the stop criterion, if \( \Delta E \) falls below ɛ, the loop is terminated and phase distribution \( \varphi_{k}^{''} \) is regarded as original phase code. Otherwise, phase \( \varphi_{k}^{''} \) will be a new guess going into next iteration:
3 Simulation results and discussion
We performed a realistic collinear non-interferometric phase retrieval experiment whose parameters are consistent with the actual experiment settings. The laser wavelength is 532 nm. The pixel pitch of SLM is 20 μm and we use 2 × 2 pixels to denote 1 phase data. We set 50 × 50 four-level phase data in the signal part and a similar amount of four-level phase data in the reference part of the data page. The pixel pitch of CMOS is 5.86 μm, and we captured twice the Nyquist size of the Fourier intensity of the input. The focal length in front of the CMOS is 150 mm.
When considering the amplitude of signal part and reference part 1:1, the simulation result is shown in Fig. 5. The input phase data page is shown in Fig. 5a. Fourier domain detected by CMOS is shown in Fig. 5b. Figure 5c is the phase retrieval result by the IFT algorithm. After the four-level phase discretizing as Fig. 5d the reconstruction results is shown in Fig. 5e. The bit-error-rate (BER) becomes 0 after 18 iterations. In the simulation, we didn’t consider the effect of the recording medium which would cause some noise such as degeneration noise mainly.
We tried to improve the weight of the reference and researched the reconstruction results. The complex amplitude distribution \( U_{k} \) in the object domain is represented by \( U_{k} = A_{\text{sig}} \exp \left( {i \times \varphi_{{{\text{sig}}\_k}} } \right) + A_{\text{ref}} \exp \left( {i \times \varphi_{{{\text{ref}}\_k}} } \right) \), where \( A_{\text{sig}} \) and \( A_{\text{ref}} \) are amplitude of signal and reference, respectively, and \( \varphi_{{{\text{sig}}\_k}} \) and \( \varphi_{{{\text{ref}}\_k}} \) are phase distributions in signal part and reference part, respectively. The specific data processing process is the same shown in Sect. 2.
Figure 6 shows the iterations under different amplitude weights of the reference (\( A_{\text{ref}} /A_{\text{sig}} \)). When the amplitude weight of the reference is improved, iterations are shortened. Because with the amplitude weight of the reference increasing, the proportion of known information increases; therefore, the phase reconstruction is accelerated and iterations are shortened. Figure 7 shows the histograms of phase retrieval data under different amplitude weight of the reference. The BER is all 0, but the accuracy of the IFTA phase retrieval result is different. As the amplitude weight of the reference beam increases, the intensity of actual signal light relatively decreases. Then the noise appears and leads to the broadening of the reconstruction value become wider. Before the broadening phase reconstruction aliases, it can still be accurately reconstructed. If aliasing occurs between different phases, the bit-error rate will appear. Due to the influence of noise, the broadening of phase value will affect the final reconstruction accuracy. Therefore, we need to set the weight of reference to achieve a balance between reconstruction speed and accuracy.
We simulated the anti-noise performance by adding random detection noise on CMOS. The CMOS gray value is 0–255. We add ± 1 pepper noise to the CMOS detection surface to simulate the actual detection noise. That is, each pixel value of the phase plane will randomly fluctuate ± 1 in the true value range. The histograms of original phase retrieval data with detection noise are shown in Fig. 8. Figure 9 shows iterations and BER under different amplitude weights of reference situations. We can see that when the amplitude weights of the reference are large enough, the BER appears and grows. Still, we need to balance iterations and BER to get the best result.
We simulated the different encoding levels from 4-level to 8-level and compared their iterations and BERs under different reference weights, as Fig. 10 shows. It has been proved that the relation between iteration times and reference weight does not change much under different coding conditions. With the increase of the weight of the reference beam, the number of iterations gradually decreases and tends to balance, as Fig. 10a shows. However, as in Fig. 10b, when the reference amplitude reached 5 times of signal, the BER started to increases with the increase of the weight of reference gradually. Moreover, the higher the coding order, the larger the BER and the faster the growth. Therefore, in the actual experiment, we need to consider the coding order, reference beam weight as well as the system BER at the same time. We calculated 10 different phase patterns in the simulation and all the results showed the same trends about these performances.
4 Conclusions
In this paper, we proposed the advanced non-interferometric phase retrieval method based on the collinear system. There are unique advantages for the collinear non-interferometric phase retrieval system. First, the code rate is increased by about 2 times, so storage density is increased. Second, embedded data can provide more modulation index including phase and amplitude to shorten iterations, so the data transfer rate is increased. In the near future, we will simulate more complex noise modes and higher phase-level code. Meanwhile, the experimental demonstration is also going to be done.
References
Haw, M.: Holographic data storage: the light fantastic. Nature 422(6932), 556–558 (2003)
Horimai, H., Tan, X.: Holographic information storage system: today and future. IEEE Trans. Magn. 43(2), 943–947 (2007)
Lin, X., Hao, J., Zheng, M., Dai, T., Li, H., Ren, Y.: Optical holographic data storage-The time for new development. Opto-Electron. Eng. 46(3), 180642 (2019)
Lin, X., Liu, J., Hao, J., Wang, K., Zhang, Y., Li, H., Horimai, H., Tan, X.: Collinear holographic data storage technologies. Opto-Electron. Adv. 3(3), 190004-1-10 (2020)
Neifeld, M., Chou, W.: Information theoretic limits to the capacity of volume holographic optical memory. Appl. Opt. 36(2), 514–517 (1997)
Gurevich, B., Gurevich, S., Zhumaliev, K., Alymkulov, S., Sagymbaev, S., Akkoziev, I.: Comparative evaluation of the volume holographic memory information capacity limits caused by different limitation factors. In: International Symposium on Optical Science & Technology 2000, pp. 167–176, San Diego, California, USA (2000)
He, M., Cao, L., Tan, Q., He, Q., Jin, G.: Novel phase detection method for a holographic data storage system using two interferograms. J. Opt. A Pure Appl. Opt. 11(6), 377–378 (2009)
Xu, X., Cai, L., Wang, Y., Meng, X., Zhang, H., Dong, G., Shen, X.: Blind phase shift extraction and wavefront retrieval by two-frame phase-shifting interferometry with an unknown phase shift. Opt. Commun. 273(1), 54–59 (2007)
Jeon, S., Gil, S.: 2-step phase-shifting digital holographic optical encryption and error analysis. J. Opt. Soc. Korea 15(3), 244–251 (2011)
Lin, X., Huang, Y., Li, Y., Liu, J.Y., Liu, J.P., Kang, R., Tan, X.: Four level phase pair encoding and decoding with single interferometric phase retrieval for holographic data storage. Chin. Opt. Lett. 16(3), 032101 (2018)
Gerchberg, R., Saxton, W.: A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 35(2), 237–246 (1972)
Fienup, J.: Phase retrieval algorithms: a comparison. Appl. Opt. 21(15), 2758–2769 (1982)
Fienup, J., Wackerman, C.: Phase-retrieval stagnation problems and solutions. J. Opt. Soc. Am. A 3(11), 1897–1907 (1986)
Lin, X., Huang, Y., Shimura, T., Fujimura, R., Tanaka, Y., Endo, M., Nishimoto, H., Liu, J., Li, Y., Liu, Y., Tan, X.: Fast non-interferometric iterative phase retrieval for holographic data storage. Opt. Exp. 25(25), 30905–30915 (2017)
Horimai, H., Tan, X., Li, J.: Collinear holography. Appl. Opt. 44(13), 2575–2579 (2005)
Horimai, H., Tan, X.: Advanced collinear holography. Opt. Rev. 12(2), 90–92 (2005)
Acknowledgements
National Key R & D Program of China (2018YFA0701800). The Open Project Program of Wuhan National Laboratory for Optoelectronics (2019WNLOKF007).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hao, J., Ren, Y., Zhang, Y. et al. Non-interferometric phase retrieval for collinear phase-modulated holographic data storage. Opt Rev 27, 419–426 (2020). https://doi.org/10.1007/s10043-020-00611-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10043-020-00611-x