A method based on iterative morphological filtering and multiple scattering for detecting layer boundaries and extinction coefficients with LIDAR

Abstract

Layer boundaries detection with LIDAR is of great significance for the meteorological and environmental research. Apart from the background noise, multiple scattering can also seriously affect the detection results in LIDAR signal processing. To alleviate these issues, a novel approach was proposed based upon morphological filtering and multiple scattering correction with multiple iterations, which essentially acts as a weighted algorithm with multiple scattering factors in different filtering scales, and applies integral extinction coefficients as media to perform correction. Simulations on artificial signals and real LIDAR signals support this approach.

1 Introduction

Detecting and quantifying the spatial distributions and sizes of clouds and aerosol particles can be useful for the climate change investigation and aeronautical meteorological research [1–4]. Many equipments have been utilized to detect the optical properties of clouds and aerosol particles, such as nephelometer and sun-photometer, but LIDAR is a popular probe that can be used to scan the spacial physical properties in three dimensions, thereby reflecting clouds and aerosol particles distribution completely [5, 6]. However, the original LIDAR signal and related retrieval parameters are affected by background noise and multiple scattering seriously. Thus, it is necessary to develop practical methods to mitigate these problems.

As a form of interference, Background noise exhibits non-linear and non-stationary. In the early research [7], windows and adaptive algorithm were proposed to denoise the LIDAR signal, which applies multiple point windows to obtain the layer base with a slope of the original signal and takes the complexities of the LIDAR signal into account. In addition, signal decomposition techniques were also introduced to eliminate signal noise, such as wavelet, empirical mode decomposition (EMD), and their variants [8–11] etc. Non-linear and non-stationary are considered, but low-pass filtering based on the allover LIDAR signal performs in these methods [8–11], thereby the boundary characteristics cannot be revealed completely. In 2010, a differential zero-crossing method [12] was demonstrated to process the LIDAR signal, which applies the signal intensity and cloud information to reduce the error. Layer boundary characteristics can be considered, but signal pre-treatment must be carried out before layer detection; some useful information of layer boundaries may be missed accordingly. Recently, some segmentation methods [13–15] about simplifying the original signal were proposed, which conduct based on characteristic points and arrange the signal simplification and layer detection in one step. Useful signal messages can be retained and reveal the layer boundary characteristics, whereas determining simplification scale is a challenge in the segmentation process. Furthermore, in the case of complicated signal, filtering approach is more mature and comprehensive than most simplification approaches.

Multiple scattering is a kind of optical interference from the layers and photons interactions. Thus, it is generally recognized that the optical properties (optical depth, extinction coefficients, LIDAR ratio, etc.) can be used to estimate multiple scattering characteristics of the cloud. The experimental model on multiple scattering was proposed in 1976 [16]. Then, the importance of considering multiple scattering effect in layer detection was first emphasized by Platt et al. [17]. Moreover, multiple scattering factors were presented with simpler and more practical description of the multiple scattering degrees [17]. In 2013, an initial scheme for correcting the cloud height by multiple scattering factors was introduced [18]. The error is described and calculated by a geometry description of part extinction coefficients. However, it is a pity that the light fluctuation of extinction coefficients is ignored in the non-cloud areas, and influences of multi-layer cirrus on multiple scattering factors are not considered.

Aiming at alleviating the noise and multiple scattering effects on layer detection, a novel scheme is introduced based on signal iterative morphological filtering and multiple scattering factors. Characteristic point detection and signal simplification perform in one step without choosing the simplifying window, and the iterative morphological filtering is employed to process the detected signal combining with the multiple scattering correction. Moreover, the overall extinction coefficients are applied to calculate the multiple scattering factors, which make the ultimate values more accurate. The layout of this paper is arranged as follows: In Sect. 2, the overall strategies of this method are shown in the flowchart. Detailed descriptions are demonstrated step-by-step. Consequently, the experiments with simulated and real signals are exhibited, respectively, in Sect. 3, and the performance evaluations of this approach are illustrated. Finally, the conclusions are shown in Sect. 4.

2 Principles and methods

The back-scatter power P(r) received by the LIDAR detector can be presented as follows:

$$P\left( z \right) = \frac{C}{{z^{2} }}\left[ {\beta_{m} \left( z \right) + \beta_{a} \left( z \right)} \right]\exp \left[ { - 2\int_{{z_{b} }}^{z} {\eta \left( {z^{\prime}} \right)\left( {\sigma_{a} \left( {z^{\prime}} \right) + \sigma_{m} \left( {z^{\prime}} \right)} \right)dz^{\prime}} } \right] + e\left( z \right)$$

(1)

where $C$ is LIDAR constant, $z$ is the range, and $z_{b}$ represents the layer base. $\beta_{a} \left( z \right)$ and $\beta_{m} \left( z \right)$ indicate the aerosol and molecule back-scattering coefficients, respectively. $\sigma_{a} \left( z \right)$ and $\sigma_{m} \left( {\text{z}} \right)$ are the aerosol and molecule extinction coefficients, respectively. $e\left( z \right)$ indicates the noise. The multiple scattering factor $\eta \left( {\text{z}} \right)$ is a significant parameter representing the degree of cloud multiple scattering. Below the cloud, the aerosol and molecular transmittance are ignored (their transmittances are set to 1). According to characteristics of the atmosphere layer as well as Eq (1), a novel layer detection method is proposed, which contains four key steps: preliminary layer detection, iterative morphological filtering, multiple scattering factors calculation, and layer boundaries correction. The flowchart of this scheme is demonstrated in Fig. 1.

Fig. 1

Flowchart of the proposed method for layer detection

2.1 Preliminary layer detection

Preliminary layer detection is a process of boundaries determining and signal simplification; the purpose of this algorithm is to search the possible boundaries of layers, and to find a similar curve with fewer points that can describe the original signal characteristics. Unlike general methods applying low-pass filter and zero-crossing, this technique only focuses on the feature-point detection in principle. It can exclude the non-feature parts of the signal and retain the possible layer boundary points that would be eliminated by low-pass filter. Detail procedures are demonstrated as the following:

Starting with a LIDAR signal that consists of n points, maxima, and minima of the signal are identified, termed $p_{1} ,p_{2} , \ldots ,p_{{n_{1} }}$ (maxima) and $v_{1} ,v_{2} , \ldots ,v_{{n_{2} }}$ (minima), respectively (Fig. 2). LIDAR signal is generally non-linear and non-stationary; thereby extremes (maxima and minima) at local waveform can carry the noise as well as the information of layers. Through investigating the relation of these extremes, the characteristics of different layers and noise are obtained. Then, the possible boundaries of layers can be discriminated by an appropriate threshold.

Fig. 2

Simulated signal (a), and its maxima and minima presented in a small scale (b)

The range-corrected signal $Pz^{2}$ is applied instead of original signal $P$ in layer detection. The relation of maxima and minima, hereafter referred to as the peak-base ratio (PBR), is considered to be:

$$r\left( {z_{{p_{i} }} ,z_{{v_{j} }} } \right) = \frac{{P_{{p_{i} }} z_{{p_{i} }}^{2} }}{{P_{{v_{j} }} z_{{v_{j} }}^{2} }}$$

(2)

where $P_{{p_{i} }} z_{{p_{i} }}^{2}$ and $P_{{v_{j} }} z_{{v_{i} }}^{2}$ represent the range-corrected signals of the maxima $p_{i}$ and minima $v_{i}$, respectively ($p_{i}$ and $v_{i}$ are the ith maxima and minima). The PBR may be an approximation, because the so-called peak or base can be effected by the noise, but it can be applied to investigate any possible layers of the LIDAR signal. In the study of PBR, Morille [11] assumed that above 7.5 km only, cloud layers contribute to the distribution of PBR; whereas under 7.5 km, both cloud and aerosol layers are components of the distribution of PBR. According to the probability density function (PDF) of PBR, Morille set a threshold value T to be 4 to separate cloud layers from aerosols for the particle layers over the full the LIDAR range, which can be translated to:

$${\text{PBR}} = \left\{ {\begin{array}{*{20}l} {\frac{{P_{p} z_{p}^{2} }}{{P_{b} z_{b}^{2} }} \ge T\;{\text{cloud}}} \hfill \\ {\frac{{P_{p} z_{p}^{2} }}{{P_{b} z_{b}^{2} }} < T\;{\text{aerosol}}} \hfill \\ \end{array} } \right.$$

(3)

where $P_{b} z_{b}^{2}$ and $P_{p} z_{p}^{2}$ are the range-corrected signals of the base and peak of a layer, respectively. In this study, 4 is selected as the threshold T based upon the previous research. Therefore, according to Eqs. (2) and (3), a novel function of layer detection is determined as:

$$z_{b} = \left\{ {z_{{v_{j} }} \left| {{ \hbox{max} }\left\{ {r\left( {z_{{p_{i} }} ,z_{{v_{j} }} } \right)\left| {r\left( {z_{{p_{i} }} ,z_{{v_{j} }} } \right) = \left( {\frac{{P_{{p_{i} }} z_{{p_{i} }}^{2} }}{{P_{{v_{j} }} z_{{v_{j} }}^{2} }}} \right),z_{{p_{i} }} > z_{{v_{j} }} } \right.} \right\} > 4} \right.} \right\}$$

(4)

$$z_{t} = \left\{ {\left. {z_{{v_{t} }} } \right|P_{{v_{t} }} z_{{v_{t} }}^{2} < P_{b} z_{b}^{2} } \right\}$$

(5)

where $z_{b}$ and $z_{t}$ are the base and top height of the layer, respectively.

2.2 Iterative morphological filtering

After determining the possible boundaries of layers, morphological filtering factors are applied to measure the morphological gaps of two peak (or valley) in non-layer areas, referred to as $\Delta_{1} ,\Delta_{2} , \ldots ,\Delta_{n}$ (Fig. 3a). Then, three important morphological filtering parameters can be expressed as:

Fig. 3

Diagram of morphological scales based on the simulated signal (a), and the smoothing process using the spherical morphological factors (b)

$$\Delta_{ \hbox{min} } = { \hbox{min} }\left\{ {\Delta_{1} ,\Delta_{2} , \ldots ,\Delta_{n} } \right\}$$

(6)

$$\Delta_{ \hbox{max} } = { \hbox{min} }\left\{ {\Delta_{1} ,\Delta_{2} , \ldots ,\Delta_{n} } \right\}$$

(7)

$$\Delta_{0} = \frac{{\Delta_{\hbox{max} } - \Delta_{\hbox{min} } }}{n - 1}$$

(8)

where $\Delta_{ \hbox{min} }$ and $\Delta_{ \hbox{max} }$ are the minimum and maximum morphological filtering scales, respectively, which determine the scale range of morphological filter and the interval $\Delta_{0}$ that can be employed to implement iterative calculation. Then, the original LIDAR signal filtering performs with the spherical factor of the scale $\Delta_{ \hbox{min} }$, and the smoothed signal $P_{0}$ is acquired. Similarly, a series of morphological filters can be used to process the original LIDAR signal with spherical morphological factors of the scales $\Delta_{ \hbox{min} } + \Delta_{0}$, $\Delta_{ \hbox{min} } + 2\Delta_{0}$,…, $\Delta_{ \hbox{max} }$; denoised signals can be termed as $P_{1}$, $P_{2}$,…, $P_{{n{ - }1}}$. Through rolling the morphological factors along the waveform, the signal can be smoothed in different scales, which is illustrated in Fig. 3b.

2.3 Multiple scattering factors calculation

The values of multiple scattering factors depend on several factors, particularly the cloud particle phase function, the cloud optical depth, and the cloud range etc [19]. Multiple scattering factors are derived through the following steps: (1) segment the simplified signal and establish the non-linear equations to compute the LIDAR ratio. (2) Compute the multiple scattering factors with the calculated LIDAR ratio.

In segmentation, three feature points: the layer base $z_{b}$, the layer top $z_{t}$, and a point in a low-altitude region (the altitude lower than $z_{b}$) $z_{c}$ are employed to divide the simplified signal. $z_{b}$ and $z_{t}$ have been obtained in the preliminary layer detection; $z_{c}$ is the $z$ corresponding to the minimum value of the function $\frac{{P\left( z \right)z^{2} }}{{\beta_{m} \left( z \right)}}$. The extinction coefficients at $z_{b}$, $z_{t}$, $z_{c}$, and the LIDAR ratio for cloud are named as $x_{1}$, $x_{2}$, $x_{3}$, and $s_{a}$, respectively; then, non-linear equations are established as follows:

$$\left\{ {\begin{array}{*{20}l} {\int\limits_{0}^{{z_{c} }} {\frac{{\exp \left( {S\left( z \right) - S\left( {z_{c} } \right)} \right)}}{{{1 \mathord{\left/ {\vphantom {1 {x_{1} }}} \right. \kern-0pt} {x_{1} }} + 2\int\limits_{z}^{{z_{c} }} {\exp \left( {S\left( {z^{\prime}} \right) - S\left( {z_{c} } \right)} \right)dz^{\prime}} }}dz + \left( {\int\limits_{0}^{{z_{c} }} {\frac{{\exp \left( {S\left( z \right) - S\left( {z_{c} } \right)} \right)}}{{{1 \mathord{\left/ {\vphantom {1 {x_{1} }}} \right. \kern-0pt} {x_{1} }} + 2\int\limits_{z}^{{z_{c} }} {\exp \left( {S\left( {z^{\prime}} \right) - S\left( {z_{c} } \right)} \right)dz^{\prime}} }}dz} } \right)^{2} } = {{x_{1} } \mathord{\left/ {\vphantom {{x_{1} } D}} \right. \kern-0pt} D}} \hfill \\ {x_{3} = - {{s_{a} \sigma_{m} \left( {z_{c} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{c} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }} + \frac{{S\left( {z_{c} } \right) \cdot \exp \left( {2\left( {{{s_{a} } \mathord{\left/ {\vphantom {{s_{a} } {s_{m} }}} \right. \kern-0pt} {s_{m} }} - 1} \right) \cdot \int\limits_{{z_{c} }}^{{z_{b} }} {\sigma_{m} \left( {z^{\prime}} \right)dz^{\prime}} } \right)}}{{{{S\left( {z_{b} } \right)} \mathord{\left/ {\vphantom {{S\left( {z_{b} } \right)} {\left( {x_{1} + {{s_{a} \sigma_{m} \left( {z_{b} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{b} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }}} \right)}}} \right. \kern-0pt} {\left( {x_{1} + {{s_{a} \sigma_{m} \left( {z_{b} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{b} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }}} \right)}} + 2\int\limits_{{z_{c} }}^{{z_{b} }} {S\left( z \right) \cdot \exp \left( {2\left( {{{s_{a} } \mathord{\left/ {\vphantom {{s_{a} } {s_{m} - 1}}} \right. \kern-0pt} {s_{m} - 1}}} \right) \cdot \int\limits_{{z_{c} }}^{{z_{b} }} {\sigma_{m} \left( {z^{\prime}} \right)dz^{\prime}} } \right)dz} }}} \hfill \\ {x_{1} = - {{s_{a} \sigma_{m} \left( {z_{b} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{b} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }} + \frac{{S\left( {z_{c} } \right) \cdot \exp \left( {2\left( {{{s_{a} } \mathord{\left/ {\vphantom {{s_{a} } {s_{m} }}} \right. \kern-0pt} {s_{m} }} - 1} \right) \cdot \int\limits_{{z_{b} }}^{{z_{t} }} {\sigma_{m} \left( {z^{\prime}} \right)dz^{\prime}} } \right)}}{{{{S\left( {z_{t} } \right)} \mathord{\left/ {\vphantom {{S\left( {z_{t} } \right)} {\left( {x_{2} + {{s_{a} \sigma_{m} \left( {z_{t} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{t} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }}} \right)}}} \right. \kern-0pt} {\left( {x_{2} + {{s_{a} \sigma_{m} \left( {z_{t} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{t} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }}} \right)}} + 2\int\limits_{{z_{b} }}^{{z_{t} }} {S\left( z \right) \cdot \exp \left( {2\left( {{{s_{a} } \mathord{\left/ {\vphantom {{s_{a} } {s_{m} - 1}}} \right. \kern-0pt} {s_{m} - 1}}} \right) \cdot \int\limits_{{z_{b} }}^{{z_{t} }} {\sigma_{m} \left( {z^{\prime}} \right)dz^{\prime}} } \right)dz} }}} \hfill \\ { - \ln \left[ {\left( {{{P_{t} z_{t}^{2} } \mathord{\left/ {\vphantom {{P_{t} z_{t}^{2} } {P_{b} z_{b}^{2} }}} \right. \kern-0pt} {P_{b} z_{b}^{2} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right] = \int\limits_{{z_{b} }}^{{z_{t} }} {\left\{ { - {{s_{a} \sigma_{m} \left( z \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( z \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }} + \frac{{S\left( z \right) \cdot \exp \left( {2\left( {{{s_{a} } \mathord{\left/ {\vphantom {{s_{a} } {s_{m} }}} \right. \kern-0pt} {s_{m} }} - 1} \right) \cdot \int\limits_{z}^{{z_{t} }} {\sigma_{m} \left( {z^{\prime}} \right)dz^{\prime}} } \right)}}{{{{S\left( {z_{t} } \right)} \mathord{\left/ {\vphantom {{S\left( {z_{t} } \right)} {\left( {x_{2} + {{s_{a} \sigma_{m} \left( {z_{b} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{b} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }}} \right)}}} \right. \kern-0pt} {\left( {x_{2} + {{s_{a} \sigma_{m} \left( {z_{b} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{b} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }}} \right)}} + 2\int\limits_{z}^{{z_{t} }} {S\left( z \right) \cdot \exp \left( {2\left( {{{s_{a} } \mathord{\left/ {\vphantom {{s_{a} } {s_{m} - 1}}} \right. \kern-0pt} {s_{m} - 1}}} \right) \cdot \int\limits_{z}^{{z_{t} }} {\sigma_{m} \left( {z^{\prime}} \right)dz^{\prime}} } \right)dz} }}} \right\}dz} } \hfill \\ {D = {{S\left( {z_{c} } \right)} \mathord{\left/ {\vphantom {{S\left( {z_{c} } \right)} {\int\limits_{0}^{{z_{c} }} {S\left( z \right)dz} }}} \right. \kern-0pt} {\int\limits_{0}^{{z_{c} }} {S\left( z \right)dz} }}} \hfill \\ \end{array} } \right.$$

(9)

where $S\left( z \right)$ is range-corrected signal computed as $S\left( z \right) = P\left( z \right)z^{2}$ and $s_{m} = {{8\pi } \mathord{\left/ {\vphantom {{8\pi } 3}} \right. \kern-0pt} 3}$ is the LIDAR ratio for molecular and assumed according to the Rayleigh scattering theory. By solving the equations, the LIDAR ratio can be obtained.

In Eq (9), the first and fifth equations determine the extinction coefficients of $z_{b}$ according to ref [20]. The second and third equations are constructed from Fernald formulation [21], with $z = z_{c}$ and $z = z_{b}$. Chen’s method [19] forms the fourth equation, which uses range-corrected signals to describe the laser transmission as well as the relation between the optical depth and extinction coefficients.

After deriving the LIDAR ratio, the extinction coefficients can be expressed as [20]:

$$\sigma \left( z \right) = \left\{ {\begin{array}{*{20}l} { - {{s^{\prime}_{a} \sigma_{m} \left( {z_{b} } \right)} \mathord{\left/ {\vphantom {{s^{\prime}_{a} \sigma_{m} \left( {z_{b} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }} + \frac{{S\left( z \right) \cdot \exp \left( {2\left( {{{s^{\prime}_{a} } \mathord{\left/ {\vphantom {{s^{\prime}_{a} } {s_{m} }}} \right. \kern-0pt} {s_{m} }} - 1} \right) \cdot \int\limits_{z}^{{z_{b} }} {\sigma_{m} \left( {z^{\prime}} \right)dz^{\prime}} } \right)}}{{{{S\left( {z_{b} } \right)} \mathord{\left/ {\vphantom {{S\left( {z_{b} } \right)} {\left( {x_{1} + {{s^{\prime}_{a} \sigma_{m} \left( {z_{t} } \right)} \mathord{\left/ {\vphantom {{s^{\prime}_{a} \sigma_{m} \left( {z_{t} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }}} \right)}}} \right. \kern-0pt} {\left( {x_{1} + {{s^{\prime}_{a} \sigma_{m} \left( {z_{t} } \right)} \mathord{\left/ {\vphantom {{s^{\prime}_{a} \sigma_{m} \left( {z_{t} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }}} \right)}} + 2\int\limits_{z}^{{z_{b} }} {S\left( z \right) \cdot \exp \left( {2\left( {{{s^{\prime}_{a} } \mathord{\left/ {\vphantom {{s^{\prime}_{a} } {s_{m} - 1}}} \right. \kern-0pt} {s_{m} - 1}}} \right) \cdot \int\limits_{z}^{{z_{b} }} {\sigma_{m} \left( {z^{\prime}} \right)dz^{\prime}} } \right)dz} }}\; + \sigma_{m} \left( {0 < z < z_{b} } \right)} \hfill \\ { - {{s_{a} \sigma_{m} \left( {z_{b} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{b} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }} + \frac{{S\left( z \right) \cdot \exp \left( {2\left( {{{s_{a} } \mathord{\left/ {\vphantom {{s_{a} } {s_{m} }}} \right. \kern-0pt} {s_{m} }} - 1} \right) \cdot \int\limits_{{z_{b} }}^{{z_{t} }} {\sigma_{m} \left( {z^{\prime}} \right)dz^{\prime}} } \right)}}{{{{S\left( {z_{t} } \right)} \mathord{\left/ {\vphantom {{S\left( {z_{t} } \right)} {\left( {x_{2} + {{s_{a} \sigma_{m} \left( {z_{t} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{t} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }}} \right)}}} \right. \kern-0pt} {\left( {x_{2} + {{s_{a} \sigma_{m} \left( {z_{t} } \right)} \mathord{\left/ {\vphantom {{s_{a} \sigma_{m} \left( {z_{t} } \right)} {s_{m} }}} \right. \kern-0pt} {s_{m} }}} \right)}} + 2\int\limits_{{z_{b} }}^{{z_{t} }} {S\left( z \right) \cdot \exp \left( {2\left( {{{s_{a} } \mathord{\left/ {\vphantom {{s_{a} } {s_{m} - 1}}} \right. \kern-0pt} {s_{m} - 1}}} \right) \cdot \int\limits_{{z_{b} }}^{{z_{t} }} {\sigma_{m} \left( {z^{\prime}} \right)dz^{\prime}} } \right)dz} }} + \sigma_{m} \;\left( {z_{b} \le z < z_{t} } \right)\;} \hfill \\ \end{array} } \right.$$

(10)

where $s^{\prime}_{a}$ is the LIDAR ratio outside the layers that is assumed to be 50. Inside the layer, the LIDAR ratio $s_{a}$ is computed using Eq (9). This technique proposes an assumed boundary $z_{c}$ to determine extinction coefficients $\sigma$ and segments the atmosphere according to layer detection.

The multiple scattering factor $\eta$ is proposed to represent the degree of atmosphere multiple scattering, which varies with the thickness and density of the layer. Outside the layer, $\eta$ is assumed to be 1. Inside, the multiple scattering factor $\eta$ can be computed as [20

$$\left\{ {\begin{array}{*{20}l} {\eta \left( {\text{z}} \right) = 1 - \frac{\ln \left( m \right)}{2\delta \left( z \right)}} \hfill \\ {\delta \left( z \right) = - \int\limits_{0}^{z} {\sigma \left( z \right){\text{d}}z} } \hfill \\ \end{array} } \right.$$

(11)

where $m$ expresses the proportion of the single scattering and multiple scattering of light transmission in the atmosphere, which can reflect the statistics microscopic state of laser transmission. The Monte Carlo (MC) approach is used to compute $\eta$ according to the “Appendix”. Table 1 presents the parameters of simulations using the MC method according to the LIDAR model.

Table 1 Parameters of MC simulation and LIDAR

Through applying the above method to $P_{0}$, $P_{1}$,…, $P_{{n{ - }1}}$, a series of multiple scattering factors and extinction coefficients can be acquired, termed as $\eta_{0}$, $\eta_{1}$,…, $\eta_{n - 1}$ and $\sigma_{0}$, $\sigma_{1}$,…, $\sigma_{n - 1}$, respectively.

2.4 The layer boundaries detection

After obtaining a series of multiple scattering factors and extinction coefficients via allover detection arrange, the corrected extinction coefficients can be calculated, according to:

$$\sigma^{\prime}_{i} \left( z \right) = \frac{{\sigma_{i} \left( z \right)}}{{\eta_{i} \left( z \right)}}$$

(12)

$\sigma^{\prime}_{i} \left( z \right)$ is the ith revised extinction coefficients, by which a series of revised returned LIDAR signals can be calculated based on:

$$P^{\prime}_{i} \left( z \right) = \frac{C}{{z^{2} }}\left[ {\beta^{\prime}_{i} \left( z \right) + \beta_{m} \left( z \right)} \right]\exp \left\{ { - 2\int_{0}^{z} {\sigma^{\prime}_{i} \left( {z^{\prime}} \right)dz^{\prime}} } \right\}\;\left( {i = 0,1, \ldots ,n - 1} \right)$$

(13)

where C is LIDAR constant, and $\beta^{\prime}_{i} \left( z \right)$ represents the ith revised aerosol back-scattering coefficients.

Applying Eqs. (2)–(5) to $P^{\prime}_{0}$, $P^{\prime}_{1}$,…, $P^{\prime}_{{n{ - }1}}$, a series of revised layer boundaries can be obtained, named as $z_{b}^{1}$, $z_{b}^{2}$,…, $z_{b}^{n}$ and $z_{t}^{2}$, $z_{t}^{3}$,…, $z_{t}^{n}$, respectively, which can outline the effect of noise with different degree of useful signal retention. Applying these corrected layer boundaries, the top and base values via the morphological scales can be acquired. Then, the final corrected top and base of layer are derived by the weighted least square method, which can be expressed as:

$$f_{0} \left( z \right) = \sum\limits_{i = 1}^{n} {\frac{{\frac{n}{2} - \left| {\frac{n}{2} - i} \right|}}{n}\left( {z - z_{t}^{i} } \right)^{2} }$$

(14)

$$f_{1} \left( z \right) = \sum\limits_{i = 1}^{n} {\frac{{\frac{n}{2} - \left| {\frac{n}{2} - i} \right|}}{n}\left( {z - z_{b}^{i} } \right)^{2} }$$

(15)

Searching the extremes of Eqs. (14) and (15), the ultimate values of layer boundaries can be expressed as:

$$z_{t} = \frac{{\sum\limits_{i = 1}^{n} {\frac{{\left( {\frac{n}{2} - \left| {\frac{n}{2} - i} \right|} \right)z_{t}^{i} }}{n}} }}{{\sum\nolimits_{i = 1}^{n} {\frac{{\frac{n}{2} - \left| {\frac{n}{2} - i} \right|}}{n}} }}$$

(16)

$$z_{b} = \frac{{\sum\limits_{i = 1}^{n} {\frac{{\left( {\frac{n}{2} - \left| {\frac{n}{2} - i} \right|} \right)z_{b}^{i} }}{n}} }}{{\sum\nolimits_{i = 1}^{n} {\frac{{\frac{n}{2} - \left| {\frac{n}{2} - i} \right|}}{n}} }}$$

(17)

where the processed layer boundaries are weighted according to the morphological filtering scales. This technique can make the corrected top and base accurate in the case of signal–noise balance.

3 Results and discussions

3.1 Experiment with simulated signals

An extensive experiment is performed to verify the proposed method using simulated signals. Three original artificial signals are produced based upon an approximate standard atmosphere model and different layers (one, two and three layers), which are simulated by linear function and quadratic function, respectively (Fig. 4). The layer boundaries of “one layer” are 4 and 6 km, those of “two layers” as well as “three layers” are 4, 4.8, 4.8, and 6, and 4, 4.5, 4.5, 5.2, 5.2, and 6, respectively, with a range resolution of 0.01 km. All of the layer intervals are set to be zero, which is beneficial for testing the denoising effects of different approaches on layer intervals. After simulating three original signals, a series of noises are mixed with them for creating the tested signals with different SNRs of 30DB, 40DB, and 50DB. Thus, nine artificial signals of different layer numbers and SNRs are formed. Figure 5 shows the results of one layer signal mixed with noises. It can be seen that in SNR = 30, the layers boundaries are very blur and many tiny peaks disturb the layer detection in the non-layer areas.

Fig. 4

Simulated signals with one ridge (a), two ridges (b), as well as three ridges (c)

Fig. 5

Adding noise to the original “one layer” simulated signal (a), with SNR = 30 DB (b), SNR = 40 DB (c), as well as SNR = 50 DB

“One layer” detection results using two methods are demonstrated in Table 2, where it can be observed that the results of our method are closer to 4 and 6 km than Xiong’s. Especially, when SNR = 40DB, the error of our method is smaller 0.1 km than the one of Xiong’s. It illustrates that the proposed method can improve the detection effect significantly in the case of fewer layers.

Table 2 “One layer” detection results using Xiong’s method with signal simplification and the proposed method

Because, layer detection is effected by complicated multiple layers and noise at the same time, the calculation errors in Tables 3 and 4 are larger than the ones in Table 2. It becomes difficult to detect the intersecting layer boundaries, such as the first-layer base and the second-layer top. Using Xiong’s approach intersecting layer boundaries are obtained with different values and have some larger deviations, while employing the proposed method the ones can be stabilized at single values regardless of the SNR degree. For example, in Table 3, when SNR = 30, the first-layer top 4.9 is larger than the second-layer base 4.87 in the right column, which is unrealistic, but in the left column, the first-layer top 4.79 nearly equals the second-layer base 4.80. Moreover, the proposed approach can also effectively restrain the background noise for multiple layers. In Table 4, when SNR = 30, at 4.5 km, it can be found that the results of our method are very close to 4.5 km, the deviations are only 0.02 and 0.02 km, while the ones of Xiong’s approach have large errors of 0.11 and 0.08 km.

Table 3 “Two layer” detection results using Xiong’s method with signal simplification and the proposed method

Table 4 “Three layer” detection results using Xiong’s method with signal simplification and the proposed method

3.2 Experiments with the real signal

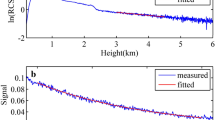
A series of experiments were performed to verify the proposed method on the layer base detection. L-band upper-air meteorological sounding system (LUMSS) was introduced as a standard equipment, which contains the GFE 1 Secondary Wind-Finding Radar and the GTS1 digital radiosonde. As a more complicated device than LIDAR, it can detect the layer boundary automatically and accurately. LUMSS has the sampling period of 1.2 s. The climbing speed and resolution of LUMSS is 400 m/min and 5 m, respectively. Due to its high-accuracy and real-time acquisition, LUMSS is arranged in radiosonde stations across China and applied to test other layer detection device as a standard system. Observations are from 15/11/06 to 15/12/14. The cloudy dates are selected. Different heights of clouds are detected by LIDAR and LUMSS. With the LIDAR and MC parameters listed in Table 5, the proposed method is used to process the real signals.

Table 5 LIDAR and MC parameters

The obtained layer base heights are shown in Table 6, where the standard values detected by LUMSS are employed to verify two methods using LIDAR. One can observe that the detection heights using the proposed approach is closer to the standard value, compared with Xiong’s method, and the mean of deviations with our method is less 45.6 m than the one with Xiong’s method (the uncertainty is 10 m). Through the above four steps, the characteristics of LIDAR signals can be selected to determine the layer boundaries. Filter, iteration, and global correction precisely retain the features of trend and multiple scattering, and thus lead the LIDAR results to approach the outcomes of LUMSS.

Table 6 Comparison results of real-signal detection

The lowest blue line, the middle green line, the middle red line, the highest light, and the blue line represent the 1st, 2nd, 3rd, 4th, and 5th detected boundaries, respectively.

An actual case can be introduced to verify our method on multiple layers. LUMSS is also used to test the performance. With the LIDAR, two layers can be exhibited clearly with a range resolution of 0.01 km in Fig. 6. After the signal correction and iteration, final-detected boundaries can be obtained as 7.72, 8.70, 8.76, and 9.72 km. In Fig. 7, detection results via the number of iterations are showed, from which one can observe that the noise vibration acting on the first boundary (approach to 7.5 km) is weakened to a value that cannot affect the layer detection through 53 iterative filtering, and other boundaries also have the similar performances. It practically illustrates that iterative morphological filtering has a good robustness making detection results stabilized at a value with the iterative number increasing. Furthermore, at the boundaries of approximate 8.7 and 9.7 km, the fluctuations of detection results are weak, which displays good performances of the intervals detection of layers.

Fig. 6

LIDAR return signal

Fig. 7

Detected layer boundaries via different iterations for the profile in Fig. 3

Detection results of real signal have been exhibited in Table 6 using the two methods. It clearly illustrates that the new approach outperforms Xiong’s method in the gaps detection of layers (8.75 and 8.77 are much closer to 8.800 than 8.90 and 8.91), because overall extinction coefficients are applied to compute the multiple scattering factors. Furthermore, using Xiong’s method, the detected layer tops can be higher than the ones using the proposed method, and closer to the standard values. It shows that the iterative morphological filtering restrains the noise better in the plat area of signals, and our method can determine the layer top at a lower altitude in the case of low-SNR.

4 Summary

A novel segmentation method based upon multiple scattering factors and iterative morphological filtering has been proposed to detect layer boundaries. This algorithm consists of four keys steps, which are the preliminary layer detection, iterative morphological filtering, multiple scattering factors calculation, and layer boundaries correction. Through the above four procedures, the waveform characteristics of the raw signal can be demonstrated in different scales, which is beneficial for combining with the multiple scattering factors to compute and revise the layer boundaries. Furthermore, as important parameters calculated, the integral extinction coefficients are employed to correct the preliminary detection results with the MC method. It is proved to be effective according to the simulations and experiments.

Appendix

As described in Fig. 8, $D_{0}$ is the initial transmission vector, $\theta_{0}$ is the initial zenith angle, and $\phi_{0}$ represents the initial azimuthal angle.

Fig. 8

Diagram of the photon scattering

$\theta_{0}$ and $\phi_{0}$ are uniformly distributed in $\left[ {0,\theta_{ed} } \right]$ and $\left[ {0,2\pi } \right]$, respectively, which can be sampled to obtain:

$$\theta_{0} = { \arccos }\left[ {1 - \zeta_{0} \left( {\cos \theta_{ed} } \right)} \right]$$

(1)

$$\phi_{0} = 2\pi \zeta_{0}$$

(2)

where $\theta_{ed}$ is the half of laser divergence angle, and $\zeta_{0}$ represents a random value that is uniformly distributed in $\left[ {0,1} \right]$. Thus, we can obtain:

$$D_{0} = \left[ {\begin{array}{*{20}c} {u_{x,0} } \\ {u_{y,0} } \\ {u_{z,0} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sin \theta_{0} \cos \phi_{0} } \\ {\sin \theta_{0} \sin \phi_{0} } \\ {\cos \theta_{0} } \\ \end{array} } \right]$$

(3)

and the coordinate of the mth scattering can be expressed as:

$$\left[ {\begin{array}{*{20}c} {x_{m} } \\ {y_{m} } \\ {z_{m} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{m - 1} + lu_{x,m - 1} } \\ {y_{m - 1} + lu_{y,m - 1} } \\ {z_{m - 1} + lu_{z,m - 1} } \\ \end{array} } \right]$$

(4)

$l$ is the length of two adjacent photon collisions, which can be expressed as:

$$l = - \frac{1}{\sigma }\ln \zeta_{0}$$

(5)

$\sigma$ expresses the extinction coefficients.

The phase function is Henyey-Greenstein (HG) function, which can be formed as:

$$P_{H - G} = {{\left( {1 - g^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {1 - g^{2} } \right)} {\left( {1 + g^{2} - 2g\cos \theta } \right)}}} \right. \kern-0pt} {\left( {1 + g^{2} - 2g\cos \theta } \right)}}^{{\frac{3}{2}}}$$

(6)

$\theta$ represents the scattering angle, and g is asymmetry factor. Therefore, the parameters of multiple scattering can be derived:

$$\theta_{m} = \arccos \left\{ {\frac{1}{2g}\left[ {\left( {1 + g^{2} } \right) - \frac{{\left( {1 - g^{2} } \right)^{2} }}{{\left( {1 - g + 2g\zeta_{0} } \right)^{2} }}} \right]} \right\}$$

(7)

$$\phi_{m} = 2\pi \zeta_{0}$$

(8)

$\theta_{m}$ and $\phi_{m}$ represent the zenith angle and azimuthal angle of the mth scattering, respectively.

Finally, we can obtain:

$$D_{m} = \left[ {\begin{array}{*{20}c} {u_{x,m} } \\ {u_{y,m} } \\ {u_{z,m} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\sin \theta_{m} \left( {u_{x,m - 1} u_{z,m - 1} \cos \phi_{m} - u_{y,m - 1} \sin \phi_{m} } \right)}}{{\sqrt {1 - u_{z,m - 1}^{2} } }} + u_{x,m - 1} \cos \theta_{m} } \\ {\frac{{\sin \theta_{m} \left( {u_{y,m - 1} u_{z,m - 1} \cos \phi_{m} - u_{x,m - 1} \sin \phi_{m} } \right)}}{{\sqrt {1 - u_{z,m - 1}^{2} } }} + u_{y,m - 1} \cos \theta_{m} } \\ { - \sin \theta_{m} \cos \phi_{m} \sqrt {1 - u_{z,m - 1}^{2} } + u_{z,m - 1} \cos \theta_{m} } \\ \end{array} } \right]$$

(9)

$$P_{n} = \frac{{P_{H - G} \left( \theta \right)\Delta \varOmega }}{4\pi }\exp \left( { - \sigma \left( {r_{n} + \sum\limits_{i = 1}^{n} {l_{i} } } \right)} \right)$$

(10)

$D_{m}$ represents the transmission vector of the mth scattering. $P_{n}$ is the probability of the nth scattering. $l_{i}$ is the segment length of the ith scattering of n scattering. $r_{n}$ is the distance form the nth scattering site to receiver. $\Delta \varOmega$ is the solid angle subtended by receiver. The sum of all the scattering events for transmitted photons expresses the LIDAR signals. Thus, applying the MC simulation, the ratio of multiple and single scattering can be obtained.