Introduction

Fractures may serve as the dominant groundwater flow and solute transport pathways in the subsurface (Weisbrod et al. 2013; Wolfsberg et al. 2017; Cohen and Weisbrod 2018), where their presence determines the total extent of groundwater circulation in hard-rock aquifers. Fractures are heterogeneous discontinuities within a rock mass, and can be generated through tectonic processes. In the context of groundwater flow modelling, incorporating heterogeneity is of key importance, where the accurate representation of naturally fractured systems in numerical models remains a complex challenge (Dou et al. 2019; Stoll et al. 2019). Hyman and Jiménez‐Martínez (2018) investigated the relative impact of geological heterogeneity on transport processes in a fractured bedrock aquifer, demonstrating that both longitudinal and transverse dispersion increased with the scale of heterogeneities. A literature review (Mineo 2023) highlighted the importance of addressing the geological variability in fractured aquifers, especially when considering contamination issues. In particular, rock masses characterized by low primary permeability are generally dominated by fluid flow through fractures (Nelson 2001). At larger scales, where rock masses are intensely fractured (high frequency and spacing of fractures), fluid flow can be approximated as an equivalent continuum medium (Hoek et al. 2002). This condition is satisfied where fractures are sufficiently numerous and interconnected so that the overall hydraulic properties are not biased to a particular direction, i.e., the rock mass responds as an isotropic, equivalent continuum (Eberhardt 2012). Equivalent porous medium approaches to numerical groundwater modeling are reasonably justified for such cases (Wellman et al. 2009). Studies combining field observations with numerical simulations demonstrate equivalent porous medium approaches to groundwater modeling can provide good correlations with experimental data (Onaa et al. 2021). However, the hydraulic continuity of fractured bedrock aquifers can be interrupted by persistent discontinuities (e.g., faults), which can function as important preferential flow pathways and barriers to groundwater flow. Such discontinuities can exert a large influence on groundwater contamination transport.

This study aims to analyze the impact of fractures and groundwater abstraction activities on groundwater flow and solute transport, for a light nonaqueous phase liquid (LNAPL) contaminant plume in a fractured carbonate aquifer in Sicily, southern Italy (Fig. 1a). Here, an anomalous trajectory of a contaminant plume was observed, that was discordant to the regional groundwater flow direction. This was expected to be influenced by (1) the rock mass heterogeneity in terms of the extent of fracturing and presence of faults, and (2) groundwater abstraction (Mineo et al. 2022). This study investigates the relative extent to which these two factors are responsible for the observed migration path of the contaminant plume. To achieve this objective, numerical groundwater models were constructed in QGIS using the FREEWAT plug-in (Rossetto et al. 2018), based on detailed hydrogeological conceptual models. The conceptual model development was guided by fieldwork data collection which included mapping the orientation of fractures present in outcropping rock masses. Different numerical model scenarios were tested to assess the role of fractures and groundwater abstraction on simulated groundwater flow and contaminant transport.

Fig. 1
figure 1

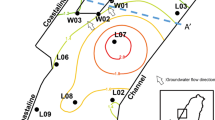
a Geographical setting of the study area (source: Google Earth); b Sketch of the LNAPL free-phase product contaminant plume path direction (modified from Mineo et al. 2022)

Full size image

Materials and methods

The case study

This study focuses on groundwater contamination by LNAPL derived from an industrial area located along the Ionian coastline of southeastern Sicily, Italy (Fig. 1a). Here, both the dissolved and free-product plumes followed an anomalous flow direction, migrating towards the southeast as opposed to the northeast, which was inconsistent with the regional hydraulic gradient. Based on multiyear monitoring, the plume was hypothesized to be driven by preferential flow pathways, represented by discontinuities in the bedrock, in combination with the local groundwater abstraction associated with the pumping of a specific well (referred to hereafter as the SE well). The SE well, no longer active, recently supplied water to a commercial area. The plume direction was found to follow linear discontinuities/faults that were identified with geophysical surveys (Mineo et al. 2022).

The contaminant plume is a mixture of light hydrocarbons methyl-t-butyl ether (MTBE) and benzene, toluene, ethylbenzene, and xylene (BTEX) with an average density of 764.86 kg/m3. Chemical analysis of groundwater samples identified the presence of dissolved contaminants within the first 25–30 m of the saturated zone. The dissolved phase of the LNAPLs is the target of the transport model presented herein.

Methodological approach

The methodological approach begins with the analysis of borehole and seismic survey data, with the aim of achieving a detailed knowledge of the bedrock geometry, with specific reference to the presence of major discontinuities. Rock mass surveys were conducted according to the International Society for Rock Mechanics (ISRM 2007) recommendations, to analyze the main discontinuity features of rock masses outcropping within the study area, to represent the structural characteristics of the bedrock aquifer. This preliminary activity facilitated the development of a detailed geological conceptual model (Fig. 2a, left). Information on the groundwater flow regime was established through the collection of piezometric data and the assessment of aquifer hydrogeological properties. Outcrop data were also used for the empirical estimation of the hydraulic conductivity along the main fractures. These data were incorporated into a hydrogeological conceptual model (Fig. 2a, right), which informed the development of numerical groundwater flow and solute transport models using the FREEWAT plugin for QGIS (Rossetto et al. 2018). Four model scenarios were simulated (Fig. 2b) to test the relative impacts of the fractures/faults and groundwater abstraction on the simulated distribution of LNAPLs in the aquifer. Finally, the observed and simulated head observations were plotted in a scatterplot and the model fit statistics were calculated to assess the reliability of the performed flow simulations.

Fig. 2
figure 2

a Methodological approach workflow; b Simulated scenarios

Full size image

Geological conceptual model

Geological framework

The study area is located on the Hyblean Plateau, a carbonate foreland basin which represents the northernmost portion of the African plate, which has been relatively undeformed following the collision with the Eurasian plate (Lentini et al. 1994). The Hyblean Plateau consists of a tectonically uplifted sequence of deep-sea clay and carbonate rocks, with intercalations of volcanic rocks (Scribano and Carbone 2020). Borehole data, providing information up to a depth of 40 m below ground level (bgl), indicated a fairly uniform stratigraphic succession. From the base of the sequence to the top, the main lithologies include (Fig. 3a):

  1. 1.

    Cretaceous submarine volcanites are represented by pillow lavas and massive basalts.

  2. 2.

    Whitish calcarenites passing upwards and laterally into algal biolithites and irregularly stratified and fractured greyish-white limestones (Miocene) belonging to the Monti Climiti Formation. This formation unconformably overlies Cretaceous lava bodies.

  3. 3.

    Cross-stratified yellowish-brown organogenic sands and calcarenites belonging to the “Panchina” Formation (Late Pleistocene).

Fig. 3
figure 3

a Geological map of the study area with inset map of the study area showing the distribution of the major discontinuity trace sets (S1–S3) identified from previous surveys; b Seismic reflection profiles with interpretations, including the distribution of potential fault planes (modified after Mineo et al. 2022)

Full size image

Structurally, the main tectonic feature of the Hyblean Plateau consists of a NE–SW-oriented extensional fault system (Scribano and Carbone 2020). On a larger scale, a NW–SE-oriented extensional fault system is present (Carbone et al. 1982). Previous seismic survey investigations and rock mass surveys specifically carried out at the plume propagation site (Fig. 3b), guided further surveying of a series of additional discontinuities. Mineo et al. (2022) commented on the results of these surveys, which reported the presence of a potential NW–SE trending fault, within the area impacted by the contamination.

Rock mass survey

Field characterization of rock mass discontinuities was carried out according to the ISRM (2007) recommendations, by sampling all the fractures identified by a scanline and analyzing their physical features, including spatial orientation, spacing, aperture, joint roughness coefficient (JRC), presence of filling material, and persistence. More specifically, the joint roughness was measured through profile gauges and then compared with typical roughness profiles to define the most suitable JRC value (Barton and Choubey 1977). Spatial data were plotted with a stereographic projection to analyze the preferential structural directions within the study area. In particular, the surveyed discontinuity poles were plotted on lower-hemisphere plots and grouped into three major sets. Their average orientation in space is approximately NE–SW for the S1 set, N–S for the S2 set and NW–SE for the S3 set (Fig. 4), which is consistent with the main regional fault directions. This suggests that the observed fracturing of the rock mass is strongly related to tectonics, and that the faults reported in previous studies are likely concordant to these directions. The bedrock outcrop fractures generally feature apertures of millimeter scales, which are locally infilled with crystalline material (calcite veins). Average fracture spacing ranges from 0.3 to 3.5 m and the exposed surface is rough to smooth, with local signs of weathering.

Fig. 4
figure 4

a–b example of surveyed limestone rock masses crossed by discontinuity sets; c Rose diagram showing the azimuthal direction of fractures mapped from bedrock outcrops

Full size image

Hydrogeological conceptual model

The studied locality of the Hyblean Plateau features significant groundwater circulation, associated with favorable bedrock permeability conditions. In particular, the carbonate lithologies provide a dual porosity aquifer, characterized by low primary permeability in the rock matrix and high secondary permeability associated with the extensive fracture development. According to literature (Mineo et al. 2022) and slug tests, the hydrogeological conceptual model of the bedrock of the study area can be divided into two main units (Fig. 5):

  • The Panchina unit, composed of highly porous sands and calcarenites, with hydraulic conductivity ranging from 10–1 to 10–3 m/s.

  • The Monti Climiti unit, consisting of fractured limestones with hydraulic conductivity ranging from 10–4 to 10–6 m/s.

Fig. 5
figure 5

a Hydrogeological map of the study area (1 M. Climiti unit, 2 Panchina unit, 3 alluvial sediments) with traces of the cross sections reported in the inset; b Representative hydrogeological profiles of the study area

Full size image

The water table lies between 3 and 0 m above sea level (asl) and recharge to the bedrock aquifer occurs from upgradient lateral inflow. Interannual monitoring highlighted an almost constant depth to groundwater subject to minor seasonal fluctuations within a range of ±0.5 m (Mineo et al. 2022). The regional groundwater flow direction is towards the coastline (E/ENE; Carbone et al. 1986). Groundwater flow occurs within the carbonate units, bound by the low permeability volcanites, outcropping in the north (Fig. 3a) and south.

To evaluate the hydraulic conductivity along a preferential direction, represented by a specific discontinuity set, Eq. (1) was used (Snow 1969; Zhang 2013 and references therein):

$$K=\frac{G{e}_{{\text{H}}}^{2}}{12v}$$
(1)

where K is hydraulic conductivity (m/s); G is the gravitational acceleration (m/\({{\text{s}}}^{2}\)); and \({e}_{{\text{H}}}\) is the equivalent hydraulic aperture of the discontinuity (m) and \(v\) is the kinematic viscosity of the fluid (1 × 10−6 m2/s for water).

The hydraulic aperture of the discontinuity was empirically calculated according to Barton et al. (1985) from Eq. (2)

$${e}_{{\text{H}}}= \frac{{e}^{2}}{{{\text{JRC}}}^{2.5}}$$
(2)

where e is the mechanical aperture of the discontinuity (m) and JRC is the joint roughness coefficient.

The results show that K is in the order of \({10}^{-2}\) m/s for all considered discontinuity sets.

Numerical simulation

Conceptualization

The aquifer system was conceptualized as an equivalent continuum medium due to the large-scale analysis (Hoek et al. 2002), and represented as an equivalent porous medium in the model domain. In this case, any individual rock piece was considered to be sufficiently small in relation to the overall size of the model domain. The fully saturated model refers to the Monti Climiti unit (Fig. 5). Boundary conditions consist of (1) lateral inflow derived from the Hyblean Mountains to the west of the study site, and (2) lateral outflow towards the eastern coast. The source term is proportional to the effective infiltration from rainfalls, while the pumping rate of the SE well constitutes a sink term. The preliminary version of the model was calibrated using available piezometric datasets.

Following these steps, four different model scenarios were implemented (Fig. 2b):

  1. 1.

    Reference scenario (RS): transient simulation of groundwater flow in a homogeneous medium (characterized by uniform hydraulic parameters), with no pumping activity in the area.

  2. 2.

    Dynamic condition (DC): transient simulation of groundwater flow in a homogeneous medium (characterized by uniform hydraulic parameters) considering the pumping activity by the SE well as a time-dependent boundary condition, where a pumping rate of 13 L/s was assigned.

  3. 3.

    Presence of major discontinuities (PD): transient simulation of groundwater flow in a heterogeneously fractured medium. The presence of key underground discontinuities (fracture/faults) is considered. These were modeled as preferential flow pathways, by assigning the corresponding cells K values that were empirically estimated according to the surveyed rock mass discontinuity features and literature sources (Mineo et al. 2022).

  4. 4.

    Cumulative model (CM): transient simulation of groundwater flow by introducing the pumping activity boundary condition of the DC model into the PD model.

Numerical model settings

The active domain of the numerical model is 1,600 × 800 m, divided into 40 × 40-m cells. The FREEWAT platform (Foglia et al. 2018) and MODFLOW-2005 (Harbaugh 2005) were used as Graphical User Interface and groundwater flow modelling code, respectively. MODFLOW solves the groundwater flow equations in three dimensions using a finite difference scheme:

$$\frac{\partial }{\partial x} \left({K}_{{\text{xx}}}\frac{\partial h}{\partial x}\right)+ \frac{\partial }{\partial y} \left({K}_{{\text{yy}}}\frac{\partial h}{\partial y}\right)+\frac{\partial }{\partial z}\left({K}_{{\text{zz}}}\frac{\partial h}{\partial z}\right)+W= {S}_{{\text{s}}}\frac{\partial h}{\partial t}$$
(3)

where Kxx, Kyy, and Kzz, are values of hydraulic conductivity along the x, y and z directions, which are assumed to be parallel with respect to the main hydraulic conductivity axis [L T−1]; h is the potentiometric head [L]; W is the volumetric flux per unit volume representing sources and sinks of water, being W < 0 for outflows for the system and W > 0 for inflows to the system (T−1); Ss is the specific storage of the porous material [L−1]; and t is time [T].

MT3DMS (Zheng and Wang 1999) was used for modelling solute transport. The partial differential equation describing the fate and transport of contaminants can be written as follows:

$$\frac{\partial \left(\theta {C}^{{\text{k}}}\right)}{\partial t}=\frac{\partial }{\partial {x}_{{\text{i}}}}\left(\uptheta {{\text{D}}}_{{\text{ij}}}\frac{\partial {C}^{{\text{k}}}}{\partial {x}_{{\text{j}}}}\right)-\frac{\partial }{\partial {x}_{{\text{j}}}}\left(\theta {v}_{{\text{i}}}{C}^{k}\right)+{q}_{{\text{s}}}{C}_{s}^{k}+\sum {R}_{{\text{n}}}$$
(4)

where θ is the subsurface medium porosity (dimensionless); \({C}^{k}\) is the dissolved concentration of species k [\({{\text{ML}}}^{-3}\)]; t is time [T]; \({x}_{{\text{i}},{\text{j}}}\) is the distance along the respective Cartesian coordinate axes [L]; \({D}_{{\text{ij}}}\) is the hydrodynamic dispersion coefficient tensor [\({{\text{L}}}^{2}{{\text{T}}}^{-1}]\); \({v}_{{\text{i}}}\) is the seepage or linear pore water velocity [\({{\text{LT}}}^{-1}]\) and it is related to the specific discharge or Darcy flux through the relationship \({v}_{{\text{i}}}\)=\({q}_{{\text{i}}}/\) θ; \({q}_{{\text{s}}}\) is the volumetric flow rate per unit volume of aquifer representing fluid sources (positive) and sinks (negative), [\({{\text{T}}}^{-1}]\); \({C}_{s}^{k}\) is the concentration of the source or sink flux for species k [\({{\text{ML}}}^{-3}]\) and \(\sum {R}_{n}\) is the chemical reaction term \([{{\text{ML}}}^{-3}{{\text{T}}}^{-1}]\).

FREEWAT and MODFLOW-2005 have been successfully used in previous studies dealing with hard-rock aquifers employing the equivalent-porous medium approach (e.g,. Arce et al. 2023; De Filippis et al. 2019; Vincenzi et al. 2022). The aquifer system under investigation was divided into three layers, according to the hydrogeological conceptual model shown in Fig. 5:

  • Layer 1: a surficial cover of sandy soil, with an average thickness of 4 m

  • Layer 2: sands and limestones, with an average thickness of 6 m (Panchina Formation)

  • Layer 3: fully saturated, fractured limestones, with an average thickness of 35 m (Monti Climiti Formation)

The hydrodynamic parameters used for these layers are provided in Table 1. Layer 3 is conceptualized with a hydraulic conductivity value of 43 m/day, a storage coefficient of 10–4/m and the specific yield and effective porosity were both assigned a value of 0.4. Here, the laboratory-determined intact rock-effective (primary) porosity value of 0.25 was increased to 0.4, to account for fractures. This was justified by borehole data reports indicating rock quality designation values lower than 25%, representing an intensely fractured rock mass. Layer 1 was defined as convertible (unconfined), whereas the second and third layers were defined as confined.

Table 1 hydraulic parameters used for the numerical simulation for each model layer. Kx, Ky and Kz are the hydraulic conductivity values (m/day); SS is the specific storage coefficient (m−1); SY is the specific yield (dimensionless); and NE is the medium porosity (dimensionless)
Full size table

A no flow limit was imposed on the active domain of the model along the northern and southern perimeters. The hydraulic exchanges between (1) the aquifer and seawater along the eastern coast, and (2) the inflow from the western hilly area were simulated using the MODFLOW constant head (CHD) package. A constant hydraulic head was defined by setting the groundwater heads to 3 m asl along the southwestern sector and to 0 m asl along the coastal northeastern sector. Recharge was implemented through the MODFLOW recharge (RCH) package and was kept constant for all the stress periods. Finally, the MODFLOW WEL package was used to simulate the prescribed flow for the SE well. Time was divided into four stress periods, each one composed a single internal time step, for a total simulation time of 115 days.

The transport model parameters are listed in Table 2. These values were not available for the investigated area and were therefore based on technical reports and literature (Spitz and Moreno 1996). The contaminated area was simulated in model layer 1 by activating the sink and source mixing (SSM) package with a constant pollutant concentration of 1 kg/m3 (value based on field observations). An initial pollutant concentration of zero was assumed for all the layers.

Table 2 Parameters used for the solute transport model. aL, is the longitudinal dispersivity (m); aTH and aTV are the ratio of the horizontal and vertical transverse dispersivity to the longitudinal dispersivity, respectively (dimensionless); DM is the molecular diffusion coefficient (m2/day); and NE is the effective porosity (dimensionless)
Full size table

Results

Flow model results

The model performance accuracy was evaluated in terms of a water balance, which showed a good closure of the water budget (no discrepancy in MODFLOW code). Furthermore, simulation results were compared to a series of head observations distributed across the model domain. The model fit, evaluated by analyzing the performance indicators reported in Table 3, resulted in a good correlation between observed and simulated values (Fig. 6). The RS scenario (Fig. 7a) shows that groundwater flows northeast from the southwestern hilly area, and then eastwards, before deviating northeast towards the coast. The simulated regional hydraulic gradient is consistent with past piezometric observations (Carbone et al. 1982), reflecting the static 2014–2020 trend (Mineo et al. 2022).

Table 3 Residual model fit statistics. SD standard deviation, SE standard error, RMS root mean square
Full size table
Fig. 6
figure 6

Flow model fit: plot of observed vs simulated residuals for all the stress periods and time steps

Full size image
Fig. 7
figure 7

Piezometric map outputs from layer three of the numerical groundwater flow model for simulation scenarios: a reference scenario (RS); b dynamic condition (DC), c presence of discontinuities (PD); and d combined action of pumping and presence of discontinuities (CM)

Full size image

Incorporating groundwater abstraction from the SE well in the DC scenario (Fig. 7b) results in a minor perturbation to hydraulic head in close proximity to the abstraction well. Neither evidence of groundwater depletion, nor perturbations to the regional hydraulic gradient, can be highlighted at the model scale.

Some interesting differences occur by invoking the presence of the fractures/faults in the PD scenario (Fig. 7c). The potentiometric contours gain an irregular trend when crossing the discontinuity traces. The S2 and S3 discontinuities that are orientated normally with respect to the regional groundwater flow direction divert groundwater flow along their trace. This produces a local rise of the water table (~20 cm), along with producing irregular variations along the hydraulic head contours. However, the hydraulic gradient resumes a northeast direction towards the coastline.

Finally, the CM scenario shows the combined action of the DC and PD scenarios (Fig. 7d), with the southeast hydraulic head perturbation associated with the fractures/faults enhanced by the pumping activity, hence favoring the groundwater flow towards the SE well, in accordance with field observations (Mineo et al. 2022).

Transport model results

The RS scenario (Fig. 8a) generates a contaminant plume with a northeastward, elongate shape, corresponding to the direction of the regional hydraulic gradient towards the coastline. Here, the source area is characterized by a relatively high groundwater LNAPL concentration of 0.09 kg/m3, and concentrations < 0.03 kg/m3 in proximity to the SE well. The DC scenario (Fig. 8b) results are broadly similar to the RS scenario, with the exception of a small perturbation in proximity to the SE well, indicating groundwater LNAPL concentrations > 0.02 kg/m3. Nevertheless, the overall northeast-trending, modelled contaminant plume in the DC scenario poorly represents the observed southeast-trending contaminant plume (Mineo et al. 2022). The PD model scenario (Fig. 8c) shows that the dissolved LNAPL contaminant plume propagation is strongly affected by the fractures/faults. Here, the contaminant plume trajectory is towards the southeast, and groundwater LNAPL concentrations > 0.06 kg/m3 are restricted to the faulted area. However, the contaminant plume does not appear to be intersected by the SE well, with groundwater LNAPL concentrations < 0.02 kg/m3. This is resolved in the CM scenario (Fig. 8d), which exhibits a similar overall contaminant plume to the PD model scenario, but with the exception of the plume being intercepted by the SE well with groundwater LNAPL concentrations > 0.03 kg/m3.

Fig. 8
figure 8

Dissolved phase contaminant concentration map outputs from the numerical solute transport model: a reference scenario (RS); b dynamic condition (DC); c presence of discontinuities (PD); d combined action of pumping and presence of discontinuities (CM). Contour values provide the contaminant concentration expressed in kg/m3

Full size image

Discussion

The RS and DC model scenarios assumed the fractured carbonate aquifer was homogeneous and isotropic with uniform hydraulic parameters. Although these scenarios simulated a satisfactory representation of the regional hydraulic gradient (i.e. from the south-west hilly area to the northeast coastline), they failed to account for the observed distribution of LNAPL contamination in the aquifer. In particular, the simulated contaminant plume was concordant with the regional hydraulic gradient as opposed to following the observed, anomalous deviation to the southeast. Groundwater abstraction from the SE pumping well in the DC model scenario did produce a minor perturbation southeast so that LNAPLs were intercepted by the well, but did not sufficiently alter the distribution of the contaminant plume to match field observations.

The southeast trajectory of the contaminant plume could only be resolved by invoking the presence of several fractures/faults into the numerical model scenarios PD and CM. These features were identified with geophysical surveys and represented as anisotropic model elements, parameterised with the results of empirical laws (Snow 1969; Zhang 2013). As the K values of the fractures/faults were two orders of magnitude greater than those from the primary permeability of the rock matrix, it is expected that the fractures/faults function as preferential groundwater flow pathways in the aquifer. As a result, the NW–SE trending S3 set produced an aquifer compartmentalisation effect, directing the contaminant plume towards the southeast as opposed to the northeast. However, the inclusion of the fractures/faults alone were insufficient to cause contaminant plume migration to the SE well. Incorporation of both the fractures/faults and groundwater abstraction into the CM model scenario extended the southeast trajectory of the plume to match field observations. Particle tracking performed on the CM model scenario (Fig. 9) shows that the SE well area of influence has an elongated capture zone in the northwest, corresponding to the S3 fault set, suggesting the pumping of the SE well increases groundwater velocity and advection of LNAPLs along these discontinuities.

Fig. 9
figure 9

Particle tracking at SE well for the combined action of pumping and presence of discontinuities (CM) model scenario

Full size image

Conclusion

This study analyzed the relative influence of two factors that were considered to be responsible for a peculiar groundwater contaminant plume trajectory using numerical groundwater flow and solute transport modelling. These factors included the presence of several fractures/faults in the fractured carbonate aquifer, and groundwater abstraction. Including both factors in the numerical models provided the most satisfactory simulation results, with the presence of fractures/faults being relatively more important for determining contaminant plume migration relative to groundwater abstraction.

Overall, the results of this study demonstrate that fractures/faults in the fractured carbonate bedrock aquifer function as preferential conduits of groundwater flow and solute transport. This study demonstrates that robust hydrogeological characterization should be regarded as the starting point for site investigation to support sustainable environmental planning and management.