Spatio-temporal modeling of groundwater quality deterioration and resource depletion

Abstract

In Hydrogeology, the analysis of groundwater features is based on multiple data related to correlated variables recorded over a spatio-temporal domain. Thus, multivariate geostatistical tools are fundamental for assessment of the data variability in space and time, as well as for parametric and nonparametric modeling. In this work, three key hydrological indicators of the quality of groundwater—sodium adsorption ratio, chloride and electrical conductivity—as well as the phreatic level, in the unconfined aquifer of the central area of Veneto Region (Italy) are investigated and modeled for prediction purposes. By using a new geostatistical approach, probability maps of groundwater resource deterioration are computed, and some areas where the aquifer needs strong attention are identified in the north-east part of the study region. The proposed analytical methodology and the findings can support policy makers in planning actions aimed at sustainable water management, which should enable better monitoring of groundwater used for drinking and also ensure high quality of water for irrigation purposes.

Abstrakt

In der Hydrogeologie basiert die Analyse von Grundwassermerkmalen auf mehreren raum-zeitlichen Daten, die sich auf korrelierte Variablen beziehen, die über einen raum-zeitlichen Bereich aufgezeichnet wurden. Daher sind multivariate geostatistische Methoden von grundlegender Bedeutung sowohl für die Bewertung der Datenvariabilität in Raum und Zeit als auch für die parametrische und nichtparametrische Modellierung. In dieser Arbeit werden drei wichtige hydrologische Indikatoren für die Qualität des Grundwassers (Natriumdbsorptionsverhältnis, Chlorid und elektrische Leitfähigkeit) sowie Daten zum Grundwasserspiegel im unbegrenzten Grundwasserleiter des zentralen Gebiets der Region Venetien (Italien) untersucht und für Prognosezwecke modelliert. Mithilfe eines neuen geostatistischen Ansatzes werden Wahrscheinlichkeitskarten der Grundwasserressourcenverschlechterung berechnet und einige Gebiete im nordöstlichen Teil der Untersuchungsregion identifiziert, in denen der Grundwasserleiter besondere Aufmerksamkeit erfordert. Die vorgeschlagene Analysemethodik und die Ergebnisse können politische Entscheidungsträger bei der Planung von Maßnahmen zur nachhaltigen Wasserbewirtschaftung unterstützen, welche eine bessere Überwachung des als Trinkwasser genutzten Grundwassers ermöglichen und eine hohe Qualität des Wassers für Bewässerungszwecke gewährleisten sollen.

Résumé

En Hydrogéologie, l'analyse des caractéristiques des eaux souterraines est basée sur de multiples données spatio-temporelles liées à des variables corrélées enregistrées sur un domaine spatio-temporel. Les outils géostatistiques multivariés sont donc fondamentaux pour l'évaluation de la variabilité des données dans l'espace et dans le temps, ainsi que pour la modélisation paramétrique et non paramétrique. Dans ce travail, trois indicateurs hydrologiques clés de la qualité des eaux souterraines (rapport d'adsorption du sodium, chlorure et conductivité électrique), ainsi que les données relatives au niveau phréatique, dans l'aquifère libre de la zone centrale de la région de Vénétie (Italie) sont étudiés et modélisés à des fins de prédiction. En utilisant une nouvelle approche géostatistique, des cartes de probabilité de détérioration des ressources en eaux souterraines sont calculées, et certaines zones où l'aquifère nécessite une attention particulière sont identifiées dans la partie nord-est de la région étudiée. La méthodologie analytique proposée et les résultats peuvent aider les décideurs politiques à planifier des actions visant à une gestion durable de l'eau, ce qui devrait permettre un meilleur suivi des eaux souterraines utilisées pour la boisson et garantir une qualité élevée de l'eau pour l'irrigation.

Resumen

El análisis de las características de las aguas subterráneas en hidrogeología se basa en múltiples datos relacionados con variables correlacionadas que se registran en un dominio espaciotemporal. Así pues, las herramientas geoestadísticas multivariantes son fundamentales para evaluar la variabilidad de los datos en el espacio y el tiempo, así como para la modelización paramétrica y no paramétrica. En este trabajo se investigan y modelizan con fines de predicción tres indicadores hidrológicos clave de la calidad de las aguas subterráneas (coeficiente de adsorción de sodio, cloruro y conductividad eléctrica), así como los datos del nivel freático, en el acuífero no confinado de la zona central de la región del Véneto (Italia). Utilizando un nuevo método geoestadístico, se calculan mapas de probabilidad de deterioro de los recursos hídricos subterráneos y se identifican algunas zonas en las que el acuífero necesita una atención especial en la parte nororiental de la región estudiada. La metodología analítica propuesta y los resultados obtenidos pueden ayudar a los responsables políticos a planificar acciones encaminadas a una gestión sostenible del agua, lo que debería permitir un mejor control de las aguas subterráneas utilizadas para beber y también garantizar una alta calidad del agua para regadío.

摘要

在水文地质学中，对地下水特征的分析基于与相关变量相关的多个时空数据，这些数据记录在一个时空域中。因此，多变量地质统计工具对于评估空间和时间上的数据变异性以及参数和非参数建模是至关重要的。本研究探讨并建立了意大利威尼托大区中部潜水含水层中地下水质量的三个关键水文指标（钠吸附比、氯离子和电导率）以及地下水位数据的预测模型。通过使用一种新的地质统计方法，计算了地下水资源恶化的概率图，并确定了研究区域东北部需要重点关注的一些地区。提出的分析方法和研究结果可以支持政策制定者制定旨在实现可持续水资源管理的行动计划，从而能够更好地监测用于饮用水的地下水，并确保用于灌溉目的的水质高质量。

Riassunto

In Idrogeologia, l'analisi delle caratteristiche delle acque sotterranee si basa su molteplici dati relativi a variabili correlate, misurate in un dominio spazio-temporale. Pertanto, gli strumenti geostatistici multivariati sono fondamentali per la valutazione della loro variabilità nello spazio e nel tempo, nonché per l'individuazione di modelli parametrici e non parametrici. In questo lavoro, si propone lo studio e la modellizzazione del livello freatico e di tre indicatori idrologici fondamentali della qualità delle acque sotterranee (rapporto di assorbimento del sodio, cloruro e conducibilità elettrica), nell'acquifero non confinato dell'area centrale della Regione Veneto (Italia). Utilizzando un nuovo approccio geostatistico, sono costruite le mappe di probabilità del deterioramento delle risorse idriche sotterranee; inoltre, nella parte nord-orientale della regione di studio sono individuate alcune aree in cui l'acquifero necessita di forte attenzione. La metodologia analitica proposta ed i risultati ottenuti possono supportare i decisori politici nella pianificazione di azioni mirate alla gestione sostenibile dell'acqua, che dovrebbe consentire un migliore monitoraggio delle risorse idriche sotterranee utilizzate per l'acqua potabile e garantire anche un'elevata qualità dell'acqua per scopi di irrigazione.

Abstrato

Em Hidrogeologia, a análise das características das águas subterrâneas é baseada em múltiplos dados espaço-temporais relacionados a variáveis correlacionadas registradas em um domínio espaço-temporal. Assim, ferramentas geoestatísticas multivariadas são fundamentais para avaliação da variabilidade dos dados no espaço e no tempo, bem como para modelagem paramétrica e não paramétrica. Neste trabalho, três principais indicadores hidrológicos da qualidade das águas subterrâneas (taxa de adsorção de sódio, cloreto e condutividade elétrica), bem como os dados do nível freático, no aquífero não confinado da área central da região de Veneto (Itália) são investigados e modelados para fins de previsão. Usando uma nova abordagem geoestatística, mapas de probabilidade de deterioração dos recursos hídricos subterrâneos são computados, e algumas áreas onde o aquífero requer maior atenção são identificadas na parte nordeste da região de estudo. A metodologia analítica proposta e as conclusões podem apoiar os formuladores de políticas no planejamento de ações voltadas para a gestão sustentável da água, o que deve permitir um melhor monitoramento das águas subterrâneas usadas para beber e também garantir alta qualidade da água para fins de irrigação.

Introduction

Groundwater is a very important worldwide resource that is used for domestic, industrial and agricultural purposes. Nowadays, several aquifers show evidence of overexploitation or pollution, often associated with changes in the climate and the water balance. Such changes, together with the impacts of other anthropic activities, can affect the soil physicochemical properties and induce negative implications for human health and development, e.g., decreasing crop yield. As a consequence, it is crucial to monitor and assess the groundwater’s qualitative and quantitative status.

Within this context, the present work aims to investigate the spatio-temporal correlation among three variables, i.e. sodium adsorption ratio (SAR), chloride and electrical conductivity (EC), which can be considered as benchmark indicators of groundwater quality for irrigation, affecting the water salinity and many natural processes related to the growth and development of plants and to the wildlife in general.

Multivariate geostatistics provides useful tools for managing and processing multivariate spatial and spatio-temporal data, which are characterized by complex patterns in space and in space-time, such as those including climatic and hydrogeological data. For this reason, the direct and cross linear correlation among variables with a spatial and temporal evolution are examined and modelled.

The first studies of multivariate space-time data can be traced back to the early 1990s (Rouhani and Wackernagel 1990; Goovearts and Sonneth 1993; Myers 1995; Xie et al. 1995). Nevertheless, spatio-temporal covariance models among variables were later proposed by De Iaco et al. (2001, 2003); Choi et al. (2009); Berrocal et al. (2010); De Iaco et al. (2019); Krupskii and Genton (2017). In addition, Fassó and Finazzi (2011) applied a spatial linear coregionalization model (LCM) by including a dynamic component in time. Indeed, among the various methods available in the literature for fitting the spatio-temporal multivariate dependence, the space-time linear coregionalization model (ST-LCM) still finds several applications for its accuracy, efficiency and above all for its flexibility (Li et al. 2008; Babak and Deutsch 2009; Gneiting et al. 2010; Emery 2010; Bevilacqua et al. 2015; Genton and Kleiber 2015; De Iaco et al. 2023).

In the past 15 years, many contributions concerning both spatial and temporal correlation among variables describing groundwater quality have been published all over the world. Most studies analyse time and space separately (Goovaerts et al. 2005; Sun et al. 2009; Hooshmand et al. 2011; Arslan 2012; Karami et al. 2018; Khorrami 2019; Kiy and Arslan 2021; Said et al. 2021; Slama and Sebei 2020; Yilmaz et al. 2020). More specifically, in Delbari et al. (2016) the spatial variability of some groundwater quality indicators—EC, SAR, sodium, chloride, bicarbonate and pH—in Fasa County (southern Iran) was investigated by means of the indicator kriging method, in order to assess the adequacy of the available groundwater for sprinkler irrigation. Mahdi (2017) proposed a space-time model (i.e. a product-sum model) suitable to quantify the risk derived from the large SAR values in the groundwater across Gaza (Palestine); this model was applied for forecasting purposes, by using spatio-temporal ordinary kriging. In Jeihouni et al. (2018) the water quality of the aquifers in a region near the Urmia Lake (Iran) were investigated by estimating some groundwater quality variables (EC, sodium and chloride) and the piezometric levels over 11 years through use of geographical information systems (GIS), geostatistics and three-dimensional (3D) modeling methods.

Furthermore, Boufekane and Saighi (2019) applied the cokriging method in comparison with two univariate geostatistical techniques (such as kriging and inverse distance weighted) to explore the spatial correlation of the groundwater quality indicators (including EC and SAR) measured in wadi Nil Plain (Jijel, north-east Algeria) and to identify the appropriate and suitable areas for agricultural purposes. Finally, more recently, the work by Bradai et al. (2022) combined some classical multivariate techniques (principal component analysis and hierarchical cluster analysis) and a geostatistical interpolation method (ordinary kriging), together with a dedicated hydrogeochemical study, to estimate groundwater sources suitable for irrigation in the western Middle Cheliff (Algeria); this was performed by analyzing the groundwater quality indicators (EC, sodium and SAR) measured in the period from April to July 2017.

However, spatio-temporal multivariate analysis, among the main variables characterizing the groundwater quality, was applied only in a few works—for example, in Jang et al. (2012) a multivariate indicator kriging was applied to describe the spatial variability of 13 hydrochemical parameters (EC, chloride, SAR and the residual sodium carbonate among others) measured in the Pingtung Plain (in southern Taiwan, China) between 1995 and 2008. Yazdanpanah (2016) used geostatistical analysis combined with a linear regression approach, in order to estimate the spatio-temporal variations of groundwater quality variables (such as sodium, calcium, bicarbonate, EC, SAR) in the aquifer that supplies Kerman (Iran) in the period from 1999 to 2010. Mastrocicco et al. (2021) proposed a multivariate statistical approach based on factor analysis, in order to pick out all the hydrogeochemical processes existing in the coastal aquifer of the Campania Plain (southern Italy) for two different years (2006 and 2016) and to estimate the trend of salinization over time, by analyzing chloride, sodium, EC, SAR and other groundwater quality parameters.

It is worth pointing out that none of these studies provide a multivariate analysis of the joint spatial and temporal evolution of significant hydrogeological variables. Thus, differently from the previously mentioned works, the present paper proposes a thorough spatio-temporal multivariate study of four relevant variables referring to water quality (chemical properties) and water quantity of an unconfined aquifer. In particular, three indicators of groundwater quality (SAR, chloride and EC) and one variable related to the quantity of available water (the phreatic level) are investigated in the central area of Veneto Region (north-eastern part of Italy). The three aforementioned indicators are measured every 6 months, i.e. in spring (April–May) and autumn (October–November) for each year from 2003 to 2021, at 69 hydrogeological stations, out of which 34 stations provide the unconfined groundwater levels, which were recorded every quarter from 1999 to 2021. The inclusion of groundwater level in the set of studied variables is justified by the dual goal of analyzing the main water parameters from the point of view of both qualitative and quantitative conditions of the aquifer.

For this reason, the novelty of this work is represented by (1) the innovative implementation of a multivariate space-time model for the hydrological variables which characterise the groundwater quality, (2) the development of a univariate space-time model for the phreatic level which determines the groundwater quantity, and (3) the construction of probability risk maps of aquifer depletion. In other terms, the proposed spatio-temporal geostatistical approach involving the analysis of some parameters related to the quality and the quantity of groundwater combines, in a unified and integrated way, multivariate and univariate spatio-temporal modeling together with parametric prediction (referring to the expected value of the variables of interest) and nonparametric estimation (referring to the probability of the occurrence of some critical hydrogeological conditions). In addition, differently from the existing multivariate procedure in De Iaco et al. (2019), the approach proposed in this study exploits the simultaneous diagonalization of the covariance matrices estimated on the standardized variables in order to easy detect the basic components of the ST-LCM. Thus, an ST-LCM with suitable models regarding the latent components of these groundwater qualitative parameters, is proposed for space-time prediction purposes. Then indicator kriging is applied for producing a joint probability deterioration map of the aquifer system in 2022, in terms of both qualitative and quantitative profiles, with respect to 12 years before.

In this paper, after a short theoretical discussion on some concepts of multivariate spatio-temporal geostatistics and the revised ST-LCM selection procedure (section ‘The ST-LCM and its fitting procedure’), the analysis focusing on the three water quality parameters combined with the groundwater level measurements from Veneto Region, is detailed (section ‘Hydrogeological framework’). The appropriate covariance models, in compliance with the main features of the sample covariances, are detected; then an assessment of the performance of the selected models, also compared with alternative models, is described (section ‘Estimation and modeling of hydrogeological features’). The spatio-temporal predictions of SAR values are computed (section ‘Prediction maps of SAR values and phreatic levels’) and the risk maps of groundwater deterioration based on a nonparametric approach are given in section ‘Probability map of groundwater deterioration’. Finally, the most original aspects of the paper are discussed in section ‘Discussion’.

In conclusion, the results of the proposed analysis will contribute on one hand to enrich the literature of the Hydrosciences and explore a new area that, to the best of the authors’ knowledge, deserves further investigation. On the other hand, the results will support policymakers in achieving sustainable water management and careful utilization of water in agriculture to protect catchment areas from overexploitation.

The ST-LCM and its fitting procedure

The observations for a given vector of variables taken for different sample locations and time points can be considered as a realization of a multivariate space-time random function (MSTRF) $\{\textbf{X}(\textbf{s}, t), (\textbf{s}, t) \in$ D$\times$T$\, \subseteq \mathbb {R}^{d}\times \mathbb {R}\}$ where $\textbf{X}(\textbf{s}, t)=[X_1(\textbf{s}, t), \ldots , X_m(\textbf{s}, t)]^\textrm{T},$ $m \ge 2,$ and $(\textbf{s}, t)$ is the point in the spatio-temporal domain D$\times$T $\subseteq \mathbb {R}^{d}\times \mathbb {R},$ with $d \le 3$.

The first and second order moments of the aforementioned MSTRF, under the second-order stationarity, are defined as follows:

$$\begin{aligned} {\varvec{\mu }}=[\mu _1, \ldots , \mu _m]^\textrm{T} \end{aligned}$$

(1)

where $\mu _i=$ E$(X_{i}), \; i=1,\ldots , m,$ and

$$\begin{aligned} \textbf{C}(\textbf{u},v) = [C_{ij} (\textbf{u}, v)] \end{aligned}$$

(2)

with

• $(\textbf{u},v)\in \mathbb {R}^{d}\times \mathbb {R}$, with $\textbf{u}=(\textbf{s}-\textbf{s}')$ and $v=(t-t')$, for any $(\textbf{s}, t)$ and $(\textbf{s}', t')$ in D$\times$T;

• $C_{ij}(\textbf{u}, v)=$ E$[(X_{i}(\textbf{s}+\textbf{u}, t+v) \cdot X_{j}(\textbf{s}, t))] - \mu _{i} \, \mu _{j}$, that is, for any $X_{i}$ and $X_{j},$ $i,j =1,\ldots , m,$ with $i \ne j$, it is the cross-covariance function, or for $i = j$, it is the direct covariance function of the $X_{i}$.

In geostatistical analysis, modeling the matrix-valued covariance function in Eq. (2) is essential when prediction purposes are of interest for the study. Towards this aim, many space-time multivariate applications use cokriging based on the ST-LCM, since this model is computationally flexible, as highlighted in Cappello et al. (2021).

The ST-LCM is constructed by the linear combination of basic scalar covariance functions; in particular, the covariance matrix $\textbf{C}$ is modeled as follows:

$$\begin{aligned} \textbf{C}(\textbf{u}, v)= \displaystyle \sum _{l=1}^L \; \textbf{B}_l \; c_l(\textbf{u}, v) \end{aligned}$$

(3)

where $c_l(\textbf{u}, v)$ are the aforementioned basic scalar covariances associated with the uncorrelated components underlying the phenomenon under study and $\textbf{B}_l = [b_{ij}^l], l=1,\ldots ,L,$ are the $(m \times m)$ positive definite matrices of coregionalization.

The model in Eq. (3) can be fitted on the basis of the steps given in the following:

• 1. Selection of basic uncorrelated components and computation of the empirical basic covariance function based on the covariance matrices estimated on the standardized observations;

• 2. Modeling the empirical basic covariances through appropriate classes of models (according to the empirical characteristics of each basic component);

• 3. Computation of admissible coregionalization matrices.

The first step starts with estimation of the matrix-valued covariance function, that is the m direct covariances and $m(m-1)/2$ symmetric cross-covariances for K-selected space-time lags. Thus, a symmetric $(m\times m)$ matrix $\widehat{\textbf{C}}(\textbf{u},v)_k = [\widehat{C}_{ij}(\textbf{u},v)_k]$, with $\textbf{u} = (\textbf{s} - \textbf{s}')$ and $v = (t-t')$, is obtained for each lag k, with $k=1,\ldots ,K$. Similarly, the matrices $\widehat{\textbf{C}}'(\textbf{u},v)_k = [\widehat{C}'_{ij}(\textbf{u},v)_k]$, with $k=1,\ldots ,K$, are computed by using the standardized values of the variables under study.

Successively, the simultaneous diagonalization (Cardoso and Souloumiac 1996) is applied to the sample covariance matrices $\widehat{\textbf{C}}'$ of the standardized variables, with the aim of detecting the latent components:

$$\begin{aligned} {\Psi }\,\widehat{\textbf{C}}'(\textbf{u},v)_k\,{\Psi }^\textrm{T} = \mathbf{\Delta }(\textbf{u},v)_k, \qquad k=1,\ldots ,K, \end{aligned}$$

(4)

where ${\Psi }$ is a $(m \times m)$ orthogonal matrix and $\mathbf{\Delta }_k$ are the diagonal $(m\times m)$ matrices. For this purpose, package Jade developed for R environment (Miettinen et al. 2017), can be very useful. From the K diagonal matrices, the sample basic uncorrelated components $\widehat{c}_l$ which correspond to the estimates of $c_l \,, l=1, \ldots , m$, can be obtained by extracting all the diagonal entries across the K matrices (Xie et al. 1995; Myers 1995).

A joint visual inspection of all $\widehat{c}_l, l=1,\ldots ,m,$ is useful to detect the $L \le m$ distinct basic components characterized by different scales of variability; in other words, by the 3D plots of all the covariance surfaces and the respective marginals in space and in time it is easy to find the different lags where the surfaces of the basic covariances decay, i.e. the scales of spatio-temporal variability.

Note that the number of basic structures obtained from this step is denoted with L ($L \le m$), since only L spatio-temporal scales of variability (the lags where the surface decays) are used in the following step.

After diagonalization, the performance is evaluated by computing some relative indices, constructed to compare the diagonal and the off-diagonal entries of the diagonalized matrices. In particular, given the $\delta _{ij,k}, i,j=1,\ldots ,m, \, k=1,\ldots ,K,$ elements of the nearly diagonalized matrices ${\varvec{\Delta }}_k$ at the K spatio-temporal lags fixed by the analyst, the following index

$$\begin{aligned} \psi _k = \frac{\displaystyle \sum _{i=1}^{m}\sum _{j=1;j\ne i}^{m} \delta ^2_{ij,k}}{\displaystyle \sum _{i=1}^{m} \delta ^2_{ii,k}}, \qquad k=1,\ldots ,K, \end{aligned}$$

(5)

can be computed. The closer to zero, the better the performance of the diagonalization.

Once the basic components $c_l, l=1,\ldots , L$, are estimated, it is necessary to proceed with their modeling (second step). The choice of a reasonable class of models to be fitted to each empirical component $\widehat{c}_l$ can be supported by analyzing the type of nonseparability (De Iaco et al. 2016).

For this aim, given the basic covariances $c_l(\textbf{u}, v)$, their spatial and temporal marginals, $c_l(\textbf{u}, 0)$ and $c_l(\textbf{0}, v)$ respectively, as well as the values at the origin $c_l(\textbf{0}, 0)$, the nonseparability ratios, as in De Iaco and Posa (2013):

$$\begin{aligned} r_l(\textbf{u}, v)=c_l({\varvec{0}}, 0)\frac{ c_l(\textbf{u}, v)}{ c_l(\textbf{u}, 0) c_l({\textbf {0}}, v)}, \qquad l=1,\ldots ,L, \end{aligned}$$

(6)

have to be inferred by considering the sample basic covariances $\widehat{c}_l$. The values of these ratios imply:

• A uniform positive nonseparability, if they are much greater than 1 for all lags;

• A uniform negative nonseparability, if they are much smaller than 1 for all lags.

In all other cases, a nonuniform nonseparability can be assumed.

As underscored in De Iaco et al. (2013), the kind of nonseparability depends on the interaction in space-time and thus on the divergence between a nonseparable covariance function and the product of the associated marginals (which represents the separable case with no interaction). In particular, the estimated ratios in Eq. (6) are represented through the construction of box plots, for the spatial and the temporal lags.

At the end, the coregionalization matrices $\textbf{B}_l, l=1,\ldots , L,$ of the model in Eq. (3) can be estimated (third step). Starting from the sample covariances $\widehat{C}_{ij}(\textbf{u}, v)$, $i,j=1,\ldots ,m,$ the elements ${b}^l_{ij}$ of $\textbf{B}_l, l=1,\ldots ,L,$ can be computed by the following ratio

$$\begin{aligned} {b}^l_{ij} = \frac{[\widehat{C}_{ij}(\text{u}, v)_{l-1}]-[\widehat{C}_{ij}(\text{u}, v)_{l}]}{[c_l(\text{0}, 0)]}, \qquad l=1,\ldots ,L, \end{aligned}$$

(7)

where $\widehat{C}_{ij}(\textbf{u}, v)_0=\widehat{C}_{ij}(\textbf{0}, 0),$ with $i,j=1,\ldots , m, \, i\le j.$

However, since the basic covariances are defined as unit-sill components, with $[c_l(\textbf{0}, 0)]=1$, the values ${b}^l_{ij}$ corresponds just to the contributions of $\widehat{C}_{ij}$ at the lth scale of variability, i.e.

$$\begin{aligned} {b}^l_{ij} = {[\widehat{C}_{ij}(\textbf{u}, v)_{l-1}]-[\widehat{C}_{ij}(\textbf{u}, v)_{l}]}, \qquad l=1,\ldots ,L. \end{aligned}$$

(8)

The positive definiteness condition of $\textbf{B}_l, l=1, \ldots , L,$ is verified by checking that their eigenvalues are non-negative. Then, by performing the following spectral decomposition

$$\begin{aligned} \textbf{B}_l=\textbf{V}_l \mathbf{\Lambda }_l \textbf{V}^\textrm{T}_l, \qquad l=1, \ldots , L, \end{aligned}$$

(9)

and computing the corresponding eigenvector matrix $\textbf{V}_l$ and eigenvalues’ diagonal matrix $\mathbf{\Lambda }_l$, it is enough to check if there are some negative eigenvalues and set them to zero. In this case, the transformed coregionalization matrix ${\textbf {B}}'_l$ is derived through the following expression

$$\begin{aligned} \textbf{B}_l'=\textbf{V}_l \mathbf{\Lambda }'_l \textbf{V}^\textrm{T}_l, \qquad l=1, \ldots , L, \end{aligned}$$

(10)

where the diagonal matrix of the eigenvalues $\mathbf{\Lambda }'_l$ is modified with respect to the original $\mathbf{\Lambda }_l$ since zeros are in place of the negative eigenvalues.

In section ‘Estimation and modeling of hydrogeological features’, the choice of an adequate ST-LCM, which could explain the direct and cross-correlation among the investigated water quality features, will be based on the aforementioned innovative procedure. This procedure helps to identify an ST-LCM, which is not strictly connected with the application of the product-sum model for the basic components, as originally developed by De Iaco et al. (2003). It is also crucial to highlight that the introduction of ex ante hypotheses on the classes of covariance models is not needed to describe the basic components.

Remarks:

• Performing the standardization is advisable in the presence of different magnitudes of the values taken for the variables under study. Moreover, the extracted basic covariances $c_l(\textbf{u}, v)$ are such that they are unit-sill components; in this way, the coregionalization matrices $\textbf{B}_l$ can better explain the contributions, in terms of variance, of the latent components.

• Once the aforementioned (1, 2 and 3) steps are completed, the defined ST-LCM is subsequently applied for prediction purposes by using cokriging.

Hydrogeological framework

In this section, the geographical area under study, the hydrogeological variables and the corresponding data are presented.

The investigated area

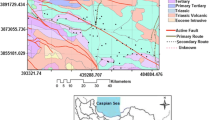
The Veneto Region is one of the four regions located in the north-east of Italy; in particular, it borders on the Italian regions of Friuli Venezia Giulia (to the north-east), Trentino-Alto Adige (to the north-west), Lombardy (to the west), Emilia-Romagna (to the south) and on the Austrian border (to the north) as shown in Fig. 1a,b. It is also the eighth largest region in Italy, with an extension of approximately 18,400 km$^2$, out of which 55% is covered by the Venetian Plain, including the subarea of interest (Fig. 1c).

Fig. 1

Maps of a northern and central Italy and its adjacent countries; b Veneto Region with altitude and its adjacent regions; c the study area and sample points, yellow circles for the stations of groundwater quality parameters and red circles for the phreatic level stations

This densely inhabited plain, characterized by intensive agricultural production, does not exceed an elevation of 100 m above sea level (m asl). Moreover, as recalled in Dal Ferro et al. (2016), the Venetian Plain was originated by the sedimentary action of the Po and Adige rivers (in the south-west), Brenta river (in the center-north) and Piave and Tagliamento rivers (in the north-east).

For what concerns the hydrogeological features, the Venetian Plain lies over two different alluvial aquifers: an unconfined aquifer which extends for 15–20 km in the upper area of the plain from the foot of the Prealps, and another aquifer system which is confined and multi-layered extending in the middle-lower area of the Venetian Plain (Dalla Libera et al. 2017). These two aquifer systems, with their huge amount of water, represent a very important hydrogeological basin and the main source of drinking and irrigation water to the Veneto Region. Moreover, in the transition subarea, namely in the area between the high and the low plains, the shallow water table meets the land surface and emerges in the most depressed zones, known as fontanili (i.e. resurgences and spring wells). Most of the investigated Venetian Plain is composed of gravelly and sandy alluvial layers (Fig. 2).

Fig. 2

Maps of: a the karst areas; b the lithological composition

Moving northwards, the hilly areas between 15 and 300 m asl are made up of calcareous, skeletal clayey and clayey soils. The mountain areas generally include sandy/clayey layers, with slightly differentiated profiles together with deeper Cambisols (valleys), as illustrated in Dal Ferro et al. (2016).

Focusing on the geolithological setting of the area under study, it emerges that the Province of Vicenza is characterized by two hydrogeological basins: the main one between the Retrone and Tesina rivers and a smaller one between the Tesina and Brenta rivers. The Vicenza Upper Plain is dominated by a high-permeability and undifferentiated sandy-gravelly alluvial bed (with a depth varying from 200 m in the northern area of Vicenza up to approximately 400 m in the eastern area, towards the Province of Padua). It includes one unconfined aquifer which extends from the upper plain to the springs line.

In the Province of Treviso there are a total of four hydrogeological basins: one between the Muson dei Sassi Creek and the Sile River, one between the Sile and Piave rivers, another between the Piave and Monticano rivers and the last one between the Monticano and Livenza rivers. The high and middle plains of Treviso represent an alluvial unit, predominantly composed of gravelly and sandy layers, with a remarkable continuity in depth until the bedrock. The low plain is characterized by a major alluvial aquifer with coarse-grained, fluvio-glacial deposits (Vorlicek et al. 2004).

Finally, the Province of Padua contains three water catchment areas: one between the Brenta River and Muson dei Sassi Creek, one between the Tesina and Brenta rivers, and the last one between the Muson dei Sassi Creek and Sile River. The superficial layers of the subsoil are composed by a greater concentration of fine sediments (silts and clays), while the sands on the surface are concentrated in small areas (Mozzi et al. 2010).

In general, for the purpose of the present study, the parent material of the soil plays an important role: layers in soils made of sandy or gravelly parent materials are relevant for the capillary dispersion of the water in the soil. Moreover, many other natural variables such as soil permeability, rainfall, temperature, and relative humidity affect the quality and quantity of the groundwater available for human and agricultural needs. Indeed, due to the high soil permeability, which is typical of the Venetian Plain, the aquifers are very vulnerable to pollution and in the last few decades, the enormous water withdrawals have caused a decrease in the quantity of available water.

Many European directives issued over the years have focused on environmental impact reduction and water quality protection (Directive 2000/60 and Directive 2006/118). In particular, these European directives were transposed in Italy by Legislative decree 152/2006, which promotes the efficiency and reuse of water. In accordance with such legislation, water resources have to be sustainably managed both to defend the environment and the ecosystem and to take care of the social and economic growth of a territory.

In the present case study, analysis of the qualitative and quantitative status of the unconfined aquifer of the subarea across the Provinces of Vicenza, Treviso and Padua, in the center-north of Veneto Region (Fig. 1c), focuses on three key hydrological indicators of groundwater quality for irrigation, in combination with the phreatic level, in order to support the water management of the Veneto Region towards a sustainable use of groundwater resources.

Space-time multivariate hydrological data

The data set under study consists of half-year values of sodium (Na$^+$), calcium (Ca$^{++}$), magnesium (Mg$^{++}$) and chloride, expressed in mg/l, as well as EC at $20\,^{\circ }$C ($\upmu$S/cm), measured at 69 hydrogeological stations located over the Venetian foothills from Vicenza to Treviso and Padua (Italy), as illustrated in Fig. 1c. These observations were collected by the Regional Agency for the Environmental Protection (Regional Agency for the Prevention and Environmental Protection of Veneto, ARPAV 2022) and refer to the period from the 1st semester 2003 to the 2nd semester 2021, where the term semester stands for half-year (the first 6 months for the first semester and the second 6 months for the second semester). Sampling takes place every 6 months, i.e. in spring (April–May) and autumn (October–November), in correspondence with the periods of maximum outflow of groundwater for the hydrogeological basins characterized by the pre-Alpine regime.

By using the measured values of Na$^+$, Ca$^{++}$ and Mg$^{++}$, the SAR has been computed, as proposed by Richards (1954), i.e.

$$\begin{aligned} \textrm{SAR} = \displaystyle {\frac{\textrm{Na}^+}{\left( \displaystyle {\frac{\textrm{Ca}^{++} \, + \, \textrm{Mg}^{++}}{2}}\right) ^{0.5}} } \end{aligned}$$

(11)

Note that SAR, chloride and EC at $20\,^{\circ }$C can be considered as the most meaningful groundwater quality indicators. Indeed, SAR is a parameter commonly used to evaluate water suitability for irrigation: the higher the SAR value, the worse the soil texture and the irrigation performance due to a decrease in the hydraulic conductivity (Bilali and Taleb 2020). Chloride concentration in groundwater is a typical indicator of slow water circulation and long paths, as well as of the presence of large dissolution surfaces. Sometimes, high chloride values are also a symptom of groundwater pollution, caused by civil or industrial sewage. EC is linked to the overall concentration of ions present in the water; therefore, it represents an indirect measure of the water’s salt content.

Groundwater level elevation (or depth), also called phreatic level, was recorded by the Agency for the Environmental Protection of the Veneto Region and has been considered as an index of the water quantity. These measurements, expressed in m, are available only at 34 sample points out of the 69 stations previously mentioned (Fig. 1c), and they were collected quarterly for the period 1999–2021 by the Agency for the Environmental Protection of the Veneto Region. Note that the depths of the wells considered in this study range from 20 to 150 m.

Estimation and modeling of hydrogeological features

A space-time multivariate study of SAR, chloride and EC is presented, in combination with the groundwater level, measured in the unconfined aquifer of the central area of the Veneto Region. Such comprehensive analysis will be executed by means of the following procedural steps:

• 1. The structural analysis of SAR, chloride and EC will be performed by estimating the direct and cross-covariance functions and then by modeling the sample covariance functions through the ST-LCM, fitted according to a revised procedure specified in section ‘The ST-LCM and its fitting procedure’;

• 2. The quarterly seasonal trend will be removed from the phreatic levels and the corresponding residuals (deseasonalized data) will be studied, after which their spatio-temporal covariance function will be estimated and modelled;

• 3. The performance of the selected models versus alternative models will be tested by means of the computation of two error metrics (the root average error and the relative mean absolute error), then the leave-one-out cross-validation of the chosen models will be carried out to check the adequacy of the fitted multivariate and univariate models;

• 4. The prediction maps concerning SAR values will be obtained through cokriging, based on the fitted ST-LCM, at the 1st and the 2nd semester of 2022 over the area under study; similarly, for the four quarters of 2022, the quarterly residuals of the phreatic levels will be predicted through the spatio-temporal kriging based on the chosen covariance model, and then the seasonal components added to the residuals in order to obtain predictions of the phreatic levels for 2022;

• 5. The probability maps of groundwater deterioration, assessed in terms of both increased SAR values and reduction of groundwater levels in 2022 with respect to 2010’s measurements, will be computed by applying spatial indicator kriging, identifying vulnerability areas with a contaminated aquifer system. Note that, for this aim, both the predicted data of SAR and phreatic level are first averaged for 2022 and then compared with the corresponding mean values recorded in 2010, in order to catch possible sites of groundwater depletion.

Spatio-temporal correlation of the groundwater quality parameters

The direct and cross-correlations among the three variables SAR, chloride and EC have been modelled through the ST-LCM which has been fitted by performing the steps previously presented (section ‘The ST-LCM and its fitting procedure’).

Covariance matrices estimation and simultaneous diagonalization

As first stage of the fitting procedure, the structural analysis of the aforementioned variables and the standardized ones has been developed. In particular, three space-time direct covariance, as well as three symmetric cross-covariance functions have been computed for a fixed number of spatio-temporal lags chosen by taking into account the geometry of the sample points over the domain under study. In this case, for eight spatial lags and eleven temporal lags, in other words for 88 spatio-temporal lags, $(K=88)$ the direct and cross-covariance functions have been estimated. Figure 3 shows the covariance surfaces of SAR, chloride and EC and their respective cross-covariance surfaces $\widehat{C}_{ij}$, $i,j=1,\ldots , m$, with $m=3$.

Fig. 3

Empirical covariance surfaces of: a SAR ($\widehat{C}_{11}$); d chloride ($\widehat{C}_{22}$); f EC ($\widehat{C}_{33}$). Empirical cross-covariance surfaces of: b SAR vs chloride ($\widehat{C}_{12}$); c SAR vs EC ($\widehat{C}_{13}$); e chloride vs EC ($\widehat{C}_{23}$)

Then, all 88 sample $(3 \times 3)$ covariance matrices computed on the standardized values have been simultaneously diagonalized by the R package Jade (Miettinen et al. 2017; Cardoso and Souloumiac 1996), in order to identify the basic uncorrelated components characterizing the phenomenon under study. The diagonalization performance has been assessed by the indices expressed in (5). Very low index values have been registered for several spatio-temporal lags: more than $87.5\%$ of the computed indices have been less than the mean value, which is equal to 0.012; hence, confirming the diagonalization’s goodness.

Basic components detection and modeling

Then, by using the following orthogonal matrix found through the simultaneous diagonalization

$$\begin{aligned} {\Psi } = \left[ \begin{array} {ccc} 0.4375874 &{} 0.8223424 &{} 0.3636897 \\ -0.7892052 &{} 0.1574239 &{} 0.5936101 \\ 0.4308973 &{} -0.5467821 &{} 0.7178836 \\ \end{array} \right] \end{aligned}$$

(12)

and the diagonalized matrices $\mathbf{\Delta }(\textbf{u},v)_k$, as in Eq. (4), three uncorrelated latent components have been obtained. In Fig. 4 the unit-sill sample covariance surfaces of the uncorrelated components $c_l$, as well as the respective spatial and temporal marginals are illustrated. Note that in modeling the covariance function, one of the aspects to be analyzed is the behavior near the origin (parabolic or linear), since the smoothness at the origin of the covariance model depends on this feature. In this case, it is evident the linear behavior at the origin of the spatial and temporal marginals, and the spatial and temporal distances at which each sample covariance decays (De Iaco et al. 2013).

Fig. 4

Empirical spatio-temporal covariance surfaces of the basic components (on the left) with the corresponding spatial (in the center) and temporal (on the right) marginals, computed on the standardized values

In addition, it has been considered reasonable to keep all the detected basic components since they have shown distinct behaviors in space and time, in terms of the distance at which they became stable. By looking at the marginals of Fig. 4, the following scales of spatio-temporal variability have been fixed:

• 1. 2 km in space, 16.5 semester in time;

• 2. 3.5 km in space, 18.5 semester in time;

• 3. 12.5 km in space, 2.5 semester in time.

Thus, given that the ST-LCM is characterized by three basic components ($L=3$), they have to be modelled and the corresponding coregionalization matrices have to be identified.

By computing the nonseparability ratios, as indicated in Eq. (6), a nonuniform nonseparability has been found for each basic component (De Iaco et al. 2013). In this case, one of the most apt classes of models to be fitted is the integrated product-sum. In particular, as in Eq. (28) of De Iaco and Posa (2013), the following integrated product-sum covariance function has been adopted for each basic component:

$$\begin{aligned} c_{_l}(\mathbf{{u}},v) = k_{1_l} \, \displaystyle {\frac{1}{\displaystyle {\frac{||\textbf{u}||}{ b_{_l}}} + \displaystyle { \frac{|v|}{a_{_l}} } +1}} + k_{2_{l}} \, \displaystyle {\frac{1}{\displaystyle {{\frac{||\textbf{u}||}{ b_{_l}} } +1}}} + k_{3_{l}} \, \displaystyle {\frac{1}{\displaystyle {\frac{|v|}{a_{_l}}} + 1}}, \; \qquad \; l= 1,2,3, \end{aligned}$$

(13)

where $k_{1_{l}}>0, k_{2_{l}}> 0, k_{3_{l}}> 0,$ while $b_{_l} > 0$ and $a_{_l} > 0$ are scaling parameters in space and time, respectively.  

By using the nonlinear regression method implemented in the SPSS package, the Statistical Package for Social Science (IBM 2015, SPSS Statistics for Windows, Version 23.0.), the models’ parameters have been estimated and their values are reported in Table 1.

Table 1 Covariance models’ parameters estimated for basic components in Eq. (13)

Note that the parameters $b_l$ and $a_l$ (with $l= 1,2,3$) in Table 1 are consistent with the scales of spatio-temporal variability previously mentioned.

At this stage of the ST-LCM, the coregionalization matrices $\textbf{B}_1$, $\textbf{B}_2$ and $\textbf{B}_3$ have to be computed; in particular, the computation of the entries $b_{ij}^l,\,$ in Eq. (8), with $\,i,j=1,2,3,\; l=1,2,3$, of the $(3 \times 3)$ coregionalization matrices, is provided in the Appendix. Finally, given the matrices $\textbf{B}_1$, $\textbf{B}_2$, $\textbf{B}_3$ and $c_1, c_2$ and $c_3$, the resulting ST-LCM in Eq. (3) is given in Eq. (14):

$$\begin{aligned} \textbf{C}(\textbf{u}, v)= & {} \left[ \begin{array}{l} 0.0871 \quad 0.6570 \qquad \qquad 10.7733 \\ \qquad \\ 0.6570 \quad 10.6902 \qquad \quad 174.1067 \\ \qquad \\ 10.7733 \quad 174.1067 \qquad 8371.4088\\ \end{array} \right] \;c_1({\textbf{u}},v) + \left[ \begin{array}{l} 0.0026 \quad 0.0567 \qquad 1.8522 \\ \qquad \\ 0.0567 \quad 1.5649 \qquad 38.8109 \\ \qquad \\ 1.8522 \quad 38.8109 \quad 1713.5202 \\ \end{array} \right] \;c_2(\mathbf{{u}},v)\;+\\+ & {} \left[ \begin{array}{l} 0.0046 \quad 0.0643 \quad 3 \\ \qquad \\ 0.0643 \quad 2.3 \qquad 170 \\ \qquad \\ \quad 3 \qquad \quad 170 \qquad 9200 \\ \end{array} \right] \;c_3({\textbf{u}},v), \nonumber \end{aligned}$$

(14)

where $c_1, c_2$ and $c_3$ are the basic covariance models defined in Eq. (13) whose parameters are reported in Table 1.

It is worth pointing out that the obtained coregionalization matrices are positive definite (the eigenvalues associated with $\textbf{B}_1$, $\textbf{B}_2$ and $\textbf{B}_3$ are all non-negative), as required for the admissibility of the fitted ST-LCM. Model Eq. (14) will be used in cokriging to obtain spatio-temporal predictions of the SAR values, as detailed in section ‘Prediction maps of SAR values and phreatic levels’.

Discussion on the use of transformed data

For comparative purposes, it is worth pointing out the effect of the simultaneous diagonalization of the covariance matrices computed on the original observations. In particular, it has been shown how the performance is affected by this choice. With this aim, it is crucial to analyze the following matrix ${\Psi }$ based on the nontransformed data:

$$\begin{aligned} {\Psi } = \left[ \begin{array}{l} 0.9989262 \qquad 0.0463189 \qquad 0.0010369 \\ -0.0463304 \quad 0.9987136 \qquad 0.0206077 \\ -0.0000811 \quad -0.0206336 \quad 0.9997871 \\ \end{array}\right]. \end{aligned}$$

(15)

Note that this matrix essentially leaves unchanged the covariance matrices $\widehat{\textbf{C}}(\textbf{u},v)_k = [\widehat{C}_{ij}(\textbf{u},v)_k]$ ($k=1,\ldots ,K$) at the K fixed lags, since it is very close to the identity matrix. This result is avoided when the standardized values are considered, as specified in section ‘Basic components detection and modeling’.

Spatio-temporal correlation of the groundwater level

As previously discussed, a thorough description of the groundwater conditions needs to take into account water chemical parameters and water quantity. With this aim, the preceding spatio-temporal analysis of the selected informative variables on water quality has been combined with a spatio-temporal analysis of the unconfined groundwater level, namely the phreatic level (P), which evidently well represents the quantitative status of the underground water resource. In particular, the quarterly measurements of the phreatic level recorded at 34 stations of the monitoring network over the Venetian foothills (a subset of the 69 stations previously analyzed) for the period 1999–2021, have been examined. It is worth pointing out that the quarterly quantitative monitoring is considered sufficient to verify the behavior of the groundwater in the various seasons. Moreover, at some locations of the study area, the quarterly time series of the phreatic layer have shown a quarterly seasonal component. In Fig. 5, the auto-correlation functions (ACF) estimated for the time series collected at two different monitored stations clearly show a periodic component with length equal to 4. For this reason, the quarterly averages have been computed for the time span, station by station, and removed from the observed values, then the residuals (deseasonalized data) have been considered in the next steps of the spatio-temporal correlation analysis.

Fig. 5

ACF computed for the time series measured at two monitored stations: a Montebelluna; b Villorba belonging to Treviso Province

The spatio-temporal covariance has been estimated for a selected set of lags, in particular, 10 spatial lags and 11 temporal lags have been chosen on the basis of the geometry of the sample points over the domain under study. The empirical spatio-temporal covariance surface of the phreatic layer, $\widehat{c}_{_\textrm{P}}$, with the corresponding marginals in space and time are illustrated in Fig. 6. The marginals show a linear behaviour at the origin and decay at very large spatial scale (~10 km) and at the 8th quarter. The nonseparability ratios computed for the sample covariance of the residuals of the phreatic layer have been positive for all the spatio-temporal lags; hence, the following integrated product-sum covariance function

$$\begin{aligned} c_{_\textrm{P}}(\mathbf{{u}},v) =k_{1_{\textrm{P}}}\, \displaystyle \frac{1}{\displaystyle \frac{||\textbf{u}||}{b_{_\textrm{P}}} + \displaystyle \frac{|v|}{a_{_\textrm{P}}} +1}+ k_{2_{\textrm{P}}}\,\displaystyle \frac{1}{\displaystyle \frac{||\textbf{u}||}{b_{_\textrm{P}}} +1}+k_{3_{\textrm{P}}}\,\displaystyle \frac{1}{\displaystyle \frac{|v|}{a_{_\textrm{P}}} +1} \end{aligned}$$

(16)

can be considered the most appropriate class of covariance model and has been adopted to describe the spatio-temporal correlation of the study variable. Note that the subscript P has been introduced to specify the model of the phreatic level variable.

Fig. 6

Empirical spatio-temporal covariance surface of the phreatic layer’s residuals (on the left) with the corresponding spatial (in the center) and temporal (on the right) marginals

Through the SPSS’s nonlinear regression method, the parameters of the model in Eq. (16) have been estimated and the following values have been found:

• $k_{1_\textrm{P}}$= 4.384 m$^2$,   $k_{2_\textrm{P}}$= 0.00013 m$^2$,   $k_{3_\textrm{P}}$= 0.14 m$^2$,

• $b_{_\textrm{P}}$= 4.105 km, $a_{_\textrm{P}}$=1.263 quarter.

Before using the models in Eqs. (14) and (16), to make predictions of the qualitative and quantitative features of the groundwater at unsampled locations and for future time points, the adequacy of both the multivariate Eq. (14) and univariate Eq. (16) models have been checked, as described in the next section.

Models’ performance assessment

The most used statistical error metrics developed to measure the goodness of fit are based on the errors computed between the fitted covariance model and the sample covariance surface: evidently the higher their discrepancy, the worse the accuracy of the fitted models. Among the error metrics proposed in the literature for the previously mentioned aim, the following have been considered in the case study:

• The root average error (RAE) proposed by Theil (1958) and computed as the square root of the ratio between the sum of the squared errors and the sum of the squared empirical values;

• The relative mean absolute error (RMAE) computed as the ratio between the sum of the absolute errors and the sum of the absolute empirical values.

Let $\widehat{c}(\mathbf{{u}},v)_k$ and $c(\mathbf{{u}},v)_k$ be, respectively, the sample covariance value and the theoretical value of the covariance computed with the fitted model at the kth spatio-temporal lag ($k=1,\ldots , K$). Hence, RAE and RMAE can be expressed as follows:

$$\begin{aligned} \text{ RAE }=\left\{ \frac{\displaystyle {\sum _{k=1}^{K}\Big [\widehat{c}(\mathbf{{u}},v)_k-{c}(\mathbf{{u}},v)_k\Big ]^{2}}}{\displaystyle \sum _{k=1}^K {\widehat{c}}^{\,2}(\mathbf{{u}},v)_k}\right\} ^{0.5}, \end{aligned}$$

(17)

$$\begin{aligned} \text{ RMAE }=\frac{\displaystyle {\sum _{k=1}^{K}\Big |\,\widehat{c}(\mathbf{{u}},v)_k-{c}(\mathbf{{u}},v)_k\Big |}}{\displaystyle \sum _{k=1}^K \Big |\,{\widehat{c}}(\mathbf{{u}},v)_k\,\Big |}. \end{aligned}$$

(18)

Note that in the case of assessing the performance of the ST-LCM fitted to the sample covariance function, $\widehat{c}(\mathbf{{u}},v)_k$ denotes the value $\widehat{c}_{ij}(\mathbf{{u}},v)_k$ of the direct (if $i=j$) or the cross (if $i\ne j$) covariance at the kth user-selected spatio-temporal lag; while $c(\mathbf{{u}},v)_k$ denotes the value ${c}_{ij}(\mathbf{{u}},v)_k$ of the covariance computed with the fitted model at the kth lag. On the other hand, in the calculation of RAE and RMAE for the covariance model fitted to the residuals of the phreatic layer, $\widehat{c}(\mathbf{{u}},v)_k$ corresponds to the value $\widehat{c}_{_\textrm{P}}(\mathbf{{u}},v)_k$ of the sample covariance at the kth spatio-temporal lag, and $c(\mathbf{{u}},v)_k$ to the value $c_{_\textrm{P}}(\mathbf{{u}},v)_k$ of the covariance computed with the fitted model at the kth lag.

At this point, the goodness of the fitted model Eq. (14) has been evaluated by performing a comparative analysis with respect to another ST-LCM, whose basic components are modelled without taking into account the type of nonseparability of the uncorrelated components. In particular, the basic components of the contender ST-LCM are modelled through the following product-sum covariance functions:

$$\begin{aligned} c^*_{l}(\mathbf{{u}},v) = k_{1_l} C_{\textrm{s}_l}(\mathbf{{u}})C_{\textrm{t}_l}(v) + k_{2_l} C_{\textrm{s}_l}(\mathbf{{u}}) + k_{3_l} C_{\textrm{t}_l}(v), \qquad l=1,2,3, \end{aligned}$$

(19)

with $C_{\textrm{s}_l}$ the spatial exponential covariance model in $\mathbb {R}^d$, $C_{\textrm{t}_l}$ the temporal exponential covariance model in $\mathbb {R}$, with practical ranges $b_{l}$ and $a_{l}$, respectively and parameters $k_{1_l}, k_{2_l}$ and $k_{3_l}, l=1,2,3,$ as indicated in Table 2. This kind of covariance model is widely used not only in environmental sciences but also in other scientific fields, such as demography (De Iaco et al. 2015). These estimates ensure the strict positive definiteness of the basic models (De Iaco and Posa 2018). It is worth pointing out that the notation $c^*_{l}$ is adopted in order to distinguish the product-sum covariance model with respect to the integrated product-sum model defined in Eq. (13).

Table 2 Covariance models’ parameters estimated for basic components in Eq. (19)

On the other hand, for the residuals of the phreatic level the following product-sum covariance model

$$\begin{aligned} c_{_\textrm{P}}^*(\mathbf{{u}},v) = k_{1_{\textrm{P}}} C_{\textrm{s}_{_\textrm{P}}}(\mathbf{{u}})C_{\textrm{t}_{_\textrm{P}}}(v) + k_{2_{\textrm{P}}} C_{\textrm{s}_{_\textrm{P}}}(\mathbf{{u}}) + k_{3_{\textrm{P}}} C_{\textrm{t}_{_\textrm{P}}}(v), \end{aligned}$$

(20)

with

• $C_{\textrm{s}_{_\textrm{P}}}$ the spatial exponential covariance model in $\mathbb {R}^d$, $C_{\textrm{t}_{_\textrm{P}}}$ the temporal exponential covariance model in $\mathbb {R}$, with practical ranges $b_{_\textrm{P}} = 14$ km and $a_{_\textrm{P}}= 12$ quarter, respectively,

• $k_{1_{\textrm{P}}} = 3.705 \, \textrm{m}^2, \, k_{2_{\textrm{P}}} =0.0041 \, \textrm{m}^2, \, k_{3_{\textrm{P}}}=0.815 \, \textrm{m}^2,$  

has been fitted and compared to the model in Eq. (16) by using the preceding error metrics RAE and RMAE.

Note that the comparative analyses to assess the fitting goodness have been performed by focusing on small spatial and temporal lags where the correlation is stronger and not for all selected lags. In particular, the two different ST-LCMs have been compared by computing errors (Eqs. 17 and 18) for the first five spatial lags and the first seven temporal lags; while for the comparison of two space-time covariance models fitted for the groundwater levels’ residuals, the first five spatial and five temporal lags have been considered.

By analyzing the statistics reported in Table 3, it is evident that the selection of the product-sum covariance model for all the latent components has determined the worst fitting, since the values of Eqs. (17) and (18) are almost always greater with respect to the case where the fitted covariance models are the integrated product-sum for all the basic components: the only exception is for the SAR, where both the aforementioned errors are smaller when three product-sum covariance basic models have been adopted. However, in general, the ST-LCM (14) with three basic integrated product-sum models is the most appropriate one for the data under study. Similarly, the adoption of model Eq. (16) for the residuals of the phreatic level represents the better choice with respect to model Eq. (20).

These results are due to the fact that Eqs. (19) and (20) are suitable in the presence of uniform negative nonseparability (De Iaco et al. 2013), thus they do not honor the type of nonseparability of the sample covariances (a nonuniform nonseparability for the basic components of the ST-LCM, and a uniform positive nonseparability for the residuals of the phreatic level).

Table 3 Statistics for models’ performance assessment

A final check of the suitability of the fitted models, both the ST-LCM in Eq. (14) for the investigated water chemical features, and the model in Eq. (16) for the phreatic level, has been made through the leave-one-out cross-validation procedure, which has been performed twice, i.e.

• 1. On the basis of the ST-LCM in Eq. (14) and the available data for SAR, chloride and EC;

• 2. On the basis of the spatio-temporal covariance model in Eq. (16) and the computed residuals of the phreatic level.

Then, the estimates of SAR obtained from the cross-validation as indicated in (1) have been compared with the recorded values and their correlation coefficient was 0.87; on the other hand, the correlation coefficient between the residuals of the phreatic level and their estimates from the cross-validation mentioned in (2) was 0.80. Hence, the high values of the correlation coefficients (significant at $1\%$ level) have confirmed the suitability of the fitted models in Eqs. (14) and (16), which can be used in the next steps of the case study, for prediction purposes.

Prediction maps of SAR values and phreatic levels

In this stage of the analysis, the models in Eqs. (14) and (16) previously defined for the multivariate and univariate cases, have been used to forecast the SAR values and phreatic levels, respectively, for 2022 over the study area. In particular, the fitted ST-LCM in Eq. (14) has been adopted to make cokriging predictions for SAR values for the 1st and the 2nd semester of 2022 (two time points after the last one available in the analyzed data set), over the investigated area. With this aim, the routine “COK2ST” of the GSLib package, proposed in De Iaco et al. (2010), has been used after properly implementing the parameter file with an ST-LCM based on three basic components modelled through the integrated product-sum covariance functions. On the other hand, the spatio-temporal covariance model in Eq. (16) has been considered to make quarterly kriging predictions of the residuals of the phreatic level in 2022; then, the quarterly mean values previously computed for all sample stations (see section ‘Spatio-temporal correlation of the groundwater level’) have been added to the estimated residuals in order to determine the phreatic levels for the four quarters of 2022. Thus, the estimated values for SAR and phreatic levels, as well as the relative error standard deviation associated to their estimates, are displayed by the contour plots shown in Fig. 7. Note that, in the case of the phreatic levels, two different quarters, the first and the third ones of 2022 (one during the winter period and the other one referring to the summer season) have been selected to show the corresponding prediction maps.

As regards the SAR values, Fig. 7a,b exhibits the highest SAR values in the central-western part of the study area, which corresponds to the high plain of Vicenza, characterized by a gravelly sandy alluvial stratum (Fig. 2b) and high permeability levels; this area represents an important site of aquifer recharge. During the last few decades, the high plain of Vicenza has been affected by the development of several urban centres and industrial activities. Similarly, the estimated SAR values are high, especially during the second semester of 2022, in the north-eastern part of the study area (the high plain of Piave in the Province of Treviso) which hosts several urban centres as well as various industrial plants specialized in the production of household appliances, electrical equipment and stainless-steel processing, as well as wine production.

Figure 7e,f shows the kriging estimates of the phreatic levels in the two selected quarters, the first and the third ones, of 2022. It is evident that the two subareas with the highest estimated SAR values exhibit low values of water quantity: as already known, the socio-economic growth of a territory is one of the main reasons for water withdrawals increasing—for civil, agricultural and industrial purposes, as well as water quality deterioration. Moreover, the lowest phreatic levels have been estimated in the south-east of the study area while the highest phreatic levels are in the central-northern part, close to the boundaries of Vicenza and Treviso. This last area can be considered as an area of discharge of the water from the Alps, and this determines the rate of increasing groundwater level. Note that cokriging and kriging prediction uncertainties, which have been measured by the relative error standard deviation associated to all predicted values, are displayed through the maps in Fig. 7c,d, for the SAR cokriging predictions, and in Fig. 7g,h for the phreatic levels kriging predictions. These uncertainty maps show very low values all over the study area, highlighting the capability of the spatio-temporal prediction procedures to determine levels of uncertainty of low magnitude, with respect to the predicted values.

Fig. 7

Prediction maps of SAR values for: a the 1st; b the 2nd semester of 2022, with the corresponding relative standard deviations (c–d). Predictions maps of phreatic levels for: e the 1st; f the 3rd quarter of 2022, with the corresponding relative standard deviations (g–h)

Finally, it is worth highlighting that all prediction maps show very slight variations in space and time: this result is due to the fact that alteration of the water quality and quantity parameters, without any accidental and extraordinary events that affect the aquifer, is a process that could occur over several years. On the basis of this consideration, the SAR values and the phreatic levels that have been predicted for 2022, have been compared with the data recorded in 2010, and some impressive results are discussed in the next section.

Probability map of groundwater deterioration

In this stage of the case study, the research aims to understand the probability of a deterioration of the aquifer system in 2022, in terms of both qualitative and quantitative profiles, with respect to the 12 years before. For this purpose, by using the results in the previous section, the analyses have been performed through the following steps:

• 1. Averaging SAR and phreatic layer predictions over the year 2022 at the sample points and defining a spatial indicator variable that is equal to 1 in case of deterioration of both qualitative and quantitative aquifer conditions for 2022, i.e. in case the yearly SAR predicted values for 2022 are greater than those measured twelve years before (2010), and yearly groundwater levels for 2022 are smaller than those measured in 2010;

• 2. Performing spatial indicator kriging over the study area in order to obtain a risk map of groundwater deterioration in 2022 with respect to 2010.

Given the spatial indicator random field I for the year 2022, which is equal to 1 in case of worsening aquifer, and equal to 0 otherwise, i.e.

$$\begin{aligned} I({\textbf {s}},t;\, \textrm{SAR}_{2010};\, \textrm{P}_{2010})=\left\{ \begin{array}{ll} 1 &{} \qquad \text{ if } \, \textrm{SAR}_{2022} > \textrm{SAR}_{2010}, \, \textrm{P}_{2022} < \textrm{P}_{2010} \\ &{} \\ 0 &{} \qquad \text{ otherwise } \end{array} \right. \end{aligned}$$

(21)

with ${\textbf {s}} \in D,$ and $t=2022,$ the indicator kriging allows for the estimation of the probability of exceeding specific threshold values over the domain under study. At an unsampled point, the probability that the variable of interest is not greater (or not smaller) than the fixed threshold can be estimated using a linear combination of neighbouring indicator variables.

Figure 8 shows the probability maps of the deterioration in 2022 of the aquifer system in Venetian Region, in terms of high SAR values (Fig. 8a), low phreatic levels (Fig. 8b), and jointly high SAR values and a low phreatic level (Fig. 8c), with respect to 2010. As regards the water quality, there is a high probability that in the north-east (in the Province of Treviso) and in the centre of the investigated area, the SAR values in 2022 are higher than those observed in 2010. In addition, the analyses herein performed have highlighted a high probability of aquifer depletion in 2022, expressed in terms of low phreatic levels with respect to 2010, over the whole study area, with the exception of a few sites in the north and in the central-east. Finally, Fig. 8c shows the probability map of both quality and quantity groundwater deterioration: it appears that in the eastern area of Vicenza Province, close to the border with Treviso and Padua, and in the north-eastern part of the analyzed area there is a high probability of worsening in 2022. On the other hand, in the south-western part of Treviso Province, above the area covered by fontanili (see section ‘The investigated area’), i.e. special water sources located between the high and the low Venetian Plain, the probability of groundwater deterioration is very low: in this part of the study area the prediction maps (Fig. 7) have shown quite small SAR values and modest levels for water quantity, especially during the second period of 2022.

Fig. 8

Probability maps of the deterioration of the aquifer system over Veneto Region in 2022, with respect to 2010, in terms of: a high SAR values; b low phreatic level; c high SAR values and low phreatic level

It is clear that the probability map obtained with the proposed application represents an effective tool for detecting areas where the groundwater needs strong controls, since it is more likely that the groundwater could suffer a degradation, in terms of quality and quantity parameters, with respect to the past.

Discussion

In this paper, a geostatistical analysis of the joint spatial and temporal behaviour of four key hydrogeological variables, concerning the water quality (chemical properties, i.e. SAR, chloride and EC) and water quantity (phreatic levels) of an unconfined aquifer, was thoroughly investigated. An ST-LCM composed of three basic integrated product-sum covariance models was constructed to describe the direct and cross-covariance in space-time among the selected chemical parameters and to predict SAR values; moreover, the integrated product-sum covariance model was also chosen to fit the spatio-temporal covariance function of the phreatic level and to forecast this last variable.

The most original aspects of the research proposed in this paper concerned: (1) the spatio-temporal modeling of some crucial factors referenced in the scientific literature (Karami et al. 2018; Dal Ferro et al. 2016; Dalla Libera et al. 2017; Boufekane and Saighi 2019) to analyze the status of an unconfined aquifer, and (2) the spatio-temporal indicator kriging (as a nonparametric spatio-temporal prediction method) carried out to determine the probability of deterioration of the unconfined aquifer over a long period.

The performed analysis allowed the identification of two sub-areas of the Veneto Region, one in the eastern part of Vicenza Province and the other one in the north-eastern part of the study area in the Treviso Province, where there is a high probability that in 2022 the SAR values are higher and the phreatic levels are smaller with respect to the corresponding values measured during 2010. These subareas of the domain under study need particular attention, since there is a very high probability that the status of the aquifer system could be damaged qualitatively and quantitatively.

Predictions of groundwater quality and quantity could help to identify appropriate areas for agriculture and avoid excessive water exploitation where the sodium concentration in the water with respect to calcium and magnesium content could dramatically increase (Boufekane and Saighi 2019). As already known, SAR affects the normal water infiltration rate in the soil; hence, water with high SAR values will decrease infiltration. Note that sodium also contributes directly to the total salinity of the water and may be toxic to sensitive crops, such as fruit trees (Ogunfowokan et al. 2013).

Evidently, various factors could affect the groundwater quality and quantity parameters. These parameters are the so-called geogenic activities, i.e., host rock, rock and water interaction, climatic effects, the hydrogeological influences, e.g., high water level, soil composition, and anthropogenic factors, reflecting the human, agricultural and industrial activities (Gautam et al. 2023). Therefore, it is extremely important for environmental sustainability to monitor the groundwater status in order to prevent serious damage to the health of people and the Earth. Further developments of the analysis method proposed in this paper will consider also important climatic variables, such as rainfall, soil and air temperature, and solar radiation, which could influence the aquifer conditions and determine the depletion and deterioration of the groundwater.

Appendix

The entries $b_{ij}^l,\,$ with $\,i,j=1,2,3,$ of $\textbf{B}_l$, defined in Eq. (8) as ${b}^l_{ij} = {[\widehat{C}_{ij}(\textbf{u}, v)_{l-1}]-[\widehat{C}_{ij}(\textbf{u}, v)_{l}]}, l=1,\ldots ,L,$ are determined by using:

• $\widehat{C}_{ij}(\textbf{0}, 0), i,j=1,2,3,$ of the sample direct and cross-covariances of the variables under study (where $i=1$ refers to SAR, $i=2$ to chloride and $i=3$ to EC);

• The values of the sample direct and cross-covariances at the three scales of spatio-temporal variability.

In particular, the entries $b_{ij}^1,\,$ with $\,i,j=1,2,3,$ of $\textbf{B}_1$ are calculated as follows:

$$\begin{aligned} \bullet \; b_{11}^{1}&=0.0943-0.0072 = 0.0871 \, \rm (mg/l)^2,\\ \bullet \; b_{12}^{1}&= {0.7780-0.1210} = 0.6570 \, \rm (mg/l)^2,\\ \bullet \; b_{13}^{1}&= {15.6255-4.8522} = 10.7733 \, \rm (mg/l \!\times \!\upmu S/cm),\\ \end{aligned}$$

$$\begin{aligned} \bullet \; b_{21}^1&= {b_{12}^{1}},\\ \bullet \; b_{22}^1&= {14.5551-3.8649} = 10.6902 \, \rm (mg/l)^2,\\ \bullet \; b_{23}^{1}&= {382.9176-208.8109} = 174.1067 \, \rm (mg/l \!\times \! \upmu S/cm),\\ \bullet \; b_{31}^1&= b_{13}^{1}, \\ \bullet \; b_{32}^1&= b_{23}^{1},\\ \bullet \; b_{33}^1&= {19284.929-10913.5202} = 8371.4088 \,\rm (\upmu S/cm)^2, \end{aligned}$$

the entries $b_{ij}^2,\,$ with $\,i,j=1,2,3,$ of $\textbf{B}_2$ are computed as follows:

$$\begin{aligned} \bullet \; b_{11}^{2}&={0.0072-0.0046} = 0.0026 \, \rm (mg/l)^2,\\ \bullet \; b_{12}^2&={0.1210-0.0643} = 0.0567 \, \rm (mg/l)^2,\\ \bullet \; b_{13}^2&={4.8522-3} = 1.8522 \, \rm (mg/l \!\times \!\upmu S/cm),\\ \bullet \; b_{21}^2&= b_{12}^{2}, \\ \bullet \; b_{22}^2&={3.8649-2.3} = 1.5649 \, \rm (mg/l)^2,\\ \bullet \; b_{23}^2&={208.8109-170} = 38.8109 \, \rm (mg/l \!\times \!\upmu S/cm),\\ \bullet \; b_{31}^2&= b_{13}^{2},\\ \bullet \; b_{32}^2&= b_{23}^{2},\\ \bullet \; b_{33}^{2}&={10913.5202-9200} = 1713.5202 \, \rm (\upmu S/cm)^2, \end{aligned}$$

and the entries $b_{ij}^3,\,$ with $\,i,j=1,2,3,$ of $\textbf{B}_3$ are found out through the following calculation:

$$\begin{aligned} \bullet \; b_{11}^3&= {0.0046-0} = 0.0046 \, \rm (mg/l)^2,\\ \bullet \; b_{12}^3&= {0.0643-0} = 0.06443 \, \rm (mg/l)^2,\\ \bullet \; b_{13}^3&= {3-0} = 3 \, \rm (mg/l \!\times \!\upmu S/cm), \\ \bullet \; b_{21}^3&= b_{12}^{3},\\ \bullet \; b_{22}^3&= {2.3-0} = 2.3 \, \rm (mg/l)^2,\\ \bullet \; b_{23}^3&= {170-0} = 170 \, \rm (mg/l \!\times \!\upmu S/cm), \\ \bullet \; b_{31}^3&= b_{13}^{3},\\ \bullet \; b_{32}^3&= b_{23}^{3},\\ \bullet \; b_{33}^3&={9200-0} = 9200 \, \rm (\upmu S/cm)^2.\\ \end{aligned}$$

Hence, the obtained coregionalization matrices $\textbf{B}_l, l=1,2,3$, are the following:

$$\begin{aligned} \textbf{B}_1= & {} \left[ \begin{array}{lll} 0.0871 &{} 0.6570 &{} 10.7733 \\ \qquad \\ 0.6570 &{} 10.6902 &{} 174.1067 \\ \qquad \\ 10.7733 &{} 174.1067 &{} 8371.4088\\ \end{array} \right], \qquad \, \textbf{B}_2 = \left[ \begin{array} {lll} 0.0026 &{} 0.0567 &{} 1.8522 \\ \qquad \\ 0.0567 &{} 1.5649 &{} 38.8109 \\ \qquad \\ 1.8522 &{} 38.8109 &{} 1713.5202 \\ \end{array} \right], \\ \textbf{B}_3= & {} \left[ \begin{array} {lll} 0.0046 &{} 0.0643 &{} 3 \\ &{}&{} \\ 0.0643 &{} 2.3 &{} 170 \\ &{}&{} \\ 3 &{} 170 &{} 9200 \\ \end{array} \right]. \nonumber \end{aligned}$$

(27)