Introduction

The quantity, quality, and the degree of spatiotemporal variability of groundwater are key factors for the wealth of human communities and ecosystems; therefore, they play a significant role in effective groundwater resources management. Both human interventions, such as excessive pumping, and natural processes, such as a decline in recharge, can cause fluctuations in groundwater levels. Level variations could be long-term (on the order of years) or short-term (on the order of months). Global studies confirm the connection between excessive groundwater pumping and variations in groundwater levels (Islam et al. 2022; Tatas et al. 2022). Dewatering efforts for underground mining operations significantly reduce groundwater levels for a long time and in many cases may dry up nearby springs. Near-mine ecosystems typically depend on groundwater for survival. Water pumping for mining activities can lead to groundwater level drops which can be harmful to local communities and ecosystems (Schrader and Winde 2015; Davies et al. 2020). Therefore, monitoring the spatial distribution of groundwater levels around mining areas is an important goal for management purposes.

Various geostatistical methods have been used to investigate changes in the spatial distribution of groundwater levels. Some studies employ Kriging methods using only primary information (Budiman et al. 2022; Evans et al. 2020), while others involve auxiliary variables (Varouchakis and Hristopulos 2013a, b; Zirakbash et al. 2020; Calzolari and Ungaro 2012; An et al. 2015) or implement hybrid machine learning approaches (Parasyris et al. 2021; Manzione and Castrignano 2019; Theodoridou et al. 2017; Tapoglou et al. 2014). In mining areas, groundwater levels distribution is usually investigated through the use of Kriging methods such as ordinary Kriging, indicator Kriging and co-Kriging (Dai et al. 2011; Abiye et al. 2018; Keegan-Treloar et al. 2021).

Geostatistical methods typically rely on the existence of data that sufficiently sample the spatial variability in the area of interest. In mining areas, the monitoring stations are often clustered around small areas of interest (pits, mines or mine sectors). This practice prevails because such areas require careful monitoring due to increased environmental risks. The clustered pattern of the measurement locations hinders the reliable estimation of the variogram model, especially if the number of data points inside each cluster is small (Goovaerts 1997; Kovitz and Christakos 2004). Another problem commonly faced by geostatistical methods is the skewness of the data distribution. This is usually handled by means of nonlinear transforms (e.g., lognormal, Box-Cox) which aim to normalize the marginal data distribution (this procedure is known as Gaussian anamorphosis; Wackernagel 2003; Chilès and Delfiner 2012).

This work has two goals: First, it presents an alternative approach for spatial groundwater levels analysis that can overcome the difficulties related to estimating spatial dependence. This approach is based on the stochastic local interaction (SLI) model. This model imposes spatial correlations by means of local couplings (interactions); the SLI model can increase the computational efficiency of spatial prediction for correlated data (Hristopulos 2015; Hristopulos et al. 2021). Secondly, a recently proposed data-driven (nonparametric), kernel-based approach is used to conduct Gaussian anamorphosis (Pavlides et al. 2022; Agou et al. 2022). This method is more flexible than nonlinear transforms based on explicit functions and does not suffer from the problems that Hermite polynomials face in the tails of the distribution.

Groundwater level data (meters below surface) from three mines operating in the same region (northern Greece), are studied. Groundwater is used to support mining activity in the study area. Groundwater levels are investigated by means of universal Kriging (UK) and SLI. Uncertainty estimates for both SLI and UK are provided. Prediction intervals (at 5 and 95% probability levels) are estimated. Leave-one-out cross-validation (LOOCV) measures indicate that the performance of UK and SLI is adequate considering the small sample size—although both methods slightly overestimate a few low values. UK performs slightly better than SLI if the entire dataset of the three mines is taken into account; however, SLI performs better than UK even for smaller sample sizes (individual mines). MATLAB code for SLI is freely available at Hristopulos (2020b).

The rest of this paper is structured as follows: section “Theory and methods” reviews the theory for the spatial prediction methods employed (UK and SLI) and for Gaussian anamorphosis; section “Data description and preprocessing” includes the data description, exploratory analysis and data normalization; section “Results: universal Kriging” presents the application of UK to the groundwater level data including cross-validation analysis; section “Results: SLI” focuses on the application of SLI over the entire area and separately to one of the three mines, along with the respective cross-validation measures. Lastly, section “Discussion” comments on the results, and the final section presents conclusions and open questions for further study.

Theory and methods

The spatial distribution of variables is used using the mathematical framework of random fields (Adler 1981; Christakos 1992; Chilès and Delfiner 2012; Hristopulos 2020a). A random field is a collection of dependent random variables distributed over the spatial domain of interest. Herein, the random field concept is used to model groundwater levels.

A scalar random field \(X(\textbf{s})\) where \(\textbf{s}\in \mathbb {R}^{d}\) is the position vector, represents a random function \(\mathcal {D} \subset \mathbb {R}^{d}\rightarrow \mathbb {R}\), where \(\mathcal {D}\) is the spatial domain; in this study \(d = 2\) and \(\textbf{s} = (s_{1}, s_{2})^\top\), where \(\top\) denotes the transpose of a vector. A random field is fully determined by means of the n-point joint probability density functions, where \(n = 1, 2, \ldots\) denotes a positive integer (the set of all positive integers is denoted by \(\mathbb {N}\)). The Gaussian assumption is often used for the joint density functions.

The data are assumed to represent a partial sample of the random field; they are denoted by the set of sampling sites \(\{\textbf{s}_{1}, \ldots , \textbf{s}_{N} \}\) and the respective water level measurements \(\{x_{1}, \ldots , x_{N} \}\) (lowercase letters denote specific realizations of the random field). The field is reconstructed on a rectangular map grid \(\mathbb {G}\) which comprises the set of points (nodes) \(\{\textbf{z}_{1}, \ldots , \textbf{z}_{P} \}\). Estimation points will be denoted in general by \(\textbf{u}\in \mathbb {R}^{d}\), where \(\textbf{u}\) refers either to a point in \(\mathbb {G}\) or one of the sampling points (e.g., for cross-validation analysis).

For practical purposes, random fields are often decomposed into a deterministic part (trend) and a stochastic part (fluctuation) as follows:

$$\begin{aligned} X(\mathbf{{s}})=m_{\!X}(\mathbf{{s}}) + X^{\prime }(\mathbf{{s}}) \end{aligned}$$
(1)

The function \(m_{\!_X} (\textbf{s})\) is assumed to represent the mathematical expectation of the random field, i.e., \(m_{\!_X} (\textbf{s}) = \mathbb {E}[X(\textbf{s})]\). The expectation \(\mathbb {E}[X(\textbf{s})]\) of a random field at the point \(\textbf{s}\) represents a stochastic average over all probable configurations of the field (as defined by means of the joint probability distribution; Hristopulos 2020a). Hence, \(m_{\!_X} (\textbf{s})\) is a deterministic function and typically it reflects slow spatial variations (trend) of the random field \(X(\textbf{s})\); usually, \(m_{\!_X} (\textbf{s})\) is modeled as a polynomial. Herein, only first-degree polynomial trends are considered, i.e.,

$$\begin{aligned} m_{\!_X}(\textbf{s})=a_0 + a_1 s_1 + a_2 s_2 \end{aligned}$$
(2)

where \({\textbf {A}} = (a_0, a_1, a_2)^\top\) is the vector of trend coefficients, and \(\textbf{s}=(s_1, s_2)\) are the coordinates of the two-dimensional (2D) position vector \(\textbf{s}\).

The fluctuation \(X^{\prime }(\mathbf{{s}})\) is a random field that represents the finer-scale, stochastic component of \(X(\textbf{s})\). It is obtained by removing the trend from \(X(\textbf{s})\) and is thus equal to the field’s residuals (Pavlides et al. 2015). Since it is assumed that \(m_{\!_X} (\textbf{s}) = \mathbb {E}[X(\textbf{s})]\), it follows that \(\mathbb {E}[X'(\textbf{s})] = 0\).

A random field is considered stationary if the joint n-point probability distributions (for all \(n \in \mathbb {N})\) do not depend on the spatial location but only the relative configuration of the points. Since this condition is not easily testable, the condition of weak stationarity is used in practice. Weak stationarity means that the expectation of the random field is constant and the covariance is a function purely of the time lag (not the particular instant in time). A stationary Gaussian random field is thus fully determined from the mean function \(m_{\!_X} (\textbf{s})\) and the covariance function \(c_{\!_X}(\textbf{r})\), where \(\textbf{r}\in \mathbb {R}^{d}\) is the space lag between two points \(\textbf{s}\) and \(\textbf{s}'=\textbf{s}+ \textbf{r}\) and \(c_{\!_X}(\cdot )\) is a positive-definite function.

It is assumed that the data sites comprise the set of points \(\{\textbf{s}_{i}\}_{i = 1}^{n}\) while the groundwater level measurements at these sites will be denoted by the data vector \(\textbf{x} = (x_{1}, \ldots x_{n})^\top\).

Variogram modeling

The models attempting to represent spatial processes rely on the spatial correlations between the data. These correlations are reflected in the covariance function that characterizes the random field; however, for practical reasons, it is more convenient to estimate the variogram function instead of the covariance function (Chilès and Delfiner 2012; Kitanidis and Vomvoris 1983).

The variogram function \(\gamma _{\!_X}(\textbf{r})\) for stationary random fields is connected to the covariance function \(c_{\!_X}(\mathbf{{r}})\) as shown in Eq. (3).

$$\begin{aligned} \gamma _{\!_X}(\mathbf{{r}})=c_{\!_X}(0)-c_{\!_X}(\mathbf{{r}}) \end{aligned}$$
(3)

where r is the distance vector between two points. Thus, the variogram function can be used interchangeably with the covariance function if the field of the fluctuations \(X'\) is considered a stationary field.

The variogram function is defined as follows

$$\begin{aligned} \gamma _{\!_X}(\mathbf{{r}})=\frac{1}{2} \text {Var} \left[ X(\mathbf{{s}})- X(\mathbf{{s+r}})\right] \end{aligned}$$
(4)

where \(\text {Var}\) is the variance operator, i.e., \(\text {Var}(X)= \mathbb {E}[X^2(\textbf{s})]- \mathbb {E}^2[X(\textbf{s})]\) Olea (2006).

The empirical (experimental) variogram is obtained from the data using Matheron’s moment estimator (Matheron 1962) or Cressie’s robust variogram estimator (Cressie 1993). The empirical variogram is then fitted to a theoretical model in order to account for all possible pair distances. Various admissible variogram models can be found in Goovaerts (1997); Chilès and Delfiner (2012); Hristopulos (2020a). The tested variogram models are fitted to the empirical variogram, using the weighted least squares method (Olea 2006). The spherical variogram model which is used herein satisfies the equation

$$\begin{aligned} \gamma _{\!_X}(\textbf{r})={\left\{ \begin{array}{ll} \sigma ^2 \left[ 1.5 (|\textbf{r}|/\xi )-0.5(|\textbf{r}|/\xi )^3\right] , &{}\ |\textbf{r}|\le \xi \, \\ \sigma ^2, &{}\ |\textbf{r}|\ge \xi \, \end{array}\right. } \end{aligned}$$
(5)

where \(\sigma ^2\) is the variance of the random field, |r| is the spatial lag, and \(\xi\) is the correlation length under the assumption of statistical isotropy (i.e., lack of directional preference; Hristopulos 2020a).

Kriging

Kriging refers to a group of stochastic spatial interpolation methods. They are by construction linear, unbiased, and minimum variance estimators. Kriging methods have a large range of applications in the mining and environmental sectors (Cressie 1990; Varouchakis et al. 2018; Varouchakis and Hristopulos 2013b). Kriging provides significant benefits compared to deterministic interpolation methods (Gong et al. 2014; Varouchakis and Hristopulos 2013a; Pavlides et al. 2015).

The value of the random field \(X(\textbf{u})\) at an unmeasured location \(\textbf{u} \in \mathbb {G}\) is estimated by means of a linear combination of the measurements at \(n(\textbf{u})\) nearby points \(\textbf{s}_{1(\textbf{u})}, \ldots , \textbf{s}_{n(\textbf{u})}\), where \(\textbf{s}_{i(\textbf{u})} \in \{\textbf{s}_{1}, \ldots , \textbf{s}_{N} \}\) is a neighbor of \(\textbf{u}\) for all \(i = 1, \ldots , n(\textbf{u})\). A map of the spatial distribution of the field is obtained by repeating the estimation process at every node of a suitably selected grid. Such maps can be accompanied by estimates of the prediction variance at each point. The variance can adequately represent the prediction uncertainty if the data probability distribution is Gaussian. If the data follow a skewed probability distribution, the Kriging-based uncertainty estimates are not reliable (Agou 2016).

Simple Kriging (SK) assumes that the random field is stationary and its mean, \(m_{\!_X}\), is known. The SK estimator is obtained by means of the following equation (Krige 1951; Cressie 1990):

$$\begin{aligned} \hat{x}({\textbf {u}})=m_{\!_X} + \sum _{i=1}^{n({\textbf {u}})} \ \lambda _{i}(\textbf{u}) \, \left( x_{i} - m_{\!_X} \right) \end{aligned}$$
(6)

In Eq. (6), \(\lambda _{i}(\textbf{u})\) are the Kriging weights at the target point \(\textbf{u}\). The Kriging weights are calculated by solving the following linear system

$$\begin{aligned} \mathbf{{C_{\!_X} \varvec{\Lambda }= C_{u}}} \end{aligned}$$
(7)

where \(\mathbf{{C_{\!_X}}}\) is the covariance (or variogram) matrix of the fluctuation random field \(X'(\cdot )\) at the data locations, i.e., \([\textbf{C}_{\!_X}]_{i,j}=c_{\!_X}(\textbf{s}_{i}-\textbf{s}_{j})\) for \(i,j = 1, \ldots , n(\textbf{u})\), \({\varvec{\Lambda }}=(\lambda _{1(\textbf{u})}, \ldots ,\lambda _{n(\textbf{u}}))^\top\) is the vector of the Kriging weights, and \(C_\mathbf{{u}}=\left( c_{\!_X}(\textbf{u}-\textbf{s}_{1}), \ldots , c_{\!_X}(\textbf{u}-\textbf{s}_{n(\textbf{u})})\right) ^\top\) is the covariance (or variogram) vector between the unknown point \(\textbf{u}\) and each of the \(n(\mathbf{{u}})\) neighbor points that contribute to the estimate (Chilès and Delfiner 2012). The Kriging estimate \(\hat{x}({\textbf {u}})\) at \(\textbf{u}\) is obtained by replacing in Eq. (6) the \(x_{i}\) with the respective data values, \(m_{\!_X}\) with the estimate of the mean, and the Kriging weights with the solution of Eq. (7) for \(\varvec{\Lambda }\).

Universal Kriging

For many datasets the constant mean assumption is not suitable; even if the assumption is reasonable, it is not always possible to accurately determine the value of the mean (e.g., if the sample is small). Several variations of Kriging have been suggested to address this issue, such as ordinary, regression, and universal Kriging (Goovaerts 1997; Schabenberger and Gotway 2004; Cressie 1990).

In this study, universal Kriging (UK) is employed, which is also known as Kriging with a drift. This method assumes that the trend \(m_{\!_X}(\textbf{s})\) depends on the coordinates \(\textbf{s}\) in terms of simple basis functions (Mesić Kiš 2016; Kitanidis 1997). Assuming a simple linear polynomial trend, \(m_{\!_X}(\textbf{s})= a_{0}+a_{1}s_{1} + a_{2} s_{2}\), where the \(a_{0}, a_{1}, a_{2}\) are real-valued, unknown coefficients, the UK estimator at location \(\textbf{u}=(u_i, u_{j})\) is

$$\begin{aligned} \hat{x}_{\!_\text {UK}}({\textbf {u}})= \sum _{k=1}^{n({\textbf {u}})} \, \lambda _{k}(\textbf{u}) x(\textbf{s}_k) \end{aligned}$$
(8)

In Eq. (8), the polynomial coefficients of the trend \(m_{\!_X}\) are considered unknown and should be estimated along with the covariance coefficients from the data, thus increasing the uncertainty of the prediction. The linear weights are calculated as the solution of Eq. (9)

$$\begin{aligned} \mathbf{{C_{\!_X} B= C_{u}}} \end{aligned}$$
(9)

where the vector \(\textbf{B}\) contains both the \(n(\textbf{u})\) weights and three Lagrange multipliers (one for each trend coefficient) used to enforce the no-bias condition. The covariance matrices \(\mathbf {C_{\!_X}}\) and \(\mathbf {C_u}\) are expressed as follows

$$\begin{aligned} \small { \left[ \begin{array}{llllll} \sigma _{\!_X}^2 &{} \dots &{} c_{\!_X}({\textbf {s}}_1,{\textbf {s}}_n) &{} 1 &{} s_{1;1} &{} s_{1;2}\\ c_{\!_X}({\textbf {s}}_2,{\textbf {s}}_1) &{} \dots &{} c_{\!_X}({\textbf {s}}_2,{\textbf {s}}_{n}) &{} 1 &{} s_{2;1} &{} s_{2;2}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ c_{\!_X}({\textbf {s}}_{n},{\textbf {s}}_1) &{} \dots &{} \sigma _{\!_X}^2 &{} 1 &{} s_{n;1} &{} s_{n;2} \\ 1 &{} \dots &{} 1 &{} 0 &{} 0 &{} 0 \\ s_{1;1} &{} \dots &{} s_{n;1} &{} 0 &{} 0 &{} 0 \\ s_{1;2} &{} \dots &{} s_{n;2} &{} 0 &{} 0 &{} 0 \\ \end{array}\right] \, \left[ \begin{array}{c} \lambda _{1} \\ \lambda _{2} \\ \vdots \\ \lambda _{n}\\ \mu _0 \\ \mu _1 \\ \mu _2 \\ \end{array}\right] =\left[ \begin{array}{c} c_{\!_X}({\textbf {s}}_1,{\textbf {u}}) \\ c_{\!_X}({\textbf {s}}_2,{\textbf {u}}) \\ \vdots \\ c_{\!_X}({\textbf {s}}_{n},\textbf{u})\\ 1 \\ u_{1} \\ u_{2} \\ \end{array}\right] } \end{aligned}$$
(10)

where \(s_{k;1}\) and \(s_{k;2}\) are the coordinates of the point \(\textbf{s}_{k}\), \(k=1, \ldots , n(\textbf{u})\). For convenience, the \(\textbf{u}\) dependence of \(\lambda _{k}(\textbf{u})\), \(k = 1, \ldots , n(\textbf{u})\), \(\mu _{1}(\textbf{u})\), \(\mu _{2}(\textbf{u})\) and \(n(\textbf{u})\) is suppressed.

The covariance (or variogram) used in Eq. (10) should be based on the residuals which are obtained by subtracting the trend from the data). However, the trend is considered unknown, and this creates a cyclical problem. Methods to address this issue are suggested in Kitanidis (1997); Goovaerts (1997). If the trend is first estimated based on the data and then removed to obtain the residuals, a more appropriate methodology is regression Kriging.

In this study, the variogram model parameters are estimated by means of maximum likelihood estimation (MLE) Fletcher (2000); Hristopulos (2020a). The spherical variogram model, given by Eq. (5), is used. The maximization of the likelihood is equivalent to the minimization of the negative logarithmic likelihood (NLL). The latter is given by

$$\begin{aligned} \text {NLL}= \frac{1}{2}(\textbf{x}-{\textbf{m}})^\top \textbf{C}_{x}^{-1} (\textbf{x}-{\textbf{m}}) + \frac{1}{2}\log ( \det \mathbf {C_x} ) + \frac{N}{2} \log (2\pi ) \end{aligned}$$
(11)

where \(\textbf{x} = (x_{1}, \ldots x_{N})^\top\) is the data vector, \(\hat{\textbf{m}}\) is the vector of the trend estimates at the sampling locations, i.e., \({m}_{i} = a_{0} + a_{1} s_{i} + a_{2}s_{j}\), and \(\det \mathbf {C_x}\) is the determinant of the covariance matrix \(\mathbf {C_x}\). The trend parameters \((a_{0}, a_{1}, a_{2})\) are estimated along with the parameters \((\sigma ^2, \xi )\) of the covariance model by minimizing the NLL.

The minimum error variance of the UK prediction, \(\sigma _{\text {UK}}^2({\textbf {u}})\), is obtained from the following equation (Kitanidis 1997, p. 127):

$$\begin{aligned} \sigma _{\text {UK}}^2({\textbf {u}}) = c_{\!_X}(0) - \sum _{k=1}^{n({\textbf {u}})} \lambda _{i}(\textbf{u}) \ c_{\!_X}(\textbf{u}-\textbf{s}_{k}) - \mu _{0}(\textbf{u}) - \mu _{1}(\textbf{u}) u_{1} - \mu _{2}(\textbf{u}) u_{2} \end{aligned}$$
(12)

Kernel functions

Kernel functions are routinely used in nonparametric estimation methods (Ghosh 2018). Herein, kernel functions are used for two purposes: (1) To define the SLI weights (see section “Stochastic local interaction model”), and (2) to estimate the cumulative distribution function (CDF) of the data. The SLI model is discussed in section “Stochastic local interaction model”. The CDF estimation is described in the following.

A kernel function \(K(\cdot ): \mathbb {R}\rightarrow \mathbb {R}\) satisfies the following requirements (Ghosh 2018):

  • K(x) is nonnegative, i.e, \(K(x) \ge 0\) and symmetric function, i.e., \(K(-x) = K(x)\) for all \(x \in \mathbb {R}\).

  • K(x) is normalized so that \(\int _{-\infty }^{+\infty }K(x)\,dx = 1.\)

  • If K(x) is a kernel function, the function \(K_{\lambda }(x) = \lambda K( \lambda x)\) is also a kernel \(\forall \lambda >0\).

The parameter \(\lambda\) adjusts the kernel’s range via the bandwidth parameter \(b = 1/\lambda\). Larger values of b imply a longer kernel range. Table 1 summarizes some kernel functions that are used in this study. At this point, a comment on notation is necessary: the symbol h is typically used to denote the bandwidth. Since in the current study kernel functions are used for CDF estimation and in SLI models, to distinguish between the two kernel bandwidths b is used for CDF estimation (b has units of [X]) and h in SLI modeling (h has units of distance).

Table 1 Common kernel functions
Full size table

Next, the nonparametric CDF estimation procedure is described. Let \(\{ x_{[i]} \}_{i = 1}^{N}\) represent the ordered sample of the water level values \(\textbf{x}\): this is defined so that for any \(i \in \{1, \ldots , N\}\) there is \(j \in \{1, \ldots , N\}\) such that \(x_{[i]} = x_{j}\) and \(x_{[1]} \le x_{[2]} \le \ldots \le x_{{[N]}}\). Then, the nonparametric, kernel-based estimate of the CDF (KCDE), \(\hat{F}_{{\text {K}}}(\cdot )\), can be obtained from the following weighted sum (Pavlides et al. 2022)

$$\begin{aligned} \hat{F}_{{\text {K}}}(x) = \sum \limits _{i=1}^{N}\dfrac{1}{N} \, \tilde{K}\left( \dfrac{x-x_{[i]}}{b} \right) \, \end{aligned}$$
(13)

where \(\tilde{K}\left( \cdot \right)\) is the CDF kernel step defined by means of the integral (Ghosh 2018; Hristopulos 2020a)

$$\begin{aligned} \tilde{K}\left( \dfrac{x-x_{[i]}}{b} \right) = \frac{1}{b} \int _{-\infty }^{x} K\left( \dfrac{x'-x_{[i]}}{b} \right) \, dx'\, \end{aligned}$$
(14)

The KCDE-based \(\hat{F}_{{\text {K}}}(x)\) has several advantages compared to the empirical staircase CDF estimate \(\hat{F}(x)\). For example, while \(\hat{F}(x)\) is discontinuous, \(\hat{F}_{{\text {K}}}(x)\) provides smoothed kernel steps by adapting the bandwidth b to the data. A continuous estimate of the CDF is especially useful for numerical simulations (Pavlides et al. 2022). For the KCDE, Eq. (13), a plug-in bandwidth b is used, based on the algorithm developed by Botev et al. (2010). This bandwidth selection method was successfully tested for non-Gaussian data (Pavlides et al. 2022).

Stochastic local interaction model

The SLI model employs a local representation that improves the computational efficiency of spatial prediction for large datasets (Hristopulos 2015, 2020a; Hristopulos et al. 2021). SLI is based on a conditional probability density function (PDF) defined by means of an energy functional that involves local interactions between neighboring sites. The energy functional represents the “probability cost” for specific spatial configurations (patterns) of field values. The local interactions are implemented by means of kernel functions with locally adaptive kernel bandwidths h.

The SLI model is expressed mathematically by means of a precision matrix \(\textbf{J}\). The term “precision matrix” refers to the inverse of the covariance matrix. In classical geostatistical analysis, the precision matrix is obtained by inverting the covariance. In contrast, in SLI the precision matrix is constructed first. This representation leads to semianalytical expression for the prediction (conditional mean) of the random field, while the conditional variance is easily expressed in terms of precision matrix elements. Assuming a Gaussian distribution, the conditional mean and variance fully determine the conditional probability distribution at the prediction point. Hence, SLI prediction avoids the computationally costly inversion of the covariance matrix required by Kriging methods.

The PDF of an SLI model is given by means of the following Boltzmann-Gibbs exponential expression (Hristopulos 2003, 2020a), where \(\textbf{v}\) is a set of model parameters

$$\begin{aligned} f_X(\textbf{x};\textbf{v})=\frac{\text {e}^{-H(\textbf{x};\textbf{v})}}{Z(\textbf{v})} \end{aligned}$$
(15)

The constant \(Z(\textbf{v})\) is a normalization factor of the PDF which is obtained by integrating \(\exp [-H(\textbf{x};\textbf{v})]\) over all possible values of the data vector \(\textbf{x}\). However, the value of \(Z(\textbf{v})\) is not needed in spatial prediction.

Precision matrix formulation

The SLI energy functional \(H(\textbf{x};\textbf{v})\), where \(\textbf{v}\) is the vector of SLI parameters (to be defined in the following), can be expressed in terms of the precision matrix as follows:

$$\begin{aligned} H(\textbf{x}; \textbf{v})=\frac{1}{2}(\textbf{x}-\textbf{m})^\top \textbf{J}(\textbf{v}') (\textbf{x}-\textbf{m}) \end{aligned}$$
(16)

In Eq. (16), \(\textbf{v}'=(c_1, \lambda , \mu , k)^\top\) is a reduced parameter vector and \(\textbf{J}(\textbf{v}')\) is a symmetric precision matrix given by the following equation

$$\begin{aligned} \textbf{J}(\textbf{v}')=\frac{1}{\lambda } \left[ \frac{\textbf{I}}{N} +c_1 \textbf{J}_1(\textbf{h}) \right] \end{aligned}$$
(17)

where \(\lambda , c_{1} >0\) are SLI parameters, \(\textbf{I}\) is the identity matrix, \(\textbf{h}\) is the vector of kernel bandwidths, and \(\textbf{J}_1\) is the interaction network matrix (gradient precision submatrix); the latter is determined by the sampling pattern, the kernel function, and the kernel bandwidth as explained in Hristopulos (2015); Hristopulos et al. (2021).

The SLI vector \(\textbf{v}=(m_X, c_1, \lambda , \mu , k)^\top\) contains the following parameters: \(m_{X}\) is the mean value (assumed constant), \(c_1\) controls the amplitude of the term which “mimics” the sum of square gradients, and \(\lambda\) controls the overall amplitude of the fluctuations. Finally, \(\mu >1\) and \(k \in \{2, 3, 4, \ldots \}\) are parameters that control the bandwidth vector \(\textbf{h}=(h_{1}, \ldots , h_{N})^\top\). The integer parameter k determines the order of the near-neighbor used to define the local bandwidth, while \(\mu\) is a global multiplication factor. The bandwidth \(h_q\) for a data point \(\textbf{s}_q\) depends on the distance of \(\textbf{s}_q\) from its k-nearest neighbor \(\textbf{s}_{k(q)}\) as follows

$$\begin{aligned} h_q = \mu \, \Vert \textbf{s}_q-\textbf{s}_{k(q)}\Vert \,,~q = 1,\ldots ,N \end{aligned}$$
(18)

In SLI estimation, k is preselected, while \(m_X\), \(\lambda\), \(c_{1}\), \(\mu\) are inferred from the data by means of MLE. If a superposition of basis functions is used to model the trend instead of a constant \(m_X\), the coefficients of the superposition can also be estimated by means of MLE. Such a trend analysis is not used in the current application of SLI.

SLI prediction

In order to predict the water level at an unmeasured point \(\textbf{s}_{\text {p}}\) (in this section \(\textbf{s}_{\text {p}}\) is used instead of \(\textbf{u}\) for notational convenience), it is inserted in the energy functional H so that it interacts with the neighboring sampling points via precision matrix elements \(J_{p,n}\), for \(n = 1, \ldots , N\). The “updated” energy function \(H(\textbf{x},x_{p};\textbf{v})\) now defines, in terms of the Boltzmann-Gibbs PDF, the marginal conditional distribution at \(\textbf{s}_{\text {p}}\). Due to the local nature of the interactions, most of the \(J_{p,n}\) values are zero. The mode of the conditional distribution at \(\textbf{s}_{\text {p}}\) is then given by the following predictive equation (Hristopulos 2015; Hristopulos et al. 2021)

$$\begin{aligned} \hat{x}_{\text {SLI}}(\textbf{s}_{\text {p}})= m_{X} - \frac{\sum _{q = 1}^N J_{q,p}(\textbf{v})(x_q-m_{X}) }{J_{p,p}} \end{aligned}$$
(19)

where \(\hat{x}_{\text {SLI}}(\textbf{s}_{\text {p}})\) is the prediction, \(x_q-m_{X}\) is the fluctuation at location \(\textbf{s}_q\) and \(J_{q,p}\), \(J_{p,p}\) represent elements of the precision matrix. Note that the SLI prediction of Eq. (19) is independent of the scale coefficient \(\lambda\).

The precision matrix uses kernel-based weights \(w_{p,q}\) to embody interactions between nearby points. More specifically, there are two weights for each pair of points \(\textbf{s}_{n}\) and \(\textbf{s}_{m}\) as follows

$$\begin{aligned} w_{n,m}(\textbf{h}) = \frac{K\left( \textbf{d}_{n,m}/h_{n}\right) }{\sum _{l = 1}^{N}\sum _{q = 1}^{N} K\left( \textbf{d}_{l,q}/h_{l}\right) }, \quad \text {for } \, n,m = 1\, \ldots , N \end{aligned}$$
(20)
$$\begin{aligned} w_{m,n}(\textbf{h}) = \frac{K\left( \textbf{d}_{n,m}/h_{m}\right) }{\sum _{l=1}^{N}\sum _{q=1}^{N} K\left( \textbf{d}_{l,q}/h_{l}\right) }, \quad \text {for } \, n,m = 1\, \ldots , N \end{aligned}$$
(21)

where \(\textbf{d}_{n,m}=\Vert \textbf{s}_{n} - \textbf{s}_{m} \Vert\) is the Euclidean distance between the points. The bandwidths \(h_{n}, h_{m}\) are determined from the sampling density in the neighborhoods of \(\textbf{s}_{n}\) and \(\textbf{s}_{m}\) respectively. Since the sampling patterns in the neighborhoods of \(\textbf{s}_n\) and \(\textbf{s}_m\) can be quite different, in general it holds that \(w_{m,n}(\textbf{h}) \ne w_{n,m}(\textbf{h})\).

The entries of the gradient precision submatrix are determined from the weights as follows (Hristopulos 2015; Hristopulos et al. 2021)

$$\begin{aligned}{}[\textbf{J}_{1}(\textbf{h})]_{n,m} = - w_{n,m}(\textbf{h}) - w_{m,n}(\textbf{h}) + \delta _{n,m} \, \sum _{l=1}^{N} \left[ w_{n,l}(\textbf{h}) + w_{l,n}(\textbf{h})\right] \end{aligned}$$
(22)

where \(\delta _{n,m} = 1\) if \(n = m\) and \(\delta _{n,m} = 0\) if \(n \ne m\) is the Kronecker delta.

The SLI conditional variance at \(\textbf{s}_{\text {p}}\) is given approximately by Hristopulos et al. (2021)

$$\begin{aligned} \sigma ^{2}_{p} \approx \frac{\lambda }{c_{1}}\, \left[ \, \sum _{q=1}^{N} \left( w_{q,p} + w_{p,q} \right) \right] ^{-1} \end{aligned}$$
(23)

As evidenced in Eq. (23), higher values of \(c_{1}\) tend to reduce the variance. This happens due to increasing energy cost for large increments in the energy functional \(H(\textbf{x};\textbf{v})\). In addition, prediction points with more neighbors (points \(\textbf{s}_{q}\) such that \(w_{q,p}>0\) or \(w_{p,q}>0\)) have lower conditional variance than prediction points in sparsely sampled regions. Similar to the Kriging variance, the SLI conditional variance does not explicitly depend on the data values. The dependence is indirect, to the extent that the data influence the estimation of the model parameters.

Gaussian anamorphosis

In many cases, spatial data follow a skewed PDF that deviates significantly from the normal distribution. In the present study, the water level distribution is clearly asymmetric (see section “Data description and preprocessing”). Nonlinear, monotonic transformations such as the logarithm, Box-Cox, normal-score, modified Box-Cox versions, and deformed logarithmic transforms are used to restore normality (Box and Cox 1964; Varouchakis et al. 2012; Goovaerts 1997; Hristopulos 2020a; Hristopulos and Baxevani 2022). The application of normalizing transforms is often referred to as “Gaussian anamorphosis”. The spatial analysis is then carried out using the transformed data. Finally, predictions in the original domain are derived by applying the inverse transformation.

In this study, Gaussian anamorphosis is performed using KCDE (see section “Kernel functions”) coupled with the normal scores transform. KCDE derives \(\hat{F}_{{\text {K}}}(x)\) from the water level data \(\{x_{1}, \ldots , x_{N} \}\), using kernel smoothing to avoid the discontinuities of the staircase CDF function. Normalized estimates, \(\{ x^{*}_{1}, \ldots , x^{*}_{N}\}\), are then calculated based on the normal scores transform. These conform with the standard normal distribution \({\mathcal {N}}(0,1)\). Spatial interpolation of the normal scores leads to predictions \(\{ x^{*}_{1}, \ldots , x^{*}_{P}\}\). Finally, an inverse transform is used to map the normalized predictions \(\{ \hat{x}^{*}_{1}, \ldots , \hat{x}^{*}_{P}\}\) back to water level values \(\{ \hat{x}_{1}, \ldots , \hat{x}_{P}\}\).

The inverse transform in Gaussian anamorphosis is implemented via a lookup table that maps the predictions of the normalized values back to water level values. The inverse transform is denoted by \(x=\hat{F}_{{\text {K}}}^{-1}\left( \Phi (x^{*})\right)\), where \(\Phi (\cdot )\) is the CDF of the standard normal distribution. Hence, the lookup table implements the mapping \(x^{*} \rightarrow x\).

To create the lookup table, the expression Eq. (13) for \(\hat{F}_{{\text {K}}}(x)\) is used to calculate the CDF for a large set of discretization points \(\{z_{l}\}_{l = 1}^L\) (herein, \(L = 10,000\)). The table thus generated comprises L rows and three columns that correspond to the discretization points \(\{z_{l}\}_{l = 1}^L\), the respective normal scores, and the corresponding CDF values \(\{ \hat{F}_{{\text {K}}}(z_l) \}\). The discretization points are linearly distributed between the minimum and maximum possible values, i.e., \(z_{\min } = x_{\min }-h\) and \(z_{\max } = x_{\max }+h\) where \(x_{\min }= \min \{x_{1}, \ldots , x_{N} \}\) and \(x_{\max }= \max \{x_{1}, \ldots , x_{N} \}\) as shown in Pavlides et al. (2022). The inverse transform of any prediction \(\hat{x}^*\) is calculated as follows: first, the respective \(\Phi (\hat{x}^*)\) is determined; next, the closest probability level to \(\Phi (\hat{x}^*)\) in the lookup table is determined; if this corresponds to \(\hat{F}_{{\text {K}}}(z_{o})\), where \(z_{o} \in \{z_{1}, \ldots , z_{L} \}\), the inverse transform of \(\hat{x}^*\) is given by \(\hat{x} = z_{o}\).

Assessment of predictions

Validation measures are used to assess the quality of the spatial prediction achieved by the models. Furthermore, stochastic methods provide estimates of the prediction uncertainty for each location.

The predictive accuracy of both UK and SLI was assessed using LOOCV (Chilès and Delfiner 2012). In LOOCV the sampling sites \(\textbf{s}_n\), \(n = 1, \ldots , N = 72\) and the corresponding measurements are cyclically removed from the data one at a time, and the water level, \(\hat{x}_{n}\) at the point removed is estimated from the remaining 71 drillholes. The estimation error \(\epsilon _n = x_{n} - \hat{x}(\textbf{s}_n)\), for \(n = 1,\ldots , 72\) is then calculated.

Ninety percent prediction intervals (i.e., based on a 90% confidence level) are used to characterize the uncertainty of the predictions. These intervals are calculated in two steps. First, prediction intervals for each point are generated for the transformed (normalized) data based on the prediction variance; the latter is given by Eq. (12) for UK and Eq. (23) for SLI. The 90% prediction interval at location \(\textbf{u}\) for either method is given by

$$\begin{aligned} \left[ \hat{x}^{*}(\textbf{u})- 1.645 \sigma (\textbf{u}), \, \hat{x}^{*}(\textbf{u}) + 1.645 \sigma (\textbf{u})\right] \end{aligned}$$
(24)

where \(\hat{x}^{*}_{0.05}(\textbf{u})=\hat{x}^{*}(\textbf{u})-1.645 \sigma (\textbf{u})\) is the \(5\%\) quantile, and \(\hat{x}^{*}_{0.95}(\textbf{u})=\hat{x}^{*}(\textbf{u}) +1.645 \sigma (\textbf{u})\) is the \(95\%\) quantile of the Gaussian predictive distribution at \(\textbf{u}\). The water level prediction intervals at \(\textbf{u}\) are obtained by applying the inverse of the normalizing transformation to the \(5\%\) and \(95\%\) quantiles, \(\hat{x}^{*}_{0.05}(\textbf{u})\) and \(\hat{x}^{*}_{0.95}(\textbf{u})\) respectively. The inversion employs the principle of quantile invariance under monotonic transformations (Hristopulos 2020a) and is implemented by means of the lookup table defined in section “Gaussian anamorphosis”. Thus, the respective water level quantiles \(\hat{x}_{0.05}(\textbf{u})\) and \(\hat{x}_{0.95}(\textbf{u})\) are obtained. To better visualize the uncertainty of the prediction, the 90% prediction interval range \(R=\hat{x}_{0.95}(\textbf{u})-\hat{x}_{0.05}(\textbf{u})\) is displayed.

Data description and preprocessing

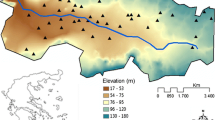
The study area comprises three mines operating in the same region in northern Greece. The area is geologically composed of various metamorphic and igneous rocks; biotite gneisses with intercalations of marble horizons are located in the area; granodiorites and acid to intermediate subvolcanic rocks intrusions into the gneisses cover small areas. The study area is characterized hydrogeologically as semipermeable, and its vertical profile comprises three hydrostratigraphic units. Secondary porosity (fractures) is responsible for hydrological connectivity. In certain areas, the rocks exhibit strong fragmentation which increases with depth thus creating pathways for slow groundwater flow (ENVECO 2010). The data used in this study comprise the 10-year average (2011–2020) of biannual water level measurements (below surface, BSL), from 72 drillholes. All the values are negative since water level is measured in terms of meters below surface. The measurement boreholes are located around the three mines operating in the area of interest (see Fig. 1b):

  • Mine A (28 drillholes)

  • Mine B (28 drillholes)

  • Mine C (16 drillholes)

Preliminary data analysis

This section presents a statistical summary of the temporally averaged water levels from the entire area. The frequency histogram and the data locations are shown in Fig. 1. The median distance of a borehole to its second-nearest neighbor (\(k = 2\)) is 488.15 m. Table 2 shows the summary statistics of the data.

Fig. 1
figure 1

a Frequency histogram of the 72 water level measurements (m below surface). b drillhole locations for the three mines: mine A (blue o), mine B (black x), mine C (red +). Coordinates are in meters

Full size image
Table 2 Summary water level data statistics. SD standard deviation
Full size table

Based on the skewness value in Table 2 and the shape of the histogram, the data deviate strongly from the normal (Gaussian) distribution. As discussed in section “Kriging”, the Kriging variance does not adequately represent the prediction uncertainty for non-Gaussian data. To address this issue, Gaussian anamorphosis is employed in order to normalize the data (see section “Gaussian anamorphosis”).

Gaussian anamorphosis of water level data

In order to address the non-Gaussian distribution of the data, the data-driven Gaussian anamorphosis method is employed. The method is described in section “Gaussian anamorphosis”. First, KCDE is applied with the triweight kernel (see Table 1) to provide a nonparametric CDF, \(\hat{F}_{{\text {K}}}(x)\), as discussed in Pavlides et al. (2022). The plug-in kernel bandwidth was calculated at \(h = 9.33\)m (h in KCDE refers to water level, not geographical distance).

Fig. 2
figure 2

Empirical staircase CDF, \(\hat{F}_{s}(x)\) (blue online) and KCDE-derived continuous CDF, \(\hat{F}_{{\text {K}}}(x)\) based on Eq. (13) (red online). The triweight kernel with bandwidth \(h = 9.33\) is used in KCDE

Full size image

Figure 2 shows the KCDE-derived \(\hat{F}_{{\text {K}}}(x)\) in comparison to the staircase \(\hat{F}_{s}(x)\). In contrast with the latter, \(\hat{F}_{{\text {K}}}(x)\) is a continuous curve which was constructed using the lookup table. Figure 3 shows the histogram and the normal probability plot for the transformed data \(\{ x^{*}_{1}, \ldots , x^{*}_{N}\}\) which are obtained after normalization. As is evident in these plots, the transformed data \(\{ x^{*}_{1}, \ldots , x^{*}_{N}\}\) conform to the standard normal distribution \({\mathcal {N}}(0,1)\). Spatial prediction is carried out using the normalized data. The predictions \(\{ \hat{x}^{*}_{1}, \ldots , \hat{x}^{*}_{P}\}\) obtained at the nodes of the map grid \(\mathbb {G}\) are transformed back to water level values \(\{ \hat{x}_{1}, \ldots , \hat{x}_{P}\}\) with the help of the lookup table as explained in section “Gaussian anamorphosis”.

Fig. 3
figure 3

a Histogram of the normalized average (over 10 years of biannual measurements) water level at 72 sites. b Normal probability plot for the normalized data

Full size image

Results: universal Kriging

The parameters of the spherical covariance model for the normalized data \(\{x^{*}_{1}, \ldots , x_{N}^{*} \}\) are obtained by maximizing the likelihood Eq. (11). The spherical covariance is obtained from the respective variogram model of Eq. (5) by means of Eq. (3). The MLE initialization values for the variogram parameters are \(\sigma ^{2}_{0} = 1.15\)m, \(\xi _{0} = 2800\)m, \(c_{o;0} = 0.11)\), where \(c_{o;0}\) is the nugget effect. The initialization parameters for the variogram have been estimated by fitting the spherical model to the experimental variogram. The initial values for the trend parameters (obtained by means of linear regression) are \(a_{0;0}=-0.93\), \(a_{1;0}=7.3\,10^{-5}\), and \(a_{2;0}=5.9\,10^{-5}\). The optimal MLE parameters for the variogram model (spherical and nugget) are \(\hat{\sigma }^2 = 0.89\), \(\hat{\xi }\) = 1,653 m, and \(c_{o} = 0.106\). The optimal variogram model (based on the MLE parameters) and the experimental variogram are compared in Fig. 4. The experimental variogram is calculated for the residuals which are obtained by subtracting from the data the MLE linear trend with coefficients \(a_{0;0} = -0.63\), \(a_{1;0}=3.98\,10^{-5}\), and \(a_{2;0}=5.00\,10^{-5}\).

Fig. 4
figure 4

Variogram of the residuals (determined by removing the MLE-based linear trend). The spherical model is shown with a continuous curve (red line), and the experimental variogram is shown by circle markers (blue circle)

Full size image

UK is then applied (using the estimated parameters) to interpolate the transformed data values \(\{ x^{*}_{1}, \ldots , x^{*}_{N}\}\) using Eq. (8). Estimates \(\{ \hat{x}^{*}_{1}, \ldots , \hat{x}^{*}_{P}\}\) are generated on a grid with \(112 \times 89\) cells (corresponding to a cell size of \(150 \times 150\) m). The range of the Kriging search neighborhood was selected at 2,400 m in order to provide adequate coverage of the mining areas and the minimum number of neighbors was set at \(K = 2\). Estimates were generated only for points \(\textbf{u}\) with search neighborhoods containing at least three points in the sampling set.

The optimal prediction \(\hat{x}_{\text {SLI}}(\textbf{u})\), as well as the estimates of the quantiles \(\hat{x}_{0.05}(\textbf{u})\) and \(\hat{x}_{0.95}(\textbf{u})\) are presented in Figs 5 and 6. The uncertainty of the predictions is visualized by means of the 90% prediction interval range \(R_{\text {UK};90}=\hat{x}_{0.95}(\textbf{u})-\hat{x}_{0.05}(\textbf{u})\) shown in Fig 5b. High values of \(R_{\text {UK};90}(\textbf{u})\) at location \(\textbf{u}\) denote higher uncertainty of the prediction. Note that the predictive distribution of \({X}({\textbf{u}})\) is not necessarily normal due to the application of the inverse transform. Hence, \(\hat{x}_{0.05}(\textbf{u})\) and \(\hat{x}_{0.95}(\textbf{u})\) are not symmetrically placed around \(\hat{x}_{\text {UK}}(\textbf{u})\) as is evident in Fig. 6. For example, the prediction at \(\textbf{u}=(10200,5400)\) is \(\widehat x(\textbf{u})=-18\) m and \(R_{\text {UK};90}(\textbf{u}) = 76\) m while \({\widehat x}_{0.05}(\textbf{u})=-78\) m and \({\widehat x}_{0.95}(\textbf{u})=-2\) m. Thus, there is \(90\%\) probability that \(X(\textbf{u})\in\lbrack-78\,\text{m},-2\,\text{m}\rbrack\), but the UK prediction is not given by the interval’s mean (i.e., −36 m) but rather by \(\widehat x(\textbf{u})=-18\,\)m which corresponds to the median of the predictive distribution.

Fig. 5
figure 5

a Map of estimated water level (m below surface) for the three mines in the study area. b Range of the 90% water level prediction intervals; high values denote higher uncertainty. Coordinates are in meters

Full size image
Fig. 6
figure 6

UK-based maps of the lower and upper limits of 90% prediction intervals: a lower quantile \(\hat{x}_{0.05}(\textbf{u})\); b upper quantile \(\hat{x}_{0.95}(\textbf{u})\). Coordinates are in meters

Full size image

UK cross-validation

The UK predictive accuracy was assessed using LOOCV (section “Assessment of predictions”). In LOOCV sampling sites \(\textbf{s}_n\), \(n = 1, \ldots , N = 72\) and the corresponding measurements are cyclically removed from the data, and the value of the water level, \(\hat{x}_{n}\) at the point removed is estimated from the remaining 71 drillholes. The estimation error \(\epsilon _n = x_{n} - \hat{x}(\textbf{s}_n)\), for \(n = 1,\ldots , 72\) is calculated.

The histogram of UK estimation errors for all mines in the study area is shown in Fig. 7. Standard validation metrics are shown in Table 3. The values of the data range from \(x_{\max } = -1\)m to \(x_{\min } = -208\)m. Most of the validation errors are in \([-50, \, 50]\,\)m, with the exception of a few locations that return errors greater than 50 m (in magnitude). The presence of few high validation errors is not surprising considering the small sample size and the significant spatial dispersion of the sampling points. These factors lead to large prediction intervals (as shown in the uncertainty map of Fig 5b). Taking into account the preceding factors, the UK interpolation performance is considered adequate.

Fig. 7
figure 7

Histogram of the UK validation errors for the three mines in the study area

Full size image
Table 3 Validation measures (LOOCV) for assessment of UK interpolation performance
Full size table

Results: SLI

The water level in the study area is estimated using SLI (see section “Stochastic local interaction model”) with the quadratic kernel (see Table 1). The transformed data values \(\{ x^{*}_{1}, \ldots , x^{*}_{N}\}\) are used for SLI interpolation and the predictions are subsequently back-transformed back to meters BSL. The SLI model parameters \(c_1, \lambda ,\mu\) and \(m_X\) are estimated by MLE. The initialization values for the MLE are: \({\textbf{v}'}_0 = (c_1 = 2.5, \lambda = 0.1, \mu = 1.25, m_X = -0.015)^\top\). The SLI model parameters estimated by MLE are \(\textbf{v}'= (c_1 = 0.926, \lambda = 0.032, \mu = 4.18, m_X = -0.015)^\top\).

Using the Eqs. (19) and (23), the optimal SLI predictions \(\hat{x}^{*}_{\text {SLI}}(\textbf{u})\) and respective variances \(\sigma _{\text {SLI}}^2(\textbf{u})\) are estimated. The same map grid \(\mathbb {G}\) is used for UK (see section “Results: universal Kriging”). In contrast with Kriging, the search neighborhood in SLI is automatically adjusted by the algorithm through the parameter \(\mu\) and the bandwidth vector \(\textbf{h}\) instead of being set by the user. For comparison purposes, the SLI predictions are used only at the map-grid nodes where UK predictions are available. The normality of the transformed data \(\{ x^{*}_{1}, \ldots , x^{*}_{N}\}\) allows using the standard deviation of the SLI predictions to determine prediction intervals using the method presented in section “Assessment of predictions”.

The results are presented in Figs. 8 and 9.

Fig. 8
figure 8

a SLI prediction map of water level (m below surface level) for the three mines. b Range of water level 90% prediction intervals. Coordinates are in meters

Full size image
Fig. 9
figure 9

SLI-based maps of the lower and upper limits of 90% prediction intervals: a lower quantile \(\hat{x}_{0.05}(\textbf{u})\); b upper quantile \(\hat{x}_{0.95}(\textbf{u})\). Coordinates are in meters

Full size image

The SLI algorithm returns large search neighborhoods as implied by \(\mu = 4.18\) (see section “Stochastic local interaction model”): the bandwidth Eq. (18) dictates that the local bandwidth \(h_u\) at the point \(\textbf{u}\) is the distance to the k-nearest neighbor (\(k = 2\)) multiplied by \(\mu\). As shown in Fig. 1, k-nearest neighbor distances vary from small (43 m) to large (2,977 m).

As is evident in Figs. 5b and 8b, the SLI prediction interval range has a minimum value, \(\min _{\textbf{u}\in \mathbb {G}}\{R_{\text {SLI};90}(\textbf{u})\}\), of 31.9 m. For UK, the prediction interval has a lower minimum, i.e., \(\min _{\textbf{u}\in \mathbb {G}}\{R_{\text {UK};90}(\textbf{u})\} = 0.7\) m. The reason is that UK explicitly minimizes the prediction variance, and thus it generates a smaller range for prediction intervals.

SLI application to mine B

Stochastic local interaction can handle large datasets due to the sparse structure of the model (Hristopulos 2015; Hristopulos et al. 2021). However, the locally adaptive nature of the SLI predictor also allows model estimation and prediction even for small samples. In this section SLI is applied to the dataset for mine B. This mine involves 28 sampling points, a sample size which is considered small for most stochastic methods. The MLE initialization values for mine B are the same as for the entire area: \(\textbf{v}_0 = (c_1 = 2.5, \lambda = 0.1, \mu = 1.25, m_X = -0.56)^\top\). The optimal SLI parameters obtained by MLE are: \(\textbf{v} = (c_1 = 2.881, \lambda = 0.046, \mu = 0.938, m_X = 0.163)^\top\).

The maps for \(\hat{x}_{\text {SLI}}(\textbf{u})\), \(\hat{x}_{0.05}(\textbf{u})\), \(\hat{x}_{0.05}(\textbf{u})\) and the range \(R_{\text {SLI};90}\) are shown in Fig. 10. The prediction of the water level values using only data from mine B is similar to the SLI implementation using the data from the entire area. The water level in the northwestern area of the mine is lower than in the southeast, although SLI for mine B gives slightly higher predictions for the low water level area in the northeast than SLI for the entire area. The prediction uncertainty using only data from mine B follows a similar spatial distribution as the interval shown in Fig. 8b. However, the uncertainty is lower in the northwestern area and the eastern part of the mine than the SLI implementation using all the data, albeit it is still relatively high. The differences for the mine B results between Figs. 8–9 and Fig. 10 are expected since the maps of Fig. 10 are produced with fewer data that determine a different SLI model.

Fig. 10
figure 10

SLI maps for mine B: a predicted water levels (m below surface); b range of the 90% water level prediction intervals; c lower quantile \(\hat{x}_{0.05}(\textbf{u})\); (d) higher quantile \(\hat{x}_{0.95}(\textbf{u})\). Coordinates are in meters

Full size image

SLI cross-validation

Leave-one-out cross-validation is used to assess the SLI predictive performance, first for the SLI model based on the entire area and then for the SLI model obtained for mine B. The validation metrics for the SLI estimation are shown in Table 4. The histograms of the errors are shown in Fig. 11. The data values for the entire area range between \(x_{\max } = -1\) m to \(x_{\min } = -208\) m. However, the lowest LOOCV prediction is \(\min _{i=\{1, 2, \ldots , N\}}{\hat{x}(\textbf{s}_i)} = -121.9\) m, i.e., the minimum is significantly overestimated. One reason for this behavior is the difficulty of estimating the minimum value, once it is removed, in a sparsely sampled area; this effect is similar to the Kriging smoothing effect (Yamamoto 2005; Pavlides et al. 2015). Another reason is that a trend function in the SLI model was not used. For mine B, the values of the data range from \(x_{\max } = -1\) m to \(x_{\min } = -142\) m. SLI again overestimated the lowest value yielding a minimum of \(-39.2\) m.

For the SLI using data from the entire area, there are a few large errors (\(\epsilon > 50\) m). For SLI predictions using only mine B data, there are three locations that return high validation errors. In both cases, the SLI overestimates the water lever in both mine B and mine C. However, considering the range of data values, the clustering of the data locations and the small number of data points (especially for mine B), and the LOOCV measures over the study areas (Table 4), the SLI performance is considered adequate overall.

Fig. 11
figure 11

Histograms of SLI leave-one-out cross-validation errors: a entire area, b mine B

Full size image
Table 4 Validation measures for the SLI estimations
Full size table

Discussion

This section provides a comparative discussion of the UK and SLI cross validation results. For ease of reference, the validation measures are gathered in Table 5. In the case of UK, the validation measures for Mine B are derived using the variogram model estimated from the entire area, as 28 data locations are considered too few to reliably estimate the variogram model. The SLI parameters were inferred separately for mine B, and thus a different set of SLI parameters was used (see section “SLI application to mine B”) than for the entire area.

UK validation measures are slightly better for the entire area. This result is attributed to the fact that UK employs a linear trend Eq. (2) to formulate predictions, while SLI is employed with a constant mean (see Eq. 19). This choice creates a disadvantage for SLI, since the spatial distribution of the data over the entire area does not seem to comply with the stationarity assumption. This shortcoming will be fixed in future implementations of SLI.

Both methods perform adequately given the small sample size, although they significantly overestimate the (few) low values as evidenced in the MaxAE values in Table 5 and the error histograms of Figs. 7 and 11. In addition, both methods give high uncertainties in areas that are distant from the sampling sites. However, these shortcomings point primarily to sampling, not methodological deficiencies.

Table 5 Leave-one-out cross validation measures for SLI and UK
Full size table

The differences between SLI and UK are illustrated in Fig. 12. As expected from the results in the previous sections, the prediction interval (PI) range of SLI, \(R_{\text {SLI}}\), is generally higher than the PI range for UK, \(R_{\text {UK}}\). Kriging methods minimize the prediction variance \(\sigma ^2_{\text {UK}}\), which affects the \(R_\text {UK}\). SLI prediction is instead based on maximizing the conditional PDF by means of the energy functional \(H(\textbf{x};\textbf{v})\) which can lead to higher prediction variances at many prediction points.

SLI gives significantly higher estimates than UK at certain points in mine B. The UK predictions drop significantly in the north of the study domain, i.e., for \(\textbf{s}_2>8000\) m (see Fig. 5), while SLI predictions remain high (see Fig. 10). The linear trend in the UK model improves the validation measures compared to a preliminary analysis based on ordinary Kriging. On the other hand, the sudden drop of the water level in the northern section of mine B, forces UK to model a significant linear slope in the trend function, leading to decreasing water levels further North. Such predicted drops cannot be verified due to the lack of data. Similar issues are present in a small part of the southern segment of mine C and the western part of mine B. It is impossible to confirm whether SLI or UK predictions are better in these areas without additional data. Figures 6 and 9 show that both UK and SLI predictions are within each other method’s prediction intervals.

Fig. 12
figure 12

Differences between SLI and UK. a Prediction: \(\hat{x}_{\text {SLI}}(\textbf{u}) - \hat{x}_{\text {UK}}(\textbf{u})\) b range: \(R_{\text {SLI}}(\textbf{u})-R_{\text {UK}}(\textbf{u})\). Coordinates are in meters

Full size image

Overall, in most cases both SLI and UK prediction intervals (based on LOOCV) include the data values at the respective point (six values outside of PI for SLI and four values for UK). For SLI, 33 of the predicted values \(\hat{x}_{SLI}\) are within the interquantile (IQ) range of \(\hat{x}_{0.25}\) to \(\hat{x}_{0.75}\). UK performs slightly worse with 30 of the predicted values \(\hat{x}_{\!_{UK}}\) inside the IQ range.

In Fig. 13, the LOOCV absolute error for each of the data sites is plotted against the range of the 90% prediction interval \(R_{\text {SLI}}(\textbf{s})\) for SLI or \(R_{\text {UK}}(\textbf{s})\) for UK. As evidenced in the figure, UK gives both the highest and lowest PI values. Furthermore, locations with high absolute error values (\(|x(\textbf{s})- \hat{x}(\textbf{s})| > 50\) m) have high PI range (\(R(\textbf{s}) > 100\) m). Thus, for both methods high absolute error values are concentrated in areas with high uncertainty.

In addition, both methods estimate prediction intervals that are wide enough to accommodate the prediction of the other method at most locations. In both cases, the LOOCV results are reasonable given the small size of the dataset. The SLI method allows for constructing a spatial model that can give reasonable predictions even with a dataset as small as that of mine B (28 points).

Fig. 13
figure 13

Validation absolute errors compared to the range of the 90% water level prediction interval (PI) for SLI (blue circle) and UK (red cross)

Full size image

Conclusions

In this research, the estimation of groundwater levels in sparsely sampled areas with mining activity is investigated. This case study involves the aggregate water level below surface for three mines in northern Greece. The recently proposed kernel-based KCDE method (Pavlides et al. 2022) is used to estimate the non-Gaussian distribution of water level and to conduct Gaussian anamorphosis. The predictive performance of two stochastic interpolation approaches is compared, UK and the more recently developed SLI method. SLI is a spatial interpolation method designed to provide computational efficiency for large spatial and spatiotemporal datasets (Hristopulos 2015; Hristopulos and Agou 2020; Hristopulos et al. 2021). While the primary objective of SLI is to efficiently extract correlations from large data, as shown herein, it can also be applied to small datasets that do not allow reliable estimation of the variogram function which is needed for the application of Kriging methods.

The cross-validation measures show evidence of reasonable interpolation performance. However, in certain areas the 90% prediction intervals are rather wide, indicating high prediction uncertainty. UK takes into account a linear trend function and minimizes the prediction variance, thus allowing for tighter prediction ranges than SLI. On the other hand, SLI provides an automatically adaptable search radius, computational efficiency, and the ability to estimate the spatial model even with the very sparse dataset of mine B. As discussed in Section “Discussion”, the introduction of a linear trend model based on a small dataset can be misleading. While UK cross-validation measures are slightly better for the entire area, application of SLI mine B leads to slightly better performance than UK. Furthermore, the trend in areas outside the data clusters leads to rapid decrease of the UK predicted water levels (see Fig. 5) that can not be confirmed based on the available data.

The SLI predictor can be modified to include trend functions as in UK—for example, promising results were obtained by incorporating a polynomial trend in the spatiotemporal SLI predictor (Hristopulos and Agou 2020). Management of water resources is important in areas of mining activity. Future studies could focus on spatiotemporal prediction methodologies in order to allow monitoring seasonal changes of the water level due to mining activities. Furthermore, the KCDE-based estimate of the CDF can be used in conjunction with conditional simulation methods, such as Kriging polarization (Chilès and Delfiner 2012; Hristopulos 2020a; Olea 2012), in order to better capture the spatial variability of water level.