Introduction

Nowadays the global concern is to maintain safe reserves of clean groundwater. The European Union (EU) Water Framework Directive 2000/60/EC aims to “achieve ‘good status’ for Europe’s rivers, lakes and groundwater by 2015” (EC 2000). One groundwater pollutant of major concern is nitrate as a consequence of overuse of fertilizer and intensive animal husbandry in agricultural regions. In fact, the status report on nitrate reports that 26.7% of the monitoring wells in agricultural regions in Germany exceed the threshold of 50 mg/L (BMUV 2020). Even though this percentage has been declining recently, effective measures still need to be taken in order to better monitor and improve the actual situation.

Accordingly, the State Geological Surveys of Germany are required to monitor groundwater quality in a suitable piezometer network to facilitate good groundwater chemical status. In the course of this task, it was required that appropriate regionalization techniques be identified in order to unify the assessment procedure within Germany while disregarding state boundaries.

Among others, deterministic interpolation methods, e.g. inverse distance weighted- (IDW) or spline interpolations were suggested. However, these methods do not quantify the reliability of the spatial estimation result. Rather they suggest an accurate spatial regionalization where local concentrations can precisely be derived from contour plots, no matter how well the data are supported, i.e. whether there is an adequate number of sample locations (piezometers). It is the major advantage of geostatistical spatial estimators such as Kriging, that they incorporate the specific spatial variability structure of regionalized variables. Applied to nitrate pollution in the groundwater of Lower Saxony in Germany, Wriedt et al. (2019) discuss the capabilities of Simple Kriging (SK) and Ordinary Kriging (OK) in order to identify regions of high contamination load. Unfortunately, they did not make use of the Kriging standard deviation \({\sigma }_{\mathrm{K}}\), which is also calculated contemporaneously in association with the actual Kriging estimate. The Kriging standard deviation represents the uncertainty that results from the data support, the sampling pattern and the specific spatial variability of the regionalized variable. Usually, it is displayed in addition to or blended with the interpolated concentration map. Webster and Oliver (2014) criticize an imprudent use of Kriging techniques in geographic information systems (GISs) and provide helpful guidance in order to consider, among others, sample support, variogram and Kriging options, respectively, especially for environmental applications.

Advanced geostatistical techniques like SIMIK+ (Bárdossy et al. 2003) not only provide a measure of uncertainty as the Kriging error (i.e. Kriging standard deviation), they can incorporate supplementary information as well, e.g. type of geology and land use. Dokou et al. (2015) present a summary of advanced Kriging techniques, which especially contribute to the spatial interpolation of nonparametrically distributed groundwater quality data, including nitrate and trace metals; specifically, the Indicator approach is well suited for questions of risk assessment. Similarly, the spatial interpolation of groundwater quality parameters based on copula estimate local-distribution functions of the target parameters (Bárdossy and Li 2008) allows for the quantification of uncertainty. This approach is further enhanced by including secondary information from correlated data (Gnann et al. 2018). Knoll et al. (2020) suggest a machine-learning approach (Random Forest) which includes environmental factors influencing nitrate in groundwater, e.g. redox status of the aquifers.

Still, it is questionable whether an interpolated contour (or pixel) map adequately reflects the spatial distribution of groundwater pollutants. The adequacy strongly depends on the objectives that are to be achieved. Interpolated maps usually suggest a more or less smooth spatial structure, which is often not realistic (Bronowicka-Mielniczuk et al. 2019), but can provide a regional overview of the contaminant distribution. Small-scale variability is better reproduced by stochastic simulation techniques, e.g. sequential Gaussian or sequential indicator simulation (Gómez-Hernández and Srivastava 2021) or multiple point simulations (Strebelle 2002; Huysmans and Dassargues 2010). These regionalization techniques are well established as parametrization tools in groundwater flow and transport models (Renard 2007). The goal of a comparative groundwater quality assessment for delineable groundwater bodies is to determine the likelihood of thresholds being exceeded and to what extent, rather than to accurately determine the pollutant concentration at a particular point location. The latter may better be achieved by the aforementioned, however elaborate, regionalization techniques.

Nitrate in groundwater, which mostly results from human activities (BMUV 2020) and is enhanced by soil features, e.g. preferential flow paths or redox status, often exhibits an erratic spatial structure. It was therefore an early proposal to present the groundwater contamination more genuinely by plotting the measurements at their respective locations without interpolation in between (Schafmeister and Pekdeger 1994). As an alternative, the pollution may be depicted spatially in Voronoi polygons, a natural neighbor technique; however, this implies an inherent error at any but the measurement location within the polygon.

Given an irregular sampling pattern, measurements can be attributed to areas of subregions around the sampling points, in which any point is closer to the sampling location than to its adjacent sampling locations. This method is named after the Russian-Ukrainian mathematician Georgy Voronoi (1868–1908) and is now known as Voronoi tessellation. Hydrologists know the same method as Thiessen polygons (after the American meteorologist Alfred Thiessen, 1872–1956) and apply it, e.g. in order to up-scale point-supported precipitation measurements from rain gauges to two-dimensional (2D) areal segments.

However, this natural-neighbor regionalization method implies a certain error at any point within the Voronoi polygon except the measurement location. This error can be expressed as the extension variance \({\sigma }_{\mathrm{e}}^{2}\) (Matheron 1971; David 1977). The extension variance quantifies the uncertainty that applies to an area (or volume) when a single-point measurement is attributed to this area (2D) or volume (3D). This approach, which combines the most plausible and simple regionalization technique with a simultaneously computed measure of uncertainty, is by no means a novel idea; however, it can easily be implemented, especially in questions of environmental risk assessment (Fuchs and Burger 2000).

The objective of this paper is to demonstrate the usefulness of the classical extension variance concept based on Voronoi-polygons as a natural-neighbor regionalization technique, in order to assess the chemical status of groundwater incorporating prediction uncertainties. This classical approach is effective and easily applicable in the course of administrative groundwater quality assessments. It was recently proposed as a standard method in Germany in the context of groundwater quality monitoring according to the goals of the EU Water Framework Directive (Zeissler and others, unpublished technical report for project 2020 0051, “Identifizierung eines Regionalisierungsverfahrens zur Bewertung des chemischen Zustands von Grundwasserkörpern nach Grundwasserverordnung und Anwendung des Verfahrens in M-V [Identification of a regionalisation procedure for assessing the chemical status of groundwater bodies according to the Groundwater Ordinance and application of the procedure in Mecklenburg-Western Pomerania]” 2021, unpublished report).

Materials and methods

Data

In order to demonstrate the concept of extension variance, a quality assessment of groundwater measurements of nitrate in the principal upper aquifer system of the state Mecklenburg-Western Pomerania (Germany) is used. Nitrate is introduced to groundwater via fertilizers and stock manure. As the oxidized species of nitrogen, nitrate is subject to redox processes and can be decomposed by lithotrophic or organotrophic means (oxidation of pyrite or organic matter, respectively). However, nitrate often reaches groundwater via preferential flow paths or if the buffering electron acceptors are missing. Under the drinking water ordinance, a concentration of 50 mg/L NO3− is considered admissible in Europe (BMUV 2010).

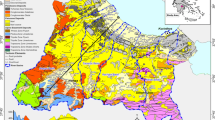
The quality assessment of groundwater is applied to smaller subregions, which can be considered delimitable with respect to the hydrogeological flow dynamics, e.g. water divides or surface waters. In Mecklenburg-Western Pomerania, which covers an area of 23,174 km2, 59 so-called groundwater bodies are identified, with an average size of 400 km2 (Fig. 1). The principal upper Pleistocene aquifer system is built up by glacial sands and gravels with moderate to high hydraulic conductivities (\(1\bullet {10}^{-4 }-5\bullet {10}^{-4}\) m/s) alternating with low-permeability tills. Locally, it is connected to deeper, pre-Quaternary sedimentary layers. The average total thickness of the principal aquifer system is 50 m. It is mostly confined by Weichselian ground moraine slabs with several tens of meter thickness. Local shallow aquifers are not considered here. Beyond the northwest–southeast striking terminal moraines, sandy and gravelly outwash plains strike out. The average annual groundwater recharge is 100–150 mm. Mecklenburg-Western Pomerania is a predominantly rural state, with more than 60% of its land used for agriculture (Stat-MV 2021).

Fig. 1
figure 1

Location of the study area. The boundary of Mecklenburg-Western Pomerania/Germany and 59 groundwater bodies are shown; colors indicate the water-table elevation

Full size image

Water samples were collected at 568 monitoring wells (Fig. 1) in Mecklenburg-Western Pomerania, which corresponds to a density of 1.2 wells per 50 km2. In accordance with BMUV (2010) the data set is compiled as the maximum concentration of relevant parameters (here nitrate) out of the annual average over a time span of 5 years (2015–2019) at each monitoring well.

Concept of extension variance

The early development of geostatistical regionalization methods for ore reserve estimations, e.g. Kriging, make use of this concept of extension variance, which expresses the error that occurs when a single measurement value is taken as an estimator for a bigger area or volume. The concept assumes that the regionalized variable Z(x) satisfies the intrinsic hypothesis, which assumes that the increments, i.e. the difference in variable values at distances h, are weakly stationary (Armstrong 1998). Here, weak stationarity of increments means that the expectation E (Eq. 1) and variance Var (Eq. 2) of \(\left[Z\left(x+h\right)-Z\left(x\right)\right]\) exist and are independent of location x.

$$\mathrm{E}\left[Z\left(x+h\right)-Z\left(x\right)\right]=0$$
(1)
$$\mathrm{Var}\left[Z\left(x+h\right)-Z\left(x\right)\right]=2\gamma \left(h\right)$$
(2)

The extension variance is based on the knowledge of the spatial variability of regionalized variables, expressed as the (semi-)variogram \(\gamma (h)\).

$${\sigma }_{e}^{2}=2 \bullet \overline{\gamma }\left(V, {x}_{0}\right)- \overline{\gamma }(V, V)$$
(3)

where \({\sigma }_{e}^{2}\) is the extension variance, \(\overline{\gamma }\left(V, {x}_{0}\right)\) is the average variogram value for all distances between all locations within the polygon V and the measurement location x0, and \(\overline{\gamma } \left(V, V\right)\) is the average variogram value for all distances possible within V, which represents the estimation volume (3D) or area (2D). In the case of natural neighbor estimation on a Voronoi-polygon, V refers to the area of this polygon. Equation 3 clearly shows that the extension variance depends on the variogram and the polygon only; it is independent of the measurement value. The extension variance is influenced by (1) the regularity of the variable, (2) the geometry of the polygon V and (3) the location of the measurement point x0 relative to V (Fig. 2). Obviously, the error (extension variance) increases with increasing size of the polygon, i.e. the larger the distance between measurement points. Equally, the more marginally the measurement point x0 is located within a polygon, the less representative it may be, i.e. the error increases; however, an irregular, i.e. less continuous variable, also increases the error.

Fig. 2
figure 2

Close-up of a Voronoi polygon and auxiliary point raster, highlighting a distances between data location x0 and all auxiliary points representing V, and b distances between all auxiliary points. (Note: for clarity, not all possible distances are shown)

Full size image

Thus, the concept of extension variance is an elegant tool to incorporate the sampling pattern into the quality assessment and can even be applied to optimize a monitoring network.

Since it is not possible to derive the average variogram \(\overline{\gamma }\) for all possible distances within a polygon, an auxiliary point raster needs to be defined that adequately represents the area of a Voronoi polygon, while still maintaining reasonable computation time. In this study, the entire investigation area was discretized into a regular 500 × 500 m2 auxiliary point raster, i.e. a Voronoi-polygon with an average size of 41 km2 is represented by 164 auxiliary points allowing for more than 13,000 possible distances h within a polygon, from which the average variogram can be determined.

Probability of exceedance

The extension variance \({\sigma }_{\mathrm{e}}^{2}\) can now be used to determine the probability that a threshold value is exceeded. Assuming a Gaussian probability distribution for \(Z\left(x\right), x\in V\), it can be concluded that with a probability of 95% Z(V) varies between \(Z\left(x\right)\pm 2{\sigma }_{\mathrm{e}}\). The probability of exceedance can easily be derived from the cumulative probability density function (Fig. 3).

Fig. 3
figure 3

Voronoi polygon and data value z(x0) (left). The extension standard deviation \({\sigma }_{e}\) quantifies the possible data range within the polygon. \(P\left(Z>{z}_{t}\right)\) is the probability that the threshold \({z}_{t}\) may be exceeded

Full size image

The final result will then reproduce the data value within a polygon V but, in addition, the uncertainty of this natural neighbor estimate, which results from the sampling pattern and the specific spatial variability structure, is visualized. All spatial analyses were run by ArcGIS Desktop 10.5.1 while the geostatistical computations are performed with R (R Core Team 2020; Ribeiro et al. 2020).

Results

Creation and adaptation of polygons to groundwater bodies

The Voronoi tessellation is performed for the 568 monitoring locations. Due to the irregular sampling pattern, some polygons are very small and others are as big as 250 km2. However, this first set of polygons needs to be adapted to the borders of the groundwater bodies. It makes sense that hydraulic boundaries which delimit the groundwater bodies should not be intersected by a polygon (Fig. 4). The final set of 568 Voronoi polygons is distributed to 59 groundwater bodies. The number of polygons which represent each individual groundwater body conforms to the number of its monitoring wells. Accordingly, some groundwater bodies can only be modelled by a single polygon, while others cover up to 16 polygons.

Fig. 4
figure 4

a Original set-up of Voronoi polygons, and b Voronoi polygons adapted to the limits of the groundwater bodies

Full size image

Characterization of spatial variability of nitrate

The data set consists of 568 monitoring wells in Mecklenburg-Western Pomerania for which nitrate concentrations are reported. These values vary between 0.01 and 480 mg/L with a modal concentration of 0.3 mg/L. Thus, the nitrate concentration locally by far exceeds the maximum admissible value of 50 mg/L; in fact, this is the case at 109 monitoring locations, corresponding to 19%.

The frequency distribution of nitrate is strongly positively skewed; therefore, the geostatistical operations are applied to the ln-transformed data (Table 1). Thereafter, the results are back-transformed to the original concentration scale.

Table 1 Frequency distribution and variogram parameters for nitrate concentrations (ln-transformed)
Full size table

Figure 5 shows the experimental and modeled variogram and the histogram of ln-transformed data. The variogram exhibits a high small-scale variability, expressed by the nugget effect, which accounts for 40% of the variance as expressed by the total sill. This high degree of spatial irregularity of nitrate concentration reflects the high local variability of influencing factors, be it the lithological structure of the soil and aquifer material, chemical zoning or the input function of nitrate.

Fig. 5
figure 5

a Variogram and b histogram of ln-transformed nitrate concentration data. The dashed red line indicates the threshold value of 50 mg/L

Full size image

Voronoi regionalization, extension variance and derived probability of exceedance

Figure 6a shows the nitrate values attributed to 568 Voronoi polygons. Following the data values, 459 polygons (81%) fall below the threshold of 50 mg/L (green shadings). These regions correspond to the aquifers below ground moraine slabs. However, two more or less W–E striking areas show values beyond 50 mg/L, with two polygons in the SW and the center, respectively, even exceeding 300 mg/L nitrate (deep red). These zones approximately trace the outwash plains.

Fig. 6
figure 6

a Voronoi polygons shaded according to their respective data values z(x0), and b the extension variance \({\sigma }_{\mathrm{e}}^{2}\) (in ln-scale). A and B point at two polygons on the island of Rügen, which exhibit high uncertainty due to the marginal position of the well within the polygon

Full size image

The extension variance as calculated in ln-scale is shown in Fig. 6b. The extension variance \({\sigma }_{e}^{2}\) lies between 3 and 6.4, respectively, i.e. extension standard deviations \({\sigma }_{\mathrm{e}}\) between 1.7 and 2.5. Clearly, the uncertainty is higher (black polygons) in scarcely sampled areas, which are represented by big polygons. However, high uncertainties are also predicted for polygons represented by a monitoring well that is located far from the polygon center, i.e. closer to the border—see for example the two medium-sized, but oddly shaped polygons in the north (Rügen Island, A and B). The level of uncertainty is clearly independent of the data values, as was specified in Eq. (3).

Figure 7 shows the probability that the threshold of 50 mg/L is exceeded within a polygon. It is derived on the basis of the local cumulative probability function (cdf) in each Voronoi polygon. As can be expected, polygons with elevated or high nitrate values (yellow and deep red, respectively, in Fig. 6a) exhibit high exceedance probabilities, e.g. higher than 50% (light and deep red). This is observed along the W–E striking outwash plain regions. Still, there are polygons that have a high level of uncertainty. However, the exceedance probability remains below 50% (A in Fig. 6a) because the data value is low. Polygon B exhibits an elevated probability of exceedance.

Fig. 7
figure 7

Map of probability of exceedance for 59 Voronoi polygons

Full size image

Quality classification of groundwater bodies

The ordinance on the protection of groundwater (BMUV 2010) requires that the assessment of the chemical status of groundwater applies to groundwater bodies. It is ruled that less than 20% surface area of a groundwater body exhibits a higher nitrate concentration than 50 mg/L. It is then classified as a ‘good status’.

The probabilities of exceedance that apply to the individual Voronoi polygons within a groundwater body are now aggregated in order to calculate the percentage \({(A}_{\mathrm{exc}})\) of the groundwater body surface area that might not fulfill the ‘good status’ criterion (Eq. 4)

$${A}_{\mathrm{exc}}=\frac{\sum\nolimits_{i=1}^{m}{ (a}_{i}\bullet {P}_{i})}{\sum {a}_{i}}$$
(4)

Aexc is calculated as an area-weighted average, where \({a}_{i}\) and \({P}_{i}\) are the weights and probabilities, respectively, applying to m Voronoi polygons within the groundwater body and \(\sum {a}_{i}\) representing its total area.

Figure 8 depicts \({A}_{\mathrm{exc}}\) for all 59 groundwater bodies. According to this assessment, only ten groundwater bodies are clearly in ‘very good status’ (green), and another ten are in ‘good status’ (yellow), which adds up to one-third of the groundwater bodies classifying as ‘good’. The remaining two-thirds of the groundwater bodies exhibit more than 20% potentially threatened by high nitrate concentrations (light and deep red). The less threatened groundwater bodies are located in the northeast and correspond to aquifers that are well protected by till sediments of the ground moraines; groundwater bodies that are highly uncertain with respect to a potential nitrate stress are identified for the less protected aquifers.

Fig. 8
figure 8

Final map which indicates the qualitative status of groundwater bodies with respect to nitrate. Groundwater bodies in which less than 20% surface area might exceed the threshold of 50 mg/L nitrate (green-yellow) are considered as ‘good chemical status’

Full size image

It is important to note that \({A}_{\mathrm{exc}}\) does not localize high loaded spots within a groundwater body, rather it reflects the potential that the threshold concentration of 50 mg/L may be exceeded. This potential is derived by merging data values with an uncertainty resulting from the variable’s structure and the spatial pattern of monitoring wells.

Discussion and conclusion

The exercise described in the preceding demonstrates a simple and straightforward method, which helps to assess groundwater quality based on measured values and the uncertainty caused by the spatial monitoring pattern and the individual variability of the considered variable. This method seems specifically well suited for groundwater pollution parameters that often reveal an erratic spatial distribution structure. Compared to variables like water-table depth, the spatial distribution of pollutants depends on a multiple set of influencing factors, one of which is the human impact. Therefore, regionalization methods which smooth the spatial variability may not be suitable to assess the quality status of groundwater bodies—overestimations as well as underestimations may occur (Li and Heap 2011). Thus, the early concept of extension variance was revisited here. Originally (Matheron 1971; David 1977), this idea was applied in questions of ore reserve estimation, where an economic balance between sampling expense and assured reserve prediction was most important.

The discussed method offers some advantages over interpolation techniques. Interpolation algorithms are generally not suitable where data are scarce, i.e. wide distances need to be bridged, which is actually an extrapolation. However, they always produce descriptive maps that suggest reliable results. Only a few interpolation algorithms additionally quantify the estimation uncertainty: Kriging produces a measure of reliability (\({\sigma }_{\mathrm{K}})\), which is, in fact, a special case of \({\sigma }_{\mathrm{e}}\) for an orthogonal estimation grid, and thus offers quantitative information on the estimation confidence. In practice, however, this is often neglected.

The variogram inference presented here (Fig. 5; Table 1) shows a spatial continuity (range of influence) of 10 km. In other words, interpolating over larger data distances goes along with null estimation confidence. With an approximate data density of 1 well per 41 km2 the overall estimation confidence in the investigation domain is generally poor.

Furthermore, contour plots based on interpolation algorithms usually produce smooth representations of the variable in question. To an unexperienced user, these types of maps might suggest that pinpointing any location on the map will render a realistic value, i.e. the interpolated concentration ‘is true’. The mosaic-like visualization of data values in Voronoi polygons, however, prevents that kind of misunderstanding from the outset, since actually no interpolation is made.

A comparison of three popular interpolation algorithms applied to the same nitrate data set that was used in this study demonstrates the dependence of the assessment on the method chosen. In order to interpolate to a grid point xi, interpolation functions calculate weights \({\lambda }_{i}\) for the neighboring data values xi:

$${\lambda }_{i}={~}^{{A(x}_{i})}\!\left/ \!{~}_{A({x}_{0})}\right.\;\;\;\;\;\;\;\mathrm{ Natural\; neighbor\; interpolation}$$
(5)

where A denotes the area of Voronoi polygons for data point xi, and the intersection of a new polygon for grid point x0 and the former data polygon A(xi).

$${\lambda }_{i}={~}^{1}\!\left/ \!{~}_{{d}_{i}^{\omega }}\right.,\;\;\;\;\mathrm{ here }\;\omega =2\;\;\mathrm{ Inverse\; distance\; interpolation}$$
(6)

Usually distances di are squared in the IDW method. In Kriging, the weights \({\lambda }_{i}\) depend on the variogram function and the individual sampling configuration:

$$\lambda_i=f\left[\gamma\left(x_0,x_i\right),\gamma\left(x_i,x_j\right)\right]\;\mathrm{Kriging}$$
(7)

with \({x}_{0}\) referring to the estimation grid point, and \({x}_{i,j}\) corresponding to the neighboring data locations.

The natural neighbor (NN) and IDW interpolation produce similar contour maps of nitrogen concentration. However, Ordinary Kriging provides extended areas where the threshold of 50 mg/L is exceeded. Actually, for the entire state Mecklenburg-Western Pomerania, the percentage of land surface in ‘good status’ is 77 and 80% according to NN and IDW, respectively. Kriging predicts only 40% of the total land surface to be in ‘good status’.

When looking closer at individual groundwater bodies (Fig. 9), e.g. 1 (center) and 2 (northeast), significant differences are revealed when the criterion that good status means less than 20% of the area exceeds 50 mg/L nitrate (BMUV 2010) is applied: For groundwater body 1, NN estimates 28% of the surface area where the threshold is exceeded, thus it is not in ‘good status’. However, according to IDW, groundwater body 1 must be considered in ‘good status (15%), and Kriging clearly certifies a poor quality (53%). For the same groundwater body, the combined Voronoi extension variance method predicts that 30% area of this groundwater body may exceed the threshold. Consequently, special attention is required here. Groundwater body 2 is clearly classified as being in ‘good status’, since apparently 50 mg/L is nowhere exceeded (NN 0.6, IDW 0.7%). In contrast, Kriging shows a high share of the area as having elevated concentrations (38%). This is due to the fact that Kriging, as all interpolation methods applied here, does not account for hydraulic borders, which delimit the groundwater bodies. However, Kriging tends to preserve the spatial continuity. The interpolated concentrations in groundwater body 2 are strongly affected by some high-concentration wells in the adjacent western groundwater body, which may lead to an overestimation here. The assessment method proposed in this paper, however, predicts a ‘good status’ for groundwater body 2. The reason being is that this groundwater body is spatially relatively well represented by 16 piezometers.

Fig. 9
figure 9

Comparison interpolated nitrate concentration, a natural neighbor interpolation, b inverse distance weighted (power 2), and c Ordinary Kriging (only the central part of Mecklenburg-Western Pomerania is shown)

Full size image

Another advantage is that, provided the spatial variability structure (the variogram) of the variable in question can be inferred from measured data, the local probability density function for all polygons can be derived based on the extension standard deviation \({\sigma }_{\mathrm{e}}\) and data value z(x0). Once the local probability density function is calculated, prescribed thresholds can be modified at any time and the resulting exceedance probability determined. Furthermore, because \({\sigma }_{e}\) is independent of the data value, it may even be calculated for additional piezometer locations and thus contribute to an optimization of the monitoring network (Schafmeister 1999; Tietze 1995).

The described method is fast and meets the groundwater protection ordinance’s requirements well; however, some aspects need to be considered. The approach, as discussed here, assumes that the variable in question follows a (1) parametric probability distribution, i.e. normal or ln-normal, and (2) is statistically homogeneous. Hydrochemical concentrations, especially for pollutants, often do not meet the former condition. If simple ln-transformation is not purposeful, a Gaussian anamorphosis (Wackernagel 2003) or the distribution independent indicator (Schafmeister 1999; Hoang et al. 2007) approach should be considered.

The condition of statistical homogeneity assumes that the distribution function of the considered variables holds throughout the entire investigation domain. Applied to groundwater quality data, this means that the physico-chemical conditions of the aquifers should be relatively constant. The principal aquifer system described previously (Mecklenburg-Western Pomerania) consists predominantly of unconsolidated porous material, which can be considered homogeneous with respect to hydrogeochemical interaction and hydrodynamic characteristics. Therefore, it seems justifiable to model the spatial variability of nitrate and other components, which were not discussed here, with a single variogram function. This variogram function is inferred from the whole investigation area, neglecting hydraulic boundaries; however, provided the intrinsic hypothesis can be assumed, it may well reflect the spatial covariance structure of the variable under consideration.

If applied to more heterogeneous geological and hydrogeochemical environments, the method needs to be constrained to statistically homogeneous regions. Investigations on the natural background values of hydrochemical compounds (Walter et al. 2012) suggest that this is especially relevant for complex fractured and karst aquifers, which dominate in the southern states of Germany.

The authorities in the state of Mecklenburg-Western Pomerania proposed the concept of extension variance (Zeissler and others, unpublished technical report for project 2020 0051, see previous details, 2021), as described in the preceding for the parameter nitrate, to be used as a standard routine method for a fast assessment of the groundwater quality according to the requirements in the groundwater protection ordinance (BMUV 2010), which attempts to assess the groundwater quality integrated for groundwater bodies. With respect to the nutrient nitrate, which is mainly applied as fertilizer, another ordinance needs to be obeyed—the Fertiliser Application Ordinance (BMEL 2017). This ordinance rules on how farmers may apply fertilizer, i.e. quantity, time and frequency; however, it requires that the actual nitrate concentration and its temporal development is known for specific agricultural land units, i.e. an accurate localization of elevated concentrations. The concept of merging extension variance with data values results in probabilities of exceedance that apply only to arbitrary Voronoi polygons whose spatial constellation is conditioned solely by the sampling pattern. The aggregation of probabilities of exceedance to groundwater bodies provides an integral evaluation of its quality rather than an exact localization of elevated concentrations. In this sense, the aforementioned method can only provide initial guesses, for which detailed information on the groundwater bodies is lacking and additional monitoring, i.e. a denser piezometer pattern and more frequent sampling, is required.

The assessment method discussed here is based on fundamental geostatistical assumptions and one of the earliest geostatistical measures of uncertainty (or estimation confidence), i.e. the extension variance. Although during seven decades of geostatistical development, many advanced approaches and tools have been developed, this classical concept is still useful, especially in questions of environmental risk assessment, when hard data are still a precious commodity.