Introduction

Unconfined detritic aquifers can be modelled as randomly heterogeneous porous media in which hydrogeological properties (e.g., transmissivity) vary spatially in a manner that is only partially understood (Kitanidis 1997). A reasonably accurate aquifer transmissivity field is essential for simulating the flow and transport of solutes (Anderson et al. 2015). Pumping tests are the main source of hard data for describing the transmissivity field of an aquifer (Renard 2005; Demir et al. 2017). However, in general, the number of pumping tests in a single aquifer is usually small (Christensen 1996; Teramoto et al. 2021); hence, transmissivity data have significant uncertainty, as will be shown by their spatial variability quantified by a variogram that shows a high nugget variance due to sampling error and/or short scales of spatial variability that is not accounted for by the available experimental data locations. Auxiliary information, however, can be used to increase the accuracy of a transmissivity field estimated from only hard transmissivity data. Of the several types of secondary information, piezometric data (water head data for the unconfined aquifer case) have often been used to improve the estimation of the transmissivity field in inverse hydrogeology approaches (Dagan 1985; Zimmerman et al. 1998; Carrera et al. 2005; among many others). When there is a correlation between the water table and topographic elevations, a digital elevation model with full coverage of elevation data can be introduced as secondary information (Renard and Jeannée 2008). Other than inverse approaches, transmissivity fields have been estimated by geostatistical co-kriging using secondary variables such as specific capacity (Ahmed and de Marsily 1987; Razack and Huntley 1991; Richard et al. 2016), connectivity data (Freixas et al. 2017) or any auxiliary data correlated with transmissivity (Kupfersberger and Blöschol 1995). Correlation and regression analysis have also been used to improve transmissivity fields by using geophysical data such as magnetic resonance (Boucher et al. 2009) or electrical resistivity (Soupios et al. 2007). Hydrofacies simulation has also been used to estimate the spatial variability of hydraulic conductivity (Zhu et al. 2016; Xue et al. 2022).

This paper shows that different types of co-kriging (the multivariate geostatistical estimator) can be used to improve the knowledge of a transmissivity field of a detritic aquifer in southern Spain (the Vega de Granada aquifer). Different aspects of the geostatistical analysis of the Vega de Granada aquifer, such as the estimation of the variogram of transmissivities and the estimation of groundwater hydraulic gradients, have been reported in Pardo-Igúzquiza et al. (2009); Pardo-Igúzquiza and Chica-Olmo 2004, 2007 and Kuhlman and Pardo-Igúzquiza (2010). This paper introduces and demonstrates several new components of the methodology in a case study of the Vega de Granada aquifer. In the methodology three types of information are used: transmissivity data from pumping tests, transmissivity data from lithofacies measured in boreholes, and water head data. These three types of information are merged in order to improve the aquifer parameter field defined by spatially variable log-transmissivities. The geostatistical approach to the inverse model has been illustrated by applying it to the Vega de Granada aquifer and the performances of the procedures have been ranked. Rather than using cross-validation to rank performance, the paper shows the use of the direct solution of the groundwater equation which is derived in this paper. In this sense, this paper presents novel results and a novel application to the Vega de Granada as a case study. The data, the methodology, the results, and the discussion are presented in the following sections.

Materials and methods

Study area

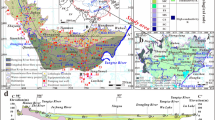
The study area is the unconfined Vega de Granada detritic aquifer in southern Spain (Fig. 1a). The aquifer has a surface area of around 200 km2 and is composed of Quaternary materials of fluvial origin (Castillo 1989; Luque-Espinar 2001; García-Soldado 2009; Pardo-Igúzquiza et al. 2011) which are part of the Granada intramountainous basin (Fig. 1b). The aquifer has an elongated shape in the E–W direction with a long axis of around 22 km and a perpendicular axis of around 8 km.

Fig. 1
figure 1

a Physical map with the general geographical location of the Vega de Granada Aquifer (VGA), Spain, inside the white square located in the southern part of the Iberian Peninsula. The colour scheme in the figure depicts topographic relief, with red colours representing higher elevations. b Image showing terrain shadows where the Vega de Granada aquifer can be seen as an intramountain basin. The polygon defines the border of the aquifer used in the modelling and the geometry of the field used for geostatistical estimation. c Drainage network and towns in the Vega de Granada aquifer. The Genil River flows from east to west through the middle of the area, where the highest transmissivities are found. The black arrow indicates an area of relatively high transmissivity that is discussed in the main text.

Full size image

The aquifer is composed of various fluvial and colluvial detritic materials such as gravel, sand, silt and clay in spatially varying proportions. The spatial variations in the material proportions imply spatial variations in porosity and hence in hydraulic conductivity and transmissivity (taking into account the thickness of saturated aquifer). At places where gravel and sand dominate, the transmissivity is high, and where silt and clay dominate, the transmissivity is low.

The Genil River (Fig. 1c) crosses the elongated central section of the aquifer from east to west. However, this river is regulated by the Canales Dam and thus the water that it contributes to the aquifer can be considered negligible. For the same reason, the Cubillas River in the northwest contributes negligible amounts of water as it is regulated by the Cubillas Dam. The remaining rivers shown in Fig. 1c (Beiro, Darro, Monachil, Dilar and Salado rivers) are ephemeral streams that carry water only after significant rainfall events. Thus, the water input from rivers has no significant effect on the methodology used in the work presented here.

Hard transmissivity data

Figure 2a shows the spatial location of the 41 measurements of transmissivity obtained from pumping tests. Most of the measurements are located around the central part of the aquifer and this zone has the highest transmissivity. Pumping tests are rare in zones that are not water productive, which implies a bias in the transmissivity data set towards relatively high transmissivity values. It should be noted that the transmissivity data are not the product of a single acquisition but have been compiled from historical records available from the office of the Spanish Geological Survey in the city of Granada. The pumping tests were conducted by different teams and the details of every test are unknown (for example, whether or not a borehole fully penetrated the aquifer); thus, these measurements have an unknown uncertainty. In addition, they are not point support data as is usually assumed, but have a specific support that is generally unknown, which implies an additional source of uncertainty if they are used as point data. The original experimental data from the pumping test were measured in m2/day and their natural logarithms (i.e. log-transmissivity data) are provided in Table 1. The histogram and the basic statistics are shown in Fig. 2b. The mean value of the log-transmissivity data is 6.96 ln(m2/day) and the variance is 2.91 ln(m2/day)2. The median is 7.29 ln(m2/day), which is close to the mean and the 25 percentile is 6.29 ln(m2/day)—that is, 75% of the measurements are greater than 6.29 ln(m2/day).

Fig. 2
figure 2

a The Vega de Granada aquifer border (solid line) and the 41 locations at which log-transmissivity was measured from pumping tests. b Histogram and basic statistics of log-transmissivity data from pumping tests. The experimental values are provided in Table 1. The units of log-transmissivity are ln(m2/day)

Full size image
Table 1 Experimental data (41 values) of log-transmissivity, with units ln(m2/day), measured from pumping tests. A map of their spatial location is shown in Fig. 2
Full size table

Transmissivity data from lithofacies measured along boreholes

The Spanish Geological Survey database contains 167 boreholes, in relation to the Vega de Granada aquifer, for which the lithofacies intersected by the boreholes were recorded during drilling. It should be noted that the boreholes were drilled over the years by different teams and, most of the time, the lithofacies were recorded by members of the drilling team who used their experience but often lacked a geological background. Thus, there was no standard terminology used for the stratigraphic column and the information has a high uncertainty, and for this reason, the categorization was performed by the authors of this paper. The lithofacies were interpreted and a code was assigned ranging from 0 (clay) to 6 (clean gravel) covering the full range of the different grain sizes sorted into seven categories (Table 2). Figure 3a shows a three-dimensional (3D) view of the boreholes and Fig. 3b shows the spatial locations of the 167 boreholes in plan within the borders of the aquifer. The log-transmissivity values in the boreholes were calculated by assigning standard values of the hydraulic conductivity, K, (Freeze and Cherry 1979) to each lithofacies and using an average aquifer saturated thickness (b) of 100 m that was determined from historical borehole and geophysics data:

$$\ln (T)=\ln (K)+\ln (b)$$
(1)
Table 2 Lithofacies codes and lithology, and the range of hydraulic conductivity (K) values typically assigned to the lithology, plus the same information in natural logarithm form. The last column gives the value selected from the interval that was assigned to the lithofacies code. This value was selected in such a way that the final mean of log-transmissivities for this data set was similar to the mean of the log-transmissivities from pumping tests
Full size table
Fig. 3
figure 3

a Three-dimensional view of the 167 boreholes for which the logarithm of transmissivity (T) was recorded (raw values in m2/day). b The Vega de Granada aquifer border (solid line) and the 167 locations at which the log-transmissivity was measured from lithofacies in the boreholes. These points are the plan projection of the boreholes (a). c Histogram and basic statistics of log-transmissivity data from hydrofacies. The experimental values are provided in Table 2. The units of log-transmissivity are ln(m2/day)

Full size image

Next, for each borehole the mean value was calculated and 4.6 (i.e., ln100) was added to give the final resulting value for the two-dimensional (2D) locations shown in Fig. 3b. Obviously, these indirect values of transmissivity also have significant uncertainty. The experimental values of the log-transmissivity data from the lithofacies are provided in Table 3. The histogram and the basic statistics are shown in Fig. 3c. The mean value of the log-transmissivity data is 7.35 ln(m2/day) and the variance is 6.08 ln(m2/day)2. The median is 7.61 ln(m2/day) and the 25-percentile is 5.58 ln(m2/day)—that is, despite similar means and medians of the log-transmissivities from the pumping test data and from the lithofacies data, there is a much larger dispersion of the log-transmissivity data from the boreholes and there is a larger proportion of relatively high values in the log-transmissivity data from the pumping test as shown, for example, by the 25% percentile. However, because of the higher dispersion of the log-transmissivity data from the boreholes, they contain more high values in absolute terms, as can be seen by comparing the 90% percentiles of both data sets.

Table 3 Experimental data (167 values) of log-transmissivity, T, in units ln(m2/day), calculated from the lithofacies data. A map of their spatial location is shown in Fig. 3b
Full size table

Piezometric head measurements

Water head measurements vary in space and time. If water head measurements for a particular date can be considered steady state, they can be related to hydraulic conductivity and transmissivity by solving the inverse problem in hydrogeology (Yeh 1986). Among the many procedures proposed for solving the inverse problem (Zimmerman et al. 1998), the geostatistical approach, explained later on, was chosen. Of the numerous water head data sets that are available for estimating the transmissivity field, the set collected in May 1970 has been chosen as it has the most (37) water head measurements (Fig. 4). The experimental values of the water head are provided in Table 4.

Fig. 4
figure 4

The Vega de Granada aquifer border (solid line) and the locations of the 37 water head measurements surveyed in May 1970. The experimental values are provided in Table 3

Full size image
Table 4 Experimental water head data (37 values). A map of their spatial locations is shown in Fig. 4
Full size table

Co-kriging

Co-kriging is a geostatistical method for optimal multivariate spatial interpolation (Chilès and Delfiner 1999). In geostatistics, a spatial variable Y(u) is modelled as a random variable. The set of all random variables Y(u) in a region χ of the space, u ∈ χ, is considered a random function or random field Y(u). With \(\chi \subset {\mathfrak{R}}^d\) and d = 2 the problem is two dimensional as is the case in the work presented here. It is assumed that Y(u) is second-order stationary with constant spatial mean

$$\textrm{E}\left\{Y\left(\textbf{u}\right)\right\}={m}_Y$$
(2)

and the two-point statistics, the covariance and the variogram functions, depend only on the vector h:

$${C}_Y\left(\textbf{u},\textbf{u}+\textbf{h}\right)={C}_Y\left(\textbf{h}\right)=\textrm{E}\left\{Y\left(\textbf{u}\right)Y\left(\textbf{u}+\textbf{h}\right)\right\}-{m}_Y^2$$
(3)
$${\gamma}_Y\left(\textbf{h}\right)={C}_Y(0)-{C}_Y\left(\textbf{h}\right)$$
(4)
$${C}_Y(0)={\sigma}_Y^2$$
(5)

where \({m}_Y,{\sigma}_Y^2,{\gamma}_Y\left(\textbf{h}\right)\) and CY(h) are, respectively, the mean, variance, variogram and covariance of the random function Y(u) and E{.} is the mathematical expectation operator.

In the simplest case for co-kriging, a variable of interest, or a primary variable (e.g.,log-transmissivity), is estimated from experimental values of the variable and experimental values of a secondary variable that is correlated with the primary variable. Obviously, the number of auxiliary variables can be increased.

The co-kriging estimator of the log-transmissivity at a given geographical location u0 = {x0, y0}, where {x0, y0} are the easting and northing coordinates respectively, can be expressed as:

$${Y}^{\ast}\left({\textbf{u}}_0\right)=\sum_{i=1}^n{\lambda}_i^0Y\left({\textbf{u}}_i\right)+\sum_{j=1}^m{\beta}_j^0Z\left({\textbf{u}}_j\right)$$
(6)

where Y(u) = ln T(u) is the natural logarithm of transmissivity T(u) and Z(u) is the log-transmissivity measured from the lithofacies. Also, as an alternative that will be assessed further on, the roles of the primary variable and the secondary variable could be swapped between both types of log-transmissivity data. The secondary variable could also be H(u), the variable that represents head data. However, the log-transmissivity data and the head data will be merged by using inverse problem co-kriging because both variables are related by the groundwater flow equations.

n and m are the number of values of the variables Y(u) and Z(u) respectively, used in the estimation in Eq. (6). Usually, these data are inside a neighbourhood centred on the estimation location u0.

The optimal weights for the linear estimation in Eq. (6) are obtained by solving the corresponding and well-known co-kriging system—see for example, Goovaerts (1997) or Wackernagel (2003). If only the primary variable is used, ordinary co-kriging collapses to ordinary kriging of the primary variable.

For co-kriging with only the two log-transmissivity data sets, the direct variograms of the two variables and the cross-variogram (or direct covariances and cross-covariance) between the two variables must be estimated from the experimental data. When the number of experimental data is small, as is the case with transmissivity data from pumping tests, the estimation of the variogram parameters by maximum likelihood (Kitanidis 1983, Mardia and Marshall 1984, Pardo-Igúzquiza 1997, 1998) is a good choice. A combination of maximum likelihood and visual fitting was used in this work to estimate the variogram model parameters.

The unbiasedness of the co-kriging estimator in Eq. (6) implies that the mean estimation error is zero:

$$\textrm{E}\left\{{Y}^{\ast}\left({\textbf{u}}_0\right)-Y\left({\textbf{u}}_0\right)\right\}=0$$
(7)

This is achieved by including the following conditions in the co-kriging system:

$$\sum_{i=1}^n{\lambda}_i^0=1$$
(8)

and

$$\sum_{k=1}^m{\beta}_k^0=0$$
(9)

The variance of the estimation error can be written as:

$$\begin{array}{l}\mathrm{Var}\left\{Z^\ast\left({\textbf{u}}_0\right)-Z\left({\textbf{u}}_0\right)\right\}=\sum\limits_{i=1}^n\sum\limits_{j=1}^n\lambda_i^0\lambda_j^0C_Y\left({\textbf{h}}_{ij}\right)+\sum\limits_{i=1}^m\sum\limits_{j=1}^m\beta_i^0\beta_j^0C_Z\left({\textbf{h}}_{ij}\right)\\+\sum\nolimits_{i=1}^n\sum\nolimits_{j=1}^m\lambda_i^0\beta_j^0C_{YZ}\left({\textbf{h}}_{ij}\right)+\sum\nolimits_{j=1}^m\sum\nolimits_{i=1}^n\beta_j^0\lambda_i^0C_{ZY}\left({\textbf{h}}_{ji}\right)\\-2\sum\limits_{i=1}^n\lambda_i^0C_Y\left({\textbf{h}}_{i0}\right)-2\sum\limits_{j=1}^m\beta_j^0C_Z\left({\textbf{h}}_{j0}\right)+C_Y\left({\textbf{h}}_{00}\right)\end{array}$$
(10)

Co-kriging is a form of data merging (Dowd and Pardo-Igúzquiza 2006, 2012)—that is, co-kriging provides an efficient means of combining different types of data to provide a new layer of information. The co-kriging system is obtained by minimizing the estimation variance in Eq. (1) subject to the unbiasedness conditions and, in matrix form (Isaaks and Srivastava 1989), is:

$$\textbf{C}\boldsymbol{\uplambda } =\textbf{B}$$
(11)

with:

$$\textbf{C}=\left[\begin{array}{ccc}\begin{array}{ccc}{C}_Y\left({\textbf{h}}_{11}\right)& \cdots & {C}_Y\left({\textbf{h}}_{1n}\right)\\ {}\vdots & \ddots & \vdots \\ {}{C}_Y\left({\textbf{h}}_{n1}\right)& \cdots & {C}_Y\left({\textbf{h}}_{nn}\right)\end{array}& \begin{array}{ccc}{C}_{YZ}\left({\textbf{h}}_{11}\right)& \cdots & {C}_{YZ}\left({\textbf{h}}_{1m}\right)\\ {}\vdots & \ddots & \vdots \\ {}{C}_{YZ}\left({\textbf{h}}_{n1}\right)& \cdots & {C}_{YZ}\left({\textbf{h}}_{nm}\right)\end{array}& \begin{array}{cc}1& 0\\ {}\vdots & \vdots \\ {}1& 0\end{array}\\ {}\begin{array}{ccc}{C}_{ZY}\left({\textbf{h}}_{11}\right)& \cdots & {C}_{ZY}\left({\textbf{h}}_{1n}\right)\\ {}\vdots & \ddots & \vdots \\ {}{C}_{ZY}\left({\textbf{h}}_{m1}\right)& \cdots & {C}_{ZY}\left({\textbf{h}}_{mn}\right)\end{array}& \begin{array}{ccc}{C}_Z\left({\textbf{h}}_{11}\right)& \cdots & {C}_Z\left({\textbf{h}}_{1m}\right)\\ {}\vdots & \vdots & \vdots \\ {}{C}_Z\left({\textbf{h}}_{m1}\right)& \cdots & {C}_Z\left({\textbf{h}}_{mm}\right)\end{array}& \begin{array}{cc}0& 1\\ {}\vdots & \vdots \\ {}0& 1\end{array}\\ {}\begin{array}{ccc}1\kern3.5em & \cdots & 1\\ {}0\kern3.5em & \cdots & 0\end{array}& \begin{array}{ccc}0\kern3em & \cdots & 0\\ {}1\kern3em & \cdots & 1\end{array}& \begin{array}{cc}0& 0\\ {}0& 0\end{array}\end{array}\right]$$
(12)
$$\boldsymbol{\lambda} =\left[\begin{array}{c}{\lambda}_1^0\\ {}\vdots \\ {}\begin{array}{c}{\lambda}_n^0\\ {}{\beta}_1^0\\ {}\begin{array}{c}\vdots \\ {}{\beta}_m^0\\ {}\begin{array}{c}{\mu}_1\\ {}{\mu}_2\end{array}\end{array}\end{array}\end{array}\right],\textbf{B}=\left[\begin{array}{c}{C}_Y\left({\textbf{h}}_{10}\right)\\ {}\vdots \\ {}\begin{array}{c}{C}_Y\left({\textbf{h}}_{n0}\right)\\ {}{C}_{YZ}\left({\textbf{h}}_{01}\right)\\ {}\begin{array}{c}\vdots \\ {}{C}_{YZ}\left({\textbf{h}}_{0m}\right)\\ {}\begin{array}{c}1\\ {}0\end{array}\end{array}\end{array}\end{array}\right]$$
(13)

where μ1 and μ2 are Lagrange multipliers or parameters that are used to include the constraints given in Eqs. (8) and (9).

The solution of the co-kriging system:

$$\boldsymbol{\uplambda} ={\textbf{C}}^{-1}\textbf{B}$$
(14)

provides the weights required in the estimator in Eq. (6).

In the geostatistical literature, the form of co-kriging summarised previously is known as “ordinary co-kriging” to distinguish it from “simple co-kriging” in which the mean mY in Eq. (2) is known (Journel and Huijbregts 1978; Goovaerts 1997; Chilès and Delfiner 1999).

Inverse problem co-kriging

In an aquifer, the head and log-transmissivity data are linked by the physical equations that describe the groundwater flow, the type of boundary conditions at the border of the aquifer and by other inputs (e.g., recharge by rainfall) and outputs (e.g., extraction of water by pumping wells or by evapotranspiration). For the case of an unconfined aquifer, the groundwater flow model with Dupuit assumptions gives the Boussinesq equation that can be written as (Cordano and Rigon 2013):

$$\frac{\partial }{\partial x}\left(K\left(\textbf{u}\right)H\left(\textbf{u}\right)\frac{\partial H\left(\textbf{u}\right)}{\partial x}\right)+\frac{\partial }{\partial y}\left(K\left(\textbf{u}\right)H\left(\textbf{u}\right)\frac{\partial H\left(\textbf{u}\right)}{\partial y}\right)=S\frac{\partial H\left(\textbf{u}\right)}{\partial t}-R\left(\textbf{u},t\right)$$
(15)

where K(u) and H(u) are the hydraulic conductivity and the water head respectively, at the spatial location u = {x, y}. R(u, t) represents the recharge or extraction term of water from the aquifer. S and t are, respectively, the specific yield (drainable porosity) and time.

For the steady-state case:

$$\frac{\partial H\left(\textbf{u}\right)}{\partial t}=0$$
(16)

and, in the absence of recharge and extraction (pumping wells or evapo-transpiration, for example):

$$R\left(\textbf{u},t\right)=0$$
(17)

and

$$\frac{\partial }{\partial x}\left(K\left(\textbf{u}\right)H\left(\textbf{u}\right)\frac{\partial H\left(\textbf{u}\right)}{\partial x}\right)+\frac{\partial }{\partial y}\left(K\left(\textbf{u}\right)H\left(\textbf{u}\right)\frac{\partial H\left(\textbf{u}\right)}{\partial y}\right)=0$$
(18)

and considering the following relationships:

$$T\left(\textbf{u}\right)=K\left(\textbf{u}\right)b$$
(19)
$$\frac{\partial \ln T\left(\textbf{u}\right)}{\partial x}=\frac{1}{T\left(\textbf{u}\right)}\frac{\partial T\left(\textbf{u}\right)}{\partial x}$$
(20)
$$\frac{\partial {\left(H\left(\textbf{u}\right)\right)}^2}{\partial x}=2H\left(\textbf{u}\right)\frac{\partial H\left(\textbf{u}\right)}{\partial x}$$
(21)

and

$$Y\left(\textbf{u}\right)=\ln \left(T\left(\boldsymbol{u}\right)\right)$$
(22)

After operating with the derivative of a product of functions and some minor calculus operations, the resulting partial differential equation is:

$$\frac{\partial Y\left(\textbf{u}\right)}{\partial x}\frac{\partial {\left(H\left(\textbf{u}\right)\right)}^2}{\partial x}+\frac{\partial Y\left(\textbf{u}\right)}{\partial y}\frac{\partial {\left(H\left(\textbf{u}\right)\right)}^2}{\partial y}+\frac{\partial^2{\left(H\left(\textbf{u}\right)\right)}^2}{\partial {x}^2}+\frac{\partial^2{\left(H\left(\textbf{u}\right)\right)}^2}{\partial {y}^2}=0$$
(23)

where T(u), and Y(u) are transmissivity and log-transmissivity respectively, at the spatial location u = {x, y}. b is the mean saturated thickness of the aquifer, which is used because it is common practice to consider time-invariant “transmissivity” values defined by the hydraulic conductivity multiplied by a time-invariant representative thickness (Pulido-Velazquez et al. 2007).

As there will be given boundary conditions at the border of the aquifer, it is assumed that any other source of recharge or extraction in the aquifer is zero. Given the boundary of the aquifer Ω and the unitary vector n normal to the boundary, the no-flow boundary condition implies:

$${\left.\frac{\partial H\left(\textbf{u}\right)}{\partial \textbf{n}}\right|}_{\Omega}=0$$
(24)

In the same way, in the parts of the boundary Ω where the boundary condition is a fixed head, the boundary condition is:

$$H\left({\textbf{u}}_i\right)={H}_i=\textrm{constant},\kern3.25em {\textbf{u}}_i\in \Omega$$
(25)

Obviously, this steady-state condition is only realistic if it is considered for a particular period of time (e.g., a day) as groundwater flow and other recharge processes are slow and it is assumed that there are no pumping wells running. Thus, the steady-state conditions can be considered realistic for the day on which the water head data were measured but a transient model should be used for longer periods of time (e.g., a week, a month, or more).

Ordinary co-kriging could be applied to the log-transmissivity and water head and ignoring Eq. (23) to estimate the covariance of log-transmissivity, the covariance of the water head and the cross-covariance between log-transmissivity and water head. However, there are several inference problems with this approach.

Firstly, the hypothesis of a constant mean water head, such as that in Eq. (2), is not realistic for an aquifer water head. Water head generally shows a spatial trend. That trend, or drift, is the difference in potential energy (for an unconfined aquifer) that results in the groundwater flowing from areas of higher potential to areas of lower potential. Thus, a spatially variable mean must be considered:

$$\textrm{E}\left\{H\left(\textbf{u}\right)\right\}={m}_H\left(\textbf{u}\right)$$
(26)

The trend is usually modelled as a low order polynomial:

$${m}_H\left(\textbf{u}\right)=\sum\limits_{i=0}^p{b}_i{f}_i\left(\textbf{u}\right)$$
(27)

where {bi; i = 0, …, p} is a set of coefficients that must be estimated and

{fi(u); i = 0, …, p} is a set of known base functions, usually monomial, of the co-ordinates—for example, {1, x, y, xy, x2, y2} are the six base functions for the case of a quadratic polynomial trend on a plane.

A trend requires new unbiasedness conditions for the co-kriging estimator—for example, for a linear trend in the secondary variable only, the co-kriging system must take into account the following unbiased conditions:

$$\sum\limits_{i=1}^n{\lambda}_i^0=1$$
(28)
$$\sum\limits_{j=1}^m{\beta}_j^0=0$$
(29)
$$\sum\limits_{i=1}^n{\beta}_i^0{x}_i=0$$
(30)
$$\sum\limits_{i=1}^n{\beta}_i^0{y}_i=0$$
(31)

Firstly, the ordinary co-kriging system that takes these unbiasedness conditions into account is universal co-kriging (Journel and Huijbregts 1978; Goovaerts 1997; Chilès and Delfiner 1999). Secondly, it can be shown (Hoeksema and Kitanidis 1984; Dagan 1985; Ahmed and de Marsily 1993; Kitanidis 1997, among others) that the groundwater flow equation that physically links the log-transmissivity and water head implies that their cross-covariance is anisotropic and antisymmetric. As it is difficult to provide a good estimate of this convoluted cross-covariance from small sets of experimental log-transmissivity and water head data, a theoretical derivation of the cross-covariance may be preferable. This problem has received significant attention in the scientific literature. Basically, there are two approaches—use various numerical methods to provide an analytical solution (Rubin 2003) or use a Monte Carlo method (Kitanidis 1997). In this sense, Dagan (1985) derived an analytical expression that considered an aquifer of infinite extent and a water head with a linear trend along one of its principal axes together with an exponential covariance for the log-transmissivity and found that the cross-covariance between log-transmissivity and water head, CYH(h), is given by:

$${C}_{YH}\left(\textbf{h}\right)={\sigma}_Y^2{\beta}_1\ell \frac{h_x}{h^2}\left[1-\left(1+h\right)\exp \left(-h\right)\right]$$
(32)

where \({\sigma}_Y^2:\) is the variance, or total sill, of the log-transmissivity Y(u) and ℓ is the range of the exponential covariance of log-transmissivity Y(u). The covariance of the log-transmissivity is:

$${C}_Y\left(\textbf{h}\right)={C}_0+{C}_1\exp \left(-h/\ell \right)$$
(33)
$${\sigma}_Y^2={C}_0+{C}_1$$
(34)

where:

C 0 is the nugget variance;

C 1 is the partial sill variance;

\(\textbf{h}=\left({h}_x,{h}_y\right)=\left(\frac{x_1-{x}_2}{\ell },\frac{y_1-{y}_2}{\ell}\right)\) is the distance vector standardized by the range of log-transmissivity;

\(h=\sqrt{h_x^2+{h}_y^2}\kern0.5em\) is the magnitude of the standardized distance vector and m H(u) = m(x, y) = β0 + β1x is the linear trend of the water head, which, in this case, is an east–west trend.

The universal co-kriging estimator can then be written as:

$${Y}^{\ast}\left({\textbf{u}}_0\right)=\sum_{i=1}^n{\lambda}_i^0Y\left({\textbf{u}}_i\right)+\sum_{j=1}^m{\beta}_j^0H\left({\textbf{u}}_j\right)$$
(35)

for which the optimal weights are obtained by solving the universal co-kriging system (in matrix form) such as given in Eq. (11) but with the following matrix elements:

$$\textbf{C}=\left[\begin{array}{cccccccccc}{C}_Y\left({\textbf{h}}_{11}\right)& \cdots & {C}_Y\left({\textbf{h}}_{1n}\right)& {C}_{YH}\left({\textbf{h}}_{11}\right)& \cdots & {C}_{YH}\left({\textbf{h}}_{1m}\right)& 1& 0& 0& 0\\ {}\vdots & \ddots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {}{C}_Y\left({\textbf{h}}_{n1}\right)& \cdots & {C}_Y\left({\textbf{h}}_{nn}\right)& {C}_{YH}\left({\textbf{h}}_{n1}\right)& \cdots & {C}_{YH}\left({\textbf{h}}_{nm}\right)& 1& 0& 0& 0\\ {}{C}_{HY}\left({\textbf{h}}_{11}\right)& \cdots & {C}_{HY}\left({\textbf{h}}_{1n}\right)& {C}_H\left({\textbf{h}}_{11}\right)& \cdots & {C}_H\left({\textbf{h}}_{11}\right)& 0& 1& {x}_1& {y}_1\\ {}\vdots & \ddots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {}{C}_{HY}\left({\textbf{h}}_{m1}\right)& \cdots & {C}_{HY}\left({\textbf{h}}_{mn}\right)& {C}_H\left({\textbf{h}}_{m1}\right)& \cdots & {C}_H\left({\textbf{h}}_{mm}\right)& 0& 1& {x}_m& {y}_m\\ {}1& \cdots & 1& 0& \cdots & 0& 0& 0& 0& 0\\ {}0& \cdots & 0& 1& \cdots & 1& 0& 0& 0& 0\\ {}0& \cdots & 0& {x}_1& \cdots & {x}_m& 0& 0& 0& 0\\ {}0& \cdots & 0& {y}_1& \cdots & {y}_m& 0& 0& 0& 0\end{array}\right]$$
(36)
$$\boldsymbol{\lambda} =\left[\begin{array}{c}{\lambda}_1^0\\ {}\vdots \\ {}\begin{array}{c}{\lambda}_n^0\\ {}{\beta}_1^0\\ {}\begin{array}{c}\vdots \\ {}{\beta}_m^0\\ {}\begin{array}{c}{\mu}_1\\ {}\begin{array}{c}{\mu}_2\\ {}{\mu}_3\\ {}{\mu}_4\end{array}\end{array}\end{array}\end{array}\end{array}\right],\textbf{B}=\left[\begin{array}{c}{C}_Y\left({\textbf{h}}_{10}\right)\\ {}\vdots \\ {}\begin{array}{c}{C}_Y\left({\textbf{h}}_{n0}\right)\\ {}{C}_{YH}\left({\textbf{h}}_{01}\right)\\ {}\begin{array}{c}\vdots \\ {}{C}_{YH}\left({\textbf{h}}_{0m}\right)\\ {}\begin{array}{c}1\\ {}\begin{array}{c}0\\ {}0\\ {}0\end{array}\end{array}\end{array}\end{array}\end{array}\right]$$
(37)

where μ1, μ2 μ3 and μ4 are Lagrange multipliers or parameters that are included in the minimization of the estimation variance subject to the constraints given in Eqs. (12) and (13). The solution of the co-kriging system is given by Eq. (14). In the geostatistical literature the co-kriging system in Eqs. (12) and (13) is known as universal co-kriging. It should be noted that in Eqs. (12) and (13) the trend is considered only in the secondary variable (i.e., water head) as there is no trend in the primary variable (i.e., log-transmissivity). Furthermore, the universal co-kriging system in which the cross-covariances between log-transmissivity and water head take into account the groundwater flow equation (i.e., the physical link between log-transmissivity and water head) is the geostatistical solution to the inverse problem in hydrogeology (Kitanidis 1996; Zimmerman et al. 1998; Rubin 2003) and hence the descriptive name of “inverse problem universal co-kriging” given to the estimator.

Results

The first result is the log-transmissivity obtained by ordinary kriging using the log-transmissivity data from the pumping tests. The estimated variogram and the fitted model for the log-transmissivity data from the pumping tests are shown in Fig. 5a. The estimated log-transmissivity field is shown in Fig. 6a. The model fitted to the estimated covariance is:

$${C}_Y(h)=1.5+1.5\exp \left(-h/3373\right)$$
(38)
Fig. 5
figure 5

a Omnidirectional experimental variogram (solid blue dots) and fitted model (solid red line) for log-transmissivity estimated from pumping tests. b Omnidirectional experimental variogram (solid blue dots) and fitted model (solid red line) for the log-transmissivity estimated from borehole lithofacies. c Omni-directional experimental cross-variogram (solid blue dots) and fitted model (solid red line) between log-transmissivity estimated from pumping tests and log-transmissivity estimated from borehole lithofacies. d Experimental variogram of water head for the four main geographical directions

Full size image
Fig. 6
figure 6

Log-transmissivity field estimated by ordinary kriging. a Using log-transmissivity data from pumping tests (OK-1 in Table 5). b Using log-transmissivity data from borehole lithofacies (OK-2 in Table 5). The black squares represent the 41 locations at which log-transmissivity was measured from pumping tests. The biased spatial locations of the pumping tests are clear because the low transmissivity regions (A, B, C and D) have no pumping tests. The units of log-transmissivity are ln(m2/day)

Full size image

i.e., an isotropic exponential covariance with a nugget variance of 1.5, a partial sill of 1.5 and a range of 3,373 m. A study of the uncertainty of the covariance parameters for log-transmissivity can be found in Pardo-Igúzquiza et al. (2009).

The second result is the log-transmissivity obtained by ordinary kriging of the log-transmissivity data from the hydrofacies data. The estimated variogram and the model fitted for the log-transmissivity data from pumping tests are shown in Fig. 5b; the estimated log-transmissivity field is shown in Fig. 6b. The model fitted to the estimated covariance is:

$${C}_Z(h)=2.14+4.98\exp \left(-h/3373\right)$$
(39)

i.e., an isotropic exponential covariance with a nugget variance 2.14, a partial sill of 4.98 and a range of 3,373 m. Both covariances were modelled with the same range because the same range must be used in the linear co-regionalization model to generate the co-kriged estimates.

Another result of estimated log-transmissivity maps is provided by ordinary co-kriging with one unbiasedness condition. In this case the estimated cross-variogram and the fitted model are shown in Fig. 5c and the fitted model is

$${C}_Y(h)=1.5\exp \left(-h/3373\right)$$
(40)

The cross-covariance between the two types of log-transmissivity data was difficult to estimate from the data as the experimental sampling plan was heterotopic (Wackernagel 2003) with few sites at which both the primary and secondary variables were sampled.

The linear model of co-regionalization was used to model the direct and cross covariances. The estimated maps are provided in Fig. 7a,b for ordinary co-kriging using both types of log-transmissivity data and considering the pumping test data and the lithofacies data as primary variables respectively.

Fig. 7
figure 7

Log-transmissivity field estimated by ordinary co-kriging with one unbiasedness condition and using log-transmissivity data from the pumping test and the borehole log-transmissivity lithofacies data. a Using log-transmissivity data from pumping tests as the primary variable (OCOK-1-2 in Table 5). b Using log-transmissivity data from borehole lithofacies as the primary variable (OCOK-2-1 in Table 5). The units of log-transmissivity are ln(m2/day)

Full size image

A fourth result is the log-transmissivity estimated by universal co-kriging using the log-transmissivity data from the pumping test and the head data. The experimental variograms of the water head for the four main geographical directions is shown in Fig. 5d. The water head clearly has a trend (Fig. 8) that provides the difference in potential energy (in an unconfined aquifer) that drives the water flow from the northern and eastern parts of the aquifer towards the south-east where the water exits the aquifer. As there is a small number (37) of water head data together with a trend and the parameters of the variogram of the residual must be estimated, the maximum likelihood estimation method was used to infer these parameters (Pardo-Igúzquiza 1997). The estimated water head trend is:

$${m}_H\left(x,y\right)=423.3874+0.006125x+00.3368y$$
(41)
Fig. 8
figure 8

a Water head map (in metres) estimated by universal kriging with a linear drift and the variogram of the residuals estimated by maximum likelihood. b Numerical model of the aquifer using a discretization of 100 m × 100 m cells. The cells of the aquifer are active cells while the cells outside of the aquifer are impervious cells that remain inactive. The coloured line (blue and red) represents the boundary Ω. The different colours represent the different boundary conditions: the blue line represents the border with a fixed head boundary condition and the red line represents the no-flow boundary condition

Full size image

where

$$\textrm{E}\left\{H\left(\textbf{u}\right)\right\}={m}_H\left(\textbf{u}\right)={m}_H\left(x,y\right)$$
(42)

The estimated isotropic variogram of the residual is:

$${\gamma}_R(h)=241.4\textrm{Sph}\left(h;7147\right)$$
(43)

i.e., a spherical model with no nugget effect, a sill of 241.4 and a range of 7,147 m. The water head field, estimated by using universal kriging with a linear trend, is shown in Fig. 8.

The cross-covariance between log-transmissivity and water head is required for the application of inverse model universal co-kriging. The estimated cross-covariance between log-transmissivity data from the lithofacies and the water head data is shown in Fig. 9a. This cross-covariance is anisotropic, antisymmetric and shows a high statistical variability because of the small amount of data in the data sets, especially in the water head data set. Consequently, instead of trying to fit a convoluted model to the experimental variogram, Dagan’s (1985) analytical solution was used. Figure 9b shows the analytical cross-covariance provided by Dagan’s solution which can be compared with the experimental cross-covariance in Fig. 9a. A comparison of Figs. 9a and 9b shows that the neat cross-covariance model in Fig. 9b can be intuited in the experimental cross-covariance in Fig. 9a. The cross-covariance is anisotropic, with higher variability in the flow direction and vanishing in a direction perpendicular to the water flow. In addition, the cross-covariance is antisymmetric with:

$${C}_{YH}(h)=-{C}_{YH}\left(-h\right)$$
(44)
Fig. 9
figure 9

a Experimental cross-covariances between log-transmissivity and water head. The different colours represent different spatial directions. Experimental variogram (solid blue dots) and fitted model (solid red line) for log-transmissivity estimated from pumping tests. b Theoretical cross-covariances between log-transmissivity and water head. Experimental variogram (solid blue dots) and fitted model (solid red line) for the log-transmissivity estimated from borehole lithofacies. c Experimental cross-covariance between log-transmissivity data from pumping tests and log-transmissivity data from lithofacies. Note the low value of the cross-covariance close to the origin indicating that the maximum correlation is reached for a distance for which one data set should be shifted with respect to the other. This explains the low correlation between the two data sets indicated by the variogram in Fig. 5c

Full size image

However, the co-kriging covariance matrix is still symmetric because for a given single entry in this matrix in relation to the cross-covariance:

$${C}_{YH}\left({\textbf{u}}_i-{\textbf{u}}_j\right)={C}_{HY}\left({\textbf{u}}_j-{\textbf{u}}_i\right)$$
(45)

The cross-covariance between log-transmissivity from the pumping tests and the water head is the imposed cross-covariance given in Eq. (7) with 3.0, 0.0061, and 3,373 m for \({\sigma}_Y^2\), β1 and ℓ, respectively. The same is valid for the cross-covariance between log-transmissivity data from lithofacies and water head but taking into account that \({\sigma}_Y^2\) is equal to 7.12. Four cases of the inverse problem by universal co-kriging have been considered:

  • Inverse problem universal co-kriging using log-transmissivity data from pumping tests and water head data. The estimated map of log-transmissivity is shown in Fig. 10a.

  • Inverse problem universal co-kriging using log-transmissivity data from lithofacies and water head data. The estimated map of log-transmissivity is shown in Fig. 10b.

  • Inverse problem universal co-kriging using log-transmissivity data from the pumping test, log-transmissivity data from lithofacies and water head data. The log-transmissivity data from the pumping test is the primary variable, the other two are secondary variables. The estimated map of log-transmissivity is shown in Fig. 11a.

  • Inverse problem universal co-kriging using log-transmissivity data from pumping tests, log-transmissivity data from lithofacies and water head data. The log-transmissivity data from lithofacies is the primary variable, the other two are secondary variables. The estimated map of log-transmissivity is shown in Fig. 11b.

Fig. 10
figure 10

Log-transmissivity (T) field estimated by inverse problem ordinary universal co-kriging with two variables: a Using log-transmissivity data from pumping tests and water head data (IP-UCOK-1 in Table 5). The white arrow shows a channel of relatively high transmissivity that is discussed in the main text. b Using log-transmissivity data from borehole lithofacies and water head data (IP-UCOK-1 in Table 5). The units of log-transmissivity are ln(m2/day)

Full size image
Fig. 11
figure 11

Log-transmissivity (T) field estimated by inverse problem ordinary universal co-kriging with three variables: log-transmissivity data from pumping tests, log-transmissivity data from borehole lithofacies and water head data. a Using log-transmissivity data from pumping tests as the primary variable (IP-UCOK-1-2 in Table 5). b Using log-transmissivity data from borehole hydrofacies as the primary variable (IP-UCOK-2-1 in Table 5). The units of log-transmissivity are ln(m2/day)

Full size image

The implications of these results are discussed in the following section.

Discussion

Although the different geostatistical estimation methods provide different transmissivity fields (Figs. 6, 7, 10 and 11), they are significantly coherent. The log-transmissivity field obtained by ordinary kriging of the log-transmissivity data (Fig. 6a) from the pumping test provides a transmissivity map with the coarsest detail and it is based on biased data in the sense of preferential sampling in areas of high transmissivity as may be seen in Fig. 6b, where low transmissivity zones A, B, C and D, in the figure, have no pumping test. The transmissivity field estimated by ordinary kriging of the log-transmissivity data from the hydrofacies data generates a map (Fig. 7b) that agrees with the general trend provided by the previous transmissivity field. It also incorporates more detail because there are more experimental data that were sampled more homogenously over the whole area rather than only in high transmissivity zones.

An improved map could be generated by ordinary co-kriging using the additional indirect transmissivity data from the hydrofacies or by using inverse problem co-kriging and head data. The estimated log-transmissivity maps for ordinary co-kriging are provided in Fig. 7a,b for the cases that consider as primary variables the experimental data from pumping tests or from lithofacies. A comparison of the ordinary kriging maps and the ordinary co-kriging maps shows that they are very similar because the cross-correlation between the two sets of log-transmissivity data is low and thus the information provided by the secondary information is low. This is especially clear by comparing Figs. 6b and 7b, which are almost identical.

With respect to the inverse problem, universal co-kriging of the four previous possibilities resulted in the log-transmissivity maps in Figs. 10 and 11. Figure 10 is a log-transmissivity map estimated by inverse problem universal co-kriging using two variables. Figure 10a uses log-transmissivity data from pumping tests and water head data while Fig. 10b uses log-transmissivity data from lithofacies and water head data. Figure 11 is the log-transmissivity map estimated by inverse problem universal co-kriging using three variables: the two log-transmissivity data sets and water head data. Figure 11a uses log-transmissivity data from pumping tests as the primary variable and in Fig. 11b the primary variable used was log-transmissivity data from the lithofacies.

The different methods could also be compared by their estimation variance for the different methodologies; however, these results depend significantly on the parameters estimated for the covariances of the different variables and a more independent comparison would be better. For this, the transmissivity fields can be used as input to the direct problem of using the groundwater flow model to estimate the May 1970 head field. The direct model solves the 2D steady-state saturated groundwater flow model in an unconfined aquifer and can be written in terms of log-transmissivities as given in Eq. (22) with the boundary conditions of no-flow and prescribed head given in Fig. 8. The area in Fig. 8 was discretized into 265 × 200 cells of 100 m × 100 m and a finite difference scheme was used to solve Eq. (22) taking into account two types of boundary conditions—no-flow and prescribed head, of which the no-flow boundary condition implies no-flow in the perpendicular direction.

The boundary conditions for the steady-state model were chosen as the specified heads as provided by the universal kriging map of water head shown in Fig. 8 and the no-flow boundaries in the borders are those determined from previous studies—Pardo-Igúzquiza et al. (2009); Pardo-Igúzquiza and Chica-Olmo 2004, 2007 and Kuhlman and Pardo-Igúzquiza (2010).

Taking each estimated log-transmissivity field as an input it is possible to estimate the water head data by solving Eq. (17) using the boundary conditions of Fig. 8. From the modelled water head field it is possible to calculate the corresponding water head values at the experimental locations where water head is known and different validation statistics can be calculated. The validation statistics considered in this work are mean error (ME), mean squared error (MSE), mean normalized squared error (MNSE), the mean absolute error (MAE), the Nash and Sutcliffe (1970) efficiency (NSE) and the Kling-Gupta Efficiency criteria (KGE) (Knoben et al. 2019):

$$\textrm{ME}=\frac{1}{N}\sum_{i=1}^N\left({h}_i^{\textrm{o}}-{h}_i^{\textrm{m}}\right)$$
(46)
$$\textrm{MSE}=\frac{1}{N}\sum_{i=1}^N{\left({h}_i^{\textrm{o}}-{h}_i^{\textrm{m}}\right)}^2$$
(47)
$$\textrm{MNSE}=\frac{1}{N}\sum_{i=1}^N\frac{{\left({h}_i^{\textrm{o}}-{h}_i^{\textrm{m}}\right)}^2}{h_i^{\textrm{o}}}$$
(48)
$$\textrm{MAE}=\frac{1}{N}\sum_{i=1}^N\left|{h}_i^{\textrm{o}}-{h}_i^{\textrm{m}}\right|$$
(49)
$$\textrm{NSE}=1-\frac{\sum_{i=1}^N{\left({h}_i^{\textrm{o}}-{h}_i^{\textrm{m}}\right)}^2}{\sum_{i=1}^N{\left({h}_i^{\textrm{o}}-\overline{h_i^{\textrm{o}}}\right)}^2}$$
(50)
$$\textrm{KEG}=1-\sqrt{{\left(r-1\right)}^2+{\left(\frac{\sigma_{\textrm{m}}}{\sigma_{\textrm{o}}}-1\right)}^2+{\left(\frac{\mu_{\textrm{m}}}{\mu_{\textrm{o}}}-1\right)}^2\ }$$
(51)
\({h}_i^{\textrm{o}}:\):

Head datum observed at the ith location

\({h}_i^{\textrm{m}}:\):

Head datum modelled by the groundwater flow Eq. (17) at the ith location

\(\overline{h_i^{\textrm{o}}}:\):

Mean of the observed values

σ o:

Standard deviation of observed values

σ m:

Standard deviation of modelled values

μ o:

Mean of observed values, i.e., equal to \(\overline{h_i^o}\)

μ m:

Mean of modelled values

N:

Number of spatial locations at which the water head was measured

The ME should be zero for an unbiased model. The MSE, MNSE and MAE should be as small as possible, whereas NSE and KGE should be as close to 1 as possible. The results obtained for the different validation statistics for the different geostatistical methodologies are shown in Table 5.

Table 5 Mean error (ME), mean square error (MSE), mean normalized square error (MNSE), mean absolute error (MAE), Nash and Sutcliffe efficiency (NSE) and the Kling-Gupta Efficiency (KGE) validation statistics for the different geostatistical methods. The geostatistical methods are ordinary kriging with log-transmissivity from pumping tests (OK-1), ordinary kriging with log-transmissivity data from boreholes (OK-2), ordinary co-kriging with log-transmissivity data from pumping tests and from hydrofacies (COK-1-2), inverse problem universal co-kriging with log-transmissivity data from pumping tests and head data (IP-UCOK-1) and inverse problem universal co-kriging with log-transmissivity data from hydrofacies and head data (IP-UCOK-2)
Full size table

A field of constant log-transmissivity was used as a reference for comparison and the validation results are also shown in Table 5. The ordinary kriging map of the log-transmissivity data from pumping tests provides a map that produces worse results (MSE = 5.4197, in Table 5) than considering a field of constant log-transmissivity (MSE = 5.2864). This implies that the image in Fig. 6a is not a good representation of the true unknown underlying log-transmissivity field and even a constant image—for example, the mean log-transmissivity value, gives better performance results. However, the ordinary kriging map of log-transmissivity obtained by using the lithofacies and shown in Fig. 6b produces the third-best result (MSE = 1.7418) of all the methods that have been tested. A comparison of Figs. 6a and 6b shows that Fig. 6b has significantly more spatial detail than Fig. 6a, especially in the elongated high log-transmissivity values in the centre of the western part of the aquifer. The use of ordinary co-kriging with the log-transmissivity data as the primary variable makes very little difference (MSE = 5.2764) when compared with ordinary kriging (MSE = 5.4197). Using ordinary co-kriging with log-transmissivity data from lithofacies gives worse results (MSE = 2.7325) than ordinary kriging (MSE = 1.7418). In fact, it seems that, despite the coherence of the basic statistics and histograms (Figs. 2b and 3c) of both log-transmissivity data sets, they have no spatial correlation for a distance of zero as may be seen in Fig. 9c, which shows the spatial cross-covariance between the two data sets. Thus, the cross-variogram (Fig. 5c) used in ordinary co-kriging does not capture the spatial shift between the two data sets and the sill of the cross-variogram indicates a low correlation of around 0.3 between the two data sets. As a result, merging the two data sets is not useful as the cross-variogram cannot capture the complexity of the cross-covariance in Fig. 9c; however, each data set can be used independently of the other. When applying inverse problem universal co-kriging, Fig. 10a is obtained by using the log-transmissivity data from pumping tests and the water head data provide the best image as measured by the validation statistics in Table 5 (MSE = 0.6305). This image is even better than the solution given by inverse problem universal co-kriging using the log-transmissivity data from the lithofacies and the water head data (MSE = 1.3799), even though the log-transmissivity from the lithofacies data were better in ordinary kriging and ordinary co-kriging. The images of the log-transmissivity fields (Fig. 10a,b) are clearly improved by including the water head data irrespective of the log-transmissivity data set used.

Finally, if the three variables (the two log-transmissivity data sets and the water head data) are used in the inverse problem universal co-kriging, the results deteriorate because of the spatial incompatibility of the two log-transmissivity data sets. When the pumping test data are used as the primary variable the results are bad (MSE = 5.9882). They are also bad when the primary variable is the lithofacies data (MSE = 2.9084). The estimated log-transmissivity fields are given in Fig. 11.

To put these results into perspective it must be said that the aquifer boundary conditions shown in Fig. 8 have a strong influence on the output of the direct modelling and even using a constant log-transmissivity field gives good results as can be seen in Fig. 12a where the scatterplot between observed versus modelled water head data can be compared with Fig. 12b, which shows the scatterplot with the best results obtained by inverse problem universal kriging using the pumping test log-transmissivities and water head data in Fig. 10a. In terms of the NSE and KGE validation statistics, the solutions provided by the different methods are very similar as can be seen in Table 5. However, the best estimated log-transmissivity field is the one in Fig. 10a, which was obtained by inverse problem universal co-kriging using the pumping test data and water head data. This figure shows remarkably well the high log-transmissivity channel that runs through the central part of the aquifer (highlighted with a white arrow in Fig. 11a) and follows the course of the Genil River (black arrow in Fig. 1c), thus confirming the conceptual model proposed by the hydrogeologists who have worked in this area over an extended period (Castillo 1986; Luque-Espinar 2001; García-Soldado 2009). This conceptual model consists of a channel of high transmissivity running through the middle of the aquifer with transmissivity decreasing towards the borders; however, Fig. 10a provides a quantitative and more complete picture than the simple conceptual scheme proposed by the hydrogeologists.

Fig. 12
figure 12

Observed water head versus modelled water head for two extreme cases of the estimated log-transmissivity field. a Constant log-transmissivity. b The method with the best performance in Table 5, that is, inverse problem universal co-kriging using log-transmissivity data from pumping tests and water head data (IP-UCOK-1)

Full size image

It is well-known that even the best estimated image, such as the one in Fig. 10a, is a smoothed version of the true but unknown log-transmissivity field. Since Delhomme (1979), geostatistical simulation has been used to generate simulated images of the transmissivity field of an aquifer in which each image reproduces the real variability of the log-transmissivity as expressed by the variogram. A representative set of these images includes the uncertainty introduced by the spatial variability of the transmissivity between the experimental data. It is possible that one of these simulated images is very close to the reality but all of them must be used because the reality is unknown. Obviously, the uncertainty of the parameters of the variogram model should also be taken into account when generating the simulated images. By using a large number of simulated images, it is, for example, possible to transfer the uncertainty in the transmissivity field into the uncertainty of the modelled water head. Thus, at each location, instead of having a single modelled water head, there is an ensemble of water heads the histogram of which provides the probability of the water head having a given interval value or being higher than a given threshold at each location. However, this is not the purpose of the work presented here, which is to identify smooth log-transmissivity images that contain as much detail as possible, and that can be used, inter alia, for modelling, optimization of observation grids and planning future geophysical campaigns.

Conclusions

Co-kriging, in its various forms, provides a means of combining different sources of hydrogeological information, which is particularly useful in estimating transmissivity fields. A case study of a detritic unconfined aquifer in southern Spain has been used as a benchmark for comparing methodologies. The transmissivity field generated from the lithofacies measured at boreholes demonstrates the importance of the indirect measures of log-transmissivity obtained from indirect data. This is particularly important because log-transmissivity data from pumping tests are biased towards high values as pumping tests are usually conducted to validate boreholes for productive water extraction. Nevertheless, the validation results show the incompatibility of the two types of information—the hard log-transmissivity data from the pumping tests and the soft log-transmissivity data from the lithofacies. Each log-transmissivity datum from the pumping tests encapsulates the permeability value (or hydraulic conductivity) and the saturated thickness at the location of the test. On the other hand, the transmissivity data from the lithofacies is proportional to the transmissivity from pumping tests (Table 3) and does not contain information on saturated thickness. A mean saturated thickness of 100 m for the aquifer is assumed in order to transform the permeability data into transmissivity data or, more exactly, data with “transmissivity units”. The incompatibility between the two log-transmissivity data sets is due to the spatial variability of the saturated thickness. The log-transmissivity data from the pumping test incorporates that spatial variability (at least in theory), whereas the log-transmissivity data from the lithofacies does not.

However, even though the log-transmissivity data sets are incompatible, if there were no pumping test data, the log-transmissivity data from the lithofacies would provide reasonable images of the log-transmissivity field that could be further improved by incorporating the water head data by inverse modelling with universal co-kriging. Nevertheless, the best results were obtained by inverse problem universal co-kriging using the log-transmissivity data from pumping tests and the water head data (Fig. 10a; Table 5). In addition, the ability of analytical solutions to obtain the cross-covariance between log-transmissivity and water head data has been demonstrated. In particular, the analytical solution of Dagan (1985) overcomes the necessity of fitting a model to a complex cross-covariance that is anisotropic, antisymmetric and difficult to visualize from the experimental cross-covariances. However, a verification of the analytical solution using the experimental data is desirable. A comparison of the different estimated log-transmissivity values can be used to improve knowledge of the transmissivity field and could be used to optimize the locations for acquiring additional experimental data—pumping test data, borehole data and geophysical data. In the interests of open science, the experimental data used in the work have been provided. This will allow others to verify the work or assess alternative methodologies to obtain more reliable log-transmissivity fields.