Joint inversion of groundwater flow, heat, and solute state variables: a multipurpose approach for characterization and forecast of karst systems

Abstract

Characterization of karst systems and forecast of their state variables are essential for groundwater management and engineering in karst regions. These objectives can be met by the use of process-based discrete-continuum models (DCMs). However, results of DCMs may suffer from inversion nonuniqueness. It has been demonstrated that the joint inversion of observations regulated by different natural processes can tackle the nonuniqueness issue in groundwater modeling. However, this has not been tested for DCMs thus far. This research proposes a methodology for the joint inversion of hydro-thermo-chemo-graphs, applying to two small-scale sink-to-spring experiments at Freiheit Spring, Minnesota, USA. In order to address conceptual uncertainty, a multimodel approach was implemented, featuring seven mutually exclusive variants. Spring hydro-thermo-chemo-graphs, for all the variants simulated by MODFLOW-CFPv2, were jointly inverted using a weighted least squares algorithm. Subsequently, models were compared in terms of inversion and forecast performances, as well as parameter uncertainties. Results reveal the suitability of the DCM approach for simultaneous inversion and forecast of hydro-physico-chemical behavior of karst systems, even at a scale of meters and seconds. The estimated volume of the tracer conduit passage ranges from approximately 46–51 m³, which is comparable to the estimate from the flood-pulse method. Moreover, it was demonstrated that the thermograph and hydrograph contain more information about aquifer characteristics than the chemograph. However, this finding can be site-specific and should depend on the analysis scale, the considered conceptual models, and the hydrological state, which are potentially affected by minor unaccountable processes and features.

Résumé

La caractérisation des systèmes karstiques et la prédiction de leurs variables d’état sont essentielles pour la gestion des eaux souterraines et l’ingénierie en région karstique. Ces objectifs peuvent être atteints par l’utilisation de modèles discrets-continus (DCM) basés sur les processus. Cependant les résultats des DCM peuvent pâtir de l’absence d’unicité de l’inversion. Il a été démontré que l’inversion conjointe d’observations contrôlées par différents processus naturels peut résoudre le problème d’absence d’unicité en modélisation hydrogéologique. Pourtant cela n’a pas encore été testé avec les DCM. Cette étude propose une méthodologie pour l’inversion conjointe des signatures hydro-thermo-chimiques qui est appliquée à deux expériences perte-source à l’échelle locale (source Freiheit, Minnesota, Etats-Unis d’Amérique). Afin de traiter l’incertitude conceptuelle, une approche multimodèle est mise en œuvre, impliquant sept variantes mutuellement exclusives. Les signatures hydro-thermo-chimiques de la source, pour toutes les variantes simulées avec MODFLOW-CFPv2, sont inversées conjointement en utilisant un algorithme des moindres carrés pondérés. Ensuite, les modèles sont comparés en termes d’inversion et de performance de prédiction, ainsi que d’incertitude des paramètres. Les résultats montrent l’adéquation de l’approche DCM pour l’inversion simultanée et la prédiction du comportement hydro-physico-chimique des systèmes karstiques, même à l’échelle des mètres et des secondes. Le volume estimé du tronçon de conduit tracé est de l’ordre de 46–51 m³, comparable à l’estimation basée sur la méthode de l’onde de crue. De plus, il est démontré que les thermogrammes et hydrogrammes contiennent plus d’informations sur les caractéristiques de l’aquifère que la chronique chimique. Cependant ce résultat peut être spécifique au site d’étude et doit dépendre de l’échelle d’analyse, des modèles conceptuels considérés et de l’état hydrologique qui peut être impacté par des processus et caractéristiques secondaires qui ne sont pas pris en compte.

Resumen

La caracterización de los sistemas kársticos y la previsión de sus variables de estado son esenciales para la gestión y la planificación de las aguas subterráneas en las regiones kársticas. Estos objetivos pueden alcanzarse mediante el uso de modelos de continuidad discreta (DCMs) basados en procesos. Sin embargo, los resultados de los DCM pueden adolecer de falta de unicidad en la inversión. Se ha demostrado que la inversión conjunta de observaciones reguladas por diferentes procesos naturales puede resolver el problema de la no unicidad en la modelización de las aguas subterráneas. Sin embargo, esto no se ha probado hasta ahora para DCMs. Esta investigación propone una metodología para la inversión conjunta de gráficos hidrotermoquímicos, aplicada a dos experimentos a pequeña escala de sumidero a manantial en Freiheit Spring, Minnesota (EE.UU.). Con el fin de abordar la incertidumbre conceptual, se aplicó un enfoque de modelos múltiples, con siete variantes mutuamente excluyentes. Los hidrotermoquimiogramas del manantial, para todas las variantes simuladas por MODFLOW-CFPv2, se invirtieron conjuntamente utilizando un algoritmo ponderado de mínimos cuadrados. Posteriormente, se compararon los modelos en términos de rendimiento de inversión y previsión, así como las incertidumbres de los parámetros. Los resultados revelan la idoneidad del enfoque DCM para la interpretación y previsión simultáneas del comportamiento hidrofísico-químico de los sistemas kársticos, incluso a escala de metros y segundos. El volumen estimado del conducto trazador oscila aproximadamente entre 46 y 51 m³, lo que es comparable a la estimación del método de pulso de inundación. Además, se demostró que el termógrafo y el hidrograma contienen más información sobre las características del acuífero que el quimógrafo. Sin embargo, esta conclusión puede ser específica de cada lugar y depender de la escala de análisis, los modelos conceptuales considerados y el estado hidrológico, que pueden verse afectados por procesos y características menores no explicables.

摘要

岩溶系统的特征和对其状态变量的预测对于岩溶地区地下水管理和工程至关重要。这些目标可以通过使用基于过程的离散连续模型(DCMs)来实现。然而，DCMs的结果可能受到反演非唯一性的影响。已经证明，由不同自然过程约束的观测数据联合反演可以解决地下水建模的非唯一性问题。然而，到目前为止，这还没有对DCMs进行测试。本研究提出了一种联合反演水-热-化学图的方法，应用于美国明尼苏达州Freiheit Spring的两个小尺度的排泄至泉的实验。为了解决概念上的不确定性，实施了一个多模型方法，具有七个相互独立的变量。使用加权最小二乘法对MODFLOW-CFPv2模拟的所有变量的泉水水-热-化学图进行了联合反演。随后，在反演和预报性能以及参数不确定性方面对模型进行了比较。结果显示，DCM方法适合于同时反演和预测岩溶系统的水文-物理-化学行为，即使是在米和秒的尺度。示踪剂传导通道的估计体积约为46至51 m³，这与洪水脉冲法的估计值相当。此外，事实证明，温度图和水文图比化学图包含更多关于含水层特征的信息。然而，这一发现可能是因地制宜的，应取决于分析尺度、所考虑的概念模型和水文状态，这些都有可能受到无法解释的小过程和特征的影响。

چکیده

Resumo

A caracterização de sistemas cársticos e a previsão de suas variáveis de estado são essenciais para o gerenciamento e engenharia de águas subterrâneas em regiões cársticas. Esses objetivos podem ser alcançados pelo uso de processos baseados em modelos discretos contínuos (MDCs). No entanto, os resultados de MDCs podem passar pela não unicidade de inversão. Tem sido demonstrado que a inversão conjunta de observações reguladas por diferentes processos naturais pode resolver o problema da não unicidade na modelagem de águas subterrâneas. No entanto, isso não foi testado para MDCs até o momento. Esta pesquisa propõe uma metodologia para a inversão conjunta de hidro-termo-quimiógrafos aplicando-se a dois experimentos em pequena escala de sumidouro para nascente em Freiheit Spring, Minnesota, EUA. Para lidar com a incerteza conceitual, uma foi implementada abordagem multimodelo, apresentando sete variantes mutuamente exclusivas. Os hidro-termo-quimiógrafos de nascente, para todas as variantes simuladas pelo MODFLOW-CFPv2, foram invertidos conjuntamente usando um algoritmo de mínimos quadrados ponderados. Posteriormente, os modelos foram comparados em termos de performance de inversão e previsão, bem como incertezas dos parâmetros. Os resultados revelam a adequação da abordagem MDC para a inversão simultânea e previsão do comportamento hidro-físico-químico de sistemas cársticos, mesmo em uma escala de metros e segundos. O volume estimado da passagem do conduto varia de aproximadamente 46–51 m³, o que é comparável à estimativa do método de pulso-inundação. Além disso, foi demonstrado que o termógrafo e o hidrograma contêm mais informações sobre as características do aquífero do que o quimógrafo. No entanto, essa conclusão pode ser específica do local e deve depender da escala de análise, dos modelos conceituais considerados e do estado hidrológico, que são potencialmente afetados por processos e feições menores e inexplicáveis.

Introduction

Karst aquifers are the source for approximately 13% of the global groundwater abstraction, supplying potable water to almost one-tenth of the world’s population (Stevanović 2019). These karst groundwater resources are generally characterized by discrete conduit networks of poorly known structure and geometry, developed within a rock matrix with presumed continuum porosity. The spatial distribution of storage and permeability fields within a karst system is not just significantly changing, but also generally unknown. Consequently, time series of hydrological (i.e., discharge and hydraulic heads) and water physico-chemical (i.e., temperature and solute concentration) state variables, in short “hydro-physico-chemical time series” or “hydro-thermo-chemo-graphs,” can vary extremely within the spatiotemporal domain, in an unfavorable and hardly forecastable fashion.

To meet the aforementioned challenges, a great deal of karst literature has been devoted to direct and indirect characterization of karst systems, especially the conduits. Speleological surveys are the most common direct method for characterizing karst conduits. Although highly informative, such surveys can be impractical when traversable conduits (i.e., caves) are absent, inaccessible, or not representative of the active flow system (Jeannin et al. 2007). Consequently, indirect characterizations based on borehole logging and geophysical surveys (Bechtel et al. 2007) and observed hydro-thermo-chemo-graphs (which is of interest in this work) are viable alternatives.

From a methodological perspective, the indirect methods based on hydro-thermo-chemo-graphs either involve the application of statistical methods (e.g., Shuster and White 1971; Mangin 1975) or the inversion of numerical models (e.g., Borghi et al. 2016; Teixeira Parente et al. 2019; Kavousi et al. 2020; Gill et al. 2021). Springs, regarded as representative monitoring sites for the global behavior of karst systems (Jeannin and Sauter 1998), comprise the only groundwater data collection point in many cases and are commonly utilized in this context.

From a driving force perspective, the indirect methods can further be categorized into two classes, either as driven by ambient recharge events, or through application of hydraulic and tracer tests (Geyer et al. 2013). Flood-pulse analysis (Ashton 1966), also called pulse-train analysis (Wilcock 1968; Ford and Williams 2007), is a conventional indirect method for estimation of phreatic conduit volume, which has been used for either recharge events (e.g., Ryan and Meiman 1996) or combined hydraulic and tracer tests (e.g., Luhmann et al. 2012). The method calculates the phreatic conduit volume as the bulk water discharged from the spring between the commencement of the hydrograph rise due to the pressure pulse and the chemograph drop due to the new water that emerged. Although the flood-pulse analysis intuitively estimates karst conduit volumes, it can result in overestimation if water is drained from the rock matrix (Birk et al. 2006) or epikarst zone (Williams 1983). Although it has not been reported, the method may theoretically underestimate the volume if new water is pushed from the conduit into the matrix due to the increased conduit head.

Several distributed numerical modeling approaches have been developed for the simulation of karst systems, as reviewed by Kovács and Sauter (2007), Ghasemizadeh et al. (2012), and Hartmann et al. (2014). Inverse application of such models has been employed for karst system characterization for over two decades (e.g., Larocque et al. 1999; Kordilla et al. 2012; Al Aamery et al. 2021; Jeannin et al. 2021); however, among the modeling approaches, only the discrete-continuum models (DCMs) can directly employ measured state variables and natural processes taking place within real-world karst systems (Kovács and Sauter 2007). Therefore, inverse modeling utilizing such process-based hybrid models can simulate not only the observed system state variables, but also support the system characterization.

Discrete-continuum models are generally composed of two compartments, i.e., discrete conduits, embedded into a rock matrix continuum (Király 1998). Over the last three decades, several DCM codes (e.g., Király et al. 1995; Liedl et al. 2003; Shoemaker et al. 2008; de Rooij et al. 2013; Reimann et al. 2018; Malenica et al. 2018; Tinet et al. 2019) and DCM-enabled general-purpose codes (e.g., Zimmerman 2006; Cornaton 2007; Therrien et al. 2010; Panday et al. 2013; Diersch 2014) have been developed. The major difference between them is their treatment of flow regimes in the conduits and the capability of accommodating coupled flow and transport simulation. As a matter of fact, only a few codes, including MODFLOW-CFPv2, in short “CFPv2” (Reimann et al. 2018), can consider both laminar and turbulent flow regimes, coupled with solute and heat transport processes.

It has been demonstrated that the joint inversion (i.e., simultaneous history matching) of different flow and transport observations can reduce the ambiguity of the inversion, i.e., parameter uncertainty and model nonuniqueness in single continuum models (Gailey et al. 1991; Harvey and Gorelick 1995; Bravo et al. 2002; Xu and Gómez-Hernández 2016). Borghi et al. (2016), utilizing the GROUNDWATER code, showed that this theory can also be supported for flow and solute transport DCMs. Considering synthetic models, they further suggested that the gradient-based linear optimization techniques are efficient and promising for karst aquifer characterization.

Utilization of hydro-thermo-chemo-graphs as the calibration target requires simultaneous simulation of flow and transport in karst systems, which is a challenging task and not supported by many DCMs. Therefore, most DCM applications have been limited to groundwater flow processes, and few joint inversion cases have been reported. Mohammadi et al. (2018) and Chang et al. (2019) successfully used CFPv2 for the joint inversion of spring hydro-chemo-graphs in Iran and China, respectively. Kavousi et al. (2020) jointly inverted the measured long-term hydro-thermo-chemo-graphs of a large-scale karst system in Iran, employing CFPv2. Their statistically robust results served as a proof of concept for the DCM approach.

The aforementioned model applications supported proof of the suitability of DCMs to simulate the integrated responses of matrix-conduit compartments for medium- and large-scale karst systems. However, simulating the individual, differential responses of a short conduit section is important for advancing understanding of karst flow and transport processes and their adequate representation in DCMs. Furthermore, these small-scale model applications enable the diagnosis of potential DCM structural inadequacies, which are not likely distinguishable for large-scale models, and have not been investigated thus far. In a large karst system, several preferential flow paths can dynamically contribute to the spring water, such that the effects (i.e., the information) of individual flow and transport processes in different parts of the system are superimposed in the observed global behavior at the spring, a theory is consistent with the theoretical backgrounds on flow and transport signal transmission in karst systems (e.g., Smart 1983) and is also supported by direct observations. Perrin et al. (2007) and Vuilleumier (2017), studying the well-defined Milandre Karst System in Switzerland, demonstrated that the superimposition of hydro-chemo-graphs recorded at different conduit tributaries yields the bulk spring signal. This superimposition may cause issues with parameter inference from inverse process-based models, such that the parameter estimates may not represent the real system; moreover, the process length- or timescales (Covington et al. 2012) of flow and transport phenomena may be exceeded in a large karst system, resulting in strong damping of hydro-thermo-chemo-graph signals. Therefore, a spatially small-scale site is chosen in this research, where the effects of relevant flow and transport processes in the observed hydro-thermo-chemo-graphs are likely preserved.

Results of inverse models can be highly affected by the chosen conceptual model. There are two major approaches to developing hydrogeological conceptual models (Enemark et al. 2019): (1) the consensus approach and (2) the multimodel approach. In the former, the current state of knowledge on the site would be integrated into a single conceptual model, such that the model would be sequentially updated to a future state of knowledge (Brassington and Younger (2010) and Enemark et al. (2019). However, in the latter, alternative plausible conceptual models are being developed and tested in parallel at any stage (Neuman and Wierenga (2003) and Enemark et al. (2019). The multimodel approach is not aimed at finding a single best model, but rather an ensemble of alternative conceptual models, accounting for the fact that “the hydrogeological functioning of a system can be interpreted in different ways” (Enemark et al. 2019). This approach is especially superior when the knowledge about the system is limited (Neuman and Wierenga 2003; Enemark et al. 2019), and hence, it is adopted in this study.

This work demonstrates the joint inversion and forecast of spring hydro-thermo-chemo-graphs from two spatiotemporally small-scale controlled experiments, pursuing the following objectives: (1) proposing and examining a methodology for joint inversion of state variables in karst systems, using a DCM approach; (2) focusing on potential model structural inadequacies for small-scale applications; (3) revealing conceptual and parameter uncertainties; and (4) inspecting the relative importance of different flow and transport state variables.

Materials and methods

This section introduces a methodology for joint inversion in karst systems using a process-based DCM approach that relies on three steps (Fig. 1):

• Step 1. Acquiring knowledge of the system, based on the hydrogeological investigations and monitoring networks of flow and transport observations. Further investigations should be carried out to close data gaps and collect information on the parameters and boundary conditions. Flow observations, including discharges (Q) and hydraulic heads (H), and transport observations, including water temperatures (T) and solute concentrations (C), are of interest. The time series of these state variables from springs and observation wells provide data for the joint inversion and forecast.

• Step 2. Building conceptual and numerical models. The knowledge acquired from the site is transferred to the conceptual multimodels, which are subsequently translated to the numerical model variants.

• Step 3. Performing joint inversion, post-inversion comparisons, and uncertainty assessment. This step incorporates joint inversion and post-inversion comparison of conceptual variants, through model performances and selection, testing, and evaluation of estimated parameters and observation data.

Fig. 1

Flowchart of proposed methodology for joint inversion of observed flow and transport state variables in a karst system, using the DCM approach (Notation: QTCH: water flux, temperature, solute concentration, and hydraulic head; BCs: boundary conditions; σ²_rel: relative parameter uncertainty variance reduction)

Acquiring knowledge of the system, based on the hydrogeological investigations and monitoring networks of flow and transport observations. Further investigations should be carried out to close data gaps and collect information on the parameters and boundary conditions. Flow observations, including discharges (Q) and hydraulic heads (H), and transport observations, including water temperatures (T) and solute concentrations (C), are of interest. The time series of these state variables from springs and observation wells provide data for the joint inversion and forecast.

Building conceptual and numerical models. The knowledge acquired from the site is transferred to the conceptual multimodels, which are subsequently translated to the numerical model variants.

Performing joint inversion, post-inversion comparisons, and uncertainty assessment. This step incorporates joint inversion and post-inversion comparison of conceptual variants, through model performances and selection, testing, and evaluation of estimated parameters and observation data.

The proposed methodology can consider multiple purposes of interpretative model applications (i.e., system understanding, parameter estimation, etc.), forecasts, and further numerical code improvements. Moreover, further conceptual model amendments and guidelines for effective parameter and observation data acquisition can be supported.

Study site

Freiheit Spring (MN23:A00041), located in SE Minnesota, United States, was chosen as the study site. Relevant information about the hydrogeological setting and utilized data are provided in the following.

Hydrogeological setting

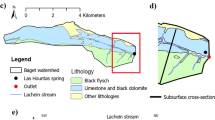
Freiheit Spring emerges from the Stewartville Formation, which is subhorizontally overlain and underlain by Dubuque-Maquoketa and Prosser-Cummingsville Formations, respectively (Steenberg and Runkel 2018). These formations are partially or entirely comprised of karstified limestone and dolostone with ubiquitous karst features such as sinkholes, sinking streams, caves, and springs—for details see Runkel et al. (2003); Mossler (2008); Steenberg (2014). Based on several qualitative and quantitative tracer tests, the areas of the Freiheit surface watershed and groundwater springshed were estimated as ~6.51 and ~0.91 km², respectively (Fig. 2).

Fig. 2

a Groundwater springshed and surface watershed of Freiheit Spring on a LiDAR-based digital terrain model from the National Elevation Dataset, NED (GIS data were retrieved from Green et al. 2018). b 3D hill-shade view of the aquifer terminal part, presenting the test sinkhole, spring, groundwater springshed, and considered conduits with colored arrows (vertical exaggeration: 1.5; camera field of view: 45°). The arrow colors (b) are based on the conduit conceptualization, as presented in the next figure. The green and yellow arrows indicate the known conduit path from the test sinkhole to the spring, while the blue and purple arrows represent potential conduits located upstream and downstream of the test sinkhole, respectively

Flow and transport in the Freiheit karst system are influenced by the effect of preferential conduit flow based on the following evidence:

• 1. Secondary solutional porosity in the geological formations is well developed (Runkel et al. (2003).

• 2. Velocities derived from tracer tests monitored at Freiheit Spring (Luhmann et al. 2012, 2015) exceed the median conduit flow velocities for 3,015 sink-to-spring tracer tests in karst systems (Worthington and Ford 2009).

• 3. Variations of the spring water quality and quantity are significant, such that the water flux, temperature, and specific conductivity during the measurement period (2008–2011) ranged from 10 to 385 L s^–1, 5.6–11.6 °C, and 0.3–0.7 mS cm^–1, respectively. Moreover, the spring water tends to be turbid during high flows, indicating relatively large opening sizes and suitable water velocities for particle transport.

Applied hydraulic and tracer experiments (observation data)

Two combined hydraulic and multitracer experiments were conducted at the downgradient end of the Freiheit karst system during a hydrograph recession—see Luhmann et al. (2012, 2015); Table 1; Fig. 2. Water with known elevated temperature and solute concentration (including salt, uranine, and deuterated water for the first experiment and salt for the second experiment) was injected into a sinkhole with ~95-m horizontal and ~19-m vertical distances to the spring. The spring responses were continuously recorded by data loggers (water flux, temperature, and specific conductivity) at a high temporal resolution (1-s periods) or collected as grab samples (concentrations of uranine, deuterium, and suspended sediment).

Table 1 Relevant characteristics of the applied hydraulic and tracer experiments (see Luhmann et al. (2012, 2015) for detailed explanation).

The main relevant features and outcomes of the experiments are summarized in the following list (for details see Luhmann et al. (2012, 2015):

• Spring discharge started to increase shortly after the injection, well before the physicochemical responses, suggesting full-pipe flow.

• Turbidity was the next signal to rise and peak, emphasizing the full-pipe flow.

• The dampened heat signal arrived later than the conservative solute signals. Moreover, the temperature signal had a much longer tailing, which shows the importance of conductive heat exchange within the rock matrix.

• The single-spike hydro-thermo-chemo-graphs imply a single conduit passage.

• The hydrodynamic conditions were very similar for both tests; however, some rainfall occurred between the two experiments, causing more background variability in the spring water before the second experiment (Table 1).

The controlled experiments documented the unique combination of hydraulic pressure, advection, dispersion, thermal conduction, and flow exchange processes in a real-world karst system at a spatiotemporally small-scale size that have not been fully simulated by a process-based model thus far. It should be mentioned that Luhmann et al. (2012) simulated the spring thermo-chemo-graphs for the first experiment, considering advective-dispersive solute transport and convective-dispersive-conductive heat transport processes within a conduit, using the COMSOL Multiphysics code. However, their discrete pipe transport model neglected the flow transfer between the conduit and its surrounding matrix. Moreover, the flow was not simulated there, but the water velocity was assumed as a spatially constant quantity at each simulation time step (Luhmann et al. 2012).

In this work, the recorded spring water flux, temperature, and chloride concentration are considered as the simulation dataset, where the first and second experiments are adopted as the history matching and forecast periods, respectively.

Conceptualization

Conceptual models were developed considering the multimodel concept. All the models are identical in terms of considered compartments, processes, and boundary conditions; however, they are distinct with respect to the conduit configuration and/or parameterization.

System compartments

The karst aquifer was conceptualized with three compartments: (1) conduit, (2) matrix, and (3) conduit-associated drainable storage (CADS). The matrix and conduit represent the main reserve and flow dynamic compartments, respectively, according to the widely accepted conceptual models of karst aquifers (e.g., Worthington 1999; Ford and Williams 2007), while the CADS compartment can be assumed as the part of the conduits that provides additional immobile storage. The matrix is assumed to be an unconfined porous medium under a laminar flow regime; however, flow in the conduit is always considered turbulent due to the recorded high flow velocities.

The CADS compartment is comparable to the “annex systems to drain” (or annex-to-drain system) in Mangin’s conceptual model (Mangin 1975), evidently reported for some karst aquifers (e.g., Raeisi et al. 1999; Maréchal et al. 2008). CADS reservoirs can be formed by solutional enlargement of fractures and cavities—for a more detailed description of the CADS conceptualization, see Reimann et al. (2014) and Kavousi et al. (2020).

Processes

Flow and transport processes within the compartments were conceptualized based on the current state of knowledge of the site and the best functionality of the adopted process-based DCM approach (Table 2).

Table 2 Groundwater flow, heat, and solute transport processes in different aquifer compartments (1D: one-dimensional)

Considering the test sinkhole connected to a submerged conduit path, advective-dispersive heat and solute transport under a turbulent flow regime were considered within the conduit compartment, such that the matrix surrounding the conduits and CADS can have diluting effects through flow transfer. Background values of spring water temperature and solute concentration were considered for inflows from the matrix continuum and initial water residing in the CADS (Table 1). In addition, heat transfer across the thermal boundary layer at the rock–water interface and heat conduction within the matrix are considered (Table 2).

Chemical reactions were ignored for solute transport because of the employed ideal tracer, i.e., chloride. Heat transport was considered with comparable 1D convective-dispersive processes; however, temperature signals are nonconservative due to the radial heat conduction within the matrix environment surrounding the conduit.

Unaccounted processes

The following processes were ignored since they were not supported by the employed state-of-the-art DCM code. Although the processes can be assumed as minor considering the following justifications, the potential impacts will be argued later (i.e., see section Discussion):

• Advective-dispersive solute and heat transport within the matrix. The conduits are expected to function as drains before the start of the experiments while the hydrograph was in recession. This means that the hydraulic head in the conduits was lower than that of the surrounding matrix. Therefore, the assumption of matrix inflow with constant background water temperature and solute concentration is justifiable. However, this assumption would be violated during flow reversals when the hydraulic heads in the conduits exceed those from the surrounding matrix because of the additional recharge input. In this case, experiment water with elevated temperature and solute concentration would penetrate into the conduit walls. Some portion of this water would still drain from the matrix when the flow reverses again to the pre-experiment draining condition; therefore, the assumption of constant matrix inflow would temporarily be violated. The periods when the conduit heads exceed the matrix heads are unknown, although they should not be long because the pool release periods were on the order of a few minutes (Luhmann et al. 2012, 2015). Moreover, the high tracer recoveries (which were ~78 and ~90% for the first and second experiments, respectively) indicate that the advective-dispersive transport processes within the matrix were of minor importance because these processes have much longer time scales in comparison to those of the conduits (Covington et al. 2012).

• Partially saturated vertical conduit flow and transport. These processes are essentially fast and cannot be monitored. In regional-scale karst models, especially when the measurement frequencies are in the range of days, these processes are disregarded (e.g., Sullivan et al. 2019; Kavousi et al. 2020). Partially saturated processes are neglected because the test sinkhole has a direct connection to the main conduit (Luhmann et al. 2012, 2015). The quick vertical flow is justifiable by the field evidence as well. Post-experiment excavations of the test sinkhole revealed a vertical conduit of ~20 cm in diameter, developed downward through a vertical joint (Luhmann et al. 2015).

Model variants

To investigate the conceptual uncertainty, seven model variants (in short “variants”) of feasible conduit configuration and zonation were conceptualized, considering a multimodel approach (Fig. 3). The conduit passage from the test sinkhole to the spring indicates the only known conduit path. The other potential conduit passages located upstream and downstream of the test sinkhole are tested by inverse modeling (Fig. 2b). The variants of conduit configuration are described in the following (Fig. 3; the inflows and recharge components will be discussed later in relation to the boundary conditions):

• Variant I is the simplest and has only one conduit (i.e., the tracer conduit), connecting the test sinkhole and spring. This single conduit is comparable to Luhmann et al. (2012).

• Variant II is similar to variant I, though the tracer conduit is further split into tracer₁ and tracer₂. This zonation aims to test the effect of changes in conduit parameters (e.g., constrictions of the passage). Indeed, adding more conduit sections results in a likely improved model fit, which is not the main objective of this research.

• Variant III is comparable to variant I, but it has an additional conduit linked to the test sinkhole, namely upstream conduit. This conduit allows checking for potential improvement in simulation by considering the back-flooding effect.

• Variant IV combines variants II and III and comprises three conduits.

• Variant V considers the test sinkhole as a sole input tributary for the experiment recharge, connected to a tributary conduit, namely lateral conduit, in the middle of the tracer conduit.

• Variants VI and VII are the combination of variants II and V, and IV and V, respectively, that test the contribution of inflows from both the upstream and lateral conduits.

Fig. 3

Conceptual model variants of conduit compartments (colored-tubes: different conduit sections; colored-texts: names of conduit sections; blue arrows: spring outflow; red arrows: experiment recharge input; gray arrows: upstream conduit inflow; purple arrows: lateral conduit inflow; red ellipses or arc lines: test sinkhole; blue ellipses: nonspring and nonsinkhole end of conduits)

The conduit configuration between the test sinkhole and spring is unknown. Indeed, more complex conduit configurations with multiple lateral conduits or constrictions may exist. The proposed conceptual variants follow the principle of parsimony, yet they enable investigation of the effects of the lateral diluting inflow or flow constrictions with only one lateral conduit and constriction. Therefore, while numerous complex configurations can be tested, all configurations can be grouped within the proposed variants. Variants I–IV assess if the test sinkhole is located over a main conduit, assuming no further conduit junctions in the tracer conduits (i.e., tracer, tracer₁, and tracer₂), while variants V–VII further test a lateral conduit contribution (Fig. 3).

It might be assumed that all the defined variants are subsets of variant VII—for example, if the diameter of the lateral conduit is set to zero, variants IV and VII are identical. However, it is emphasized that, since the conduit diameter and wall roughness height are being separately estimated, the conduit diameter cannot be reduced to a diameter of zero—for example, an unfeasible high value of wall roughness height coinciding with a low value of conduit diameter (i.e., a ratio of > ~3:1) causes model failure due to numerical instabilities. Nevertheless, variants II and IV, which have been chosen to investigate potential conduit constriction, can be assumed as the subsets of variants I and III, respectively.

Numerical modeling

CFPv2 was employed for simultaneous simulation of groundwater flow, heat, and solute transport processes. The code is the updated version of MODFLOW-2005 CFP-M1, flow model (Shoemaker et al. 2008), which has been further enhanced by the built-in subroutines for solute and heat transport, originating from the conduit aquifer void evolution (CAVE) model (Birk 2002; Liedl et al. 2003; Birk et al. 2006). The basics of the implemented groundwater flow, heat, and mass transport processes in the model code are given in the electronic supplementary material (ESM).

Numerical model discretization

The history-matching period was temporally discretized by three stress periods, whereby the first one was considered as steady-state. This period, which is justifiable by the aquifer hydraulic state and the short period of the experiment, is required to reproduce a matrix head for the remaining simulations. The following transient stress periods lasted 214 s for the injection and 6,986 s for the pulse transmission. A gradual increase in time step length was adopted to increase the accuracy of calculations while reducing the computation time.

The springshed, i.e., the aquifer zone, was considered as the model domain (Fig. 2), and was spatially discretized by 100 m² (10 m × 10 m) cells in two layers. The Stewartville Formation together with the overlaying unconsolidated sediments and Prosser Formation comprise the first and second model layers, respectively. Based on the three-dimensional (3D) geological data (Steenberg 2014), the thickness of the first model layer ranges from ~20.3 to ~73.8 m, while the second layer has a thickness of ~32.0 m.

The spatiotemporal discretization in the heat and solute transport modules was much finer to achieve accurate calculations. Transport modules in CFPv2 take user-defined values for spatial discretization and internally calculate the temporal discretization (i.e., size of transport time steps), avoiding undesirable numerical dispersion (Reimann et al. (2018) for a detailed description of transport discretization).

Finer spatiotemporal transport discretization generally results in a notable increase in computation time; therefore, a balance between transport discretization and model accuracy is necessary. This balance is achieved by step-by-step refinement of spatial discretization, such that the model converges toward a unique result. Accordingly, any conduit segment between two conduit nodes was subdivided into 125 and 70 subsegments for heat and solute transport calculations, respectively. Moreover, 100 radial cells with 1-cm increments were considered to capture the heat conduction within the matrix. One forward model computation time was approximately a couple of minutes to several hours, depending on the variants and selected parameter values, using an Intel Core-i7 @ 2.30GHz.

Boundary conditions

A no-flux (second-type Neumann) boundary condition was assumed for the model domain, underpinning the spatiotemporal scale of the experiments, which was limited to the aquifer downgradient part for only 2 h. Freiheit Spring was regarded as a specified-head (first-type Dirichlet) boundary condition.

The recharge consisted of two components: the antecedent recharge (accounting for the pre-experiment spring discharge) and the injected water into the test sinkhole, as described in the following.

Antecedent recharge component

Before the experiments, an antecedent pre-experiment recharge supported the spring discharge to the karst system. Two hours after the first injection, spring discharge was recessed by ~5% (~1.2 L s^–1). This slight discharge reduction was taken into account via a changing flux antecedent recharge for the first test. However, the pre- and postexperiment spring discharges for the second experiment were almost unchanged; therefore, a specified-flux antecedent recharge was assumed for the forecast simulations. The antecedent recharge is further apportioned between two subcomponents of the distributed recharge and localized conduit inflows. The distributed recharge determines the initial head distribution in the matrix. This subcomponent is defined by the estimated annual recharge of the region, which was ~0.31 m during the year of interest—calculated based on the modified Thornthwaite-Mather soil-water-balance approach at a spatial resolution of 1 km by Smith and Westenbroek (2015). The conduit inflows account for the recharge drained by the conduits of distant aquifer parts, which are of unknown configuration and not simulated to reduce the computation time. Accordingly, the long-term distributed recharge over the model domain accounts for ~9.1 L s^-1 of spring discharge, while the rest (~17.7 L s^-1) is defined as the conduit inflows at the nonspring conduit ends. Considering the pre-experiment spring water temperatures of the first and second experiment, constant values of 9.08 and 9.31 °C were assumed as the initial condition of the rock matrix and reserved water in all aquifer compartments, as well as the specified heat-flux for the antecedent recharge of the first and second experiments, respectively. Similarly, the chloride concentration of the first and second pre-experiment recharge and the corresponding reserved water was set to the background values of 11.8 and 5.46 ppm, respectively (Table 1).

Recharge component of the experiments

Recharge from the experiments was considered by a specified-flux (second-type Neumann) boundary condition, approximated by uniform rectangular functions. The recharge period was 214 s for the first experiment, based on the observed flooding period of the test sinkhole. However, the periods of flooding were not reported for the first and second pulses of the second experiment; therefore, the recharge period for these pulses was estimated based on the ratio of the time difference between the hydrograph and chemograph rise times (i.e., 625 s) to the observed flooding period for the first experiment (i.e., 214 s). Accordingly, the duration of the first and second pulses of the second experiment was calculated as 172 and 159 s (considering the corresponding time differences between the hydrograph and chemograph rise times of 502 and 464 s). Table 1 mentions solute concentrations and temperatures of the experiments’ recharge water. It is worth noting that the concentrated recharge from the experiment can reach conduits and/or the CADS at the test sinkhole node.

Model joint inversion and post-inversion comparisons

Joint inversion method

A least squares-based parameter inversion was adopted (Aster et al. (2018), where the objective function (Φ) was defined as the weighted sum of squared differences between measured and simulated spring water flux (Q), temperature (T), and chloride concentration (C), i.e., hydro-thermo-chemo-graphs. Observation weights were specified as reciprocal of the measurement standard deviation (Aster et al. 2018), such that the uniform weights for Q, T, and C observation time series were 1/(0.0027 m³ s^–1), 1/(0.66 °C), and 1/(0.156 kg m³), respectively. This Bayesian weighting scheme is especially meaningful because the observations from different groups are orders of magnitude different.

Matrix or conduit hydraulic heads were not recorded in the Freiheit karst system; therefore, the outlet elevation—i.e., 359.66 m above sea level (masl)—was instead assumed to represent the matrix head at the spring discharge node as an additional observation. This assumption would further constrain the inverse problem to stick with realistic head distributions.

Minimization of the objective function was performed via the Levenberg-Marquardt search algorithm (Levenberg 1944; Marquardt 1963), implemented in the Parameter ESTimation (PEST) suite of software in parallel mode (Doherty 2019). It has been revealed that such a linearized gradient-based inversion scheme can provide efficient and promising results for discrete-continuum models (Borghi et al. 2016).

To increase the estimability of parameters and to capture realistic results, two pieces of prior information were supplemented to the objective function—for details see Doherty (2015). Prior information was utilized to avoid the case where the combined share of conduit and CADS recharges exceeded the whole experiment recharge. The second prior information was designated for estimation of inflow to upstream (Q_Upstream) and lateral (Q_Lateral) conduits in variants VI and VII, such that the summation of these inflows approaches the recharge subcomponent of localized conduit inflow, i.e., 17.7 l s^–1 (see section ‘Boundary conditions’).

Adjustable parameters

All the candidate parameters in the assumed processes were considered (see section ‘Processes’). Accordingly, 12 adjustable parameters were estimated, including seven, two, and three parameters for conduit, CADS, and matrix compartments, respectively (Table 3). The following points should be taken into account when inspecting the adjustable parameters in Table 3:

• All parameters can potentially control flow, heat, and solute transport processes except for the rock-specific heat and thermal conductivity, which can only affect heat transport.

• All parameters are homogeneously distributed across the domain except for the first five parameters in the table, which were parameterized based on the conduit sections for variants II–VII. Accordingly, the number of adjustable parameters was successively 10, 15, 15, 20, 20, 22, and 27 for variants I–VII.

• CADS is associated with all conduit nodes.

• Conduit inflows (i.e., Q_upstream and Q_lateral) are only estimated for variants VI and VII, where the total inflow can be shared between Q_upstream and Q_lateral. In other words, the inflow allocation ratio in variants VI and VII is not fixed, but estimated via inversion. Q_upstream or Q_lateral are not estimated and treated as fixed for the other variants because only one such parameter was introduced there to deliver all the inflow.

• The experiment recharge components can be diverted to the test sinkhole as concentrated recharge fractions to the conduit (as CRCH) and/or CADS (as CADS-RCH), such that the inversion quantifies them. The model inversion can further support the diversion of the experiment water to the matrix, too.

• All parameters were considered as log-transformed except for the inflows (i.e., Q_upstream and Q_lateral), such that they can even be estimated as zero.

• Matrix specific yield (S_y) has been considered as an adjustable parameter in the preliminary models. However, it was entirely “insensitive” in the course of inversion of all variants, and therefore, excluded to reduce the inversion dimensionality. A fixed value of 0.05 was considered for the parameter based on the two pumping tests on the wells drilled in the same geological strata in the region—see MDH (2016, 2019). The insensitivity of S_y is justifiable by the fact that the period of the dynamic response to the experiment was only 2 h when the water reserves of the conduit and CADS compartments could react and regulate the system behavior more effectively than that of the matrix.

• A pumping test ~30 km southeast of Freiheit Spring provided a horizontal hydraulic conductivity (K_h) ranging between 4.0 × 10^–7 and 1.6 × 10^–6 m s^–1 for the combined Stewartville, Prosser, and Cummingsville formations (MDH 2019). However, another pumping test ~31 km northwest of Freiheit Spring estimated larger K_h values ranging between 3.0 × 10^–5 and 1.1 × 10^–4 m s^–1 for the combined Maquoketa, Dubuque, Stewartville, Prosser, and Cummingsville formations (MDH 2016). Since the model layers (i.e., Stewartville and Prosser formations) have quite comparable lithology and their K_h have not separately been estimated, only one K_h zone, characterized by a typical vertical anisotropy ratio of 1:10 (A. Runkel, Minnesota Geological Survey, personal communication, 2021), was considered for the entire model domain. Indeed, natural heterogeneity and anisotropy may play a significant role in the matrix and conduit heads and associated flow transfers between matrix and conduit compartments at large spatiotemporal scales. However, considering the small scale of the experiment, the sink-to-spring nature of the experiments, and the lack of data (on hydrodynamic parameters of the layers and head observations), the simplifying assumptions about the homogeneity and the typical anisotropy ratio are justifiable while the simulations still allow 3D flow in the matrix compartment.

• The parameter bounds cover a wide range, which even goes beyond the range of reported values for conduit tortuosity (τ_c), rock specific heat (c_p,rock), and rock thermal conductivity (λ_rock). Those parameter ranges are deliberately extended beyond physical limits because preliminary model inversions demonstrated that the respective estimated values hit their defined boundaries. This incidence is usually a sign of parameter compensation effects and often a sign of missing processes.

• Several inversions were performed for each variant with different (random) initial parameter values to decrease the risk of being trapped in a local minimum value of the objective function.

Table 3 Model parameters in the inversion process

Model performance, selection, and testing

The ability of variants to match hydro-thermo-chemo-graphs was separately compared using three commonly used metrics for the model performance assessment: (1) the root mean square error (RMSE); (2) the Nash-Sutcliffe efficiency (NSE; Nash and Sutcliffe 1970); and (3) the Kling-Gupta efficiency (KGE; Gupta et al. 2009). The RMSE is expressed in the measured value units, while the NSE and KGE are normalized metrics. The smaller the RMSE and the higher the KGE or NSE values (i.e., the more approaching unity), the better the model performance (Wöhling et al. 2013). Unlike the NSE, which ranges from zero to one, the KGE can reach negative values. Knoben et al. (2019) demonstrated that the traditional mean flow benchmark that results in an NSE = 0, i.e., the likely origin of the “bad/good” model performance, yields a $\textrm{KGE}=1-\sqrt{2}\approx -0.41$.

Model performance can generally be improved by introducing more adjustable parameters to the model; however, this can result in overparameterization and give rise to uncertainty because the information on observations would be distributed through more parameters (Engelhardt et al. 2014). This issue can be tackled by the principle of model parsimony, i.e., keeping the model “as simple as possible, but as complex as necessary” (Hill and Tiedeman 2007; Höge et al. 2018). For this reason, model dimensionality (i.e., the number of adjustable parameters) should be increased in a stepwise way, starting with a model with homogeneous parameter domains—see Sun et al. (1998). Subsequently, different parameter dimensionalities can be compared and ranked using model selection criteria (e.g., Engelhardt et al. 2014; Kavousi et al. 2020).

Model selection criteria, also called information criteria (IC), seek the optimum trade-off between model complexity and goodness of fit. The smaller the IC, the more suitable the model (Hill and Tiedeman 2007). Model complexity will grow by increasing the number of adjustable parameters included in the ICs as a penalty term. However, an additional parameter may substantially improve the goodness of fit, hence overwhelming the penalty. In this work, the Akaike Information Criterion (AIC; Akaike 1974), corrected AIC (AICc; Hurvich and Tsai 1989), Bayesian Information Criterion (BIC; Schwarz 1978), and Kashyap’s Information Criterion (KIC; Kashyap 1982) were utilized. All the inverted variants were used to forecast the hydro-thermo-chemo-graphs for the second experiment. The forecasting results were compared in terms of the RMSE, NSE, and KGE values of each observation (i.e., Q, T, and C), as well as the average KGE values.

Uncertainty analysis

Parameter uncertainties were investigated by the 95% confidence intervals of parameters (in short, 95% CI), calculated based on the same linearity assumption used for the inversion, and therefore, implemented with no additional computational burden. When a linear approximation to the posterior covariance matrix was achieved, confidence limits can be reported as post-inversion statistics— see James et al. (2009); Doherty (2015); Aster et al. (2018). However, with a nearly singular normal matrix, the post-inversion confidence limits were calculated by considering uncertainty variance as the square of the standard deviation (Doherty 2015).

Observations considered in an inverse problem would change prior and posterior uncertainties in which the parameters are being estimated. Relative parameter uncertainty variance reduction, σ²_rel, can be used to estimate the change of parameter uncertainty variances as (Doherty 2015):

$${\left({\sigma^2}_{\textrm{rel}}\right)}_i=1-\frac{{\left({\sigma^2}_{\textrm{prior}}\right)}_i}{{\left({\sigma^2}_{\textrm{posterior}}\right)}_i}$$

(1)

where (σ²_prior)_i and (σ²_posterior)_i are the prior and posterior uncertainty variances for the ith parameter, respectively. σ²_prior and σ²_posterior are expressed as the diagonal elements of the covariance matrix associated with preinversion and postinversion probability distribution of parameters, respectively (details of the calculation procedure are beyond the scope of this work and can be found in Doherty (2015), among others).

σ²_rel ranges from zero to one, with zero indicating no reduction of parameter uncertainty and a value one indicating a complete reduction of uncertainty (Doherty 2015). This intuitive criterion was here preferred to the other comparable post-inversion statistics, such as identifiability and relative error variance reduction, because it is believed to be a more robust metric for assessing parameter significance—see Doherty and Hunt (2009) and Doherty (2015).

Value of observation data

Data worth analyses in multitype monitoring networks are often conducted to assess and reduce predictive uncertainty (e.g., Wöhling et al. 2016); however, it is believed that multitype monitoring designs can also yield narrower parameter uncertainty posteriors because parameter compensation is expected to happen less likely across different physical process descriptors of the same system. Parameter uncertainty reduction is expected to depend on the observation types, the model parameters, and the functional relationship between the two. Multitype observations may not always lead to narrower parameter posteriors if the number of process-related parameters increases with additional processes in the coupled model.

The joint inverse problem in this work has three simultaneous observation time series, namely Q, T, and C. Accordingly, all potential combinations of observation data sets (subsequently referred to as “observation cases”), i.e., Q, T, C, TC, QC, QT, and QTC, were considered for all the variants. No changes were made to the estimated parameter values obtained using the full observation dataset, i.e., the QTC observation case. However, the Jacobian matrices were recalculated for each case and used to evaluate the value of observation data based on the extent of parameter uncertainty reduction. For this purpose, the 95% CI for different observation cases, normalized to the respective estimated values, were compared via normalization relative to the same base parameter estimates for each variant, which was achieved by the inversion based on all observations (i.e., the QTC observation case). It should be noted that the observation cases without Q (i.e., T, C, and TC) are uncommon and undesirable monitoring setups; however, they are also analyzed to assure a comprehensive assessment.

Results

Model performance, selection, and testing

All the variants were jointly inverted based on the measured Q, T, and C from the first experiment and found to be acceptable in terms of the calculated fitting statistics (Table 4); however, variants VII, IV, VI, and II successively achieved better performances than the others in terms of Φ. It should be mentioned that the AIC, AICc, BIC, and KIC information criteria demonstrated the same model variant rankings as suggested by Φ (Table 4), thus they are not discussed in detail to avoid redundancy. Nevertheless, among the top four variants with relatively better performance, variant II is the simplest, and thus might be preferred, considering the principle of model parsimony (Table 4). The considered model variants suggest that the inverse model performance can be improved by further zonation of the tracer conduit—compare variants I and III with variants II and IV, respectively (Table 4; Fig. 3).

Table 4 Weighted least squares objective function (Φ), model selection criteria (i.e., AIC, AICc, BIC, and KIC), and model performance criteria of different observations (i.e., RMSE, NSE, and KGE with respect to Q, T, and C) across the variants. Φ and information criteria (ICs) are only calculated for the inversion period. Model variants are ranked from the best to the worst according to the Φ and average KGE (KGE_Ave) in the inversion and testing periods, respectively

Figure 4 presents the measured and jointly inverted hydro-thermo-chemo-graphs for variants I and II. The figure illustrates the ability of the model to reproduce the spring observations simultaneously; moreover, it demonstrates better fits for variant II (the simplest variant among the top four variants) than variant I, considering one additional conduit section. The occasional deviations between the measured and simulated graphs, especially near the peaks, can be observed, which went slightly beyond the measurement error just for C (Fig. 4). It should be noted that only variants I and II were plotted in Fig. 4 to ease the visual interpretation, because there was not a sharp difference between variant II and the better-performed variants with two tracer conduits (compare the objective function values in Table 4, for example). Variant III with one tracer conduit was also comparable to variant I (cf. Table 3).

Fig. 4

Measured and joint inverted a hydro- b thermo- c chemo-graphs of the first experiment for variants I and II. Time series of residuals (i.e., measured minus simulated values) are presented as gray subplots above each plot. The recharge rate is indicated by an inverted right y-axis (a). The measured and simulated recoveries of thermal energy and salt tracer are also presented (b–c), respectively. Reported measurement errors were ±10%, ±0.4 °C, and ±5%, respectively (a–c)

Remarkably, the inverted recoveries for the thermo-chemo-graphs were very close to the observed ones, demonstrating that the difference between T and C processes was well captured by the model (Fig. 4). The measured and simulated recovered salt tracer mass within the two hours of history matching were ~78 and ~77%, while the comparable values for thermal energy were ~54 and ~56%, respectively. This dampening of the thermal signal by heat conduction within the rocks surrounding the conduit was simulated well.

According to all the inversion performance criteria, Q fitting was slightly weaker than C and T (Fig. 4; Table 4), which can be explained by the following:

• 1. The measured Q rise had a 3.25-min delay relative to the beginning of the experiment, which is attributed to the time required for recharge water to reach the phreatic conduits. The hydraulic pulse was then assumed to propagate along the flow path at the speed of sound under submerged conditions (Luhmann et al. 2012). The simulated Q delay was inevitably shorter since the partially saturated vertical conduit flow was ignored in the simulations (see section ‘Processes’).

• 2. Small oscillations in the measured Q likely resulted from the measurement method, which consisted of a 120° v-notch weir and pressure transducer data logger (for details see Luhmann et al. (2012).

• 3. An unusual Q drop from the pre-experiment level was observed, followed by some recovery (~60–90 min). Luhmann et al. (2012) attributed this odd flow behavior to siphoning, flow inertia, or hysteresis effects associated with the transition of some portion of the conduit from full-pipe to open-channel flow. These processes are neither distinguishable at the current state of knowledge of the site nor covered by the available model tools.

Nevertheless, the reported ±10% error in Q measurements (Luhmann et al. 2012) is still larger than the maximum residual error for all the variants (Fig. 4).

It is possible to achieve slightly better fitting statistics by introducing additional parameters or spatial parameterization schemes, e.g., with multiple conduit constrictions. However, this would inflate the dimensionality of the inversion problem, which then could be countered by regularization constraints, e.g., Tikhonov regularization (Doherty 2003; Moore et al. 2010). Nevertheless, the simple parameterization scheme of a few sections is preferred here, as it yields acceptable results with fewer adjustable parameters (as parsimonious models) and at lower computational cost.

All the jointly inverted variants were tested against the hydro-chemo-thermo-graphs of the second experiment as the forecast period (see section ‘Applied hydraulic and tracer experiments (observation data)’). Comparing the normalized performance criteria, i.e., the NSE and KGE values, the following results can be summarized (Table 4):

• KGEs for the testing periods are smaller than the comparable values for the inversion periods because the information behind the system behavior at different periods may not be the same. The minimum, i.e., the worst KGE for a forecasted observation, is ~0.46, which is not overly large, but higher than the mathematical threshold between the “good” and “bad” model performances (i.e., KGE ≈ –0.41).

• On average, variant V, which has conduit inflow solely as Q_Lateral, has the highest forecast performance among the variants. However, this variant had the worst inversion fitting statistics among the variants with Q_Lateral (i.e., V, VI, and VII), which will be discussed below (see section ‘Distribution and plausibility of estimated parameters’).

• Q and C have the highest and the lowest forecast performances for each variant, respectively (except for variant III, where the KGE_T is slightly greater than the KGE_Q). The slight discrepancy between T and C observations resulted from the difference in the involved processes (see section ‘Processes’).

Figure 5 shows the measured and forecasted hydro-thermo-chemo-graphs, where the following features can be highlighted:

• 1. Forecasted peaks are slightly lower than the observed ones for all observation types in almost all the variants.

• 2. Considering the measurement errors, Q is reasonably forecasted by all the variants.

• 3. Some delayed time shifts of forecasted transport spikes are evident. There are ~0.5 to ~6 min and ~1 to ~6 min delays between the measured and forecasted T and C, respectively. These deviations potentially result from the uncertainties in the recharge functions, which were assumed rectangular for both inversion and forecast periods (see section ‘Boundary conditions’).

• 4. Variant V is the best-performed variant because the transport peaks are less time-lagged (all the other variants may be grouped around a similar peak lag); however, variant V is performing the worst at predicting the amplitude of the peaks.

• 5. The unaccountable flow process (e.g., siphoning) potentially causes discrepancies between measured and forecasted Q (cf. the drop and recovery in the measured Q between ~45 and ~90 min).

• 6. The unaccountable transport processes in the history matching period also affected the forecast period results (see section ‘Processes’ and also section ‘Discussion’)

Fig. 5

Measured and forecasted a hydro- b thermo- c chemo-graphs of Freiheit Spring. The forecasted results of all the variants are presented with gray-scale colors, except for those of variant V, which had the highest performance criteria (Fig. 6). The recharge rate is indicated by an inverted right y-axis (a). The plotted measurement errors were ±10%, ±0.4 °C, and ±5%, respectively (a–c)

Figure 5 shows the results for all the model variants (unlike Fig. 4) because the model performances in the testing period were diverse (cf. Table 4). However, the residual side-plots were not included in the figure because there are obvious shifts in the simulated transport signals, i.e., high residuals, while the models could still reflect the transmission of tracer and heat inputs by some delay (as explained previously).

Distribution and plausibility of estimated parameters

Analyzing the estimated parameter values and 95% CI across all the variants, the following results can be highlighted (Fig. 6; see Table S1 in the ESM):

• All estimated values are within their reported ranges, except for the rock specific heat (c_p,rock) and tortuosity of the tracer conduits (i.e., τ_c, τ_c1, and τ_c2), which is detailed in section ‘Discussion’.

• Diameters of the tracer conduits (i.e., D_c, D_c1, and D_c2) have the most constant and certain estimates across the parameters (Fig. 6a–c).

• The wall roughness heights are generally high, especially for the tracer conduits (i.e., k_c, k_c1, and k_c2).

• The lower confidence limits for τ_c,upstream and τ_c,lateral are slightly beyond the lower feasible range.

• In variants I and II, which had neither upstream nor lateral conduits, the estimated parameters are on average associated with the highest certainties across all the variants.

• In variants III–VII, which had upstream and/or lateral conduits, the parameters corresponding to the tracer conduits (i.e., tracer, tracer₁, and tracer₂) exhibit a narrower 95% CI than those of the upstream and lateral ones, except for the conduit tortuosity (Fig. 6a–y).

Fig. 6

Estimated parameter values and their 95% confidence intervals. Note that in the first five rows of the plots (i.e., a–y), each row presents parameterized values for the same parameter type on a similar y-scale range (Table 2; Fig. 3). The gray and reddish regions indicate the parameter spaces that exceed the reported values and infeasible range of values, respectively

The relative parameter uncertainty variance reduction (σ²_rel) of all the variants was also calculated, and the following results can be considered (Table 5):

• The level of uncertainty reduction is different, yet remains considerable for many parameters in all the variants.

• All the parameters of variants I and II feature a σ²_rel > 0.8, indicating that the parameters are effectively sensitive for the current conceptual model and dataset.

• Almost all parameters from the upstream and lateral conduits have smaller σ²_rel compared to the equivalent parameters in the same variants, and therefore, are less sensitive (the σ²_rel for the water transfer coefficient of the upstream conduit, i.e., α_{ex, upstream}, in variants IV and VII are exceptions, slightly exceeding their equivalent values for the tracer conduits).

Table 5 Relative parameter uncertainty variance reduction (σ²_rel) for all the variants

Value of hydro-thermo-chemo-graphs

Figure 7 presents a bar chart of normalized 95% CI for variant II, at seven cases of observation data availability (in short “observation cases”, as mentioned in section ‘Value of observation data’). This variant, which was chosen as an example plot, had two tracer conduits laid solely along the tracer path from the test sinkhole to the spring. The variant achieved a relatively narrow 95% CI for the QTC observation case compared to variants III to VII, which had upstream and/or lateral conduits (Fig. 6). Inspecting the results of different observation cases for variant II, the following outcomes can be summarized (Fig. 7):

• 1. Among the single observation cases (i.e., Q, T, and C), the Q and C cases on average yield the narrowest and widest 95% CI, respectively.

• 2. In general, the joint use of different observation types increases the certainty at which the parameters are estimated. According to the average rank of parameter uncertainty, the CT, QT, and QC observation cases reduce parameter uncertainty more than the single observation cases.

• 3. Q observation is the most valuable data type. This observation case reduces parameter uncertainty even more than the combined CT case.

• 4. Although the T observation case is substantially more valuable than the C, the combined QC case is only slightly favored over the QT case.

• 5. The normalized 95% CI values for the full (QTC) observation case are the narrowest for all parameters (Fig. 7). There is only a slight increase of parameter uncertainty for the QT and QC cases compared to QTC.

Fig. 7

The 95% confidence intervals of parameters for variant II, normalized to the respective estimated values for different cases of observation data availability. The values within each case were sorted based on the average rankings across all the cases (as presented in the legend and bars), such that the higher parameter uncertainty is more to the right and has warmer color. The cases were also sorted based on the average ranking of parameters within each case, such that the C and the combined QTC cases exhibit the least and the highest reduction of parameter uncertainties, respectively. Note that the c_p,rock and λ_rock parameters are absent for the C, Q, and QC cases, and therefore, they are not considered in the ranking and are presented by gray colors at the right-most end of the relevant cases (with legend symbols of cp and λ, respectively). The bars indicated by the red star (for the C case) exceed the y-axis range (i.e., 2). Moreover, the cases without Q data (indicated by a light gray background) are not the usual data acquisition scheme for karst springs

The value of observation data was also investigated for the other variants. It is worth mentioning that there were five incidences of the nearly singular normal matrix, which happened only for the Q observation cases of variants III–VII. Figure 8 presents the cumulative probability (i.e., the exceedance probability) of normalized 95% CI of all the variants for the different observation cases. This kind of probability plot is utilized because the parameters do not behave similarly for different observation cases. The normalized 95% CI could reach unacceptably high values, especially for the parameters of lateral and upstream conduits in variants III–VII (Fig. 8). For simplicity in comparisons, the subsequent general rule can be stated: the more the cumulative probability line shifts to the right, the less uncertainty reduction for the corresponding observation case. Comparison of the uncertainty reduction of parameters in the different variants can be summarized as follows:

• Among all single observation cases, C is the least valuable in all the variants. Q is the most valuable in variants I and II, while T is the most valuable in the other variants.

• Although the combined use of observation types generally results in higher uncertainty reduction for most of the estimated parameters, the T observation case even more effectively reduces the uncertainty of parameters in comparison to dual observation cases in some variants. Specifically, the T observation case is the second most important observation case (after the QTC) for variant III.

• The QC observation case is the second closest case to the QTC in variants I and II, in terms of the average value and ranking of parameter uncertainty reduction. However, the QT is comparable to the QTC in all the other variants, and therefore, it is preferable to the QC, considering the prevailing conceptual uncertainty.

Fig. 8

Cumulative probability of normalized 95% confidence interval of parameters at different cases of observation data availability for all the variants

Discussion

There are very limited observations of the size and location of the conduits inside the Freiheit karst system; therefore, none of the candidate variants can be disregarded as their performances were statistically acceptable. However, as the assumed variants cover a reasonable range of feasible conduit configurations, they can provide insight on the aquifer characteristics and functioning in its terminal part, as discussed in the following.

Model structure identification and conceptual uncertainty

Parameter uniqueness

Inspecting parameter values demonstrates that some parameters could be almost uniquely estimated across the variants, while others were significantly diverse. Specifically, conduit-related parameters for the tracer conduits were estimated at comparable values and with a lower degree of uncertainty when compared to the same parameters in the upstream and lateral conduits. These results suggest that the conducted experiment is more appropriate for inferring parameters of the tracer conduits than the upstream or lateral conduits. Combining these findings with those of the model performances, one may prefer variant II to the others, even if its performance was slightly weaker than variants IV, VI, and VII.

Inflow from upstream and lateral conduits

Considering the joint inversion results, the estimated value of lateral inflow (Q_lateral) in the variants with both parameters, i.e., variants VI and VII, was ~13.5 L s^–1 and ~14.0 L s^–1, respectively (see Table S1 in the ESM). Thus, ~77.1 and ~79.7% of the total conduit inflow were respectively allocated to Q_lateral in these variants, which means that the joint inversion tended to favor Q_lateral over upstream inflow (Q_upstream) in these variants. However, variants I, II, III, and IV, which have no lateral conduit (i.e., 100.0% Q_upstream), and variant V, which has no upstream conduit inflow (i.e., 100.0% Q_Lateral), also successfully inverted the hydro-thermo-chemo-graphs.

The model performances for the testing, i.e., the forecast period, differed from those of the inversion period. Variant V, which is the only variant without Q_upstream, had distinctively superior forecast performance (see ‘Model performance, selection, and testing’). Therefore, the forecasts tend to favor the conceptual model with solely Q_lateral. It should be noted though that this conclusion is valid only as long as the aquifer is at the current hydraulic level, as other inactive vadose passages may connect with the spring to create epiphreatic to phreatic conditions during high flows. Moreover, variant V is the best-performed variant for the peak timing, but the worst performed for the peak amplitude. Depending on the modeling purpose, the peak time or the peak amplitude could be of interest; therefore, the other model variants may still be preferred, despite the worse model performance metrics as given in Table 4.

Significance of CADS

The estimated values for the CADS width were 1 mm to ~10 cm across all the variants. This may lead to the assumption that the CADS is not important in the simulated experiment (see Table S1 in the ESM); therefore, a CADS-free version of variant II was constructed and inverted to test the hypothesis.

Results suggest that the CADS-free model cannot simultaneously adhere to the spring hydro-thermo-chemo-graphs, such that in comparison to the CADS-bearing version of variant II, the objective function value was increased to 77.41, which means over a four-time increase (Table 4). The thermo-chemo-graphs can partially be simulated with the CADS-free model; however, the hydrograph cannot be jointly simulated at all. The inadequacy of the CADS-free model generally highlighted the importance of this compartment in the overall aquifer functioning and DCM.

Uniformity and reasonability of tracer conduit size

Conduit passage collapses, sediment breakdowns, and insoluble blocks may constrict karst conduits, consequently regulating the observed spring hydro-physico-chemical behavior. Model simulations have indicated that these features may control the observed behavior of some karst aquifers (Halihan and Wicks 1998; Covington et al. 2009; Chen and Goldscheider 2014; Kavousi et al. 2020).

Potential constriction in the conduit path was investigated by comparison of the diameters of the tracer conduits (i.e., D_c, D_c1, and D_c2). Although conduit parameterizations may result in better model performance, D_c, D_c1, and D_c2 were almost uniform in size, ranging from 30.5 to 39.7 cm for variants I to V. However, D_c1 and D_c2 were more diversed for variants VI and VII, where the values range from 30.0 to 50.2 cm (Fig. 6; see Table S1 in the ESM). Therefore, the inverse model revealed an important role of conduit diameters and their potential variability along the tracer path, but it did not indicate narrow constrictions within the conduits.

It is worth mentioning that Luhmann et al. (2012), using sole-pipe transport simulations by COMSOL Multiphysics, suggested a conduit diameter of 7–8 cm, based on the first experiment results. These values are obviously smaller than the estimates here and highlight the difference of using a process-based DCM compared to a sole-pipe transport model, with a simplifying assumption of uniform velocity across the flow path during each calculation time step.

Excavation of the test sinkhole by a track hoe revealed a vertical solution conduit ~20 cm in diameter developed along a vertical joint (Luhmann et al. 2015). This direct observation for the vertical shaft of the vadose zone supports this model’s results, because a diameter of >20 cm can be a reasonable estimate for the saturated zone conduits beneath the test sinkhole, where groundwater is permanently moving and developing its passage toward the spring.

The volume of tracer conduits, along with their pertinent 95% CI, were calculated by multiplying the length of tracer conduits by the relevant estimates for the tortuosity and cross-sectional areas of conduits (Fig. 9). The conduit volumes ranged from 45.64 to 50.79 m³, while their 95% CI ranged from 13.14 to 25.86 m³ across all variants. These values were similar to a former estimate by the flood-pulse analysis, which was 47±4.7 m³ (Luhmann et al. 2012; Fig. 9).

Fig. 9

Comparison of estimated volume of tracer conduit passage from the flood-pulse analysis (Luhmann et al. 2012) with those of this study (i.e., CFPv2 DCM). The 95% confidence intervals of model estimates and error bars of the flood-pulse analysis are indicated

Highly-rough surfaces of conduits

The friction factors for flow and transport simulations are estimated based on the mean roughness height of the conduit walls’ microtopography, in short “wall roughness height (k_c)” (see the combined form of Darcy-Weisbach and Colebrook-White equations as Equation S2 in ESM). The Colebrook-White equation has been proposed for pipe networks, where k_c is much lower than that of natural karst conduits. Although the validity of the equation has not been proven for highly roughened walls, previous research has still suggested it as a first approximation for flow and transport simulations (Bergman et al. 2011).

Based on the direct observation from Goliath’s Cave, a few kilometers away from Freiheit Spring, the conduit walls in the Stewartville Formation are extremely rough at the few centimeter scale, due to the differential weathering of ubiquitous fossil worm burrows in the bedrock (Alexander et al. 2015). This so-called “Stewartville Knobblies” feature is an unambiguous field marker for the upper Stewartville Formation (Alexander et al. 2015).

The k_c value was generally high in the models developed here, approaching a value of one meter (especially for the tracer conduits; see section ‘Distribution and plausibility of estimated parameters’). The k_c has been widely investigated in open-channel and river hydraulics, where values in the range of a few meters have been reported for gravel-bed rivers (Lee and Ferguson 2002); however, few studies have investigated the k_c for karst conduits. Atkinson (1977) found a k_c to diameter ratio of about three for conduit passages in Mendip Hill, UK, whereas Jeannin (2001) reported a ratio of one quarter in the Hölloch cave system, Switzerland. The ratio in models reported here was generally within these ranges. The tracer conduits have a minimum, average, and maximum ratio of 0.6, 1.8, and 3.2, respectively, while the respective values for the other conduits were 0.4, 0.6, and 1.4.

Necessity of additional heat exchange

Modeling results indicated that to have a successful joint inversion of hydro-thermo-chemo-graphs for the conducted experiment, extraordinarily large values for the tortuosity of tracer conduits (i.e., τ_c, τ_c1, and τ_c2) are required (see Table S1 in the ESM). On the other hand, all the variants reached their upper bound for estimation of rock-specific heat, which was set at a large value of 5,000 J kg^–1 K^–1 (which is slightly larger than that of water, i.e., 4,195.2 J kg^–1 K^–1). Moreover, the estimated rock thermal conductivity ranged from 2.920 W m^–1 K^–1 to 3.632 W m^–1 K^–1, comparable to the reported large values for carbonate rocks (Robertson 1988). The tendency toward large values of tortuosity and rock thermal parameters suggests that the inversion tries to consider more heat exchange, which can be attributed to the following justifications:

• 1. Overlooked impact of added surface area due to macroscopic roughened conduit walls. The Stewartville Knobblies may result in conduit surface areas of several times larger than the calculated area based on the macroscopic conduit dimensions, which is believed to be of greater impact in smaller conduits (C. Alexander, Jr., University of Minnesota, personal communication, 2022). The state-of-the-art DCM codes still neglect such “macrotopographic” features of the conduit walls.

• 2. Neglected vertical flow and transport processes. No extensive analysis on cave sinuosity has been carried out in the studied karst region (Luhmann et al. 2012); however, since the models here neglect the vertical passage of water in the vertical shaft, some large estimates of saturated tortuosity are expected to compensate for the ignored loss of heat signals via this vertical passage. As a rough estimate, if one considers the reported median value for tortuosity by Worthington (2014), based on 85 major cave flow paths (which was 1.44), given the elevation difference and horizontal distance between the test sinkhole and spring outlet (which are 19 and 95 m, respectively) and the straight model length (which is 90 m), a reasonable model tortuosity should be around 1.8 to account for both vertical and horizontal paths. However, the calculated tortuosity for variants I and III (with only the tracer conduit) was 5.4 and 5.2, respectively. Therefore, adopting a large tortuosity, the model tried to provide some extra flow path length, i.e., additional area for heat exchange, which evidently exceeded the assumed loss of heat for the combined horizontal and vertical conduits.

• 3. Assumption of circular conduits. Freiheit Spring emerges from a bedding plane parting, suggesting that a wide rectangular conduit cross-sectional shape may be more appropriate than a circular one (Luhmann et al. 2012). Excavation of an abandoned steephead (i.e., blind valley) just southwest of Freiheit Spring by a track hoe exposed a solutionally enlarged bedding plane parting with a height on the order of centimeters (Luhmann et al. 2015). Water flowing through rectangular conduits would obviously have an additional heat exchange area compared to circular conduits at the same hydraulic radius; however, CFPv2 currently assumes only circular conduits.

• 4. Neglected transport processes in the matrix. These processes were assumed to be of minor importance considering the high mass recovery of salt tracer and the distinct difference in the timescale of these processes within the matrix continuum and conduits (see section ‘Processes’). However, it was expected that some parameters try to compensate for the missed processes to obtain a better inversion performance.

Limitations and future outlook for spatiotemporally small-scale DCM applications

The approach described here simulates most of the hydraulic and transport processes occurring in a karst aquifer. Its application to a spatiotemporally small-scale real-world case highlighted the importance of some model structures and processes at that scale, which are typically overlooked:

• 1. Noncircular conduit cross-sectional shapes. Real-world karst conduits can be of different cross-sectional shapes. Jouves et al. (2017) investigated the geometrical shape of a cumulative length of 621 km of cave passages from France, Spain, and Italy. They demonstrated that the average width-height ratio for water table, looping, and maze conduit networks ranges from ~1.6 to 1.9. Luhmann et al. (2012) showed that the rectangular conduit shape could suggest enhanced heat transport for Freiheit Spring, which appears to be a relevant factor in joint simulations of flow and heat transport, as shown in this work.

• 2. Partially saturated vertical flow and transport processes in conduits. Although these processes may have a very short time scale, they can significantly change the input signal characteristics, i.e., the presumed boundary conditions for the recharge signal that reaches to the saturated zone. Rectangular recharge functions were assumed here, affecting both inversion and forecast results.

• 3. Syphoning and inertia processes for conduits and CADS. Odd spring hydrograph fluctuations upon passage of the hydraulic pulses were previously attributed to the likely siphoning and/or inertia effects in conduit flow processes (Luhmann et al. 2012). Although the current version of CFPv2 can consider partially saturated conduits to some extent, flow processes in such conduits need to be adequately monitored and thoroughly understood for an effective real-world simulation (Reimann et al. (2011).

• 4. Transport processes within the matrix. Advective-dispersive solute and heat transport processes in porous media are not supported in CFPv2. These processes are evidently of minor importance for the case studied here; however, they can be of vital importance in cases where conduit-matrix exchange, particularly flow reversal, is important.

The aforementioned model limitations broaden the outlook of required CFPv2 improvements, and any other DCM in general, for spatiotemporally small-scale applications.

Conclusions

A methodology for the application of joint-inversion to time-series data of hydrological and physicochemical state variables observed in karst systems was proposed. To illustrate and test the methodology, CFPv2 DCM was applied for the joint inversion of spring hydro-thermo-chemo-graphs in response to a sink-to-spring hydraulic and tracer injection experiment at a spatiotemporally small scale. Adopting a multimodel concept, different conduit configurations were considered and compared in terms of model inversion performance and parameter uncertainties, and forecast capability for a second, more complex experiment at the same site.

Although the forecast capability of all the variants was acceptable statistically speaking, the approach is preferably intended for interpretation, i.e., as an engineering calculator for site characterization, a screening tool for proof of concept, and diagnosis of potential structural inadequacies for a process-based DCM approach at spatiotemporally small-scale applications.

The main modeling outcomes for the studied case can be summarized as follows:

• 1. High certainty and uniqueness of estimated values for the conduit diameter of the tracer passage

• 2. Unlikely conduit restriction in the tracer passage

• 3. Potential inflow from both upstream and lateral conduits with higher support for contribution from the latter

• 4. Importance of conduit-associated drainable storage, CADS, in aquifer hydrodynamic behavior

• 5. The necessity of considering some additional surface areas for heat exchange

• 6. Importance of using heat data in joint inversion

• 7. Consistency of the estimated volumes of the tracer conduit passage with those of the conventional flood-pulse method

Considering the models as engineering calculators, the most notable result was that the volume of the active conduit of the models is comparable to that estimated by Ashton’s intuitive method. However, former studies have claimed that this conventional hydraulic-based method tends to overestimate the conduit volume, ignoring the contribution from the fissure system during the hydraulic pulse transmission (e.g., Williams 1983; Birk et al. 2006). While the results support the flood-pulse method, more model investigations are required to thoroughly test the hypothesis under different conceptual models and parameter combinations.

As an additional part of this research, the value of water flux, temperature, and solute concentration data on the certainty of model adjustable parameters was investigated. Results suggest that the water flux and temperature data generally reduce posterior parameter uncertainties more than the solute concentration data. Moreover, the parameter estimates had the highest degree of certainty if the combined observation datasets were used through the joint inversion. Results further suggest that if the solute concentration data were excluded from the inversion, the estimated parameters could be recovered at almost the same degree of certainty compared with the case of the full observation dataset. Therefore, considering the objective of data acquisition planning for spring flow and transport simulation, it is concluded that the continuous record of spring water temperature is of higher priority than the solute concentration. This result is likely case-specific and depends on the current dataset, system state, and considered conceptual models. However, further application of the proposed methodology to other karst aquifers will show to what extent these findings can be generalized, thus providing guidance for effective parameter and observation data acquisition in karst systems.