Introduction and background

In carbonate hydrogeology, interactions between groundwater and surface water are complicated by interconnected, heterogeneous fracture networks capable of quickly transmitting large water volumes. Effective water resource management of carbonate aquifers relies on a robust understanding of fracture complexities, particularly in arid climates where water scarcity is expected to further stress human and environmental systems (Vörösmarty et al. 2000; Jury and Vaux 2005; Meixner et al. 2016). Such dynamics are evident in the Basin and Range carbonate-rock aquifer system in the western United States (Harrill and Prudic 1998; Welch et al. 2007), including Snake Creek in Great Basin National Park.

Except during periods of unusually high runoff, all the natural surface-water flow in the upper part of the Snake Creek drainage entirely infiltrates into the subsurface as it crosses a losing reach overlying permeable carbonate bedrock. Until recently, this water had been assumed to flow south and then east through the deep subsurface, eventually recharging the regional Great Basin carbonate and alluvial aquifer system near the Nevada-Utah border (Heilweil and Brooks 2011; Prudic et al. 2015). This previously proposed deep subsurface pathway was largely based on the outcropping of low-permeability quartzite in the drainage and the assumption that the generally north–south-trending Snake Range detachment fault was a hydrological barrier to groundwater flow from the higher elevations of the Snake Creek drainage to the eastern springs in the drainage near the valley lowland (Prudic et al. 2015).

Quantitative tracer tests are powerful tools to estimate groundwater/surface-water fluxes and provide insight into subsurface characteristics critical to solute transport. Such tests are well documented in fractured carbonate systems and can employ a variety of tracers including fluorescent dyes, ionic salts, dissolved gases, stable and radiogenic isotopes, and particles (Zötl 1961; Mull et al. 1988; Maloszewski et al. 1992; Käss 1998; Goldscheider et al. 2008; Taylor and Greene 2008; Rasmuson et al. 2020; Benischke 2021). Each tracer has advantages and disadvantages related to the purpose of the test, ease of injection, detection limit, and conservative behavior. The combined use of multiple tracers with varied chemical properties not only increases the likelihood of successfully estimating volumetric fluxes, but can constrain important subsurface properties related to contaminant transport such as fracture characteristics, matrix porosity, fluid velocity, and groundwater transit times (Garnier et al. 1985; Jardine et al. 1999; Becker and Shapiro 2000).

In this study, two tracers were injected to estimate the quantity of Snake Creek infiltration that is recovered at Spring Creek Spring (SCS), 9.8 kilometers (km) down drainage: dissolved sodium bromide (NaBr) for analysis of the bromide anion (Br–) and fluorescein dye. Fluorescein dye can easily be detected in very low (parts per billion) concentrations and is relatively conservative when used in underground applications although it photodegrades when exposed to sunlight and is susceptible to analytical interferences (Mull et al. 1988; Goldscheider et al. 2008). While the detection limit of Br– is higher than fluorescein dye, Br– is considered a more conservative tracer (Leis and Benischke 2004) and is relatively free of analytical interferences (Goldscheider et al. 2008). Although sorption of Br– has been documented in soils with low pH and in the presence of iron oxides (Boggs and Adams 1992; Korom 2000), there is little evidence to support Br– sorption in fractured carbonates (Payne 1968; Schmotzer et al. 1973; Leap 1992).

The breakthrough curve (BTC) of a tracer can provide useful information on subsurface transport phenomena. Many artificial tracer studies in karstic terrain are on the kilometer scale (Käss 1998; Worthington and Ford 2009) and these BTCs can be evaluated for tracer velocity and conduit interconnections. Other studies have examined the declining limb (or “tail”) of the BTC to determine physical transport processes such as heterogeneous advection, fracture channeling, and chemical diffusion, but the majority of these studies are at 10–100-meter (m) scales (e.g., Birgersson and Neretnieks 1990; Maloszewski et al. 1999; Becker and Shapiro 2000, 2003; Neretnieks 2006). The physical processes described by power law scaling of the BTC tail control mass-transfer from mobile to immobile zones of the aquifer and should be considered to accurately quantify the volumetric water flux through the system but are seldom field-tested at the kilometer scale (Bodin et al. 2003).

This study describes an artificial and quantitative dual-tracer test over a straight-line distance of 9.8 km from Snake Creek to SCS. At this scale, diffusive flux of the tracer from mobile to immobile zones of the aquifer may become increasingly important. To estimate this diffusive flux, the observed breakthrough data were applied to an analytical model for transient contaminant transport (Sudicky and Frind 1982; Toran 2005). The resulting best-fit solutions were used to estimate the theoretical total tracer recovery given infinite time. This study presents (1) quantitative results of the Snake Creek dual-tracer injection, (2) analytical modeling results of advection-dispersion-diffusion transport, (3) the application of previously reported power law scaling to the empirical (unmodeled) BTCs of both tracers, and (4) a revised geologic cross section for the proposed subsurface flow path of losing water from Snake Creek to SCS.

Site description

Great Basin National Park (GBNP) is in the southern Snake Range in east-central Nevada near the town of Baker, approximately 10 km west of the Utah border. This study focuses on the Snake Creek drainage basin (84.7 km2) which lies on the eastern side of the mountain crest between the Big Wash drainage to the south and the Baker Creek drainage to the north (Fig. 1). Average annual precipitation is less than 20 cm near the bottom of the Snake Creek drainage near Garrison (US Climate Data 2021) and greater than 75 cm in the higher elevations of the drainage (Prudic et al. 2015). Streams, springs, and seeps within the Snake Creek drainage are valuable water resources that maintain diverse biological communities, enhance the abundance of geologic features, and provide water for park operations (Elliott et al. 2006). Snake Creek waters also provide irrigation supply to crops grown in the valley below.

Fig. 1
figure 1

Site map and location of Snake Creek and Spring Creek Spring in the Snake Creek drainage in Great Basin National Park, Nevada, USA, using Google Earth satellite imagery. Geology simplified from McGrew and Brown (1995)

Full size image

Prudic et al. (2015) describes a regional detachment fault that divides the geology between upper plate and lower plate carbonate units (Fig. 1). The Snake Creek channel crosses from the lower plate carbonates to a fault block that contains a low permeability quartzite unit that creates a partial impediment to groundwater flow (Elliott et al. 2006; Prudic et al. 2015). Downstream of this fault block, a large Tertiary normal fault crosses the drainage from southeast to northwest (McGrew 1993; Miller et al. 1999; Prudic et al. 2015). Several springs are located along the fault strike including SCS. Diversions from Snake Creek and SCS provide water for a Nevada Department of Wildlife managed fish-rearing station and for irrigation in Snake Valley.

Surface-water flow in upper Snake Creek is diverted around a losing reach of the stream channel underlain by permeable carbonate rock through a 15-inch pipeline reported to convey as much as 400 liters per second (L s–1 ) (Dahl Zohner, Assistant District Ranger, Humboldt National Forest, personal communication, 1961). Snake Creek mean annual discharge is 85 L s–1 with a range of 20–1,303 L s–1 (Prudic et al. 2015). Typically, all Snake Creek water above the pipeline is diverted into the pipeline except during periods of seasonally high discharge which can occur in May or June. Prior to the construction of the pipeline, surface water in Snake Creek above the pipeline intake would infiltrate the streambed through the permeable carbonate rock and provide some support for the local riparian vegetation (Schook et al. 2020). The direction of movement and terminal discharge point of this infiltrated water was undetermined until now.

Methods

Overview

At the injection site, Snake Creek flows into a large concrete collection box with outflow controlled by a headgate. When the headgate is closed, the water level in the collection box rises until it is diverted into the pipeline. The headgate can be manually opened to the desired level to release some or all the flow back into the natural channel. Ideally, the headgate would be opened well in advance of the injection; however, the exact timing of release of the Snake Creek water into the natural channel was constrained by downstream water use until the end of the irrigation season. As a result, the headgate was partially opened on October 2, 2020, and fully opened on October 9, 2020, 19 days and 12 days before the injection, respectively (Table 1). The headgate was closed, and all flow returned to the pipeline on May 17, 2021. The injection point was located several hundred meters above the point where all streamflow was lost to the subsurface through the cobbly channel bottom (Fig. 2).

Table 1 Timing of flow release and tracer injection
Full size table
Fig. 2
figure 2

Injection site schematic showing the relative locations of the diversion, pipeline, headgate to control the flow into the losing reach, bromide and fluorescein dye injections, and the losing reach of Snake Creek. Schematic is not drawn to scale. Photo credit: US Geological Survey

Full size image

Dual-tracer injections

Contemporaneous injections of Br– and fluorescein dye were made in Snake Creek on October 21, 2020 when Snake Creek discharge was stabilized at approximately 22.7 L s–1. The Br– was released as a continuous injection of brine over an 8.5-hour (h) period from 07:44 to 16:14, and the powdered fluorescein dye was mixed with stream water and injected over a 30-minute (min) interval from 09:15 to 09:45. The brine was injected continuously, rather than as a slug, to avoid undesirable density differences that could cause the brine, and thus the Br– tracer, to separate from the natural water in the stream. The amount of tracer selected for injection was based on the discharge at predetermined outlet point(s), the distance between the injection point and the known recovery point(s) corrected for assumed sinuosity of the underground flow path, and the desired peak tracer concentration at the output point(s). The locations of the tracer recovery points were determined from a qualitative reconnaissance fluorescein dye tracer test conducted in 2019 (Gardner et al. 2023). A total of 0.567 kilogram (kg) of powdered fluorescein dye and 196.7 kg of Br– were injected. The fluorescein dye concentration in Snake Creek was calculated to be 13.9 parts per million (ppm) and the Br– concentration in Snake Creek was 260.7 ppm as measured by ion chromatography (Table 2). Additional details on the tracer injection methods, including how the solid tracers were dissolved into an aqueous form and then thoroughly mixed into Snake Creek, can be found in Humphrey et al. (2023).

Table 2 Tracer injection summary
Full size table

Sample recovery and analysis

Water samples for tracer analysis were collected with models 6712 and 3700 ISCO autosamplers at SCS from October 2, 2020 to March 3, 2021 starting 19 days before injection and ending 133 days after the injection. The paired autosamplers were placed near the outlet of SCS and adjacent to a flume where discharge was measured. The outlet of Squirrel Spring was also equipped with an autosampler, but the spring did not flow during the sampling period. Background samples were collected once a day beginning on October 2, until the start of the injection on October 21, 2020. Thereafter, spring water samples were collected every 3–12 h at increasing intervals until the end of the monitoring period on March 3, 2021. The Br– concentration at SCS was also monitored with a TempHionTM ion probe to detect the timing of principal components of the BTC and to inform sample collection intervals for both tracers. Programmed intervals were 6 and 8 h during the early part of the monitoring period (rising limb to peak concentration) to 12 and 24 h during the falling (recession) limb and extended tail of the BTC. The samplers were set up on the same, but offset intervals to increase the overall sampling frequency (e.g., samples were effectively collected every 3, 4, 6, and 12 h throughout the sampling campaign).

The flow rate at SCS was monitored using a submersible pressure transducer to record stage in a permanently installed, level 9-inch Parshall flume. These data were converted into a 15-min discharge record using standard discharge tables that relate stage above the throat of the flume to discharge with a 3–5% accuracy (Bureau of Reclamation 2001). Stage measurements recorded using the transducer were field-checked 15 times between the end of September 2020 and mid-February 2021.

Water samples for fluorescein dye were analyzed on a Turner Designs TD-700 filter fluorometer in the Utah Water Science Center laboratory using standard methods (Wilson et al. 1986). Additional details on fluorescein dye quality control and assessment can be found in Humphrey et al. (2023). Water samples for Br– were syringe filtered (0.45 µm) and analyzed by ion chromatography (IC) at the University of Utah. Laboratory check standards and one consistently repeated natural sample were analyzed with each batch of samples to ensure accuracy of IC measurements and to account for potential instrument drift. To confirm sample concentrations on the falling limb of the BTC, five samples at low concentrations (<0.10 ppm) were also analyzed for Br– by mass spectrometry.

Tracer uncertainty quantification

To quantify the uncertainty of recovered tracer mass, possible error was considered from the following sources: tracer mass injected into Snake Creek (Minj), recovered tracer concentration at SCS (ci), background tracer concentration at SCS (cb), and discharge (flow rate) at SCS (Qi). For the Br– tracer, the uncertainty of Minj required propagating the standard deviation of the injection rate and the concentration of Br– injectant at the 95% confidence intervals (2σ) using standard methods (Meyer 1975; Kline 1985). The Minj of the fluorescein dye tracer contains uncertainty associated with sorption on streambed alluvium and photodegradation as the fluorescein dye moved downstream in the channel to the point of total streamflow loss. These losses are not quantifiable; however, because stream water was shaded from direct sunlight and quickly infiltrated into the subsurface, these losses are likely relatively small (Smith and Pretorius 2002). The analytical uncertainty of cb and ci at SCS was determined at the 95% confidence intervals (2σ) by calibration standards and determined to be 0.01 ppm for Br– and 0.03 parts per billion (ppb) for fluorescein dye. The IC detection limit for Br– is 0.01 ppm and the fluorometer detection limit for fluorescein dye is 0.01 ppb (Neal et al. 2007; Goldscheider et al. 2008).

Normally distributed random error with bounds of 2σ was applied to the four identified error sources. The total uncertainty of percent tracer recovered was estimated from Monte Carlo simulations (n = 100,000) performed in MATLAB (2019). The 95% confidence intervals were determined from the simulations to yield the uncertainty of the total tracer recovered.

Estimation of the breakthrough curve and characteristic parameters

Interpolated BTCs were generated by aggregating background-corrected tracer concentration and time data from SCS samples. The background concentration of Br– was 0.034 and ~0.01 ppb for fluorescein dye. An hourly BTC was created by linear interpolation between measured sample concentrations using the griddedInterpolant function in MATLAB (2019). This interpolated curve is useful to simplify the calculation of characteristic parameters from the mathematical integration of discharge, concentration, and time data to summation notation. The interpolated BTC was used to estimate time of leading edge (i.e., first arrival, TL), peak concentration (Tp), mean transit time (\(\overline{t}\)), centroid (Tc), and trailing edge (Tt) (US Environmental Protection Agency 2002; Kilpatrick and Wilson 1989; Taylor and Greene 2008).

The mass of the recovered tracer (MR) is given by the integration of the tracer flux over time (Goldscheider et al. 2008). In practice, MR is expressed by numerical integration in Eq. (1) (modified from Mull et al. 1988):

$${M}_{\textrm{R}}=\sum_{i=1}^n{Q}_i\left({c}_i-{c}_{\textrm{b}}\right)\Delta t$$
(1)

where i is the ith sampling interval, n is the cumulative number of samples until Tt, Qi is spring discharge (flow rate) at SCS, ci is recovered tracer concentration, cb is background tracer concentration, and Δt is duration of the sampling interval (consistent for interpolated BTC). The interpolated vector of hourly concentration data was multiplied by the hourly discharge at SCS. The resulting flux vector was multiplied by the sampling interval (1 h) and summed to yield the total mass recovered (Eq. 1). The percent mass recovery (%MR) is calculated by dividing MR by the total mass injected. The equations for mean transit time (\(\overline{t}\)) (Appendix, 1st equation therein) and mean tracer velocity (\(\overline{v}\)) (3rd equation) along with the variance (4th and 5th equations, respectively) of these two parameters can also be found in the Appendix.

The injections were assumed to be impulse releases (i.e., “slugs”) because the duration of the injections (8.5 h for Br– and 0.5 h for fluorescein dye) was substantially less than the principal components of the BTC (e.g., the duration of the Br– injection was 1.5 orders of magnitude less than the time to peak tracer concentration). This was verified by comparing the calculations of Br– characteristic parameters based on both impulse and short-pulse assumptions and finding the differences to be negligible—for example, the mean tracer velocity for Br– under impulse assumptions was 0.8% less than the mean tracer velocity under short-pulse assumptions.

The power law slope of the declining limb of the BTC can indicate the physical processes (e.g., chemical diffusion) affecting tracer transport (e.g., Hadermann and Heer 1996; Becker and Shapiro 2000). The BTCs can be normalized by computing the mass flux rate (MF,i) for a given sampling interval:

$${M}_{\textrm{F},i}=\frac{c_i{Q}_i}{M_{\textrm{inj}}}\kern0.5em$$
(2)

where Minj is the tracer mass injected. The apparent power law slope was found by plotting MF,i vs time in log-log space and fitting a power law curve to the declining limb of the breakthrough data using the polyfit function in MATLAB. This method yields the “apparent” power law slope because a robust analysis of other statistical distributions to the breakthrough curve tail was not performed as summarized by Pedretti and Bianchi (2018).

Breakthrough curve simulations

The effects of matrix diffusion on both BTC geometry and total tracer recovery were investigated by applying the analytical solution for transient contaminant transport, known by the computer code “CRAFLUSH” (Sudicky and Frind 1982), to the injection parameters of this study. This solution considers advective transport and hydrodynamic dispersion along two parallel fractures as well as molecular diffusion between the fracture and the matrix as defined by the last two equations of the Appendix. Toran (2005) applied the analytical solution given by the CRAFLUSH model in a processing program called CRAFIT, which uses a Latin hypercube sampling scheme to vary five model parameters (fracture aperture, fracture spacing, fracture and matrix retardation, and matrix porosity) and finds the minimum error between simulated and observed BTCs. The measure of error calculated by CRAFIT is the absolute value of the minimum orthogonal distance between interpolation points and the modeled BTC (Toran 2005).

CRAFIT was used to determine possible fracture/matrix properties that could be used in the forward model by Sudicky and Frind (i.e., CRAFLUSH) to investigate the effects of tracer flux between fractures and the surrounding porous matrix. By incorporating the known injection parameters (initial tracer concentration, rate of injection, injection duration, and tracer diffusion coefficients) and subsurface assumptions (system volume, system length, longitudinal dispersivity, and tortuosity) along with a range of possible fracture/matrix properties (fracture aperture, fracture spacing, and matrix porosity; Table 3) into CRAFIT, the program can provide the best-fit values of fracture aperture, fracture spacing, and matrix porosity that fit the observed breakthrough curves. These best-fit fracture/matrix parameters can then be applied to the analytical solution by Sudicky and Frind (1982) to model the effects of molecular diffusion on the transport of fluorescein dye and Br– from Snake Creek to SCS. The initial input tracer concentrations to the model must consider the fraction of the total injected tracer recovered at SCS, thus the initial injected tracer concentration (Co) for CRAFIT simulations must be proportional to the amount of tracer recovered, which is given by:

$${C}_{\textrm{o}}=\%{M}_{\textrm{R}}\times {C}_{\textrm{meas}}$$
(3)
Table 3 CRAFIT initial parameters
Full size table

where %MR is the mass fraction of recovered tracer and Cmeas is the tracer concentration in Snake Creek. This accounts for the fraction of initially injected tracer that is not recovered at SCS and is presumed to move into the deeper subsurface.

The injection rate was set equal to the flow rate of Snake Creek as measured 10 m upstream from the diversion structure. The longitudinal dispersivity (αL) was assumed to be 100 m and tortuosity was assumed to be 1.5. The free-water diffusion coefficient (Dw) of Br– and fluorescein dye are 1.6 · 10−4 and 3.6 · 10−5 m2 day–1, respectively (Casalini et al. 2011; Lide 2004). The system volume was calculated by multiplying the measured distance from the losing section of Snake Creek to SCS (10,000 m) by an assumed cross-sectional area (5,000 m2). The cross-sectional area was determined by using the cubic law (Witherspoon et al. 1980) with a fracture spacing of 1.6 m and a fracture aperture of 0.6 mm. In other words, with the aforementioned fracture parameters and maximum hydraulic gradient between the injection point and SCS, a cross-sectional area of 5,000 m2 is required to transmit the observed flow through fractures to SCS. The system length and cross section provided a volume for input to CRAFIT (Table 3).

Parameter ranges typical for fractured carbonates in the region (Prudic et al. 2015) and consistent with the required volume flux of Snake Creek were applied to the five CRAFIT variable parameters. The fracture aperture was given a range of 0.1–1.0 mm, the fracture spacing was given a range of 0.1–2 m, and the matrix porosity was given a range of 0.05–1.00%. Fracture and matrix retardation was set to 1 based on the assumption of nonreactive tracer transport and these parameters were not varied in the simulations.

A single set of model subsurface parameters (i.e., fracture aperture, fracture spacing, and matrix porosity) was chosen to isolate the effects of matrix diffusion on tracer subsurface transport. A second simulation of the Br– injection was conducted maintaining the initial Br– concentration and injection duration but substituting the Dw of fluorescein dye. A third simulation of the Br– injection was conducted with a Dw near zero, simulating the hypothetical BTC with no matrix diffusion. The same two additional simulations were conducted for the fluorescein dye tracer: (1) a simulation maintaining initial fluorescein dye injection parameters but substituting the Dw of Br–, and (2) a simulation of fluorescein dye injection parameters substituting a near-zero Dw.

Results

Breakthrough curves and Spring Creek Spring response

First arrival of Br– at SCS occurred at 9.1 days after injection with a peak concentration of 0.91 ppm after 12.6 days (Fig. 3; Table 4). Breakthrough of fluorescein dye occurred 9.9 days after injection with a peak concentration of 5.01 ppb after 12.7 days. The BTCs are most similar at early times and deviations could be a result of analytical error (e.g., sampling time and small background uncertainties). Differences between the two tracers are evident in the tail of the BTC and calculated parameters that rely on the entirety of the BTC. The time to trailing edge of Br– was 133.3 days and 73.4 days for fluorescein dye. The mean transit time \(\Big(\overline{t}\Big)\) of Br– was 35.5 days (σ = 30.9 days) and mean tracer velocity (v̅) was 24.9 m h–1 (σ = 17.2 m h–1). The mean transit time \(\Big(\overline{t}\Big)\) of fluorescein dye was 17.8 days (σ = 8.0 days) and mean tracer velocity (v̅) was 33.0 m hr–1 (σ = 9.7 m h–1).

Fig. 3
figure 3

a Interpolated breakthrough curve (BTC) and cumulative recovery of both tracers at Spring Creek Spring with characteristic parameters. b Enlarged view of BTC from 5–40 h after injection. Characteristic parameters include time to leading edge (i.e., first arrival, TL), time to peak concentration (Tp), time to centroid (Tc), mean transit time (\(\overline{t}\)), and time to trailing edge (Tt) with the appropriate tracer indicated (bromide [Br–], fluorescein dye [F])

Full size image
Table 4 Summary of tracer results
Full size table

The discharge at SCS declined from 36.9 L s–1 on October 2, 2020, when water was diverted from the pipeline back into the losing reach of Snake Creek, to 36.2 L s–1 on October 12, 2020 (Fig. 4). After this period, discharge at SCS increased rapidly to 43.6 L s–1 on November 24, 2020, and then gradually increased to 45.8 L s–1 on March 31, 2021. Historical observations of SCS indicate that discharge of the spring generally declines from September through December until mid-January when early snowmelt events cause an increase in spring discharge. In this case, the uncharacteristic rise of SCS discharge in early October occurred 10 days after Snake Creek water was diverted back into the losing reach. The time of first tracer arrival at SCS occurred 9.1 and 9.9 days from injection (Table 4).

Fig. 4
figure 4

Summary of hydraulic response at Spring Creek Spring (SCS) and timing of important diversion and tracer events

Full size image

Tracer recovery

The total measured percent mass recovery (%MR) of Br– and fluorescein dye was 16.4% (2σ = 2.6%) and 20.4% (2σ = 1.3%), respectively. A Monte Carlo uncertainty analysis (as previously described) was used to determine if the difference in %MR could be the result of analytical and/or random error. The null hypothesis is \(\%{M}_{\textrm{R}}^{\textrm{Fl}}\ne \%{M}_{\textrm{R}}^{\textrm{Br}}.\)The resulting probability density functions (PDFs) show the spread of possible %MR values given perturbations in the input parameters (Fig. 5). Because the 95% confidence intervals for the tracer recoveries do not overlap, the null hypothesis cannot be rejected with 95% confidence indicating that the difference in the Br– and fluorescein dye recoveries is not simply the result of measurement error.

Fig. 5
figure 5

The probability density functions (PDFs) of total percent tracer recovery (%MR) for the bromide and fluorescein dye tracers at Spring Creek Spring from Monte Carlo uncertainty analysis. The maximum of each curve indicates %MR and is the mean value (μ) of the PDF represented by a vertical dotted line. The 95% confidence interval (C.I.) for each curve is equal to ±2σ and is plotted as a vertical dashed line

Full size image

Modeling results

The best-fit model parameters of both tracers were found from 1,000 iterations in CRAFIT. The results indicate slight differences in modeled fracture aperture (0.6 and 0.8 mm for Br– and fluorescein dye, respectively), matrix porosity (0.8 and 0.9% for Br– and fluorescein dye, respectively), and fracture spacing (1.6 and 1.9 m for Br– and fluorescein dye, respectively). Considering the modest effect that the differences in these three parameters have on the BTC of each tracer (Humphrey et al. 2023), the best-fit model parameters of Br– were arbitrarily chosen for subsequent diffusion models for both fluorescein dye and Br–. The simulated BTC was compared to the observed BTC for each tracer (Fig. 6).

Fig. 6
figure 6

Observed tracer concentration and CRAFIT modeled concentration [C(t)] for a Br– and b fluorescein dye. The dotted black line in each plot represents the theoretical tracer recovery given the effective diffusion coefficient (Dw) of the other tracer

Full size image

A hypothetical BTC was simulated for each tracer using the Dw of the other tracer (Fig. 6). The simulations demonstrate that, by simply applying the Dw of fluorescein dye to the Br– injection parameters, the resulting peak concentration of Br– is 110% higher than the peak concentration when the true Dw of Br– is used in the model. In addition, the Br– concentration on the last sampling day (133 days from injection) is 52% lower for the Br– simulation with the Dw of fluorescein dye than the Br– simulation with the true diffusion coefficient. These diffusional effects are inverse for the fluorescein dye simulations. The fluorescein dye peak is 57% lower and the concentration of the BTC tail at day 133 is 62% higher when simulated with the Dw of Br– compared to the Dw of fluorescein dye.

The initial tracer concentration (Co) for CRAFIT simulations is the measured fraction of tracer mass recovered multiplied by the measured concentration in Snake Creek (Table 3); Eq. (3). Therefore, Co is also the fraction of recoverable tracer at SCS and excludes tracer that does not surface in the study area. In other words, Co is the fraction of injected tracer that does not move to an undetected location (e.g., continues moving downgradient to enter the valley basin-fill aquifer) and will eventually discharge at SCS. The results of simulated tracer recovery under the assumed conditions of fracture transport with diffusion indicate that at 133 days from the injection 0.89 Co of fluorescein dye is recovered and 0.84 Co of Br– is recovered (Fig. 7). Furthermore, the estimated total recovery of fluorescein dye and Br– at 550 days is 0.93 Co and 0.92 Co, respectively, indicating that even at long sampling intervals the entirety of the tracer will not be 100% recovered when matrix diffusion has a significant effect on groundwater transport. When Dw of each tracer is set to near zero, it is estimated that >0.95 Co of both tracers would be recovered after 12.5 days (i.e., time to peak concentration) and >0.99 Co of each tracer would be recovered at 133 days (the end of sampling in this study).

Fig. 7
figure 7

Results from CRAFIT simulations of bromide and fluorescein dye tracers show the theoretical recovery at the date of last sample (133 days from injection shown as a dashed line) and up to 550 days from injection. Also shown is the theoretical recovery at 133 days from injection in the hypothetical scenario where the effective diffusion coefficient of each tracer is near zero (no diffusion) shown as a dotted line. The theoretical recovery is the total recoverable tracer at Spring Creek Spring that does not flow to other areas of the system such as the deep regional aquifer

Full size image

These results suggest that the measured mass percent of recovered tracer should be adjusted to consider the effects of diffusion. The measured mass percent recoveries of Br– and fluorescein dye at the 95% confidence intervals are 13.8–19.0% and 19.1–21.7%, respectively (Fig. 5). If the effect of diffusion is considered, the theoretical recoveries of Br– and fluorescein dye at the 95% confidence intervals are 16.9–22.1% and 21.7–24.3%, respectively, and the null hypothesis (\(\%{M}_{\textrm{R}}^{\textrm{Fl}}\ne \%{M}_{\textrm{R}}^{\textrm{Br}}\)) can be rejected. These theoretical recoveries indicate that, given infinite time, the recoveries would be statistically identical, and any differences could be attributed to analytical error. This statistical similarity is evidence that diffusional effects should be considered to accurately quantify total tracer recovery.

Apparent power law scaling

The log-log plot of normalized mass flux rate versus time from injection shows the declining limbs of the tracer BTCs at high resolution (Fig. 8). Power law slopes were calculated starting at 13 days from injection or approximately 1 day after peak concentration. The slope of fluorescein dye is well-fit (R2 = 0.98) by a single value equal to –3.58. The Br– breakthrough tail inflects at 23 days from injection and cannot be well-fit by a single slope value. The apparent power law slope of early time regime Br– data (13–23 days from injection) is –3.05 (R2 = 0.99) and decreases to –1.17 (R2 = 0.94) during the late-time regime (23–133 days from injection).

Fig. 8
figure 8

Breakthrough curves in log-log space for fluorescein dye and bromide tracers. The apparent power law slope of the fluorescein dye declining limb (black line) is well-fit by a single slope value. The apparent power law slope of the bromide declining limb inflects after 23 days from injection and the change in slope is shown

Full size image

Discussion and conclusions

Physical implications of apparent power law slopes

The elongated tracer breakthrough tails may be attributed to several physical processes including hydrodynamic dispersion (Becker and Shapiro 2000; Bodin et al. 2003), the effects of channeling in a fracture network (Abelin et al. 1994; Tsang and Neretnieks 1998), and diffusion into either the porous matrix or stagnant water zones in fractures (Maloszewski and Zuber 1993; Neretnieks 2006). For several decades, researchers have used the power law decay rate of the declining limb (i.e., the slope of the declining limb in log-log space) to differentiate between the effects of these physical processes on tracer recovery. Early studies attributed a power law slope of –1.5 to diffusive exchange between mobile and immobile zones of the system (e.g., Hadermann and Heer 1996). More recent studies have attributed a straight-line slope of –2 on log-log plots to heterogeneous advection or channeling (Becker and Shapiro 2003; Guihéneuf et al. 2017; Shapiro et al. 2008; Willmann et al. 2008). Most of these studies conducted experimental tracer tests on the order of 1–100 m under forced gradient conditions. This study examined tracer breakthrough on the order of 10 km under a natural gradient and finds slight but potentially significant deviations from previously reported power law slopes.

The initial slope of the Br– tail in log-log space is –3.05 and the slope of fluorescein dye in log-log space is –3.58, which are steeper than the power law slopes proposed for heterogeneous advection, channeling, or diffusion cited previously. The magnitude and similarity of these slopes indicate that physical transport along the entire length of the flow path is controlled by similar physical processes for both tracers at early times. The decay of the fluorescein dye declining limb is well-fit by a single power law slope of –3.58 for the entirety of tracer recovery suggesting that advection-dispersion is the dominant, but not singular, process throughout the transport of this tracer. Advection-dispersion modeling from CRAFIT (with Dw ≈ 0) indicates that, in the absence of diffusion, the power law slope of both tracers is less than (more negative) –6.0, which indicates greater transport complexity than can be explained by only advection-dispersion.

Although the apparent power law slope of fluorescein dye is well-fit by a single value, the apparent power law slope of the Br– tail inflects after 23 days and the slope becomes –1.17. The deviation of this slope from the abundance of reported –1.5 slopes may be attributed to the combined effects of long advection times with chemical diffusion into immobile zones of the aquifer. Hyman et al. (2019) proposed that deviations from –1.5 at late-time tailing may be the result of slowly decaying advective travel time distributions under the influence of chemical diffusion. Furthermore, Pedretti and Bianchi (2018) suggest that subsampling of empirical data, particularly at late times, may limit the ability to differentiate between a power law model and other statistical distributions. While the solute-transport model (CRAFLUSH/CRAFIT) used in this study strongly suggests that variations between the breakthrough curves of Br– and fluorescein dye can be largely attributed to differences in the diffusion coefficients of each tracer, additional statistical modeling of this tracer experiment may be needed to draw conclusions on the physical processes that yield such a deviation in apparent power law slope from those values reported in the literature and demonstrate whether other statistical distributions may also be appropriate.

One such physical influence on the apparent power law slopes may be the effects of conduits that act as a network of pipes in karstic terrains (Onac and Van Beynen 2021). The potential effects of these conduits on BTCs are summarized in Benischke (2021), which describes both the combination of dispersion with matrix diffusion in conduits and the superposition of multiple flow paths from a single source to an outlet to produce BTCs with elongated tails. In GBNP, conduits up to 3.2 km in length have been observed in lower plate carbonates in the Lehman Creek drainage 10 km to the north, but the existence and extent of these conduits in the Snake Creek drainage are unknown. Groundwater flow through fractures, not conduits, has been observed in upper plate carbonates in Snake Creek Well No. 5 (Prudic et al. 2015), located 3.7 km down drainage from SCS (Fig. 9). Should conduits exist along the proposed Snake Creek losing-water flow path, they likely exist in the lower plate carbonates below the losing section of Snake Creek. However, these conduits are not observed in upper plate carbonates (albeit with only a single observation well as reference) and are likely not persistent at scales larger than have been observed in other areas of the park (3.2 km in length). Rather, groundwater flow in the system is likely controlled by millimeter-scale fractures along the flow path that delay peak tracer arrival sufficiently for matrix diffusion to have a disproportional effect on the BTC tails of two tracers with different diffusion coefficients.

Fig. 9
figure 9

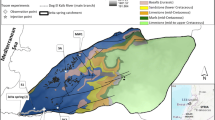
Geologic map showing potential subsurface flow paths (1) north and (2) south of exposed low-permeability siliciclastic units that could connect the losing reach of upper Snake Creek to Spring Creek Spring. The geologic cross section shows the more likely southern flow path from map view (flow path 2) and a possible flow path for the fraction of Snake Creek water that arrives at Spring Creek Spring (upper flow path) and a possible flow path for the fraction of Snake Creek water that is not recovered (lower flow path). The cross section showing flow path 2 follows from the work of Prudic et al. (2015), which proposed a flow path southeast toward the Big Wash drainage. Geologic structures and units are from McGrew and Brown (1995)

Full size image

The fate of lost Snake Creek water

The entirety of Snake Creek surface-water loss along the pipeline reach was previously assumed to flow southward, leaving the Snake Creek drainage through underlying and connected carbonate units, to enter the regional carbonate aquifer (Prudic et al. 2015). This proposed flow path assumed that the low permeability Prospect Mountain Quartzite and the Snake Range detachment fault (outcropping mid-canyon near the downstream end of the pipeline) would prevent groundwater from discharging at down-drainage springs or to the alluvial aquifer near the mouth of Snake Creek Canyon. The existence of a subsurface hydrologic connection between upper Snake Creek and SCS that approximately follows the stream channel would require flow across the southern Snake Range detachment fault and through the low-permeability Pioche Shale and Prospect Mountain Quartzite siliciclastic units (Fig. 9). Furthermore, the Snake Range detachment fault is also considered to be a hydrological barrier (Prudic et al. 2015). The low-permeable nature of these features suggests that this path is unlikely. Alternative flow paths include (1) subsurface flow that bypasses the shale and quartzite to the north, crosses the detachment fault where lower plate carbonate rocks are in direct contact with highly faulted upper plate carbonate rocks, or (2) subsurface flow that bypasses the shale and quartzite to the south, moving beneath the detachment fault and crossing from the Pole Canyon Limestone into the Lincoln Peak Limestone (a member of the lower plate carbonates in depositional contact with the Pole Canyon Limestone) before entering upper-plate carbonate rocks where they are obscured by Quaternary and Tertiary sediments just south of the Snake Creek drainage divide. These potential flow paths are shown on the plan view geologic map in Fig. 9.

The results of this tracer study indicate that a significant fraction of the Snake Creek stream loss occurring near the head of the pipeline travels through the subsurface across the karst limestone zone to discharge farther downstream within the Snake Creek drainage at SCS. Previous field work has demonstrated the low permeability of the Prospect Mountain Quartzite and provided little evidence to support the existence of late-time faulting that could structurally segment the detachment fault within the karst-limestone hydrogeologic zone near Snake Creek itself (McGrew and Brown 1995; Prudic et al. 2015). Therefore, groundwater flow originating from upper Snake Creek likely bypasses these impermeable features along one of the potential flow paths proposed previously. Because the northern flow path crosses the Eureka Quartzite, another siliciclastic unit known to be a local barrier to groundwater flow that controls spring discharge (Prudic et al. 2015), the southern flow path is preferred and illustrated in the cross section in Fig. 9. The complex normal faulting that occurs in the upper plate carbonates may disrupt continuity of the older detachment surface and create a permeable pathway so that water moving along this flow path can continue downgradient to discharge at SCS. The remaining fraction of upper Snake Creek stream loss likely continues to move eastward through an unspecified combination of fractured Cambrian and Paleozoic carbonate rocks before entering the Snake Valley alluvial aquifer east of the Snake Creek Well.

The amount of infiltrating Snake Creek water discharging from SCS can be estimated from the percentage of tracer recovered (Brown et al. 1969; Smart 1988). Based on both cumulative tracer recovery and diffusion modeling, 16.9–24.3% of the infiltrating flow from upper Snake Creek is estimated to be recovered at SCS. During the period of this test, the flow rate of upper Snake Creek was 22.7 L s–1, thus 3.8–5.5 L s–1 of the total flow at SCS is estimated to originate from upper Snake Creek. This estimate was determined under base-flow conditions in a particularly dry year in Great Basin National Park and may not be reflective of total flow recovered under different hydrological conditions (e.g., higher precipitation throughout the year or during spring snowmelt). Finally, the modeled diffusive flux indicates that additional tracer is likely stored in immobile zones of the aquifer and is remobilized only at large timescales on the order of years.

Summary and conclusions

In this study, the total flow of Snake Creek was diverted from a pipeline into the natural channel and simultaneous, short-pulse injections of two tracers (Br– and fluorescein dye) were made in a losing reach of Snake Creek underlain by permeable carbonate rocks. Flow into the losing reach remained steady for the duration of the test and all streamflow was lost to groundwater recharge within the reach. Apparent tracer recoveries for the Br– and fluorescein dye at Spring Creek Spring, approximately 10 km down drainage, were 16.4±2.6% and 20.4±1.3%, respectively, and early BTC characteristics were similar for the two tracers. Differences in the normalized peak concentration, BTC tail duration and power law slope, and apparent tracer recovery can be partially rationalized by the effects of tracer diffusion into immobile zones of the aquifer.

These results suggest that the percent recoveries calculated using standard methods account for only 0.84 Co of the Br– and 0.91 Co of the fluorescein dye expected in the eventual complete recovery of these tracers. The total expected recovered flow from Snake Creek at Spring Creek Spring is therefore 16.9–24.3% under the hydrological conditions of this test. These recoveries may not reflect the total flow recovered from Snake Creek under different hydrological conditions, particularly during snowmelt runoff. These findings imply that additional consideration of the diffusive tracer flux in fracture-dominated flow may improve the ability to quantify tracer recovery.

Finally, a geologic cross section is proposed showing that flow diverted underground in a losing reach in the upper part of the Snake Creek drainage could bypass the quartzite at the southern edge of the drainage through fractured carbonate rock and likely crosses the Snake Range detachment fault. This suggests the potential for other previously dismissed hydrological connections between groundwater and surface water in the Snake Range.