Geographic and hydromorphologic controls on interactions between hyporheic flow and discharging deep groundwater

Abstract

Hyporheic exchange flow (HEF) at the streambed–water interface (SWI) has been shown to impact the pattern and rate of discharging groundwater flow (GWF) and the consequential transport of heat, solutes and contaminants from the subsurface into streams. However, the control of geographic and hydromorphological catchment characteristics on GWF–HEF interactions is still not fully understood. Here, the spatial variability in flow characteristics in discharge zones was investigated and averaged over three spatial scales in five geographically different catchments in Sweden. Specifically, the deep GWF discharge velocity at the SWI was estimated using steady-state numerical models, accounting for the real multiscale topography and heterogeneous geology, while an analytical model, based on power spectral analysis of the streambed topography and statistical assessments of the stream hydraulics, was used to estimate the HEF. The modeling resulted in large variability in deep GWF and HEF velocities, both within and between catchments, and a regression analysis was performed to explain this observed variability by using a set of independent variables representing catchment topography and geology as well as local stream hydromorphology. Moreover, the HEF velocity was approximately two orders of magnitude larger than the deep GWF velocity in most of the investigated stream reaches, indicating significant potential to accelerate the deep GWF velocity and reduce the discharge areas. The greatest impact occurred in catchments with low average slope and in reaches close to the catchment outlet, where the deep GWF discharge velocity was generally low.

Résumé

Il a été démontré que le flux d’échange hyporhéique (HEF) à l’interface entre le lit du cours d’eau et l’eau (SWI) a un impact sur les modalités et le taux d’écoulement des eaux souterraines (GWF) et le transport consécutif de la chaleur, des solutés et des contaminants de la subsurface vers les cours d’eau. Cependant, le contrôle des caractéristiques géographiques et hydromorphologiques des bassins versants sur les interactions GWF–HEF n’est pas encore totalement compris. Ici, la variabilité spatiale des caractéristiques d’écoulement dans les zones de décharge a été étudiée et moyennée sur trois échelles spatiales dans cinq bassins versants géographiquement différents en Suède. Plus précisément, la vitesse de décharge du GWF profond au niveau de la SWI a été estimée à l’aide de modèles numériques en régime permanent, tenant compte de la topographie multi-échelle réelle et de la géologie hétérogène, tandis qu’un modèle analytique, basé sur une analyse spectrale de puissance de la topographie du lit du cours d’eau et des évaluations statistiques de l’hydraulique du cours d’eau, a été utilisé pour estimer le HEF. La modélisation a donné lieu à une grande variabilité des vitesses GWF en profondeur et HEF, à la fois au sein des bassins versants et entre eux, et une analyse de régression a été effectuée pour expliquer cette variabilité observée en utilisant un ensemble de variables indépendantes représentant la topographie et la géologie du bassin versant ainsi que l’hydromorphologie locale du cours d’eau. De plus, la vitesse du HEF était environ deux ordres de grandeur plus grande que la vitesse du GWF profond dans la plupart des tronçons de cours d’eau étudiés, ce qui indique un potentiel significatif pour accélérer la vitesse du GWF profond et réduire les zones de décharge. L’impact le plus important s’est produit dans les bassins versants à faible pente moyenne et dans les tronçons proches de l’exutoire du bassin versant, où la vitesse de décharge du GWF profond était généralement faible.

Resumen

Se ha demostrado que el flujo de intercambio hiporreico (HEF) en la interfaz entre el cauce y el agua (SWI) influye en el patrón y la tasa de descarga del flujo de agua subterránea (GWF) y en el consiguiente transporte de calor, solutos y contaminantes desde el subsuelo hacia los cursos de agua. Sin embargo, el control de las características geográficas e hidromorfológicas de la cuenca sobre las interacciones GWF–HEF aún no se conoce en su totalidad. En este caso, se investigó la variabilidad espacial de las características del flujo en las zonas de descarga y se promedió a lo largo de tres escalas espaciales en cinco captaciones geográficamente diferentes de Suecia. En concreto, la velocidad de descarga del GWF profundo en el SWI se estimó mediante modelos numéricos de estado estacionario, teniendo en cuenta la topografía de múltiples escalas y la geología heterogénea del lugar, mientras que para estimar el HEF se utilizó un modelo analítico, basado en el análisis espectral de potencia de la topografía del cauce y en evaluaciones estadísticas de la hidráulica del arroyo. La modelización dio como resultado una gran variabilidad en las velocidades profundas del GWF y del HEF, tanto dentro de las cuencas como entre ellas, y se realizó un análisis de regresión para explicar esta variabilidad observada utilizando un conjunto de variables independientes que representaban la topografía y la geología de la cuenca, así como la hidromorfología local del arroyo. Además, la velocidad del HEF fue aproximadamente dos órdenes de magnitud mayor que la velocidad del GWF profundo en la mayoría de los tramos de arroyo investigados, lo que indica un potencial significativo para acelerar la velocidad del GWF profundo y reducir las áreas de descarga. El mayor impacto se produjo en las cuencas con baja pendiente media y en los tramos cercanos a la salida de la cuenca, donde la velocidad de descarga de la GWF profunda era generalmente baja.

摘要

已证明在河床-水界面(SWI)处的潜流交换流(HEF)会影响排泄型地下水流(GWF)，以及从地下到河流的热流，溶质和污染物传输的模式和速率。然而，仍然尚未完全了解对GWF -HEF相互作用的地理和水文学形态特征的控制。在这里，研究了排泄区流动特征的空间变异性，并在瑞典五个地理学流域的三个空间尺度上平均。具体而言，使用稳定流数值模型估算了SWI处的深GWF排泄速度，考虑了实际的多尺度地形和异质性地质，而基于河床地形的功率谱分析和河流水力学的统计评估的分析模型，被用来估计HEF。该建模导致在集水区内和流域之间的深部GWF和HEF速度的差异很大，并且通过使用一组代表集水区地形和地质学的自变量以及局部河流水文形态学来解释这种观察到的可变性。此外，在大多数研究的河流中，HEF速度大约比GWF速度大约两个数量级，这表明有显著的潜力可以加速深部GWF的速率并降低排泄区范围。最大的影响发生在平均斜率低的集水区和靠近流域出口的区域，那里的深部GWF排泄速度通常很低。

Resumo

Foi demonstrado que o fluxo de troca hiporreico (FTH) na interface leito-água (ILA) afeta o padrão e a taxa de descarga do fluxo de águas subterrâneas (FAS) e o consequente transporte de calor, solutos e contaminantes do subsolo para os riachos. No entanto, o controle das características geográficas e hidromorfológicas da bacia nas interações FAS–FTH ainda não é totalmente compreendido. Aqui, a variabilidade espacial nas características de fluxo nas zonas de descarga foi investigada e calculada a média em três escalas espaciais em cinco bacias hidrográficas geograficamente diferentes na Suécia. Especificamente, a velocidade de descarga profunda do FAS na ILA foi estimada usando modelos numéricos de estado estacionário, representando a topografia multiescala real e a geologia heterogênea, enquanto um modelo analítico, baseado na análise espectral de potência da topografia do leito do rio e avaliações estatísticas da hidráulica do fluxo, foi usado para estimar o FTH. A modelagem resultou em grande variabilidade nas velocidades profundas do FAZ e do FTH, tanto dentro como entre as bacias hidrográficas, e uma análise de regressão foi realizada para explicar essa variabilidade observada usando um conjunto de variáveis independentes representando a topografia e geologia da bacia, bem como a hidromorfologia do córrego local. Além disso, a velocidade do FTH foi aproximadamente duas ordens de grandeza maior que a velocidade do FAS profundo na maioria dos trechos de fluxo investigados, indicando potencial significativo para acelerar a velocidade do FAS profundo e reduzir as áreas de descarga. O maior impacto ocorreu em bacias com baixa declividade média e em trechos próximos à saída da bacia, onde a velocidade de descarga profunda do FAS foi geralmente baixa.

Introduction

Groundwater flow circulation within a catchment occurs over a wide range of spatial and temporal scales, creating flow paths that are nested in a hierarchical flow cell structure (Tóth 1963, Winter et al. 1998, Wörman et al. 2007). Groundwater recharges over relatively large areas, while it generally discharges in low-elevation areas and often in surface-water features such as streams, wetlands, or lakes (Marklund et al. 2008; Uchida et al. 2003). Previous studies have shown that the local flow of surface water through the sediments of streams and wetlands, commonly referred to as hyporheic exchange flow (HEF; Boano et al. 2014), can converge the groundwater flow (GWF) close to the streambed–water interface (SWI), reduce the groundwater discharge area, and increase the discharge velocity (Bhaskar et al. 2012; Boano et al. 2008; Mojarrad et al. 2022). HEF is driven by hydraulic head gradients at the SWI that are created by spatial variability in the streambed topography and the overlying surface water (e.g., Boano et al. 2014; Packman et al. 2004; Ward et al. 2019). The surface water that flows into the streambed in zones of high pressure and the discharging groundwater close to the SWI will interact and alter the direction and velocity of both upwelling and downwelling water, which will in turn influence stream biogeochemistry and benthic ecological functions (e.g., Bhaskar et al. 2012; Boano et al. 2008; Fleckenstein et al. 2010; Winter et al. 1998). The impact of HEF on deep GWF pathways can therefore be important to consider when evaluating the transport and fate of specific deep groundwater contaminants that flow into the biosphere. One critical application is the long-term safety assessment of nuclear waste repositories where high-level radioactive waste (HLRW) is isolated hundreds of meters deep in the bedrock. When quantifying the possible leakage of such radioactive compounds in regard to humans and other living organisms, a critical consideration in the assessment models is the groundwater flow through the upper parts of Quaternary deposits (QD; Alexander et al. 2003; Kautsky et al. 2013; Wörman et al. 2019). Another common groundwater contaminant is excess nitrogen in agricultural soils that reaches the stream network through GWF. In certain agricultural areas, so-called legacy nitrogen can be transported to streams with relatively deep and old groundwater after accumulating in the root zone for several decades (Van Meter et al. 2016; Tesoriero et al. 2013). The fate of groundwater nitrogen can then be substantially modified after passing through the hyporheic zone (Hedin et al. 1998; Krause et al. 2013), and the exact hyporheic transport times are thus essential to assess upwelling groundwater quality. Furthermore, the temporal variation in deep groundwater discharge areas due to interactions with HEF affects the stability and diversity of ecological habitats of benthic and aquatic organisms (Krause et al. 2011; Poole et al. 2006).

A relevant measure of the interactions between groundwater and surface water is the ratio $\overline{W_{\mathrm{dGWF}}}/{\left\langle W\right\rangle}_{\mathrm{HEF}}$, where $\overline{W_{\mathrm{dGWF}}}$ is the average deep groundwater flow (dGWF) discharge velocity and 〈W〉_HEF is the flow-weighted average hyporheic exchange velocity (Mojarrad et al. 2019). If $\overline{W_{\mathrm{dGWF}}}/{\left\langle W\right\rangle}_{\mathrm{HEF}}$<<1, then an increased convergence of the dGWF close to the SWI is expected, whereas if $\overline{W_{\mathrm{dGWF}}}/{\left\langle W\right\rangle}_{\mathrm{HEF}}$>>1, then the HEF has an insignificant or only a slight effect on the dGWF discharge pattern. The impact of the HEF on the dGWF discharge pattern and transport through QD is likely to have a substantial spatial variability, since both GWF and HEF are known to depend on spatially varying geographic and hydromorphological characteristics of the catchment and stream network (e.g., McGlynn et al. 2003; Wondzell et al. 2019). Furthermore, a general relationship may exist between $\overline{W_{\mathrm{dGWF}}}/{\left\langle W\right\rangle}_{\mathrm{HEF}}$ and independent geographic and hydromorphological variables, which would provide valuable guidance in elucidating the conditions in which HEF is important to consider when modeling groundwater transport through QD.

To the authors’ knowledge, no studies have yet specifically investigated the impact of regional catchment characteristics on dGWF discharge velocities and spatial patterns. However, several studies have found statistical linkages between catchment characteristics and other aspects of regional GWF, such as the average groundwater residence time (e.g., McGlynn et al. 2003; McGuire et al. 2005; Tetzlaff et al. 2009) and stream discharge (Laudon et al. 2007; Lacombe et al. 2014). Increasing the median subcatchment area (i.e., the median drainage area of all points along the stream network within a catchment) has been shown to cause, for example, increases in both the average groundwater residence time within a catchment (McGlynn et al. 2003) and the proportion of groundwater contribution to stream discharge (Laudon et al. 2007). Furthermore, the average distance to the stream network (DtS), the average elevation above the stream network (EaS), and the average gradient to the stream network (GtS = EaS/DtS) have been shown to control the average groundwater residence time within catchments (McGuire et al. 2005). Spatial trends in groundwater discharge into surface-water systems have also been linked to simple variables such as the average catchment slope and catchment area. A recent study found a higher proportion of deep groundwater in streams in large watersheds with low slopes than in small watersheds with high slopes (Hare et al. 2021). A wide variability in deep groundwater contributions has also been observed within single catchments, suggesting a greater contribution of deep groundwater in the main river valley than in the steep headwaters (Marklund et al. 2008). Finally, the catchment average groundwater residence time is also affected by the catchment geological characteristics, and it increases with both soil permeability and soil depth (i.e., thickness of QD; Tetzlaff et al. 2009).

As is the case with GWF, the residence time, rather than the velocity, has been the focus of most regression studies that consider HEF as the dependent variable. The average residence times of HEF can scale positively with measures of the local hydromorphologic complexity (e.g., stream slope, bed roughness, and sinuosity; Gooseff et al. 2007), as well as with hydraulic aspects of the streamflow defined by different types of inverse Reynolds numbers (O’Connor and Harvey 2008; Packman et al. 2004) and inverse Froude numbers (Sawyer et al. 2011; Wörman et al. 2002). Parameter groups accounting for both geological and hydraulic factors, such as the Darcy-Weisbach friction factor and the stream power, have also been shown to explain HEF well (Harvey et al. 2003; Zarnetske et al. 2007). Finally, recent studies have shown that the fractal properties of streambed elevation can explain a large part of the variability in HEF between stream reaches that differ in hydromorphological character (Lee et al. 2020; Marzadri et al. 2014).

The general aim of the present study is to investigate the degree of spatial variability in GWF–HEF interactions between and within catchments and how these interactions are controlled by specific hydromorphological and geographic characteristics. One particular aim was to identify conditions when HEF has a prevalent impact on the dGWF discharge; therefore, the focus of the study was to analyze the ratio between the dGWF discharge velocities and HEF velocities, here defined as an indicator of this impact. This aim was fulfilled by modeling the regional GWF and the local HEF for a wide range of spatial scales in five Swedish catchments with different topographic and hydromorphological characteristics. The average velocity of dGWF discharge and HEF, as well as the ratio between them, was subsequently statistically related to independent estimations of the catchment and local stream characteristics using regression analysis. An additional aim of the study was to investigate how the geographic and hydromorphologic controls might vary depending on the spatial scale at which the dependent and independent variables were averaged. Therefore, all analyses were performed at three specific scales: the stream reach, the intermediate catchment, and the regional catchment scale.

Methods

The methodology of this study consists of three separate steps: (1) modeling the GWF and HEF and numerically tracing deep groundwater flow paths discharging at the SWI; (2) calculating relevant independent variables in terms of catchment characteristics that might control the GWF–HEF interactions; and (3) investigating the correlations between catchment and local stream characteristics and the GWF–HEF interactions through multivariate power-law regression analysis. This section describes these steps in detail, following a description of the study catchments and the geographic and hydrological data used.

Study catchments and data

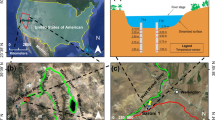
Five different catchments from different parts of Sweden were selected as the study areas (Fig. 1a). The catchments were chosen to cover a range of various characteristics, including topographic elevation, depth of the QD, land use, and stream slope and discharge. Data on discharge, land cover, and soil types presented in this section are all available from the Swedish Meteorological and Hydrological Institute (SMHI; Strömbäck et al. 2013), and soil depths were extracted from the soil depth model provided by the Geological Survey of Sweden (Daniels and Thunholm 2014). All topographic data originate from a digital elevation model (DEM) with a resolution of 2 m × 2 m (GSD-Elevation data, grid 2+, ©Swedish Mapping, Cadastral, and Land Registration Authority). The data for the five catchments are found in Table 1, which summarizes a more thorough description found in Text S1 in the electronic supplementary material (ESM).

Fig. 1

a The regional catchment locations in Sweden, and b Säva Brook regional catchment with stream network, subcatchments of each stream link, and intermediate subcatchments. The red lines represent the part of the stream network where topographic surveying was performed to calculate the topographic power spectral density used to validate the magnitude and slope of the DEM power spectral density. Detailed maps of all other catchments can be found in the Figs. S2–S5 in the ESM

Table 1 Summary of the characteristics of the five investigated catchments

The stream networks of the five catchments were generated from the DEM files by calculating the accumulated upstream area for all pixels and setting a flow accumulation threshold above which pixels were defined as streams. Comparable results for the five catchments were generated by relating the flow accumulation threshold area to the stream discharge so that only streams with an annual mean low discharge, Q_ML (m³/s), higher than 0.5 L/s were included in the analysis. The average annual mean low discharge and annual mean discharge, Q_M (m³/s), of each reach were calculated as the arithmetic mean of the distributed discharge within each reach. The distribution of the discharge was determined by scaling the annual mean or mean low discharge at the catchment outlet—Q_{M, out} (m³/s) and Q_{ML, out} (m³/s), respectively, obtained from the Hydrological Predictions for the Environment (HYPE) model; Lindström et al. (2010)—with the normalized flow accumulation area according to Text S2 in the ESM.

The effect of different spatial scales on GWF–HEF interactions was examined by conducting the investigations at three distinct spatial scales: the reach scale, the intermediate scale, and the regional catchment scale. Reaches were defined as stream segments in the network that did not have any tributaries. Four reaches with stream lengths <50 m were removed (for practical modeling purposes), leaving reaches with lengths varying between 61 and 9,318 m, with an average of 1,230 m in all five catchments. The local catchment areas of those reaches varied between 0.0051 and 7.714 km², with an average of 1.317 km². Clustering adjacent subcatchments, guided by the stream network, was performed to create intermediate catchments, which had areas ranging between 6.68 and 37.75 km², with an average of 19.03 km². Finally, the regional scale simply consisted of the five regional catchments, which had areas ranging between 68 and 193 km². The final stream network, reach catchments, and intermediate subcatchments in the Säva Brook regional catchment are presented in Fig. 1b, and maps of the four remaining catchments are found in Figs. S2–S5 in the ESM.

Hydrological modeling

The modeling framework of this study included a steady-state multiscale approach to cover a wide range of spatial scales that influence groundwater/surface-water interactions. The governing field equation for three-dimensional (3D) incompressible flow within porous media at steady state can be represented by:

$$\frac{\partial }{\partial x}\left(-{K}_{\mathrm{x}}\frac{\partial H}{\partial x}\right)+\frac{\partial }{\partial y}\left(-{K}_{\mathrm{y}}\frac{\partial H}{\partial y}\right)+\frac{\partial }{\partial z}\left(-{K}_{\mathrm{z}}\frac{\partial H}{\partial z}\right)=0$$

(1)

where H (m) denotes the hydraulic head, K (m/s) is the hydraulic conductivity, and x (m), y (m), and z (m) are the spatial directions, in which x and y lie on the horizontal plane, while z is aligned with the vertical direction (positive upward). Darcy’s law can be used to evaluate the subsurface flow in saturated porous media and is described with isotropic and homogeneous hydraulic conductivity as:

$$\textbf{q}=-\textbf{K}\left(\frac{\partial H\left(x,y,z\right)}{\partial x}+\frac{\partial H\left(x,y,z\right)}{\partial y}+\frac{\partial H\left(x,y,z\right)}{\partial z}\right)$$

(2)

where q (m/s) is the Darcy velocity vector and K is the tensor of hydraulic conductivity.

Regional groundwater flow modeling

The GWF models were developed for the five different catchments in COMSOL Multiphysics^®. The models consist of two different layers representing QD and bedrock. Isotropic and heterogeneous hydraulic conductivities were considered for the QD layer, according to the existing soil type map and previously estimated hydraulic conductivity values (Table S1 in the ESM). It was assumed that hydraulic conductivity decays exponentially with depth, according to Saar and Manga (2004), and that the decay function is different for the QD and bedrock. Hence, the hydraulic conductivity of the different layers in this study was described as:

$${K}_i(z)={K}_{\mathrm{i},\mathrm{top}}\ {e}^{\frac{\left(z-{z}_{\mathrm{i},\mathrm{top}}\right)}{\delta_i}}$$

(3)

where z_i,top (m) is the topographic elevation at the top of the layer, δ (m) is the earth skin depth, and index i represents different individual layers (i.e., bedrock or QD). Saar and Manga (2004) suggested that δ for QD and bedrock layers is in the range of 200–300 m. In this study, δ = 250 m was considered for both QD and bedrock layers. In addition, the porosity of the QD was assumed to be 0.2, reflecting the porosity of tills (Kilfeather and van der Meer, 2008), which are the most common soil types in Sweden. Furthermore, the bedrock porosity was assumed to be 0.001, which is meant to reflect the porosity of granite, estimated by others to vary between approximately 0.03 and 0.1% (Abelin et al. 1991; Ofterdinger et al. 2014).

The catchment modeling was conducted using a nonuniform numerical mesh size varying in a range of 2–17 and 17–403 m for the QD and bedrock layers, respectively. In general, the water table is controlled by either topographic fluctuations or recharge intensity, depending on the ratio of climatic conditions to geological and topographic conditions (Haitjema and Mitchell-Bruker 2005; Bresciani et al. 2016a, b). Therefore, in this study, the top boundary condition of the regional groundwater flow numerical model was set as the landscape topography, H(x,y,z = 0) = Z_B(x,y), for areas of groundwater discharge but smoothed for areas of groundwater recharge. The smoothing of the water table was performed in line with Mojarrad et al. (2022), where an iterative approach to reduce the DEM resolution was conducted to satisfy the annual mean infiltration rates of the catchments estimated by the SMHI. The total depth of the model (D_T) including both QD and bedrock thicknesses, varied spatially within different catchments, but D_T = 850 m was set at the locations with the lowest elevation in each catchment. A no-flow boundary was assumed at the horizontal flat surface at the bottom of the model (${\left.\frac{\partial H}{\partial z}\right|}_{\mathrm{z}=-{D}_{\mathrm{T}}}=0$), but the importance of this condition for groundwater discharge is overruled by the depth-decaying hydraulic conductivity. A constant head boundary was also applied to the lateral surfaces of the domain, according to ${\left.\mathrm{H}\left(x,y,z\right)\right|}_{x=0,{\mathrm{L}}_x\ \mathrm{and}\ y=0,{\mathrm{L}}_y}={Z}_{\mathrm{B}}\left(x,y\right)$, where L_x and L_y denote the length of the catchment in the x and y directions, respectively.

Particle tracing was conducted for all catchments by releasing 10,000 inert particles from a flat horizontal surface located at 500 m depth from the lowest topographic elevation (100 × 100 uniformly spatially distributed particles in each direction). The aim of particle tracing was to evaluate the deep groundwater flow paths, as well as the main discharge zones and the vertical velocity of the particles once they reached the topographic bed surface. This velocity is denoted W_dGWF(p) (m/s), where p is the index of the particle. Particle tracing was performed for 320 million years to allow all particles to leave the domain.

Hyporheic exchange flow modeling

The HEF was modeled separately from the larger-scale regional groundwater flow for two reasons. First, the HEF acts at much smaller spatial and temporal scales than what could be accounted for in the catchment numerical model. Second, the main part of the HEF is driven by local hydraulic head fluctuations at the streambed controlled by the hydraulic and hydromorphologic characteristics of the stream, which are not reflected by the top boundary of the regional groundwater model. Thus, solving the governing equation for the HEF first required estimating the hydraulic head variations along each stream reach.

Here, to capture the range of scales involved in HEF, the spectral approach presented in Morén et al. (2021) was applied to each stream segment, specifying the hydraulic head at the SWI and the HEF velocity across the streambed as power spectral densities (PSDs), distributed over different wavelengths λ (m). The flow-weighted average exchange velocity, 〈W_HEF〉 (m/s), was then calculated for each reach by integrating over the HEF velocity PSD (${S}_{{\mathrm{W}}_{\mathrm{HEF}}}\left(\lambda \right)$) between the smallest and largest wavelengths of the spectrum, λ_min (m) and λ_max (m), according to:

$$\left\langle {W}_{\mathrm{HEF}}\right\rangle =\sqrt{\int_{\lambda_{\mathrm{min}}}^{\lambda_{\mathrm{max}}}\frac{S_{{\mathrm{W}}_{\mathrm{HEF}}}\left(\lambda \right)}{\lambda^2} d\lambda}$$

(4)

In line with Morén et al. (2021), ${S}_{{\mathrm{W}}_{\mathrm{HEF}}}\left(\lambda \right)$ was calculated from the hydraulic head PSD, S_h(λ), as:

$${S}_{{\mathrm{W}}_{\mathrm{HEF}}}\left(\lambda \right)={\left(2\pi {K}_{\mathrm{h}\mathrm{z},\kern0.5em \mathrm{top}}\right)}^2\alpha {\left(\lambda \right)}^2\frac{S_{\mathrm{h}}\left(\lambda \right)}{\lambda^2}$$

(5)

where K_hz, top is the hydraulic conductivity at the SWI, and α(λ) (-) is a geological damping factor accounting for a decrease in HEF velocity with depth into the streambed according to:

$$\alpha \left(\lambda \right)={e}^{\left(-\frac{c\lambda}{4\pi }+\sqrt{{\left(\frac{c\lambda}{4\pi}\right)}^2+1}\right)\frac{2\pi y}{\lambda }}$$

(6)

Equation (6) results from an exponential decay in hydraulic conductivity with depth according to K_hz(z) = K_hz, tope^–cz, where the constant c (m^–1) was estimated for each reach by fitting the exponential equation to two points of hydraulic conductivity within the streambed. At the surface (z = 0 m), the hydraulic conductivity was assumed to be K_hz, top = 10^–4 m/s in all reaches, as this is approximately what has been measured previously, on average, in streambeds (Riml et al. 2013; Morén et al. 2021; Stewardson et al. 2016; Ward et al. 2019). At a depth of 1 m, the hydraulic conductivity was set to that of the underlying soil (from the soil map), namely, K_hz(z =  –1 m) = K_{QD, top} (Table S1 in the ESM).

The estimated hydraulic head PSD, S_h(λ), accounted for both static head fluctuations resulting from variations in the water-surface profile (WSP) and dynamic head fluctuations resulting from drag forces created when the streaming water interacts with the rough streambed. Both types of hydraulic head fluctuations were in this study estimated from the DEM, and the total hydraulic head PSD was defined as the sum of the static and dynamic head PSDs according to ${S}_{\mathrm{h}}\left(\lambda \right)={S}_{{\mathrm{h}}_{\mathrm{s}}}\left(\lambda \right)+{S}_{{\mathrm{h}}_{\mathrm{d}}}\left(\lambda \right)$. Elevation data were first extracted along the thalweg of each reach, and the PSDs of the data, S_DEM(λ) (m³), were then calculated using the Welch method (Welch 1967) and specifically the MATLAB function pwelch. Then, a comparison with PSDs calculated from streambed topography and water elevation profiles measured in nine reaches within the investigated catchments (Text S4 and Fig. S1 in the ESM) confirmed that the elevation data extracted along the stream network captured the general characteristics of the WSP, rather than the streambed elevation. Mathematically, the static hydraulic head PSD was thus defined as ${S}_{{\mathrm{h}}_{\mathrm{S}}}\left(\lambda \right)={S}_{\mathrm{WSP}}\left(\lambda \right)={S}_{\mathrm{DEM}}\left(\lambda \right)$ and the streambed topographic PSD was subsequently calculated as ${S}_{{\mathrm{z}}_{\mathrm{b}}}\left(\lambda \right)={S}_{\mathrm{WSP}}\left(\lambda \right)/{C}_s$. The transformation factor (C_s) was defined as a constant and related to the mean difference in the variations of the stream bottom and WSP elevation, in the nine investigated streams (see Text S4 and Fig. S1 in the ESM). Finally, the dynamic hydraulic head PSD, ${S}_{{\mathrm{h}}_{\mathrm{d}}}\left(\lambda \right)$, was calculated as ${S}_{{\mathrm{h}}_{\mathrm{d}}}\left(\lambda \right)={C}_{\mathrm{d}}{S}_{{\mathrm{z}}_{\mathrm{b}}}$, where the transformation coefficient C_d was estimated using a semiempirical equation transforming the topography to dynamic head. The equation can be found in the ESI (Text S4 and Equation S7 in the ESM) and includes the gravitational acceleration g (m/s²), the average stream velocity U (m/s), the average stream depth d (m), and the standard deviation in the bottom elevation ${\sigma}_{{\mathrm{z}}_{\mathrm{b}}}$(m)(Elliott and Brooks 1997a, b). The standard deviation in the bottom elevation, ${\sigma}_{{\mathrm{z}}_{\mathrm{b}}}$, was calculated from the 2 m × 2 m DEM extracted along the stream reach, and a regression model was used to estimate the average stream depth and stream velocity from flow discharge (estimated as described in section ‘Study catchments and data’) and geographic location of the catchment (Round et al. 1998).

Using this approach to calculate the HEF velocity also provides a way to account for head variations across small spatial scales not included in the DEM (Morén et al. 2021). The resolution of the DEM was 2 m × 2 m, which results in a minimum wavelength of the spectrum λ_min = 2Δx^∗ = 4 m, according to the Nyquist–Shannon sampling theorem, where Δx^∗ is the distance between measurements along the stream segment. However, since the streambed topography was observed to be fractal at wavelengths smaller than approximately 20 m in the majority of the PSDs of the DEM, a power law function was fitted to that part of each PSD (4 m < λ < 20 m) according to:

$${S}_{\mathrm{WSP}}\left(\lambda <4\right)={a}_{\mathrm{WSP}}{\lambda}^{b_{\mathrm{WSP}}}$$

(7)

where a_WSP and b_WSP are constants unequally estimated for each reach. Equation (7) was subsequently used to calculate the variations in the WSP not captured by the DEM (scales 0.01–4 m).

Independent catchment and reach characteristics

A large number of catchment and reach characteristics were derived from the independent data of the five watersheds to be tested as explanatory variables for the GWF–HEF interactions. The characteristics can be divided into three specific groups that reflect the catchment topography, the catchment geology, and the stream hydromorphology. Catchment topography and geology were mainly assumed to control the large-scale groundwater flow, while the stream hydromorphological variables were believed to control mainly the hyporheic flow. The definition of these variables, how they were derived from available data, and why they are relevant to consider as controls on the GWF–HEF interactions are described in detail in Text S5 in the ESM, and summarized in Table 2. Independent and dependent variables were averaged at the three spatial scales, as described in section ‘Averaging dependent and independent variables over three different scales’.

Table 2 Calculated independent variables, origin of the data, and calculation methods

Averaging dependent and independent variables over three different scales

The independent variables (Table 2) were averaged slightly differently depending on the variable of interest as well as the spatial scale over which it was evaluated (reach, intermediate or regional catchment scale). Stream hydromorphological variables were derived directly as an average at the reach scale (Text S5 in the ESM) and noted with the reach index r. Area distributed variables (i.e., variables that were derived for each 2 m × 2 m pixel) were averaged as the arithmetic mean of all pixels within the area. If the area corresponded to the catchment of the stream reach, the variables were indexed r, while they were indexed IC or RC if the averaging area was the intermediate or regional catchment, respectively.

For the dGWF discharge velocity, the average for each subcatchment was taken as the arithmetic mean of the discharging velocity of all particles at the SWI in that subcatchment and denoted ${\overline{W_{\mathrm{dGWF}}}}_r$,${\overline{W_{\mathrm{dGWF}}}}_{IC},$ and ${\overline{W_{\mathrm{dGWF}}}}_{RC}$. The velocity ratio at the reach scale was then derived according to:

$${\delta}_{W,r}={\overline{W_{\mathrm{dGWF}}}}_r/{\left\langle {W}_{\mathrm{HEF}}\right\rangle}_r$$

(8)

Finally, the velocity ratio, stream hydromorphological variables, and flow-weighted average hyporheic exchange velocity (Eq. 4) at the intermediate or regional catchment scale were averaged by taking a length-weighted average, defined as:

$${\overline{\zeta}}_{\mathrm{scale}}=\frac{\sum_{r=1}^R{L}_r{\zeta}_r}{\sum_{r=1}^R{L}_r}$$

(9)

where R is the number of reaches in the intermediate catchment (scale = IC) or regional catchment (scale = RC), L_r is the length of reach r, and ζ_r is the variable of interest, calculated or averaged at the reach scale.

Statistical analysis

Regression analysis was used to investigate if and to what degree the independent variables control the dependent variables, i.e., the average dGWF discharge velocity, the average HEF velocity, and the ratio between them. Since the data were observed to be approximately log-normally distributed (Fig. S8 in the ESM), independent of the scale of averaging, regression analysis was performed on the logarithm of the dataset (see the equation for the regression model, Text S6 in the ESM). To study the groundwater/surface water interactions specifically in deep groundwater discharge zones, reach-scale subcatchments with no upwelling of deep groundwater were removed from the analysis. This resulted in a decrease in the number of reaches in all catchments from 393 to 293 and the number of subcatchments from 29 to 25, while the number of regional catchments was unchanged. In addition, 23 independent geographic and hydrogeological characteristics were initially calculated, as described in section ‘Independent catchment and reach characteristics’. Regression analysis should preferably be applied to independent (noncorrelated) variables. Principal component analysis (PCA) was therefore performed at the three spatial scales to obtain an initial understanding of the intercorrelation between the supposed independent variables and to limit the number of variables to include in further analysis. PCA was conducted on the standardized datasets and was depicted as a distance biplot (Fig. S6 in the ESM). From the distance biplot, 13 different independent variables were selected based on their relatively low intercorrelation (A, S, GtS, MSC, K, D_QD, U, Fr, Re , Ω, f, a_WSP, and b_WSP), subjectively indicated by a relatively large angle between them. Last, the variance inflation factor (VIF) was calculated. A VIF above 10 indicates a high correlation with one or several of the other variables (Montgomery et al. 2012), and thus the variables with VIF above 10 were removed one at a time, starting with the in-stream velocity (U) then the stream power (Ω) and finally the Reynolds number (Re). This resulted in 10 independent variables that were further tested in the regression analysis. The same variable set was used at all three scales to allow comparison of the results, although the PCA and VIF at the larger scales did indicate some multivariability (Table S3 and Fig. S7 in the ESM).

The regression analysis was performed both through single-variate regression analysis (i.e., n = 1 in Equation S9 in the ESM) and through pairwise and multivariate regression analysis (i.e., n > 1 in Equation S9 in the ESM). Single-variate regression analysis was performed to provide information on linearity between each of the independent variables and the three dependent variables, as linearity should exist for the inclusion of the independent variables in the multivariate regression analysis. Multivariate regression analysis was subsequently performed using all 10 independent variables to begin with. The number of variables was then reduced through backward elimination, where the least statistically significant variable (i.e., the variable with the highest p-value) was removed after each regression analysis. Models in which all variables had p-values lower than 0.05 were considered statistically significant. The performance of the statistically significant models was quantified by deriving three different scorings: the regular coefficient of determination (R²) the adjusted coefficient of determination (R²_Adj) and the predictive coefficient of determination, R²_Pred (see equations in Text S6 in the ESM). The model with the highest adjusted and predictive R² value, in which all included variables contributed significantly to the model’s explanation and prediction power, was defined as the best model for each of the three dependent variables averaged over the three different scales. A significant contribution was specified here as a decrease in both the adjusted and predictive R² values of more than 2% upon the removal of any of the variables from the model. Since relatively few models with more than two independent variables showed statistical significance at the intermediate catchment scale, all possible combinations of two variables were also tested as possible explanations for the three dependent variables. This evaluation was referred to here as pairwise regression analysis.

Results

Variability in the GWF–HEF interactions within and between catchments

The modeling of the regional GWF shows the significance of DEM resolution on GWF velocity at the water table. In particular, the results demonstrated that decreasing the DEM resolution (larger mesh size) of the water table used as the head boundary condition in recharge areas substantially decreased the mean absolute value of the vertical velocity at the water table, $\overline{\left|{W}_{\mathrm{GWF}}\right|}$ . The required mesh size satisfying the infiltration constraint varied between 74 and 94 m among the considered catchments in this study.

The location of the dGWF discharge points was evaluated using a particle-tracing method (section ‘Regional groundwater flow modeling’). The results of this analysis indicated that the majority of dGWF reached the topographic surface in locally low-elevation areas, such as lakes and streams (Fig. S9 in the ESM), and that 41–63% of all those particles (depending on the catchment) did so within the catchment boundaries (Table S4 in the ESM). Depending on the catchment, 75% to approximately 100% of the particles that discharged within the catchments did so at or close to the stream network (not including lakes), thereby highlighting the possibility of mutual interference between the GWF and HEF and motivating an investigation of their velocity ratio.

Examination of the velocities of the upwelling particles, as well as the average HEF velocities, revealed a large variation both within and between the five investigated regional catchments. The cumulative distribution of the reach average dGWF discharge velocities, ${\overline{W_{\mathrm{dGWF}}}}_r,$ covered seven orders of magnitude, ranging between 10^–9 and 10^–5 m/s in the majority of the reaches (Fig. 2a). The highest velocities were generally found in the catchments of Krycklan and Bodals Brook, in which ${\overline{W_{\mathrm{dGWF}}}}_r$ values were higher than 10^–7 m/s in more than 60 and 45% of all reaches, respectively. Lower velocities were found in the catchments of Tullstorps Brook and Säva Brook, in which ${\overline{W_{\mathrm{dGWF}}}}_r$ values were higher than 10^–7 m/s in approximately 20 and 10% of all reaches, respectively. Finally, the lowest velocities were estimated in the catchment of Forsmark, where all reaches had ${\overline{W_{\mathrm{dGWF}}}}_r$ values lower than 10^–7 m/s. Note, however, that the distribution was very wide in the catchment of Tullstorps Brook, and in some reaches, the discharging velocities exceeded the values in Krycklan Catchment and Bodals Brook. This difference in distribution width was also reflected in the average values. Because of the approximate log-normal distribution, the average dGWF discharge velocity at the regional catchment scale was higher than the median of the distribution and ranged between 2.39 × 10^–8 m/s in the catchment of Forsmark and 1.5 × 10^–6 m/s in the catchment of Tullstorps Brook. Compared to the dGWF discharge velocity, the reach-averaged HEF velocities were generally much higher and ranged between approximately 10^–7 and 10^–3 m/s in all catchments (Fig. 2b). The hyporheic exchange velocities clearly varied between catchments and increased from lowest to highest in the following order: Forsmark, Säva, Bodals, Tullstorps, and Krycklan. The regional averages of the HEF velocities, ${\overline{\left\langle {W}_{\mathrm{HEF}}\right\rangle}}_{\mathrm{RC}}$, (average calculated using Eq. 9) ranged between 9.27 × 10^–7m/s in Forsmark and 2.51 × 10^–5 m/s in Tullstorps Brook.

Fig. 2

Cumulative distribution function of a reach average dGWF discharge velocity, b reach average HEF velocity, and c the ratio between the reach average dGWF discharge velocity and the reach average HEF velocity in the five different catchments: Bodals Brook (BB), Säva Brook (SB), Tullstorps Brook (TB), Forsmark Brook (FB) or Krycklan (K)

The general magnitude difference between the velocities of the two investigated types of flows led to velocity ratios (i.e., ${\delta}_{\mathrm{W},r}={\overline{W_{\mathrm{dGWF}}}}_r/{\left\langle {W}_{\mathrm{HEF}}\right\rangle}_r$) that were far below 1 in most reaches (Fig. 2c), indicating that convergence of the upwelling deep groundwater due to HEF is strong in most reaches of the investigated catchments. A relatively wide distribution of ratios was also evident within the five catchments, ranging between approximately 10^–4 and 10, except in the Forsmark catchment, where the range was narrower and most ratios were between 10^–3 and 10^–1. The length-weighted average (Eq. 9) of the velocity ratio over the full regional catchment ranged from 0.2 in Forsmark to 0.76 in Bodals Brook.

Regression analytical results

Both single and multivariate regression analyses were performed to study the factors controlling the observed variation in HEF–GWF interactions that were quantified in terms of three variables—i.e., the average dGWF discharge velocity, the average HEF velocity, and their ratio. Furthermore, the analyses were performed at three different scales: the reach scale, intermediate catchment scale, and regional catchment scale. At the regional scale, the limited number of five samples (regional catchments) prevented multivariate regression analysis; thus, only the results from the single-variate-regression analysis are presented here. Note that the regression analysis was performed on dimensional variables, and therefore, the estimated regression coefficients have units, which can be derived from the units of the included variables (see Table 2).

Regression models for the deep groundwater discharge velocity

The single-variate regression analysis resulted in five significant relationships (p < 0.05) between the reach-scale average dGWF discharge velocity, ${\overline{W_{\mathrm{dGWF}}}}_r$, and different independent variables (Fig. S10 in the ESM). However, only the correlation between ${\overline{W_{\mathrm{dGWF}}}}_r$ and K_r, which had an R² value of 0.40, explained more than 10% of the variability in ${\overline{W_{\mathrm{dGWF}}}}_r$. When independent and dependent variables were averaged at the intermediate catchment scale (Fig. S11 in the ESM), ${\overline{{\mathrm{W}}_{\mathrm{dGWF}}}}_{\mathrm{IC}}$ was still correlated with K_IC, and the correlation had an R² value of 0.48, which was higher than at the reach scale. In addition, ${\overline{W_{\mathrm{dGWF}}}}_{\mathrm{IC}}$ was also significantly correlated with GtS_IC, and this correlation also had an R² value of 0.33. Finally, ${\overline{f}}_{\mathrm{IC}}$ was significantly correlated with ${\overline{W_{\mathrm{dGWF}}}}_{\mathrm{IC}}$, but had an explanatory power of only 14%.

As expected, the regular R² value increased when more variables were included in the multivariate regression analysis. The best model at the reach scale had a ${\overline{W_{\mathrm{dGWF}}}}_r$ that was positively related to the topographic indices S_r and to the hydraulic conductivity of the local catchment K_r (Fig. 3a). The small difference between the regular R² value (0.45), the adjusted R² value (0.45) and the predictive R² value (0.44) confirms that the model was stable. However, the relatively low magnitudes of all scoring parameters revealed that, in general, the independent geographic and hydromorphological variables failed to explain most of the observed variability in the dGWF discharge velocity at the reach scale. At the intermediate scale, the pairwise regression analysis revealed two different significant models, which both included a close to linear and positive correlation between K_IC and ${\overline{W_{\mathrm{dGWF}}}}_{\mathrm{IC}}$. The best significant model also included GtS_IC and predicted approximately half of the variability in ${\overline{W_{\mathrm{dGWF}}}}_{\mathrm{IC}}$ (Fig. 3b). The regular R², adjusted R², and predictive R² values were 0.67, 0.61, and 0.51, respectively, which was higher than the best reach scale model; however, the relatively large differences between scoring parameters indicate that the model is more uncertain than the reach scale model.

Fig. 3

Best regression models for the dGWF discharge velocity, where dependent and independent variables were averaged at a the reach scale, b the intermediate catchment scale and c the regional catchment scale. The gray line indicates the 1:1 relationship and the different colored markers indicate if the data originated from Bodals Brook (BB), Säva Brook (SB), Tullstorps Brook (TB), Forsmark Brook (FB) or Krycklan (K)

At the regional catchment scale, the single variate regression analysis resulted in no significant correlations between ${\overline{W_{\mathrm{dGWF}}}}_{\mathrm{RC}}$ and the independent variables with a 95% level of confidence (Fig. S12 in the ESM). However, the best correlation in terms of both significance and R² values was that between GtS_RC and ${\overline{W_{\mathrm{dGWF}}}}_{\mathrm{RC}}$ (Fig. 3c).

Regression models for the hyporheic exchange velocity

The single-variate regression analysis showed that seven of the ten tested variables were significantly related to 〈W_HEF〉_r (p < 0.05) (Fig. S13 in the ESM); however, most correlations had explanatory power lower than 10%. Exceptions were the level and slope of the water-surface elevation PSD (a_{WSP, r} and b_{WSP, r}) which explained 60 and 67% of the observed variability in 〈W_HEF〉_r, respectively. Another important variable was the Darcy-Weisbach friction factor (f_r) which explained 13% of the variability. When averaged at the intermediate scale, the same three variables (${\overline{a}}_{\mathrm{WSP},\mathrm{IC}}$, ${\overline{b}}_{\mathrm{WSP},\mathrm{IC}}$ and ${\overline{f}}_{\mathrm{IC}}$) were significantly correlated to 〈W_HEF〉_IC, and R² values were 0.63, 0.48 and 0.49. (Fig. S14 in the ESM). In addition, the gradient to stream (GtS_IC) and the depth of the Quaternary deposit (D_{QD, IC}) were significantly correlated with 〈W_HEF〉_IC and had R² values of 0.48 and 0.44, respectively.

The multivariable regression models for 〈W_HEF〉_r had higher scoring values than the single-variate regression model, as expected. The model with the highest scoring values showed a positive correlation between 〈W_HEF〉_r and variables a_{WSP, r}, K_r, and A_r, and a negative correlation between 〈W_HEF〉_r and b_{WSP, r}. However, the catchment area did not significantly contribute to the explanatory power and was not included in the best model, which is plotted in Fig. 4a and shows that the PSD of the water-surface-elevation profile along the reach (a_{WSP, r} and b_{WSP, r}), together with the hydraulic conductivity, provided the major control of 〈W_HEF〉_r. At the intermediate scale, several models with two predictors were found that explained the variability in ${\overline{\left\langle {W}_{\mathrm{HEF}}\right\rangle}}_{\mathrm{IC}}$ relatively well, although models with higher scoring values were found that explained the inter-reach variability. The model with the highest explanatory and predictive powers showed an increase in ${\overline{\left\langle {W}_{\mathrm{HEF}}\right\rangle}}_{\mathrm{IC}}$ with increasing ${\overline{a}}_{\mathrm{IC}}$ and decreasing S_IC. However, since there was low correlation between ${\overline{\left\langle {W}_{\mathrm{HEF}}\right\rangle}}_{\mathrm{IC}}$ and S_IC in the single variate regression analysis (Fig. S14 in the ESM), this model was considered uncertain, and therefore, the model with the second highest R² values was selected as the best model. The chosen model showed an increase in ${\overline{\left\langle {W}_{\mathrm{HEF}}\right\rangle}}_{\mathrm{IC}}$ with increasing ${\overline{a}}_{\mathrm{IC}}$ and increasing ${\overline{f}}_{\mathrm{IC}}$, as illustrated in Fig. 4b.

Fig. 4

Best regression models for the average HEF velocity, where dependent and independent variables were averaged at a the reach scale, b the intermediate catchment scale and c the regional catchment scale

At the regional catchment scale, only ${\overline{f}}_{\mathrm{RC}}$ was statistically correlated with the dependent variable, ${\overline{\left\langle {W}_{\mathrm{HEF}}\right\rangle}}_{\mathrm{RC}}$, at the 95% confidence level, and it explained 96% of the variability in ${\overline{\left\langle {W}_{\mathrm{HEF}}\right\rangle}}_{\mathrm{RC}}$ (Fig. 4c); however, D_{QD, RC}, GtS_RC and ${\overline{b}}_{\mathrm{RC}}$ were also statistically correlated with ${\overline{\left\langle {W}_{\mathrm{HEF}}\right\rangle}}_{\mathrm{RC}}$ at the regional catchment scale if the confidence level was decreased to 90% (Fig. S15 in the ESM).

Regression models for the velocity ratio

The single-variate regression analysis of the correlation between the velocity ratio (${\delta}_{\mathrm{W},r}={\overline{W_{\mathrm{dGWF}}}}_r/{\left\langle {W}_{\mathrm{HEF}}\right\rangle}_r$) and each independent variable showed that six of the ten tested variables were significantly correlated with the velocity ratio at the reach scale (Fig. S16 in the ESM). The variables K_r, a_{WSP, r}, and b_{WSP, r} explained 21, 22 and 20% of the variability in δ_{W, r}, respectively, while the rest of the significant correlations had R² values < 5%. At the intermediate catchment scale, only K_r and GtS_r were significantly correlated to the ratio between the dGWF discharge velocity and the HEF velocity (${\overline{\delta_{\mathrm{W}}}}_{\mathrm{IC}}$) and the correlations had R² values of 0.20 and 0.17, respectively (Fig. S17 in the ESM).

The best multivariate regression model for δ_{W, r} included four independent variables and a positive correlation to S_r, K_r and b_{WSP, r} and a negative correlation to a_{WSP, r} (Fig. 5a). Additionally, it had an adjusted R² value of 0.53 and a predictive R² value of 0.51. The multivariate regression analysis at the intermediate scale resulted in two significant models, where the one with the highest explanation power and lowest p-values displayed an increase with K_IC and GtS_IC and had an adjusted R² value of 0.31 and a predictive R² value of only 0.03 (Fig. 5b).

Fig. 5

Best regression models for the ratio between the dGWF velocity at the SWI and the average HEF velocity, where dependent and independent variables were averaged at a the reach scale and b the intermediate catchment scale

Single-variate regression analysis with the velocity ratio averaged at the regional catchment scale (${\overline{\updelta_{\mathrm{W}}}}_{\mathrm{RC}}$) resulted in no statistically significant correlations at the 95% or 90% confidence level (Fig. S18 in the ESM).

Discussion

Variations in deep groundwater upwelling velocities between and within catchments and implications for the spread of deep groundwater contaminants

In agreement with previous studies (Marklund et al. 2008; Uchida et al. 2003), the particle tracing performed in this study showed that deep groundwater discharge zones coincided well with the river network and lakes in all study areas in the upstream and downstream parts of the catchments. Furthermore, dGWF velocities at the SWI, averaged at the reach scale, varied greatly both within and between catchments (section ‘Variability in the GWF–HEF interactions within and between catchments’), and the variability might be even larger than that estimated due to the possible existence of intact bedrock and fracture networks in the subsurface that were not accounted for here. Fractures within the bedrock can result in preferential flow paths, where velocities are faster than in other parts of the catchment (Selroos et al. 2002; Welch et al. 2012). The observed large variation in upwelling groundwater velocity agrees with a recent study by Hare et al. (2021), who identified both regional trends and great spatial heterogeneity in the magnitude of deep groundwater discharging into streams.

Relatively small velocity ratios (${\delta}_{\mathrm{W},r}={\overline{W_{\mathrm{dGWF}}}}_r/{\left\langle {W}_{\mathrm{HEF}}\right\rangle}_r$) were found in most stream reaches, indicating that the HEF can have a large impact on the discharge of the dGWF by converging the flow close to the SWI and thereby accelerating the discharge velocity and reducing the discharge area. This is relevant when considering the spread of radionuclides in the biosphere. If the local-scale HEF velocity field is not accounted for in hydrological models used to parameterize dose assessment compartment models for HLRW safety assessment, then the transport rates defined for the area close to the stream might be underestimated. Since the velocity is generally lower for groundwater discharge than for surface water, the exact values of the transport rates through the area closest to the stream will affect the total residence time of the radionuclides in the biosphere as a whole, which is especially the case in areas with shallow QD, reflecting the environmental conditions in landscapes that were covered by inland ice in the past. Accounting for HEF in groundwater transport models is also essential when estimating the discharge of nitrogen from deep groundwater to the stream, which can be significantly modified when traveling through the hyporheic zone (Hedin et al. 1998; Krause et al. 2011). Furthermore, the finding that the HEF is large enough in most stream reaches to potentially modify the groundwater discharge patterns is of relevance for stream ecology. Since the HEF is controlled partly by stream hydraulics, which is discussed in the following sections, the position and area of discharging deep groundwater will probably change over relatively short timescales and can affect the temporal stability of the habitat patch structure in the streambed, which depends on the biogeochemical and thermal conditions within the hyporheic zone (Poole et al. 2006).

The large difference between the HEF and dGWF velocity is not a surprising result, given the very low hydraulic conductivities along some of the deep groundwater flow paths compared to the hydraulic conductivity of the streambed, which was assumed to be 10^–4 m/s everywhere. Nevertheless, in order to know the exact velocities, the full geometry of the groundwater flow needs to be understood, and for that, a model of some type is essential. It should also be noted that the presented dGWF discharge velocities result from particles released at a 500-m depth, which could only be found from particle tracing through the calculated flow field. Shallower groundwater flow will probably have higher discharge velocities, since the hydraulic conductivity of shallower layers are lower, and will thus be relatively less impacted by the HEF. This difference between shallow and deep groundwater, as well as the wide range of deep upwelling velocities within a single catchment (Fig. 2a), highlights that transport rates derived from average velocities over a larger area are most likely uncertain. Note that this study also uses average values and merely points out the variability in discharge rates that can be expected in most catchments, leading to the need to present a distribution of transport rates and to carefully consider the area of averaging in studies where the aim is to estimate specific transport rates and times.

Hydromorphological and geographic controls on dGWF–HEF interactions

In addition to modeling HEF and dGWF within and between five catchments, this study investigated which independent stream characteristics control the variance in these two flows using regression analysis. The results imply that both the dGWF velocity and HEF velocity were mainly controlled by spatial variability in elevation and the resulting elevation gradients were quantified by different variables (S, GtS, a_WSP, and b_WSP). The secondary control was the geological characteristics, i.e., the stream hydraulic conductivity (K) and depth of Quaternary deposits (D_QD). Finally, the hydraulics of the stream network specifically controlled the HEF velocity but to some extent also the dGWF velocity.

Controls on the dGWF velocity

The average hydraulic conductivity of the topsoil exerted major control on the dGWF discharge velocity, independent of the catchment scale over which variables were averaged. It explained 39 and 48% of the variability in ${\overline{W_{\mathrm{dGWF}}}}_r$ and ${\overline{W_{\mathrm{dGWF}}}}_{\mathrm{IC}}$, respectively (Figs. S10–S11 in the ESM) and was included in the best multivariate regression model at the reach scale as well as the intermediate catchment scale (Fig. 3a, b). The inclusion of the top hydraulic conductivity in the regression models was not self-evident (although expected), since the groundwater velocity at a specific point is controlled by the harmonic mean of the hydraulic conductivity along the full stream tube, and not just the local hydraulic conductivity. Additionally, other studies have identified soil properties as an important control on groundwater flow; in certain catchments more dominant than the catchment topography (Tetzlaff et al. 2009). However, here, the explanatory power increased considerably when a topographic variable was included in the multivariate analysis (Fig. 3), which highlights that the variability in groundwater flow is dependent on both the topographic and geological conditions. Finally, the dGWF discharge velocity depended somewhat on the hydromorphological characteristics of the local stream reach, but the control was less important (lower R² values) and of lower significance (higher p-values) than the control of the catchment characteristics.

Controls on the HEF velocity

In contrast to the dGWF, the variables that best explained the variability in the HEF velocity at the reach and intermediate catchment scales were the characteristics of the local reach and specifically the fractal properties of the stream-water-surface elevation—i.e., the spectral level a_WSP and spectral slope b_WSP (Fig. 4a, b). Since the integral of a PSD equals the variance of the signal, the positive correlation between a_WSP and the average hyporheic exchange velocity shows an increase with variance in the WSP along the streambed. The predominant control of a_WSP and b_WSP on the HEF over other variables is interesting. These other variables include the stream-flow velocity and depth and the head gradients over wavelengths larger than approximately 20 m (indicated, for example, by the stream slope or normalized standard deviation of the stream longitudinal elevation). This finding agrees with previous studies that concluded that static head gradients, rather than the dynamic head gradients, drive the main part of the HEF (Marzadri et al. 2014; Mojarrad et al. 2019), and that gradients over shorter scales accounted for the main part of the hyporheic flux (Morén et al. 2021). Previous regression analyses have also shown that fractal properties of the streambed topography (or water-surface elevation) can function as indices for hyporheic exchange (Lee et al. 2020; Marzadri et al. 2014). Although the methods and included variables in those studies differed slightly from the ones used in the present study, the general conclusions were the same—the hyporheic exchange flux was generally higher in reaches with high elevation variability, distributed equally over all scales, than in reaches where the elevation variability was centralized to a certain point along the reach or related to general landscape variability. Another important variable for HEF was the Darcy-Weisbach friction factor, which caused an increased HEF at all three spatial scales and was specifically important at the intermediate and regional catchment scales, which is in contrast to previous studies that found an increase in the HEF residence time with increasing Darcy-Weisbach friction factor within specific streams (Harvey et al. 2003; Zarnetske et al. 2007). Thus, variability in streambed topography between stream segments inserted a primary control on the HEF compared to differences in discharge, depth and stream velocity, which could have a physical explanation, but could also be due to the model setup. In general, the stream velocity varied relatively little between stream segments due to the way it was estimated using a regression model. Furthermore, the dynamic velocity and stream depth only had an indirect control on the HEF velocity through the dynamic hydraulic head distribution at the streambed interface, which was generally much smaller than the static head gradients, and therefore had little impact on the results.

Controls on the velocity ratio

In general, the regression models developed in this study to explain the ratio between the dGWF discharge velocity and the HEF velocity mirrored the regression models developed for the two types of flows separately. At the reach scale, the velocity ratio increased with increasing S_r and K_r (Fig. 5a), and the same trend was seen for the dGWF discharge velocity. Similarly, the ratio decreased with a_{WSP, r} and increased with b_{WSP, r}, which reflects the relationship between these variables and the nominator of the ratio, i.e., 〈W_HEF〉_r. Thus, the velocity ratio was the smallest, and the impact of the HEF on the dGWF pattern was highest in reaches with high variability in the WSP occurring over relatively short spatial scales and not correlating with landscape topographic variations.

At the intermediate scale, the velocity ratio did not correlate with the topographic variation along the stream thalweg and was instead correlated with the average local slope of the catchment (Fig. 5b). It seems intuitive that when variables are averaged over larger scales, the influence of catchment characteristics increases and becomes more dominant in controlling the HEF–dGWF interactions compared to the local stream characteristics. However, it should be noted that the intermediate catchment-scale model for the velocity ratio was considered uncertain due to the large difference between the adjusted and predictive R² values. This is probably because higher multicollinearity was found at the intermediate scale compared to the reach scale, which infers uncertainty in all derived models at the intermediate scale.

The only previous regression analysis (to the authors’ best knowledge) on the relationship between the velocity ratio and catchment characteristics (Mojarrad et al. 2019) concluded that the catchment mean elevation and stream order were the two most important independent variables, both causing a decrease in the velocity ratio. Here, the catchment elevation was removed from the analysis after PCA because of its high positive correlation with other independent variables, such as GtS and the local slope S, especially at the intermediate and regional catchment scales. The local slope was one of the variables included in the best regression models of this study at the reach scale (Fig. 5a), thus indicating consistency with the findings of Mojarrad et al. (2019). The stream order was not included in this study because it was not possible to use at the intermediate and regional catchment scales; however, at the reach scale, the stream order was slightly correlated with the fractal properties of the streambed. A higher a_{WSP, r} and a lower b_{WSP, r} were found in lower order reaches, implying that the velocity ratio decreased with stream order.

Impacts of spatial scale on the control on GW–HEF interactions

An interesting aspect of the regression results is how the derived models varied in explanation power and included different variables when analyses were performed at the three different spatial scales. Other studies that have discussed how the spatial scale can influence the results of regression analysis of groundwater flow (McGlynn et al. 2003; McGuire et al. 2005; Tetzlaff et al. 2009) have generally concluded that at hillslope scales, transport times mainly depend on the catchment area or flow path length (McGlynn et al. 2003). Subsequently, when averaged over larger catchment areas, clearer dependencies are evident between the topographic indices and groundwater flows (McGuire et al. 2005), which is in agreement with the results of the present study when moving from the reach to the intermediate catchment scale. In this study, the catchment area did not significantly control the flow velocities at the discharge sites at any scale; however, increasing the scale used for averaging the variables from the reach scale to the intermediate scale resulted in an increase in the adjusted R² value. For the HEF velocity and the velocity ratio, however, the trend was the opposite, and the explanatory power decreased when averaging over the intermediate catchment scale instead of the reach scale. The relationships found at the regional catchments generally had high explanation power, which is interesting but uncertain due to the low number of catchments included in the analysis; therefore, studies based on a larger number of catchments should be conducted in the future to validate the results reported here.

Limitations and uncertainties

This study used well-established models, which were partly validated within the studied catchments and supported with observed landscape and stream network topography, to highlight the large variability in dGWF discharge velocity that can be found within and between catchments and the possible effects of HEF on this discharge. Nevertheless, the lack of site-specific data to calibrate the models and validate the estimated velocities is a limitation that can influence the regression results. This can partly explain the relatively low R² values (adjusted R² < 0.61) found in this study, mainly related to models explaining variability in dGWF velocity and the velocity ratio at the SWI at reach and intermediate catchment scales. Thus, although the best available data and state-of-the-art models were used in this study and the results generally conform to the concurrent understanding of the hydrological system, a need remains for more research on the spatial variability in GWF–HEF interactions in areas where more data are available.

When studying processes within streams across large scales, one challenge is how to define the exact extension of the stream network. Here, the stream network was mapped from high-resolution elevation data using ArcGIS and manually controlled to follow the lowest part of the landscape, so that topographical variations would reflect the stream and not the surrounding land. However, the stream was modelled as a polyline without width and it was assumed that all particles that discharged within a local catchment (related to a local stream segment) did so specifically at the stream bottom. In reality, it is likely that some of the deep groundwater discharges adjacent to the stream network where it will not be impacted by the processes in the stream. Furthermore, the flow accumulation threshold used to define the upper limit of the stream network was, in this study, related to a small discharge of 0.5 L/s at low flow conditions. Since deep groundwater discharged in upstream as well as downstream parts of the catchment, choosing another threshold would probably influence the result slightly, which is an uncertainty of this study. Future studies could improve this by performing a sensitivity analysis on the threshold or taking into account factors like climate and soil type when defining it (e.g., Vogt et al. 2003).

Another limitation is that the two models used in this study do not account for any temporal variability of the hydrological variables. The landscape topography was used to reflect the phreatic water surface and the top boundary condition in the GWF models, which is in line with both the analytic and numeric solutions of previous studies (Cardenas and Jiang 2010; Craig 2008; Wang et al. 2011) and is justified by the relatively flat topography, shallow soils, and humid climate in the studied catchments (Haitjema and Mitchell-Bruker 2005). Furthermore, the model used here also accounted for the fact that the water table is controlled by the recharge rate in the infiltration zone, making it more realistic than many previous studies. Adapting the grid resolution until satisfying the estimated runoff values by the SMHI for each catchment could also be seen as a type of calibration process of the models.

The assumption of stationary longitudinal stream WSPs, which was assumed here to be reflected by the elevation data extracted from the DEM, infers uncertainties in the estimations of HEF. This is because the DEM reflects only the surface-water elevation at the specific time the LIDAR measurements were taken and because the relationship between stream-flow discharge and HEF velocities is still debated. On the one hand, studies have shown that in cases of stable groundwater discharge, yearly variations in stream base flow only had a limited impact on the average hyporheic exchange flux (Marzadri et al. 2014; Storey et al. 2003; Tonina and Buffington 2009). This would imply that although head gradients at the streambed interface might be over- or underestimated due to misinterpretation of the topographic data, the general result that HEF velocities are considerably higher than dGWF discharge velocities prevails in most reaches. On the other hand, recent studies have shown that fast changes in stream flow related to specific discharge events can substantially impact HEF (e.g., Singh et al. 2019; Trauth and Fleckenstein 2017), thus leading to temporal variability in both the velocity ratio and the pattern of discharging dGWF. This variability is not accounted for in the present study but is an important question that should be extensively studied in the future. Another uncertainty is the 20-m wavelength limit, which was used when extrapolating the head variation spectrum towards lower scales. This limit could have large impact on the HEF, since the smallest scales were shown to be the most important. To minimize this uncertainty, future studies should include a sensitivity analysis on using different cut-off wavelengths.

The uncertainties in the estimation of HEF also relate to stream-flow velocity and depth, which are estimated using statistical relationships based on a limited dataset and result in rather small variations in the two variables between reaches. Uncertainties in the stream velocity and depth are subsequently reflected in several of the independent variables, which might have impacted the final results of the regression analysis and limits the results specifically to Swedish hydrological conditions. However, at this point, using the presented regression model along the lines of Lindström et al. (2010), for example, was the best option available for overcoming the lack of spatially distributed observations of channel characteristics. Finally, although the model used for calculating the HEF velocity was validated in Morén et al. (2021), it was demonstrated in that study that the model might underestimate the HEF velocity in reaches with high discharge and depth and low slopes. This would in turn indicate that the velocity ratio might be overestimated in the high-order stream reaches, as well as generally in flat regional catchments (such as Forsmark). However, this potential underestimation of the HEF velocity would not influence either the general conclusion that the HEF velocities are considerably higher than the dGWF discharge velocity, or in which reaches and catchments the impact is largest.

Conclusions

In this study, the use of physically based steady-state models that were supported by topographic, geological, and hydraulic data showed that the velocity of discharging dGWF varied substantially both within and between five regional catchments in Sweden. Furthermore, the dGWF discharge velocities were considerably smaller than the HEF velocities, indicating that HEF can have a substantial impact on the pattern of the discharging dGWF in most stream networks considered here. The main effect of the hyporheic zone in this context is that it confines the dGWF discharge areas and thereby accelerates the discharge velocity at the SWI. This is, for example, relevant information for analyses examining the spreading of radionuclides originating from HLRW located in deep bedrock, the upwelling of legacy nitrogen and the temporal stability and distribution of the patchy structure of benthic habitats.

A large number of significant regression models were derived to explain the relationships between catchment and stream-reach hydromorphological and geographic variables and the targeted dependent parameters—dGWF discharge velocity, HEF velocity, and the ratio between the two velocities averaged at three spatial scales. The regression analysis could explain some but not all of the modelled variability in the dependent variables, with explanation powers varying between 70 and 90% for the HEF models and between 40 and 50% for the dGWF models. The one regression model found for the velocity ratio explained approximately 50% of the variability. Thus, more research is needed to understand these phenomena and the derived models should be applied with caution. Note also that results are limited to reaches where deep groundwater was upwelling from a depth of 500 m and that some of the variables used to limit the models were estimated using semiempirical equations and theoretical assumptions. Thus, the resulting models should be applied specifically in discharge zones and should not be used in other hydrological conditions than the one found in Sweden. Nevertheless, the regression models indicated that upwelling groundwater velocity increases mainly with the hydraulic conductivity of the topsoil but that the explanatory power increases when topographic information is also accounted for. Furthermore, the regression analyses indicate that the fractal properties of the longitudinal water-surface elevation along the stream network regulate the HEF velocities to a large extent, thereby also exerting primary control over the velocity ratio and convergence of deep groundwater close to the SWI. In more generalized terms, the regression analytical results lead to two conclusions. One is that both the dGWF discharge velocities and HEF velocities are larger in steep subcatchments with highly variable stream slopes, which are often headwaters or low-order streams, than in flatter areas close to the catchment outlet. The other is that the impact of HEF on the dGWF discharge velocities was highest in areas where the landscape elevation variability was low, that is, in areas where the upwelling groundwater velocity was low but where relatively high variability was present in the local elevation along the stream reaches.