Introduction

Step-drawdown pumping tests, sometimes also called step-discharge or well-performance tests, are a widely used method to determine the maximum allowable pumping rate of a water well (Batu 1998; Kruseman and de Ridder 2000; Kasenow 2010). The well is successively pumped at several, commonly three to six, increasing pumping rates. In the ideal case, drawdown becomes constant at the end of each step before the rate is increased.

Jacob (1947) found that the total well drawdown (sw) obtained from such a test has two components

$$ {s}_{\mathrm{w}}=B\cdotp Q+C\cdotp {Q}^2 $$
(1)

where the first component involves the aquifer loss coefficient B [T/L2] and the pumping rate (Q), and the second component involves the pumping rate and the well loss coefficient C [T2/L5].

It was originally proposed that the term BQ describes the drawdown caused by the formation, which is assumed to be linear-laminar (Darcian) losses within the aquifer. For screened and gravel-packed wells constructed in uniform unconsolidated aquifers, the CQ2 term is commonly described as the sum of all losses caused by the well itself (“well losses”), e.g. by gravel pack, wellbore skin, screen and casing; also the constriction of annular flow caused by the motor of a submersible pump. The square dependency on the pumping rate indicates that these losses should include a turbulent component, as, for example, addressed in the Darcy-Weisbach equation (Weisbach 1845).

Based on the approximation of the Theis (1935) equation by Cooper and Jacob (1946), Jacob (1947) obtained B as

$$ B=\frac{1}{4\pi \cdotp T}\cdotp \left[\ln \left(\frac{4\cdotp T\cdotp t}{{r_{\mathrm{w}}}^2\cdotp S}\right)-0.5772\right] $$
(2)

with

T:

Aquifer transmissivity [L2/T]

t:

Time of pumping [T]

rw:

(Effective) well radius [L]

S:

Aquifer storativity

Jacob (1947) also defined the specific capacity Q/sw, which basically describes which flow rate Q [L/T] is obtained for a meter of drawdown sw (or unit of lift energy). At high pumping rates, the importance of non-Darcian flow will increase and the Q/sw ratio will increasingly deviate from a linear relationship.

The coefficients B and C are usually obtained graphically, by plotting sw/Q as a function of Q for each step, assuming equal duration, obtaining B as the intercept of the resulting line with the sw/Q axis and C as its slope (Bierschenk 1963).

Rorabaugh (1953) modified the Jacob equation by proposing the more general form

$$ {s}_{\mathrm{w}}=B\cdotp Q+C\cdotp {Q}^n $$
(3)

Rorabaugh (1953) found values between 2.4 and 2.8 for n, except for low discharges where n may approach one. Lennox (1966) found a maximum of n = 3.5. Based on a set of 290 step-drawdown tests from the United Arab Emirates, Kurtulus et al. (2019) reported a wide range of exponents from 0.35 to 6.01 and a broadly semilogarithmic correlation between C and n. The maximum, however, was found at around n = 2, with 96% in the range of 0.5–3. Allowing such a wide range of exponents can be treacherous, however, and would allow overfitting or even fitting erroneous tests.

Other authors, however, confirmed the value proposed by Jacob (1947) of n = 2.0 (Bierschenk and Wilson 1961; Clark 1977). Louwyck et al. (2010) reviewed the analysis of the step-drawdown test by Clark (1977) as performed by several later authors and found that most arrived at values for n closely around 2, including themselves. According to Kaergaard (1982) and Rushton and Rathod (1988), deviations from the Theis or Cooper-Jacob simplified model for aquifer response are the most likely cause of apparent differences from the value of 2. Another strong argument in favor of n = 2 is that several equations describing nonlinear losses, especially the Forchheimer equation and the Orifice equation, show a square dependency; therefore, n = 2 is assumed here in the following.

Alternatively, iterative numerical methods are available (Labadie and Helweg 1975; Miller and Weber 1983). Avci et al. (2010) proposed taking the derivative of drawdown with respect to time and integrating this to obtain a continuous function, which can then be used to derive both the aquifer and well loss parameters. Louwyck et al. (2010) used a numerical model to successfully model step-drawdown tests. They state that, compared to methods based on analytical solutions, the inverse numerical model allows a more representative aquifer schematization, usage of all parts of the drawdown curve, and a comprehensive analysis of parameter uncertainty. These approaches, however, are significantly more computationally demanding than the analysis after Jacob (1947) and Rorabaugh (1953). Free and commercial software based on this approach is available for certain aquifer regimes.

There is considerable debate about what the coefficients B and C actually mean and what information they contain (Mogg 1969; Ramey 1982; Driscoll 1986; Helweg 1994; Kawecki 1995; Shapiro et al. 1998; Mathias et al. 2008; Mathias and Todman 2010). Several authors pointed out that not all well losses are necessarily turbulent and that coefficient B could contain some linear well losses (Mogg 1969; Driscoll 1986). On the other hand, losses in the aquifer may, at high intake velocities, contain turbulent losses, which would have to be included in C (Mathias et al. 2008; Mathias and Todman 2010).

Some of the older references mentioned previously only distinguish between linear laminar (Darcy) and turbulent flow. In reality, there is a transitional nonlinear laminar flow regime between them (Bear 1988, 2007), described by the Forchheimer equation (Forchheimer 1901a, b). For steady-state radially symmetric flow, the Engelund Eq. (4) can be used to describe linear and nonlinear laminar flow to a well (Engelund 1953; Barker and Herbert 1992). It should be noted that with a very small contribution of inertial forces (β* ≈ 0), Eq. (4) reduces to the well-known Dupuit-Thiem equation which describes fully laminar (Darcian) radial well flow (Dupuit 1863; Thiem 1870; Tügel et al. 2016).

(4)

with

r1,r2:

Radius (r2 > r1) [L]

β*:

Inertial factor or Forchheimer coefficient

It is striking that Eq. (4) has the same form as the Jacob (1947) equation, since it contains one summand (= B) with a linear dependency on Q and one summand (= C) with a square dependency on Q.

In the following, this will be refined further by considering the contributions of all components located around the well. The head loss measured as drawdown stot in a well is the sum of the losses caused by the different components of the aquifer-well system (Eq. 5) that the groundwater has to pass through (Barker and Herbert 1992; Houben 2015b).

$$ {s}_{\mathrm{tot}}={s}_{\mathrm{aq}}+{s}_{\mathrm{sk}}+{s}_{\mathrm{gp}}+{s}_{\mathrm{sc}}+{s}_{\mathrm{up}} $$
(5)

with

saq Head loss caused by the aquifer [L]

ssk Head loss caused by the wellbore skin layer [L]

sgp Head loss caused by the gravel pack(s) [L]

ssc Head loss caused by the screen inflow [L]

sup Head loss caused by upflow in the unscreened casing [L]

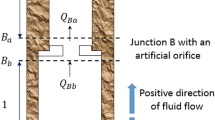
Flow in the aquifer, the wellbore skin and the gravel pack could in general include both viscous (linear laminar) and inertial (nonlinear laminar) flow components. For each component, losses could be calculated using the appropriate equations for steady-state or transient flow, respectively. However, Houben (2015b) computed Reynolds numbers as a function of distance from the well for a variety of common well set-ups and found that flow right up to the borehole wall is commonly fully laminar and that nonlinear laminar flow commonly becomes relevant only in the gravel pack. In this case, the steady-state flow in the aquifer and the wellbore skin can be described by the Dupuit-Thiem equation. Flow in the gravel pack is described by the Forchheimer-Engelund approach and thus contains a linear and a square term. Flow in the screen (slots) and in the well interior is fully turbulent under almost all circumstances; therefore, the orifice equation (Barker and Herbert 1992) and the Darcy-Weisbach equation (Weisbach 1845), respectively, have to be applied, which both display a square dependency on Q. The latter has to be calculated separately for flow inside the screen, inside the casing sections, and in the annulus around the pump motor. Note that, unlike in the casing, not the whole volume of water flows upwards for the entire length of the screen. Assuming uniform screen inflow, the effective screen length is one third of its actual length. Intuitively, one would assume that the roughness and thus the friction factor of the screen are higher than those for the casing; however, the inflow into perforated pipes can actually decrease friction (Su and Gudmundsson 1998). Separating the linear and square summands and factoring out the pumping rate yields Eq. (6):

$$ {s}_{\mathrm{tot}}=\left({s}_{\mathrm{aq}}+{s}_{\mathrm{sk}}+{s}_{\mathrm{gp}-\mathrm{lin}}\right)+\left({s}_{\mathrm{gp}-\mathrm{nonlin}}+{s}_{\mathrm{sc}}+{s}_{\mathrm{up}}\right)= BQ+C{Q}^2 $$
(6)

with

sgp-lin Head loss caused by linear (Darcian) flow in the gravel pack [L]

sgp-nonlin Head loss caused by nonlinear (non-Darcian) flow in the gravel pack [L]

Using the explicit formulations of the terms that appear in Eq. (6) from Houben (2015b, their Eq. 35), and factoring out some constants yields:

(7)

with

ApOpen screen area (fractional)

bThickness of aquifer [L]

Cc Contraction coefficient (typically ≈ 0.6)

CvVelocity coefficient (≈ 0.98 for screen slots)

diDiameter of casing section, if telescopic casing is used

dsDiameter of screen [L]

dcDiameter of casing [L]

fDDarcy friction factor of pipe surface (fD,s = screen, fD,c = casing)

gAcceleration of gravity [L/T2]

Kxyhydraulic conductivity of component xy: aq = aquifer, gp = gravel pack, sk = wellbore skin [L/T]

LcLength total casing (distance from screen top to pump inlet) [L]

LiLength of casing section (if telescopic diameters are used) [L]

LsLength screen [L]

nc,dNumber of (telescoping) casing sections with different diameters (i = 1, 2, 3, …)

rxRadius of component x: b = borehole, s = screen, sk-in = inner diameter skin layer,, sk-out = outer diameter skin layer [L]

r0Radius of influence [L]

β*Inertial factor or Forchheimer coefficient

Head losses caused by the convergence of flow paths to the screen slots (Boulton 1947) were not considered here, due to their usually very limited contribution to the total loss (Houben 2015b). In case nonlinear losses extend into the aquifer, a Forchheimer-Engelund term for this can be added to Eq. (7). If the casing has telescoping diameters, this has to be addressed by loss terms (Weisbach equation) for each diameter, as indicated by the summation.

The objective of this study is to (1) answer the question: What is contained in the terms B and C? and, (2) to test a fully explicit analytical model based on Houben (2015b) against actual field step-drawdown tests, including an assessment of its limitations.

Transient flow

A general disadvantage of steady-state models discussed in the preceding is that they cannot treat well tests where the pumping steps have not reached stable drawdown, which seldom occurs during the typical short duration step-drawdown tests, especially in fractured-rock aquifers. For transient flow, the linear laminar terms after Dupuit-Thiem used in Eq. (7) for flow through the aquifer, wellbore skin and gravel pack would have to be replaced by the Theis (1935) equation, or to make things simpler, by the Cooper and Jacob (1946) approximation, as proposed by Eden and Hazel (1973) and Brereton (1979). It should be noted that this involves a change in boundary conditions from an aquifer bounded by a recharge boundary (Dupuit-Thiem) to an infinite aquifer (Theis). Mathias et al. (2008) modified the nonlinear laminar term after Engelund (1953) in Eq. (7) and thus obtained Eq. (8), valid for transient drawdown of a well pumped at a constant rate for sufficiently large times.

(8)

with

β´Inertial factor or Forchheimer coefficient [L−1]

Again, the similarity to the Jacob (1947) Eq. (1) is immediately apparent, since Eq. (8) also contains one summand (= B) with a linear dependency on Q and one summand (= C) with a square dependency on Q. Mathias and Todman (2010) therefore applied the Eq. (8) to step-drawdown tests. They also defined a critical minimum time for the step duration, which can be used to assess the validity of applying the Jacob (1947) method.

One limitation of this approach is that they attributed all nonlinear losses to the near-field of the well, without distinguishing between individual components such as aquifer, wellbore skin and gravel pack. Introducing the explicit terms from Houben (2015b) for these contributions expands Eq. (8) to Eq. (9):

(9)

with

TxyTransmissivity of component xy: aq = aquifer, gp = gravel pack, sk = wellbore skin [L/T]

SaqAquifer storativity

The Mathias et al. (2008) approximation, however, is only valid for larger times, where flow in the near-field of the well has already become constant. After a few minutes, the pump will extract at a constant rate; flow through the near-field (wellbore skin, gravel pack, screen, well interior) will thus quickly become constant and drawdown from them can be considered the same as for steady state. Additionally, assuming a storage of water in the wellbore skin and gravel pack is not really useful. The transient drawdown signal will continue to travel outward only through the aquifer. With this simplification, Eq. (9) becomes Eq. (10), a mix of transient terms for the far field (aquifer) and steady-state terms for the near field (wellbore skin, gravel pack, screen, well interior).

(10)

Assuming that, for most cases, screen entrance and upflow losses are small, this equation can be simplified to

(11)

Comparison to actual steady-state step-discharge tests

Barker and Herbert (1992) were probably the first to realize that a formulation of the type of Eq. (7) can be used to emulate step-drawdown tests from the field, although they did not provide an explicit definition of B and C. They compared their model to several field tests and obtained a reasonably good fit (r2 = 0.92), although relative differences of individual data pairs were relatively high. This deviation may be due to the presence of a wellbore skin, something which their model did not address.

Therefore, it was decided to use actual step-drawdown tests to investigate the performance of Eq. (7). Unfortunately, many published step-drawdown tests do not include the full data set needed. Often information on casing, screen and borehole radius, screen length and grain sizes of gravel pack and aquifer is missing (Clark 1977; Helweg 1994). Others did not reach steady state at the end of the steps (e.g. Shapiro et al. 1998), thus violating the steady-state assumptions of the Jacob (1947) model. Four sufficiently documented tests were found (Table 1). They all had steps of long duration (several hours to tens of hours), which each reached steady state, thus avoiding problems related to transient conditions (Mathias and Todman 2010). Another problem is that a priori information on the presence, thickness and hydraulic conductivity of a skin layer is almost never available (Houben et al. 2016). In the following calculations, the skin layer is thus initially assumed to be absent and the gravel pack is the main optimization parameter. If this, however, leads to an unreasonably low hydraulic conductivity of the gravel pack, this can be interpreted as an indication of the presence of a skin layer. The resulting losses could thus be interpreted as caused by a near-well zone, comprised of gravel pack and skin layer. Losses due to screen entrance and upflow in both screen and casing were calculated based on provided data or reasonable assumptions. As will be shown below, these contributions are small, which is in good accordance with Houben (2015b). They were thus summarized under “in-well losses” in the tables. In all cases, the commonly employed n = 2 was used for the CQn term, although using higher values after Rorabaugh (1953) could have, in some cases, led to better fits.

Table 1 Input data for the four-example step-discharge tests
Full size table

The first example is taken from Vukovic and Soro (1992), in which almost all terms present in Eq. (7) are calculated explicitly from knowledge of the well construction. The well, PEB-3, is located in the Kamenicka Ada well field, near the city of Novi Sad, Serbia. It was drilled in 1983 to a depth of 30 m. A screen of 15.7 m length was installed in the lower part of the drillhole. The aquifer consists of an upper fine-to-medium sand layer of 9.5 m thickness and a basal layer of 7 m of gravelly sand. The aquifer is overlain by clayey sand; drawdown compared to initial saturated thickness is relatively small and confined conditions can thus be assumed safely. No information on the grain size of the gravel pack was given. The step test involved four pumping rates. The measured and calculated data are given in Table 2.

From the linear regression of a plot of s/Q versus Q (Fig. 1a), the linear loss coefficient B was obtained as 68.4 s/m2 and the nonlinear coefficient C as 1,010 s2/m5, respectively. Vukovic and Soro (1992) obtained similar values with B = 69 s/m2 and C = 1,000 s2/m5, respectively, from a graphical analysis. Figure 1b shows that the measured drawdowns show a marked deviation from a linear relationship early on. In-well losses are found to be negligible (<2 mm). Considering the small screen entrance and upflow losses, these additional losses are basically controlled by the gravel pack conductivity, which was optimized to Kgp = 1.35 · 10−3 m/s to obtain the total loss curve in Fig. 1b. This value is only slightly higher than that of the aquifer, which would be unusual for any gravel pack material. The presence of a skin layer is therefore probable.

Fig. 1
figure 1

Step-drawdown test PEB-3, Kamenicka Ada: a evaluation after Bierschenk (1963), b measured and calculated drawdown (head losses). The difference between calculated total and linear losses describes the nonlinear losses

Full size image

The second example, well HB5, is located in the Kirchdorf wellfield, near the city of Sulingen, Germany (Table 1; Fig. 2). The aquifer is 20 m thick and consists mainly of medium sand, with some coarse sand admixed. It is capped by a 5-m-thick clay layer and remained confined during the test. A stainless-steel wire-wound screen of 10 m length with a diameter of 0.40 m was installed in the lower part of the drillhole. The quartz gravel pack consists of an outer (grain size 1–2 mm) and an inner layer (3.15–5.6 mm) and was installed between 44 and 58 m depth. The step test involved three pumping rates, each of which reached steady-state drawdown. The measured and calculated data are given in Table 3 and Fig. 2, together with a calculated virtual fourth step. From the linear regression of a plot of s/Q versus Q, the linear loss coefficient B was obtained as 49.2 s/m2 and the nonlinear coefficient C as 191.4 s2/m5, respectively (Fig. 2a). This shows that the well produces markedly lower well losses than the PEB-3 well, despite the shorter screen. The hydraulic conductivity of the gravel pack was optimized to Kgp = 3.0 · 10−3 m/s to obtain the curve shown in Fig. 2. This is only slightly higher than that of the aquifer but the difference in mean grain size between the aquifer material (d50 = 0.6 mm) and the outer filter sand (1–2 mm) is not very high. Again, screen and upflow losses are negligible (<2 mm).

Fig. 2
figure 2

Step-drawdown test Kirchdorf HB5: a evaluation after Bierschenk (1963), b measured and calculated drawdown (head losses). The difference between calculated total and linear losses describes the nonlinear losses

Full size image
Table 2 Data and results for step-drawdown test PEB-3, Kamenicka Ada
Full size table
Table 3 Data and results for step-drawdown test HB5, Kirchdorf
Full size table
Table 4 Data and results from step-drawdown test Horkesgath 4
Full size table
Table 5 Data from step-drawdown test Murschnitz 3
Full size table

The third step-drawdown test comes from an experimental well that was equipped with a novel screen design made of compacted porous plastic granulate (Tholen and Treskatis 1998). It is located in the Horkesgath wellfield, near the city of Krefeld, Germany (Table 1). It is capped by a 4.5-m-thick clay layer and thus confined (initial water level 9.45 m below surface). A PVC screen of 10 m length was installed in the lower part of the drillhole (22–32 m). The aquifer consists mainly of medium sand, with some interspersed fine and coarse sand layers. The quartz gravel pack has a grain size range of 2.0–3.15 mm and was installed between 19 and 34 m depth. The step test involved four pumping rates, each of which reached steady-state drawdown. The measured and calculated data are given in Table 4 and Fig. 3. Even at the rather low initial pumping rate of Q = 30 m3/h, the well already shows nonlinear losses, which become quite severe at higher pumping rates. This is probably due to a combination of low aquifer conductivity, short screen length, small screen and borehole diameter (compared to the Kirchdorf well) and the hydraulically not advantageous gravel pack, which in combination produce high approach velocities and nonlinear losses. The model using Eq. (8) only reproduces the results of the first two steps well, but seemingly underestimates the drawdown of the third and fourth step (Fig. 3b). This, however, is easily explained by the drawdown, which at the second step has reduced the water saturated thickness at the well by half, at the third stage reaches into the top of the gravel pack, and at the fourth stage already starts dewatering the screen, since drawdown is then higher than the initial water level above the screen top. The aquifer is thus not confined anymore and significant vertical flow develops around the nearfield of the well, potentially accompanied by the development of a seepage face, which can cause additional losses (Houben 2015a). These deviations are beyond the capabilities of the model used in Eq. (8). From the linear regression of a plot of s/Q versus Q, the linear loss coefficient B was obtained as 378.6 s/m2 and the nonlinear coefficient C as 9,905 s2/m5, respectively (Fig. 3a). The very high value for C highlights the hydraulic stress the well is suffering. Again, in-well losses are smaller by orders of magnitude.

Fig. 3
figure 3

Step-drawdown test Horkesgath 4: a evaluation after Bierschenk (1963), b measured, corrected and calculated drawdown (head losses). The difference between calculated total and linear losses describes the nonlinear losses

Full size image

Since the Horkesgath aquifer becomes unconfined at the second step, additional drawdown caused by the decrease of transmissivity and vertical flow around the well occurs. This could be addressed by applying the correction factor introduced by Jacob (1944) for water-table aquifers. The corrected drawdown s′ is obtained via Eq. (12).

$$ {s}^{\prime }=s-\frac{s^2}{2b} $$
(12)

For the Horkesgath test, the corrected drawdowns (b = 20 m) yield a more or less straight line, close to the calculated linear losses (Fig. 3b). This is indirect proof that the transition to unconfined conditions and the development of vertical flow does cause some of the deviations between measured and calculated drawdowns. The corrected values, however, fail to emulate the drawdowns at higher pumping rates, where the model according to Eq. (7) performs better.

Figures 1, 2, 3 show that Eq. (8) can emulate both the absolute drawdowns and the relative contribution of linear and nonlinear losses measured in actual wells quite closely. The definitions of B and C obtained from Eq. (8) have the general advantage that they give a physical meaning to the coefficients proposed by Jacob (1947). They therefore allow a quantitative assessment of the impact of individual components such as the borehole diameter, the hydraulic conductivity of the gravel pack and the presence or absence of wellbore skin. The equations can thus be used to implement virtual step-drawdown tests, even before the well has been built, or to deduce loss components from actual well tests in a post audit (Figs. 1, 2, 3). Both can help in designing better, more energy-efficient wells. It can be argued, however, that many of the parameters required are difficult, if not impossible to obtain, e.g. the hydraulic conductivity of the gravel pack, the Forchheimer coefficient, and both the conductivity and the thickness of the wellbore skin (Houben et al. 2016). Reasonable estimates can, however, be obtained in most cases, allowing at least an order-of-magnitude analysis of losses.

There are, of course, cases such as the Horkesgath well, when the boundary conditions of actual step-drawdown tests deviate strongly from those assumed in the analytical models used here. Another, deliberately extreme example comes from well Murschnitz 3, near the city of Chemnitz, Germany, where groundwater was extracted from granulite, a highly metamorphic consolidated rock type. The aquifer hydraulic conductivity was set to Kaq = 2 · 10−5 m/s. The borehole had a diameter of 0.62 m (11–30 m) and 0.52 m (30–70 m) in the screened interval (slotted steel), which ranged from 11 to 70 m, with a uniform screen diameter of 0.40 m. The annulus was filled with very coarse gravel (7–10 mm), for which a hydraulic conductivity of Kgp = 1 · 10−2 m/s was assumed. Initially, the water level was 3.65 m below ground surface, so that the well had an initial water column of 66.35 m. According to the geological log, groundwater entered the well through various fractures and mylonitic zones. The step test involved four pumping steps. The measured data are found in Table 5 and Fig. 4 and show very strong nonlinear behavior. The calculated results clearly show that Eq. (8) is not able to recreate the course of the step-drawdown test, except for the first and second step, where drawdowns are still small. Due to the low pumping rates, the model even predicts the absence of nonlinear losses, indicated by the small value for C (Fig. 4b). The reasons for this deviation from reality are manifold. The analytical model assumes confined conditions, a constant aquifer thickness and transmissivity, while in reality the saturated thickness near the well had decreased to about 50% of the initial at the highest pumping rate, thus reducing transmissivity. The observed strong nonlinear contribution is likely to stem from processes in the fractures located close to the well. At high pumping rates, some fractures might run dry and, in others, flow might become nonlinear or even turbulent. Additionally, a vertical flow component and a seepage face might have developed in and near the well, which would also contribute additional head losses (Houben 2015a). While the effect of the changing transmissivity could be addressed in the model by manually adapting the saturated thickness for each drawdown step, the other deviations cannot be overcome. This shows the limitations of the approach. Further details on step drawdown tests in fractured rocks can be taken from, e.g. Dougherty and Babu (1984) and Hammond (2018).

Fig. 4
figure 4

Step-drawdown test Murschnitz 3: a unsuccessful evaluation after Bierschenk (1963), b measured and calculated drawdown (head losses), here only linear losses

Full size image

Data requirements and uniqueness

A general problem with analytical models like the one in Eq. (7) is the multitude of parameters involved, which can all be varied to some degree to obtain a fit to measured data. Therefore, some doubt remains regarding the uniqueness of the values chosen for a curve fit. Some parameters are easy to obtain, e.g. the length and diameter of casing and screen, which are provided by the manufacturer, the pump position and the aquifer thickness, which can be read off from well logs. Others like pump rates and water levels can be measured in the field with sufficient accuracy. Some, like the hydraulic conductivity of the aquifer and the radius of influence, can at least be constrained, e.g. by a pump test, analytical models and empirical approaches, etc.

Not all parameters are equally important. The radius of influence only appears in a logarithmic term and is thus of limited influence. As the analysis of the example tests showed, many parameters are of very limited influence, e.g. the ones regarding screen entrance and upflow losses.

The most important handles remaining are the hydraulic conductivity of the gravel pack and the wellbore skin. Mathias and Todman (2010) solved this problem elegantly by assigning all nonlinear losses to the near-field of the well, without addressing their individual contributions. The conductivity of the gravel pack material is rarely measured. Since it is most often a well-sorted, uniform material, the Kozeny-Carman equation is a useful tool for its calculation (Houben 2015a, b). This equation also allows different degrees of compaction to be addressed by varying the porosity. The wellbore skin is very difficult to assess since its presence and properties are commonly unknown (Houben et al. 2016). Here, by using the hydraulic conductivity of the gravel pack as the main optimization parameter (and ignoring the wellbore skin in this first step), this study makes use of the usually very high conductivity of gravel packs, especially immediately after well construction, when most step-discharge tests are done. If the optimization yields an inexplicably low conductivity for it, this is a strong indicator that a wellbore skin layer has formed during construction and was not removed during well development. Since their thickness rarely exceeds a few millimeters (Houben et al. 2016), their low hydraulic conductivity can then be used as a second optimization parameter. For older wells, a reduction of gravel pack conductivity by incrustations may need to be considered.

Conclusions

The study of the contribution of the individual components of a well to the drawdown measured in a step-discharge test could finally settle the question as to what the terms B and C of Jacob (1947) represent. For radially symmetric flow at steady state to a fully penetrating screened and gravel-packed well in a horizontal and homogeneous aquifer, one obtains the “linear loss” term B of Jacob (1947) as

$$ B=\frac{1}{2\uppi \cdotp b}\cdotp \left[\frac{1}{K_{\mathrm{aq}}}\cdotp \ln \left(\frac{r_0}{r_{\mathrm{b}}}\right)+\frac{1}{K_{\mathrm{s}\mathrm{k}}}\cdotp \ln \left(\frac{r_{\mathrm{s}\mathrm{k}-\mathrm{out}}}{r_{\mathrm{s}\mathrm{k}-\mathrm{in}}}\right)+\frac{1}{K_{\mathrm{gp}}}\cdotp \ln \left(\frac{r_{\mathrm{b}}}{r_{\mathrm{s}}}\right)\right] $$
(13)

The analysis showed that B indeed is solely composed of linear losses, albeit from different components. This confirms the findings of Driscoll (1986), who pointed out that B does not solely comprise effects of the aquifer but also includes the effects of linear laminar flow in the gravel pack and wellbore skin (the latter if present). However, the aquifer will always be the dominant contributor.

For the “well loss” coefficient C of Jacob (1947), the following definition is obtained:

$$ C={\left(\frac{1}{2\uppi \cdotp b}\right)}^2\cdotp \left[\frac{\beta^{\ast }}{{K_{\mathrm{gp}}}^2}\cdotp \left(\frac{1}{r_{\mathrm{s}}}-\frac{1}{r_{\mathrm{b}}}\right)+\frac{1}{{\left({r}_{\mathrm{s}}\cdotp {C}_{\mathrm{v}}\cdotp {C}_{\mathrm{c}}\cdotp {A}_{\mathrm{p}}\right)}^2\cdotp 2g}+\left(\frac{1}{3}\cdotp \frac{f_{\mathrm{D},\mathrm{s}}\cdotp 32\cdotp {L}_{\mathrm{s}}\cdotp {b}^2}{{d_{\mathrm{s}}}^5\cdotp g}+\sum \limits_i^{n_{\mathrm{c},\mathrm{d}}}\frac{f_{\mathrm{D},\mathrm{c}}\cdotp 32\cdotp {L}_{\mathrm{i}}\cdotp {b}^2}{{d_{\mathrm{i}}}^5\cdotp g}\right)\right] $$
(14)

In the form of Eq. (14), C contains all nonlinear and turbulent losses occurring in the gravel pack, the screen and the casing(s). It could easily be expanded to include nonlinear losses in the aquifer, if this is indicated by the Reynolds numbers. Therefore, C is not only a “well loss” coefficient but includes all nonlinear and turbulent losses of all components around the well. The screen losses, which are commonly quite small (Clark and Turner 1983; Houben 2015b), could be omitted from the definition of C, without compromising the accuracy much. For shallow wells with short screen and casing lengths, large diameters and smooth surfaces, even the contribution of upflow will often be small enough to be neglected, as the examples showed. In this case, C would only depend on the nonlinear losses of the gravel pack and would take a form similar to the definition of C by Mathias and Todman (2010).

As the examples from unconsolidated aquifers show, the model based on Eq. (7) is able to recreate or even predict step-drawdown tests, provided that the boundary conditions do not deviate strongly from the ones the analytical models assume, e.g. horizontal flow, constant transmissivity and nonleaky (quasi-)confined conditions. For fractured aquifers with their strongly localized well inflow and unconfined aquifers with high drawdown, its use is not indicated.

For transient cases, the steady-state Dupuit-Thiem terms can be replaced by (simplified) Theis terms, although this involves a change of boundary conditions. For larger times, flow in the well itself (skin, gravel pack, screen, well interior) can be assumed to be steady state, with transient flow only occurring in the aquifer.

An Excel spreadsheet that allows easy calculations of Eq. (7), including all terms, is attached to this study as electronic supplementary material (ESM). It is an expanded version of the ESM from Houben (2015b). One of the improvements is that virtual step-drawdown tests can now be calculated, allowing predictions on the potential yield of planned wells or post-audits of existing wells. The tool was also expanded to allow the calculation of some required but often a priori unknown parameters, e.g. the hydraulic conductivity of the gravel pack (using the Kozeny-Carman equation) and the radius of the cone of depression, based on analytical equations.