Abstract
Anisotropic fast-marching algorithms are computationally efficient tools for generating realistic maps of karst conduit networks, constrained by both the spatial extent and the orientation of karstifiable geologic units. Existing models to generate conduit network maps are limited either by high computational requirements (for chemistry-based models) or by their inability to incorporate the effects of elevation and orientation gradients (for isotropic fast-marching models). The new anisotropic fast-marching approach described here provides a significant improvement, though it imitates rather than reproduces actual speleogenetic processes. It can rapidly generate a stochastic ensemble of plausible networks from basic geologic information, which can also be used as input to karst-appropriate flow models. This paper introduces an open-source, easy-to-use implementation through the Python package pyKasso, then describes its application to a well-mapped geologically complex long-term study site: the Gottesacker alpine karst system (Germany/Austria). Groundwater flow in this system is exceptionally well understood from speleological investigations and tracer tests. Conduit formation primarily occurs at the base of the karst aquifer, following plunging synclines. Although previous attempts to reproduce the conduit network at this site yielded implausible network maps, pyKasso quickly generated networks faithful to the known conduit system. However, the model was only able to generate these realistic networks when the inlet-outlet connections of the system were correctly assigned, highlighting the importance of pairing modeling efforts with field tracer tests. Therefore, a model ensemble method is also presented, to optimize field efforts by identifying the most informative tracer tests to perform.
Zusammenfassung
Anisotrope Fast-Marching-Algorithmen sind recheneffiziente Werkszeuge zur Generierung realistischer Karströhren-Netzwerke, die durch die räumliche Verbreitung und die Orientierung verkarstungsfähiger geologischer Einheiten eingeschränkt sind. Existierende Ansätze zur Generierung von Karströhren-Netzwerken sind entweder durch ihren sehr hohen Rechenaufwand limitiert (Modelle, die auf der chemischen Lösungskinetik basieren), oder durch die fehlende Möglichkeit, die Effekte von topografischen und strukturellen Gradienten zu berücksichtigen (isotrope Fast-Marching-Modelle). Der neue anisotrope Fast-Marching-Ansatz, der hier vorgestellt wird, ist daher ein wesentlicher Fortschritt, wobei speläogenetische Prozesse eher imitiert als physikalisch reproduziert werden. Er kann aus einfachen geologischen Informationen schnell ein stochastisches Ensemble plausibler Netzwerke generieren, das auch für karstspezifische Strömungsmodelle verwendet werden kann. Dieses Paper stellt eine leicht nutzbare Open-Source-Implementierung mithilfe des Python-Pakets pyKasso vor und beschreibt dann seine Anwendung auf ein gut untersuchtes, geologisch komplexes Untersuchungsgebiet: das alpine Karstsystem Hochifen-Gottesacker (Deutschland/Österreich). Das unterirdische Entwässerungsnetz in diesem Karstgebiet ist aufgrund von speläologischen Beobachtungen und zahlreichen Markierungsversuchen außergewöhnlich gut bekannt. Karströhren bilden sich dort vor allem an der Basis des Karstaquifers und folgen dem Schichtfallen und den abtauchenden Synklinal-Achsen. Während frühere Versuche, das Karströhren-Netzwerk in diesem Gebiet zu reproduzieren, zu implausiblen Ergebnissen führten, konnte pyKasso sehr schnell Netzwerke generieren, die mit dem bekannten Karströhren-Netzwerk gut übereinstimmen. Allerdings war dies nur möglich, wenn die Einlass-Auslass-Verbindungen des Systems korrekt vorgegeben wurden, was zeigt, dass Karst-Modellierungen sinnvollerweise mit Markierungsversuchen kombiniert werden sollten. Daher wird auch eine Modell-Ensemble-Methode vorgestellt, um Geländeuntersuchungen zu optimieren, indem die jeweils aussagekräftigsten Markierungsversuche identifiziert werden.
Résumé
Les algorithmes de fast-marching anisotropes sont des outils de calcul rapides et efficaces pour générer des cartes de réseaux de conduits karstiques plausibles au sein d’une formation géologique en prenant en compte le pendage des roches karstifiables. Les modèles existants capables de générer des réseaux de conduits karstiques sont limitées soit par un temps de calcul élevé (dans le cas des modèles génétiques) soit par leur incapacité de représenter les effets des gradients topographiques et du pendage des roches (dans le cas des modèles de fast-marching isotropes). La nouvelle méthode utilisant un fast-marching anisotrope et présentée dans cet article représente une avancée importante même si elle imite les mécanismes de la spéléogenèse plutôt que de les simuler en détail. Cette méthode est capable de générer rapidement un ensemble de réseaux vraisemblables à partir de données géologiques simples, ensemble qui peut ensuite servir de point de départ pour la modélisation de l’écoulement des eaux souterraines en utilisant des modèles adaptés aux aquifères karstiques. Cet article présente une implémentation libre et facile à utiliser de la méthode: le module Python pyKasso. Les capacités de ce module sont démontrés en modélisant une région de karst alpin bien cartographié située dans un contexte géologique complexe: le système Gottesacker (Allemagne/Autriche). L’écoulement des eaux souterraines sur ce site est exceptionnellement bien connu, grâce à de nombreuses données de traçage et d’explorations spéléologiques. Le développement des conduits se concentre à la base de l’aquifère karstique, le long des axes plongeants de synclinaux. Bien que des efforts précédents de simulation du réseau karstique sur ce site aient rendu des cartes de réseaux improbables, pyKasso a pu rapidement générer des réseaux qui se conformaient au réseau connu. En revanche, le modèle n’a pu générer ces réseaux vraisemblables qu’une fois que chaque point d’entrée du système ait été attribué à la source correcte. Cette limitation surligne le lien essentiel entre la modélisation et les données de traçage acquises sur le terrain. Par conséquent, une méthode est proposée pour l’optimisation du travail de terrain, en utilisant un ensemble de modèles pour identifier les traçages les plus informatifs.
Resumen
Los algoritmos de avance rápido a nivel anisotrópico son herramientas computacionalmente eficientes para generar mapas realistas de redes de conductos kársticos, limitados tanto por la extensión espacial como por la orientación de las unidades geológicas karstificables. Los modelos existentes para generar mapas de redes de conductos están limitados por los elevados requisitos computacionales (para los modelos basados en la química) o por su imposibilidad de incorporar los efectos de los gradientes de elevación y orientación (para los modelos isotrópicos de avance rápido). El nuevo enfoque de avance rápido a nivel anisotrópico descrito aquí supone una mejora significativa, aunque no reproduce los procesos espeleogenéticos reales, sino que los simula. Puede generar rápidamente un conjunto estocástico de redes plausibles a partir de información geológica básica, que también puede utilizarse como entrada para modelos de flujo apropiados para el karst. Este artículo presenta una implementación de código abierto y fácil de usar a través del programa Python pyKasso, y luego describe su aplicación a un sitio de estudio a largo plazo bien cartografiado y geológicamente complejo: el sistema kárstico alpino de Gottesacker (Alemania/Austria). El flujo de aguas subterráneas en este sistema se conoce excepcionalmente bien gracias a las investigaciones espeleológicas y a las pruebas de trazadores. La formación de conductos se produce principalmente en la base del acuífero kárstico, siguiendo la pendiente de los sinclinales. Aunque los intentos anteriores de reproducir la red de conductos en este lugar dieron lugar a mapas de red poco plausibles, pyKasso generó rápidamente redes fidedignas al sistema de conductos conocido. Sin embargo, el modelo sólo fue capaz de generar estas redes reales cuando se asignaron correctamente las conexiones de entrada-salida del sistema, lo que pone de manifiesto la importancia de acoplar los esfuerzos de modelado con las pruebas de trazadores de campo. Por lo tanto, también se presenta un método de conjunto de modelos para optimizar los trabajos de campo mediante la identificación de las pruebas de trazadores más significativas que deben realizarse.
摘要
各向异性快速行进算法是用于生成岩溶管道网络的真实地图的计算有效的工具, 该网络受可溶地质单元的空间范围和分布控制。生成管道网络图的现有模型要么受限于高计算要求(基于化学的模型), 要么受限于它们无法考虑高程和方向梯度的影响(对于各向同性快速行进模型)。这里描述的新的各向异性快速行进方法提供了显著的改进, 尽管它模仿而不是再现实际的洞穴发生过程。它可以从基本地质信息中快速生成合理网络的随机集合, 也可以用作适合岩溶流动模型的输入。本文通过 Python 包 pyKasso 介绍了一个开源、易于使用的实现, 然后描述了在一个细致绘制、地质复杂的长期研究场地:Gottesacker 高山岩溶系统(德国/奥地利)的应用。从洞穴学调查和示踪测试中可以非常清楚地了解该系统中的地下水流。管道的形成主要发生在岩溶含水层的底部, 并沿向斜倾斜。尽管以前在该场地再现管道网络的尝试产生了难以置信的网络图, 但 pyKasso 迅速生成了符合已知管道系统认识的网络。然而, 只有在正确分配系统的入口-出口连接时, 该模型才能生成真实的网络, 这突出了将建模工作与现场示踪试验联合的重要性。因此, 还提出了一种模型集成方法, 通过确定要执行的最大信息量的示踪试验来优化现场工作。
Resumo
Algoritmos anisotrópicos de marcha rápida são ferramentas computacionalmente eficientes para gerar mapas realistas de redes de condutos cársticos, restringidos tanto pela extensão espacial quanto pela orientação das unidades geológicas cársticas. Os modelos existentes para gerar mapas de rede de condutos são limitados por altos requisitos computacionais (para modelos baseados em química) ou por sua incapacidade de incorporar os efeitos de gradientes de elevação e orientação (para modelos isotrópicos de marcha rápida). A nova abordagem de marcha rápida anisotrópica descrita aqui fornece uma melhoria significativa, embora imite em vez de reproduzir processos espeleogenéticos reais. Ele pode gerar rapidamente um conjunto estocástico de redes plausíveis a partir de informações geológicas básicas, que também podem ser usadas como entrada para modelos de fluxo apropriados para o carste. Este artigo apresenta uma implementação de código aberto e fácil de usar por meio do pacote Python pyKasso e descreve sua aplicação em um local de estudo de longo prazo geologicamente complexo e bem mapeado: o sistema cárstico alpino Gottesacker (Alemanha/Áustria). O fluxo de águas subterrâneas neste sistema é excepcionalmente bem compreendido a partir de investigações espeleológicas e testes de traçadores. A formação de condutos ocorre principalmente na base do aquífero cárstico, seguindo sinclinais profundas. Embora as tentativas anteriores de reproduzir a rede de conduítes neste local produzissem mapas de rede implausíveis, o pyKasso rapidamente gerou redes fiéis ao sistema de conduítes conhecido. No entanto, o modelo só foi capaz de gerar essas redes realistas quando as conexões de entrada-saída do sistema foram corretamente atribuídas, destacando a importância de emparelhar esforços de modelagem com testes de rastreadores de campo. Portanto, também é apresentado um método de conjunto de modelos, para otimizar os esforços de campo, identificando os testes de traçador mais informativos a serem realizados.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Motivation and context
Numerical modeling is a powerful, widely used tool for the understanding and management of groundwater resources; however, applying numerical flow models in karst aquifers is challenging (Scanlon et al. 2003; Jeannin et al. 2021). Unlike in porous aquifers, groundwater flow in karst occurs primarily through conduits dissolved into a rock matrix. The matrix can also include fissures and intergranular pores, resulting in double- or even triple-porosity systems, which leads to complex, heterogeneous behavior that is highly dependent on the spatial structure of the conduit network (Ford and Williams 2007).
Existing approaches to modeling groundwater flow in karst aquifers generally take a lumped, distributed, or semidistributed approach (Kovács and Sauter 2007; Jeannin et al. 2021). Lumped models transfer an input timeseries (typically recharge/precipitation and snowmelt) into an output timeseries (typically spring discharge) at the scale of the entire karst system, without explicitly describing the conduit network (Hartmann et al. 2014). This approach has the advantage of being able to represent the overall water balance and dynamics of the system using minimal data, but does not capture spatial variability in hydraulic head or directions and rates of groundwater flow within the aquifer (Scanlon et al. 2003). Distributed models discretize the model domain and apply spatially dependent parameters to each cell, thereby enabling them to simulate the spatial dimensions of groundwater flow in triple-porosity systems. To achieve this, they require the spatial distribution of matrix and conduit geometry and hydraulic properties, which produces far more data than is needed by lumped models (Hartmann et al. 2014). Semidistributed models take an intermediate approach, simulating flow through a spatially distributed pipe network representing the conduits, but simplifying matrix flow, either by neglecting it entirely or by representing it as a lumped entity (Jeannin et al. 2021). This makes them most appropriate for dual-porosity karst systems where the matrix porosity is low.
The often-prohibitive data requirements of distributed and semidistributed models have limited their use primarily to either synthetic cases or well-understood, extensively-studied systems such as the one presented in the second part of this paper (Chen and Goldscheider 2014). Even in well-studied systems, the conduit network is impossible to fully map, because small-diameter conduits (<0.5 m) are inaccessible and difficult to detect by geophysical methods (Jaquet and Jeannin 1994). A relatively new approach for overcoming this difficulty is the use of karst conduit evolution models to generate probable maps of the conduit network based on the geologic setting of the study system (Borghi et al. 2012). These simulated networks then serve as input for distributed groundwater flow models, reducing the data requirements of the modeling project.
Previous work reveals two significant hurdles to using conduit evolution models as input to distributed groundwater flow models: (1) uncertainties in the conduit network structure contribute significantly more to prediction uncertainty than uncertainties in the hydraulic parameters (Refsgaard et al. 2006; Fandel et al. 2021); and (2) existing conduit evolution models either are extremely computationally and data intensive—if they solve the physical and chemical equations driving speleogenesis (Borghi et al. 2012; Dreybrodt et al. 2005)—or yield hydrogeologically implausible networks in complex geologic settings (Fandel et al. 2021). The strong influence of conduit network structure on groundwater flow and transport predictions means that relying on a single conduit map does not adequately capture the range of possible behaviors in a system. However, this problem can be addressed by using a multimodel approach, in which an ensemble of competing structures is used to generate a range of predictions (Enemark et al. 2019), following the method of multiple working hypotheses advocated for by Clark et al. (2011). This method was applied to karst systems in a previous publication (Fandel et al. 2021). The topic of the present publication is the second hurdle: generating realistic conduit networks using fewer data and computational resources than existing models.
Challenge
The goal of this paper was to develop a karst conduit network simulator that yielded hydrogeologically plausible networks while requiring minimal data and computational power, so that it could be run numerous times to generate an ensemble. Six criteria for plausibility were defined, which the simulated networks needed to meet, based on published conceptualizations of cave formation processes (Audra and Palmer 2011):
-
1.
Conduits should connect chosen inlets to outlets by the most efficient path.
-
2.
Conduits should seek the steepest path down the hydraulic gradient towards the outlets.
-
3.
Conduits should seek more soluble formations and avoid less soluble formations.
-
4.
Conduits should seek high-conductivity features such as fractures.
-
5.
Newly-forming conduits should seek to merge with existing conduits.
-
6.
Conduits should connect into a cohesive network linking multiple inlets and outlets.
Previous work
The evolution of karst conduit networks can be described by several different conceptual models, depending on the geologic and hydrologic setting. Generally, solutional conduit networks form through a positive feedback loop in which greater discharge along one path results in faster enlargement, thus capturing more discharge and further increasing the enlargement rate, and so on. However, the shape of the resulting conduit network also depends on (1) the type of initial porosity (intergranular, bedding plane partings, or fractures), (2) the source of solutionally aggressive water (focused surface recharge, diffuse recharge through an overlying unit, or deep-seated hypogenic sources), (3) whether the conduit is forming under vadose (unsaturated) or phreatic (saturated) conditions, and (4) the amount of time that has passed since solutional enlargement began. These factors combine to produce five common network morphologies: branchwork systems, network systems, anastomotic systems, spongework/ramiform systems, and single-passage systems (Palmer 1991). When generating simulated conduit networks, care must be taken to choose a method appropriate for the geologic and hydrologic conditions being modeled.
Existing methods of generating karst conduit network maps generally rely either on manual delineation based on a conceptual model of the aquifer (Jeannin et al. 2013), simulation of hydrochemical dissolution processes (Duan et al. 2020; Dreybrodt et al. 2005), or geostatistical approximations based on simplified, spatially distributed representations of the karst medium (Pardo-Igúzquiza et al. 2012). While the first two approaches yield realistic conduit networks and can be applied in a wide range of hydrogeologic settings, they tend to lead towards a single conceptual model of the karst system, which may obscure important structural uncertainties (Enemark et al. 2019). Most chemistry-based simulations are also extremely computationally intensive and require knowledge of past conditions during which the conduits formed, limiting their application to advancing the understanding of basic processes governing speleogenesis in more hypothetical or schematized systems (Dreybrodt et al. 2005; de Rooij and Graham 2017). For the purposes of efficiently generating numerous possible conduit networks in real geologic settings with limited data availability, stochastic geostatistical approaches remain one of the most viable options.
Stochastic conduit generation models can be divided into structure-imitating and process-imitating approaches (de Rooij and Graham 2017). Structure-imitating models use geostatistical methods such as diffusion-limited aggregation (Pardo-Igúzquiza et al. 2012) or nonlooping invasion percolation (Ronayne 2013) to reproduce the structure of the networks. Process-imitating approaches mimic speleogenesis without solving the underlying physical and chemical reaction equations, instead using iterative positive-feedback mechanisms. As a result, they yield maps of the conduit network at a certain point in time (generally after the system has reached a stable maximum enlargement rate), but provide little insight into how such a network came to exist. Examples of this approach include lattice-gas automata (Jaquet et al. 2004), heuristic erosion potential functions (Lafare 2011), and fast-marching algorithms (Borghi et al. 2012).
This study focuses on improvements to the process-imitating fast-marching approach, which has the advantages of being designed to model real study sites constrained by the regional geologic setting, being able to be conditioned to available data but not requiring in-depth initial data availability, and being computationally efficient (Borghi et al. 2012). While this approach is able to recreate both vadose and phreatic settings, it is not applicable to karst systems in which the presolutional porosity is primarily intergranular, or where the source of water is primarily diffuse or hypogenic inflow—such systems tend to form anastomotic, ramiform, or spongework morphologies, and make up only a small percentage of all cave systems worldwide (Palmer 1991). This approach is also not appropriate for the purposes of modeling single-passage systems early in their formation, nor is it intended to simulate the geochemical dissolution reactions that drive speleogenetic processes. The fast-marching approach is most appropriate for branchwork caves, which, in number and in aggregate length, exceed all other cave morphologies combined (Palmer 1991). Branchwork caves form in settings where the source of presolutional porosity is dominated by fractures and bedding planes, and where groundwater flow through caves originated primarily from concentrated surface recharge through features such as sinkholes and sinking streams. While it may be possible to adapt this approach to network systems, the second-most-common morphology worldwide, both the synthetic example and the real karst system presented in this paper are branchwork systems, and no testing has yet been done on network systems.
Isotropic fast marching
The initial fast-marching approach presented by Borghi et al. (2012), known as the Stochastic Karst Simulator (SKS), mimics conduit evolution based on the assumption that water will follow a minimum-effort path within the boundaries of the karstifiable units, as computed by an isotropic fast-marching algorithm (Sethian 1996). Fast-marching algorithms are a family of numerical techniques originally designed to track the evolution of expanding interfaces—such as the surface of a growing soap bubble, or the front wave of an earthquake—through a medium (Fig. 1a). The medium may be heterogeneous, in that the expanding front can travel more or less easily through different regions, but it must be isotropic, in that the ease of travel is the same in each direction. Fast-marching algorithms address the problem by calculating a map of arrival times based on the map of travel cost, where each location on the map is assigned a value indicating how long it takes to get from the point of origin (e.g. the center of a bubble or the epicenter of an earthquake) to that map location (Sethian 2006; Fig. 1b). The shortest path from any given point to the point of origin can then be calculated by following the gradient of the travel time map (Fig. 1c).
A simple example of isotropic fast marching. a An expanding front travels away from the point of origin through a heterogeneous medium. b The time at which the front reaches each cell in the domain is recorded, resulting in a travel time map. c Based on the travel time map, the fastest path from any point to the point of origin can be calculated
To apply fast-marching methods to karst conduit generation, the outlet draining the system is used as the starting point of the front propagation, and each model cell is assigned a travel cost based on the geology (Borghi et al. 2012). Karstifiable formations have a lower travel cost than nonkarstifiable formations and fractures have a lower travel cost than matrix, etc. The travel time map is then used to calculate the fastest path from each inlet to the system (e.g. dolines or sinkholes) to the outlet, resulting in a network of conduits converging at the outlet.
Isotropic fast marching works well in many settings, but cannot account for local structural controls on conduit orientation such as when karst development follows a stratigraphic slope. Furthermore, it requires simulating the saturated and unsaturated zones separately to obtain a correct representation (Borghi et al. 2012). In the extensively studied Gottesacker karst system in the German-Austrian Alps, an ensemble of 100 networks generated using the isotropic fast-marching method yielded only a single plausible configuration—all other networks in the ensemble included conduits climbing up and across large anticlines, rather than following synclinal axes, as would be expected from groundwater flowpaths controlled by the dip direction of the underlying impermeable unit (Fandel et al. 2021). To demonstrate the problem, consider a simple synthetic system, consisting of a single outlet draining a valley. There are only three geologic units—highly karstifiable limestone folded into a syncline along the valley axis, underlain by nonkarstifiable shale, with an obstacle in the form of a nonkarstifiable granite intrusion. Five inlets are randomly distributed across the upper part of the valley (Fig. 2). In this example, conduits would be expected to travel towards and along the synclinal axis before reaching the outlet (Fig. 2a). However, the isotropic fast-marching algorithm returns conduits that instead follow the most direct path to the outlet as the crow flies (Fig. 2b).
Synthetic example problem: a simple valley with three geologic units, drained by a single outlet at the contact between the karstifiable unit and the underlying marl. a A 3D block view of the valley. b A 2D map view of the conduit network expected to form based on synclinal geologic structure. c The 2D conduit network returned by the isotropic fast-marching algorithm
Other limitations of the existing fast-marching-based conduit-model implementation, are that it requires treating the unsaturated and saturated zones separately, which is computationally inefficient. Furthermore, the SKS code is written as a procedure-oriented code in the proprietary MATLAB language, limiting its widespread applicability, and it lacks some useful features—for example, the code does not easily allow assigning specific inlets to specific outlets, which limits the use of tracer test data to condition and/or test the model.
New approach to karst modelling: the anisotropic fast-marching algorithm
This paper addresses the limitations of existing stochastic karst conduit generation models with an open-source Python-based tool for generating ensembles of conduit network maps in complex geologic settings using anisotropic fast-marching algorithms. The new tool, pyKasso, is so named partly based on the acronym python karst stochastic simulator, and partly because, like the great painter, it aims to extract only the lines that make up the essence of a thing. It relies on an object-oriented code structure described in detail by Miville (2020) and the Adaptive Grid Discretization package, described by Mirebeau and Portegies (2019), which implements a suite of isotropic and anisotropic fast-marching algorithms. The karstnet package is used to compute statistical indicators for comparing karst networks, described in Collon et al. (2017), and to analyze the quality of the results. By combining these features, pyKasso enables quick iteration, stochastic fracture network generation, conditioning to field observations, calculation of network statistics, and visualization and storage of results.
The principles of the approach used in this paper were introduced by Borghi et al. (2012). For the sake of brevity, the underlying mathematical formulas and computations are therefore not described in detail here. Instead, this paper focuses on novel work: the use of anisotropic fast-marching.
Anisotropic fast marching
Anisotropic fast marching allows the ease of travel through a medium to vary by direction. It can be used, for example, to calculate optimal paths for remote-controlled-undersea-exploration robots operating in strong currents—traveling with the current is easier than traveling against it (Garrido et al. 2020). In the context of karst systems, the anisotropy field informs the preferential direction of conduit formation at any given location (Fig. 3). Conduits should form in the direction of the maximum downward hydraulic gradient, towards the outlet (Fig. 2). For shallow, unsaturated karst systems such as the example presented here, the hydraulic gradient generally coincides with the topographic gradient. The anisotropy field is therefore generated based on a proxy such as the topography of the lower boundary of the karstifiable unit. These data are converted into a vector field, from which the maximum downward gradient at each location is calculated.
Anisotropic fast-marching. a An expanding front travels away from the point of origin through a heterogeneous, anisotropic medium. b The time at which the front reaches each cell in the domain is recorded, resulting in a travel time map. c Based on the travel time map, the fastest path from any point to the origin can be calculated. Note that the fastest path through an anisotropic medium may not be the same as the fastest path through an isotropic medium
Implementation
Following Borghi et al. (2012), to simulate karst conduit networks, the spatially distributed properties of the medium must be defined, the inlets and outlets of the system identified, and multiple generations of conduit formation iterated over using fast-marching. The primary advance in this paper is the use of anisotropic fast marching. The code structure consists of several classes describing different components of the model (grid, points, geology, fractures, karst network, etc.), each with built-in methods. The result is an efficient code that allows rapid iteration over multiple versions of the same model, without having to reload all inputs and variables at each iteration (Miville 2020). The code and a complete set of example input data and files can be found in the pyKasso GitHub repository (GitHub 2021).
Inputs
The main inputs are a geologic model, in this case, constructed using the implicit method described in de la Varga et al. (2019), indicating which lithologic unit is present in each cell, the coordinates of the known inlets and outlets to the system, the statistics describing the fracture network—discussed in more detail in Bonnet et al. (2001)—and the relative travel costs associated with different geologic features. The anisotropy is expressed by computing a vector field derived from the gradient of a potential—see section ‘Initial calculations’ for more detail. Travel costs are given in reference to travel in the direction parallel to the vector field (maximum gradient) in each cell. A cost ratio is therefore also needed, to calculate the travel cost perpendicular to the gradient.
In the synthetic example, the problem is further simplified to consider only a two-dimensional (2D) geologic map, with the elevation of the lower boundary of the limestone unit as the scalar field (Fig. 4). The fracture statistics are given in Table 1, and the travel costs in Table 2.
Initial calculations
First, pyKasso generates a set of arrays describing the medium through which conduits will evolve (Fig. 5). A discrete fracture network is stochastically generated independent of the travel cost map or the anisotropy field, based on the density, orientation range, and length range of each fracture family. A cost map is then created by calculating the difficulty with which a conduit could traverse each cell. Low-cost regions are easy for conduits to form in, while high-cost regions are more difficult and are therefore avoided by evolving conduits. Generally, the karstifiable unit should have a lower travel cost than nonkarstifiable units, fractures should have a lower travel cost than the surrounding matrix, and existing conduits should have the lowest travel cost. The travel cost also increases with increasing elevation, to discourage conduits from traveling upwards. Finally, a vector field describing the anisotropy of the system is calculated based on the input scalar array. The scalar array represents a crude approximation to the hydraulic potential surface. In shallow, unsaturated systems, several proxies may be used to represent this surface: the land surface topography, the topography of the bottom of the karstifiable unit, or the potential array returned by geologic modeling software such as GemPy (de la Varga et al. 2019) or GeoModeller (Calcagno et al. 2008). In this example, the lower boundary of the limestone unit is used.
Iteration structure
Although the entire conduit network could be simulated in a single iteration, this approach rarely yields realistic results. In real karst systems, the network often has a hierarchical structure. In many cases, there are known connections between certain inlets and outlets. Occasionally, the purpose of the modeling is to reconstruct different phases of karst development. In all of these situations, it is preferable to iterate over several phases of conduit formation, updating the travel cost map and travel time map at each step. The iteration structure of pyKasso is highly flexible to accommodate a range modeling needs.
Conduit formation can be separated into stages by outlet, by inlet, or a combination of the two. If there are multiple outlets from the system, each outlet can be given its own iteration and assigned specific inlets (or the order may instead be shuffled). Conduits will then form in the first iteration from the first set of inlets to the first outlet, the cost map will be updated to reflect the new low-cost travel paths along the new conduits, and the next iteration will model the conduits from the second set of inlets to the second outlet, and so on, stopping when all inlets and all outlets have been accounted for. Within the outlet iterations, it is also possible to iterate over the set of inlets assigned to that outlet. Each inlet can be run in its own iteration, or inlets can be grouped into stages, with several inlets per iteration (Fig. 6). Each iteration stops once the conduits departing from each inlet reach their assigned outlet. It is already apparent at this stage that the conduits are behaving as expected, based on Fig. 2a.
Conduit formation over three rounds of inlet iteration. After each iteration, the cost map is updated so that cells containing a conduit have a very low travel cost, attracting conduits during later iterations and creating a hierarchical branching structure. A similar process allows for iteration over multiple outlets
The conduit paths generated by the fast-marching algorithm all go the entire way from inlet to outlet, overlapping when they are attracted to the path of an older conduit, resulting in a collection of disconnected paths rather than a single cohesive network. A special function is required within pyKasso to connect the paths into a network and convert it into a sequence of nodes and edges composing a graph. This function iterates over each path and follows it towards the outlet. At each point on the path, it adds a node and links it to the previous node by an edge. If there is already a node in that location, it links the existing node to the previous node and skips to the next point (see Appendix, which describes the process of the path to network conversion).
Outputs
At the end of the model run, pyKasso outputs a karst network object, which stores the conduit network as a graph composed of nodes and edges (Fig. 7a). The network object also stores a simplified version of the graph with intermediate nodes removed. The simplified network is useful for flow modeling, where the reduction in computation time gained from reducing the number of nodes may outweigh the loss of high-resolution spatial information that was contained in the original network. Figure 7b, and a set of statistical metrics (Collon et al. 2017) describing the geometry and topology of the network, were all calculated using the karstnet package v.1.1.0 (Table 3). Notice that the network returned by pyKasso using anisotropic fast marching is much more reasonable than the network returned using isotropic fast marching (Fig. 8). Although inlet iteration can create the expected branching structure in an isotropic simulation, new conduits can run uphill to join existing conduits, because the algorithm has no information about the structure and orientations of the base of the aquifer (Fig. 8a). The anisotropic simulation, by contrast, results in conduits that follow the gradient to merge with one another (Fig. 8b).
Influence of parameters on model results
The simple one-valley system presented in the preceding can be modified to demonstrate the influence of the various options and parameters available in pyKasso. Five are highlighted here: inlet/outlet assignment, fracture travel cost, conduit travel cost, and cost ratio. Two other ways to use pyKasso are also demonstrated: to simulate a vertical cross-section of the system in which conduits form through both the unsaturated and saturated zones, and to generate probability maps of conduit locations through iteration.
-
1.
Inlet/outlet assignment. While the outlets draining a karst system are usually easily identifiable (springs), not every karst system has distinct inlets corresponding to hydrogeologic features identifiable in the field such as sinkholes, sinking streams, ponors, etc. In many cases, the entire land surface acts as a diffuse recharge area. Inlets can therefore be simulated in one of three ways: (1) if specific inlet locations are known, they can be directly specified as inputs to the model, (2) if the entire area is receiving diffuse recharge, inlets can be randomly generated across the recharge area, and (3) a combination of known inlet locations and randomly generated inlets can be used. Specific inlets or groups of inlets can then be assigned to specific outlets (again, either explicitly specified if the connections are known from field data such as tracer tests, or randomly assigned if not). To demonstrate the importance of inlet/outlet assignment, a second, randomly generated outlet is added to the example system. By default, the inlets will be assigned to the outlets in the order they are given in the model input, giving the same result every time. Shuffling the order, however, can result in strikingly different networks (Fig. 9). In this example, the five inlets are randomly split between the two outlets—two to one outlet, three to the other. The order in which the outlets are created is indicated by the outlet number. All conduits going to a given outlet are simulated in a single iteration (though one could easily choose to simulate each inlet in its own iteration as well). Outlet 0 is created first, and all inlets labeled 0 go to outlet 0. Outlet 1 is created next, and all inlets labeled 1 go to outlet 1. While randomly pairing inlets and outlets can be useful in exploring a wide range of possible networks (Fig. 9a,b), caution is needed, because the networks can quickly become implausible if an inlet that would not logically connect to a certain outlet is accidentally assigned to it (Fig. 9c)—the fast-marching algorithm will attempt to connect the inlet to the outlet, no matter how unrealistic the resulting conduit. The two outlets may also be disconnected (Fig. 9b), because the algorithm has no reason to connect them. If a connected network draining to both outlets is desired, an inlet connected to the lower outlet can be co-located with the upper outlet (in Fig. 9b, for example, this would connect outlet 0 to outlet 1).
-
2.
Fracture travel cost. The cost of travel through fractures is by default set higher than the cost of travel through conduits, but lower than the cost of travel through the karstifiable matrix (Fig. 10b). A lower travel cost will encourage conduits to follow fractures more closely at the expense of merging with existing conduits (Fig. 10a), while a higher travel cost simulates cemented fractures that conduits will try to avoid (Fig. 10c).
-
3.
Conduit travel cost. The cost of travel through the conduits controls how strongly younger conduits will be attracted to older conduits (Fig. 11). By default, the conduit travel cost is set lower than any other feature. If the conduit cost is dramatically lower than the travel cost through any other feature, younger conduits will take unrealistic routes through obstacles or upgradient in order to reach older conduits more quickly (Fig. 11a). If the travel cost is only slightly lower through conduits than through other features, younger conduits will seek to merge with older conduits through realistically branching paths (Fig. 11b). If the conduit travel cost is higher than the travel cost through the surrounding rock, conduits will seek to avoid each other (Fig. 11c).
-
4.
Travel cost ratio. The travel cost ratio is the travel cost parallel to the gradient over the travel cost perpendicular to the gradient (Fig. 12). If the ratio is one, the system behaves as though it were isotropic. If the ratio is less than one, the travel cost is lower parallel to the gradient, and conduits will try to follow the direction of the steepest gradient (Fig. 12a,b). The smaller the ratio, the stronger the influence of the anisotropy field on conduit formation, and the less likely conduits will be to deviate from the steepest path. If the ratio is greater than one, the travel cost is lower perpendicular to the gradient, and the conduits will try to traverse along contour lines (Fig. 12c).
-
5.
Simulating the unsaturated zone. Thus far, the test system has been considered only in map view, using the lower boundary of the limestone unit to generate an anisotropy field. However, the system can also be modeled in cross-section, to simulate conduit development in the unsaturated zone. Generally, mostly vertical conduits are expected to form, descending from the surface inlets to the water table, then making their way to the outlet by the most direct path. Previously, to achieve this with the isotropic Stochastic Karst Simulator, the unsaturated zone was simulated first, with the target being the entire water-table surface rather than the system’s outlet, then the saturated zone was simulated separately, with the inlets being replaced by the endpoints of the unsaturated zone conduits. While this approach works, it is computationally inefficient. Instead, an anisotropy field can be created to impose a strong downward gradient in the unsaturated zone, while leaving the saturated zone unaffected (Fig. 13a). The resulting conduits travel mostly downwards until they reach the water table, at which point they curve toward the outlet (Fig. 13b).
-
6.
Probability maps. Part of the appeal of using fast-marching methods for conduit network simulation is computational efficiency. If little is known about the karst system being modeled, tens or hundreds of networks can quickly be generated to establish an initial range of possibilities (Fig. 14). While each of the networks in this initial ensemble has a low probability of reproducing the true network, taken all together and displayed visually, they can still provide useful information. For example, they may be used to identify potential hazard zone boundaries or to guide additional, carefully targeted, data collection such as tracer tests, that would allow the rejection of networks that do not match the new information.
Influence of inlet/outlet assignment and iteration order on the final network structure. The number next to each outlet indicates the order in which the outlet was created. The number next to each inlet indicates which outlet that inlet was assigned to. The arrows indicate the direction of conduit formation. a An interconnected network with intersecting conduits. b Two disconnected networks. c A misleadingly plausible-looking network with loops that nevertheless involves a path crossing the syncline and climbing back up to outlet 0 via an existing conduit from the first iteration—this example highlights the importance of inlet/outlet assignments
Influence of the travel cost through fractures on the final network structure. a A fracture travel cost equal to or lower than the conduit travel cost results in conduits closely following fractures. b A fracture travel cost between the conduit cost and the matrix cost results in conduits following fractures only when an existing conduit is not available to follow. c A fracture travel cost higher than the matrix travel cost results in conduits avoiding fractures
Influence of the travel cost through conduits on the final network structure. a A very low conduit travel cost results in younger conduits traversing obstacles or moving upgradient to rejoin existing conduits. b A conduit travel cost only slightly lower than the fracture or matrix cost results in younger conduits seeking older conduits when possible, forming a realistically branching network. c A conduit travel cost higher than the surrounding matrix results in conduits avoiding each other
Influence of the travel cost ratio on the final network structure. a A cost ratio much lower than one results in conduits that follow the steepest gradient almost to the exclusion of all else, ignoring fractures or obstacles to do so. b A cost ratio slightly lower than one results in conduits that prefer to follow the gradient, but will also avoid obstacles or follow fractures if they offer a less resistant path. c A cost ratio greater than one results in conduits that follow contours, attempting to form perpendicular to the gradient
Application to a real-world karst system
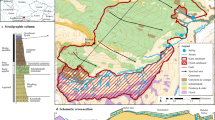
The new approach was tested on a real, complex example: the extensively studied Gottesacker karst system in the German/Austrian Alps (Goldscheider 2005). This system consists of a series of plunging synclines and anticlines draining to the Schwarzwasser Valley, which cuts roughly perpendicularly across the fold axes. The karst aquifer lies north and northwest of the valley in a limestone unit locally overlain by sandstone and younger units, and underlain by nonkarstifiable marl and older units. Three major springs drain the system. South of the valley, nonkarstifiable flysch lithology prevents conduit development—for a full description of the geologic setting, see Goldscheider (2005). Several other geologic units and small springs are present, but for the purposes of generating conduit network maps, the geology is represented by a simplified model focused on delineating the boundaries of the karstifiable limestone unit (Fig. 15).
A simplified geologic model of the Gottesacker karst system (Fandel et al. 2021). The karst aquifer is located in the limestone unit, and drains to the three springs in the lower part of the system. The model quality is fairly good within the karst catchment (north of the stream), but is poorer south of the stream due to lower data resolution in that area. b Location of the study site within central Europe. c Schematic cross-section of the fold and drainage structure (after Goldscheider 2005)
Numerous tracer studies (Goldscheider 2005; Goeppert and Goldscheider 2008; Goeppert et al. 2020) have yielded a good understanding of the conduit network, which has been used successfully for previous groundwater flow modeling efforts (Chen and Goldscheider 2014) (Fig. 16a). The outlets in this flow model correspond to the three major springs draining the system, while the inlets correspond either to tracer injection sites or to locations selected based on a conceptual understanding of the system. However, efforts to model the conduit system using the isotropic Stochastic Karst Simulator yielded networks that, while able to reproduce observed discharge dynamics at the three major springs, did not match the spatial configuration of the known network (Fandel et al. 2021; Fig. 16b).
a Expected conduit network in the Gottesacker karst system, as determined by tracer tests, field observations, and previous modeling work (after Chen and Goldscheider 2014). A major conduit parallels the stream along the valley, and is fed by a set of four conduits draining the upper part of the aquifer along synclinal axes, which coincide roughly with the major surface valleys. b A representative sample of networks returned by previous modeling efforts using the isotropic Stochastic Karst Simulator (Fandel et al. 2021). Note that they do not follow synclines, and differ widely from the expected network
To simulate the Gottesacker karst system with pyKasso, the problem is considered in a simplified form—in two dimensions, using a map view of the geologic model, the inlet and outlet locations used in previous flow modeling efforts, the fracture statistics reported in Goldscheider (2002), and the surface topography as a proxy for the hydraulic potential field (because in vadose systems the topographic gradient is an acceptable representation of the hydraulic gradient, and in this system, the surface topography roughly parallels the lower surface of the karstifiable unit, with a few localized exceptions). A few iterations with different inlet/outlet assignments immediately yielded a result quite visually similar to the expected network (Fig. 17).
To test the influence of changing the simulation parameters, two parameters of interest were selected: the fracture network, and the inlet/outlet assignments. An ensemble was created by iterating over two sets of 10, 50, and 100 simulations. In the first, only the fracture network was regenerated at each run (Fig. 18a). In the second, the inlet/outlet pairings were also randomly shuffled for each run (Fig. 18b). The resulting probability maps suggest that inlet/outlet assignment has a much stronger influence than the fractures over the structure of the simulated conduit networks, and that varying the inlet/outlet assignment order adds diversity to the model ensemble even with a small number of realizations. However, random inlet/outlet pairings also introduce networks that are geologically implausible—for example, conduits that climb up and over anticlines. Caution and validation with field data are therefore needed when using this feature. Many other parameters could also be modified to add variety to the resulting conduit networks: the relative travel costs of different features, the travel cost ratio, the surface used to generate the anisotropy field, or the fracture network statistics, for example.
Influence of fracture network and inlet/outlet assignment on simulated network structure. a When the inlet/outlet assignments are kept fixed, the fractures add only a small amount of variability to the conduit network structure. b When the inlet/outlet assignments are randomly shuffled, the ensemble is more diverse, but includes many networks that do not resemble the known network and many networks that are structurally implausible
In addition to visually assessing the similarity of the simulated networks to the expected network, their statistical similarity was compared (Table 4). For both groups of 100 simulations—one with variability due only to the fracture network, the other with variability due to both the fracture network and the inlet/outlet assignment order—the mean value and standard deviation of the statistical metrics returned by pyKasso were calculated, and compared to the values of each metric for the base model.
Several complicating factors must be considered regarding the application of these metrics in this example. First, the expected network map is simplified to only the major branches and connections, and does not represent the detailed network geometry; therefore, only topological (rather than geometric) indicators were considered. Second, the mean number of nodes in simulated networks was more than double the number of nodes in the expected network, even after the simulated networks were simplified. This is due to the difficulty of automating graph simplification—the simulated networks were automatically simplified from the complex rendering returned by pyKasso, while the expected network was hand-drawn and was already very simple. The difference in number of nodes does not indicate actual discrepancies in complexity of the networks. It does, however, mean that the number of nodes and the average shortest path length are applicable only when comparing between networks that were generated using methods with similar resolutions (in terms of the number of nodes and edges per length of conduit); thus, networks simulated with pyKasso can be compared to each other, but not to the expected network. Third, the simulated networks sometimes include loops, a common feature of real karst systems, which increases the value of the mean node degree. The simplified expected network, however, does not include loops (the real conduit network undoubtedly has them, but their locations are difficult to determine without firsthand cave exploration). The mean node degree of the simulated networks is therefore not easily comparable to that of the expected network. These multiple considerations indicate that caution is required when making statistical comparisons between the expected network and the simulated network, but comparisons across simulated networks remain of interest.
Since the ensemble of simulated networks with fracture-induced stochasticity only (ensemble A) was less visually diverse than the networks simulated with fracture-induced and inlet/outlet assignment-induced stochasticity (ensemble B), it might be expected that the standard deviation of the statistical metrics for ensemble B would be higher. This was indeed the case, with the standard deviations 8–70% higher than in ensemble A. However, a simple two-sample t-test indicated that the two ensembles were only significantly statistically different from each other according to two metrics: central point dominance and mean degree (both higher for ensemble B). This is likely because shuffling the inlet/outlet connections tends to result in more loops and intersections within the network.
Since the simulated networks in ensemble A were also more visually similar to the expected network than the simulations in ensemble B, one might expect the mean statistical metrics for ensemble A to also be more similar to the expected network. However, while this assumption generally held true, the differences were slight, and, as already explained, comparing networks with such different levels of complexity is inadvisable in this case. Therefore, this study does not draw any conclusions about structural similarity between the expected and simulated networks based on metrics of statistical similarity.
Discussion and conclusion
Advantages and limitations
This paper demonstrates that using anisotropic fast marching to generate stochastic simulations of karst conduit networks has several advantages. Most of the previous advantages of the Stochastic Karst Simulator developed by Borghi et al. (2012) remain—compared to existing conduit network generation models, less input data is required, and the algorithm is computationally efficient. As compared to the original SKS algorithm (based on isotropic fast marching), the use of anisotropic fast marching yields karst networks that better follow geological structures such as synclines or dipping layers, and are therefore more realistic. Furthermore, anisotropic fast marching can represent the unsaturated zone in a simple manner. This simplifies the algorithm and makes the calculations more efficient. These novel features are implemented in the pyKasso Python package, which is open-source and freely available.
These characteristics make this approach widely applicable to modeling a variety of karst systems where minimal information is available and resource limitations restrict the time, software, and computational power that can be dedicated to a modeling effort. It is useful for generating a range of hypotheses as to the conduit network structure, which can be used as a starting point for further study, or to guide data collection. It is also effective in systems with strong elevation gradients and a complex geologic structure, particularly where conduit formation is structurally controlled.
The approach documented here is not, however, an accurate representation of the speleogenetic process. It does not simulate the physical and chemical reactions driving conduit formation, nor does it simulate any internal conduit properties such as diameter or roughness. If the inlet/outlet pairings are not well understood, it is likely to generate many networks that differ significantly from the true conduit network. It is therefore not recommended when the goal of the modeling effort is to generate a single most-probable network. If the goal is to generate networks to serve as inputs to a flow model, it is strongly recommended that an ensemble approach be used, in which flow simulations are run on many competing possible networks.
Possible application: guiding data collection
In the ensembles tested in this study, the inlet/outlet assignment has a strong influence on the resulting network, and certain inlet/outlet pairings yield geologically implausible networks—when, for example, a randomly assigned pairing forces a conduit to connect an inlet to an outlet in a different subwatershed. The ability to control the network structure based on inlet/outlet pairings is an important feature, because inlet/outlet pairings are relatively easy to test in the field using tracer methods, and do not require continuous flow monitoring or additional flow or transport modeling in order to be useful—for example, in the case of the Gottesacker karst system, if the network configuration and inlet/outlet connections were not already known, the simulated network ensemble would encompass several dominant possibilities (Fig. 19; Table 5).
Some of these possibilities should be rejected immediately because they are geologically implausible—for example, in No. 4b (Table 5), the conduits leading from inlet 4 to merge with the conduits from inlet 3. These conduits are the result of random inlet/outlet pairing assigning inlet 4 to outlet 0 or outlet 1, thereby forcing a connection across the anticline and the nonkarstifiable marl unit that lie between inlet 4 and these two outlets. Each of the remaining possibilities can be tested in the field with tracer methods, in order of informativeness. Inlet 3, for example, appears to have a roughly equal number of iterations with conduits following the two main paths—Nos. 3a and 3b (Table 5)—which merge with the main conduit above and below outlet 1, respectively. Previous tracer studies found that in fact the correct path connects above outlet 1; however, if there was no prior information about the site, and if limited resources restricted the number of tracer tests that could be performed, inlet 3 would be a good choice to test first, as it would allow the rejection of a large number of networks and provide information about the source of water at outlet 1. Conversely, there would be little point in injecting a tracer at inlet 0 or inlet 4, because nearly all of the geologically plausible iterations agree on the path of the conduit departing from those inlets. Data collection needs can therefore be reduced from five tracer tests to three (Fig. 19).
In this example, a tracer injected at inlet 3 would be found at outlets 1 and 2, allowing all networks in which inlet 3 is not connected to outlet 1 to be rejected. A similar process would narrow down the model structure based on tracer tests at inlets 1 and 2.
If not enough resources were available to perform any additional tracer tests, the model ensemble would still be useful in guiding decision-making because it identifies a range of possibilities to consider and enables their presentation in an easily digestible visual format. Potential hazard zones (Fig. 19) can be identified from the conduit probability map: these are zones that the model ensemble suggests are likely to have a subsurface conduit network present and therefore are potentially at higher risk for sinkhole hazards, potential contamination pathways, etc. Identifying these zones could be useful, as one example, in choosing the location of future infrastructure projects.
Future work
The anisotropic fast-marching method, combined with the code structure of pyKasso, allows for a wide range of applications to karst modeling problems. One logical next step is to test flow through the simulated conduit networks. The node/edge data structure returned by pyKasso to describe the network can be easily used as input to a distributed flow model that can consider discrete flow structures and can therefore be used in karst—two examples of such models are MODFLOW-CFP (Reimann and Hill 2009) or SWMM (Rossman 2015). The next logical step is to simulate solute transport as well as flow—considering transport can reduce the nonuniqueness of simulated behaviors significantly more than flow modeling alone (Kavousi et al. 2020; Sivelle et al. 2020). However, flow and transport models require internal information about the conduits such as diameter and roughness. Creating an add-on to pyKasso that could estimate these parameters would therefore be a useful next step. Because groundwater flow models are computationally intensive, it would also be interesting to test whether any statistical metrics describing the network geometry and topology are correlated with how well the network is able to reproduce observed flow patterns such as discharge at the system outlet. Finally, although the examples in this paper are two-dimensional, a 3D version of pyKasso will be released in the near future.
References
Audra P, Palmer AN (2011) The pattern of caves: controls of epigenic speleogenesis. Géomorphol Relief Process Environ 17:359–378. https://doi.org/10.4000/geomorphologie.9571
Bonnet E, Bour O, Odling NE, Davy P, Main I, Cowie P, Berkowitz B (2001) Scaling of fracture systems in geological media. Rev Geophys 39:347–383. https://doi.org/10.1029/1999RG000074
Borghi A, Renard P, Jenni S (2012) A pseudo-genetic stochastic model to generate karstic networks. J Hydrol 414–415:516–529. https://doi.org/10.1016/j.jhydrol.2011.11.032
Calcagno P, Chilès JP, Courrioux G, Guillen A (2008) Geological modelling from field data and geological knowledge. Phys Earth Planet Inter 171:147–157. https://doi.org/10.1016/j.pepi.2008.06.013
Chen Z, Goldscheider N (2014) Modeling spatially and temporally varied hydraulic behavior of a folded karst system with dominant conduit drainage at catchment scale, Hochifen–Gottesacker. Alps J Hydrol 514:41–52. https://doi.org/10.1016/j.jhydrol.2014.04.005
Clark MP, Kavetski D, Fenicia F (2011) Pursuing the method of multiple working hypotheses for hydrological modeling. Water Resour Res 47. https://doi.org/10.1029/2010WR009827
Collon P, Bernasconi D, Vuilleumier C, Renard P (2017) Statistical metrics for the characterization of karst network geometry and topology. Geomorphology 283:122–142. https://doi.org/10.1016/j.geomorph.2017.01.034
de la Varga M, Schaaf A, Wellmann F (2019) GemPy 1.0: open-source stochastic geological modeling and inversion. Geosci Model Dev 12:1–32. https://doi.org/10.5194/gmd-12-1-2019
de Rooij R, Graham W (2017) Generation of complex karstic conduit networks with a hydrochemical model: generation of karstic conduit networks. Water Resour Res 53:6993–7011. https://doi.org/10.1002/2017WR020768
Dreybrodt W, Gabrovšek F, Romanov D (2005) Processes of speleogenesis: a modeling approach. Založba ZRC; Inštitut za zariskovanje krasa ZRC SAZU, Ljubljana, Postojna, Slovenia
Duan R, Shang G, Yu C, Wang Q, Zhang H, Wang L, Xu Z, Dong Y (2020) Reactive transport simulation of cavern formation along fractures in carbonate rocks. Water 13:38. https://doi.org/10.3390/w13010038
Enemark T, Peeters LJM, Mallants D, Batelaan O (2019) Hydrogeological conceptual model building and testing: a review. J Hydrol 569:310–329. https://doi.org/10.1016/j.jhydrol.2018.12.007
Fandel C, Ferré T, Chen Z, Renard P, Goldscheider N (2021) A model ensemble generator to explore structural uncertainty in karst systems with unmapped conduits. Hydrogeol J 29:229–248. https://doi.org/10.1007/s10040-020-02227-6
Ford D, Williams P (2007) Karst hydrogeology and geomorphology Derek Ford. Wiley, Chichester, UK
Garrido S, Alvarez D, Moreno LE (2020) Marine applications of the fast marching method. Front Robot AI 7:2. https://doi.org/10.3389/frobt.2020.00002
GitHub (2021) pyKasso. https://github.com/randlab/pyKasso. Accessed December 2021
Goeppert N, Goldscheider N (2008) Solute and colloid transport in karst conduits under low- and high-flow conditions. Ground Water 46:61–68. https://doi.org/10.1111/j.1745-6584.2007.00373.x
Goeppert N, Goldscheider N, Berkowitz B (2020) Experimental and modeling evidence of kilometer-scale anomalous tracer transport in an alpine karst aquifer. Water Res 115755. https://doi.org/10.1016/j.watres.2020.115755
Goldscheider N (2002) Hydrogeology and vulnerability of karst systems: examples from the Northern Alps and the Swabian Alb. PhD Thesis, Universität Karlsruhe, Karlsruhe, Germany
Goldscheider N (2005) Fold structure and underground drainage pattern in the alpine karst system Hochifen-Gottesacker. Eclogae Geol Helvetiae 98:1–17. https://doi.org/10.1007/s00015-005-1143-z
Hartmann A, Goldscheider N, Wagener T, Lange J, Weiler M (2014) Karst water resources in a changing world: review of hydrological modeling approaches: karst water resources prediction. Rev Geophys 52:218–242. https://doi.org/10.1002/2013RG000443
Jaquet O, Jeannin PY (1994) Modelling the karstic medium: a geostatistical approach. In: Armstrong M, Dowd PA (eds) Geostatistical simulations, quantitative geology and geostatistics. Springer Netherlands, Dordrecht, The Netherlands, pp 185–195. https://doi.org/10.1007/978-94-015-8267-4_15
Jaquet O, Siegel P, Klubertanz G, Benabderrhamane H (2004) Stochastic discrete model of karstic networks. Adv Water Resour 27:751–760. https://doi.org/10.1016/j.advwatres.2004.03.007
Jeannin P-Y, Eichenberger U, Sinreich M, Vouillamoz J, Malard A, Weber E (2013) KARSYS: a pragmatic approach to karst hydrogeological system conceptualisation: assessment of groundwater reserves and resources in Switzerland. Environ Earth Sci 69:999–1013. https://doi.org/10.1007/s12665-012-1983-6
Jeannin P-Y, Artigue G, Butscher C, Chang Y, Charlier J-B, Duran L, Gill L, Hartmann A, Johannet A, Jourde H, Kavousi A, Liesch T, Liu Y, Lüthi M, Malard A, Mazzilli N, Pardo-Igúzquiza E, Thiéry D, Reimann T et al (2021) Karst modelling challenge 1: results of hydrological modelling. J Hydrol 600:126508. https://doi.org/10.1016/j.jhydrol.2021.126508
Kavousi A, Reimann T, Liedl R, Raeisi E (2020) Karst aquifer characterization by inverse application of MODFLOW-2005 CFPv2 discrete-continuum flow and transport model. J Hydrol 587:124922. https://doi.org/10.1016/j.jhydrol.2020.124922
Kovács A, Sauter M (2007) Modelling karst hydrodynamics, in: methods in karst hydrogeology. Taylor and Francis, London, pp 201–222
Lafare A (2011) Modélisation mathématique de la spéléogenèse: une approche hybride à partir de réseaux de fractures discrets et de simulations hydrogéologiques [Mathematical modeling of speleogenesis: A hybrid approach based on discrete fracture networks and hydrogeologic simulations]. PhD Thesis, Université de Montpellier, Montpellier, France
Mirebeau J-M, Portegies J (2019) Hamiltonian fast marching: a numerical solver for anisotropic and non-holonomic Eikonal PDEs. Image Process Line 9:47–93. https://doi.org/10.5201/ipol.2019.227
Miville F (2000) Modélisation stochastique du bassin versant karstique de la source du Betteraz (JU) [Stochastic model of the Betteraz spring karst catchment, Jura]. MSC Thesis, Université de Neuchâtel, Neuchaâtel, Switzerland
Palmer AN (1991) Origin and morphology of limestone caves. Geol Soc Am Bull 103:1–21. https://doi.org/10.1130/0016-7606
Pardo-Igúzquiza E, Dowd PA, Xu C, Durán-Valsero JJ (2012) Stochastic simulation of karst conduit networks. Adv Water Resour 35:141–150. https://doi.org/10.1016/j.advwatres.2011.09.014
Refsgaard JC, van der Sluijs JP, Brown J, van der Keur P (2006) A framework for dealing with uncertainty due to model structure error. Adv Water Resour 29:1586–1597. https://doi.org/10.1016/j.advwatres.2005.11.013
Reimann T, Hill ME (2009) MODFLOW-CFP: a new conduit flow process for MODFLOW-2005. Ground Water 47:321–325. https://doi.org/10.1111/j.1745-6584.2009.00561.x
Ronayne MJ (2013) Influence of conduit network geometry on solute transport in karst aquifers with a permeable matrix. Adv Water Resour 56:27–34. https://doi.org/10.1016/j.advwatres.2013.03.002
Rossman LA (2015) Storm water management model user’s manual version 5.1 (no. EPA-600/R-14/413b). EPA, Cincinnati, OH
Scanlon BR, Mace RE, Barrett ME, Smith B (2003) Can we simulate regional groundwater flow in a karst system using equivalent porous media models? Case study, Barton Springs Edwards aquifer, USA. J Hydrol 276:137–158. https://doi.org/10.1016/S0022-1694(03)00064-7
Sethian JA (1996) A fast marching level set method for monotonically advancing fronts. Proc Natl Acad Sci 93:1591–1595. https://doi.org/10.1073/pnas.93.4.1591
Sethian J (2006) Level set methods: an act of violence. Am Sci 85(3):254–263
Sivelle V, Renard P, Labat D (2020) Coupling SKS and SWMM to solve the inverse problem based on artificial tracer tests in karstic aquifers. Water 12:1139. https://doi.org/10.3390/w12041139
Acknowledgements
The authors wish to thank the journal editor and two anonymous reviewers, whose comments greatly improved the manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant DGE-1143953, and by the Deutscher Akademischer Austauschdienst (DAAD) One-Year Doctoral Research Grant Program (C.F.). This work is also a contribution to the KARMA Project (Karst Aquifer Resources availability and quality in the Mediterranean Area), which is financially supported by the Federal Ministry of Education and Research (BMBF) and the European Commission through the Partnership for Research and Innovation in the Mediterranean Area (PRIMA) program under Horizon 2020 (grant agreement number 01DH19022A; N.G.). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
No conflicts of interest to report.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fandel, C., Miville, F., Ferré, T. et al. The stochastic simulation of karst conduit network structure using anisotropic fast marching, and its application to a geologically complex alpine karst system. Hydrogeol J 30, 927–946 (2022). https://doi.org/10.1007/s10040-022-02464-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-022-02464-x























