Abstract
Horizontal wells play an often overlooked role in hydrogeology and aquifer remediation but can be an interesting option for many applications. This study reviews the constructional and hydraulic aspects that distinguish them from vertical wells. Flow patterns towards them are much more complicated than those for vertical wells, which makes their mathematical treatment more demanding. However, at some distance, the drawdown fields of both well types become practically identical, allowing simplified models to be used. Due to lower drawdowns, the yield of a horizontal well is usually higher than that of a vertical well, especially in thin aquifers of lower permeability, where they can replace several of the latter. The lower drawdown, which results in lower energy demand and slower ageing, and the centralized construction of horizontal wells can lead to lower operational costs, which can make them an economically feasible option.
Abstrakt
Horizontalfilterbrunnen spielen eine oft übersehene Rolle in der Hydrogeologie und der Altlastensanierung, sind aber eine interessante Option für viele Anwendungen. Diese Studie bewertet bauliche und hydraulische Aspekte, die sie von Vertikalfilterbrunnen unterscheiden. Die Fließwege in ihrem Umfeld sind deutlich komplizierter als bei Vertikalfilterbrunnen, was ihre mathematische Beschreibung deutlich schwieriger macht. Allerdings sind die Absenkfelder beider Brunnentypen in einer gewissen Entfernung praktisch identisch, so dass dann auch einfachere Modelle genutzt werden können. Durch die geringeren Absenkungen ist die Leistung von Horizontalfilterbrunnen gewöhnlich höher als die von Vertikalfilterbrunnen, besonders in geringmächtigen und gering durchlässigen Grundwasserleitern, so dass ein einzelner Horizontalbrunnen mehrere Vertikalbrunnen ersetzen kann. Die geringere Absenkung, die in einem verminderten Energiebedarf und langsamerer Alterung resultiert, kann zu geringeren Betriebskosten führen, die sie auch aus wirtschaftlicher Sicht zu einer interessanten Option machen.
Resume
Les puits horizontaux jouent souvent un rôle méconnu en hydrogéologie et dans la remédiation des aquifères mais ils peuvent constituer une option intéressante pour de nombreuses applications. Cette étude passe en revue les aspects de construction et d’hydraulique qui les distinguent des puits verticaux. Les schémas d’écoulements qui se produisent vers eux sont beaucoup plus compliqués que ceux des puits verticaux, ce qui rend leur traitement mathématique plus exigeant. Cependant, à partir d’une certaine distance, les champs de rabattement des deux types de puits deviennent pratiquement identiques, autorisant le recours à des modèles simplifiés. Du fait de rabattements moindres, le rendement des puits horizontaux est. généralement supérieur à celui d’un puits vertical, en particulier dans les aquifères peu épais de faible perméabilité, où ils peuvent remplacer plusieurs de ces derniers. Le rabattement moindre, dont résultent une demande en énergie plus faible et une obsolescence plus lente, et la construction centralisée des puits horizontaux peuvent conduire à des coûts d’exploitation inférieurs, ce qui peut en faire une option économiquement intéressante.
Resumen
Los pozos horizontales desempeñan un papel a menudo olvidado en la hidrogeología y en la rehabilitación de acuíferos, pero pueden ser una opción interesante para muchas aplicaciones. Este estudio revisa los aspectos constructivos e hidráulicos que los distinguen de los pozos verticales. Los patrones de flujo hacia ellos son mucho más complicados que los de los pozos verticales, lo que hace que su tratamiento matemático sea más exigente. Sin embargo, a cierta distancia, los campos de depresión de ambos tipos de pozos son prácticamente idénticos, lo que permite utilizar modelos simplificados. Debido a las menores depresiones, el rendimiento de un pozo horizontal suele ser mayor que el de un pozo vertical, especialmente en acuíferos finos de menor permeabilidad, donde pueden sustituir a varios de estos últimos. La menor depresión, que se traduce en una menor demanda de energía y un envejecimiento más lento, y la construcción centralizada de los pozos horizontales pueden dar lugar a menores costes de explotación, lo que los convierte en una opción económicamente viable.
摘要
水平井在水文地质学和含水层修复中发挥着经常被忽视的作用, 但对于许多应用来说可能是一个有趣的选择。本研究评述了将与垂向井区分的构造和水力因素。 他们的流态型比垂向井的复杂得多, 因此数学处理要求更高。 然而, 在一定距离处, 两种井型的降深在实际中类似, 因此可以采用简化模型。 由于较小的降深, 水平井的产量通常高于垂直井的产量, 尤其是在更低渗透率的薄层含水层, 因此水平井的效果相当于几个垂向井的。较小的降深引起较低的能源需求和较慢的老化, 水平井的集中建设可以降低运营成本, 可从经济上作为可行的选择。.
Resumo
Poços horizontais desempenham um papel frequentemente esquecido na hidrogeologia e na remediação de aquíferos, mas podem ser uma opção interessante para muitas aplicações. Este estudo revisa os aspectos construtivos e hidráulicos que os distinguem dos poços verticais. Os padrões de fluxo em direção a eles são muito mais complicados do que os de poços verticais, o que torna seu tratamento matemático mais exigente. No entanto, a alguma distância, os campos de rebaixamento de ambos os tipos de poço tornam-se praticamente idênticos, permitindo o uso de modelos simplificados. Devido a rebaixamentos menores, o rendimento de um poço horizontal é geralmente maior do que o de um poço vertical, especialmente em aquíferos finos de baixa permeabilidade, onde podem substituir vários destes últimos. O rebaixamento menor, que resulta em menor demanda de energia e envelhecimento mais lento, e a construção centralizada de poços horizontais podem levar a menores custos operacionais, o que pode torná-los uma opção economicamente viável.
Аннотация
В гидрогеологии и при очистке водоносных пластов от загрязнения могут быть успешно применены горизонтальные скважины, несмотря на то, что обычно их возможности зачастую не осознаются практиками. В настоящем обзоре описаны конструктивные и гидравлические особенности таких скважин в сравнении с вертикальными. Схемы фильтрации к горизонтальным скважинам намного сложнее, чем к стандартным вертикальным. Соответственно, математические расчеты горизонтальных скважин гораздо изощреннее, чем вертикальных. Вместе с тем, на достаточном удалении от горизонтальной скважины поле характеристик водопонижения практически идентично таковому от вертикальной скважины того же расхода, что позволяет использовать упрощенные модели в фильтрационных расчетах. Продуктивность горизонтальных скважин обычно выше, чем у вертикальных, особенно в тонких пластах малой проницаемости, где одна горизонтальная скважина может заменить целый куст вертикальных. Меньшее водопонижение в пласте означает снижение энергии, необходимой на откачку воды, удлинение срока эксплуатации без ремонтных работ, что вкупе с централизацией процесса конструирования горизонтальных скважин дают выигрыш и в снижении операционных затрат. Это интегрально может сделать горизонтальную скважину экономически более выгодной альтернативой.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Horizontal wells (HW), including radial collector wells (RCW) and horizontal directionally drilled wells (HDDW) are, from a hydraulic and economical point of view, an interesting alternative to vertical wells for a variety of hydrogeological situations. In the groundwater sector, their potential is, however, often overlooked, due to the scarcity of practical examples, qualified companies and specialized planners. Even in some drilling textbooks, such as Driscoll (1987) and Roscoe Moss (1990), they are mentioned only in passing. While a myriad papers, many of them from the oil and gas industry, discuss the hydraulics of such wells, there is a lack of a comprehensive description of all aspects of HWs from the groundwater perspective. This study aims at closing this gap by addressing: the evolution of HWs and their fields of application; the general construction techniques; their particular hydraulic conditions and design criteria, and how they can be modeled properly. The electronic supplementary material (ESM) contains an appraisal of construction and operational costs and the aging processes, and what can be done about them. Other non-vertical extraction techniques, such as covered drainage ditches, drip galleries, Maui tunnels and slant wells, will also be considered here.
The focus here will be single-phase groundwater flow, although many technical developments and mathematical models for horizontal wells come from the oil and gas industry, where the operators are interested in both single-phase (crude oil) and multiphase flow (secondary and tertiary stages of hydrocarbons recovery) from porous/fractured formations. The review incorporates a wealth of older literature, which is often overlooked as they are only available in German, French, Russian or Polish (Falcke 1962; Nöring 1953; Polubarinova-Kochina 1955, 1977; Stack 1958; Borisov et al. 1964; Schneebeli 1966; Grigoryan 1969; Wiederhold 1966a, 1966b; Kotowski 1985, 1988; Iktisanov 2007; Khisamov et al. 2017).
In the groundwater sector, horizontal wells are used for
-
water supply (especially river bank filtration), for public, industrial and agricultural purposes
-
drainage (groundwater level control)
-
contaminant removal (especially skimming)
-
subsurface seawater intake, e.g. for desalinization plants (Spiridonoff 1964; Missimer et al. 2013; Williams 2013, 2015)
-
managed groundwater recharge (injection well)
-
pressure relief around subsurface infrastructure, e.g. tunnels, deep basements (e.g. Nemecek 2006)
-
geothermal applications (Huber et al. 2015; Sun et al. 2018).
The general advantages and disadvantages of HWs are summarized in Table 1.
History and types of non-vertical wells
Horizontal drainage systems, in the form of the khanats and kharezes, are amongst the oldest employed by man to extract groundwater. A more detailed description can be found in the ESM. In most areas of the world, vertical dug and shaft wells became the most commonly used instruments to access groundwater, when no springs were available. As water demand increased rapidly in the second half of the nineteenth century in many countries, due to population growth, urbanization, industrialization and higher hygienic standards, dug and shaft wells were ill-suited to cover this demand due to their poor yields. Drilled vertical wells, as we know them today, developed slowly from the drive points introduced in the 1860s as Norton or Abyssinian wells but became practical and widespread in use only from the 1880s onwards (Houben 2019). Therefore, people turned their attention to horizontal captures, in the form of covered drainage trenches (Campbell and Lehr 1983; Houben 2019). Therefore, perforated pipes were laid into excavated trenches, embedded in permeable material, often with several layers of gravel and sand, and finally covered with impermeable material to prevent the inflow of water from the surface. A more detailed description of the historical systems can be found in the ESM. The popularity of the technique at its time, e.g. in the USA and especially in Germany, motivated Adolf Thiem (1870) and Philipp Forchheimer (1886) to develop the first mathematical models of groundwater flow to horizontal drains (details see below).
Besides the high costs, drainage ditches have some other disadvantages. If located close to exfiltrating surface water bodies, their yield may decrease significantly at times of low flow. Secondly, they can only tap relatively shallow groundwater, which is often contaminated by anthropogenic activities. Therefore, they are hardly used for water supply anymore. One remarkable exception is the extraction of fresh groundwater from the thin freshwater lenses on oceanic islands. Compared to vertical wells, the smaller and spatially more evenly distributed drawdown curbs the upconing of underlying saltwater (Griggs and Peterson 1993; Stoeckl and Houben 2012; Pauw et al. 2016; Hendizadeh et al. 2016). Horizontal extraction galleries are thus used on many Caribbean and Pacific islands (Fil 1950; Mather 1975; Lloyd et al. 1993). For general dewatering and infiltration purposes, e.g. in agriculture, civil engineering and mining, drainage trenches are still commonly used. Another mostly historical horizontal water extraction technique, drip tunnels in consolidated rocks, are described in the ESM.
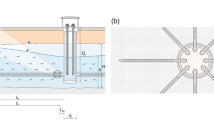
Horizontal drilling was a common technique in the mining industry before the twentieth century (see ESM). The inventor and pioneer of the RCW, as we know it today, is Leo Ranney, an American geologist and engineer, who, in 1927 used horizontal boreholes to extract oil from sandstone formations in Ohio (Todd 1959; Hunt 2003). His first oil RCW had a shaft of 40 ft. (12 m) diameter and 70 ft. (21.6 m) depth, from which 16 lateral bores were driven into the formation in a radial pattern. His first RCW for water supply was completed in 1934 in London, England (UK), with more wells in other European countries following, mostly after World War 2. The first groundwater RCW in the USA was drilled in 1936 (Hunt 2003). Figure 1 shows a typical RCW in cross sectional and plan view. A much more detailed technical drawing is shown in Fig. S4 of the ESM.
Typical set-up of a radial collector well: (a) cross section, (b) plan view, (c) wet shaft and (d) dry shaft (modified after Houben and Treskatis 2007)
A radial collector well consists of a number of horizontal arms, called manifolds or, more commonly, laterals, which are open to the aquifer, all connected to a vertical cylindrical caisson. The number and spatial arrangement of laterals depends on the water demand, technical and financial constraints and the presence of boundary conditions, e.g. infiltrating rivers or impermeable rocks. The classical star-shaped RCW has laterals of equal length evenly distributed over its circumference (Fig. 2). If many laterals are needed, it is sometimes useful to install them in two different height levels above the caisson floor, if the aquifer thickness permits. Lee et al. (2010) describe a RCW with six laterals installed at a depth of 12 m and six at 20 m. During operation, groundwater enters the well through the slots in the laterals and flows into the caisson, where one or more pumps are installed, often with variable-speed capability. In low-permeability media, the water volume stored in the RCW shaft provides a limited storage volume.
In reality, often one or more of the laterals does not reach the intended length, e.g. due to obstacles. An example is shown in Fig. 2 (arrangement a´). In many bank filtration cases, laterals may extend underneath the river (Fig. 2, arrangement d´). In a very few cases, the RCW is placed in the river (Kollis 1961).
Another type of non-vertical wells are inclined or slant wells. Inclined drilling is not uncommon in the mining industry and in geoengineering and is often used for exploration and dewatering (e.g. Müller et al. 2009; Zingg and Anagnostou 2018). Slant wells are sometimes used as intakes for desalination plants (Williams 2013, 2015) and to reach contaminant plumes under built-up industrial sites (Furukawa et al. 2017). They are rarely considered for water supply and have received limited attention in literature outside the oil and gas industry (e.g. Joshi 1988; Zhan and Zlotnik 2002; Tsou et al. 2010; Blumenthal and Zhan 2016; Liang et al. 2017). A more detailed description is found in the ESM.
Horizontal directionally drilled (HDD) wells are a rather late addition to the field of hydrogeology, arriving around the mid 1990s. The technique was originally developed in the hydrocarbon industry and first adapted for trenchless cable and pipeline laying. They proved particularly useful for contaminated site remediation, since the screens can be placed underneath active industry complexes, airport runways or landfills without compromising their functioning (e.g. Fournier 1997, 2002; Lubrecht 2012; Divine et al. 2018). HDD wells are also used for dewatering in geotechnical applications and surface mines (e.g. Struzina and Drebenstedt 2008a; Müller et al. 2009). Applications for water supply are scarce (e.g. Sass and Treskatis 2000a, 2000b; Licht et al. 2001; Birch et al. 2007). Figure 3 shows the most common concepts of HDDWs.
Horizontal directionally drilled well concepts used in water supply and aquifer remediation: (a) discontinuous (blind), (b) continuous, (c) with central collector shaft, consisting of two individual HDDW driven into the shaft from two starting pits (b and c modified after Houben and Treskatis 2007)
A general problem of inclined wells is the placement of the pump. Most pumps are designed for a strictly vertical “hanging” position. In an inclined position, the bearings and drive shafts suffer from an uneven load, which can lead to uneven wear and reduce their life-time. Therefore, an alternative method is to put a caisson between the strings, so that the pumps can be placed in an upright position (Fig. 3c). Additionally, the caisson allows for easier maintenance and rehabilitation of the strings. A well of this type was described by Licht et al. (2001), constructed at the same site in Germany as described above. First, a shaft was constructed. After its placement, two strings were drilled directionally towards it.
Construction techniques
Construction of RCW
The reinforced concrete shaft of a RCW, commonly called caisson, used to be poured in-place and in sections (Spiridonoff 1964). This tedious and time-consuming procedure has been replaced by using pre-fabricated rings (segments) of reinforced concrete which can be easily assembled on-site (Figs. 4 and 5). The diameter of the caisson strongly influences building costs. The minimum diameter has to be sufficient to accommodate the machinery for lateral placement (including a ladder for the operators) and – later – the pumps. The smallest RCWs have shaft diameters of 1.5 m. Diameters of 3 to 6 m (10 to 20 ft) are more common. Larger diameters are rare, although the RCW in Warsaw, Poland, has a diameter 11 m (Kollis 1961). Wider shafts enable the installation of longer casing and screen sections, thus reducing the number of expensive and potentially leaking joints. The first (later: bottom) segment acts as a cutting ring, and therefore it is heavily reinforced and may weigh several tons. Using a clamshell, soil material is removed from the interior of the segment, which then slides downwards, upon which the next segment is added (Fig. 4). The following segments are usually higher, e.g. 2.5 m (8 ft) instead of 1.5 m (5 ft) for the bottom segment. Bentonite suspensions are sometimes used to diminish the friction between segments and surrounding soil. The bentonite later also helps sealing the zone damaged during caisson sinking, diminishing the downward flow of unwanted surface water. Wall thicknesses may range from 0.3 m (12 in.) for shallow and 0.6 m (24 in.) for deeper shafts. Metal reinforcement of the concrete has to be strong to withstand not only water and soil pressure, but also the forces occurring during uneven sinking and the later insertion of the laterals. A segment of 3.4 m outer diameter, 0.3 m wall thickness and 2.5 m in height may weigh up to 18 tons, illustrating the need for heavy machinery. The bottom of an RCW, installed after the emplacement of the last segment, is a heavily enforced concrete slab, poured on site to prevent ground failure due to groundwater inflow from below. Deviations of the shaft from the vertical may occur in heterogeneous subsurface strata. A RCW built for the water supply of Salzburg, Austria, showed a deviation of almost 2.5 m at the final depth of 47 m (Nemecek 2006). The resulting cracks in the concrete were, however, sealed, and the well equipped with 22 laterals of up to 40 m length and put into use. Some special and rare types of caisson construction are discussed in the ESM.
Typical steps in the construction of a radial collector well: (a) setting of foundation and first tubing (with cutting ring base), excavation of aquifer material from within the tubing, leading to its downward movement, (b) emplacement of following segment (repeated until final depth is reached), (c) caisson completed, emplacement of impermeable bottom plug, dewatering from caisson (not shown), (d) insertion of laterals from inside of caisson
Laterals are commonly installed about 1 m (3–4 ft) above the caisson floor. The portholes are usually prefabricated and not drilled into the caisson. They are sealed by plugs during sinking of the caisson. Lateral ports are spaced at least 22.5 degrees apart, equivalent to a maximum of 16 laterals, to ensure structural integrity (Spiridonoff 1964), although RCW with 20 laterals have been built in South Korea from a 3.5 m caisson (Hang-Tak et al. 2020). More common are 6 to 12 laterals, however. When a higher number is desired, it is common practice to install the laterals in two or more different height levels. Sometimes, more portholes than planned laterals are installed as a back-up, e.g. if a lateral becomes stuck or collapses during installation. The most common length of laterals is between 30 and 70 m (100 to 200 ft., see below), although longer laterals of up to 275 m (900 ft) are possible under ideal conditions with current technologies. In such long laterals, the frictional head losses within the narrow screen consume the gains in flow obtained by the longer screen length (for details, see section ‘Design criteria’).
The original Ranney concept of RCW construction involved driving the screens directly into the aquifer using hydraulic jacks. The diameter was usually not more than 0.2 m. Usually, two drive jacks, e.g. each of 1000 to 1500 kN, were used to push in the laterals (Spiridonoff 1964; Huisman 1972). Resistance was highest for the first few meters of penetration, it then usually decreased somewhat, but, for longer laterals, the increasing jacket friction of the casing increased it again. Depending on the soil type, maximum lateral lengths of 40 to 80 m were possible (Huisman 1972). Due to the mechanical forces acting upon it, the screen needed to have a thick wall, often around 6 to 10 mm. Originally, copper alloy or mild steel was mostly used. The number of slots had to be restricted in order to not compromise the stability. Slots were cut with a saw or angle grinder, with a width of 6 to 9.5 mm and a length of 38.1 mm (1.5 in.) (Spiridonoff 1964; Huisman 1972). The open area would be around 15–20% in the best cases (Spiridonoff 194; Huisman 1972). During construction, a rubber “sand line” was inserted into the pipe to block the screen slots, allowing water and aquifer material to enter only through perforations in the tip (pilot). From there, water and sand were transported to the caisson through an inside hose. Opening the valve of the inside hose at the caisson end induced a flow through the pilot perforations, driven by the static water head (Huisman 1972). The resulting high flow velocities at the tip, up to 5 m/s according to Huisman (1972), induced the removal of aquifer material, which lowered the force needed to drive in the lateral and improved the hydraulic conductivity around it. For each meter of inserted pipe, a volume of 0.3 to 0.7 m3 of fine sand was usually removed (Spiridonoff 1964; Huisman 1972). Due to the large slot widths and the limited well development, problems with sand intake during production were not uncommon for Ranney wells, especially in uniform fine to medium sand aquifers. The method worked best for coarse sediments with mean grain sizes larger than 1.0 mm, or better 3.0 mm, where the finer grains could be removed by development, leaving a coarse, highly permeable zone behind. If the sand intake was only local, this section could be sealed by a later but costly installation of a liner casing. The relatively poor hydraulics of the Ranney screens also made later rehabilitations, e.g. in the case of incrustations, difficult. Since stainless steel would have been too expensive, considering the high wall thicknesses of the Ranney screens, the mild steels employed often suffered from strong corrosion. One way to overcome the sand intake problems of the Ranney method is to use a screen in screen solution. Moses and Riegert (2004) used a six-inch (15 cm) wire-wound-screen inserted into an eight-inch (20 cm) outer screen. The space between the screens was prepacked with ceramic beads.
To overcome the limitations of the Ranney method, a proper well screen was inserted under the protection of a temporary casing, which was later retracted. At first, it was tried to push both protective casing and screen into the aquifer together, the so-called Nebolsine well (Bieske 1959). This proved impractical. Therefore, it was decided to separate the steps of screen and protective casing installation. Swiss engineers thus introduced the Fehlmann concept in the late 1940s (Fehlmann and Fehlmann 1959). The first well of this type was installed in the year 1947, near Bern, Switzerland (Fehlmann and Fehlmann 1959). In this concept, a sturdy mild steel temporary casing (15 to 20 mm wall thickness) is driven in first (Huisman 1972). Unlike in the Ranney method, the pilot head is not screwed to the casing and can be moved independently, allowing limited work around obstacles, e.g. boulders. Water flow can be reversed to induce a jetting effect at the tip. Removing a volume of 0.15 to 0.3 m3 of fine sand for each meter of inserted pipe was usually sufficient to keep the driving force below 400 kN (Huisman 1972). Using telescoping diameters, lateral lengths of 100 m and more became possible. After reaching the final position, the inside hose is removed. A well screen of smaller diameter is inserted and the temporary casing is pulled. The drilltip remains in the aquifer (lost tip). The big advantage is that the final screen can be made of much thinner material with higher open area, as it does not have to withstand the mechanical forces of driving it through the aquifer. Therefore, more expensive but more corrosion resistant screen materials such as stainless steel became possible. Hydraulically advantageous screen types, e.g. wire-wrapped, thus became feasible, which facilitated well development and later rehabilitation. After installation, the well is developed by pumping, which leads to the removal of fines from the vicinity of the lateral. The development, however, works best in coarser sediments with limited percentages of fine material, e.g. in alpine gravel deposits. The method is therefore still being used, for example, in Switzerland (Conrad 2010).
The Fehlmann concept was further refined by German engineers in the early 1950s by installing an artificial gravel pack between casing and screen (Preussag concept). The temporary casing therefore has to have a larger diameter, usually 0.4 m, thus requiring a higher driving force. After reaching the final position, the screen is inserted. A constant distance between temporary casing and screen is maintained by centralizers. Into this annular space, gravel material is flushed using a small-diameter feeder pipe. During gravel pack installation both the gravel pipe and the temporary casing are slowly pulled back, the tip remains. The gravel pack allows much better sand control, as it can be adjusted to the surrounding aquifer material. This made RCWs in fine-grained and non-uniform material possible. The tip can be equipped with a jetting nozzle to facilitate the propagation through denser sediments, e.g. silt lenses.
In all previously described methods, the loosened sediment is transported only by the groundwater that enters at the tip of the string and flows towards the caisson, due to the induced gradient. Therefore, dry zones pose a problem. Another problem is that boulders or consolidated (cemented) portions of the aquifer cannot be passed easily. In the case of boulders, common in glacial deposits, the drillers try to remove as much material as possible around it by intensive flushing, hoping that the obstacle sags down, allowing the string to pass above it. However, many laterals of RCWs are shorter than intended because the obstacle could not be removed.
Therefore, the water hydraulic drilling (WHD) technique was developed in Germany to overcome these problems (Huber and Schätz 2009). Here, a water-driven rotary drill head is attached to the tip of the string. The water used as drilling fluid is used to rotate the drill tip (up to 200 l/min at 200 bar, torque 10,500 Nm, 36 rpm) and is also used to transport material away from the string. The drilling diameter is up to 480 mm. The tip angles can be adjusted to keep the drilling in its intended path using a laser. This technique now allows the installation of RCWs in (semi-)consolidated and even dry formations. The drilling tool is 2.5 m long and thus requires a caisson diameter of at least 2.8 m.Two further, recently developed methods are described in detail in the ESM.
For all methods, the last few meters of the lateral near the caisson are usually installed with unslotted casing (blind casing), which is intended to keep surface water away, which might flow downwards along the disturbed zone around the caisson.
After finishing the laterals, the in-caisson infrastructure is installed, including pumps, electrical supply, lighting, measuring equipment and access ladders. The majority of RCWs have a “wet shaft”, meaning that water from the laterals runs directly into the caisson interior, collects there and is pumped by standard submersible pumps from this reservoir (Daffner et al. 2010a, 2010b). In most cases, the laterals can be closed individually by a valve (Fig. 6). Inspections and repairs require a diver, the installation of a lock for an individual lateral or the closure of all laterals and pumping out of the water inside the caisson. In the much less common and more expensive “dry shaft” system (Daffner et al. 2010a, 2010b), each lateral is connected individually to a pipeline system connected to the pumps (Figs. 1 and 6). The caisson is not filled with water and can be inspected at any time using permanently installed ladders and platforms. This system is often used when the groundwater quality would negatively affect the concrete shaft or when it contains high concentrations of iron and manganese, which would precipitate in the shaft when exposed to oxygen. Due to the pipelines and ladders, the open space in a dry shaft is limited, which makes the accessibility, e.g. for repairs, more difficult. In all systems, the electrical and electronic components of the RCW are usually installed in an extension of the caisson above surface.
An even rarer compromise is the “wet basement”, where the lower part of the caisson is closed by a lid and flooded (Remde 1959; Huisman 1972; Daffner et al. 2019b). The laterals are connected to the basement and the pumps extract water from there. The upper part is dry and accessible for maintenance.
Some statistical data on the number of RCW worldwide, the range of caisson depths and diameters as well as lateral lengths and diameters are discussed in the ESM.
Construction of HDDWs
HDDW drilling is usually performed in stages (Fig. 7). The first involves the drilling of a thin-diameter pilot borehole, by jetting or roller bit, depending on the subsurface material (Fig. 7a). The location of the drillbit can be detected from the surface by electromagnetic tools, either using the natural or an induced magnetic field. The direction of the drillbit can be adjusted in all angles during the drilling process to keep the drillhole within the intended track. This allows a very exact positioning. Licht et al. (2001) were able to hit 40 × 40 cm windows in a shaft at 12 m depth with two strings of 170 m length each. The pilot borehole is then widened by a second drilling (or overwashing) starting from the end pit (going backwards), a process that can be repeated if necessary (Fig. 7b). Finally, a protective casing is installed and the final casing and screen pulled into it (Fig. 7c). The protective casing is then removed and the well developed.
Since the bending capacity of both drillstring and casing material is limited, a certain horizontal distance between the starting point and the end point at the final depth is required, the so-called setback. Usually, the ratio of a horizontal unit of length to vertical penetration depth is around five, e.g. a projected final depth of 10 m requires a minimum horizontal distance of 50 m between the drilling rig and the target point.
The maximum depth for a HDDW is around 30 m for a twin well as shown in Fig. 4 c and may be up to 600 m for a single, blind HDDW (Fig. 3a). Drilling diameters of up to 400 mm and screen diameters between 100 and 300 mm are common. The casing and screen is often composed of steel, although experiments with PVC have also proven feasible (Hang-Tak et al. 2020). The maximum length of one string can be up to 600 m. Gravel packs are difficult to be emplaced and the well thus commonly requires natural development. Drilling fluids are indispensable to stabilize the borehole. As a consequence, the probability of wellbore skin formation is higher. Therefore, usually biodegradable polymers are used instead of bentonite. Well development remains, however, an indispensable step.
A well of the type shown in Fig. 3b was built in Krefeld, Germany, by Sass and Treskatis (2000a, 2000b). The unconfined aquifer at this location was very thin (13 m), with only 3.5 to 7 m saturated thickness, depending on the level of the nearby river. Due to the low saturated thickness, vertical wells would have produced high drawdowns, which would easily have aerated the short screened intervals. A disproportionate number of small vertical wells would thus have been needed to produce a sufficient yield. It was therefore decided to build a HDDW. Both the entry and the exit angle of the drill string were 11°, while the 45 m of screen were more or less horizontal at a depth of around 10.5 m. Total drilling length was 262 m. The drilling was begun with a 171 mm (6 3/4″) pilot borehole, followed by a 305 mm (12″) overwash. The screen (110 mm diameter) was then pulled into the borehole, the overwash removed and the well developed.
Fournier (2005) states that around 2000 horizontal wells were drilled for environmental remediation purposes between 1988 and 2005 with maximum drilling lengths of up to 1500 ft. (460 m) and screen lengths of up to 840 ft. (250 m).
General observations on the hydraulics of horizontal screens
Differences compared to vertical wells
The geometry and technical features of a HW – and especially those of a RCW – differ significantly from a vertical well and make their mathematical treatment more complicated. Figure 8 shows the typical geometry of a RCW in a bank filtration site. It also describes the terms used in the following.
General dimensions and terms for a RCW, here in a bank filtration scheme (modified after Collins and Houben 2020). Dc = depth of caisson, dc = diameter of caisson, H = initial water-saturated thickness, h = dynamic head, Ll = total length of lateral, Lf = screened length of lateral, Lbc = length of unscreened part of lateral (blind casing), rgp = radius gravel pack, ds = diameter screen lateral
In the ideal case, a vertical well drains a cylindrical aquifer volume and radial symmetry of groundwater flow can be assumed (Thiem 1870). The catchment of a horizontal lateral is much more complex (Fig. 9). Even in the simple case of a fully penetrating horizontal drain, it captures water from an ellipsoidal zone of influence (Forchheimer 1886). As a lateral ends within the aquifer, it always represents a partially penetrating well, with an essentially 3-D groundwater flow. A lateral is positioned at a certain depth above the aquifer base, and therefore it receives water from above and below as well as from both sides of the lateral. The tip of the lateral can be considered as a mathematical singularity if the lateral is modeled as a line sink.
Three-dimensional path lines to a radial collector well with two sets of laterals at different levels, depicting the complicated pattern of flow lines near the laterals. The three laterals at the higher level are 80 m long, the four laterals at the lower level are 50 m long, and the aquifer is 20 m thick. Pathlines are started from two locations at nine elevations. The orange path lines flow to one of the three laterals at the higher level and the blue pathlines flow to one of the four laterals at the lower level. Solution was obtained with the multi-layer analytic element model TimML (Bakker and Strack 2003), using the approach of Bakker et al. (2003)
In the case of a RCW, the flow towards one lateral can be influenced by neighboring laterals. Flow inside a well screen, both for vertical and horizontal wells, will always be turbulent. For vertical wells, the additional head losses caused by turbulent flow within and very close to the well can often be ignored, as they are usually quite small (Barker and Herbert 1992a, 1992b; Houben 2015a, 2015b). For HWs, this simplification is often not possible, as laterals tend to be very long, often several tens of meters, and mostly have much thinner diameters than vertical wells. This implies that the mostly horizontal Darcian matrix flow in the surrounding aquifer is connected to a discrete pipeline feature with turbulent axial flow via a transitional converging flow regime around the lateral. To obtain a full solution, all three features need to be considered together, as one affects the other. The major challenge lies in the conjugation of the three flow domains:
-
Darcian groundwater flow in the bulk aquifer,
-
non-Darcian seepage in the vicinity of the gravel pack or the screen slots of a lateral (where the magnitude of the specific discharge vector may be very large)
-
viscous fluid flow inside the screened pipe
For the latter, the classical fluid mechanic methods of constant rate flow in a pipe with a certain roughness, standardized in the Darcy-Weisbach, Moody or Colebrook-White empiric equations, can be used. They should, however, consider the following complication: both the pressure (static) head losses along the lateral and the flow rate are a part of the solution. Moreover, if in a standard steady state laminar or turbulent pipe flow, the head losses depend linearly on the length of the pipe and the flow rate is constant, in HW and RCW, this is not the case. Specifically, the along-axis gradient of the head losses depends on the rate of the pipe flow. This rate, in turn, depends on the “far field” of the problem, that is the seepage into the pipe (the “near field”) from the formation, as well as on an empiric coefficient (friction factor), which is not fixed - as in standard pipes with impermeable walls - but also depends on the relative roughness of the pipe and the Reynolds number of the in-pipe flow. Owing to the perforation of the walls of the “pipe”, the mass of water and impulse vary along the axis of the lateral. Consequently, the conjugation problem becomes mathematically convoluted and is aggravated by the paucity of experimental data from the in-pipe manometry and measurements of the progressively (from the tip to the caisson) increasing longitudinal flow rate of water, which infiltrates into the pipe.
Finally, the long laterals and the caisson provide a significant volume of water stored in an idle RCW. A RCW with a caisson of 4 m diameter with a level of 10 m of water inside, equipped with 10 laterals, each 50 m long and of 0.3 m diameter, provides a storage of 125.7 m3 + 35.3 m3 = 161 m3. This wellbore storage will influence the initial stage of a pumping test and should thus be taken into account when the early time of a pumping test needs to be considered (e.g. Park and Zhan 2002; Giese et al. 2019).
Lateral inflow distribution
The distribution of groundwater inflow over the length of a lateral is a difficult but crucial parameter (Huisman 1972; Antipov et al. 1996; Collins and Houben 2020). While the early analytical model by Forchheimer (1886) clearly made the case for a non-uniform inflow distribution, many later models assume a uniform distribution of influx over the screen length (e.g. Hantush and Papadopulos 1962; Daviau et al. 1988; Odeh and Babu 1990; Langseth 1990; Cleveland 1994; Schafer 2006; Zhan 1999). However, the assumption of a specified head along the lateral is more realistic, in particular, a uniform head (Hantush and Papadopulos 1962; Steward and Jin 2001). As it is mathematically more difficult to incorporate into analytical models, it is less frequently considered (Bischoff 1981; Rosa and Carvalho 1989; Tarshish 1992; Steward and Jin 2001).
Measuring the inflow within a lateral is far from trivial. The flowmeter needs to be installed onto a little cart, which is moved through the lateral. Especially in thin laterals, the system can obstruct flow to a degree that it influences the actual measurements. Some of the secondary peaks observed at the end of the blind casing in Figs. 10c and 11a might thus be artefacts. The few available flowmeter measurements in actual HWs and most physical models show that the uniform inflow assumption is indeed not realistic (e.g. Falcke 1962; Krebs 1957; Stack 1958; Nemecek 2006; D’Alessio et al. 2018; Collins and Houben 2020). The field examples shown in Fig. 11 show that influx is commonly highest at the tip of the lateral, being up to more than eight times higher than that close to the caisson wall and often more than two times higher than the average flux. D’Alessio et al. (2018) investigated the inflow distribution in three RCWs with 6, 8 and 10 laterals (mostly around 50 m long) and repeated all measurements after five years. Their 48 flow meter curves basically all show a very similar inflow distribution to the one shown in Fig. 11d. The bulk of the inflow occurs in the first 5–10 m of the laterals, counted from the tip, while the remainder shows a gently decreasing inflow, which can be approximated by a constant inflow rate. The ratio of peak to base inflow was as high as ten or more. Huisman (1972) stated categorically “Under practically all circumstances, the inflow of groundwater will be much greater near the tip of the collector than near the central shaft. In fact, near the latter point the collector may just as well be made of blind pipe, reducing the cost of construction without lowering the capacity.” The reason behind the uneven inflow is that it is easier for the water to flow through the lateral than through the aquifer, thus following the path of least resistance. Only the analytical models assuming non-uniform inflow are able to recreate such profiles, e.g. the ones by Forchheimer (1886), Steward and Jin (2001) and Tarshish (1992). The latter author also included the pipe flow resistance of a lateral, through which the inflow rate varies depending on the flow within the lateral.
Measured inflow distribution along the length of (a, b) two laterals of a RCW in Berlin, Germany (Krems 1972; Collins and Houben 2020), (c) a lateral in Hannover, Germany (Stack 1958), (d) an anonymous RCW from Austria (Nemecek 2006) and (e) a lateral from RCW 5, Sonoma County, USA (D’Alessio et al. 2018). In all graphs, the caisson is to the left and the tip of the lateral to the right. All laterals, except (d), have a portion of blind casing at the caisson
Measured inflow distribution along the length of (a) a lateral of an anonymous RCW in eastern Germany, at two pumping rates, diameter 250 mm (b) an anonymous RCW, with two pumping rates and a losing section (negative flow) close to the caisson, where water re-infiltrates into the aquifer and (c) an anonymous RCW lateral (Diameter 283–299 mm) from Switzerland with a reversed inflow pattern. In all graphs, the caisson is to the left and the tip of the lateral to the right. Data: Bohrlochmessung Storkow GmbH
The examples from Berlin, Germany, shown in Fig. 10a, b and the study by D’Alessio et al. (2018) show that the different laterals of one RCW usually show the same patterns of inflow distribution. The influence of different pumping rates is investigated in Fig. 11a, b. The example of Fig. 11a shows the typical inflow distribution shown in Fig. 10, although a minor second peak occurs close to the caisson. Increasing the pumping rate from 120 to 204 m3/h does not change the general inflow pattern. Only the secondary peak close to the caisson becomes less prominent. The example of Fig. 11b shows a relatively standard inflow distribution at a pumping rate of 50 m3/h, which, however, becomes more uniform at 90 m3/h.
The model study by Steward and Jin (2001) showed that the uniform head approach can lead to the occurrence of losing sections in laterals, when there is a natural background groundwater flow with a component in the direction along the lateral. Such losing sections exfiltrate water back to the aquifer. This would be, of course, unwanted in actual water supply wells due to the inherent inefficiency and especially in decontamination applications, where it could lead to a redistribution of contaminants. Conditions favorable for the development of losing sections are long laterals and low pumping rates (Steward and Jin 2001), if not lateral variations of the permeability of the aquifer are responsible. Above a threshold pumping rate, losing sections should disappear altogether. Figure 11b shows a rare field example of such a losing section, here located close to the caisson and present at both pumping rates.
Several authors have compared the results of using the uniform flux versus the uniform head assumption (Kawecki 2000). They generally conclude that for the uniform head case, the head in the well is equal to that in a uniform flux well at a distance y along the lateral given by
with
- F:
-
correction factor
- Ll:
-
length of lateral [m]
The correction factor ranges around 0.7 (Gringarten et al. (1974) report 0.73; Daviau et al. (1988) report 0.67–0.72; and Rosa and Carvalho (1989) report 0.65–0.71).
In the strict sense, the uniform head assumption is also only an approximation, as the lowest head must occur at the caisson, and head losses will occur inside the lateral (Kim et al. 2008; Rushton and Brassington 2013a, 2013b). Head measurements over the length of a lateral are scarce. For the relatively low discharge rate of 9.6 m3/h, Mohamed and Rushton (2006) found a difference in hydraulic head of 0.042 m for a lateral of 150 m length and 0.15 m diameter. Based on a model, they found that doubling the discharge rate would increase the head difference to 0.24 m. The resulting inflow profile, however, still showed that inflow at the tip was higher than near the caisson. This was only reversed to more inflow at the caisson side when the lateral length was increased to 300 m and the head loss within the lateral reached 0.62 m. In this case, energy minimization favors flow through the aquifer. Rushton and Brassington (2013a, 2013b) found an extreme example, where the drawdown along a 300 m lateral amounted to 1.7 m. This, however, can be attributed to the poor hydraulic characteristics of the screen, for which a corrugated plastic drainage pipe of 160 mm diameter was used. The overall perforation was as low as 0.48% and additionally impeded by a geotextile wrapping. Božović et al. (2020) found that internal resistance effects within a lateral are practically negligible. They found average head losses of less than 1.5 cm along their laterals of 50 m length, and concluded that a uniform head approach, represented by a constant head boundary condition in their model, is therefore close enough to reality.
It should be noted that measuring the actual head distribution along the length of an active lateral is far from trivial. It is usually done by moving a pressure sensor mounted onto a little cart against the turbulent flow. The sensor, however, measures the pressure exerted by the column of water above it, including the elevation head above a level of reference. Practical experience has shown that laterals are often not perfectly horizontal. Both upward and downward facing laterals have been found, as well as bent ones. In inclined laterals, an uneven head distribution might thus just be an artefact of the variations in elevation head. Small head differences, such as the ones reported by Mohamed and Rushton (2006) and Božović et al. (2020), therefore need to be treated with caution.
Wang and Zhan (2017) introduced a Mixed-Type Boundary Condition (MTBC), which tried to address the issues of both uniform flow and uniform head boundary conditions. Chen et al. (2003) proposed to assign an equivalent hydraulic conductivity to the lateral, which can be made dependent on the Reynolds number or, in other words, the degree of turbulence. In their numerical model, they actually produced an inflow distribution that is the reverse of the ones shown in Figs. 10 and 11a, with the highest specific influxes occurring at the caisson side. However, the lateral they considered was very long (116 m) and of extremely small diameter (0.05 m), which inevitably must produce very high in-lateral losses. While such small diameters are unrealistic, the case might show what happens when the inside of a lateral becomes clogged by incrustations or sand accumulation. The sandtank experiments by Kim et al. (2008) also produced a reverse inflow distribution. Again, the very small lateral diameters considered, 10, 20 and 30 mm, are the probable explanation. The very long (300 m), thin (0.15 m diameter) and poorly designed well screen (0.48% open area) described by Rushton and Brassington (2013a, 2013b) also showed a stronger inflow close to the pump side. Field examples of such a reversed inflow pattern are rare. Figure 11c shows results from a RCW lateral installed in extremely coarse alpine gravels. The lateral has a relatively short net length, promoting turbulent losses although the lateral diameter is quite high at 283–299 mm. Here, most of the inflow occurs close to the caisson. Stack (1958) found a similar inflow distribution for an RCW in Hannover-Ricklingen (not shown), which he attributed to the very permeable sediment. The most probable explanation for the reversed inflow pattern is probably the presence of extremely coarse and highly permeable sediment, which imposes less piezometric head losses than the axial pipe flow losses inside the lateral.
Using a flow net analysis, Huisman (1972) concluded that with the general case of the aquifer material causing higher head losses than the pipe flow inside the lateral, the uneven flow pattern shown in Fig. 10 is inevitable. Only in aquifers of poor hydraulic conductivity will the inflow become more uniform (Birch et al. 2007; Kim et al. 2008). A more even inflow could be enforced by reducing the diameter of the laterals, at the expense of higher pipeline losses. Numerical and physical models by Chen et al. (2003) and Kim et al. (2008) confirm this. However, Huisman admits that finding the ideal combination between aquifer and lateral losses is next to impossible, due to natural heterogeneity and practical constraints of screen diameters available on the market. Huisman (1972) also mentions that an eventual clogging of the lateral tips will smoothen the inflow curve, as more water will be diverted away from the blocked tips. A gravel pack will have the same effect.
Collins and Houben (2020) compared the effects of three different boundary conditions for lateral inflow on the flow field in a numerical model. They compared uniform inflow, uniform head and a chain of point sources. For the first, the extraction rate was distributed evenly over a number of point sinks along the lateral; for the third, the distribution was uneven and based on a flowmeter profile shown in Fig. 10a (lateral 10). For the uniform head, the extraction was simulated by placing a single pumping cell at the caisson and treating the laterals as discrete features. Turbulent in-lateral losses were not considered. The equipotentials shown in Fig. 12 demonstrate that all boundary conditions result in different drawdown patterns but basically only between the laterals and up to a distance of roughly 1.3 times the lateral length. Farther outside, the effect of the different boundary conditions becomes negligible. Even between the laterals, the difference between the most unrealistic (Fig. 12a) and the most realistic (Fig. 12c) boundary conditions is not dramatic.
Drawdown around a RCW with four laterals considering three boundary conditions: (a) uniform flux, (b) uniform head, (c) non-uniform flow. Based on numerical models by Collins and Houben (2020). Caisson in the lower left corner; laterals are thick black lines. ©BGS
Finally, an explicit treatment of pipe flow in the lateral is possible using the Navier-Stokes equation (Hayati-Jafarbeigi et al. 2020). This approach is more realistic than the previously discussed boundary conditions, but is computationally more demanding.
Localized velocity peaks at the tip can be important, because high flow velocities can induce non-linear laminar losses, promote the growth of incrustations and the mobilization of fines from the aquifer (Houben 2006; Houben and Treskatis 2007; Houben and Weihe 2010; Houben 2015a).
Contribution of individual laterals to total yield
The contribution of individual laterals to the total yield of RCWs was investigated by D’Alessio et al. (2018), on the same RCWs mentioned above. In an RCW with ten laterals, the most productive ones contributed around 20% of the total yield and the least productive ones around 5%. They found that the contribution is a function of the lateral length but is also positively affected by the orientation towards infiltrating surface water bodies. A numerical model study by Park et al. (2015) came to even more pronounced differences. In a star-shaped RCW with eight laterals, of which three were facing the river, the latter produced 83% of the total yield. The hydrochemical quality of water from different laterals, despite all tapping the same depth, can vary significantly, (e.g. Hünerberg 1959; Bietmann (2009).
Special problems of bank filtration sites
The common use of RCWs for bank filtration poses some special issues. In many cases, the laterals extend to underneath the river bed (Figs. 2 and 8). The subsurface residence time going from the river bed to the lateral has to be long enough to safeguard the filtration of particles and microorganisms, the decay of organic substances and the adsorption of metals and pesticides, a condition which, however, is not always met (e.g. Gidley 1952; Verstraeten et al. 1999). Most of the mechanical filtration occurs not in the aquifer but the river bed. Natural sedimentation and filtration induced by the RCWs can thus lead to the clogging of the river bed by silt and clay particles and biomass, which may increase over time (Hubbs 2006). Despite its minute thickness, the low permeability of the stream bed layer can have a substantial influence on the efficiency of a bank filtration system. It is therefore explicitly considered in many of the models discussed below. Huang et al. (2012) found that the steady-state infiltration from the river is a function of the ratio of streambed and aquifer permeability.
One might think that after several years or decades of operation, all bank filtration sites should become inoperable due to successive growth of the clogging layer. However, this problem is mostly overcome naturally through floods which break up the clogging layer and wash it away. In Warsaw, Poland, small boats are sometimes used to stir up the bottom sediment during periods of low water levels around a RCW situated in the river Vistula.
Transient pumping phases
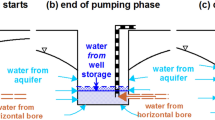
The pumping tests of HWs can have several stages which show up as individual segments in the drawdown curve. Several authors have developed equations for each particular phase (e.g. Hantush and Papadopulos 1962; Odeh and Babu 1990; Kawecki 2000) and care must be taken to select the appropriate one. Hantush and Papadopoulos (1962) developed solutions for short and long times of pumpage. Odeh and Babu (1990) distinguish four phases: early radial flow, early linear flow, late pseudo-radial and finally late linear (Fig. 13). In the early radial phase, water is released from aquifer storage close to the lateral and the water table is not yet affected. In the early linear phase, the upper and lower boundary conditions start influencing the flow pattern towards the lateral but flow parallel to the lateral remains insignificant. In the late pseudo-radial phase, the dimensions of the area affected by pumping become much larger than the length of the laterals and the drawdown field outside the laterals shows a pattern similar to that caused by a vertical well. In the late linear phase, drawdown has reached the boundary conditions and flow becomes basically steady-state. Depending on the circumstances some phases may not be distinguishable. According to Odeh and Babu (1990) the first phase might be too short to be noticeable and the second might not show up if the length of the laterals is significantly greater than the aquifer thickness. According to Kawecki (2000), the early linear phase might not develop if water from beyond the lateral tips enters the well before drawdown reaches the boundary conditions. Under particularly adverse boundary conditions, none of the phases might develop properly, rendering the pumping test not analyzable (Odeh and Babu 1990).
Transient phases of pumping from a horizontal well screen in a confined aquifer: (a) early radial flow, (b) early linear flow, (c) late pseudo-radial flow (redrawn and modified after Kawecki 2000). The image for the fourth, late linear phase, will look the same as for the pseudo-radial phase. Left images = cross-sectional view, right = plan view. Grey bars indicate impermeable layers, inflow from left and right. In an unconfined aquifer, the upper boundary is the water table
The spatially limited influence of the laterals and the transient pumping phase have some implications on pumping tests for HWs and RCWs. The drawdown field around an HW becomes equivalent to that of a vertical well at a relatively short distance away from the tip of the lateral. If the observations wells are located outside the perimeter influenced by the laterals and the pumping has reached the pseudo-radial phase, the classical transient pumping test methods by Theis and Cooper-Jacob for vertical wells may be used without overly compromising accuracy. The well radius has to be replaced by an ersatzradius as described below.
Design criteria
Aquifer conditions and well yield
The first design criteria for a horizontal well are of course the thickness and the depth of the aquifer. Thin aquifers are actually a positive criterion for RCW, as the smaller and more evenly distributed drawdown limits aquifer dewatering (Steward and Jin 2003). In deep aquifers, the construction of a caisson or a HDDW becomes prohibitively expensive. Aquifers with cemented parts, clay lenses and large boulders are to be avoided, as laterals tend to get stuck by these obstacles.
The yield of a horizontal well will usually be greater than that of a vertical well. Offerhaus (1961) compared both by investigating options that lead to the same drawdown for both. He considered a RCW with eight laterals of 30 m length each, all located at a height of 30% of the aquifer thickness above its bottom. He obtained its yield using the empirical equation by Falcke (1962). The vertical wells had a drilling diameter of 0.5 m and the maximum permissible drawdown was determined after Sichardt (1928, details see following section). Figure 14 shows on the horizontal axis the yield of a RCW divided by that of a vertical well at the same drawdown. The horizontal axis can tentatively also be used to estimate how many vertical wells a RCW may replace. Varying the saturated aquifer thickness (vertical axis in Fig. 14) and the hydraulic conductivity of the aquifer, Offerhaus (1961) found the ratio of horizontal to vertical well capacity is greatest for relatively thin aquifers with low hydraulic conductivity. Using their analytical model, Beljin and Losonsky (1992) arrived at the same conclusion. In such environments, vertical wells fail to produce much water or lead to excessive drawdown. Only in very thick and highly permeable aquifers will vertical wells have well capacities close to those of horizontal wells. Under such conditions, only a few vertical wells are needed to replace a RCW and the cost-benefit analysis will favor the vertical wells (details see economic appraisal in the ESM).
Head losses and entrance velocity
As with vertical wells, one of the most important design criteria is minimizing the head losses, thus ensuring an energy-efficient operation. In horizontal wells they can occur in the (a) aquifer, (b) skin layer (if present), (c) gravel pack or developed zone, (d) screen, (e) interior of lateral, (f) blind casing (before shaft entrance), (g) inlet to the caisson, (h) the caisson, and finally, (i) riser pipes and pump.
The aquifer losses are, of course, a natural precondition. Only the area immediately around the lateral is affected by drilling-related processes that affect its hydraulic conductivity (Renard and Dupuy 1991). Since laterals are often driven and not drilled, the aquifer material suffers from compaction. On the other hand, material removed during insertion and later development, especially fine-grained material, leads to an improvement of conductivity. The deposition of fines mobilized from the aquifer and from drilling fluid additives (e.g. bentonite, polymer) can lead to the occurrence of a positive skin layer around the lateral, which has a hydraulic conductivity significantly lower than that of the aquifer material (Houben et al. 2016). It is less probable than for most vertical wells because the laterals are usually inserted without the use of drilling fluid additives (exception: HDDW). Due to the commonly lower flow rate per unit of length of screen in horizontal wells, the effect of such a skin layer should be less pronounced than for vertical wells. A negative skin layer (hydraulic conductivity higher than aquifer) occurs when the removal of fines during the insertion of the lateral or a later development was effective. Several of the models described below allow the effects of a skin layer to be addressed (Odeh and Babu 1990; Beljin and Losonsky 1992; Park and Zhan 2002). In several models the skin factor is used – or, maybe better, abused – to include effects that are not related to the deposition or removal of fines at the wellbore but are difficult to quantify. These can include non-Darcy losses and wellbore damage (Hayati-Jafarbeigi et al. 2020). If used in this wider sense, it should be referred to as pseudo-skin factor.
Head losses in the gravel pack should be very small, considering its high hydraulic conductivity and small thickness (Houben 2015b). Similar to vertical wells, the losses caused by the well screen slots are probably negligible (Barker and Herbert 1992a, 1992b; Chen et al. 2003; Houben 2015b). Turbulent losses within long laterals with high pumping rates and small diameters, however, can be significant (Bakker et al. 2005). They can be calculated using the Darcy-Weisbach equation (Weisbach 1845) or similar equations, taking into account the friction of the pipe surface through the surface roughness (Chen et al. 2003; Bakker et al. 2005; Lee et al. 2010; Houben 2015a). Here, of course, the diameter of the lateral plays a major role and a small increase in diameter significantly reduces in-lateral losses. The short blind casing before the shaft entrance can be treated in a similar fashion. Finally, the head losses caused by the outflow from the lateral into the caisson have to be considered (Bakker et al. 2005).
As with vertical wells, the entrance velocity, that is the velocity of groundwater entering the screen, is often used as a design criterion for HWs. Huisman (1972) therefore divides the total flow rate by the total surface area of the laterals; the latter is simply the product of the circumference and length of all laterals. This approach does not, however, consider an unevenly distributed inflow. The resulting velocity should be lower than described by the empirical and dimensionally inconsistent criterion defined by Sichardt (1928).
with
- Q:
-
pumping rate, well discharge (L3/T)
- vcrit:
-
critical or maximum permissible (average) entrance velocity (L/T)
- rl:
-
radius of lateral (L)
- n:
-
number of laterals
- Ll :
-
length of laterals (L)
- Lbc:
-
length of blind casing (L)
- K:
-
hydraulic conductivity of aquifer (L/T)
- C:
-
empirical constant (values of 15, 30 and 60 common)
A further design criterion proposed by Huisman (1972) is the maximum permissible flow velocity inside the laterals, intended to limit turbulent losses. For the sake of simplicity it is calculated at a location immediately before the entrance into the caisson, usually a short blind casing. He recommends values not exceeding 0.75 to 1.0 m/s. While DVGW (2008) recommends 0.7 m/s, Kim et al. (2008, 2012) arrived at a value of 1.0 m/s. These values are significantly smaller than the recommended upflow velocity in vertical wells of 1.5 m/s (Houben 2015a, 2015b). The reason behind this is the commonly much smaller diameter of the laterals of HWs. The diameter has a decisive influence on turbulent pipeline losses (Weisbach 1845).
with
- vcrit:
-
maximum permissible flow velocity in lateral at entry to caisson (L/T)
Lateral geometry
The ideal height of the laterals above the aquifer base is a contested issue. In unconfined aquifers, placing them too high might incur the risk of running dry, if the drawdown becomes too high. The minimum remaining water column above the lateral during pumping should not be less than 1 m. This avoids the intake of air which can disrupt pump operation and cause massive iron oxide clogging (Houben 2003). Placing them too low, at the aquifer base, might lead to unwanted hydraulic interferences with the basal aquitard. Low placement also incurs the danger of striking the aquitard while driving in the laterals, if the aquitard top is not perfectly horizontal or the string deviates. This can lead to the string getting stuck or to later intake of fines from the aquitard during production. Based on his sandtank experiments for homogeneous isotropic aquifers, Falcke (1962) obtained an optimum height of hl-opt = 0.46 of the saturated thickness, that is roughly in the middle. DVGW (2008) recommend a height right between the water table at maximum drawdown and the basal aquitard. The minimum distance to the latter should at least be 1 m. Based on an analytical element model (AEM) and practical experience, Moore et al. (2011) generally support placing the laterals in the middle of the aquifer to avoid interferences from the upper and lower limits. However, they found that a higher lateral position slightly increases the total well yield. A contrasting view is formulated by Birch et al. (2007), who recommend, based on numerical modeling of a bank filtration site, placing the laterals as deep as possible in the aquifer, within 0.5 to 2.5 m above the basal aquitard.
The lateral length is one of the most important parameters, both from a cost and a hydraulic perspective. The yield of a lateral generally grows with its length. This is truer for several laterals, as their interference becomes smaller at increasing distances from the caisson. At some point the gains of longer laterals are diminished disproportionally by the increasing turbulent losses in the lateral, which themselves strongly depend on the diameter. Several authors point out that for each well an optimum lateral length exists, beyond which the flow rate increases very little (Falcke 1962; Dikken 1990; Birch et al. 2007; Kim et al. 2008). For a field-scale model with a lateral of 0.3 m diameter, Bakker et al. (2005) computed the additional discharge caused by extending the lateral. They found that an extension always resulted in an increase of the total discharge. However, for a lateral length beyond 170 m, the relative increase in discharge of an additional 20 m lateral decreased. Many RCWs have smaller diameters than the 300 mm used by Bakker et al. (2005), so in those cases the maximum useful length would be much shorter. This is confirmed by a numerical model study by Birch et al. (2007), who found optimum lengths of 75, 125 and 250–300 m for lateral diameters of 100, 200 and 300 mm, respectively, in an aquifer of good hydraulic conductivity (K = 1 × 10−3 m/s). In aquifers of poor conductivity (K = 1 × 10−6 m/s) the optimum length exceeds 500 m for all three diameters, since the (negative) influence of the aquifer losses overrides the lateral losses. It should be noted, that actual lateral lengths for groundwater applications (Fig. S5 of the ESM) rarely reach the optimum lengths discussed here, so this more a theoretical discussion. Results by Mohamed and Rushton (2006) and Rushton and Brassington (2013a, 2013b) showed that doubling the length from 150 to 300 m for a lateral of 0.15 m diameter increased head losses disproportionally from 0.24 to 0.62 m. There is, however, one point in favor of longer screen lengths. They will distribute drawdown over a larger area and minimize maximum drawdown (e.g. Lee et al. 2010). In very shallow aquifers, this can help prevent the well running dry, e.g. during drought conditions (Rushton and Brassington 2013a, 2013b).
The influence of the number and spatial arrangement of RCW laterals was investigated by Moore et al. (2011), Huang et al. (2012) and Park et al. (2015). It should be noted that these three studies considered bank filtration scenarios only. Moore et al. (2011) studied twelve variations of five different lateral arrangements (Fig. 2), one star-shaped set-up, five fans, one deadman, four pecten and one mousetrap. They found that a six-arm fan and five and six-arm pecten-shaped lateral arrangements facing the river provide the highest total and yields. The mousetrap arrangement yielded the worst performance.
Huang et al. (2012) found that a fan-shaped arrangement with the laterals directed towards the river produces a lower drawdown than the star-shaped and deadman-style arrangements as well as fan-shaped arrangements with laterals facing away from the river. This confirms the results by Moore et al. (2011).
Using numerical models, Lee et al. (2010) and Park et al. (2015) studied different fan-shaped lateral arrangements of the type shown in Fig. 2 of a RCW located near a river. They found that increasing the number of laterals increases the well yield, here expressed as total well yield, but the gain is very minor above five laterals (Fig. 15), probably a reflection of the interferences between them. The specific intake rate per meter of lateral decreases almost linearly with the number of laterals due to their interference (Fig. 15). Considering that additional laterals significantly increase the cost of the RCW, a number of five laterals facing the river is probably the optimum, at least under the conditions studied by Park et al. (2015). Both Lee et al. (2010) and Park et al. (2015) investigated the effect of the angle between individual laterals facing an infiltrating boundary conditions. Lee et al. (2010) found that a decreasing angle (laterals more closely spaced) increases the total drawdown due to the increased hydraulic interference between them but that the overall effect is small. For three laterals, Park et al. (2015) came to a similar conclusion. They found that an angle of 45° yielded the best specific intake rates, although the difference to an angle of 22.5°, equivalent to 16 laterals in a star-shaped RCW, was small. Angles below 22.5° are usually not feasible due to constructional restrictions, as they would endanger the caisson stability (Spiridonoff 1964).
Influence of the number of laterals on total yield and specific yield per meter of lateral length for a fan-shaped RCW facing an infiltrating boundary condition (after data from a numerical model by Park et al. 2015)
The infiltration rate from the river is a function of the ratio of streambed and aquifer permeability (Huang et al. 2012). The percentage of river-borne water in the pumped water is an important piece of information (e.g. Lee et al. 2010). For smaller rivers, the stream depletion caused by bank filtration can negatively affect baseflow and endanger its ecology. Since river water and groundwater often differ in hydrochemistry, e.g. in hardness or anthropogenic pollution, it is important to know their respective percentages in the bulk water to properly set up the water treatment plant.
Modelling groundwater flow to horizontal wells
Introduction
Practically all modeling techniques available in groundwater hydrology have been applied on horizontal wells. Electro-analog models, which are only of historical interest, are discussed in the ESM.
Problems in modeling HW arise from several issues. The first is the problem of scale: while the laterals are very thin, often in the range of 0.1 to 0.3 m, the laterals can be up to 100 m long and the affected aquifer can be kilometers wide. Secondly, HWs are always partially penetrating wells (Hantush and Papadopulos 1962), which prevents the use of simplifying geometries such as radial symmetry, which can be used for vertical wells. Especially the tip(s) of the lateral pose a problem, since flow around them is three-dimensional or axisymmetric. In this sense, they are a kind of singularity of a line sink in the flow field. The inflow distribution over the length of a lateral is also difficult to address and several approaches have been developed (see section ‘General observations on the hydraulics of horizontal screens’). Since most HWs, especially RCWs, have several laterals, sometimes even at different height levels, their 3D interference needs to be considered. In combination, these problems make the mathematical treatment of HWs much more complicated than that of vertical wells.
Many models presented in the following calculate drawdown around one single lateral. For a RCW with several laterals, the total drawdown field in a confined aquifer can be obtained by superimposing the drawdown fields of the individual laterals, of course, taking into account their different angles and lengths (and boundary conditions of the natural flow field). This sounds tedious but can be solved with the help of spreadsheet calculators or computational software.
It should be noted that in almost all of the mathematical models described in the following, a lateral is not represented as a line sink in the strict sense. As described above, it is simulated by a chain of a finite number of point sinks, for which individual drawdowns can be computed and then superimposed (e.g. Polubarinova-Kochina 1955; Wildenhahn 1972; Tarshish 1992; Schafer 2006). Image wells can be used to address the effects of impermeable boundaries. If all sinks have the same strength, a uniform inflow results. Non-uniform flow can be emulated by introducing sinks of varying strengths, for which linear and polynomial relationships have been used, which vary the sink strength as a function of distance along the lateral (Steward and Jin 2001). The problem of the very high inflow rate at the lateral tips can be addressed by assigning a powerful mathematical function to these singularities, e.g. a square function (Haitjema and Kraemer 1988).
Physical sand tank models
Physical models of RCWs were done by Falcke (1962), Nemecek (1961), Kotowski (1982, 1983, 1985, 1988), Chen et al. (2003), Birch et al. (2007), Kim et al. (2008) and Müller et al. (2009). Often, these experiments studied only one lateral. The most comprehensive study is probably the one by Falcke (1952) who performed dozens of experimental variations (for details see ESM). Unlike most analytical models, which assume uniform influx over the length of the lateral, Falcke (1952) realized that most inflow and thus the highest velocities occur at the tip of the lateral. He attributed this to the fact that losses in the aquifer are higher than those in the pipes. The relative importance of losses in the lateral and the aquifer can be quantified by assessing the ratio of the two friction factors, which in the case of the aquifer is the hydraulic conductivity. Lateral inflow becomes more uniform with increasing aquifer flow velocity, decreasing number of laterals, decreasing diameter and increasing lateral length. The non-uniform flow was found to be more pronounced when the lateral is surrounded by a zone of higher hydraulic conductivity (e.g. desanded zone, gravel pack). More flowlines then converge towards the lateral tip. However, more of the water entering at the tip then flows through the desanded zone in the direction to the shaft, before entering the screen, making screen inflow more even. He also found that the yield of an individually operated lateral is significantly higher than that of the same lateral when operating together with neighboring laterals. A better yield can also be obtained by placing the lateral at 46% of the aquifer thickness (above bottom). This is, however, not possible in thin aquifers when high drawdowns in the aquifer are expected. In his experiments, Falcke (1962) found that the relationship between drawdown and pumping rate (yield) is linear up to a drawdown (at the shaft) of 40% of the initial saturated thickness. At higher drawdowns, non-Darcian losses start to occur in the aquifer and turbulent losses in the laterals increase. He also investigated the influence of variations of lateral number, length and diameter on the well yield. Yield initially increases with increasing lateral length but finds a limit due to increasing losses in the lateral itself. The yield is more sensitive to the number of laterals. A higher yield can thus be obtained more easily by increasing the number of laterals rather than by increasing the lateral length. The influence of the lateral diameter is rather weak. Doubling it leads to only a 30% higher yield. This is explained by a more even inflow with lower diameters, leading to lower losses.
Kotowski (1982, 1985) used a 1:25 scale model of an unconfined aquifer, which encompassed a quarter of a cylinder of 4 m radius and 1 to 3 laterals. Otherwise, the set-up was similar to that of Falcke (1962). Buried pressure sensors were used to measure the piezometric head distribution. In all of his set-ups, the yield-drawdown relationship was practically linear, indicating the absence of non-Darcian losses. Similar to Falcke (1962) he found that lateral inflow is not uniform and is influenced by the ratio of the hydraulic resistances of aquifer and lateral. Again, higher inflow peaks were found at the tip of the lateral, especially in longer laterals. Contrary to Falcke (1962), he found that longer laterals are more likely to result in a higher yield than a higher number of laterals. This discrepancy can probably be attributed to the different maximum number of laterals considered, seven by Falcke (1962) and twelve by Kotowski (1985). With an increasing number of laterals, their hydraulic interferences become more pronounced. Both authors agree, however, that the cumulative length of all laterals is the decisive parameter. In a second physical model series, Kotowski (1983, 1988) simulated a horizontal well where the aquifer is overlain by an open water body, e.g. a river or infiltration basin. This also allowed studying the impact of a colmation layer at the river bed. With increasing degree of colmation, the flow to the laterals becomes more uniform, a feature predicted by the model by Kacimov and Obnosov (2008).
Both Falcke (1962) and Kotowski (1982, 1983, 1985, 1988) transferred their model findings to the field scale through empirical equations, which are only of historical interest and thus presented in the ESM.
Chen et al. (2003) used a very large sand tank of 4.5 m length and especially studied the influence of in-lateral head losses and the distribution of Reynolds’ numbers there. Similarly, the physical model by Kim et al. (2008) investigated the influence of lateral length and diameter and the contrast in hydraulic conductivity between aquifer and lateral. The probably largest physical model of horizontal wells was done at the Technical University of Freiberg, Germany, to study their application in the dewatering of lignite mines (Struzina and Drebenstedt 2008b; Müller et al. 2009). They used a concrete basin of 6 m × 6 m × 2.5 m and studied different types and arrangements of screens, including slant wells. They found that the dewatering efficiency increases as an almost linear function of the lateral length. On the other hand, efficiency decreases linearly with decreasing water head above the lateral. Inclined screens showed a slightly better efficiency than vertical ones and the effect becomes more pronounced with increasing inclination. The presence of a gravel pack aids in better dewatering. They also tried a combination of a horizontal drain with a vertical well, the latter right above the former (Struzina and Drebenstedt 2008b; Müller et al. 2009). The expected gain in efficiency due to the vertical screen acting as some kind of pre-collector could not be verified, in fact the efficiency decreased slightly.
Stoeckl and Houben (2012) compared the influence of pumping from vertical and horizontal screens on the freshwater-saltwater interface in a sand tank model. They found that the more evenly distributed drawdown of the horizontal screen leads to less upconing of saltwater.
Ersatzradius method
The effect of the individual laterals on the flow field becomes smaller with increasing distance from the well and at some point the effects are the same as if the RCW was one vertical well of large diameter. Huisman (1972) postulated that the difference becomes negligible at a distance of 1.5 lateral lengths. The numerical models by Collins and Houben (2020), which compared the effects of different boundary conditions for lateral inflow, show actually a factor of only 1.3, which is already sufficient. Some of the first mathematical approaches thus tried to substitute the horizontal well with an equivalent vertical well, for which analytical solutions already existed. Therefore, a so-called “ersatzradius” (analog or equivalent well radius, ersatz = German for replacement) was defined to replace the well radius of the horizontal well by an equivalent, fully penetrating vertical well. The drawdown around the horizontal well in a confined aquifer at steady-state is then given by the Dupuit-Thiem equation (Thiem 1870), assuming horizontal, radially symmetric flow in an isotropic island aquifer.
with
- Q:
-
pumping rate, well discharge (L3/T)
- r0:
-
radius of cone of depression = radial distance from well center to location where drawdown is zero (L)
- rw:
-
radius of (analog) well (L)
and
with
- Fe:
-
correction factor for ersatzradius (L)
- Ll:
-
(average) length of laterals (L)
The radius of the ersatz well is always smaller than the length of the lateral of the HW (Fe < 1). Forchheimer (1886) proposed that a horizontal drainage of a length fD can be considered equivalent to a vertical well with a diameter of half the length of the drainage. Solving Eq. 1 for rw and using some standard parameters, Huisman (1972) arrived at the conclusion that the correction factor should range between 1/6 and 1/3 of the lateral length, measured from the center of the caisson. However, based on experimental and field evidence, several authors proposed correction factors greater than 0.6, which are now commonly used. Nöring (1953) arrived at
with
- nl:
-
number of laterals (−)
- Ll:
-
length of lateral [L]
Mikels and Klaer (1956) used correction factors Fe ranging from 0.75 to 0.80, while Hantush and Papadopulos 1962proposed 0.75. McWhorter and Sunada (1977) suggested a value of 0.61. While these models only consider the lateral length, the model by Wiederhold (1966a, 1966b) considers also the blind casing part of the lateral and the caisson radius.
with
- Lbc:
-
length of blind casing on lateral (L)
- rc:
-
radius of caisson (L)
Collins and Houben (2020) obtained an ersatzradius model, which was trained to emulate the analytical model by Hantush and Papadopulos (1962). It produces a better fit than the previously mentioned ersatzradius methods, especially close to the laterals, at distances as low as 0.75 Ll (Fig. 16).
Comparison of several ersatzradius methods and varying correction factors, and the analytical model by Hantush and Papadopulos (1962). Calculated for a radial collector well with 12 laterals, a caisson of radius 2 m and a lateral length of 33 m. Black line on x axis indicates the length of the lateral
Figure 16 compares several ersatzradius models for a typical radial collector well with 12 laterals, a caisson of radius 2 m, and a lateral length of 35 m. The fit of the ersatzradius model is dependent on the ratio of the caisson radius/cased length of laterals to the filtered length of laterals, as shown by Collins and Houben (2020). The coefficients suggested in the literature of 0.61–0.8, discussed above, would require a very large caisson and relatively short laterals to provide a good fit or, alternatively, several meters of blind casing on the laterals that is not included in the calculation. Two more, less frequently used methods to calculate the ersatzradius are presented in the ESM.
Although the ersatzradius approach is a simplifying approximation, several authors found that the difference between the drawdown field for a horizontal well and that of a vertical well is small for locations far away from the well (Hantush and Papadopulos 1962; Huang et al. 2012; Collins and Houben 2020). Such analog models are thus sufficient for studying the general impact of HW on the aquifer flow field but not for the immediate vicinity of the well, especially not between the laterals.
The ersatzradius approach can also be used for transient conditions, using the Theis (1935) approach for the ersatz vertical well. For a RCW with at least two laterals, Hantush (1964) found that at a distance of r > 5 (rc + Ll), drawdown can be described using the Theis model without correction. Collins and Houben (2020) compared the Theis model to field data from two RCWs and found that it yielded a reasonable fit already at a distance of only 0.5Ll. At the tip of the laterals, the much more complex Hantush and Papadopulos (1962) approach provided no advantage over the Theis vertical well model.
While all ersatzradius models make use of the similarity between the drawdown fields of a vertical and a horizontal well at some distance from the laterals, it should be taken into account that this similarity only develops later during a pumping test, in the pseudo-radial phase (Kawecki 2000). The ersatzradius therefore cannot be applied for pumping tests of short duration, where this stage has not been reached yet.
The ersatzradius method works best when the extraction is distributed evenly over the circumference of the RCW. This does not apply to RCW with a non-uniform spatial orientation of the laterals, e.g. more facing in one direction, as common in bank filtration, or with laterals of significantly different lengths. In this case, more advanced modeling tools may be required.
Analytical and semi-analytical models
Probably the oldest models to describe groundwater flow to a horizontal drain were developed by Adolf Thiem (Thiem 1870) and Philipp Forchheimer (Forchheimer 1886). The most frequently cited analytical model is that of Hantush and Papadopoulos (1962). Details on these models and further models by Polubarinova-Kochina (1955), Ferris (1962), Borisov et al. (1964), Schneebeli (1966), Gringarten et al. (1974), Odeh and Babu (1990), Beljin and Losonsky (1992) and Williams (2013) are discussed in the ESM. Discussing all analytical and semi-analytical (using Laplace transforms) models for 3D flow towards horizontal wells would overstretch the scope of this study and therefore some will only be referenced here, e.g. Wildenhahn (1972), Rückert (1977), Daviau et al. (1988), Strack (1989), Kawecki (2000), Park and Zhan (2003), Steward and Jin (2003), Kawecki and Al-Subaikhy (2005), Anderson (2013), Morozov (2018) (see also brief review in Huang et al. 2012). Zhan et al. (2001) were the first to directly solve the problem of flow to a horizontal well in an anisotropic, confined aquifer. Zhan and Zlotnik (2002), Zhan and Park (2003) and Park and Zhan (2002) derived semi-analytical solutions for 3D flow towards horizontal wells in unconfined and leaky aquifers. Zhan and Zlotnik (2002) developed a solution for unconfined aquifers that accounted for the effect of instantaneous drainage or delayed yield when the free surface declines. Park and Zhan (2002) developed a semi-analytical drawdown solution considering the effects of a finite diameter, the wellbore storage and a skin zone around a horizontal well in anisotropic leaky aquifers. They found that those effects cause significant change in drawdown at an early pumping period. Zhan and Park (2003) provided a general semi-analytical solution for pumping-induced drawdown in a confined aquifer, an unconfined aquifer on a leaky bottom and a leaky aquifer. More recently, Huang et al. (2011, 2012, 2016) published analytical models that consider a horizontal well close to a river, rather than in an infinite aquifer, and Blumenthal and Zhan (2016) derived a rapidly computed analytical solution for drawdown caused by a partially or fully penetrating directional wellbore (vertical, horizontal, or slant) via the Green’s function method. For a range of commonly used analytical and semi-analytical models, Table S1 of the ESM summarizes the applicability in terms of aquifer type, considered parameters and boundary conditions. Figure S7 of the ESM compares several models to Hantush and Papadopulos (1962).
Analytical element models
Analytical elements models (AEM) of RCW have been published by Steward (1999), Luther and Haitjema (1999), Steward and Jin (2001), Bakker et al. (2005), Patel et al. (2010), Moore et al. (2011) and Ameli and Craig (2018). The AEM is based on the superposition of analytic solutions (e.g., Strack 2003). Each analytic solution represents a feature in the aquifer and has at least one free parameter. The free parameters may be specified or computed from specified field conditions. For example, the Thiem solution for a fully penetrating well is an analytic element. The free parameter is the discharge of the well, which may either be specified or computed from, e.g., the head specified at the well. All unknown free parameters in a model must be computed simultaneously as, e.g., the discharge of one well may affect the head at another well or vice versa.
Two of the most useful analytic elements are wells, also referred to as point sinks, and line-sinks. A point-sink extracts water at a point while a line-sink extracts water along a line. The distribution of the extraction along a line-sink, referred to as the inflow, is commonly approximated by a polynomial. Line-sinks exist for two-dimensional flow, three-dimensional flow, and multi-layer flow. Line-sinks are ideally suited to simulate HWs or RCWs. Each well or arm may either be approximated by one line-sink where the distribution of the inflow is approximated by a polynomial of higher order, or by a string of connected short line-sinks where the inflow is uniform along each line-sink. The free parameters (the coefficients of the polynomial or the inflow along each line-sink of a string) are computed from the specified condition at a number of control points along each lateral. The specified condition can be any of the commonly applied conditions, including specified inflow, specified head just outside the lateral, uniform head inside the lateral, or a varying head inside the lateral based on turbulent head losses.
In two-dimensional solutions, HWs are essentially simulated as fully penetrating ditches or galleries. Special line-sinks have been developed to simulate the high inflow rates near the end points of the laterals (Strack 1989) or to simulate the concentrated inflow using a polynomial of very high order (Janković and Barnes 1999). Steady two-dimensional solutions of RCWs may be useful for regional studies, where the exact three-dimensional flow field near the collector well is not of interest. Specification of an effective entry resistance may yield reasonable approximations of the head in the well (following Haitjema et al. 2010). Two-dimensional solutions were applied, e.g., to study the performance of different layouts of laterals (Patel et al. 2010; Moore et al. 2011).
In three-dimensional solutions, HWs are simulated with three-dimensional line-sinks that may have arbitrary orientation. Special three-dimensional line-sinks were developed to simulate the high inflow rates near the ends (Haitjema and Kraemer 1988). The horizontal top and bottom of the aquifer may be simulated with the method of images (Haitjema 1985), by placing an array of imaginary alternating sinks-sources whose action ensures impermeability of both the bedrock and caprock. Polubarinova-Kochina (1977) presented a similar superposition of point sinks and sources for the case of a physical point sink placed between a bedrock and equipotential plane modeling a ponded soil surface. A phreatic top boundary can be simulated with a modified version of the method of images (e.g., Luther and Haitjema 1999) or using series solutions (Ameli and Craig 2018; Iktisanov 2020). Three-dimensional line-sinks were used to study the capture zone of horizontal wells (Steward 1999) and the existence of losing sections of horizontal wells (Steward and Jin 2001).
In practice, multi-layer analytic elements are the most versatile for the simulation of HWs and RCWs. Multi-layer line-sinks were developed for steady flow (Bakker and Strack 2003) and transient flow (Bakker 2013a). The aquifer is divided into a number of layers, where the thickness of the layer at the depth of a lateral is equal to the diameter of the lateral; line-sinks that represent a lateral are placed in this layer. Each layer may have different aquifer properties, which are piecewise constant in each layer. Vertical flow between layers is simulated using a finite difference approximation. The Dupuit-Forchheimer approximation is applied in each layer, so that three-dimensional pathlines may be simulated (following Strack 1984); the three-dimensional plot of Fig. 9 was created using this technique. Slanted laterals may be simulated by discretizing the aquifer in many thin layers and by approximating the angle well by a sequence of horizontal line-sinks in a stepwise manner.
Multi-layer analytic element solutions for steady flow to radial collector wells are compared to a three-dimensional analytic element solution in Bakker et al. (2005), which shows that the multi-layer solution is a very accurate approximation of the three-dimensional solution, even for unconfined conditions, as the drawdown of the water table is commonly small for horizontal wells or collector wells. A multi-layer analytic element solution for transient flow to a horizontal well in an unconfined aquifer is compared to the semi-analytic solution of Zhan and Zlotnik (2002) in Bakker (2013b); a close match between the two solutions was obtained using only 12 layers.
Numerical modeling
Compared to the analytical models presented above, numerical models are more flexible with regard to the geometries of the HW and the types and locations of boundary conditions that can be treated. All types of grid discretization have been used for numerical modeling of RCW, finite difference (Eberts and Bair 1990; Cunningham et al. 1995; Kawecki and Al-Subaikhy 2005; Mohamed and Rushton 2006; Su et al. 2007; Patel et al. 2010; Kelson 2012; Collins and Houben 2020; Božović et al. 2020), polygon finite difference (Chen et al. 2003), finite element (Ophori and Farvolden 1985; Birch et al. 2007; Lee et al. 2010, 2012; Dimkić et al. 2013) and finite volume (Hayati-Jafarbeigi et al. 2020). In rectangular finite difference (FD) grids, RCW laterals may not align with the rows and columns of the model grid, or in other words, are not at right angles to the grid cells. This can be problematic, especially when modeling converging flow to a lateral and require additional grid refinement (Kelson 2012).
A general problem for including HW and RCW in grid-based numerical models is the range of scales involved. The laterals have diameters of a few decimeter and lengths of several tens of meters. Due to the often high pumping rates, the area of the aquifer affected can easily reach several square kilometers. As an example of the scale problem, Lee et al. (2012) studied a RCW with laterals of 0.2 m diameter and 25 m of length but had to consider a model area of 46 km2. These different scales can invoke problems with the spatial discretization of the grid, which needs to be very fine around the laterals. The scale range of up to four orders of magnitude may require a grid refinement likely to strain computational resources (Haitjema et al. 2010). As stated above, flow in the aquifer matrix around a HW is likely to be linear-laminar (Darcy flow), while turbulent flow will prevail in the long and thin laterals. A full treatment of both laminar aquifer flow and discrete turbulent flow in one model is mathematically and computationally demanding.
The treatment of laterals in the numerical models thus differed considerably. While Eberts and Bair (1990) simply modeled their RCW as one very large model cell (330 m × 330 m), Ophori and Farvolden (1985) modeled the lateral as three point sinks of equal strength. Chen et al. (2003) modeled the laterals as an equivalent porous medium with the hydraulic conductivity depending on the flow rate. The latter was done to address the different flow regimes, e.g. laminar and turbulent. Birch et al. (2007) used a similar approach; they calculated the head losses in the laterals using the Darcy-Weisbach equation and re-expressed them via an equivalent hydraulic conductivity, which, when plugged into the numerical model, would result in the initially calculated head losses. Mohamed and Rushton (2006) considered three flow regimes, laminar flow in the aquifer (MODFLOW model), transition from aquifer to lateral, expressed via a resistance coefficient and finally turbulent pipe flow, expressed through the Hazen-Williams equation. The three parts were coupled through a successive calculation of pipe flow, transitional and aquifer flow, looped for each time step until convergence.
In their 3D models, Lee et al. (2010, 2012) also considered laminar, transitional and turbulent flow regimes. They used an empirical coefficient to describe the inflow of groundwater from the aquifer to a lateral, with the in-lateral head losses obtained from the Darcy-Weisbach equation. Since the friction factor is a function of the Reynolds number and thus the flow velocity, they were able to vary it with the pumping rate. The friction factor and the lateral losses were then updated iteratively between the model steps. By applying very low pumping rates (36 m3/h), they were even able to induce laminar flow in some parts of the laterals. Such low rates, however, are not very realistic for a RCW. The differences in the friction factor caused by going from laminar to turbulent lateral flow had a small effect on the head loss and the inflow distribution. The influence of pipe roughness was also small.
In their finite element models, Kojić et al. (2007) and Dimkić et al. (2013) combined 3D models of the aquifer with 1D elements representing the RCW laterals. Dimkić et al. (2013) compared a discretization of the laterals versus their simulation as 1D elements and found that the latter approach was reasonably accurate, provided that the modeled system size is significantly greater than the screen dimensions. The axial flow within the laterals was emulated by assigning them with a high conductivity. The connection between the laterals and the aquifer was obtained via shared model cell nodes. The effects of a skin layer was also addressed. Kelson (2012) proposed using a head-dependent flux boundary condition for the laterals within a Dupuit model. For his MODFLOW model he chose the DRN package. With this approach, a fine grid discretization can be avoided, making the model computationally less demanding. The effects of converging flow around the lateral were replaced by an entry resistance, similar to Haitjema et al. (2010). The results compared well to those obtained from a 3D AEM model and a MODFLOW model with a finely discretized grid. Božović et al. (2020) used a similar approach by employing MODFLOW-USG for the aquifer flow and the Connected Linear Network Process package for the laterals. This proved useful to study clogging effects of the zone close to the laterals.
Several authors tested their numerical models against analytical models. Examples include the finite difference model by Kawecki and Al-Subaikhy (2005), which was tested against the analytical solution by Kawecki (2000). Lee et al. (2010) compared their numerical model against the Hunt (2005) model, and Collins and Houben (2020) theirs against Hantush and Papadopulos (1962).
An explicit treatment of the flow in the lateral by the Navier-Stokes equation has been demonstrated by several authors, mostly from the oil and gas industry (Hayati-Jafarbeigi et al. 2020). This approach removes the problem of the more or less approximating boundary conditions of lateral inflow (uniform vs. constant head) and the equivalent conductivity discussed above, but is, of course, computationally much more demanding. Flow in the aquifer is commonly considered to be purely Darcy flow and effects of non-Darcy flow around the lateral are subsumed in a pseudo-skin factor.
Conclusions
Horizontal captures are one of the oldest techniques employed for groundwater recovery. Today, they have been mostly replaced by vertical wells. Their construction requires special techniques (emplacement of caisson and horizontal laterals), which differ significantly from those for vertical wells and are provided by few companies. A single HW or RCW is more expensive but can replace several vertical wells, which result from their lower drawdown and the possibility of installing several long laterals in one well. The lower drawdown makes HW and RCW especially feasible in thin shallow aquifers, where vertical wells are hydraulically limited and also for the prevention of the upconing of saltwater.
The mathematical treatment of HW and RCW is also significantly more elaborate, mostly due to the more complicated geometry of the flow field and the different scales involved, although simplified solutions are available. The issues mentioned above probably prevent many planners from considering HW and RCW as an alternative to vertical wells, although they can be quite competitive when considering their benefits. Further information on the cost-benefit analysis of RCW vs. vertical wells can be found in the ESM, together with a discussion of ageing processes and rehabilitation measures, which also affect the lifetime costs. Hopefully, this study can overcome some prejudices against HW and RCW and can convince some well owners and planners alike to give them a chance in the future.
References
Ameli AA, Craig JR (2018) Semi-analytical 3D solution for assessing radial collector well pumping impacts on groundwater-surface water interaction. Hydrol Res 49(1):17–26
Anderson EI (2013) Stable pumping rates for horizontal wells in bank filtration systems. Adv Water Resources 54:57–66
Antipov DM, Ibragimov AI, Panfilov MB (1996) Model of coupled fluid flow in a reservoir and inside a horizontal well. Fluid Dynamics 31(5):718–723
Bakker M (2013a) Analytic modeling of transient multilayer flow. In: Advances in hydrogeology. Springer, New York, pp 95–114
Bakker M (2013b) Semi-analytic modeling of transient multi-layer flow with TTim. Hydrogeol J 21(4):935–943
Bakker M, Strack OD (2003) Analytic elements for multiaquifer flow. J Hydrol 271(1–4):119–129
Bakker M, Kelson VA, Luther KH (2005) Multilayer analytic element modeling of radial collector wells. Ground Water 43(6):926–934
Ball K (2012) Louisville launches innovative RBF project. J Am Water Works Assoc 104(3):60–67
Barker J, Herbert R (1992a) Hydraulic tests on well screens. Appl Hydrogeol 0:7–19
Barker J, Herbert R (1992b) A simple theory for estimating well losses: with application to test wells in Bangladesh. Appl Hydrogeol 0:20–31
Beljin MS, Losonsky G (1992) HWELL: a horizontal well model. In: Solving groundwater problems with models. International Groundwater Modeling Center and the Association of Groundwater Scientists and Engineers, Colorado, USA, pp 45–54
Bieske E (1959) Horizontalfilterbrunnen, ihre Herstellungsverfahren und Bauformen [Horizontal filter wells, their manufacturing processes and designs]. Gas- und Wasserfach 100(34):876–880
Bietmann A (2009) Modellierung der Grundwasserströmung und Charakterisierung der hydrochemischen Verhältnisse des Grundwassers im Wassergewinnungsgebiet Ahlintel (Emsdetten) bei der Anwendung einer neu entwickelten Betriebsweise eine Horizontalfilterbrunnens [Modelling of groundwater flow and characterization of groundwater hydrochemistry in the well field Ahlintel (Emsdetten) during the application of a newly developed mode of operation of a radial collector well]. Münster. Forsch. Geol. Paläontol. 104: p. 129 [PhD thesis Münster University]
Birch S, Donahue R, Biggar KW, Sego DC (2007) Prediction of flow rates for potable water supply from directionally drilled horizontal wells in river sediments. J Environ Eng Sci 6(2):231–245
Bischoff H (1981) An integral equation method to solve three dimensional flow to drainage systems. Appl Math Model 5:399–404
Blumenthal BJ, Zhan H (2016) Rapid computation of directional wellbore drawdown in a confined aquifer via Poisson resummation. Adv Water Resour 94:238–250
Borisov YP, Pilatovskii VP, Tabakov VP (1964) Oil production using horizontal and multiple deviation wells. Nedra, Moscow, p 364 [in Russian]
Božović Đ, Polomčić D, Bajić D, Ratković J (2020) Hydrodynamic analysis of radial collector well ageing at Belgrade well field. J Hydrol 582:124463
Chen HC (2008) Pump induced tilt and pore pressure variations at Fuhrberg, north of Hannover and their modeling in layered half space. PhD thesis Leibniz University Hannover, 115 p
Chen C, Wan J, Zhan H (2003) Theoretical and experimental studies of coupled seepage-pipe flow to a horizontal well. J Hydrol 281(1–2):159–171
Chen HC, Kümpel H-J, Krawczyk CM (2010) Field layout of a tiltmeter array to monitor micro-deformation induced by pumping through a horizontal collector well. Near Surf Geophys 8(4):321–330
Chittaranjan R, Melin G, Linsky RB (2002) Riverbank filtration – improving source-water quality. Kluwer, Dordrecht
Cleveland TG (1994) Recovery performance for vertical and horizontal wells using semianalytical simulation. Ground Water 32(1):103–107
Collins SL, Houben GJ (2020) Horizontal and radial collector wells: simple tools for a complex problem. Hydrogeol J 28:1925–1935
Cooper HH, Jacob CE (1946) A generalized graphical method for evaluating formation constants and summarizing well field history. Am Geophys Union Trans 27:526–534
Cunningham WL, Bair ES, Yost WP (1995) Hydrogeology and simulation of ground-water flow at the south well field, Columbus, Ohio USGS WRI-95–4279
Daffner T, Hüper G, Scheppat-Rosenkranz B, Leibenath C (2010a) Erfahrungen bei der Planung von Horizontalfilterbrunnen in Nass- und Trockenaufstellung [experiences in planning radial collector wells with wet an dry shafts] (part 1). Bbr 05/2010:42-49
Daffner T, Hüper G, Leibenath C, Scheppat-Rosenkranz (2010b) Erfahrungen bei der Planung von Horizontalfilterbrunnen in Nass- und Trockenaufstellung [Experiences in planning radial collector wells with wet an dry shafts] (Part 2). bbr 06/2010:48–53
Daffner T, Klee M, Scheppat-Rosenkranz, Leibenath C (2019a) Rezente Erfahrungen bei der Planung von Horizontalfilterbrunnen – Teil 1 [Recent experiences in the planning of radial collector wells - Part 1]. bbr 10/2019:26–33
Daffner T, Klee M, Scheppat-Rosenkranz, Leibenath C (2019b) Rezente Erfahrungen bei der Planung von Horizontalfilterbrunnen – Teil 2 [Recent experiences in the planning of radial collector wells - Part 2]. bbr 11/2019:48–52
Daviau F, Mouronvai G, Bourdarot G, Curutchet P (1988) Pressure analysis for horizontal wells. SPE Formation Eval 3(4):716–724
Dikken BJ (1990) Pressure drop in horizontal wells and its effect on production performance. J Petrol Techn 42(11):1426–1433
Dimkić M, Pušić M, Vidović D, Isailović V, Majkić B, Filipović N (2010) Numerical model assessment of radial-well ageing. ASCE J Comput Civil Eng 25(1):43–49
Dimkić M, Pušić M, Obradović V, Djurić D (2011) Several natural indicators of radial well ageing at the Belgrade groundwater source, part 2. Water Sci Technol 63(11):2567–2574
Dimkić M, Pušić M, Obradović V, Kovačević S (2012) The effect of certain biochemical factors on well clogging under suboxic and mildly anoxic conditions. Water Sci Technol 65(12):2206–2212
Dimkić M, Ranković V, Filipović N, Stojanović B, Isailović V, Pušić M, Kojić M (2013) Modeling of radial well lateral screens using 1D finite elements. J Hydroinf 15(2):405–415
Divine CE, Roth T, Crimi M, DiMarco AC, Spurlin M, Gillow J, Leone G (2018) The horizontal reactive media treatment well (HRX well®) for passive in-situ remediation. Groundwater Monitor Remed 38(1):56–65
Dugat WD (2009) Interactions and implications of a collector well with a river in an unconfined aquifer with regional background flow. PhD Thesis, Texas A&M University
DVGW (2008) Bau und Ausbau von Horizontalfilterbrunnen [Construction and completion of radial collector wells]. Technische Regel Arbeitsblatt W128, DVGW, Bonn
D'Alessio M, Lucio J, Williams E, Warner J, Seymour D, Jasperse J, Ray C (2018) Flow analysis through collector well laterals: A case study from Sonoma County Water Agency, California. Water (Switzerland), 10(12), art. no. 1848
Eberts SM, Bair ES (1990) Simulated effects of quarry dewatering near a municipal well field. Ground Water 28(1):37–47
Etschel G, Heimberg S (2013) Mechanische Regenerierung eines Horizontalfilterbrunnen [Mechanical rehabilitation of a radial collector well]. Energie Wasser-Praxis 09/2013
Falcke (1962) Modellversuche an Brunnen mit horizontalen Fassungsträngen unter besonderer Berücksichtigung der geometrischen und physikalischen Veränderlichen [Model experiments on wells with horizontal intakes with special emphasis on geometric and physical variables]. PhD thesis, TH Karlsruhe
Falta RW (1995) Analytical solutions for gas flow due to gas injection and extraction from horizontal wells. Ground Water 33(2):235–246
Fehlmann H, Fehlmann JH (1959) Subterranean water collector. Water Sewage Works 106(2):60–64
Fil JF (1950) Horizontal wells reduce salt water intrusion into Guam's water supply. Civil Eng 20:454–455
Fournier LB (1997) Horizontal well technology comes of age. Int Ground Water Technol 3(2):20–21
Fournier LB (2002) Directionally drilled horizontal wells offer cost savings and technical advantages over alternative soil and groundwater remediation systems. Remediation 13(1):87–98
Fournier LB (2004) Can a horizontal well provide the same benefits as a vertical well? Water Well J 58(8):42
Fournier LB (2005) Horizontal wells in water supply applications. Water Well J 59(6):34–36
Furukawa Y, Mukai K, Ohmura K, Kobayashi T (2017) Improved slant drilling well for in situ remediation of groundwater and soil at contaminated sites. Environ Sci Poll Res 24(7):6504–6511
Giese M, Reimann T, Liedl R, Dewandel B, Maréchal J-C, Sauter M (2019) An approximation of inner boundary conditions for wells intersecting highly conductive structures. Groundwater 58(4):611–621
Griggs JE, Peterson FL (1993) Ground-water flow dynamics and development strategies at the atoll scale. Ground Water 31(2):209–220
Grigoryan AM (1969) Development of formations by multilateral and horizontal wells. Nedra, Moscow [in Russian]
Gringarten AC, Ramey HJ, Raghavan R (1974) Unsteady-state pressure distributions created by a well with a single infinite-conductivity vertical fracture. Soc Petrol Eng J 14(4):347–360
Haitjema HM (1982) Modeling three-dimensional flow in confined aquifers using distributed singularities. PhD thesis, Depart Civil Eng, University of Minnesota
Haitjema HM (1985) Modeling three-dimensional flow in confined aquifers by superposition of both two-and three-dimensional analytic functions. Water Resourc Res 21(10):1557–1566
Haitjema HM, Kraemer SR (1988) A new analytic function for modeling partially penetrating wells. Water Resourc Res 24(5):683–690
Haitjema H, Kuzin S, Kelson V, Abrams D (2010) Modeling flow into horizontal wells in a Dupuit-Forchheimer model. Ground Water 48(6):878–883
Hang-Tak J, Hamm S-J, Hong S-O, Lee SY, Kim H-S (2020) Groundwater productivity and rehabilitation of radial collector wells for agriculture near Okseong underground dam. J Korean Earth Sci Soc 41(4):381–390
Hantush MS (1965) Wells near streams with semi-pervious beds. J Geophys Res 70(12):2829–2838
Hantush MS, Papadopulos IS (1962) Flow of ground water to collector wells. Proc Am Soc Civil Eng, J Hydraulics Div HY5:221–224
Hayati-Jafarbeigi S, Mosharaf-Dehkordi M, Ziaei-Rad M, Dejam M (2020) A three-dimensional coupled well-reservoir flow model for determination of horizontal well characteristics. J Hydrol 585:124805
Herbert R (1990) Dug well vs. collector well performance: ODA R & D Project No. 90/11, Development of horizontal drilling rig for alluvial aquifers of high permeability. British Geol. Survey Tech. Rep. WD/90/34, 20 p
Houben G (2003) Iron oxide incrustations in wells, part 1: genesis, mineralogy and geochemistry. Appl Geochem 18(6):927–939
Houben G (2006) The influence of well hydraulics on the spatial distribution of well incrustations. Ground Water 44(5):668–675
Houben G (2015a) Review: hydraulic of water wells - flow laws and influence of geometry. Hydrogeol J 23:1633–1657
Houben G (2015b) Review: hydraulic of water wells - head losses of individual components. Hydrogeol J 23:1659–1675
Houben G, Treskatis C (2007) Water well rehabilitation and reconstruction. McGraw Hill Professional, New York
Houben G, Weihe U (2010) Spatial distribution of incrustations around a water well after 38 years of use. Ground Water 48(5):53–58
Houben G, Halisch M, Kaufhold S, Weidner C, Sander J, Reich M (2016) Analysis of wellbore skin samples - typology, composition, and hydraulic properties. Groundwater 54(5):634–645
Huang CS, Chen YL, Yeh HD (2011) A general analytical solution for flow to a single horizontal well by Fourier and Laplace transforms. Adv Water Resour 34:640–648
Huang CS, Tsou PR, Yeh HD (2012) An analytical solution for a radial collector well near a stream with a low-permeability streambed. J Hydrol 446:48–58
Huang CS, Chen JJ, Yeh HD (2015) Analysis of three-dimensional groundwater flow toward a radial collector well in a finite-extent unconfined aquifer. Hydrol Earth Syst Sci 12:7503–7540
Huang C-S, Chen J-J, Yeh H-D (2016a) Approximate analysis of three-dimensional groundwater flow toward a radial collector well in a finite-extent unconfined aquifer. Hydrol Earth Syst Sci 20(1):55–71
Huang C-S, Tsou P-R, Yeh H-D (2016b) Erratum: corrigendum to “an analytical solution for a radial collector well near a stream with a low-permeability streambed” (J Hydrol (2012) 446–447 (48–58) (S0022169412003034) (10.1016/j.jhydrol.2012.04.028)) J Hydrol 542, 1002
Hubbs SA (2006) Changes in riverbed hydraulic conductivity and specific sapacity at Louisville. In: Hubbs SA (eds) Riverbank filtration hydrology. Nato science series: IV: earth and environmental sciences, vol 60. Springer, Dordrecht
Huber M, Daffner T (2012) Regenerierung eines Horizontalfilterbrunnens in Trockenaufstellung [rehabilitation of a radial collector well with dry shaft]. bbr 12/2012: 46-55
Huber M, Schätz M (2009) Neues horizontales Bohrverfahren im ersten Praxiseinsatz [New horizontal drilling technique in first practical application]. bbr 04/2009: 22-28
Huber M, Walter P (2013) Neubau eines Horizontalfilterbrunnens zur Grundwasserabsenkung in Oberhausen [construction of a new radial collector well for groundwater level control]. bbr 12/2013: 48-53
Huber M, Niespor R, Stadler M (2015) Geothermische Nutzung von Horizontalfilterbrunnen [Geothermal use of radial collector wells]. bbr 06/2015: 56–61
Huisman L (1972) Groundwater recovery. MacMillan, London
Hünerberg K (1959) Untersuchungen an Horizontalfilterbrunnen im Berliner Raum [investigations on radial collector wells in the area of Berlin]. Gas- und Wasserfach 100(34):862–870
Hunt H (2003) Leo Ranney Water Well J 57(10):60
Hunt B (2005) Flow to vertical and nonvertical wells in leaky aquifers. J Hydrol Eng 10:477–484
Hunt H (2006) American experience in installing horizontal collector wells. Water Sci Technol Libr 43(1):29–34
Hüper G, Haertl, Zerobin W, Hladej M (2005) Bau von acht Horizontalfilterbrunnen auf der Donauinsel in Wien [Construction of eight radial collector wells on the Danube Island, Vienna]. bbr 2/2005: 32–39
Iktisanov VA (2007) Hydrodynamic studies and modeling of multilateral horizontal wells. Pluton, Kazan [in Russian]
Iktisanov VA (2020) Description of steady fluid flow towards wells of various configurations and various screening. Proc Mining Inst 243:305–312 [in Russian]
Janković I, Barnes R (1999) High-order line elements in modeling two-dimensional groundwater flow. J Hydrol 226(3–4):211–223
Jasperse J (2009) Planning, design and operations of collector 6. Sonoma County Water Agency NATO Sci Peace Security Ser:169–202
Javandel I, Zaghi N (1975) Analysis of flow to an extended fully penetrating well. Water Resour Res 11(1):159–164
Joshi SD (1988) Augmentation of well productivity with slant and horizontal wells. J Petroleum Technol 40(6):729–739
Joshi SD (1991) Horizontal well technology. PennWell Books, Tulsa
Kacimov AR, Obnosov YV (2008) Leaky-layer seepage: the Verigin function revisited. J Eng Math 62:345–354
Kawecki MW (2000) Transient flow to a horizontal water well. Ground Water 38(6):842–850
Kawecki MW, Al-Subaikhy HN (2005) Unconfined linear flow to a horizontal well. Ground Water 43(4):606–610
Kelson V (2012) Predicting collector well yields with MODFLOW. Ground Water 50(6):918–926
Khisamov RS, Khakimzyanov IN, Petrov VN, Sheshdirov RI, Ziyatdinov AG (2017) 25-year formation experience of drilling wells with horizontal end in the republic of Tatarstan. Georesourc 19(3):159–165
Kim SH, Ahn KH, Ray C (2008) Distribution of discharge intensity along small diameter collector well laterals in a model riverbed filtration. J Irrig Drain Eng –ASCE 134(4):493–500
Kim SH, Ahn KH, Prasher SO, Patel RM (2012) Extending riverbed filtration design velocity for horizontal wells from model to prototypes. Can Biosyst Eng 54:1.1–1.6
Kojić M, Filipović N, Stojanović B, Ranković V, Krstić M, Otaševic L, Ivanović M, Nedeljković M, Dimkić M, Tričković M, Pušić M, Boreli-Zdravković D, Durić D (2007) Finite element modeling of underground water flow with Ranney wells. Water Sci Technol Water Supply 7(3):41–50
Kollis W (1961) Wasserfassung durch einen Horizontalfilterbrunnen unter dem Weichselflußbett zur Wasserversorgung Warschaus [capture of water by a radial collector well under the bed of the Vistula River for the water supply of Warsaw]. WWT 11(3):117–120
Kompani-Zare M, Zhan H, Samani N (2005) Analytical study of capture zone of a horizontal well in a confined aquifer. J Hydrol 307(1):48–59
Kotowski A (1982) Modelowanie fizyczne infiltracyjnych ujęć promienistych wody [Physical modeling of the infiltration of water into radial collector wells]. Archiwum Hydrotechniki 29(3):219–240
Kotowski A (1983) Badania modelowe wpływu uszczelnienia dna źródła infiltracji na działanie ujęć promienistych wody [model studies on the influence of the colmation of the infiltration source floor on the efficiency of radial collector wells]. Archiwum Hydrotechniki 30(3):175–191
Kotowski A (1985) Modellversuche über Horizontalfilterbrunnen bei geringer Grundwassermächtigkeit [Model experiments on radial collector wells at small groundwater thickness]. gwf. Wasser/Abwasser 129(12):804–810
Kotowski A (1988) Modellversuche mit einem Horizontalfilterbrunnen, dessen Filterrohre unter einem Infiltrationsbecken liegen [experiments with a horizontal well with laterals underneath the bottom of an infiltration pond]. GWF Wasser/Abwasser 129(12):804–810
Kotowski A (2017) Simulation studies into the effect of infiltration source bottom seal on radial water intakes performance. Arch Hydrotechn 30:175–191
Krebs H, Serbser J, Jäkel G (1957) Bemerkenswerte Brunnenerneuerung im Wasserwerk Naunhof bei Leipzig durch Vortrieb horizontaler Filterstränge [remarkable well reconstruction in the Naunhof water works, near Leipzig, through insertion of horizontal screens]. Wasserwirtsch Wassertech 7(8):323–325
Lee E, Hyun Y, & Lee K-K, Shin J (2012) Hydraulic analysis of a radial collector well for riverbank filtration near Nakdong River, South Korea. Hydrogeology Journal. 20. https://doi.org/10.1007/s10040-011-0821-3
Lee E, Hyun Y, Lee KK (2010) Numerical modeling of groundwater flow into a radial collector well with horizontal arms. Geosci J 14(4):403–414
Liang X, Zhan H, Zhang Y-K, Liu J (2017) On the coupled unsaturated and saturated flow process induced by vertical, horizontal, and slant wells in unconfined aquifers. Hydrol Earth Syst Sci 21(2):1251–1262
Licht F, Treskatis C, Knopf O. (2001) Einsatz der gesteuerten Horizontalbohrtechnik im Brunnenbau [Utilization of the directional drilling technique in well construction]. bbr 2001 (1): 27-32
Lloyd JW, Yu YH, Peach DW (1993) The management of groundwater abstraction in islands using trenches: a Bahamian example. In: Custodio E, Galofré A (eds.) Proc. 12th saltwater intrusion meeting, Barcelona 1992: 489–503
Lubrecht MD (2012) Horizontal directional drilling: a green and sustainable technology for site remediation. Environ Sci Technol 46(5):2484–2489
Luther K, Haitjema HM (1999) An analytic element solution to unconfined flow near partially penetrating wells. J Hydrol 226(3–4):197–203
Maliva RG, Missimer TM (2015) Well intake systems for SWRO systems: design and limitations. Environm SciEngi (Subseries: Environm Sci) 149:147–162
Maroney CL, Rehmann CR (2017) Stream depletion rate for a radial collector well in an unconfined aquifer near a fully penetrating river. J Hydrol 547:732–741
Mather JD (1975) Development of the groundwater resources of small limestone islands. Qtl J Eng Geol 8:141–150
Missimer TM, Ghaffour N, Dehwah AHA, Rachman R, Maliva RG, Amy G (2013) Subsurface intakes for seawater reverse osmosis facilities: capacity limitation, water quality improvement, and economics. Desalinisation 322:37–51
Missimer TM, Maliva RG, Pankratz T (2015) Innovations in design and operation of SWRO intake systems. Environm Scie Eng (Subseries: Environm Sci) 149:351–360
Mohamad Faizal TB, Mohd Nordin A, Nor Azizi Y, Zaidi E (2019) Feasibility study of riverbed filtration technique at Sungai Kampar Perak by using numerical modelling. J Phys: Conf Series 1351(1):012047
Mohamed A, Rushton K (2006) Horizontal wells in shallow aquifers: field experiment and numerical model. J Hydrol 329:98–109
Moore R, Kelson V, Wittman J, Rash V (2011) A modeling framework for the design of collector wells. Ground Water 50(3):355–366
Morgan JH (1992) Horizontal drilling applications of petroleum technologies for environmental purposes. Ground Water Monit Rev 12(3):98–102
Morozov PE (2018) Steady fluid flow to a radial system of horizontal wells. J Appl Mech Tech Phy 59:273–280
Moses G, Riegert DS (2004) Bringing new life to an old collector well. Water Well J 58(6):14–16
Müller M, Drebenstedt C, Struzina M, Mansel H, Preußler F, Bach F, Kretschmer T, Wagner S, Schramm R, Kummer S (2009) Entwicklung eines umweltschonenden und effzienten Verfahrens zur Entwässerung oberfächennaher Lockergesteine im Bergbau und Bauwesen unter Nutzung der verlaufsgesteuerten Horizontalbohrtechnik (HDD-Brunnen) [Development of an environmentally friendly and efficient method for the drainage of near-surface unconsolidated rocks using directionally drilled horizontal wells (HDD wells)]. Final report of project „Erste Phase der Entwicklung einer umweltschonenden und effzienten Horizontalfilterbrunnentechnik zur Entwässerung oberflächennaher Lockergesteine im Bergbau und Bauwesen. Deutsche Bundestiftung Umwelt. https://www.dbu.de/projekt_22473/01_db_2848.html
Muralidharan D, Rangarajan R, Murthy JVS, Prabhakar Rao Y (2005) Mapping of hydrodynamic changes around radial arms of collector well by streaming potential survey. Curr Sci 88(12):1901–1904
Nahrgang G, Falcke FK (1954) Modellversuche über die Strömungsvorgänge an Horizontalbrunnen [Model experiments on flow processes around horizontal wells]. gwf. Wasser/Abwasser 95(4):111–119
Nemecek EP (1961) Horizontalfilterbrunnen zur Grundwassergewinnung [radial collector wells for groundwater exploitation]. Wasserwirtsch Wassertechn 11:99–107
Nemecek EP (1987) Groundwater utilisation and protection. 277-346, In: Novak P developments in hydraulic engineering- 4, Elsevier, London
Nemecek EP (2006) Horizontalfilterbrunnen [Radial collector wells]. Schriftenreihe Wasserwirtschaft TU Graz 45, TU Graz, Graz
Ng MC, Aguilera R (1999) Well test analysis of horizontal wells in bounded naturally fractured reservoirs. J Can Pet Technol 38(7):20–24
Nöring F (1953) Geologische und hydrologische Voraussetzungen für Horizontalfilterbrunnen [Geological and hydrogeological prerequisites for radial collector wells]. gwf. Wasser/Abwasser 107(32):605–612
Odeh AS, Babu DK (1990) Transient flow behavior of horizontal wells: pressure drawdown and buildup analysis. Society of Petroleum Engineers Formation Evaluation, March: 7–15. (SPE paper 18802)
Ophori DU, Farvolden RN (1985) A hydraulic trap for preventing collector well contamination: a case study. Ground Water 23(5):600–610
Park E, Zhan H (2002) Hydraulics of a finite-diameter horizontal well with wellbore storage and skin effect in leaky aquifers. Adv Water Resourc 25:389–400
Park E, Zhan H (2003) Hydraulics of horizontal wells in fractured shallow aquifer systems. J Hydrol 281:147–158
Park JY, Choi S-M, Kim J-M, Kim GB (2015) Evaluation of impacts of radial arm configurations on performance and efficiency of radial collector wells using a detailed numerical modeling technique. J Geol Soc Korea 51(1):81–92
Patel HM, Eldho TI, Rastogi AK (2010) Simulation of radial collector well in shallow alluvial riverbed aquifer using analytic element method. J Irrigation Drainage Eng 136(2):107–119
Pauw PS, van der Zee SEATM, Leijnse A, Oude Essink GHP (2016) Saltwater upconing due to cyclic pumping by horizontal wells in freshwater lenses. Groundwater 54(4):521–531
Polubarinova-Kochina P (1955) Zadacha o sisteme gorizontal‘nykh skvazhin [the problem of the horizontal well system]. Archiwum Mechaniki Stosowanej. Polska Akademia Nauk 7(3):287–300
Polubarinova-Kochina P (1977) Theory of ground water movement, Second edn. Nauka, Moscow [in Russian]
Remde C (1959) Neuartiger Schacht für Horizontalfilterbrunnen [Novel shaft type for radial collector wells]. Gas- und Wasserfach 100(34):875–876
Renard G, Dupuy JM (1991) Formation damage effects on horizontal-well flow efficiency. J Petrol Technol 43(0): 786–869
Rosa AJ, Carvalho RDS (1989) A mathematical model for pressure evaluation in an infinite-conductivity horizontal well. SPE Formation Eval 4(4):559–566
Rückert H (1977) Die Bemessung von Horizontalfilterbrunnen [The dimensioning of horizontal wells]. PhD thesis, Technical University of Leipzig
Rushton K, Brassington F (2013a) Hydraulic behaviour and regional impact of a horizontal well in a shallow aquifer: example from the Sefton coast, Northwest England (UK). Hydrogeol J 21(5):1117–1128
Rushton K, Brassington F (2013b) Significance of hydraulic head gradients within horizontal wells in unconfined aquifers of limited saturated thickness. J Hydrol 492:281–289
Rushton K, Brassington F (2016) Pumping from unconfined aquifers of limited saturated thickness with reference to wellpoints and horizontal wells. Hydrogeol J 24:335–348
Sass I, Treskatis C (2000a) Verlaufsgesteuerte Trinkwasserbrunnen als neues Fassungsorgan für die Grundwassererschließung [Directionally drilled drinking water well as new capture tool for groundwater exploitation]. Grundwasser 5:17–23
Sass I, Treskatis C (2000b) Herstellungs- und Bemessungsgrundlagen für einen verlaufsgesteuerten Trinkwasserbrunnen als Pilotversuch an einem Standort in Krefeld [Fundamentals of construction and dimensioning of a prototype directionally drilled drinking water well at Krefeld]. Grundwasser 5:24–34
Sawyer CS, Lieuallen-Dulam KK (1998) Productivity comparison of horizontal and vertical ground water remediation well scenarios. Ground Water 36(1):98–103
Schafer DC (2006) Use of aquifer testing and groundwater modeling to evaluate aquifer/river hydraulics at Louisville water company, Louisville, Kentucky, USA. NATO Sci. Ser. IV Earth Environ Sci 60:179–198
Schneebeli G (1966) Hydraulique souterraine [Subsurface hydraulics]. Ed. Eyrollea, Collection du Centre de Recherches et d'Essais de Chatou
Spiridonoff SV (1964) Design and use of radial collector wells. J Am Water Works Ass 56(6):689–698
Stack H (1958) Hydraulische Untersuchungen an zwei Horizontalfilterbrunnen [Hydraulic investigations on two radial collector wells]. gwf. Wasser/Abwasser 99(12):265–268
Steward DR (1999) Three dimensional analysis of the capture of contaminated leachate by fully penetrating, partially penetrating, and horizontal wells. Water Resour Res 35(2):461–468
Steward DR, Jin W (2001) Gaining and losing sections of horizontal wells. Water Resour Res 37(11):2677–2685
Steward DR, Jin W (2003) Drawdown and capture zone topology for nonvertical wells. Water Resour Res 39(8):SBH91–SBH911
Stoeckl L, Houben G (2012) Flow dynamics and age stratification of freshwater lenses: experiments and modeling. J Hydrol 458-459:9–15
Strack OD (1984) Three-dimensional streamlines in Dupuit-Forchheimer models. Water Resourc Res 20(7):812–822
Strack ODL (1989) Groundwater mechanics. Prentice Hall, Englewood Cliffs
Strack OD (2003) Theory and applications of the analytic element method. Rev Geophys 41(2):1–19
Struzina M, Drebenstedt C (2008a) Horizontal wells installed by horizontal directional drilling (HDD) as an alternative mine dewatering technology. In: ISCSM - 9-th Int Symp continuous surface mining, University of Petrosani, Romania
Struzina M, Drebenstedt C. (2008b) Large scale laboratory tests for development of dewatering system for open pit mines based on horizontal filter wells installed by horizontal directional drilling. In: Mine water and the environment, 10-th mine water Assoc Congr, Technical University of Ostrava
Sufi AB, Latif M, Skogerbie GV (1998) Simulating skimming well techniques for sustainable exploitation of groundwater. Irrigat Drainage Syst 12:203–226
Sun F, Yao Y, Li G, Li X (2018) Geothermal energy extraction in CO2 rich basin using abandoned horizontal wells. Energy 158:760–773
Szanyi ML, Hemmingsen CS, Yan W, Walther JH, Glimberg SL (2018) Nearwellbore modeling of a horizontal well with computational fluid dynamics. J Petrol Sc Eng 160:119–128
Tarshish M (1992) Combined mathematical model of flow in an aquifer-horizontal well system. Ground Water 30(6):931–935
Theis CV (1935) The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage. Am Geophys union transact, 16th Ann meeting, part 2, 519–524
Thiem A (1870) Die Ergiebigkeit artesischer Bohrlöcher, Schachtbrunnen und Filtergalerien [The yield of artesian boreholes, shaft wells and filter galleries]. J Gasbeleuchtung Wasserversorgung 13:450–467
Todd DK, Mays LW (2005) Groundwater hydrology. Wiley & Sons, New Jersey
Trüeb E (1969) Aus der praxis von Grundwassererschließung und Brunnenbau [Practical aspects of groundwater exploration and well construction]. Schweizerische Bauzeitung 87(22):429–432
Tsou PR, Feng ZY, Yeh HD, Huang CS (2010) Stream depletion rate with horizontal or slanted wells in confined aquifers near a stream. Hydrol Earth Syst Sci 14(8):1477–1485
Verstraeten IM, Carr JD, Steele GV, Thurman EM, Bastian KC, Dormedy DF (1999) Surface water-ground water interaction: herbicide transport into municipal collector Wells. J Environ Qual 28(5):1396–1405
Wang Q, Zhan H (2017) Intrawellbore kinematic and frictional losses in a horizontal well in a bounded confined aquifer. Water Resour Res 53(1):127–141
Wang J-Z, Jiang X-W, Wan L, Wang X-S, Li H (2014) An analytical study on groundwater flow in drainage basins with horizontal wells. Hydrogeol J 22:1625–1638
Weisbach J (1845) Lehrbuch der Ingenieur- und Maschinen-Mechanik [Textbook of engineering and machine mechanics]. Friedrich Vieweg, Braunschweig
Wiederhold W (1966a) Zur Hydraulik des Horizontalfilterbrunnens – Auswertung von Feldversuchen [On the hydraulics of radial collector wells – evaluation of field tests]. gwf. Wasser/Abwasser 107(28):782–787
Wiederhold W (1966b) Zur Hydraulik des Horizontalfilterbrunnens – Auswertung von Pumpversuchen [On the hydraulics of radial collector wells – evaluation of pumping tests]. gwf. Wasser/Abwasser 107(32):888–891
Wildenhahn E (1972) Beitrag zur Berechnung von Horizontalfilterbrunnen [Contribution to the computation of horizontal wells]. PhD thesis, University of Stuttgart
Williams DE (2013) Drawdown distribution in the vicinity of nonvertical wells. Groundwater 51(5):745–751
Williams DE (2015) Slant well intake systems: design and construction. Environm Sci Eng (Subseries: Environm Sci) 49:275–320
Wright EP, Herbert R, Murray KH, Ball D, Carruthers RM, McFarlane MJ, Kitching R (1989) Final report of collector well project 1983-1988. Brit Geol Surv Techn Report WD/88/31
Yale R (1958) Use of radial collector well in Skagit County, wash. Am Water Works Assoc 50(1):125–128
Yeh HD, Chang YC (2013) Recent advances in modeling of well hydraulics. Adv Water Resour 51:27–51
Zhan H (1999) Analytical study of capture time to a horizontal well. J Hydrol 217(1):46–54
Zhan H, Cao J (2000) Analytical and semi-analytical solutions of horizontal well capture times under no-flow and constant-head boundaries. Adv Water Resour 23(8):835–848
Zhan H, Park E (2002) Vapor flow to horizontal wells in vadose zones. Soil Sci Soc Am J 66(3):710–721
Zhan H, Park E (2003) Horizontal well hydraulics in leaky aquifers. J Hydrol 281:129–146
Zhan H, Zlotnik VA (2002) Groundwater flow to a horizontal or slanted well in an unconfined aquifer. Water Resourc Res 38(7):1108–1129
Zhan H, Wang LV, Park E (2001) On the horizontal-well pumping tests in anisotropic confined aquifers. J Hydrol 252(1–4):37–50
Zingg S, Anagnostou G (2018) Effects of the hydraulic capacity of advance drainage boreholes on tunnel face stability. Tunn Undergr Space Technol 71:518–530
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflicts of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
ESM 1
(PDF 1681 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Houben, G.J., Collins, S., Bakker, M. et al. Review: Horizontal, directionally drilled and radial collector wells. Hydrogeol J 30, 329–357 (2022). https://doi.org/10.1007/s10040-021-02425-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-021-02425-w