Introduction

Fractured and karstified carbonate aquifers constitute major drinking water resources worldwide (Goldscheider et al. 2020). As with other groundwater resources, carbonate aquifers are at risk of pollution by anthropogenic compounds such as nitrate (Vías et al. 2006; Husic et al. 2019). Nitrate contamination has evolved to become a global environmental and health problem (Ward et al. 2018) due to continuing expansion of agricultural production over the last few decades (Morris et al. 2003; OECD 2008). Under oxic conditions, nitrate (NO3−) is usually transported conservatively with percolating water or along groundwater flow paths. In the absence of oxygen, NO3− may be degraded by microbially mediated processes, which leads to the formation of more reduced compounds such as N2 (by denitrification) or NH4+ (by dissimilatory nitrate reduction to ammonium; Korom 1992; Kuypers et al. 2018). The reduction of nitrate constitutes an important natural mechanism for the attenuation of high NO3− concentrations in groundwater in general (Rivett et al. 2008) and specifically in carbonate rock aquifers (Einsiedl and Mayer 2006; Heffernan et al. 2012). Therefore, a better understanding and estimation of the nitrate reduction potential is imperative for safeguarding groundwater quality and the supply of drinking water.

The nitrate reduction potential is mainly governed by the occurrence of suitable redox conditions (e.g., low oxygen concentrations), a sufficient amount of electron donors near groundwater flow paths, and the presence and activity of microbial communities capable of coupling nitrate reduction to the oxidation of bioavailable electron donors. While natural organic matter (NOM) is the most common electron donor for (heterotrophic) denitrification in shallow alluvial aquifers (Smith and Duff 1988; Zarnetske et al. 2011), ferrous iron [Fe(II)] and reduced sulfur [S(-I)] bearing minerals such as pyrite were found to dominate (autotrophic) denitrification in aquifers with low amounts and limited bioavailability of NOM. This includes fractured aquifers in carbonate rocks (Baker et al. 2012; Kim et al. 2016; Opazo et al. 2016), and crystalline bedrock (Pauwels et al. 2000; Orr et al. 2016), but also porous aquifers (e.g., Schwientek et al. 2008; Zhang et al. 2013). The presence of denitrifying microorganisms within fractured carbonate aquifers was confirmed by studies investigating microbial communities in the major conduit and fracture network (Farnleitner et al. 2005; Jakus et al. 2021) or attached to the limestone rock matrix (Herrmann et al. 2017; Starke et al. 2017). However, only a few studies have provided sound estimates of the amount of electron donors available in the aquifer matrix for the observed nitrate reduction processes (e.g., Kludt et al. 2016). Particularly for fractured aquifers, detailed information on the extent of nitrate turnover and the inventory of available electron donors is usually sparse, which often limits the estimation of the nitrate reduction potential to geostatistical or stochastic modeling approaches (Rivas et al. 2017; Loschko et al. 2019).

The Middle Triassic carbonates of the Upper Muschelkalk form an important regional fractured aquifer in southwest Germany, which is used for drinking water supply. The main objective of this study was to assess and estimate the available nitrate reduction potential protecting drinking water wells and springs of the Middle Triassic carbonate aquifer, taking into account the porosities and the contents of Fe(II) and S(-I)-bearing minerals in the major sedimentological facies types of the aquifer’s rock matrix.

Principle approach

To provide realistic estimates of the parameters required for the assessment of the nitrate reduction potential of the Upper Muschelkalk aquifer, first, the major sedimentological facies types of the aquifer’s rock matrix were characterized with respect to hydraulically relevant features and to the content of reactive minerals. The inventory of electron donors available for nitrate reduction within the aquifer was determined by analyzing the abundance of Fe(II) and S(-I) together with the porosity of the rock matrix using thin section microscopy and EDX spectra of rock samples from the main sedimentological facies types (see sections “Type, occurrence, and characterization of reactive minerals”, “Major facies types and distribution of reactive minerals”, and “Evidence of reactivity”). Since nitrate (and oxygen) transport in the aquifer is mainly linked to groundwater flow along fractures, the rock matrix adjacent to these flow paths forms the major zones contributing electron donors for the potential redox processes. The location and distribution of the predominant flow paths were derived from flowmeter logs in three wells extracting groundwater from the Upper Muschelkalk. Gamma logs were used to relate the observed groundwater flow paths with the known lithological and facies profiles from quarries and drilling cores (see section “Groundwater flow paths with advective nitrate transport”). With these data and information, hydraulically active fractures could be interrelated with the measured porosity and Fe(II) and S(-I) concentrations of the respective facies in order to identify potential zones of high nitrate turnover within the aquifer (see section “Zones of high nitrate turnover in the aquifer”). Finally, nitrate degradation processes were evaluated using model simulations of the electron donor/acceptor mass balance along groundwater flow paths for the different facies types. These simulations provided estimates of the remaining nitrate reduction potential as a function of nitrate input concentrations and the time over which this nitrate input might persist (see section “Remaining nitrate reduction potential of the aquifer ”).

Study area

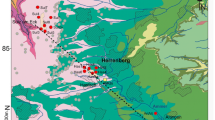
The study area “Oberes Gäu” is an intensively agriculturally used region located in Baden-Württemberg, southwest Germany. It is located near the town of Herrenberg, approximately 25 km SW of the city of Stuttgart and 20 km west of the city of Tübingen (Fig. 1).

Fig. 1
figure 1

a Geologic map of the study area (LGRB 2019) with major tectonic elements and location of sampling sites; b Paleogeography of the Muschelkalk (Middle Triassic; white area) in central Europe (after Hagdorn 1991). The red frame indicates the study area

Full size image

Geological setting

The up to 90-m-thick carbonates of the Upper Muschelkalk (Middle Triassic) shown in Fig. S1 of the electronic supplementary material (ESM) have been extensively investigated with respect to sedimentology (e.g., Köhrer et al. 2010; Palermo et al. 2012; Warnecke and Aigner 2019). The sedimentation area of the Upper Muschelkalk of southwest Germany is interpreted as a shallow marine storm-dominated carbonate ramp (Aigner 1985). It developed on the NW margin of the Vindelician-Bohemian Massif in the semi-enclosed intracratonic Germanic Basin, which was sporadically linked to the Tethys Ocean in the south via the Silesian-Moravian (SiMo), East Carpathian (E-Ca), and the Burgundy seaways or “gates” (Ziegler 1990; Fig. 1b). The gently inclined paleoslope was dipping at less than 1° to the NW into the basin. On a section from SE to NW, different facies zones from the shallow marine to the deep basin can be observed. The succession of the Upper Muschelkalk starts with the shallow marine Zwergfauna-Member and the Haßmersheim-Member, which is characterized by a prominent clay horizon. These are followed by the ramp deposits of the Trochitenkalk Formation, an alternation of more basinal marlstones, mudstones, and crinoidal limestone beds forming an overall fining-upward sequence (Palermo et al. 2012) of stacked meter-scale stratigraphic cycles. The subsequent Meißner Formation forms an overall coarsening upward sequence (Palermo et al. 2012) made up of marlstones, fine-grained limestones, and shoal carbonates. The top of the Muschelkalk is formed by the peritidal dolomites of the Rottweil Formation (“Trigonodusdolomit”), which are overlain with a sequence boundary (Aigner and Bachmann 1992) by the clastic and gypsum deposits of the Keuper Group (Upper Triassic).

As a consequence of tectonic events, such as the rifting of the Atlantic in the Jurassic-Early Cretaceous and the formation of the Upper Rhine Graben in late Eocene-Quaternary, the area was affected by intense fracturing and brittle deformation of the sedimentary cover resulting in the gentle dipping (1–3°) of the lithostratigraphic units to the SE. Faults with horizontal and often lateral displacements up to several tens of meters, e.g. the Swabian Lineament, are trending mainly NW–SE, ENE–WSW and NNE–SSW (Reicherter et al. 2008; Schwarz 2012; Ring and Bolhar 2020). This was accompanied by the rise of hydrothermal fluids (Staude et al. 2009; Pfaff et al. 2010; Bons et al. 2014). In the study area, escaping mantle-born CO2 (Lübben and Leven 2018), which was used by D’Affonseca et al. (2020) to verify the existence of unmapped faults, might be related to these processes.

Hydrogeological setting

The limestone and dolomite rocks of the Upper Muschelkalk constitute a regional fractured aquifer of about 150 km2 in size. In the NW of the study area, the Upper Muschelkalk outcrops below a usually shallow soil cover (0.3–1.8 m) over a distance of 2–4 km and gently dips to the SE, where it is increasingly covered by low-permeability sedimentary Upper Triassic rocks (Fig. 1a). The base of the aquifer is formed by impermeable clayey subrosion residues of the evaporite-dominated formations of the Middle Muschelkalk. The uncovered part of the Upper Muschelkalk constitutes the main recharge area and karstification of the limestone rocks caused numerous dolines and other karstic structures (sinkholes and karstic springs) in this area. Towards the SE the fractured carbonate aquifer becomes confined or even artesian. D’Affonseca et al. (2020) report a mean bulk hydraulic conductivity of 3 × 10−6 m/s for the covered (not karstified) part of the Upper Muschelkalk aquifer, which mainly represents the fracture network of the carbonate formations. A higher mean value of 4 × 10−5 m/s was reported in Villinger (1982) if also the karstified part of the aquifer is taken into account. The porous rock matrix itself can be expected to be much less permeable and only accessible by molecular diffusion. Generally, the groundwater flow direction is from NW to SE following the dipping of the Triassic formations. In addition to karstic features, regional groundwater flow is influenced by numerous tectonic structures and their associated fault systems (D’Affonseca et al. 2020). Most fractures visible in quarries or boreholes follow the ENE–WSW and NW–SE directions of the fault zones. Spacing of the mainly subvertical fractures typically ranges between 1.5 and 5.0 m. No reliable data on fracture apertures were available because of weathering or mechanical stress of the rock faces at quarries.

Sources and cycling of nitrate

Dominant agricultural land use (about 67%; Visser et al. 2021) over the entire study area leads to the release of NO3− from inorganic fertilizers or manure into the karstic aquifer. Groundwater nitrate concentrations decline with increasing distance from the recharge area from elevated values (approximately 35 mg/L on average) to low concentrations in the range of 0–2 mg/L in the confined part of the aquifer. Dissolved organic carbon (DOC) concentrations are generally low (mean of 1.1 mg/L), and no correlation was observed between NO3− and DOC concentrations (Visser et al. 2021), suggesting that electron donors other than DOC might play a role for nitrate reduction. Evidence that the decrease in nitrate is due to microbially mediated nitrate reduction coupled to oxidation of Fe(II) or S(-I) was provided by geochemical and isotopic investigations (Visser et al. 2021) and by microbial enrichment cultures (Jakus et al. 2021) from the aquifer. Nitrate concentrations of up to 80 mg/L are also present in overlying aquifers of the Lower and Middle Keuper. This suggests that dilution with nitrate-poor groundwater by mixing with groundwater from a different recharge area is unlikely to cause the low nitrate concentrations in the confined part of the Upper Muschelkalk aquifer. Moreover, tritium concentrations ranging from 6 to 16 TU (samples collected from 2004 to 2011; unpublished data of the water supplier) indicate that most of the groundwater was recharged after the start of intense fertilizer application about 60 years ago. Access to the groundwater is provided by an artesian monitoring well (ArtAlt) and two production wells (TBEnt1, TBAlt3), which were used for flowmeter logging and chemical monitoring.

Data collection and experimental methods

Petrographical analyses

To investigate the occurrence, amount, and origin of reactive, iron- and sulfur-containing minerals in rocks of the Upper Muschelkalk, rock samples from different locations within the study area were collected from quarries near Herrenberg and Mötzingen and from a recently drilled Muschelkalk core near Reusten (Fig.1). Special care was taken during sampling to consider lithologies that vary in facies type and visible porosity and to select samples from areas with different degrees of tectonic stress. From the samples, about 30 uncovered thin sections mounted on glass-slides 26 × 48 mm and 50 × 50 mm and polished on grinding powder of grit size 100–1,200 to a final thickness of 35 μm were prepared. Thin sections were analyzed with a polarizing light microscope (Leitz Laborlux 12 Pol S) using transmitted and reflected light at a magnification of 50–200 according to lithology and Dunham texture (Dunham 1962), in order to (1) identify type and content of iron-bearing minerals, (2) to estimate macro-porosity and (3) to evaluate sedimentary features of the selected rock samples and identify the facies type. For porosity determination, thin sections were pretreated with blue dyed resin. Thin sections selected for energy dispersive X-ray spectroscopy (EDX) were polished with diamond suspensions of 6–15 μm and 3-μm grain diameter. To prevent the electrically nonconductive samples from becoming charged during electron beam bombardment, the samples were cleaned with acetone, dried and coated with a thin layer of carbon using a Sputter Coater (BAL-TEC Model SCD 005/CEA 035). Analyses of the iron minerals and matrix composition were carried out using a scanning electron microscope (LEO 1450 VP) and EDX-system (OXFORD Instruments INCA Energy300).

Fraction of organic carbon in rock samples

To quantify the organic carbon content (foc) rock samples were crushed using a jaw crusher, dried at 60 °C in an oven, pulverized (ZrO2 ball mill), decarbonized (HCl 16%), purged with deionized water and redried (60 °C). Measurements were performed with an elemental analyzer (Elementar Vario EL; thermal oxidation at 950 °C and CO2 quantification using a heat conductivity detector). Results are reported in wt.%; LOQ = 0.003 wt.%.

Chemical analyses of sulfur as proxy for pyrite concentrations

The determination of pyrite concentrations in rock samples according to the AVS/CRS method was done at Aarhus University, Denmark. The inorganic sulfur was divided into two fractions, acid volatile sulfides (AVS): H2S, FeS, and chromium reducible sulfides (CRS): S0, FeS2. Their digestions were performed following a two-step procedure. In a first step, AVS were distilled from a weighed amount of homogenized rock powder. In a second step, the CRS were determined in the sediment slurry remaining after AVS distillation as described by Fossing and Jorgensen (1989). The total concentration of pyrite was calculated from the total concentration of CRS assuming that pyrite was the only source of chromium-reducible inorganic sulfur in the sample.

Flowmeter and video logging

Flowmeter logging was used to identify groundwater inflow horizons and quantify the corresponding water fluxes at three groundwater wells completed in the Upper Muschelkalk aquifer (see Fig. 1 for their locations). A flowmeter with a hot wire sensor (Berghof Analytik & Umweltengineering GmbH, Tübingen, Germany) using the principle of anemometry (Agarwal and Olin 2014) was used to measure vertical flow rates in the 45-m-deep water supply well TBEnt1 and in the artesian well ArtAlt in April and July 2014, respectively. The 60-m-deep ArtAlt has a completed well casing down to 19 m below ground surface (bgs) corresponding to the base of the Upper Triassic (Lower Keuper) sediments. The remaining 41 m within the Upper Muschelkalk are left unscreened as an open borehole with a diameter of 330 mm (from 19 to 28 m bgs) and 220 mm (from 28 to 60 m bgs). At the 60-m-deep water supply well TBAlt3, an impeller flowmeter (Mount Sopris Instruments, Denver, USA) was used to measure vertical flow rates in Jan 2019. Details on the construction of the wells TBEnt1 and TBAlt3 are provided in Figs. S3 and S4 of the ESM. In total, four flowmeter logs were conducted at each well, at ArtAlt under natural artesian outflow conditions of about 6 L/s, at TBEnt1 and TBAlt3 during groundwater extraction by a submersible pump (Grundfos GmbH, Erkrath, Germany) installed in the well casing a few meters below the groundwater table with a rate of 6.0 and 6.6 L/s, respectively. Each log consisted of continuous measurements with data recording every 5–10 cm starting at least 2 m above and ending 2 m below the screened sections or open borehole. Prior to groundwater extraction, baseline flowmeter logs were measured at TBEnt1 and TBAlt3 under ambient conditions without pumping. At ArtAlt, a video log (Wiggerich Video-Inspektionssysteme, Arnsberg, Germany) was additionally performed in March 2014, which in combination with the results of the flowmeter logging, allowed to visualize the horizons of groundwater inflow.

Depth-specific groundwater sampling

Groundwater samples for hydrochemical and tritium analysis were taken from the artesian well ArtAlt in July 2014, directly after the flowmeter logging. Groundwater was collected from three different depths (17.5 m, 30.5 m, 46.0 m bgs) to capture the changes caused by inflowing groundwater from the major fractures. The samples were taken from all three depths simultaneously with a flow rate of about 0.1 L/min using a set of custom-made pneumatically controlled, miniaturized double-valve pumps. For the pneumatic activation of the pumps, nitrogen gas with a purity of 99.999% was used. Dissolved ions were quantified in the laboratory by ion chromatography (Thermo Scientific Dionex DX-120; Anions: Dionex IonPac A523 analytical column with a Dionex IonPac AG23 guard column; Cations: Dionex IonPac CS12A-5-μm analytical column with a Dionex IonPac CG12A-5-μm guard column; LOQ = 0.1 mg/L).

Tritium was analysed with the 3He-ingrowth method (Sültenfuß et al. 2009). Samples of 500 g of water were degassed and stored for 3He accumulation in dedicated He-free glass bulbs. After a storage period of 2–6 months, 3He was analyzed with the mass spectrometric system at the Bremen Mass spectrometry facility. This method achieves a detection limit of 0.01 TU (tritium unit). The uncertainty is typically less than 3% for samples of >1 TU.

The concentration Cs of an ion (e.g., NO3−, SO42−) or tritium in the collected water samples from depth s represents a mixture of groundwater from the inflow Qn, directly at the sampling depth (with concentration Cn), and the cumulated vertical groundwater flux from other inflow horizons:

$$C_s\;Q_s=C_nQ_n+\sum_{i=1}^{n-1}C_i\;Q_i$$
(1)

where Qs is the cumulative groundwater flux corresponding to the value measured by the flowmeter log at depth s. The concentrations Ci were derived by rearranging Eq. (1) for each inflow horizon i and solving the system of linear equations for the unknown concentrations.

Gamma logging

Logging of the natural gamma radiation was applied for assessment and assignment of the lithological and stratigraphic setting at the artesian well ArtAlt using a slim gamma probe (Mount Sopris Instruments, Denver, USA). Logging was performed over the entire depth of the well with the smallest possible logging speed of approximately 1.8 m/min and a depth resolution of approximately 5 cm. For the analysis, four logs were averaged for improving the signal-to-noise ratio.

Modeling approach

Conceptional setup of geometry and reaction fronts

Advective transport in the carbonate aquifer is restricted to the fracture network of the carbonate rocks. Due to the small permeability of the carbonate formations, water flow in the matrix is assumed to be very low and is therefore neglected. Access to the electron donors in the rock matrix is provided by slow diffusive exchange between mobile water in the fractures and pore water in the rock matrix. Due to reactions between electron donor-bearing minerals in the rock matrix and electron acceptors (O2 or NO3−) entering the porous matrix by diffusion, a moving reaction front will develop along the hydraulically active fractures (Sidborn and Neretnieks 2007, 2008). The extent of rock matrix contributing to the reduction capacity of the aquifer is growing with time and increasing electron acceptor/donor ratio. On time scales of decades or at high electron donor concentration, reduction is restricted to a narrow zone around the fractures, which is usually substantially smaller than the total extent of the aquifer (Fig. 2).

Fig. 2
figure 2

a Schematic display of a typical section across the oxic and the confined part of the fractured carbonate aquifer. The dashed blue line represents the capture zone of a hypothetical well Pm. b Location of electron donor depletion fronts in the rock matrix along a fracture/bedding plane as assumed in the electron acceptor/donor balance model (vertical scale exaggerated). The sketch shows the situation when the front has just reached the location xm of the well. Note that the depths of the fronts within the rock matrix are additive, i.e. the depletion due to reactions of O2 and NO3− only would form a triangular depletion area, as indicated by the dotted line. Note further that the size of this depletion area is ½ zmxm

Full size image

In general, the penetration depth z of a solute or a reaction front into the rock matrix after time t can be expressed based on the mean square displacement (e.g., Grathwohl 1998; Sidborn and Neretnieks 2007):

$$z=\sqrt{2\ {D}_{\mathrm{a}}\ \mathrm{t}}=\sqrt{2{D}_{\mathrm{e}}\frac{C_{\mathrm{a}}}{C_{\mathrm{d}}}\ t}$$
(2)
$${D}_{\mathrm{e}}={D}_{\text{aq}}\frac{\varepsilon }{\tau}\approx {D}_{\text{aq}}\ {\varepsilon}^2$$
(3)

where Da and De are the apparent and effective diffusion coefficients, respectively. The reciprocal of the acceptor/donor ratio Ca/Cd accounts for retardation of the electron donor depletion front in the rock matrix. De is derived from the aqueous diffusion coefficient Daq by accounting for the porosity ε and tortuosity τ of the rock matrix (Rügner et al. 1999; Boving and Grathwohl 2001). After onset of the current hydrological cycle, the oxidation of electron donors by O2 followed by the reduction of natural (nonanthropogenic) NO3− formed a sequence of depletion fronts in the rock matrix along fractures. Due to high concentrations, the recently added anthropogenic NO3− lead to an accelerated penetration of the nitrate depletion front into the matrix as depicted in Fig. 2b. The thickness of the rock matrix contributing to nitrate reduction is considered to reach a maximum value zm at time txm when the depletion front along the fracture reaches a hypothetical well Pm at xm. Given that the reaction front can be approximated by a linear decrease of z with increasing distance along the fracture as shown in Fig. 2b (see also Sidborn and Neretnieks 2007), the total area of NO3− depletion in the rock matrix may be represented by half of the depth zm; hence, the factor ½ in Eq. (5). The prolonged exposure of reactive minerals to O2 and natural NO3− since the onset of the current groundwater flow regime resulted in the depletion of electron donors in parts of rock matrix along the fractures. The degradation of anthropogenic NO3− leads to the depletion of minerals further inside the rock matrix and is additive to the previous mineral depletion. Correspondingly, the depth of the depletion front zm in the rock matrix is calculated independently of any previous mineral depletion (see Fig. 2). This approach is justified by the relatively fast nonreactive diffusion of NO3− across the depleted porous matrix with a pore diffusion coefficient of De/ε (Grathwohl 1998).

Electron acceptor/donor mole balance

The nitrate reduction potential of the fractured carbonate aquifer is assessed by quantifying the moles of electron donors in the rock matrix along hydraulically active fractures, which allow the transport of known quantities of the electron acceptors dissolved oxygen (O2) and nitrate (NO3−). A mole balance is applied to groundwater extracted or discharging naturally from a typical aquifer section forming the capture zone of a hypothetical well Pm (or other discharge point) as shown in Fig. 2. The number of moles of NO3− (or of any other electron acceptor) Na that are transformed in the aquifer section over time t can be derived by:

$${N}_{\mathrm{a}}={C}_{\mathrm{a}}\ Q\ t$$
(4)

where Ca is the concentration of NO3− in mol/L in the groundwater entering the fractures (nitrate input). The discharge Q (in L/year) constitutes the groundwater flux emerging from the fracture network at xm. Note that in Eq. (4) the nitrate input Ca and discharge Q are assumed to remain constant over time or to represent time averaged values. The nitrate reduction potential protecting the well Pm is governed by the volumetric molar concentration of electron donor equivalents Cd in mol NO3−/L, which comprises the concentration Ci of all electron donors in the rock matrix next to the effective fractures and the stoichiometric factors γi of each reaction (moles of NO3− that can be reduced by one mole of donor i): Cd =  ∑ Ciγi. The number of moles of electron donor equivalents Nd that is available for nitrate reduction before the nitrate front reaches the well at Pm can be expressed as:

$${N}_{\mathrm{d}}=2\ {C}_{\mathrm{d}}\ w\ {x}_{\mathrm{m}}\frac{z_{\mathrm{m}}}{2}{n}_{\mathrm{f}}$$
(5)

where w denotes the width of the cross section providing Q (perpendicular to flow but parallel to fracture planes), xm is the distance (parallel to flow) between the well Pm and the boundary to the oxic zone at x = 0 (see Fig. 2), zm is the penetration depth of the nitrate reduction front into the rock matrix at x = 0 for the time when the reaction front reaches the well at Pm, and nf is the number of hydraulically active fractures. The width w of the capture zone of well Pm is related to discharge Q by Darcy’s law:

$$Q=A\ K\ I=d\ {n}_{\mathrm{f}}\ w\ K\ I$$
(6)

where A is the cross-section of the capture zone of well Pm, K is the mean bulk hydraulic conductivity of the fractured aquifer, d the mean fracture spacing, and I the hydraulic gradient along the capture zone. Under the assumption of a network of (parallel) fractures with laminar flow and a mean effective aperture b, the hydraulic conductivity of the fractured aquifer is given by:

$$K=\frac{g}{12\ \vartheta}\frac{b^3}{d}$$
(7)

where g is the gravitational acceleration and ϑ the kinematic viscosity of water at 10 °C.

Assuming a quasi-steady state where the nitrate input concentration, groundwater discharge rate, and groundwater flow paths stay constant over the considered time t, the remaining fraction of protection potential rPP = 1 – Na/Nd along all groundwater flow paths contributing to Q can be quantified by combining Eqs. (4–6):

$${r}_{\text{PP}}=1-\frac{C_{\mathrm{a}}}{C_{\mathrm{d}}}\ \frac{Q\ t}{n_{\mathrm{f}}\ w\ {x}_{\mathrm{m}}\ {z}_{\mathrm{m}}}=1-\frac{C_{\mathrm{a}}}{C_{\mathrm{d}}}\ \frac{d\ K\ I\ t}{x_{\mathrm{m}}\ {z}_{\mathrm{m}}}$$
(8)

By definition, the well protection potential is depleted (i.e. nitrate concentration ≥ 0) when the reaction front has arrived at xm after time t = txm. For this situation, rPP in Eq. (8) becomes zero and thus can be used to determine txm after inserting Eqs. (2) and (3) for zm = z(txm) into Eq. (8):

$${t}_{\text{xm}}=2\ {D}_{\text{aq}}\ \frac{C_{\mathrm{d}}}{C_{\mathrm{a}}}\ {\left(\frac{\varepsilon\ {x}_{\mathrm{m}}}{d\ K\ I}\right)}^2$$
(9)

Inserting this expression into Eq. (2), the average penetration depth of the reaction front zm can also be written as:

$${z}_{\mathrm{m}}=\frac{2\ {x}_{\mathrm{m}}\ {\varepsilon}^2\ {D}_{\text{aq}}}{d\ K\ I}$$
(10)

Now zm is independent of Ca/Cd for a given value of xm. Provided that the different fractures contributing to discharge Q can be represented by “averaged fractures” with an effective aperture and flow velocity, zm constitutes a representative mean of the considered aquifer section. Note that the derivation of Eqs. (9) and (10) is based on the assumption that the reaction with minerals is instantaneous and that the NO3− concentration in the pore water of the rock matrix is much smaller than the concentration of electron donors in the rock. As such it represents an optimal case for nitrate reduction. Inserting Eq. (10) into Eq. (8), the remaining well protection potential rPP becomes:

$${r}_{\text{PP}}=1-\frac{C_{\mathrm{a}}}{C_{\mathrm{d}}}\ {\left(\frac{d\ K\ I}{\varepsilon\ {x}_{\mathrm{m}}}\right)}^2\frac{t}{2\ {D}_{\text{aq}}}$$
(11)

Parameter assignment and model scenarios

The parameters required to calculate rPP can usually be obtained from basic hydrogeological studies or monitoring programs. In this work, rPP was determined for the aquifer matrix of a typical well catchment situated in the confined part of the aquifer. Modeling was performed for the geological and geochemical conditions determined for three of the four investigated facies (aggregating shoal and backshoal facies). In addition, for each facies two different nitrate input scenarios were considered: (1) low natural nitrate concentrations (~1.0 mg/L) that presumably prevailed during onset of the current groundwater flow regime, and (2) high anthropogenic nitrate concentrations (>10 mg/L) that started about 60 years ago. Regional groundwater flow is assumed to take place mainly in horizontal fractures or bedding planes. A spacing of hydraulically active fractures/bedding planes d of 10 m was used, corresponding to a mean value determined from flowmeter logs at the three studied wells. Hydraulic conductivity of the fractured aquifer was set to 2.0 × 10−5 m/s, which is in the upper range of values reported for the confined part of the aquifer (D’Affonseca et al. 2020). The length of the effective bedding planes xm was taken to be about 5,000 m corresponding to the average distance of the production wells from the start of the confining layers preventing oxygen replenishment along karstic features. The hydraulic gradient I of 1.0% was derived from water table contours (D’Affonseca et al. 2020).

The depth of the rock matrix potentially contributing to nitrate reduction was determined using Eq. (10). The effective diffusion coefficient De has been estimated as 0.004–1.0 × 10−10 m2/s for a nitrate diffusion coefficient Daq of 1.5 × 10−9 m2/s (in pure water at 10 °C; e.g., Picioreanu et al. 1997) and mean porosities ε of 23, 5, and 1% of the shoal/backshoal, tempestite, and basinal facies, respectively. Similar values for De were reported by Hill (1984) for a chalk aquifer in the UK. The concentration of electron donor equivalents Cd was determined from measured concentrations of reactive minerals by assuming that nitrate reduction is coupled to the oxidation of reduced iron Fe(II) and sulfur S(-I) contained in pyrite (FeS2) and iron-rich dolomites Ca(Fe,Mg)(CO3)2 according to the following reactions (Straub et al. 1996; Appelo and Postma 2005):

$$5\text{Fe} {\mathrm{S}}_2+14 {\text{NO}}_3+4{\mathrm{H}}^{+}\kern0.5em \to \kern0.5em 10{\text{SO}}_4+7{\mathrm{N}}_2+5{\text{Fe}}^{2+}+2\mathrm{H}_{2}{\mathrm{O}}$$
(12)
$$10{\text{Fe}}^{2+}+2{\text{NO}}_3+24{\mathrm{H}}_2\mathrm{O}\kern0.5em \to \kern0.5em 10\text{Fe}{\left(\text{OH}\right)}_3+{\mathrm{N}}_2+18{\mathrm{H}}^{+}$$
(13)

Based on the stoichiometry of these reactions, Cd in mol/L can be calculated from the average abundance of reactive minerals Cpyr and Cdol (in wt.%) as follows:

$$C_{\mathrm d}=\left(C_{\text{Fe}\left(\text{II}\right)}\cdot\frac{1}{5}+C_{\mathrm S\left(-\mathrm I\right)}\cdot \frac{7}{5}\right) \it{\rho}_{\mathrm r}\left(1-\varepsilon\right)$$
(14)

with:

$${C}_{\text{Fe}\left(\text{II}\right)}=\left({C}_{\text{pyr}}\cdot 0.465+{C}_{\text{dol}}\cdot 0.059\right)\cdot \frac{1000}{55.845}$$
(15)
$${C}_{\mathrm{S}\left(-\mathrm{I}\right)}=\left({C}_{\text{pyr}}\cdot 0.535\right)\cdot \frac{1000}{32.065}$$
(16)

where CFe(II) and CS(−I) are the molar concentrations (in mol/g) of reduced iron and sulfur, respectively. The mean density of the carbonate minerals was set to ρr = 2.7 g/cm3.

Results and discussion

Type, occurrence, and characterization of reactive minerals

Concentrations of organic carbon foc in the Upper Muschelkalk rock matrix are rather low with values in the range of 0.04–0.31 wt.% (three samples from the Herrenberg quarry) and 0.02–0.18 wt.% (six samples from the Mötzingen quarry). The mean foc value of 0.12 wt.% is in good agreement with data from Kleineidam et al. (1999a, b), who reported foc values in Muschelkalk rock fragments from the same region in the range of 0.03–0.09 wt.%. They also showed that, due to burial history, the organic matter in the carbonates of the Muschelkalk is mainly composed of kerogen (inert amorphous organic matter) and of limited bioavailability.

Results from pyrite (FeS2) quantification via sulfur measurements performed in four rock samples from the Herrenberg quarry indicate that considerable amounts of pyrite are present in the rock matrix. The concentration ranges between 0.6 and 1.6 wt.%. Bivalent iron (Fe2+) might also be present as a substitute of Mg2+ in the crystal lattice of dolomites, particularly in the Rottweil Formation (Schauer and Aigner 1997). However, iron concentrations were too low to be quantified (Fig. S2 of ESM), suggesting that these dolomites may not significantly contribute as electron donors. In addition to pyrite, marcasite, a metastable form of FeS2, and saddle dolomite, an iron-bearing dolomite characterized by a higher Fe2+ content, are considered to constitute the main reactive minerals in the Upper Muschelkalk of the study area (Fig. 3).

Fig. 3
figure 3

Thin-section photomicrographs of a Backshoal facies: dolo-mudstone with intercrystalline porosity (blue), Herrenberg quarry (transmitted light). b Shoal facies: bioclastic grainstone with vuggy porosity (blue), Mötzingen quarry (transmitted light). c Shoal facies: saddle dolomite from Mötzingen quarry (transmitted light, crossed polarized light). d Tempestite facies: bioclastic pack- to wackestone with shell debris and crinoid in micritic matrix and brown limonite rims in vuggy porosity, drilling core Reusten (transmitted light). e Tempestite facies with saddle dolomite from drill core Reusten in plane polarized light. f Tempestite facies: thin layer of syn-depositional pyrite (appearing as white-yellow spots) lining rim of shell component from drill core Reusten (reflected light, oil). g Basinal facies with syn-depositional pyrite appearing as white-yellow spots, from Mötzingen quarry (reflected light, oil). h Basinal facies with post-depositional pyrite/marcasite in fracture, from drill core Reusten (transmitted light). i Basinal facies with saddle dolomite as fracture fill from Mötzingen quarry (crossed polarized light)

Full size image

Pyrite occurs as finely distributed crystals of 1–40 μm in size, as framboidal pyrite, in fecal pellets, or along C-rich layers in shell fragments. The subhedral to euhedral, mostly uncorroded pyrite minerals are precipitated in anoxic to suboxic marine sediments at the water-sediment interface and during shallow burial (Berner 1985; Fig. 3g).

Marcasite, an orthorhombic metastable form of FeS2, often is present as aggregates and can be found together with pyrite in fractures and veins indicating a post-sedimentary transport of iron along tectonic pathways.

Saddle dolomite is an iron-bearing dolomite with a considerable Fe2+ content (1.7–2.6 wt.% as obtained from EDX analyses; Fig. S2 of ESM). In thin sections, saddle dolomite shows the typical oscillatory extinction in x-polarized light (Fig. 3c). Characteristic are large mm-sized cloudy crystals, curved cleavage plains, and crystal surfaces often with limonite staining. Coatings with limonite can also occur around the edges of the vugs (Köhrer et al. 2010). Saddle dolomite forms from hypersaline fluids at elevated temperatures from 60° up to 180 °C (Radke and Mathis 1980; Spötl and Pitman 1998; Gregg and Shelton 1990; Davies and Smith 2006), which can be caused by burial diagenesis, a higher geothermal gradient, or by upward movement of hydrothermal fluids (Machel and Lonnee 2002). In the study area, only temperatures of about 60 °C were reached during burial by the maximal 1,000-m-thick sedimentary overload of the Keuper and Jurassic formations (Geyer and Gwinner 2011) at an expected geothermal gradient of 30–40 °C/1,000 m. As already suggested by Zeeh and Geng (2001), it has therefore to be assumed that in the region “Oberes Gäu” percolating hydrothermal fluids supported the precipitation of the saddle dolomite as well as the pyrite/marcasite precipitation in fractures and veins of the Upper Muschelkalk.

Major facies types and distribution of reactive minerals

The occurrence and type of reactive minerals varies across different facies types. In order to describe the reactivity of the Upper Muschelkalk with respect to nitrate reduction, four lithological and geochemical distinct facies types were considered. By regrouping and merging of the original 21 facies types (Warnecke and Aigner 2019), the following four facies types cover the almost complete sequence of the Upper Muschelkalk in the study area: (1) backshoal facies, (2) shoal facies, (3) tempestite facies, and (4) basinal facies. These facies types differ mainly by the depositional environment but also by porosity and type and content of Fe(II) minerals (Table 1).

Table 1 Typical ranges of porosity, pore size, abundance of pyrite (Pyr) and saddle dolomite (sDol) as well as grain sizes of reactive minerals for the main facies types of the Middle Triassic carbonate rocks in the study area
Full size table

Backshoal facies

The low-energy backshoal facies (Fig. 3a) is represented by the dolomitic mud- to packstones of the Rottweil Formation, which were deposited in a peritidal and lagoonal setting. Porosity is high due to intercrystalline pores. Analysis of thin sections from the study area revealed a porosity of 15–28% for this facies type. Values from previous published studies range from 0.1 to 32% (Schauer and Aigner 1997; Köhrer et al. 2010). Pyrite was observed in thin sections in amounts of up to 1 wt.% as small anhedral pyrite crystals in the matrix. Saddle dolomite sometimes is present in pore spaces originating from bioturbation or anhydride solution and in fissures and fractures in an amount of up to 1 wt.%. Zeeh and Geng (2001) give iron content values in the Rottweil Formation of 0.6–0.7 wt.%.

Shoal facies

Towards the basin follow the bioclastic dolomites and limestones of the high energy shoal facies (Fig. 3b, c). Porosity is high due to interparticle and moldic pores. Visual inspection of thin sections suggests a porosity of 15–30%. Previously published studies give porosity values ranging from 4 to 30% (Braun 2003; Kostic and Aigner 2004; Köhrer et al. 2010; Palermo et al. 2012). Pyrite was observed in thin sections in amounts of 1–2 wt.% including early diagenetic pyrite as well as late diagenetic pyrite associated with vuggy and moldic pore spaces. Saddle dolomite is present in fractures and as pore fillings in amounts of up to 2 wt.%.

Tempestite facies

The poorly sorted to graded bioclastic packstones to wackestones of the tempestite facies in the studied rock samples (Fig. 3d–f) are sedimented as proximal to distal storm deposits of the mid to deeper ramp (Aigner 1985; Köhrer et al. 2010). Thin-section examination suggests a porosity value of 0.5–10%. Porosity values from previous published studies range from 0.5 to 20% (Braun 2003; Kostic and Aigner 2004; Köhrer et al. 2010). Pyrite concentrations of 1–2 wt.% were observed in the tempestite facies in reducing micro-environments as early diagenetic pyrite and as pyrite and marcasite in fractures. Saddle dolomite occurs in pore space and in fissures in an amount of 0–2 wt.%.

Basinal facies

The mud-dominated sediments of the basinal facies (Fig. 3g–i) are suspension deposits of the low-energy deeper ramp below the storm wave base. Porosity is low with values of 0.5–5%, which corresponds to ranges from previous published studies (Braun 2003; Kostic and Aigner 2004). However, values in the very low range could not be accurately determined from thin sections. Pyrite occurs as early diagenetic, finely dispersed unaltered subhedral to euhedral crystals of 1–40 μm in size (up to 4 wt.%) or in fractures (Fig. 3g, h). Saddle dolomite is rare but can occur in fissures and fractures (Fig. 3i) and rarely in cavities from bioturbation in an amount of up to 0.5 wt.%.

Evidence of reactivity

In rock fragments and thin sections of the shoal and the tempestite facies, alteration of the saddle dolomite resulted in dark brown limonite rims in the moulds and vugs due to oxidation processes. In general, fresh limestone rock fragments of the Upper Muschelkalk show a medium-to-dark-grey colour, which partly turns to light brown at the surfaces due to weathering. This is believed to be caused by ferric oxyhydroxide accumulating at rims or along fissures. Brownish weathering surfaces are described in other studies, e.g., from the Jurassic Lincolnshire limestone by Baker et al. (2012), and usually attributed to the oxidation of pyrite. Sulfide is converted to aqueous sulfate and removed from the rock matrix whilst ferrous iron is converted to solid ferric oxyhydroxide phases (Baker et al. 2012). On the fracture surfaces a pyrite-depleted brownish high-porosity coating will develop. The contribution of denitrification to the oxidation of pyrite is difficult to assess and the observed coatings most likely resulted from exposure to atmospheric or dissolved oxygen during the present and past hydrological cycles.

Groundwater flow paths with advective nitrate transport

Depth profiles of groundwater inflow and nitrate concentrations at the artesian well ArtAlt, located in the confined part of the aquifer, indicate that only a few fractures significantly contribute to groundwater flow (Fig. 4b). Based on flowmeter logging, four major active fractures were identified (Table 2), which under artesian conditions produced a natural groundwater discharge of 5–50 L/s (2014–2019). Fracture spacing ranges from about 3–16 m with a mean value of 10 m.

Fig. 4
figure 4

a Schematic borehole profile of the artesian well ArtAlt. b Flowmeter log at ArtAlt at natural outflow conditions. Zones of significant groundwater inflow are characterized by steep increases in (vertical) groundwater flux and indicated by blue-shaded areas. The percentages represent the relative increase of the flow rate in relation to the total outflow of about 6 L/s. Variability of the baseline limits the detection of inflows with a contribution of >5%. The sharp drop at 28.5 m as well as the sharp increase in vertical flux at 20 m (dashed lines) are solely caused by changes in borehole diameter at these depths. Red arrows indicate the depths where three groundwater samples for chemical analyses were taken directly after flowmeter logging. c Pictures of the fractures at 26.5–28.0 m and 32.0–33.5 m bgs taken from the video log

Full size image
Table 2 Summary of vertical fluxes representing groundwater inflow Qin, relative contribution of fractures fin, and concentrations of nitrate (NO3−), sulfate (SO4−), and tritium in water samples or calculated for the individual groundwater inflows using Eq. (1) at different depths of the artesian well ArtAlt
Full size table

The video-logging revealed that depths of high inflow correspond with horizontal, partly karstified open bedding planes (Fig. 4c). These “fractures” most probably evolved above thin interbeddings of low-permeability marl or clay layers within the carbonate rocks. This is confirmed by a gamma profile of the borehole at ArtAlt. A correlation with the gamma profile measured at the quarry in Mötzingen (Köhrer et al. 2010; Fig. 5) indicates that the two uppermost flow paths are located within the dolomite rocks of the Rottweil Formation mainly consisting of high-porosity backshoal facies.

Fig. 5
figure 5

a Facies distribution at Mötzingen quarry (lower part not shown here); b Gamma log at Mötzingen quarry; and c Gamma log at groundwater well ArtAlt. Indicator clay horizons (CH) are shown as green lines for orientation. Blue bars indicate the locations of the observed groundwater inflows at ArtAlt. The depth scale is related to the boundary between Upper Muschelkalk (mo) and Lower Keuper (ku). The Mötzingen data were modified after Köhrer et al. (2010)

Full size image

Besides the four active bedding planes, the video logging shows ten additional open bedding planes, which did not produce a clear signal in the flowmeter logs and apparently do not contribute (or only to a minor extent) to groundwater inflows. According to the gamma profile, most of these structures are also associated with bedding planes of carbonate rock overlying clay horizons, as indicated by peaks in gamma counting rates near the bottom of the fractures. However, the data at ArtAlt do not provide evidence that the active bedding planes below the top of the dolomite rocks, including the two lower flow paths, have contact with high-porosity tempestite or low-porosity micritic (basinal) facies.

Nitrate concentrations were low (1–3 mg/L) for all groundwater inflows (see Table 2), suggesting that conditions for nitrate retardation by reactive processes and matrix diffusion are similar at all groundwater flow paths. Moreover, the rather constant sulfate concentrations (agreement within analytical uncertainties) in all sampled groundwater inflows indicate that nitrate reduction is coupled to oxidation of a similar amount (or absence) of pyrite along the different flow horizons. Tritium concentrations between 3 and 6 TU confirm that most of the groundwater extracted from the well ArtAlt is younger than 60 years. The lower tritium content in the upper flow horizon could be due to the location of the bedding plane in the high-porosity backshoal facies intensifying loss of tritium because of matrix diffusion.

The findings in ArtAlt with respect to number and properties of flow paths as well as their position within the Upper Muschelkalk were confirmed at two other locations (production wells TBAlt3, TBEnt1) at about 1.5 and 5.5 km distance from ArtAlt (Fig. 1). In both wells three to four active horizontal flow paths were identified by the flowmeter logging (Figs. S3 and S4 of ESM). Main groundwater inflow again was observed in or close to the high-porosity dolomites of the backshoal facies at the top of the Upper Muschelkalk (Rottweil Formation). These findings suggest that a few partly karstified bedding planes control horizontal flow in the Muschelkalk aquifer at a regional scale. Similar primary flow and transport along major horizontal fractures was inferred from tracer tests and flow logs in a limestone aquifer in Denmark (Mosthaf et al. 2018). Although no vertical fractures were observed at the well, such fractures, when roughly aligned with the general flow direction, may additionally contribute to regional groundwater flow. Moreover, due to the tectonic block structure at the study site (D’Affonseca et al. 2020), the horizontal flow is possibly intercepted on the 1–10-km scale by vertical flow and mixing at fault zones with significant vertical displacements.

Zones of high nitrate turnover in the aquifer

While oxic conditions usually prevail in the uncovered part of karstic or fractured groundwater systems, conditions favourable for denitrification (e.g., low dissolved oxygen) are restricted to the anoxic zone, which is often situated within the confined parts of an aquifer (Rivett et al. 2007; Henson et al. 2019). This is also the case at the study site where high concentrations of dissolved oxygen (3–9 mg/L) and of nitrate (up to 60 mg/L) were measured in groundwater samples from the unconfined part of the Muschelkalk aquifer (Visser et al. 2021). Although Visser et al. (2021) found evidence for potential denitrification in niches where (near) anoxic conditions might develop, e.g., beyond the O2 depletion front in the pore matrix along fractures of the phreatic zone or epikarst, a strong decline in groundwater O2 and NO3− concentrations to values close to the detection limit were only found in the confined part of the aquifer (e.g., well ArtAlt). In this part, the replenishment of oxygen due to fast transport along karstic features or vertical fractures across the vadose zone is prevented by the overlying sediments.

High absolute nitrate turnover rates can be expected to occur at those locations where flow in fractures coincides with high abundance of reactive minerals in the rock matrix. Most likely, ferrous iron and reduced sulfur-bearing minerals in the rock matrix (Table 1) are the main electron donors in the carbonate aquifer. Particularly, the divalent iron minerals pyrite/marcasite and saddle dolomite provide a considerable electron donor capacity for nitrate reduction. Therefore, zones of oxygen consumption and subsequent nitrate reduction in the fractured aquifer are attributed to the occurrence and spatial distribution of these minerals, which can be found (1) in the porous backshoal, shoal and tempestite facies, where the saddle dolomite can be dissolved and the released Fe(II) is subsequently oxidized; the occurrence of these reactions is documented by the limonite rims in vuggy and moldic pore spaces, (2) along fractures filled with post-sedimentary saddle dolomite and pyrite/marcasite, precipitated from ascending hydrothermal fluids, and (3) in the micritic basinal carbonates along fractures and bedding planes, where exposed crystals of syn-sedimentary pyrite can be oxidized to limonite, while pyrite in the central parts of the rock matrix remains unaltered (Baker et al. 2012).

For turnover processes to take place, the reactive minerals are assumed to come into contact with O2 or NO3−, which are transported with groundwater along the horizontal, karstified bedding planes or vertical fractures in the general flow direction. High diffusive fluxes and therefore high nitrate turnover due to a higher effective diffusion constant in Eqs. (2) and (3) can be expected for the high-porosity shoal and backshoal facies, which were found to host the largest part of groundwater flow at the investigated wells in the confined part of the aquifer. However, due to uncertain flow paths between the recharge zone and the studied wells, fractures or bedding planes passing other facies types might contribute substantially to O2 and NO3− depletion, particularly if associated with Fe(II)-rich hydrothermal precipitates near fault zones.

Remaining nitrate reduction potential of the aquifer

The temporal development of the aquifer’s potential to protect wells against nitrate was calculated for the capture zone of a hypothetical water supply well in the confined part of the aquifer, 5 km distant from the uncovered oxic part (Fig. 2). To this end, Eq. (11) was applied with measured porosities and concentrations of pyrite and saddle dolomite of each facies type and a fracture spacing d = 10 m observed at the investigated wells. In Fig. 6, the remaining well-protective nitrate reduction potential rPP of each facies is shown for two nitrate input scenarios: “long-term (~100,000 years) natural background” and “short-term (~100 years) anthropogenic input”. The simulations show that the time required to deplete the nitrate reduction capacity strongly depends on the porosity of the facies constituting the rock matrix. By contrast, the variation of reactive mineral abundances between the facies is small (Table 1) and therefore only of minor importance for the differences in rPP. For NO3− background concentrations below 1 mg/L, the higher-porosity shoal and backshoal facies retains more than 80% of the reduction capacity even for groundwater flow that started prior to the last interglacial (Fig. 6a). If the background NO3− is transported along fractures in the low-porosity basinal facies, the reduction capacity of the aquifer section becomes depleted after about ten thousand years (Fig. 6c).

Fig. 6
figure 6

Remaining well-protective nitrate reduction potential rPP (in %) as a function of the NO3− concentration (y-axis) and time (x-axis). a–c Contours for long-term natural NO3− input concentrations for the different facies. The dashed red line assumes low NO3− background values in groundwater (1 mg/L) over long periods of time. d–f Contours for high NO3− concentrations resulting from anthropogenic N additions for the different facies. The dashed red line highlights the approximate time of high average NO3− concentrations in the study area (35 mg/L). Values for txm and zm(x = 0) refer to the time when the well-protective nitrate reduction will be entirely depleted (rPP = 0) and the depth the reaction front has propagated into the matrix at the upgradient boundary of the anoxic zone at this time

Full size image

When high anthropogenic NO3− concentrations are considered, which entered the groundwater as a consequence of the increased fertilizer application since the 1960s, the reduction capacity remains nearly unaltered for the shoal/backshoal and tempestite facies (Fig. 6d, e). The results for the low-porosity basinal facies indicate a decrease to about 60–70% after anthropogenic NO3− input of approximately 60 years (Fig. 6f). The preservation of the reduction potential in the tempestite, and particularly the shoal/backshoal facies, is a consequence of high matrix porosities—note that the effective diffusion coefficient De increases nonlinearly with porosity in Eq. (3). The higher the matrix porosity, the larger is the volume of the rock matrix that contributes to nitrate reduction and the larger is the quantity of available electron donors. This is indicated by the substantially larger penetration depth of the depletion front of zm = 38 cm in the shoal/backshoal rock matrix as compared to the basinal facies with zm = 0.07 cm.

Calculating the average mineral depletion depth in the rock matrix for different porosities at x = 0 yields: zm(O2) + zm(NO3) = 0.002 to 1.1 m, which is much smaller than the spacing of the fractures. This means that only a small part of the aquifer volume contributes to oxygen consumption and nitrate reduction and hence to the protection of the water supply well against a nitrate breakthrough.

The estimated rPP values shown in Fig. 6 are based on the assumption that all electron donors are used up directly in the rock matrix in instantaneous reactions. Therefore, these estimates represent optimal conditions for the considered nitrate reduction scenarios. Lower rPP values are expected in case of unfavourable conditions for mineral dissolution or reactivity, or if microbial access is limited because only a fraction of the electron donors is available for the reactions. Due to their generally low concentrations, sedimentary organic carbon and DOC are believed to be of no relevance for nitrate reduction in the Upper Muschelkalk aquifer. The maximum potential contribution of sedimentary organic carbon to nitrate reduction (e.g., by additional heterotrophic denitrification) would only amount to about 15% of the overall electron donor capacity assuming a mean foc of 0.1 wt.% as was determined for the Upper Muschelkalk rock matrix.

The results shown in Fig. 6 are sensitive to the hydraulic aquifer parameters, d, K, and I (rPP depends on the square of these parameters); however, thanks to the well logging campaigns and previous work in the study area reported in D’Affonseca et al. (2020), these parameters could be estimated reasonably well. Against this background, it is believed that the rPP values presented here represent good, but optimum estimates. However, the general trends are assumed to be well represented by Fig. 6, which also demonstrates the large differences between the facies types. Additional uncertainties remain due to often low accuracy of the contributing variables such as the hydraulic conductivity K.

The flowmeter logs of three investigated wells at the study site show that a large fraction of groundwater flow takes place in the backshoal facies. Since all wells are located in the confined part of the aquifer, about 5–10 km from the boundary of the uncovered oxic part, the modeling results indicate that for these wells the nitrate reduction potential can be expected to remain fully intact for at least several hundreds of years. However, if groundwater flow towards the wells also includes flow through bedding planes or fractures located in facies of lower porosity, the aquifer’s nitrate reduction potential that can be utilized to protect the wells might diminish over a much shorter period of time. Figure 4 and Figs. S3 and S4 of ESM also show that total groundwater discharge is not distributed equally among the flow paths but is usually dominated by one of the contributing bedding planes. Under the assumption that discharge from all but one groundwater flow path is negligible, the calculation of rPP using Eq. (11) has to account for an increase of the fracture spacing d (by a factor equal to nf= 4), in order to maintain the average hydraulic conductivity K of the aquifer section. In this case, the reduction potential protecting a supply well in the basinal facies would be fully depleted already after 30 years of well operation for NO3− concentrations above 10 mg/L (Fig. 7). Although the aquifer has an almost infinite nitrate reduction potential, this again shows the large uncertainty in predicting reactive nitrate transport in such an aquifer system.

Fig. 7
figure 7

Remaining well-protective nitrate reduction potential rPP (in %) as a function of the NO3− concentration and time, calculated for a larger fracture spacing of d = 40 m as compared to the base case in Fig. 6 (d = 10 m). a–c Contours for long-term natural NO3− input concentrations for the different facies. The dashed red line assumes low NO3− background values in groundwater (1 mg/L) over long (but unknown) periods of time. d–f Contours for high NO3− concentrations resulting from anthropogenic N additions for the different facies

Full size image

Conclusions

Based on investigations of the fractured Upper Muschelkalk aquifer in SW Germany, the nitrate reduction potential is mainly controlled by (1) the presence of Fe(II) or S(-I) bearing mineral phases such as pyrite, marcasite, or saddle dolomite formed under anaerobic conditions in shallow marine sediments or from percolating low-temperature hydrothermal fluids, (2) the diffusion coefficients and thus the matrix porosity of the different carbonate facies, and (3) the spacing of groundwater flow paths (along fractures or bedding planes) and their spatial interrelation with the different facies types. The major facies types show large differences in relevant parameters, and hence in the degradation of nitrate. With the simple electron acceptor/donor balance approach presented in this study, the nitrate reduction potential for water supply wells or other receptors of interest could be estimated. Using observed data from the study site, the results of the estimation show that concentrations of Fe(II)-minerals in the range of 1–4 wt.% represent a high nitrate reduction potential and that to date only a minor part of the nitrate reduction potential of the fractured aquifer has been consumed. Particularly, if large parts of groundwater flow take place in high-porosity facies, the nitrate reduction capacity will most likely remain high over centuries. In contrast, if matrix porosities are low and flow is restricted to one or just as few fractures or bedding planes, then the nitrate reduction capacity protecting a well will be depleted within a few years to decades depending on nitrate concentration. These findings likely also apply for comparable fractured limestone aquifers which have been formed under similar conditions.