Abstract
Formal policy analysis can aid resource management where groundwater is used intensively. Approaches for developing equitable and effective pumping allocations for drought are evaluated in the context of the 2012–2016 drought in Tulare County, California, USA. Potential economic impacts of policy alternatives on two user groups with conflicting interests are considered. Tradeoffs between losses of agricultural profit and response costs for domestic wells that run dry are estimated for various maximum groundwater depth policies. A welfare maximizing approach for identifying policies that limit depth to groundwater is evaluated and found to be ineffective because agricultural opportunity costs are much larger than domestic well costs. Adding a fee for additional drought groundwater pumping is proposed as a more impactful and balanced management policy approach. For the case study presented, a fee range of $300 to $600/acre-foot ($300–$600/1,233 m3) yielded an effective groundwater management policy for reducing domestic well impacts from drought and balancing agricultural impacts of drought with the need to replenish additional drought pumping in wetter years. Recent management policies enacted in the study area agree with this finding. These results may provide a useful perspective for analytically examining and developing groundwater management policies near the study area and elsewhere.
Résumé
Une analyse formelle de la politique peut aider à la gestion des ressources là où les eaux souterraines sont utilisées de manière intensive. Les approches pour le développement d’allocations équitables et efficaces de pompage lors de sécheresse sont évaluées dans le contexte de la sécheresse de 2012–2016 dans le Comté de Tulare, Californie, Etats-Unis d’Amérique. Les impacts économiques potentiels des alternatives de politique sur deux groupes d’usagers aux intérêts conflictuels sont examinés. Les compromis entre les pertes de profit agricole et les coûts associés à l’asséchement des puits domestiques sont estimés pour des politiques concernant différentes profondeurs maximales d’eaux souterraines. Afin d’identifier les politiques limitant la profondeur d’exploitation des eaux souterraines, une approche de maximisation du bien-être social a été évaluée et s’avère inefficace du fait que les coûts d’opportunité agricole sont bien plus importants que les coût des puits domestiques. L’ajout d’une redevance pour un pompage supplémentaire des eaux souterraines en période de sécheresse est proposé comme une approche de politique de gestion plus efficace et plus équilibrée. Pour l’étude de cas présentée, une gamme de redevance de 300 à 600$ par acre-pied ($300–600$/1,233 m3) a abouti à une politique de gestion des eaux souterraines efficace permettant de réduire les impacts de la sécheresse sur les puits domestiques et équilibrer les impacts de la sécheresse sur l’agriculture avec la nécessité de reconstituer l’impact d’un pompage supplémentaire en période de sécheresse au cours des années plus humides. Les politiques de gestion récemment adoptées dans la zone d’étude vont dans le sens de ce constat. Ces résultats peuvent fournir une perspective utile pour l’examen analytique et le développement de politiques de gestion des eaux souterraines près de la zone d’étude et ailleurs.
Resumen
El análisis de políticas formales puede ayudar a la gestión de los recursos cuando las aguas subterráneas se utilizan de forma intensiva. Los enfoques para desarrollar dotaciones de bombeo equitativas y eficaces para la sequía se evalúan en el contexto de la sequía de 2012–2016 en el condado de Tulare, California, Estados Unidos. Se consideran los posibles impactos económicos de las alternativas políticas en dos grupos de usuarios con intereses contrapuestos. Se estiman las compensaciones entre las pérdidas de beneficios agrícolas y los costes de respuesta para los pozos domésticos que se secan para varias opciones de profundidad máxima de las aguas subterráneas. Se evalúa un enfoque de maximización del bienestar para identificar las políticas que limitan la profundidad de las aguas subterráneas y se descubre que es ineficaz porque los costes de oportunidad agrícolas son mucho mayores que los costes de los pozos domésticos. Se propone añadir una tasa por el bombeo adicional de aguas subterráneas durante la sequía como un enfoque político de gestión más impactante y equilibrado. Para el caso de estudio presentado, una tasa de entre $300 y $600 por acre-pie ($300–$600/1,233 m3) dio lugar a una política de gestión de las aguas subterráneas eficaz para reducir los impactos de la sequía en los pozos domésticos y equilibrar los impactos agrícolas de la sequía con la necesidad de reponer el bombeo adicional de la sequía en los años más húmedos. Las recientes políticas de gestión promulgadas en la zona de estudio coinciden con esta conclusión. Estos resultados pueden ofrecer una perspectiva útil para el examen analítico y el desarrollo de políticas de gestión de las aguas subterráneas cerca de la zona de estudio y en otros lugares.
摘要
正式的政策分析可以辅助地下水强开采区的资源管理。在美国加利福尼亚州Tulare县 2012–2016 年干旱情景下,对制定应对干旱公平有效抽水方案的方法进行了评估。考虑了政策替代方案对具有冲突利益的两个用户群体的潜在经济影响。针对各种最大地下水埋深政策,估计了农业利润损失与干涸私有井的响应成本之间的权衡。用于确定限制地下水埋深的政策的利益最大化方法被评估为无效的,因为农业机会成本远大于私有井成本。建议提高额外干旱地下水开采量使用费,作为一种更有影响力和平衡的管理政策方法。对于所提供的案例研究,每英亩-英尺 300 至 600 美元(每 1,233 m3 300 至 600 美元)的费用范围产生了有效的地下水管理政策,以减少干旱对私有井的影响并平衡干旱对农业的影响,以此在丰水年份补充增加的枯水期开采量。研究领域最近颁布的管理政策与本研究一致。这些结果可能为分析检查和制定研究区和附近其他地方的地下水管理政策提供有用的参考。
Resumo
Resumo A análise das políticas formais pode auxiliar na gestão de recursos onde as águas subterrâneas é utilizada intensivamente. Abordagens para desenvolver alocações de bombeamento justo e eficiente para seca foram avaliadas no contexto de seca de 2012–2016 no Condado de Tulare, California, EUA. Impactos econômicos potenciais de políticas alternativas em dois grupos de usuários com interesses conflitantes foram considerados. Acordos entres as perdas do lucro agrícola e custos respostas para poços domésticos que secam foram estimados para várias políticas de profundidade máxima de águas subterrâneas. Uma abordagem de maximização do bem-estar para a identificação de políticas que limitem a profundidade para as águas subterrâneas é avaliada e mostrou-se ineficaz pois os custos das oportunidades agrícolas são muito maiores que os custos dos poços domésticos. Adicionar uma taxa para bombeamento adicional de águas subterrâneas em período de seca foi proposto como a abordagem de políticas de gestão mais impactante e equilibrada. Para o estudo de caso apresentado, uma taxa entre $300 e $600 por acre-pé ($300–$600/1,233 m3) rendeu uma política de gestão de águas subterrâneas eficaz para reduzir os impactos dos poços domésticos da seca e equilibrar os impactos agrícolas da seca com a necessidade de reabastecimento de bombeamento adicional no período de seca em anos mais úmidos. Políticas de gestão recentes decretadas na área de estudo concordam com essa descoberta. Esses resultados podem fornecer uma perspectiva útil para o exame e desenvolvimento analítico das politicas de gestão das águas subterrâneas próximas à área de estudo e outros lugares.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction and objectives
Groundwater resources are used intensively worldwide (Wada et al. 2012; Döll et al. 2014) and are often becoming degraded as a result (Foster and Chilton 2003). This has been the case in California (USA) where the recent 2012–2016 drought exacerbated existing problems from declining groundwater levels (Hanak et al. 2019). The drought, one of the most severe and the warmest on record, had especially pronounced impacts on soil moisture and snowpack (Lund et al. 2018). Streamflows reached record lows in some parts of the state and surface-water deliveries for agricultural irrigation were greatly reduced (Lund et al. 2018; Hanak et al. 2019). Global demand for many of California’s crops prompted increased groundwater pumping to replace surface-water shortfalls and sustain profitable crop production (Medellín-Azuara et al. 2016; Gumidyala et al. 2020). This substitution for irrigation supplies accelerated groundwater overdraft and a range of related problems (Moran et al. 2014) that included domestic well failure (Gailey et al. 2019) and land subsidence (Smith et al. 2017).
An outcome of the drought in California was passage of the Sustainable Groundwater Management Act (SGMA) in 2014 (California Department of Water Resources 2018a). SGMA requires local groundwater management policies to achieve sustainability over a 20-year period and then maintain sustainable conditions for another 30 years. It defines six groundwater sustainability indicators (chronic lowering of groundwater levels, reduction of groundwater storage, seawater intrusion, degraded water quality, land subsidence, and depletions of interconnected surface water) which must be addressed to prevent undesirable results (California Department of Water Resources 2017). Local groundwater sustainability agencies (GSAs) are tasked with planning to manage groundwater resources such that these undesirable results do not become “significant and unreasonable” relative to baseline conditions at the beginning of 2015 (California Department of Water Resources 2017). GSAs must develop management policies that include groundwater depth sustainability criteria over the long-term and maximum depth limits for shorter-term increases in groundwater use to address supply shortages. The GSAs also are allowed to collect fees for groundwater pumping. Basins designated as critically overdrafted were required to submit sustainability plans for review early in 2020 while the deadline for other basins is early in 2022 (Hanak et al. 2019).
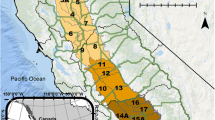
In regions where agriculture is a large part of the local economy and groundwater depletion has occurred for many years, policy evaluation tools may be helpful, if not essential, for successful planning. One such region is the San Joaquin Valley of California, USA (Fig. 1) where most groundwater basins are critically overdrafted. Gailey et al. (2019) suggested an approach for groundwater management policy analysis in part of this region within the context of addressing supply interruptions and economic impacts from domestic wells running dry. For Tulare County, California during the 2012–2016 drought, policies were explored as a range of depth to groundwater (DTGW) limitations to constrain agricultural pumping. The relationship between economic impact to domestic well owners and DTGW policies was presented as a domestic well cost curve for a range of groundwater depths. This curve was considered along with an oppositely sloped agricultural-opportunity cost curve representing costs to agriculture from restricted irrigation pumping. The opportunity cost curve indicated forgone agricultural profits as a result of DTGW policies that constrained irrigation pumping to protect domestic wells. Using information from the two curves, economic interests of the two user groups (domestic well owners and agriculture) relative to DTGW policies were expressed as a single tradeoff curve. While domestic well costs were quantified, agricultural opportunity costs were considered only illustratively. The work presented herein quantifies agricultural opportunity costs using economic optimization analysis, pairs these results with the previous work of Gailey et al. (2019) to extend the analysis of possible DTGW management policies and provide insight for future groundwater management in California and elsewhere.
Methods
Focusing on Tulare County, California during the 2012–2016 drought, an agricultural opportunity cost curve is constructed, a tradeoff curve for the economic interests of the two user groups (domestic well owners and agriculture) is developed, and policies that maximize overall economic welfare are identified. Hydrologic and crop production data from the drought are used to estimate agricultural surface-water deliveries, crop water demands, and groundwater use. With these data, an agricultural profit maximization model is created to develop the agricultural cost curve as a function of groundwater use. Along with this base model, two additional versions of the model are developed to include cropping flexibility and groundwater recovery costs. Using the resulting agricultural cost curves along with the previously developed domestic well cost curve, tradeoff curves are presented for each modeling scenario and the welfare-maximizing DTGW policy for each scenario is identified. The following sections present details of the study area, analysis period, analysis steps (Fig. 2), and key assumptions and limitations. Stone (2019) presents more details on methods and data processing.
Study area and analysis period
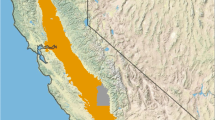
The study area includes much of the Central Valley floor within Tulare County, California (Fig. 3). Agricultural production is the major local industry (Medellín-Azuara et al. 2016). This study focuses on the most recent 2012–2016 drought in California with implications for managing through future droughts. Potential groundwater management decisions and subsequent economic impacts to agriculture and domestic well owners are analyzed by simulating the hydrologic conditions of this recent drought.
Study area (red boundary) within Central Valley floor of Tulare County, California (gray boundary). Orange triangle indicates the representative well location selected by Gailey et al. (2019)
Data collection and estimation
Crop demands and surface-water deliveries
Irrigation in the study area is supplied by surface-water deliveries and groundwater pumping (California Department of Water Resources 2015). Groundwater pumped for agriculture during the drought was estimated as the difference between crop demand and surface-water deliveries. To estimate crop demand in the study area during the drought, land use was first determined using the California Department of Water Resources (CADWR) land use data for 2014 (California Department of Water Resources 2019a). After identifying each land use and corresponding coverage within the study area, the categories that comprise approximately 95% of land use in the study area were selected as a simplifying approximation and scaled to represent the entire study area. Land use categories included 12 crops plus idle and urban uses. Non–crop categories, idle and urban, were omitted from the crop demand calculation, assuming these non–crop categories require little water. Although annual urban water use for Tulare County is about 134 thousand acre-feet (TAF, 0.17 × 106 m3), annual agricultural water use is approximately 2,690 TAF (3.32 × 106 m3) according to 2005–2010 data (California Department of Water Resources 2015). Each of the 12 crops was classified as annual or perennial (Tulare County Agricultural Commissioner 2016). Crop coverages in the study area for each year of the drought were estimated by scaling the 2014 coverage data for the study area relative to annual changes in coverage for the entire county reported in the Tulare County Agricultural Commissioner crop reports (Table 1).
Evapotranspiration (ETc), Eq. (1), was calculated for each year of the drought for each of the 12 crops using crop coefficients (Kc) and daily reference evapotranspiration (ET0) while accounting for precipitation (Orang et al. 2013; Doll 2017; California Department of Water Resources 2019b). Total crop demand per year was calculated as the summation of the products of each crop coverage and corresponding ETc, Eq. (2), and is shown in Table 1 and Fig. 4. The total coverage for annual and perennial crop types vary throughout the drought. While temporal fluctuations of annual crop type coverage can be attributed to fallowing, temporal fluctuations of perennial crop type coverage are most commonly attributed to fallowing older, less long-term productive perennials and planting new perennials in a given year (Sanchez 2017).
where:
- i:
-
is crop type (1–12)
- t:
-
is year (0–5)
- ETc,i,t:
-
is evapotranspiration for each crop i in each year t [AF/acre]
- Kc,i:
-
is the crop coefficient curve for each crop i
- ET0,i,t:
-
is the reference evapotranspiration for each crop i in each year t [AF/acre]
- Ac,i,t:
-
is coverage for each crop i in each year t [acre]
Irrigation districts (IDs) provide much of the surface water to agriculture as farm-gate deliveries and review of local agricultural water management plans indicated the main sources of farm-gate deliveries are local sources (i.e., creeks, rivers, and reservoirs) and the federally operated Friant-Kern Canal.
Farm-gate delivery data were obtained for the IDs in the study area from 2011 to 2016 (California Department of Water Resources 2018b, c, 2019d). However, documentation of farm-gate deliveries for the IDs was temporally and spatially sparse with the largest coverage consisting of 2013 delivery data for 13 IDs, representing 85% of the study area. These select 2013 farm-gate deliveries were scaled, based on area, to reflect farm-gate deliveries for the entire study area in 2013. By a similar process, 2011–2016 Friant Kern deliveries for IDs, with available data, were scaled, based on area, for the entire study area using delivery data from the US Bureau of Reclamation (US Bureau of Reclamation 2019). The temporal trends of Friant-Kern deliveries were used to temporally scale farm-gate deliveries (Fig. 5). These scaled farm-gate deliveries represent surface-water deliveries to the study area from 2011 to 2016.
Groundwater pumped over time and depth to groundwater
The groundwater volume pumped per year in the study area (Fig. 6) was estimated for 2011 to 2016 by assuming that differences between crop demands and surface-water deliveries are supplied from pumping groundwater (Eq. 3).
DTGW values for the study area were estimated using a representative groundwater hydrograph selected by Gailey et al. (2019). The selected well was in the central part of the study area (Fig. 3) and is assumed to represent the entire area. Use of groundwater level data (California Department of Water Resources 2019c) allowed estimation of year-end DTGW values and temporal trends of DTGW values for the study area. Given spatially varying hydrogeologic and pumping characteristics of the study area groundwater system, these DTGW values are simplified estimates of real-world conditions. Assumptions used to develop DTGW values for the study area apply only to the agricultural opportunity cost curve and not the domestic well cost curve from Gailey et al. (2019). Figure 6 presents estimated groundwater pumped and well hydrograph DTGW values during the drought. The relationship of DTGW and groundwater pumped during the drought was approximated through linear regression with DTGW as the dependent variable and cumulative groundwater pumped as the independent variable (Fig. 7).
As expected, with increasing cumulative groundwater pumping, DTGW values increase. The slope of the regression, 6.05 × 10−6 ft./AF (1.84 × 10−6 m/1,233 m3), represents the DTGW decrease for each additional unit of groundwater pumped. This slope was used in the agricultural profit model to provide a relationship between groundwater pumped and subsequent DTGW increase to evaluate DTGW policy compliance.
Agricultural profit optimization model
Each DTGW policy considered represents a limit that requires groundwater users to stop pumping groundwater when the limit is reached. To obtain a relationship between agricultural opportunity costs and DTGW policies, an agricultural profit optimization model was developed. Three versions of the model were created representing different cropping options and groundwater pumping costs. These are discussed in the following sections.
Base model (model 1) formulation
The model formulation is mathematically defined as follows:
subject to:
where:
- GW:
-
is groundwater pumped from year t = 1 to t = 5 (vector of GWt), [AF]
- Π:
-
is profit from year t = 1 to t = 5, [$]
- t:
-
is year (1–5)
- r:
-
is discount rate, [%]
- i:
-
is crop type (1 = annual, 2 = perennial)
- Ai,t:
-
is coverage of crop i in year t, [acre]
- Ri:
-
is net return per acre of crop i, [$/acre]
- Wi,t:
-
is water available for crop i in year t, [AF]
- ATi,t:
-
is total available coverage of crop i in year t, [acre]
- CDi,t:
-
is water demand per acre of crop i in year t, [AF/acre]
- SWt:
-
is surface water available in year t, [AF]
- DTGW0:
-
is initial DTGW, [ft]
- DTGWt:
-
is depth to groundwater change from year t – 1 to t, [ft]
- DTGWpolicy:
-
is allowed maximum DTGW, [ft]
The model is formulated as a nonlinear optimization problem. The objective, Eq. (4), is to maximize agricultural profit (Π) from crop production during the drought by selecting annual groundwater pumping volumes (GW). Discount rate (r), crop coverage (Ai,t), and net return (Ri) are used to calculate agricultural profit for each annual time step (t). The model considers two crop types (i): (1) annual and (2) perennial. Net returns for each of the two crop types were estimated by obtaining historical net returns for crop subtypes from UC Cooperative Extension Cost and Return Studies (University of California Cooperative Extension 2019) and weighting by 2014 coverages. Net return for annual and perennial crops were estimated as $180 and $2,085/acre ($445 and $5,152/ha), respectively.
Total water available (Wi,t) in each time step includes the estimated surface water delivered (SWt) and the optimal volume of groundwater pumped (GWt). The total water available is proportionally allocated between the two crop types based on water available and respective crop type demands in the 2011 base year (Eq. 5). Crop coverages were calculated for each time step as the water available for the respective crop type divided by the crop demand (CDi,t; Eq. 6). Annual crop demands were estimated for 2012–2016, using the method discussed in section ‘Crop demands and surface-water deliveries’, by classifying each of the 12 crop types as either annual or perennial (Tulare County Agricultural Commissioner 2016) and weighting based on respective crop coverage. Actual annual and perennial crop coverages were estimated by scaling 2014 coverages using temporal scaling factors from Tulare County Agricultural Commissioner crop reports, as discussed in section ‘Crop demands and surface-water deliveries’. The upper limit for annual crop type coverage was the actual annual crop type coverage for the respective year (AT1,t; Eq. 7). The upper limit for perennial crop type coverage was the modeled perennial crop type coverage of the previous time step (A2,t–1; Eq. 8). The perennial crop type coverage upper limit accounts for the fact that once fallowed, newly planted perennials are not immediately profitable and thus are not successively fallowed and replanted in a short time period, as opposed to annual crops which may be successively fallowed and replanted (Sanchez 2017).
For each model simulation, a DTGW policy (DTGWpolicy) is specified. For each annual time step, the summation of initial DTGW (DTGW0) and incremental DTGW change (DTGWt), resulting from the groundwater pumped, cannot exceed the specified DTGW policy, Eq. (9). The incremental DTGW change, in each time step, is determined using the relationship between groundwater pumped and DTGW described in section ‘Groundwater pumped over time and depth to groundwater’ (Eq. 10). Lastly, the model is subject to constraints based on initial crop coverages (Ai,0; Eqs. 11–12) and non-negativity (Eqs. 13–15).
Parametric analysis provided information for developing the agricultural cost curves. A set of model runs incrementally examined a range of DTGW policies with pumped groundwater volumes and total agricultural profit being estimated for the 2012–2016 annual time steps. To estimate agricultural opportunity cost, each modeled agricultural profit was subtracted from the maximum agricultural profit. The maximum short-term agricultural profit was estimated from the model run of the largest (most lenient) DTGW policy threshold derived by relaxing Eq. (9) until it was nonbinding. The agricultural opportunity costs and respective DTGW policies were compiled to form the agricultural opportunity cost curve.
Model 2: allowing annual crops to replace perennials
Model 2 includes the same formulation as the base model but allows for planting annual crops to replace fallowed perennial crop coverage in each time step. This additional model element increases cropping flexibility since replacing older, less productive perennials with annual crops may be beneficial during drought. The constraint on the upper limit of annual crop coverage, shown previously as Eq. (7), was updated as follows:
The new term in Eq. (16), \(\sum_1^t\left({A}_{\mathrm{T}2,t}-{A}_{2,t}\right)\), represents the cumulative fallowed perennial crop coverage from year 1 to year t. Agricultural opportunity cost curves were compiled for different discount rates (0, 3 and 6%) to evaluate sensitivity to discounting.
Model 3: including post-drought groundwater recovery costs for drought pumping
Model 3 includes the same formulation as model 2, but also incorporates a groundwater recovery cost for the volume of pumped groundwater that exceeds a base volume. For this analysis, the base groundwater use is the pumped volume in 2011 before the drought. Since sustainable groundwater use entails ending long-term overdraft, a groundwater recovery cost is added to simulate the costs of replenishing groundwater after the drought to predrought conditions. The agricultural user group is assumed responsible for the groundwater recovery cost. To implement this addition, the objective function Eq. (4) was updated as follows:
where:
- Cw:
-
is unit groundwater cost per volume [$/AF]
- Xt:
-
is pumped groundwater volume exceeding the base value, in year t [AF]
- GW0:
-
is pumped groundwater volume in base year 2011 [AF]
The new term in Eq. (17), CwXt, represents the groundwater recovery cost, in units of dollars, and is subtracted from the crop profit term. Specifically, Cw is the unit groundwater recovery cost per volume, in dollars per AF (dollars per 1,233 m3), and Xt is the pumped groundwater volume exceeding the base volume in year t, in units of AF (1,233 m3), as shown in Eq. (18). Different values of Cw, ranging from $0 to $900/AF ($0–$900/1,233 m3), were used in successive model runs. In general, Cw can be considered either as (1) an excess groundwater pumping fee (the cost per unit volume of water to purchase and recharge a basin), or (2) a proxy for future agricultural opportunity costs due to the water scarcity caused by current management decisions. These Cw values used here are exploratory.
Tradeoff curve and policy evaluation
With the agricultural opportunity cost curves developed from the optimization models and the domestic well cost curve from Gailey et al. (2019), a tradeoff (Pareto) curve of respective agricultural and domestic costs for each DTGW policy and approach was developed. Then the DTGW policy along the curve that minimized total cost to the two user groups was identified for each of the three model systems. To estimate this DTGW policy, the total cost to agriculture and domestic well owners was calculated for each DTGW policy and the policy, rounded to the nearest 1 ft. (0.3 m), that corresponded to the minimum total cost was identified as the welfare-maximizing DTGW policy.
Sensitivity analysis
Two sources of uncertainty in the agricultural profit optimization model are: (1) the crop demand for perennial and annual crops and (2) surface water (farm gate deliveries) for the study area. For both crop demand and surface-water data, which were available only for parts of the study area, proportionality was assumed for extrapolating to the entire study area—for example, the weighted perennial crop demand (AF/acre) for the portion of the study area where data was available (95% of the study area) was assumed for the entire study area.
An analysis was done to illustrate model output sensitivity to surface water (SWt) and crop demand (CDi, t) input variables. To vary the surface water and crop demand inputs, the highest and lowest individual values in each respective aggregation (instead of previous proportionality method) were used to scale the available data to the entire study area. For example, instead of using the weighted perennial crop demand, calculated for the part of the study area where the data was available (95% of the study area), for the entire study area, it was assumed that the remaining 5% of the study area had either the highest perennial crop demand or the lowest perennial crop demand, to calculate the perennial crop demand bounds. Perennial crop demand bounds varied from ±1%, annual crop demand bounds varied from ±3%, and surface-water inputs varied from −12 to 34% of the base model formulation.
The range in adjusted inputs were combined in model 3 to simulate worst-case groundwater pumping scenarios: upper-bound (lower surface water, higher crop demand) and lower-bound (higher surface water, lower crop demand). These scenarios simulated groundwater recovery costs (Cw), ranging from $0 to $600/AF ($0–$600/1,233 m3).
Assumptions and limitations
The following sections outline key assumptions and limitations of the methods used in this analysis. Most result from data and modeling simplifications.
Negligible drawdown effect from domestic groundwater pumping
It is assumed that domestic groundwater pumping is a negligible portion of overall groundwater use and adds little to drawdown. In the analysis, DTGW values throughout the drought are driven solely by agricultural groundwater pumping. Agricultural groundwater pumping has historically been much larger than domestic groundwater pumping (Gailey et al. 2019). Assuming each of the 5,774 domestic wells in the study area supports one household, with an annual water demand of about 0.89 AF (1,098 m3; California Department of Water Resources 2014), the estimated annual domestic water demand for the study area is about 5.1 TAF (6,291 m3). Compared to the average annual agricultural groundwater pumped during the drought (Fig. 6), about 1,602 TAF (1.98 × 106 m3), the domestic water demand is minimal.
Limitations of pumped groundwater and DTGW regression
The regression model does not fully encompass the complexity of the groundwater system in the study area. Since the mathematical relationship is based on estimations of pumped groundwater and DTGW values, the regression does not account for all groundwater flow dynamics, hydrogeological processes, and other aquifer-specific characteristics. For example, the data in Fig. 7 suggests a concave relationship between DTGW and cumulative groundwater pumped which may be the result of land subsidence that has occurred in the study area (Smith et al. 2017). However, as shown in Fig. 7, the linear regression’s R2 of 0.94, suggests a reasonable fit to the data for this study. Additionally, pumping outside the study area can influence drawdown inside the study area; thus, the regression tends to overestimate drawdown from pumping within the study area. It is also noted that the selected well hydrograph is assumed to represent the entire study area as a simplification.
Agricultural profit optimization model limitations
The main assumptions of the agricultural profit model are fixed crop net returns and the crop water allocation method. The crop net return values, described in section ‘Base model (model 1) formulation’, were fixed for the modeling period by weighting historical crop net return values by coverage during the drought. By using fixed net return values, real-world temporal fluctuations in crop yield and market price were not considered. In addition, the crop water allocation method, described in section ‘Base model (model 1) formulation’, was assumed to be proportional based on 2011 crop water use. This simplified approach provided a consistent allocation rule, but may not reflect all real-world allocation conditions and decisions.
Five limitations of the agricultural profit model are (1) simplified crop types, (2) the crop coverage decision method, (3) the assumption of no deficit irrigation, (4) the limited modeling time period, and (5) model sensitivity to initial conditions. The model considers only two general crop types, annual and perennial, when allocating water and coverage. By limiting crop types, the model does not reflect the entire range of crop varieties. In addition, the primary method to determine crop coverage, Eq. (6), is based on water allocated to the crop and respective crop demand. Although the model versions have different crop coverage constraints, the primary method remains the same and may not accurately reflect all planting decisions. Specifically, for models 2 and 3, in which annual crops may replace fallowed perennial coverage, replanting costs and other operational considerations are not included in the formulation. Furthermore, demands are assumed to be fully satisfied with no consideration of deficit irrigation that may occur during drought. The 5-year modeling time period, may introduce uncertainty in agricultural opportunity cost results since perennials in the study area can produce and be profitable for approximately 20 years. Lastly, the model is sensitive to initial variable values at the onset of optimization which can slightly influence results. Many of these uncertainties and limitations could be explored for more extensive applied policy studies.
Results
Estimated pumped groundwater during drought
Figure 8 indicates crop water use, surface-water deliveries, and estimated groundwater pumping during the drought. Crop demand steadily increased, which may be partly due to increased perennial crop planting that generally hardens water demands. As shown in Fig. 4, perennial and total crop coverage generally increased in the study area during the drought. Surface-water deliveries decreased significantly from predrought 2011, reached a minimum in 2014 and 2015, and slightly increased in 2016 near the end of the drought. As a result, estimated groundwater pumping increased during the drought and reached a maximum in 2014 and 2015.
Agricultural cost curves and tradeoff curves of DTGW policies
Figures 9, 10, 11 show, for each model, the agricultural cost curves, for each model version, the domestic well cost curve, total cost curves, and resulting Pareto trade-off curves. The cost curves are presented for DTGW policies ranging from 112 ft. (34.1 m) to 200 ft. (61.0 m). The DTGW value in 2011 was 112 ft. (34.1 m) and the actual maximum DTGW during the drought was 162 ft. (49.4 m) (Fig. 6); therefore, the range of DTGW policies bracketed the drought conditions. Each model system used a discount rate of 3%, except for model 2, which used three different discount rates, as shown in Fig. 10. As noted in the figures, the agricultural and domestic costs are presented in different units (billions and millions of dollars, respectively).
Agricultural cost curves and total cost curves
For all model versions, allowing less groundwater drawdown increases agricultural costs and reduces domestic well costs. Agricultural costs increase because reduced groundwater availability limits crop production and profits. Domestic well costs decrease because the DTGW increase during drought is limited, which limits supply interruptions and accompanying costs from groundwater drawdown (Gailey et al. 2019). Conversely, larger DTGW policy values decrease agricultural costs and increase domestic well costs. The total cost curves (sum of agricultural and domestic well costs) are highly influenced by the agricultural costs because of larger order of magnitude compared to domestic well costs.
The base model and model 2 have similar results with slight differences. The agricultural cost curve and the total cost curve shift downward since less agricultural cost is generated for policies that limit DTGW. This shift occurs because model 2 allows for planting annual crops to replace fallowed perennial coverage which can increase agricultural profit. Results are similar for a range of discount rates (Fig. 10a).
Figure 11a shows agricultural and total costs curves from model 3, which incorporates a unit groundwater recovery cost (Cw), reflecting a cost to recover additional groundwater pumped during the drought. Agricultural cost curves, with different Cw values, $0 to $600/AF ($0 to $600/1,233 m3), are plotted along with corresponding total cost curves. The results from model 2 are included as a base case (without groundwater recovery costs), whereas model 3 results are significantly different. The added groundwater recovery cost reduces agricultural profit (increases opportunity cost) as Cw increases and the agricultural cost curves level off at thresholds where the recovery costs for groundwater exceed the profit gained from the additional pumped groundwater. Inspection of the results indicates that, for DTGW values less than that which maximizes welfare, the DTGW policy compliance constraint, Eq. (9), is binding. Such a groundwater recovery fee can accomplish three objectives: (1) reducing groundwater drought drawdown effects on domestic wells and the aquifer overall, (2) provide funds for reducing agricultural pumping or increasing aquifer recharge in wetter years to recover groundwater storage, and (3) provide funds for the relatively modest costs of remedying agricultural pumping impacts on domestic and community wells.
Tradeoff curves and welfare-maximizing DTGW policies
Tradeoff curves for each model are presented in Figs. 9, 10, 11. These curves plot agricultural and domestic costs for each DTGW policy. Agricultural and domestic costs are in units of billions and millions of dollars, respectively. The tradeoff curves were used to evaluate the cost allocation tradeoff for welfare-maximizing DTGW policies.
The welfare-maximizing DTGW policies, total cost, cost breakdown between users, maximum agricultural profit, and total groundwater recovery cost for each model system appear in Table 2. The unregulated case results are from the base model using a nonoptimal DTGW policy of 162 ft. (49.4 m), which was the actual maximum DTGW value from the drought.
The welfare-maximizing DTGW policy corresponds to the minimum sum of costs for the two user groups. These policies are indicated on the total cost and tradeoff curves for the three sets of model results on Figs. 9, 10, 11. As discussed, the total cost curve is driven by the agricultural cost curve since agricultural costs greatly exceed domestic well costs. Therefore, the welfare-maximizing DTGW policies heavily weight minimizing agricultural cost, as indicated in the total cost breakdown in Table 2. There is negligible cost to agriculture, and little change in groundwater use, unless there is a charge for pumping.
The welfare-maximizing DTGW policy for model 2 is only slightly less than for the base model due to a small benefit from more cropping flexibility. In contrast, the policy value changes greatly over the range of Cw values explored for model 3. As the cost of additional pumping (Cw) increases, the amount of groundwater used for irrigation diminishes to the base groundwater pumping volume (3,133 AF over 5 years for a Cw of $600; Table 2). This occurs because the profit gained from pumping more groundwater eventually does not outweigh the groundwater recovery costs incurred. Allowing significant drawdown during drought is valuable for agriculture, but only if the recovery cost is not too great. The total agricultural groundwater pumped stabilizes for Cw values of $600/AF ($600/1,233 m3) or greater, with an estimated DTGW of 131 ft. (39.9 m). For all model systems, the welfare-maximizing DTGW policy is less than the unregulated 162 ft. (49.4 m) DTGW observed during the drought.
Additional Cw values in the range of $0–$900/AF ($0–$900/1,233 m3) were used with model 3 to clarify results. The total costs of minimizing DTGW policy, maximizing agricultural profit, and total groundwater recovery cost were estimated for each Cw value (shown in Fig. 12). As Cw increases, the optimal DTGW policy decreases to a threshold value of 131 ft. (39.9 m) at $600/AF ($600/1,233 m3). This threshold represents a DTGW where no agricultural groundwater pumping occurs above the no-fee base amount. Similarly, as Cw decreases, the optimal DTGW policy increases to a threshold value of approximately 157 ft. (47.9 m) at $300/AF ($300/1,233 m3). This DTGW policy results in significant groundwater pumping for agricultural irrigation demand. A drought pumping fee (Cw) of less than $300/AF ($300/1,233 m3) would be ineffective in reducing domestic well costs, although it might raise funds to compensate affected domestic well owners and fund groundwater recovery after the drought, with some short-term loss of agricultural profit. For Cw values between $300 and $600/AF ($300 and $600/1,233 m3), the policy reduces groundwater pumping and drought drawdown, while raising more money for groundwater recovery and domestic well compensation. If Cw exceeds $600/AF ($600/1,233 m3), the policy would be excessive, eliminating additional groundwater pumping as the fee cost exceeds the profit gained from additional drought agricultural pumping.
The sensitivity analysis results in Fig. 12d as the upper-bound (lower surface water, higher crop demand) and lower-bound (higher surface water, lower crop demand) ranges of total agricultural groundwater pumped. These scenarios were simulated for Cw, ranging from $0 to $600/AF (0–$600/1,233 m3). The cone of uncertainty increases as the quantity of groundwater pumped increases (i.e., Cw decreases). Both the upper-bound and lower-bounds converge on the model 3 results as Cw increases and less groundwater is pumped, but the upper-bound and lower-bounds converge on the model 3 results at different Cw values (Cw = $300 and $400/AF, respectively). This difference occurs because the upper-bound conditions (lower surface water, higher crop demand) specify a scenario that is more sensitive to increases in Cw than do the lower bound conditions.
Limit to the maximum welfare approach
The order of magnitude difference in cost for the two user groups (agricultural and domestic well users) is a challenge for the welfare-maximization approach (Gailey et al. 2019). A welfare maximizing DTGW policy minimizes total cost for the two groups and occurs when the first-order optimization criterion in Eq. (19) is met:
By defining total cost as the sum of agricultural opportunity and domestic costs and rearranging Eq. (19), the resulting Eq. (20) indicates that the optimization criterion is met when marginal costs for agricultural and domestic well users are equal.
This condition is problematic for models 1 and 2. Inspection of Figs. 9a and 10a, recalling the different orders of magnitudes of the left and right vertical axes, shows that the slopes for agricultural and domestic costs are only equal when the agricultural cost curve approaches zero. Therefore, Eq. (20) can only be satisfied when agricultural opportunity cost is essentially zero. Said another way, the agricultural opportunity cost from shorting a unit of water far exceeds the domestic well costs from this agricultural use, so maximization of total welfare always satisfies agricultural demand at the expense of domestic well users. Introducing a groundwater pumping fee is one approach to avoid this problem and could be viewed as a Pigouvian tax to compensate affected domestic well users. Another approach to account for the difference in cost magnitudes is discussed in section ‘Potential for negotiated cost allocation among user groups’.
Discussion
Several points regarding effective groundwater management policy may be derived from these results.
Potential for negotiated cost allocation among user groups
As discussed in section ‘Limit to the maximum welfare approach’, potential agricultural losses skew DTGW policies developed with a welfare-maximizing approach to favor agriculture because domestic well costs are relatively small. As a result, equitable sharing of the common-pool groundwater resource benefits may not occur. Negotiated cost allocations, or compensation, between user groups may be a more appropriate approach. Since domestic costs are much less than agricultural opportunity costs, agricultural users could compensate domestic users at a negotiated percentage of domestic costs (Gailey et al. 2019). For example, using the tradeoff curve from model 2, a line with slope equal to –1 is extended from the maximum-welfare DTGW policy to the agricultural costs axis to represent a compensation range from 0 to 100% (Fig. 13).
Negotiated cost allocation of welfare-maximizing policy for model 2 system. 100% cost allocation indicates full compensation, 0% cost allocation indicates no compensation. Discount rate (r) = 3%. See Fig. 10b for a larger-scale view of results
The cost allocation line is referred to as “negotiated” because the percentage of compensation provided by agricultural users may be a matter of negotiation involving user groups and regulators (Gailey et al. 2019). One potential method to estimate a socially equitable negotiated cost allocation would be to model groundwater drawdown caused by agricultural and domestic users and allocate domestic well costs proportionally to drawdown impacts. Costs allocated to agriculture could be addressed by creating a compensation fund with revenues from excess pumping fees collected according to model 3. Based on these results, a Cw value in the “effective policy” range between $500 and $600/AF may suffice (Fig. 12a,c). In this case, pumping fee and negotiated approaches would be consistent.
Fees needed for effective policy
Global agricultural demand drives prices which are largely unaffected by local drought, and significantly influence cropping decisions and groundwater use (Lund et al. 2018). Consistent with this expectation, the study area’s crop coverage and water use increased during the drought (Table 1; Fig. 8). As discussed in section ‘Agricultural profit optimization model limitations’, the agricultural profit model does not include changes in crop net returns over time and the market influences that occurred during the drought are not fully reflected in the model. This limitation has the potential to influence estimation of the fees required to curb excessive groundwater pumping (model 3); however, the results of this study appear reasonable since the penalty fee structure recently enacted in the study area is consistent with the findings (Henry 2020). The estimated bounds for effective policy ($300–$600/AF, Fig. 12) compares well with the enacted fee structure ($245–$500/AF) reported by Henry (2020).
Additional cost considerations for groundwater management
The results presented here, while case-specific and particular to the management formulation used, illustrate useful insights from policy analysis for achieving groundwater sustainability and reducing drought impacts. Depending on case-specific challenges, there may be additional costs to consider. For example, land subsidence in the study area has damaged the Friant-Kern Canal which conveys surface water within the study area (Kern Groundwater Authority 2020). Costs for canal repair could also be considered when developing management policies. Where they exist, impacts of groundwater-dependent ecosystems also could be represented in the analysis.
Short-term versus long-term effects on policy development
Addition of the penalty fee (Cw) to the management formulation (model 3) would help internalize externalities caused by additional groundwater pumping during droughts. Considerations for setting the value of Cw include (1) replenishment of extra water pumped, (2) replacement of domestic wells that run dry with deeper wells, and (3) other costs created by short-term additional pumping (i.e., additional pumping lift or canal damage from land subsidence, environmental mitigation). The focus of the welfare maximization is short-term because the droughts are assumed to have limited duration (e.g., 1–5 years) and the additional pumping is defined relative to a base amount of sustainable groundwater use. In contrast, the planning horizon for sustainable groundwater management is long-term (50 years for California’s SGMA program), and some short-term costs may cease to be relevant during the course of management—for example, well replacement could be completed after only a few drought cycles. In cases where justification for a management policy (i.e., pumping charge to address dry wells) ceases after the short-term, another policy must be available to support the long-term management goals. Limiting maximum groundwater depth is an attractive choice. From an administrative perspective, however, enforcement of a groundwater depth limitation for individual pumpers may be more challenging than influencing overall user group behavior through collection of pumping fees for purchasing replacement water to replenish groundwater storage.
Conclusions and future work
This study produced three main conclusions:
-
1.
Analysis of the economics that drive groundwater use and the resulting hydrologic conditions can provide guidance for developing and evaluating groundwater management policies.
-
2.
Economic considerations of various user groups may be so different that attempts to maximize total welfare while developing policies may not by itself produce widely accepted or fair results.
-
3.
Implementing a carefully selected groundwater use fee and redistributing the collected funds to address economic externalities created by the resource use may more effectively achieve equitable allocation of the limited common-pool resource.
For the study area in Tulare County, California, agricultural opportunity costs exceed domestic well costs by almost three orders of magnitude. This severely limits application of pure welfare maximization as a groundwater management approach; however, application of a groundwater pumping fee on additional drought pumping in the range of $300–$600/acre-foot ($300–$600/1,233 m3) appears quite effective. These results agree with recently enacted groundwater management policies in the study area.
Groundwater managers often have limited opportunities to enact and adjust policies; thus, research results that identify more likely effective policies are useful. The analysis presented here may provide a useful starting point for groundwater management policy planning by GSAs in California or other regulatory entities elsewhere where groundwater is limited and profit maximization is applicable. Such work would likely include additional model complexities and a different range of approaches for selecting policies. As discussed previously, the agricultural profit model is simplified and additional details (i.e., more crop type options, perennial crop age, planting decisions, and cost categories, as well as more accurate land use data and temporal variation in market price) could be included. Also, the prediction of depth to groundwater is based on a linear relationship between groundwater pumped and resulting drawdown. A more accurate relationship could be developed that includes aquifer-specific parameters and groundwater flow principles. Moreover, this study only considers agricultural and domestic user groups, while additional users and stakeholders, such as the environment and other industries, could be considered.
While the study focused on the economic concept of welfare-maximization to select optimal policies, additional and supplemental approaches, could be simulated. As proposed previously (Gailey et al. 2019), exploring the dynamics of negotiated or regulated cost allocations among user groups may provide additional insights for selecting optimal policies.
References
California Department of Water Resources (2014) California Water Plan: update 2013, vol 3: resource management strategies. https://water.ca.gov/-/media/DWR-Website/Web-Pages/Programs/California-Water-Plan/Water-Plan-Updates/Files/Update-2013/Water-Plan-Update-2013-Volume-3.pdf. Accessed 2 May 2019
California Department of Water Resources (2015) California’s groundwater update 2013: a compilation of enhanced content for California Water Plan Update 2013: Tulare Lake hydrologic region. https://water.ca.gov/-/media/DWR-Website/Web-Pages/Programs/California-Water-Plan/Docs/Update2013/GroundwaterUpdate/Californias-Groundwater-Update-2013%2D%2DTulare-Lake-Regional-Report.pdf. Accessed 2 May 2019
California Department of Water Resources (2017) Best management practices for the sustainable management of groundwater: sustainable management criteria draft. https://water.ca.gov/-/media/DWR-Website/Web-Pages/Programs/Groundwater-Management/Sustainable-Groundwater-Management/Best-Management-Practices-and-Guidance-Documents/Files/BMP-6-Sustainable-Management-Criteria-DRAFT_ay_19.pdf. Accessed 28 Nov 2020
California Department of Water Resources (2018a) Sustainable groundwater management website. California Department of Water Resources. California Department of Water Resources. https://www.water.ca.gov/Programs/Groundwater-Management/SGMA-Groundwater-Management/. Accessed 31 Mar 2018
California Department of Water Resources (2018b) California counties: datasets—California Natural Resources Agency open data. https://data.cnra.ca.gov/dataset/california-counties. Accessed 1 May 2019
California Department of Water Resources (2018c) Water districts: datasets—California Natural Resources Agency open data. https://data.cnra.ca.gov/dataset/water-districts. Accessed 1 May 2019
California Department of Water Resources (2019a) 2014 CADWR land use viewer. https://gis.water.ca.gov/app/CADWRLandUseViewer/. Accessed 1 May 2019
California Department of Water Resources (2019b) California Irrigation Management Information System (CIMIS) station reports. https://cimis.water.ca.gov/WSNReportCriteria.aspx. Accessed 1 May 2019
California Department of Water Resources (2019c) Water data library: groundwater level data. http://wdl.water.ca.gov/waterdatalibrary/groundwater/index.cfm. Accessed 1 May 2019
California Department of Water Resources (2019d) WUEdata: water use efficiency data. https://wuedata.water.ca.gov/. Accessed 1 May 2019
Doll D (2017) Pistachio irrigation: determining water needs and managing drought. https://ucanr.edu/sites/PistachioShortCourse/files/274447.pdf. Accessed 2 May 2019
Döll P, Schmied HM, Schuh C, Portmann FT, Eicker A (2014) Global scale assessment of groundwater depletion and related groundwater abstractions: combining hydrological modeling with information from well observations and GRACE satellites. Water Resour Res 50:5698–5720. https://doi.org/10.1002/2014WR015595
Foster SSD, Chilton PJ (2003) Groundwater: the processes and global significance of aquifer degradation. Philos Trans R Soc B 358(1440):1957–1972. https://doi.org/10.1098/rstb.2003.1380
Gailey RM, Lund JR, Medellín-Azuara J (2019) Domestic well reliability: evaluating supply interruptions from groundwater overdraft, estimating costs and managing economic externalities. Hydrogeol J 27:1159–1182. https://doi.org/10.1007/s10040-019-01929-w
Gumidyala S, Ruess PJ, Konar M, Marston L, Dalin C, Wada Y (2020) Groundwater depletion embedded in domestic transfers and international exports of the United States. Water Resour Res 56(2). https://doi.org/10.1029/2019WR024986
Hanak E, Escriva-Bou A, Gray B, Green S, Harter T, Jezdimirovic J, Lund J, Medellín-Azuara J, Moyle P, Seavy N (2019) Water and the future of the San Joaquin Valley. https://www.ppic.org/wp-content/uploads/water-and-the-future-of-the-san-joaquin-valley-february-2019.pdf. Accessed 2 May 2019
Henry L (2020) Proposed agreement could boost funds to fix Friant-Kern Canal. SJV Water, December 15, 2020. https://sjvwater.org/proposed-agreement-could-boost-funds-to-fix-friant-kern-canal/. Accessed 16 Feb 2021
Kern Groundwater Authority (2020) Groundwater Sustainability Plan. http://www.kerngwa.com/assets/kga-umbrella-gsp_final.pdf. Accessed 23 Feb 2020.
Lund J, Medellín-Azuara J, Durand J, Stone K (2018) Lessons from California’s 2012–2016 drought. J Water Resour Plann Manag 144(10). https://doi.org/10.1061/(ASCE)WR.1943-5452.0000984
Medellín-Azuara J, MacEwan D, Howitt R, Sumner D, Lund J (2016) Economic analysis of the 2016 California drought on agriculture. UC Davies, Davis, CA. https://watershed.ucdavis.edu/files/DroughtReport_20160812.pdf. Accessed 13 Sept 2020
Moran T, Choy J, Sanchez C (2014) The hidden costs of groundwater overdraft: understanding California’s groundwater. Water West.http://waterinthewest.stanford.edu/groundwater/overdraft/.. Accessed 5 July 2017
Orang MN, Snyder RL, Geng S, Hart QJ, Sarreshteh S, Falk M, Beaudette D, Hayes S, Eching S (2013) California simulation of evapotranspiration of applied water and agricultural energy use in California. J Integr Agric 12(8):1371–1388. https://doi.org/10.1016/S2095-3119(13)60742-X
Sanchez N (2017) Changes in evapotranspiration of agricultural crops in Kern County during the 2014–2015 drought years. MSc Thesis, University of California Davis, Davis, CA. https://watershed.ucdavis.edu/shed/lund/students/NadyaSanchezMS2017.pdf. Accessed 2 May 2019
Smith R, Knight R, Chen J, Reeves JA, Zebker HA, Farr T, Liu Z (2017) Estimating the permanent loss of groundwater storage in the southern San Joaquin Valley, California. Water Resour Res 53:2133–2148. https://doi.org/10.1002/2016WR019861
Stone K (2019) Economic tradeoffs in groundwater management during drought: Tulare County, California. MSc Thesis, University of California Davis, CA. https://watershed.ucdavis.edu/shed/lund/students/KStone_Thesis2019.pdf. Accessed 6 June 2021
Tulare County Agricultural Commissioner (2016) 2015 Tulare County annual crop and livestock report. https://agcomm.co.tulare.ca.us/ag/index.cfm/standards-and-quarantine/crop-reports1/crop-reports-2011-2020/2015-tulare-county-annual-crop-and-livestock-report-pdf/. Accessed 2 May 2019
University of California Cooperative Extension (2019) Current cost and return studies: San Joaquin Valley south region. https://coststudies.ucdavis.edu/en/current/region/san-joaquin-valley-south/. Accessed 1 May 2019
US Bureau of Reclamation (2019) Central Valley Operations (CVO)Mid-Pacific region: monthly delivery tables. https://www.usbr.gov/mp/cvo/deliv.html. Accessed 1 May 2019
Wada Y, van Beek LPH, Bierkens MFP (2012) Nonsustainable groundwater sustaining irrigation: a global assessment. Water Resour Res 48(6):W00L06. https://doi.org/10.1029/2011WR010562
Acknowledgements
The authors thank Nadya Alexander Sanchez for assisting with crop evapotranspiration calculations as well as Josué Medellín-Azuara and Jon Herman for providing advice on other elements of the research.
Funding
This work was supported by the State of California, S.D. Bechtel Foundation, UC Davis Center for Watershed Sciences, UC Davis Department of Civil and Environmental Engineering, and the Public Policy Institute of California.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stone, K.M., Gailey, R.M. & Lund, J.R. Economic tradeoff between domestic well impact and reduced agricultural production with groundwater drought management: Tulare County, California (USA), case study. Hydrogeol J 30, 3–19 (2022). https://doi.org/10.1007/s10040-021-02409-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-021-02409-w