Abstract
Hydraulic properties of coastal, urban aquifers vary spatially and temporally with the complex dynamics of their hydrogeology and the heterogeneity of ocean-influenced hydraulic processes. Traditional aquifer characterisation methods are expensive, time-consuming and represent a snapshot in time. Tidal subsurface analysis (TSA) can passively characterise subsurface processes and establish hydro-geomechanical properties from groundwater head time-series but is typically applied to individual wells inland. Presented here, TSA is applied to a network of 116 groundwater boreholes to spatially characterise confinement and specific storage across a coastal aquifer at city-scale in Cardiff (UK) using a 23-year high-frequency time-series dataset. The dataset comprises Earth, atmospheric and oceanic signals, with the analysis conducted in the time domain, by calculating barometric response functions (BRFs), and in the frequency domain (TSA). By examining the damping and attenuation of groundwater response to ocean tides (OT) with distance from the coast/rivers, a multi-borehole comparison of TSA with BRF shows this combination of analyses facilitates disentangling the influence of tidal signals and estimation of spatially distributed aquifer properties for non-OT-influenced boreholes. The time-series analysed covers a period pre- and post-impoundment of Cardiff’s rivers by a barrage, revealing the consequent reduction in subsurface OT signal propagation post-construction. The results indicate that a much higher degree of confined conditions exist across the aquifer than previously thought (specific storage = 2.3 × 10−6 to 7.9 × 10−5 m−1), with implications for understanding aquifer recharge, and informing the best strategies for utilising groundwater and shallow geothermal resources.
Résumé
Les propriétés hydrauliques des aquifères côtiers urbanisés varient dans l’espace et dans le temps en fonction de la complexité de leur dynamique hydrogéologique et de l’hétérogénéité des processus hydrauliques influencés par l’océan. Les méthodes traditionnelles de caractérisation des aquifères sont coûteuses, chronophages et représentent un instantané temporel. L’analyse des marées souterraines (AMS) peut caractériser passivement les processus souterrains et établir des propriétés hydrogéomécaniques à partir des chroniques de la charge des eaux souterraines mais elle est généralement appliquée à des puits individuels situés à l’intérieur des terres. L’AMS présentée ici est appliquée à un réseau de 116 forages d’eau souterraine afin de caractériser spatialement le degré de confinement et l’emmagasinement spécifique au sein d’un aquifère côtier à l’échelle de la ville de Cardiff (Royaume Uni) à l’aide d’un ensemble de données chronologiques enregistrées sous haute fréquence sur une durée de 23 ans. L’ensemble des données englobe les signaux terrestres, atmosphériques et océaniques, dans le cadre de l’analyse menée dans le domaine temporel en calculant les fonctions de réponse barométrique (FRB) et dans le domaine fréquentiel (AMS). En examinant l’amortissement et l’atténuation de la réponse des eaux souterraines aux marées océaniques (MO) en fonction de la distance à la côte et aux rivières, la comparaison multi-forages de AMS et de FRB montre que cette combinaison d’analyses facilite la distinction entre l’influence des signaux de marée et l’estimation des propriétés de l’aquifère distribuées spatialement pour des forages non influencés par les MO. La chronique analysée concerne une période couvrant l’avant et l’après mise en eau des rivières de Cardiff par un barrage, qui montre la réduction conséquente de la propagation du signal MO souterrain après sa construction. Les résultats indiquent qu’il existe un degré beaucoup plus élevé des conditions confinées dans l’aquifère qu’on ne le pensait auparavant (coefficient d’emmagasinement = 2.3 × 10−6 à 7.9 × 10−5 m−1), avec des implications pour comprendre la recharge de l’aquifère et pour éclairer au mieux les stratégies d’utilisation des eaux souterraines et des ressources géothermiques peu profondes.
Resumen
Las propiedades hidráulicas de los acuíferos costeros y urbanos varían espacial y temporalmente con la compleja dinámica de su hidrogeología y la heterogeneidad de los procesos hidráulicos influenciados por el océano. Los métodos tradicionales de caracterización de acuíferos son costosos, requieren mucho tiempo y representan una instantánea en el tiempo. El análisis del subsuelo en función de las mareas (TSA) puede caracterizar de forma pasiva los procesos del subsuelo y establecer las propiedades hidrogeomecánicas a partir de las series temporales de las aguas subterráneas, pero suele aplicarse a pozos individuales en el territorio. Aquí se presenta la aplicación del TSA a una red de 116 pozos de agua subterránea para caracterizar espacialmente el confinamiento y el almacenamiento específico en un acuífero costero a escala de ciudad en Cardiff (Reino Unido), utilizando un conjunto de datos de series temporales de alta frecuencia de 23 años. El conjunto de datos comprende señales terrestres, atmosféricas y oceánicas, y el análisis se realiza en el dominio del tiempo, mediante el cálculo de las funciones de respuesta barométrica (BRF), y en el dominio de la frecuencia (TSA). Al examinar la amortiguación y la atenuación de la respuesta de las aguas subterráneas a las mareas oceánicas (OT) con la distancia a la costa/río, una comparación de TSA con BRF en varios pozos muestra que esta combinación de análisis facilita la separación de la influencia de las señales de las mareas y la estimación de las propiedades del acuífero distribuidas espacialmente para los pozos no influenciados por las OT. Las series temporales analizadas cubren un período anterior y posterior a la construcción de una presa en los ríos de Cardiff, lo que revela la consiguiente reducción de la propagación de la señal de OT en el subsuelo después de la construcción. Los resultados indican que existe un grado mucho mayor de condiciones de confinamiento en el acuífero de lo que se pensaba (almacenamiento específico = 2.3 × 10−6 a 7.9 × 10−5 m−1), con consecuencias para la comprensión de la recarga del acuífero y para fundamentar las mejores estrategias de utilización de las aguas subterráneas y los recursos geotérmicos poco profundos.
摘要
沿海城市含水层的水力特性随其水文地质学的复杂动态和受海洋影响的水力过程异质性而在空间和时间上发生变化。传统的含水层表征方法昂贵和耗时, 而且能及时反映变化。潮汐地下分析(TSA)可以被动地表征地下过程并根据地下水水头时间序列建立水文地质力学特性, 但通常应用于内陆的单个井。本文介绍TSA 应用于 116 个地下水钻孔网络, 以使用 23 年高频时间序列数据集在空间上表征卡迪夫(英国)城市尺度沿海含水层的承压和单位存储性质。该数据集包括地球、大气和海洋信号, 通过计算气压响应函数(BRF)在时域和频域(TSA)进行分析。通过检查地下水对海洋潮汐 (OT)与海岸/河流距离响应的阻尼和衰减, TSA 与 BRF 的多钻孔比较表明这种分析的组合有助于分离潮汐信号的影响和空间分布含水层的估计不受 OT 影响钻孔的特性。分析的时间序列涵盖了卡迪夫河流被拦河坝蓄水前和蓄水后的一段时期, 揭示了施工后地下 OT 信号传播的减少。结果表明, 整个含水层存在比以前认为的更高程度的封闭条件(单位储水系数 = 2.3 × 10−6 到 7.9 × 10−5 m−1), 这对地下水和浅层地热资源利用中了解含水层补给和告知最佳策略具有重要意义。
Resumo
As propriedades hidráulicas dos aquíferos costeiros e urbanos variam espacial e temporalmente com a dinâmica complexa de sua hidrogeologia e a heterogeneidade dos processos hidráulicos influenciados pelo oceano. Os métodos tradicionais de caracterização de aquíferos são caros, demorados e representam um instantâneo no tempo. A análise de subsuperfície de maré (ASM) pode caracterizar passivamente os processos de subsuperfície e estabelecer propriedades hidrogeomecânicas de séries temporais de cabeceira de água subterrânea, mas é normalmente aplicada a poços individuais no interior. Apresentado aqui, a ASM é aplicada a uma rede de 116 furos de água subterrânea para caracterizar espacialmente o confinamento e o armazenamento específico em um aquífero costeiro em escala de cidade em Cardiff (Reino Unido) usando um conjunto de dados de séries temporais de alta frequência de 23 anos. O conjunto de dados é composto por sinais terrestres, atmosféricos e oceânicos, sendo as análises realizadas no domínio do tempo, por meio do cálculo das funções de resposta barométrica (FRBs), e no domínio da frequência (ASM). Ao examinar o amortecimento e a atenuação da resposta das águas subterrâneas às marés oceânicas (MO) com a distância da costa/rios, uma comparação de furos múltiplos da ASM com FRB mostra que esta combinação de análises facilita o desemaranhamento da influência dos sinais de maré e estimativa de aquíferos espacialmente distribuídos propriedades para furos de sondagem não influenciados por MO. A série temporal analisada cobre um período pré e pós represamento dos rios de Cardiff por uma barragem, revelando a consequente redução na propagação do sinal da MO subterrânea pós-construção. Os resultados indicam que existe um grau muito maior de condições confinadas em todo o aquífero do que se pensava anteriormente (armazenamento específico = 2.3 × 10−6 a 7.9 × 10−5 m−1), com implicações para a compreensão da recarga do aquífero e informando as melhores estratégias para a utilização de águas subterrâneas e recursos geotérmicos rasos.
Абстрактный
Гидравлические свойства прибрежных городских водоносных горизонтов меняются в пространстве и во времени из-за сложной динамики их гидрогеологии и неоднородности гидравлических процессов под влиянием океана. Традиционные методы определения характеристик водоносных горизонтов являются дорогостоящими, отнимают много времени и дают представление о положении дел лишь в определенный момент времени. Приливный подповерхностный анализ (tidal subsurface analysis, TSA) может пассивно охарактеризовать подземные процессы и установить гидрогеомеханические свойства на основе временных рядов уровня грунтовых вод, однако обычно данный анализ применяется в отношении отдельных удаленных от океана скважин. В данном исследовании TSA применяется к сети из 116 скважин для наблюдения за грунтовыми водами, чтобы пространственно охарактеризовать замкнутость и коэффициент упругой емкости пласта в прибрежном водоносном горизонте в масштабе города в Кардиффе (Великобритания) с использованием охватывающего 23 года набора данных высокочастотных временных рядов. Набор данных включает земные, атмосферные и океанические сигналы, при этом анализ проводится как во временной области путем расчета функций барометрического отклика (barometric response functions, BRF), так и в частотной области (TSA). Изучение затухания и ослабления реакции грунтовых вод на океанские приливы на разном расстоянии от берега океана и рек на основании данных из многочисленных скважин показывает, что комбинация анализов TSA и BRF облегчает различение влияния приливных сигналов и оценку пространственно распределенных свойств водоносного горизонта для скважин, не подверженных влиянию океанских приливов. Анализируемые временные ряды охватывают период до и после подпруживания рек Кардиффа, показывая сокращение подземного распространения сигнала океанских приливов, последовавшее за сооружением плотины. Результаты показывают, что в водоносном горизонте существует гораздо более высокая степень замкнутых условий, чем считалось ранее (коэффициент упругой емкости пласта = от 2.3 × 10−6 до 7.9 × 10−5 m−1), что имеет значение для понимания динамики подпитки водоносного горизонта и разработки наилучших стратегий использования подземных вод и источников геотермальной энергии неглубокого залегания.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
As competitive use of underground urban spaces increases, better understanding of the subsurface and its processes is needed to de-risk development and ensure sustainability. Coastal environments present additional challenges for hydrogeological interpretation due to the dynamic and heterogeneous nature of their aquifers and the impacts of ocean tides (OT) on the subsurface pressure signals. Traditionally, subsurface and hydraulic properties are determined from aquifer tests which are expensive, time consuming, require specifically drilled extraction wells and only provide data from a single time period. Geophysical measurements can also be used as a proxy for direct measurement, but these rely on indirect, and often ambiguous, relationships between geophysical and hydromechanical subsurface properties (McMillan et al. 2019). Traditional methods also often fail to account for the effects of barometric pressure on groundwater level measurements resulting in errors in estimating total head and groundwater flow direction (Rasmussen and Crawford 1997), which can be significant in areas of flat topography (Spane 2002) and therefore have implications for contaminant pathway assessment, groundwater resource management, the use of sustainable urban drainage systems (SuDS) and the implementation of ground source heating systems.
An alternative approach is to use the groundwater level response to tides to estimate aquifer characteristics in a ‘passive’ sense, without the need for additional investigation beyond the collection of sufficient high measurement and time resolution head datasets—for example, the use of groundwater head response to barometric pressure in determining barometric efficiency (BE; e.g. Hsieh et al. 1987; Acworth and Brain 2008) can be used to determine subsurface compressibility and therefore specific storage if a value of porosity can reliably be assumed. As shown by Gonthier (2007), there is also a need to remove Earth tides (ET) from groundwater level analysis when considering the effects of barometric pressure on head. Acworth et al. (2016), later advanced by Acworth et al. (2017) and Rau et al. (2020a), therefore developed a frequency domain method to disentangle the impact of Earth and atmospheric tides (AT) on groundwater head for inland aquifers. By determining the groundwater response to Earth and atmospheric tides, it is possible to calculate BE from which a range of hydraulic properties, such as aquifer compressibility, specific storage and confinement may be derived. McMillan et al. (2019) refer to this as tidal subsurface analysis (TSA), expressing its suitability for a range of applications but noting it is a promising, yet underused, tool. This passive approach repurposes, and has the potential to add value to, commonly collected atmospheric and groundwater monitoring data enabling detailed rapid characterisation of subsurface conditions at a high spatial and temporal resolution.
The aim of this study is to map spatial variance in hydro-geomechanical properties for a coastal, sand and gravel aquifer, with particular interest in how these change with distance from the coast/river boundaries, and to demonstrate how these have changed due to human intervention. To this end, TSA has been applied to derive spatially distributed hydraulic properties (e.g. BE, aquifer compressibility and storativity) across the aquifer using a high-resolution, 23-year-longtime-series dataset from a preexisting groundwater monitoring network (Mitchell 1996), now incorporated in a geothermal energy observatory in Cardiff, UK (Patton et al. 2019), comprising 234 boreholes. Data from 116 of these have been considered here, based on the availability of continuous data for the maximum number of boreholes monitoring the glaciofluvial sand and gravel aquifer and the made ground. Given its coastal setting, methods have been developed here to account for the added complication of the impact of OT-influences on the head time series (Gonthier 2007). The Cardiff case study dataset presents an additional opportunity to explore the use of TSA on coastal aquifers owing to the construction of a barrage adjacent to the coastline which impounds the city’s rivers and reduces the OT input on the aquifer. Groundwater head data for Cardiff cover a period before and after the barrage construction allowing for TSA to be applied both pre- and post-impoundment enabling observation of the related changes in OT signal propagation.
Previous studies have focused on either a time (e.g. Clark 1967; Rasmussen and Crawford 1997; Gonthier 2007) or frequency (e.g. Quilty and Roeloffs 1991; Acworth et al. 2016) domain methodology for estimating BE. When comparing different methods Turnadge et al. (2019) concluded that frequency-domain based approaches provide the most accurate BE estimates. To substantiate this, results of the TSA for Cardiff were also compared with barometric response functions (BRF) calculated using the Rasmussen and Crawford (1997) method providing the first spatially distributed comparison of the two methods for the determination of BE under additional influence of OT.
Materials and methods
Study area
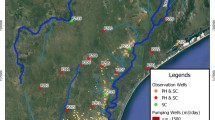
Cardiff is the capital city of Wales and is located adjacent to the Bristol Channel at 51.4816° N, 3.1791° W (WGS84) (Fig. 1). Cardiff has a temperate, maritime climate with an average annual daytime temperature of 14.7 °C and a total annual rainfall of 1,150 mm (Met Office, UK 2020). The city has an area of approximately 140 km2, the majority of which is low-lying, built on a former coastal floodplain, being bounded by hills to the east, north and west. To the southeast of the city lies Cardiff Bay, an artificially impounded freshwater lagoon created in 1999 by the construction of the Cardiff Bay Barrage, isolating the city from the sea. Into this lagoon drain two of the city’s three rivers: the Taff and the Ely. Prior to impoundment, the Taff and the Ely were strongly OT-influenced. The River Rhymney still discharges into the Bristol Channel.
Map of the Cardiff (Wales, UK) study area identifying the locations of all analysed boreholes coded by the unit monitored by each installation. [The UK comprises England, Wales, Scotland and Northern Ireland.] Weather stations; sea, river and bay level gauges; geological map; principal water bodies and areas identified by Cardiff Harbour Authority as historical clay pits are also shown. Coordinate system: British National Grid. Contains DiGMapGB 1:50000 British Geological Survey © NERC & Ordnance Survey data © Crown Copyright & database rights (2021) Ordnance Survey (100025252)
Cardiff’s bedrock comprises folded Silurian, Devonian and Carboniferous strata unconformably overlain by the low-permeability Triassic-aged Mercia Mudstone Group, in turn overlain by Devensian glacial till and glaciofluvial sand and gravels, and by Holocene tidal flat deposits and river alluvium (Waters and Lawrence 1987; Kendall 2015). The glaciofluvial sand and gravels form the target aquifer for this study, which is typically 9–10 m thick (Boon et al. 2019), comprising dense, poorly sorted sandy gravel with cobbles (Heathcote et al. 2003). The tidal flat deposits are thought to be of generally low to intermediate permeability, confining the aquifer to the south of the city centre (Edwards 1997). In some areas these deposits are absent (shown as former clay pits in Fig. 1). This results in hydrogeological connectivity between the sand and gravel aquifer and made ground (Williams 2008). Groundwater levels across Cardiff are 3–4 m below ground level (bgl) at 1.8–6.9 m aOD (above Ordnance Datum; average 4.5 m aOD), and the hydraulic conductivity of the glaciofluvial sand and gravel aquifer averages 50 m/day(Heathcote et al. 2003).
Cardiff has a groundwater monitoring network comprising 234 boreholes with hourly time-series groundwater level data spanning a 23-year period (1996–2019). The network is no longer monitored but data are available on request from Cardiff Harbour Authority (part of the County Council of the City and County of Cardiff, UK). The boreholes were installed across the city prior to the construction of the barrage to monitor its long-term impacts on groundwater levels (Heathcote et al. 1997) and cover an area of around 20 km2. Level data are available pre- and post-impoundment allowing changes in the OT-influence on the aquifer to be observed. The boreholes are variably screened to monitor the glaciofluvial sand and gravel aquifer, till and Mercia Mudstone Group bedrock, as well as the overlying tidal flat deposits, river alluvium and made ground (anthropogenic deposits). This study uses data from 116 of these boreholes, primarily screened within the glaciofluvial sand and gravels, till and Mercia Mudstone Group (Fig. 1). Some analysis of made ground boreholes is also illustrated. These boreholes were selected as they provide the longest unbroken data record for the largest number of boreholes.
Borehole drilling logs, available from the National Geoscience Data Centre, were used to characterise the lithologies at each site. A three-dimensional(3D) geological model for Cardiff produced by the British Geological Survey (Kendall et al. 2018) was used to evaluate the wider geological context for the city. The availability of high-resolution groundwater level data from the Cardiff study area has made it possible to test, compare and develop the methodologies described in the following sections, and hydraulically characterise the city’s aquifer.
Time and frequency domain analysis
Using the available groundwater level data from Cardiff, time (BRF) and frequency (TSA) domain methods of calculating BE were compared to establish values from which to further determine hydraulic properties. Their spatial and temporal variability was then mapped across the aquifer at the city-scale as well as establishing the extent of aquifer confinement. Cardiff’s coastal setting gave the context for both methods to be used to identify OT signal propagation and demonstrate how this has changed post-impoundment.
Tidal subsurface analysis (TSA)
TSA as described by Acworth et al. (2016), subsequently generalised further by Rau et al. (2020a), was applied to the Cardiff dataset. TSA is a frequency domain approach to disentangle the impacts of Earth and atmospheric tides (EATs) on groundwater levels using a spectral analysis of EAT components to obtain individual component amplitudes and phases, and calculate BE, from which subsurface properties can further be derived. For this study BE is calculated using Eq. (1) (Acworth et al. 2016)
where \( {S}_2^{\mathrm{GW}} \) is the S2 amplitude(m) observed in the groundwater, \( {S}_2^{\mathrm{ET}} \) is the S2 amplitude (m) in the ET, \( {S}_2^{\mathrm{AT}} \) is the S2 amplitude (m) in the AT, \( {M}_2^{\mathrm{GW}} \) is the M2 amplitude (m) in the groundwater, \( {M}_2^{\mathrm{ET}} \) is the M2 amplitude (m) in the ET, and ∆∅ is the phase difference in radians between \( {S}_2^{\mathrm{ET}} \) and \( {S}_2^{\mathrm{AT}} \). TSA derives amplitudes and phases for \( {M}_2^{\mathrm{GW}} \)and \( {S}_2^{\mathrm{GW}} \)using a harmonic least-squares(HALS) approach. Compared to the Fast Fourier Transform (FFT), this method offers unbiased signal amplitudes and phase estimates because the frequencies of the components are precisely known (Schweizer et al. 2021). The HALS approach minimises the sum the squared residuals between a model blending harmonics with known frequencies, and with measured data points (Schweizer et al. 2021). Schweizer et al. (2021) found the harmonic least square approach to be superior both in terms of the analysis and its ability to handle data gaps; therefore, values derived from this approach are adopted for analysis. TSA has been applied here to EATs in the groundwater time-series in the frequency domain using the atmospheric pressure data and a synthetic ET record generated using PyGTide (Rau 2018). PyGTide is based on ETERNA PREDICT (Wenzel 1996) and uses a comprehensive table of frequency components to calculate theoretical ETs in the time domain. The mathematics behind ETERNA PREDICT are sophisticated and the code has been validated comprehensively and is used as the gold standard for theoretical gravity in geodesy (McMillan et al. 2019). The results are highly accurate due to precise knowledge of the relative movement of celestial bodies established by the astronomical sciences. Indeed, the literature shows that differences between theoretical gravity changes and measurements can reveal Earth processes due to the high accuracy of the predictions. In this work, PyGTide is used to disentangle possible ET influences on the S2 component which is discussed in Rau et al. (2020a). They note that TSA assumes a groundwater pressure head representative of subsurface pore pressure which may not always be a simple relationship. TSA works by cleaning the S2 signal from ET-influence. The smaller these are, and the higher hydraulic conductivity is, the greater the accuracy in estimated BE (Rau et al. 2020a). In the Cardiff aquifer, permeability values are sufficiently high to enable reliable calculations of BE with the Acworth et al. (2016) method. The effects of precipitation are filtered out from TSA during the signal processing, which extracts only harmonics rather than randomly distributed events, and thus does not impact the results. Examples of the frequency spectra derived using TSA are shown (Fig. 2) for a typical non-OT borehole and an OT-influenced borehole from Cardiff.
Conceptual model representing groundwater head measured in a borehole drilled into a confined aquifer under the influence of a strains caused by ETs, b barometric loading caused by ATs, and c strains caused by OTs. Examples of the TSA outputs for boreholes where each of the tides is dominant are shown for each case. The plots illustrate \( {M}_2^{\mathrm{GW}} \) and \( {S}_2^{\mathrm{GW}} \) amplitudes derived from the TSA method and show how the groundwater head time-series responds to changes in EATs
A visual quality assessment of the output results is needed to determine confinement conditions. Where M2 or S2 signals can be seen above the background noise in the spectral plots the aquifer is assumed to be confined. Where no discernible signal is present, the location is considered unconfined and BEs are disregarded.
With respect to the construction of the Cardiff Bay Barrage the pre-impoundment subset of data covered a period just over 2 months (1 March–6 May 1997). A post-impoundment data period was chosen covering a 1-year period 20 years later (1 January–31 December 2017) as these dates provided the longest unbroken dataset for the greatest number of boreholes. Turnadge et al. (2019) note that TSA results can be sensitive to different time-series lengths. To account for this possible uncertainty, 1-year, 1-month and 6-month data windows were explored to determine the optimum time-series length required for accurate TSA, which would enable consistent results with the shortest required data capture period. Atmospheric pressure, sea level and river stage data were provided by Cardiff Harbour Authority for the same time periods, and post-impoundment level data from the Cardiff Bay freshwater lagoon were also supplied for inclusion in the analysis (Fig. 1).
Barometric response function (BRF)
Rasmussen and Crawford (1997) developed a regression deconvolution method to characterise groundwater pressure responses to changes in barometric pressure. BE is calculated as a function of the delay between the change in barometric pressure and the change in groundwater head as illustrated by Eq. (2) (Rasmussen and Crawford 1997).
where BE is the barometric efficiency, ∆B is a change in barometric pressure (mbar) at the land surface during an arbitrary unit of time and ∆W(m) is the corresponding change in groundwater level. The Rasmussen and Crawford (1997) method evaluates the time delay between changes in barometric pressure and the corresponding groundwater response by convolution. The time-lag response coefficients between barometric pressure changes and groundwater level responses are then estimated using regression deconvolution.
BRFs were determined for the study areas from the groundwater head and atmospheric pressure data using (Rasmussen and Crawford 1997)
where ∆W(t) is the change in detrended groundwater level (m) between time t and the previous time when a measurement was taken (τk = tk − k∆t), ∆B(t − k∆t) and ∆E(t − k∆t) are the changes in the detrended barometric pressure head (mbar) and ET gravity potential (J/kg) between t − k∆t and the previous time when a measurement was taken [t − (k + 1)∆t], αk and βk are the unit (impulse) barometric pressure and ET response functions at lag k, K is the maximum number of time lags for the barometric pressure and ET response, and ∆t is the time between adjacent measurements (Butler Jr. et al. 2011). From this, in a confined aquifer, BE is determined as follows (Rasmussen and Crawford 1997):
where BRF(τk) is
The time domain-based BRF method was applied to the same boreholes for the same time periods as the frequency domain-based TSA method and the BE results were then compared.
Turnadge et al. (2019) and Rau et al. (2020a) have shown TSA-derived BEs to be superior in accuracy to those generated by other time domain-based solutions and thus all hydraulic properties calculated from BEs (see section “Aquifer properties”) are based on TSA values. However, both methods have also been compared here in a spatially distributed assessment of the two, and BRF was also used to complement TSA in the identification of OT signals and to establish aquifer confinement from BRF plot shapes as follows.
Barometric response function was plotted against time lag for each borehole to investigate whether the theory of Rasmussen and Crawford (1997) would hold for Cardiff. Four styles of plot shape were observed, and each borehole assigned to one of the categories based on the shape of its BRF plot. The first three of these categories were identified by Rasmussen and Crawford (1997) and can be described as: (1) ‘rising’, i.e., depicting a profile of increasing gradient with time, suggesting a confined aquifer but with a delay in groundwater response caused by borehole storage or skin effects; (2) ‘flat’, i.e., where the gradient is relatively consistent with time, found at confined locations with an immediate groundwater head response to changes in barometric pressure; and (3) ‘falling’, i.e., where the gradient falls with time, indicative of unconfined boreholes where the decreasing response to barometric pressure with time is the result of the delay in the signal being transmitted through the unsaturated zone. Since this study applies BRF analysis to a coastal aquifer for the first time (based on available knowledge) here an additional fourth ‘peaked’ category has been defined, where the profile shows one or more peaks and troughs (Fig. 3). Boreholes displaying this pattern were found to be located adjacent to the coastal/riverboundary and coincide with boreholes identified by Mitchell (1996) as OT-influenced(Fig. 3). It is, therefore, concluded that these peaks are caused by OT-influences which is an unaccounted force when calculating the BRF using Eqs. (3)–(5). This assumption has been confirmed by mathematically generating a synthetic OT signal and adding this to an existing AT-dominate borehole’s groundwater level response. When the BRF is applied to this artificially OT-influenced signal, the result is a BRF plot that shows an OT peak and trough pattern overprinting the rising profile of a confined borehole with storage effects (Fig. 4). This pattern does not fully replicate the ‘peaked’ profile of an OT borehole but is rather a hybrid of ‘peaked’ and ‘rising’.
a Example of a BRF plot for an AT-dominant borehole (borehole no. CS303). b BRF plot for the same borehole contaminated with a synthetic OT signal. In this example the BRF plot shape has changed with the addition of a synthetic OT signal to show a hybrid of its original signal overprinted with a peak and trough pattern. As this borehole originally displayed a rising profile associated with a confined borehole with storage effects, this signal combines with the synthetic OT to produce this combination of ‘rising peaked’. The error bars on the plot have increased and the BE is no longer reliable
Several BRF plots could not be assigned to any category as the shapes produced were inconclusive. These may be where OT signal is confounded with other influences to produce hybrid results or where other diurnal or semidiurnal forces affect the result. By mapping the distribution of the BRF plot shapes, it has been possible to assess aquifer confinement across the city.
Disentangling tidal components
Whereas TSA has only previously been applied to noncoastal aquifers, in Cardiff the majority of pre-impoundment, and several post-impoundment, boreholes are OT-influenced. Hence, sea level data were also included in the analysis to determine its influence on groundwater level variations.
The TSA methodology works by estimating the groundwater response to the principle solar (S2) and principle lunar (M2) tidal components of EATs. The S2 component occurs at 2.00 cycles per day (cpd) and is found in both ET and AT, while the 1.93277-cpd M2 component is only found in the ET. As M2 is not found in the AT, it is possible to determine how much influence each of the two tides has on groundwater using the relationship between the two signals (Acworth et al. 2016; Rau et al. 2020a). This relationship is complicated in coastal settings as the M2 tidal component is also found in OTs. Since the OT part of the signal gets damped and attenuated by the aquifer away from any ocean-tide-influenced boundaries, to an unknown extent, it cannot be reliably disentangled by TSA and the method cannot currently provide accurate BE values where OT signals are present.
Previous investigations have also found an increasing M2 magnitude with depth due to decreasing consolidation (Rahi and Halihan 2013; McMillan et al. 2019). Recent literature (e.g., Rau et al. 2020a) shows that permeability affects the phase of the signal but not the amplitude. Therefore, it is plausible that increasing M2 could be due to an increase in consolidation with depth, but for the Cardiff case, the boreholes analysed are very shallow so one can expect this to be very limited in effect. Since most boreholes in this work are screened in reasonably shallow unconsolidated sediments, the ET-based influence can be considered as limited. Here, use is made of the fact that an increased M2 amplitude in groundwater (\( {M}_2^{\mathrm{GW}} \)) is indicative of OT-influence and is therefore useful for identifying boreholes where BE values derived from TSA may be subject to too much uncertainty. To identify the dominant tide at each location the following approach was developed. In addition to those calculated for groundwater, TSA computed M2 and S2 amplitudes for ET, AT and OT. The ratio of the two tidal components for each tide type are termed \( {M}_2^{\mathrm{ET}} \):\( {S}_2^{\mathrm{ET}} \), \( {M}_2^{\mathrm{AT}} \):\( {S}_2^{\mathrm{AT}} \) and \( {M}_2^{\mathrm{OT}} \):\( {S}_2^{\mathrm{OT}} \). These values (2.22, 0.04 and 2.85, respectively) were then compared to the magnitude of M2:S2 found in groundwater (\( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \)) and it was assumed the resultant ratio closest to 1 for each borehole reveals the dominant tide type, i.e. if there is a 1:1 ratio for (\( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \)):(\( {M}_2^{\mathrm{AT}} \):\( {S}_2^{\mathrm{AT}} \)) the aquifer would be AT-dominant at that location.
Using this approach, it is possible to clearly identify AT- and OT-dominant boreholes; however, boreholes with a ratio close to that of the ET, may be either ET- or OT-dominant as their ratios are similar. Through comparison with BRF plot shapes, it was possible to further differentiate between these two to identify OT-dominant boreholes and eliminate them from further analysis using TSA-derived BEs. This has been validated by rerunning the TSA analysis for the boreholes with the synthetic OT signal added to the AT groundwater level response. The resulting \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \)is as one expected of an OT-dominate borehole.
Aquifer properties
From the BEs derived from the TSA methods, several parameters can be determined, including loading efficiency (Eq. 6), aquifer compressibility (Eq. 7) and specific storage (Eq. 8).
where γ is the loading efficiency (dimensionless). Rearranged from Acworth et al. (2016), it is found that:
where α is the formation compressibility (Pa−1), θ is the aquifer porosity (−) and β is the fluid compressibility (Pa−1). Porosity values of 0.2 for the glaciofluvial sands and gravels, and 0.5 for the alluvium, tidal flat deposits and made ground, are taken for Cardiff from Boon et al. (2019) and Kreitmair et al. (2020), while fluid compressibility is 4.58 × 10−10 Pa−1(Young and Freedman 2000).
Specific storage (Ss, m−1), can also be determined as follows (Cooper 1966):
where ρ is the mass density of water (constant assumed value of 1,000 kg/m3) and g is gravitational acceleration (constant assumed value of 9.8 m/s2). This, in turn, allows for estimates of storativity (Eq. 9) and hydraulic diffusivity (Eq. 10).
where b is aquifer thickness, D is hydraulic diffusivity (m2/day) and T is transmissivity. These relationships allow a hydro-geomechanical aquifer characterisation using the groundwater response to EAT (McMillan et al. 2019).
Results
Parameter sensitivity to time-series length
The sensitivity analysis to the choice of time-series duration used for TSA indicated only a weak correlation between the results of 1 month and 1 year with no statistical significance (R(39) = 0.314, p = 0.062). For 6 months and 1 year there is a very strong correlation (R(39) = 0.801, p = 0.000), indicating that 6 months would be an ample dataset but 1 month is insufficient at this location. Pre-impoundment, the longest period of continuous data capture was for 2 months; however, the results indicated that whilst time-series length was important for the accuracy of output M2 and S2 amplitude and phase values, duration had little impact on the determination of dominant tides, which remained consistent across the different time-periods tested. Therefore, the pre-impoundment data were only used to identify changes in OT-influence post-impoundment, and not for deriving hydraulic parameters.
When comparing BRF results over the different time windows, strong or very strong correlations were seen between all subsamples therefore it may be more appropriate than TSA for shorter time-series (1 month versus 6 months was R(39) = 0.732, p = 0.000, while 6 months versus 1 year was R(39) = 0.989, p = 0.000).
Identifying OT-influence in \( {M}_2^{\mathrm{GW}} \)
\( {M}_2^{\mathrm{GW}} \) amplitudes were found to vary across the aquifer in the pre-impoundment data, decreasing with distance from the coast/river boundaries as would be expected due to hydraulically diffusive damping of the hydraulic responses. There is also a significant reduction in \( {M}_2^{\mathrm{GW}} \) amplitudes in the post-impoundment data suggesting the higher \( {M}_2^{\mathrm{GW}} \) amplitudes near the boundaries may also be the result of OT-influence(Fig. 5) despite the emplacement of the barrage. During the pre-impoundment data window, sea levels fluctuated by 13.4 m, compared with 1.0 m in water level change in Cardiff Bay post-impoundment; however, the OT-influence appears to penetrate through to the aquifer beneath the bay. The boreholes closest to the coast/rivers have \( {M}_2^{\mathrm{GW}} \) amplitudes greater than \( {S}_2^{\mathrm{GW}} \), while the reverse is true for boreholes located further from the boundary. \( {M}_2^{\mathrm{GW}} \) was greater than \( {S}_2^{\mathrm{GW}} \) in fewer boreholes post-impoundment than prior to the barrage (Fig. 6). As high \( {M}_2^{\mathrm{GW}} \) amplitudes may be as a result of either OT or ET influence, \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) was found to be more indicative of OT-dominance than \( {M}_2^{\mathrm{GW}} \) alone. \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) resembling the M2:S2 found in one of the three tide records reflects the dominant tide driving groundwater responses at each borehole.
Plot showing how the strength of the ratio between \( {M}_2^{\mathrm{GW}} \) and \( {S}_2^{\mathrm{GW}} \) amplitudes varies across the city with distance from the coast/river boundary, and how this has changed from pre-impoundment, shown on the left side of each borehole marker, to post-impoundment, shown on the right. © Ordnance Survey data © Crown Copyright & database rights (2021) Ordnance Survey (100025252)
Boreholes where \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) was closest in value to \( {M}_2^{\mathrm{OT}} \):\( {S}_2^{\mathrm{OT}} \) were found throughout Cardiff pre-impoundment, while a reduction was seen in the number of these boreholes post-impoundment, when these sites are limited to those near the coast/rivers. Figure 7 shows the spatial distribution of dominant tides at each borehole location and illustrates a reduction in OT-influence post-impoundment.
a The change in dominant tide at each borehole location as defined by the combined analysis of TSA \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) and BRF plot shape. Pre-impoundment dominant tide is shown on the left side of each borehole marker, while post-impoundment tides are shown on the right. Empty halves are shown where data were only available for either pre- or post-impoundment. b The spatial changes in barometric efficiency (BE) as derived from TSA on the left and BRF on the right. Only non-OT-influenced boreholes are shown therefore a comparison of BEs derived from the two methods from unpolluted groundwater response is possible. The histogram shows the distributions of the calculated BEs using both methods. Contains DiGMapGB 1:50000 British Geological Survey © NERC & Ordnance Survey data © Crown Copyright & database rights (2021) Ordnance Survey (100025252)
When TSA was applied to boreholes monitoring made ground, \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) revealed OT-dominance at only four sites (Fig. 8).
Map showing dominant tide at each borehole location based on \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \)for made ground boreholes, identifying areas of hydraulic connection with the aquifer. Contains DiGMapGB 1:50000 British Geological Survey © NERC & Ordnance Survey data © Crown Copyright & database rights (2021) Ordnance Survey (100025252)
Identifying characteristic BRF shapes
Barometric response functions shapes were used to identify aquifer confinement, and to confirm and clarify OT-influence, pre- and post-impoundment. A map showing the distribution of these shapes pre- and post-impoundment is shown (Fig. 9). Pre-impoundment, a total of seven boreholes had ‘peaked’ BRF plots denoting an OT-influence, while post-impoundment there were 20 ‘peaked’ plots. These boreholes all coincided with those defined as OT-dominant using the \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) approach, indicating that both methods may provide for robust analysis where OT signals are dominant enough. Pre-impoundment, 17 boreholes produced BRF plot shapes that could not be assigned to any of the defined categories, likely due to OT-influence combining with other factors such as evapotranspiration, which confound BRF analysis. Post-impoundment there were seven such boreholes. These boreholes were also identified by their \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) as OT-dominant and are located close to the river/coast.
Map showing the confinement status across the aquifer as defined from the BRF plot shapes for each borehole. Pre-impoundment results are shown on the left and post-impoundment on the right of each borehole marker. Contains DiGMapGB 1:50000 British Geological Survey © NERC & Ordnance Survey data © Crown Copyright & database rights (2021) Ordnance Survey (100025252)
A vast difference in the plot shapes between the pre- and post-impoundment results, following a reduction in OT signal propagation is noted; however, given that BRFs do not consider the impacts of OTs, BE values were not derived for OT dominant boreholes for further analysis. Of the remaining pre-impoundment BRF plots one showed an unconfined ‘falling’ profile, seven had ‘flat’ profiles identifying them as confined, while six had ‘rising’ profiles meaning they were confined with borehole storage or skin effect. Post-impoundment, one borehole had a ‘falling’ profile, nine had ‘flat’ profiles, while 32 had ‘rising’ profiles.
Spatial patterns of aquifer confinement did not change post-impoundment, although a small number of boreholes changed with respect to apparent borehole storage/skin effects, possibly the result of silting of the boreholes over time. Most boreholes were found to be confined except for two boreholes found close to the River Taff (Fig. 9); however, more data on confinement was available for the post-impoundment dataset as the absence of the OT-influence allowed confinement to be identified more easily in the BRF plot shape. It is possible that some of the boreholes close to the coast/river boundaries may be unconfined, but this cannot be verified through this method, due to the influence of the OT signal in these locations.
TSA-derived BEs (non-OT boreholes)
The TSA-derived BEs for non-OT boreholes ranged between 0.01 and 0.60, with a mean of 0.27, standard deviation of 0.16 and median of 0.21. Low values are seen across most of the aquifer, as would be expected for this unconsolidated formation. This is especially true for the northwest of the city, around the area marked as alluvium on the geological map (BGS 2016) and immediately south of this (Fig. 7). BEs were shown to be slightly higher further south and east, closer to the coastline. Local pockets of higher BE can be seen in the areas where the alluvium and tidal flat deposits are absent, and around the docks and train line where extensive made ground is likely present.
Comparison of TSA with BRF
The BE values derived using the various dataset sample lengths produced differing values for the TSA, while sample length had less impact on BRFs. Comparing results of the different sample lengths with each other and between the TSA and BRF derived BEs, it was found that longer time-series yield more accurate results. When comparing TSA with BRF for non-OT boreholes for the 1-month window, there was only a weak positive correlation which was statistically not significant: R(39) = 0.346, p = 0.039. This improved when using 6 months’ worth of data to R(39) = 0.426, p = 0.010. One year offers a further improvement indicating that the longer the time-series, the better the correlation between the results and the more reliable the TSA-derived BE, however 6 months appears to offer reasonable results as there is no significant improvement gained by using the 1-year time-series length.
When considering only non-OT boreholes, the two methods compared well (R(23) = 0.752, p = 0.000; Fig. 10). The spatial pattern also shows broad agreement (Fig. 7) although local discrepancies are observed. The inset histograms show the range and distribution of BE values from both methods. For TSA BEs were found to be left-skewed, while those for BRF are closer to normal distribution, but with some outliers. BRF appears to result in higher BE particularly in those boreholes with storage/skin effects. Both methods highlight greater formation compressibility towards the northwest of the study area and an area of lower compressibility to the east, but TSA suggests a greater degree of compressibility for those boreholes located between the two rivers in the central part of the study than those indicated by the BRF estimations.
Barometric response functions analysis detected only one unconfined borehole in the post-impoundment data; however, when applying TSA to the dataset, no tidal signals could be identified in 15 boreholes, suggesting these to be unconfined.
Hydraulic properties
With the OT-influenced boreholes identified and removed, it was possible to calculate the formation compressibility, specific storage, storativity and hydraulic diffusivity for the remaining locations using Eqs. (6)–(10) in conjunction with porosity estimates. Compressibility ranged from 9.9 × 10−11 to 8.0 × 10−9 Pa−1, averaging at 9.3 × 10−10 Pa−1, which is in line with values reported by Freeze and Cherry (1979) as typical for a sand and gravel aquifer. Specific storage varied across the aquifer (Fig. 11), ranging from 2.3 × 10−6 to 7.9 × 10−5 m−1, averaging at 1.1 × 10−5 m−1, although most sites were below this value, with the average skewed by an area of high specific storage as shown in Fig. 11 around Riverside, Canton and Leckwith. This is consistent with typical values reported by Batu (1998) for similar deposits. Storativity was calculated from specific storage for all sites where aquifer thickness was proven in borehole logs. This ranged from 4.4 × 10−6 to 8.11 × 10−5, averaging at 3.0 × 10−5(Fig. 11). A map showing the hydraulic diffusivities derived from the calculated storativity values and an assumed transmissivity of 370 m2/day—based on the average hydraulic conductivity for the aquifer of 50 m/day(Heathcote et al. 2003 using Eq. 10 is shown in Fig. 12). These results are based on the measured saturated thickness from boreholes logs for each location.
a Map of specific storage (Ss) values (m−1) calculated from TSA-derived BEs. Only non-OT boreholes are shown. The region depicted by the green polygon shows the area of higher specific storage between Canton, Riverside and Leckwith. The histogram shows the distributions of the calculated Ss. b Map of storativity (S) values (−) calculated from TSA-derived BEs. Only non-OT boreholes are shown. The histogram shows the distributions of the calculated S. Contains DiGMapGB 1:50000 British Geological Survey © NERC & Ordnance Survey data © Crown Copyright & database rights (2021) Ordnance Survey (100025252)
Map of hydraulic diffusivity (D) values (m2/s) calculated from TSA-derived BEs. Only non-OT boreholes are shown. The histogram shows the distributions of the calculated D. Contains DiGMapGB 1:50000 British Geological Survey © NERC & Ordnance Survey data © Crown Copyright & database rights (2021) Ordnance Survey (100025252)
The main uncertainty in these ranges of hydraulic properties by this analysis is in the assumed porosity. For Cardiff, extensive existing data on porosity has been summarised by the British Geological Survey (Boon et al. 2019; Kreitmair et al. 2020) and was found to vary across the aquifer between 0.2 and 0.3, translating to an uncertainty of 20% for all properties calculated using porosity. For aquifers with more heterogenous porosity this could result in a far larger uncertainty unless site specific data is known for each borehole location, thus values may be calculated on a case-by-case basis. The other notable uncertainty in this work comes from the assumed value for transmissivity, as this is derived from a reported discrete value for hydraulic conductivity from Heathcote et al. (2003) with no reference to an upper and lower limit. However, Heathcote et al. (2003) note that results from pump tests demonstrated that hydraulic conductivity of the glaciofluvial sand and gravels was relatively consistent across the aquifer. Whatever uncertainty exists in this estimate will also directly impact the uncertainty of the derived diffusivity values.
Discussion
Identifying OT signals
Tidal subsurface analysis has previously only been applied to inland settings (Acworth et al. 2016) and currently, without knowing the relative proportions of OT and ET M2 signals within a groundwater level time series. TSA cannot be used to derive BEs for OT-influenced boreholes, and BRF also fails to account for OT-influence. The OT driver signal cannot be included in these methods as the OT signal propagates horizontally into the aquifer at a rate dependant on the aquifer’s horizontal hydraulic properties. The magnitude of changes in groundwater head caused by OTs decays with distance from the coastal boundary (Rotzoll and El-Kadi 2008) and the further from this boundary a borehole is, the more difficult it is to distinguish head changes induced by OT from ET signals (Liao and Wang 2018). The attenuation of OT amplitude and the lag in OT phase are products of aquifer thickness and hydraulic conductivity (Solórzano-Rivas et al. 2021), which in turn is dependent on porosity and compressibility, which can vary considerably across an aquifer, even over small distances. Furthermore, conditions close to the boundary may be substantially different to those further inland, for example Rotzoll et al. (2013) noted significant OT damping near the coast at their study area. Results from Cardiff show that \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) can be used to identify boreholes that are definitely AT- or OT-dominant, where ratios are either close to 1:1 or where values are too low to be anything other than AT-dominant, or too high to be anything but OT-dominant. This method fails where the groundwater M2:S2 ratio lies between those of the ET and OT ratios as these values are similar. Therefore, it is not always possible to distinguish ET- from OT-dominant locations; however, it has been shown here that BRF plot shapes can be used to differentiate between the two. This allows TSA to be applied to coastal aquifers where a proportion of the boreholes show no OT signal, by establishing the extent of the OT signal propagation across the aquifer.
The amplitude of \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \)(Fig. 6) decreases with distance from the coast/river boundary and is lower in the post-impoundment data. This signifies that this method is suitable for identifying the amplitude and propagation of OT signals inland and, for Cardiff, shows how much the OT-influence has decreased since the construction of the barrage. The majority of the southern three quarters of the city was OT-influenced pre-impoundment with all boreholes around the coast/rivers in this region OT-dominant(Fig. 7). The area coincides with mapped tidal flat deposits (BGS 2016). Post-impoundment, the OT signal is seen in fewer boreholes, found only adjacent to the coast/river boundary, with the signal strength greatly reduced. Due to the proximity of these boreholes to the coast/river boundary, and the reduction in signal strength and propagation post-impoundment, it is possible to conclude that \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) is indicative of OT-influence. It is demonstrated that impoundment has changed the groundwater level response to tidal forces.
made ground boreholes were assessed to test the hypothesis that strong \( {M}_2^{\mathrm{GW}} \) signals were indicative of OT-influence, as follows. As made ground is generally of low permeability it was not expected to see much hydraulic connectivity with the aquifer and thus little OT-influence; therefore, if \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) truly are indicative of tidal dominance, low values would be expected within made ground boreholes. Only four made ground boreholes were found to be OT-dominant(Fig. 8), despite proximity to the coast/river boundary, while the others showed no OT dominance despite their proximity to OT-dominant glaciofluvial sand and gravel boreholes. This suggests that the strong M2 signal seen in the aquifer is derived from OTs.
Complete disentanglement of ET, AT and OT from groundwater level measurements has yet to be achieved but this study has demonstrated a reasonable method of identifying OT-influenced boreholes, enabling TSA to be applied to any non-OT boreholes. The combined approach of using BRF with TSA to identify OT signals has the potential to be useful for further development of the TSA method to account for OT signals.
Rasmussen and Crawford (1997) only had one example of the ‘peaked’ BRF profile and theorized that the effect could be due to transmission of barometric pressure through the unsaturated zone or potentially a tidal influence. In Cardiff, the boreholes which display this shape are clustered around the coast/rivers and coincide with boreholes identified by TSA as OT- or, to a lesser extent, ET-dominant. It is therefore evident that these peaks do represent OT signals and can, therefore, be used to distinguish between ET and OT boreholes designated as possible ET by TSA.
When running the simulated data for an AT borehole polluted with a synthetic OT signal, the plot shape also changes to show the peaked effect. There is 89% agreement between peaked BRF shapes and TSA OT designation using \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \), with the remaining 11% all explainable. Each of the exceptions can be accounted for by local anomalies including a borehole adjacent to a known sewer with direct connection to the sea (Mitchell 1996), proximity to a dock, the OT peak being masked by borehole storage and unreliable data as a result of operator error or compromised borehole casing (Table 1).
Comparison of TSA with BRF
When comparing methods of BE characterisation, Turnadge et al. (2019) found that BRF, and other regression deconvolution methods, were confounded by diurnal and/or semidiurnal signals being present. In contrast, TSA was found to be reliable with BEs consistent with those derived from pumping tests. BEs calculated from TSA and BRF for OT-influenced boreholes are not meaningful, thus the approach was taken to identify OT-influence and exclude these boreholes from BE calculations. However, both methods produced reasonable estimates for non-OT boreholes, with results showing moderate correlation. This illustrates the potential usefulness of using a regression between the two sets of results in identifying OT signals, as OT-dominate boreholes will not correlate. However, for those individual non-OT sites where the methods did not compare as well, in particular, for those boreholes found to be confined with borehole storage/skin effects, BRF tended to overestimate BE (Figs. 7 and 9). The Cardiff dataset has demonstrated that TSA and BRF compare favourably for non-OT boreholes without borehole storage/skin effects. While TSA yields more precise BE estimates, BRFs are useful for identifying aquifer confinement and for supporting TSA in highlighting OT-dominance. However, TSA indicated unconfined conditions at 15 boreholes not identified by BRF, suggesting that the assessment of confinement may be frequency dependant, with BRF more sensitive to lower frequencies, and supports the use of both methods in combination for aquifer characterisation.
Acworth et al. (2016) suggest a 15-day time-series is sufficient for TSA, while Schweizer et al. (2021) conclude that a minimum of 20 days is required, with a sampling rate of no fewer than six samples per day, and Rau et al. (2020b) suggest 60 days of data may be needed. However, by comparing results of different time-series lengths, it is shown here that whilst 60 days is sufficient to establish which tide is dominant at a given location, a 6-month-longtime-series yields more accurate BE results in this location. In contrast, BRF was found to be as consistent for shorter time-series as longer ones. Rau et al. (2020b) note that BRF only requires a time-series length with a minimum duration of 5 days. Therefore, whilst TSA may be more accurate when long time-series are available, where the time-series is short, BRF may be more suitable.
Hydraulic properties of Cardiff
Boreholes previously identified as OT-influenced by Cardiff Harbour Authority (Mitchell 1996) were confirmed as such using TSA; however, four additional sites were also revealed. The tidal analysis of the made ground boreholes highlighted four locations where OT signals are detected. These are found close to the boundary, and in one case inside a former river meander, suggesting a previously unidentified localised hydraulic connectivity between the made ground and the aquifer (Fig. 8).
From the BRF plot shapes, just two boreholes were identified as unconfined (one pre- and one post-impoundment, both found close the River Taff within the groundwater control zones; Fig. 9), coinciding with areas of the city where it is suspected some of the confining clays may have been removed for industrial purposes. Furthermore, some areas of Cardiff that were previously assumed to be unconfined (e.g. Hydrotechnica. 1991; Mitchell 1996) were shown to exhibit a degree of confinement.
Barometric efficiencies across Cardiff were found to be low, as would be expected for a relatively compressible, unconsolidated lithology and are consistent with the findings of Rau et al. (2018). By contrast, BRF-derived BEs, whilst broadly consistent with those of TSA, tended to be higher, particularly where borehole storage was observed.
Much of the aquifer had relatively uniform hydraulic properties; however, a zone of higher specific storage than the Cardiff average was found around Canton, Riverside and Leckwith. This had not previously been identified in the existing mapping (Waters and Lawrence 1987) and reflects the potential heterogeneity of coastal, urban aquifers. There are a number of potential explanations for this:
-
1.
The degree of compositional variability in the glaciofluvial sand and gravels could account for this localised trend since borehole logs in this area show a slightly higher sand content compared with the rest of the city, and, therefore, greater porosity and compressibility. However, the aquifer unit shows great variability in clast size and assemblage, and no particle size distribution data are available to fully test this relationship.
-
2.
The area is close to a mapped deposit of till (BGS 2016); therefore, it is possible that localised compositional variability within the extremely heterogenous unit is responsible for the higher specific storage.
-
3.
The area described is one of the oldest and most developed parts of the city and substantial compaction and reworking of the ground, as well as buried services may have altered the hydraulic regime.
-
4.
Prior to its current use as a residential and commercial area, the land was agricultural with a network of drainage ditches crisscrossing the site, altering natural drainage patterns. Cardiff is also home to many buried valleys, one of which is known to be present close to the area of high specific storage (Waters and Lawrence 1987). Another possible explanation for the zone is a paleo-oxbow lake of the present-day River Taff from the last Ice Age, and its associated fluvial deposits. Any buried channels, natural or anthropogenic, could be infilled with alluvial material of higher porosity and compressibility which may account for the high specific storage values in this area.
It is only possible to speculate about the cause of the zone of high specific storage; however, TSA has identified an area of the city that could require further investigation prior to the development of shallow geothermal energy networks proposed by Farr et al. (2017), as the groundwater and heat flow models required for this development need to account for heterogeneity in hydraulic properties. This highlights the importance of TSA as a rapid, passive method of characterising groundwater systems and deriving subsurface properties at scale.
Limitations
The inability of either TSA or BRF to accurately determine BE for OT-influenced boreholes is a major limitation to the use of this type of methodology in coastal aquifers. However, the combined approach of TSA with BRF is useful for identifying OT-influenced boreholes and eliminating them for further investigation, before calculating BE for any non-OT boreholes highlighted by the method. Furthermore, \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) may be used to map OT-signal propagation with distance from the coastal/river boundary, and this needs to be explored deeper with future investigations. Further work is necessary to fully disentangle tidal signals if TSA is to be applied to deliver estimates of BE in OT-influenced boreholes.
Another potential drawback of TSA is the assumption that groundwater pressure head is representative of subsurface pore pressure (Rau et al. 2020a). Whilst this has not presented an issue in Cardiff due to the sufficiently high permeability found throughout the city, this may be of concern in other locations. Additionally, uncertainty exists in the estimation of BE from TSA and it has not been possible to quantify this. However, Turnadge et al. (2019) have shown that in comparisons with other methods of deriving BE, TSA performs very well.
The uncertainties surrounding assumed porosity and transmissivity values are a limitation of this methodology, and where these are high, the calculated hydraulic properties may be less certain. However, in the Cardiff study, uncertainty is low and the estimated properties may be considered acceptable. As such, where uncertainties are high, it may be more appropriate to report a range for estimated hydraulic property values, which, while less quantitative, is still of use for the qualitative characterisation of hydro-geomechanical parameters to support groundwater modelling.
Conclusions
-
1.
TSA and BRF applied in combination provide a powerful tool for the hydro-geomechanical characterisation of coastal aquifers, where individually these techniques would be more limited. BEs derived from the TSA and BRF methods for non-OT-influenced boreholes compare moderately well (R = 0.75); however, BEs calculated by the TSA method are considered more reliable (Turnadge et al. 2019). Neither method can produce reliable BEs for boreholes affected by an OT signal.
-
2.
By comparing the magnitude of \( {M}_2^{\mathrm{GW}} \):\( {S}_2^{\mathrm{GW}} \) with \( {M}_2^{\mathrm{ET}} \):\( {S}_2^{\mathrm{ET}} \), \( {M}_2^{\mathrm{AT}} \):\( {S}_2^{\mathrm{AT}} \) and \( {M}_2^{\mathrm{OT}} \):\( {S}_2^{\mathrm{OT}} \) it is possible to identify AT-dominant boreholes, and those boreholes with a definite and obvious OT-influence. BRF plot shapes can then be used to differentiate between ET- and OT-dominance in the remaining boreholes. This enables TSA-derived BEs to be calculated for non-OT-influenced boreholes in a coastal aquifer setting.
-
3.
The use of TSA for the large spatial characterisation of hydraulic properties across an aquifer has been demonstrated for the first time. TSA-derived BEs, aquifer compressibility, specific storage, storativity and hydraulic diffusivity have been mapped across the Cardiff aquifer. Through the identification of OT signals in boreholes monitoring the made ground, it is possible to detect areas of the study site where there is hydraulic connectivity between the aquifer and the made ground, and thus detect local hydro-geomechanical variations within units. In Cardiff, some previous assumptions about the aquifer and the confining overlying clays have been confirmed, while others have been improved, and a discrete zone of high storage has been identified.
Through the spatial aquifer characterisation, input parameters for hydrogeological and subsurface heat transport models may be more representative of localised variations, than otherwise possible using traditional methods of parameterization, allowing for more robust modelling of aquifer responses to natural and anthropogenic change. Spatial patterns of hydraulic properties can be used to constrain model calibration and afford statistically correlated spatial parameter distribution for prior uncertainty analysis. Where uncertainties over porosity and transmissivity are high, an estimated range may be more appropriate for each hydraulic property. These are still of use in the supporting groundwater models.
-
4.
TSA has been shown to be effective in detecting the effects of anthropogenic interventions on the hydraulic responses and regime. In Cardiff, this is illustrated by the comparison of pre- and post-impoundment tidal signals, where a distinct reduction in OT signal is observed after the construction of the barrage, both in terms of signal strength and distance from the source. The combined TSA/BRF approach allows for the identification of OT signals and their amplitude to be mapped with distance from the coast/river boundary.
-
5.
There remain uncertainties in the precise delineation of OT-influence within coastal aquifers where the OT signal strength is of a similar order of magnitude to ET-signals. Further research is required to establish whether complete tidal disentanglement in the presence of OT is possible. If this were to be achieved, TSA could be used to derive BEs and other hydraulic properties from OT-influenced boreholes. Additionally, more research into the way the degree of aquifer confinement could be established from \( {M}_2^{\mathrm{GW}} \) and \( {S}_2^{\mathrm{GW}} \) phases could be developed through the combined approach of TSA and confinement identified from BRF plot shapes.
-
6.
TSA has an advantage over traditional methods of aquifer characterisation. It is noninvasive, making use of often routinely drilled groundwater monitoring boreholes instead of bespoke installations which are costly and cumbersome to complete in built-up areas. The ‘passive’ technique is quick to apply and yields large amounts of geotechnical data from minimal input, making it a cost-effective addition to existing ground investigation methods.
References
Acworth RI, Brain T (2008) Calculation of barometric efficiency in shallow piezometers using water levels, atmospheric and earth tide data. Hydrogeol J 16(8):1469–1481. https://doi.org/10.1007/s10040-008-0333-y
Acworth RI, Halloran LJS, Rau GC, Cuthbert MO, Bernardi TL (2016) An objective frequency domain method for quantifying confined aquifer compressible storage using earth and atmospheric tides. Geophys Res Lett 43(22):11671–11678. https://doi.org/10.1002/2016GL071328
Acworth RI, Rau GC, Halloran LJS, Timms WA (2017) Vertical groundwater storage properties and changes in confinement determined using hydraulic head response to atmospheric tides. Water Resour Res 53(4):2983–2997. https://doi.org/10.1002/2016WR020311
Batu V (1998) Aquifer hydraulics: a comprehensive guide to hydrogeologic data analysis. Wiley, New York, 727 pp
Boon DP, Farr GJ, Abesser C, Patton AM, James DR, Schofield DI, Tucker DG (2019) Groundwater heat pump feasibility in shallow urban aquifers: experience from Cardiff, UK. Sci Total Environ 697:133847. https://doi.org/10.1016/j.scitotenv.2019.133847
British Geological Survey (BGS) (2016) Digital geological map of Great Britain 1:50 000 scale (BGS Geology 50k) data. Version 8.24. Release date 16-01-2017, British Geological Survey, Keyworth, UK. https://doi.org/10.5285/455f9151-61ae-479f-9916-f01d612ab66a
Butler JJ Jr, Jin W, Mohammed GA, Reboulet EC (2011) New insights from well responses to fluctuations in barometric pressure. Ground Water 49(4):525–533. https://doi.org/10.1111/j.1745-6584.2010.00768.x
Clark WE (1967) Computing the barometric efficiency of a well. J Hydraul Div 93(4):93–98
Cooper HH (1966) The equation of groundwater flow in fixed and deforming coordinates. J Geophys Res 71(20):4785–4790. https://doi.org/10.1029/JZ071i020p04785
Edwards RJG (1997) A review of the hydrogeological studies for the Cardiff Bay barrage. Q J Eng Geol Hydrogeol 30:49–61. https://doi.org/10.1144/GSL.QJEGH.1997.030.P1.05
Farr GJ, Patton AM, Boon DP, James DR, Williams B, Schofield DI (2017) Mapping shallow urban groundwater temperatures, as case study from Cardiff, UK. Q J Eng Geol Hydrogeol 50:187–198. https://doi.org/10.1144/qjegh2016-058
Freeze RA, Cherry JA (1979) Groundwater. Prentice Hill, Englewood Cliffs, NJ, 604 pp
Gonthier G (2007) A graphical method for estimation of barometric efficiency from continuous data - concepts and application to a site in the Piedmont, Air Force Plant 6, Marietta, Georgia (Tech. Rep. 2007-5111). US Geological Survey, Marietta, GA. https://doi.org/10.3133/sir20075111
Heathcote JA, Lewis RT, Russell D, Soley RWNS (1997) Cardiff Bay barrage: groundwater control in a thin tidal aquifer. Q J Eng Geol Hydrol 30:63–77
Heathcote JA, Lewis RT, Sutton JS (2003) Groundwater modelling for the Cardiff Bay barrage, UK: prediction, implementation of engineering works and validation of modelling. Q J Eng Geol Hydrogeol 36(2):159–172. https://doi.org/10.1144/1470-9236/2002-29
Hsieh PA, Bredehoeft JD, Farr JM (1987) Determination of aquifer transmissivity from earth tide analysis. Water Resour Res 23(10):1824–1832. https://doi.org/10.1029/WR023i010p01824
Hydrotechnica (1991) Cardiff Bay Barrage groundwater modelling final report. Reference 12057/R3 Final. Hydrotechnica Ltd for Cardiff Bay Development Corporation, Cardiff
Kendall RS (2015) Conceptual cross-sections of superficial deposits in Cardiff. British Geological Survey open report OR/15/045, BGS, Keyworth, UK
Kendall RS, James L, Thorpe S, Patton A (2018) Model metadata report for Cardiff superficial deposits. British Geological Survey open report, OR/ 16/031, BGS, Keyworth, UK
Kreitmair MJ, Makasis N, Bidarmaghz A, Terrington RL, Farr GJ, Scheidegger JM, Choudhary R (2020) Effect of anthropogenic heat sources in the shallow subsurface at city-scale. E3S web conference, 205 07002. https://doi.org/10.1051/e3sconf/202020507002
McMillan TC, Rau GC, Timms WA, Andersen MS (2019) Utilizing the impact of earth and atmospheric tides on groundwater systems: a review reveals the future potential. Rev Geophys 57:281–315. https://doi.org/10.1029/2018RG000630
Met Office (2020) Met Office: averages 1981–2010. https://wwwmetofficegovuk/research/climate/maps-and-data/uk-climate-averages/gcjszmp44. Accessed 12 November 2020
Mitchell RCS (1996) Cardiff Bay barrage groundwater characterisation. Entec technical report for Cardiff Bay Development Corporation, Cardiff, UK
Patton AM, Farr G, Boon DP, James DR, Williams B, James L, Kendall R, Thorpe S, Harcombe G, Schofield DI, Holden A, White D (2019) Establishing an urban geo-observatory to support sustainable development of shallow subsurface heat recovery and storage. Q J Eng Geol Hydrogeol 53(1):49–61. https://doi.org/10.1144/qjegh2019-020
Quilty EG, Roeloffs EA (1991) Removal of barometric pressure response from water level data. J Geophys Res Solid Earth 96(B6):10209–10218. https://doi.org/10.1029/91JB00429
Rahi KA, Halihan T (2013) Identifying aquifer type in fractured rock aquifers using harmonic signals. Ground Water 51:76–82. https://doi.org/10.1111/j.1745-6584.2012.00925.x
Rasmussen TC, Crawford LA (1997) Identifying and removing barometric pressure effects in confined and unconfined aquifers. Ground Water 35(3):502–511. https://doi.org/10.1111/j.1745-6584.1997.tb00111.x
Rau GC (2018) PyGTide: a Python module and wrapper for ETERNA PREDICT to compute synthetic model tides on earth. https://doi.org/10.5281/zenodo.1346260
Rau GC, Acworth RI, Halloran LJS, Timms WA, Cuthbert MO (2018) Quantifying compressible groundwater storage by combining cross-hole seismic surveys and head response to atmospheric tides. J Geophys Res Earth Surf 123:1910–1930. https://doi.org/10.1029/2018JF004660
Rau GC, Cuthbert MO, Acworth RI, Blum P (2020a) Technical note: disentangling the groundwater response to earth and atmospheric tides to improve subsurface characterisation. Hydrol Earth Syst Sci 24:6033–6046. https://doi.org/10.5194/hess-2020-256
Rau GC, Cuthbert MO, Post VEA, Schweizer D, Acworth RI, Andersen MS, Blum P, Carrara E, Rasmussen TC, Ge S (2020b)Future-proofing hydrogeology by revising groundwater monitoring practice. Hydrogeol J 28:2963–2969. https://doi.org/10.1007/s10040-020-02242-7
Rotzoll K, El-Kasi AI (2008) Estimating hydraulic properties of coastal aquifers using wave setup. J Hydrogeol 353:201–213. https://doi.org/10.1016/j.jhydrol.2008.02.005
Rotzoll K, Gingerich SB, Jenson JW, El-Kadi AI (2013) Estimating hydraulic properties from tidal attenuation in Guam Lens aquifer, territory of Guam, USA. Hydrogeol J 21:643–654. https://doi.org/10.1007/s10040-012-0949-9
Schweizer D, Ried V, Rau GC, Tuck JE, Stoica P (2021) Comparing methods and defining practical requirements for extracting harmonic tidal components from groundwater level measurements. Math Geosci 2021. https://doi.org/10.1007/s11004-020-09915-9
Solórzano-Rivas SC, Werner AD, Irvine DJ (2021) Estimating hydraulic properties from tidal propagation in circular islands. J Hydrol. https://doi.org/10.1016/j.jhydrol.2021.126182
Spane FA (2002) Considering barometric pressure in groundwater flow investigations. Water Resour Res 38(6):14.1–14.1418. https://doi.org/10.1029/2001wr000701
Turnadge C, Crosbie RS, Barron O, Rau GC (2019) Comparing methods of barometric efficiency characterization for specific storage estimation. Groundwater 57(6):884–859. https://doi.org/10.1111/gwat.12923
Waters RA, Lawrence DJD (1987) Geology of the South Wales coalfield, part III, the country around Cardiff: memoir for the 1:50 000 geological sheet 263, England and Wales, 3rd edn. HMSO, London
Wenzel HG (1996) The Nanogal software: earth tide data processing package ETERNA 3.30. Bull Inform Marées Terrestres 124:9425–9439 http://www.eas.slu.edu/GGP/ETERNA34/MANUAL/ETERNA33.HTM. Accessed September 2021
Williams B (2008) Cardiff Bay barrage: management of groundwater issues. Water management. ICE Proc 161:313–321. https://doi.org/10.1680/wama.2008.161.6.313
Young H, Freedman R (2000) Sears and Zemansky’s university physics with modern physics, 10th edn. Addison-Wesley, Boston
Liao X, Wang CY (2018) Seasonal permeability change of the shallow crust inferred from deep well monitoring. Geophys Res Lett 45:11130–11136. https://doi.org/10.1029/2018GL080161
Acknowledgements
The authors would like to thank the following: C. Abesser, A. Holden, G. Farr and L. Oliver from the British Geological Survey, and D. James from the County Council of the City and County of Cardiff, as well as the reviewers of this manuscript. A.M.P. publishes with the permission of the executive director, British Geological Survey (NERC). Groundwater level data have been provided by, and are used with, the permission of Cardiff Harbour Authority, County Council of the City and County of Cardiff.
Funding
M.O.C. gratefully acknowledges funding for an Independent Research Fellowship from the UK Natural Environment Research Council (NE/P017819/1). Funding from the British Geological Survey, Natural Environment Research Council. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 835852.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Patton, A.M., Rau, G.C., Cleall, P.J. et al. Hydro-geomechanical characterisation of a coastal urban aquifer using multiscalar time and frequency domain groundwater-level responses. Hydrogeol J 29, 2751–2771 (2021). https://doi.org/10.1007/s10040-021-02400-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-021-02400-5