Abstract
A three-dimensional variable-density finite element model was developed to study the combined effects of overabstraction and seawater intrusion in the Pingtung Plain coastal aquifer system in Taiwan. The model was generated in different layers to represent the three aquifers and two aquitards. Twenty-five multilayer pumping wells were assigned to abstract the groundwater, in addition to 95 observation wells to monitor the groundwater level. The analysis was carried out for a period of 8 years (2008–2015 inclusive). Hydraulic head, soil permeability, and precipitation were assigned as input data together with the pumping records in different layers of the aquifer. The developed numerical model was calibrated against the observed head archives and the calibrated model was used to predict the inland encroachment of seawater in different layers of the aquifer. The effects of pumping rate, sea-level rise, and relocation of wells on seawater intrusion were examined. The results show that all layers of the aquifer system are affected by seawater intrusion; however, the lengths of inland encroachment in the top and bottom aquifers are greater compared with the middle layer. This is the first large-scale finite-element model of the Pingtung Plain, which can be used by decision-makers for sustainable management of groundwater resources and cognizance of seawater intrusion in coastal aquifers.
Résumé
Un modèle tridimensionnel à éléments finis et à densité variable a été développé pour étudier les effets combinés de la surexploitation et de l’intrusion d’eau de mer dans le système aquifère côtier de la plaine de Pingtung à Taïwan. Le modèle a été généré avec différentes couches pour représenter les trois aquifères et les deux aquitards. Vingt-cinq puits de pompage multicouches ont été affectés à l’exploitation des eaux souterraines, en plus des 95 puits d’observation du suivi du niveau des eaux souterraines. L’analyse a été réalisée sur une période de 8 ans (2008–2015 compris). La charge hydraulique, la perméabilité du sol et les précipitations ont été utilisées comme données d’entrée, ainsi que les enregistrements de pompage dans les différentes couches de l’aquifère. Le modèle numérique développé a été calibré par rapport aux archives des charges hydrauliques observées et le modèle calibré a été utilisé pour prédire la pénétration de l’eau de mer à l’intérieur des terres au sein des différentes couches de l’aquifère. Les effets du débit de pompage, de l’élévation du niveau de la mer, et de la relocalisation des puits sur l’intrusion de l’eau de mer ont été examinés. Les résultats montrent que toutes les couches du système aquifère sont affectées par l’intrusion d’eau de mer ; cependant, les longueurs de la pénétration à l’intérieur des terres au sein des aquifères supérieurs et inférieurs sont plus importantes que dans la couche intermédiaire. Il s’agit du premier modèle à éléments finis à grande échelle de la plaine de Pingtung, qui peut être utilisé par les décideurs pour la gestion durable des ressources en eaux souterraines et la connaissance de l’intrusion de l’eau de mer dans les aquifères côtiers.
Resumen
Se elaboró un modelo tridimensional de elementos finitos de densidad variable para estudiar los efectos combinados de la sobreexplotación y la intrusión de agua de mar en el sistema acuífero costero de la llanura de Pingtung en Taiwán. El modelo se generó en diferentes capas para representar los tres acuíferos y los dos acuitardos. Se asignaron 25 pozos de bombeo multicapa para extraer las aguas subterráneas, además de 95 pozos de observación para monitorear el nivel de las aguas subterráneas. El análisis se llevó a cabo durante un período de ocho años (2008–2015 inclusive). Se utilizaron como datos de entrada la altura hidráulica, la permeabilidad del suelo y la precipitación, junto con los registros de bombeo en las diferentes capas del acuífero. El modelo numérico desarrollado se calibró frente a los registros de la carga hidráulica observada y el modelo calibrado se utilizó para predecir la invasión de agua de mar en las diferentes capas del acuífero. Se analizaron los efectos de la tasa de bombeo, la elevación del nivel del mar y la reubicación de los pozos en la intrusión marina. Los resultados muestran que todas las capas del sistema acuífero se ven afectadas por la intrusión de agua marina; sin embargo, la longitud de la intrusión hacia el interior en los acuíferos superiores e inferiores es mayor en comparación con la capa media. Se trata del primer modelo de elementos finitos en gran escala de la llanura de Pingtung, que puede ser utilizado por los responsables de la toma de decisiones para la gestión sostenible de los recursos hídricos subterráneos y el conocimiento de la intrusión marina en los acuíferos costeros.
摘要
为了研究台湾屏东平原沿海含水层系统中过量开采和海水入侵的综合影响, 建立了三维变密度的有限元模型。该模型采用不同的层来模拟三个含水层和两个隔水层。研究区有95眼观测井监测水位, 还有25眼多层开采地下水的抽水井。分析期为8年(即2008–2015年)。将水头, 土壤渗透率和降水与在不同含水层中的开采记录一起作为输入数据。基于观察的水头结果, 完成了数值模型的校准, 并使用该校准模型来预测在不同含水层中内陆的海水入侵。研究了开采量, 海平面上升和井的重新布局对海水入侵的影响。结果表明, 含水层系统的所有层位都受到海水入侵的影响; 但是, 与中间层相比, 顶部和底部含水层的内陆入侵长度更大。这是屏东平原的首个大尺度有限元模型, 决策者可以将其用于地下水资源的可持续管理以及沿海含水层中海水入侵规律的认识。
Resumo
Um modelo tridimensional de elementos finitos de densidade variável foi desenvolvido para estudar os efeitos combinados de superabstração e intrusão de água do mar no sistema aquífero costeiro da Planície de Pingtung, em Taiwan. O modelo foi gerado em diferentes camadas para representar os três aquíferos e dois aquitardos. Foram especificados 25 poços de bombeamento multicamada para captar as águas subterrâneas, além de 95 poços de observação para monitorar o nível das águas subterrâneas. A análise foi realizada por um período de 8 anos (2008–2015 inclusive). Cargas hidráulicas, permeabilidade do solo e precipitação foram atribuídas como dados de entrada, juntamente com os registros de bombeamento em diferentes camadas do aquífero. O modelo numérico desenvolvido foi calibrado contra os registros das cargas observadas e o modelo calibrado foi usado para prever a invasão da água do mar no continente em diferentes camadas do aquífero. Os efeitos da taxa de bombeamento, aumento do nível do mar e realocação de poços na intrusão de água do mar foram examinados. Os resultados mostram que todas as camadas do sistema aquífero são afetadas pela intrusão da água do mar; no entanto, os comprimentos de invasão continental nos aquíferos superior e inferior são maiores em comparação com a camada intermediária. Este é o primeiro modelo de elementos finitos em larga escala da Planície de Pingtung, que pode ser usado pelos tomadores de decisão para o gerenciamento sustentável dos recursos hídricos subterrâneos e o conhecimento da intrusão da água do mar nos aquíferos costeiros.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Developing industrial, agricultural and tourism activities together with human settlements in coastal areas has led to overexploitation of aquifers, increasing seawater intrusion (SWI) and decreasing groundwater quality. The sea-level rise (SLR) due to climate change associated with global warming is expected to exacerbate the problem (Stocker 2014). The coastal plain of Pingtung in Taiwan currently suffers from SWI due to overexploitation of the aquifer system by a significant number of pumping wells screened through the aquifers, at different pumping rates and depths, and using different well types. There are two different methods commonly used for analysing SWI: “sharp interface” and “variable density” methods (Sherif et al. 2012). In the sharp interface method, the saltwater and freshwater are considered as immiscible fluids with a sharp interface separating them in a homogeneous unconfined aquifer. This method is used when the width of the transition zone between saltwater and freshwater is small compared to the aquifer thickness (Bear 1979), and hence the effect of the interface (transition zone) is ignored. It can be assumed that the flow is substantially horizontal in the system (Dupuit assumption) and the vertical gradient is negligible (Vacher 1988). Based on the literature, due to the dominantly laminar pattern of groundwater flow in aquifers, where the width of the mixing zone is relatively smaller than the aquifer thickness, the boundary can be delineated as a sharp interface with a slope, where the two liquids may be considered as two immiscible fluids (Das and Datta 1999; Kacimov and Sherif 2006). Under this condition and due to pressure balance on both sides, it can generally be assumed that this sharp interface is static and there is no flow across it (Dogan and Fares 2008). The Ghyben-Herzberg method was the first analytical formulation of SWI (Bear 1979), and provides a quick estimation of the location of the freshwater–saltwater interface under steady-state conditions.
However, this method is not applicable to cases with a wider interface between freshwater–saltwater (Cooper 1959), as is the case in this study where the freshwater–saltwater interface occupies a greater depth than the thickness of the aquifer system. Therefore, the variable density approach was employed to analyze the mixing of freshwater and saline water (as miscible fluids), which is controlled by hydrodynamic dispersion, which is the combination of mechanical dispersion and physico-chemical dispersion (Bear 1979). This zone is created between freshwater and saltwater in the form of a transition zone and it is closer to the physical behaviour of the flow and solute transport in reality. The fluid density in the transition zone (freshwater–saltwater interface) varies in time and space as a function of the fluid’s temperature, concentration, and pressure (Kooi et al. 2000; Voss and Souza 1987; Pool and Carrera 2011; Diersch and Kolditz 2002; Barazzuoli et al. 2008); therefore, a variable-density flow and transport model is imperative for an appropriate representation of the saltwater intrusion mechanism (Kolditz et al. 1998; Voss and Souza 1987; Langevin and Guo 2006; Simmons et al. 2001).
While there are many natural and manmade factors affecting SWI in coastal aquifers, the main natural factors are aquifer geometry, geological parameters, depth of aquifer along the coast, hydraulic and hydrogeological parameters, and sea-level rise (Mehnert and Jennings 1985; Sherif et al. 2012; Paniconi et al. 2001a, b; Zhou et al. 2000; Tber et al. 2008; Narayan et al. 2007; Collins and Gelhar 1971). Moreover, artificial recharge, controlling water runoff from the surface and excessive pumping are some of the man-made factors affecting SWI (Sherif et al. 2012). The progress of the freshwater–seawater interface in coastal aquifers can be directly affected by changes in all of the aforementioned factors (Kim et al. 2009). Identifying the effects of these factors on SWI plays an important role in the effective management of groundwater resources.
Sea-level rise is one of these factors that reduces the land surface and affects groundwater resources (Werner and Simmons 2009; Chang et al. 2011; Ferguson and Gleeson 2012; Essink 2001). By 2100, sea levels are expected to rise globally from 0.09 to 0.88 m (Solomon et al. 2007). SLR can also increase the hydrostatic head of the sea which would, in turn, result in inland movement of the saltwater interface (Priyanka and Mahesha 2015). SLR has a negative effect on aquifers’ hydraulic equilibrium condition, in line with various natural parameters such as tides and manmade activities like overpumping (Werner et al. 2013). SLR coupled with overexploitation of groundwater has been proven to be a key factor in extending the transition zone in unconfined aquifers (Bobba 2002; Yechieli et al. 2010; Loáiciga et al. 2012; Carretero et al. 2013; Rasmussen et al. 2013; Sefelnasr and Sherif 2014; Uddameri et al. 2014). Loss of wetlands, impeded drainage, erosion, land-surface inundation and SWI are all problems caused by sea-level rise (Fitzgerald et al. 2008; Bricker 2009; Nicholls 2010, 2015). The lateral encroachment of seawater will be accelerated by increasing the hydraulic head of the saltwater in coastal boundaries due to SLR. It has been shown that a 0.5-m SLR could increase the lateral saltwater intrusion in the Nile aquifer by about 9,000 m (Sherif and Singh 1999) and change the inland penetration of the saline toe by approximately 5 km (Werner and Simmons 2009). In another study, it was shown that a 1-m SLR within the Mediterranean Sea would cause a 400-m intrusion for the Mediterranean coastal aquifer in Israel (Yechieli et al. 2010).
A number of numerical simulation codes such as SUTRA (Voss and Provost 1984), FEFLOW (Diersch 2006), and SEAWAT (Langevin et al. 2008) have been applied to simulate variable-density flow and solute transport in aquifers. Despite the availability of powerful numerical modelling tools, due to the lack of adequate and accurate data, relatively few studies have been published on the large-scale simulation of SWI (Ababou and Al-Bitar 2004; Kopsiaftis et al. 2009; Sherif et al. 2012). In general, collecting hydrogeological data for large-scale three-dimensional (3D) case studies is very expensive, time-consuming and in some cases impossible due to limited accessibility. In this study, the encroachment of saltwater at different layers of the multilayer aquifer system in the Pingtung Plain in Taiwan, is simulated in 3D using FEFLOW, considering the density-dependent flow and solute transport in the aquifer.
Study area
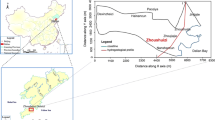
The Pingtung Plain, with an area of 1,210 km2 (width of 20 km and length of 55 km), is located in the southwest of Taiwan. The plain extends as a 2-km deep alluvial wedge bounded by two active faults named “Feng Shan” and “Chao-Chou” from the north-west and south-east, respectively. The Taiwan Strait extends along the south border of the domain boundary. The foothills and river valleys bound the plain in the north. There is a mountain range adjacent to the alluvial deposit plain (Fig. 1), which itself can be categorised as a valley due to its position, being surrounded by hills with four specific topographic zones which are the northern mountainous region, eastern mountainous area, the western foothills and the Pingtung Valley (Ting et al. 1998b). The plain is a relatively flat area with less than 100-m elevation and is drained by three main rivers, the Kaoping, Donggang, and Linbian. The Kaoping, with a length of approximately 50 km, is the longest river within the Pingtung Plain area, originating from the mountain range and discharging to the Taiwan Strait. These rivers divide the Pingtung Plain into three zones of proximal fan, mid fan, and distal fan (Fig. 1).
The Pingtung Plain’s subsurface geology has been identified from the examination of the outcrops and interpretation of borehole tests and available wells (Ting et al. 1998b). According to Kuo and Wang (2001), sandy gravel with more than 60% gravel and 20% sand forms the proximal fan material with a transmissivity of about 9,000 m2/day and a storage factor of 6.5 × 10−3(Hsieh et al. 2010). However, decreasing grain size from north to south and east to west leads to having 40% gravel and 40% sand in the mid fan zone (Kuo and Wang 2001) with 2,300 m2/day transmissivity and a 9.5 × 10−4 storage factor, while the distal fan is mainly comprised of silt and clay, with a transmissivity of about 1,200 m2/day and a storage factor of about 0.00005 (Hsieh et al. 2010). The afore-mentioned storage factors are based on previous studies (Hsu 1961; Ting 1992; Ting et al. 1998b) which were defined as characteristic properties of the upper aquifer only, while the values of this parameter are not available for the other layers. Due to the lack of data, value of 0.0001 m−1 (default value in FEFLOW) was assigned for specific storage (Ss) for the entire model.
Being located south of the Tropic of Cancer, the Pingtung Plain has a subtropical climate with an average temperature of 24 °C, reaching its highest value (28 °C) in July and lowest value (19 °C) in January. The plain receives, on average, 2,400 mm/year of natural precipitation; nonetheless, this amount reaches 3,000 mm/year or higher in the mountain areas, with 90% of the total annual precipitation occurring during the wet (monsoon) season (from May to October) due to typhoons (Yu et al. 2006).
The recharge pattern is highly dependent on the permeability of the soil (Hsieh et al. 2010). As the right side of the plain, the proximal fan is composed of gravel and sand, it has higher potential for recharge and percolation of precipitation and river flow (Ting et al. 1997; Hsieh et al. 2010). Also, the monitored groundwater level in the eastern part is much higher than in the western side of the plain (zone of overpumping), comprised of silt and clay with fine sediments in all aquifers (Hsieh et al. 2010; Chang et al. 2017). The precipitation follows an unsteady pattern in this area and the ratio of rainfall in the wet season to dry season is 9:1, which is much higher than the ratio in other areas in Taiwan (Huang and Chiu 2018; Fig. 2).
The rainfall distribution is a significant factor in controlling the availability of the Pingtung Plain’s groundwater resources (Hsu et al. 2007). The plain is enclosed by mountainous regions in the east and north and foothills in the west, which contain a thick series of black slate with very low porosity (Tu et al. 2011). Accordingly, the cleavages and local joints are the only options for water storage (Ting et al. 1998b), a feature that results in most of the precipitation running off the surfaces towards the rivers and streams and along the plain (Chang et al. 2004). The entire groundwater aquifer underlying the Pingtung Plain area is comprised of unconsolidated sediments. The direct infiltration of rainfall in the north and east of the plain (due to the unconsolidated deposits) through the foothills is the main mechanism of groundwater recharge. Additionally, river seepage, as local penetration in the upper regions of the plain, is another source of surface water for recharging groundwater.
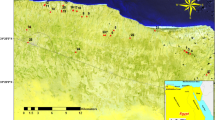
Faults with impervious bedrock surround the plain from the east and west. This, together with the low permeability soil along the north boundary, creates no lateral flux boundary conditions in these parts of the domain (Hsu et al. 2007). The outflow includes abstraction via numerous pumping wells, evaporation losses and the seaward movement of brackish water. The groundwater has been extracted at a rate of 4,000 million liters per day (MLD) within the entire Pingtung Plain area, which is significantly higher than the natural recharge rate of 2,730 MLD (Hsu et al. 2007), which also strongly depends on the precipitation rate. Due to lack of data on the transient pumping rates for the simulation period (2008–2015) and depth of the wells, the pumping data of the year 1996 (the only available data) for the 25 townships in the Pingtung Plain (Figs. 1 and 3; Table 1) were used as input. The wells were considered screened through the aquifer’s whole depth (through three aquifers and two aquitards), for both steady-state and transient models. Based on Taiwan’s Water Resource Bureau (MOEA), the applied abstraction rate has not changed significantly in the last decade. Therefore, in this study, it was assumed that the rates of abstraction from the pumping wells were constant for the simulation period. However, to address the uncertainty in the data, the study included cases of a 30% increase and decrease in the abstraction rate in order to examine the importance of this parameter for the SWI.
Seawater intrusion in the Pingtung Plain
The availability of a large amount of water, the soil texture, and the climatic conditions make the Pingtung Plain one of the highly productive areas for agriculture (Hsieh et al. 2010). Surface-water supplies only 20% of the demand which emphasises the significant dependency on groundwater resources (Lin et al. 2011) for agriculture, industry, fish breeding and drinking water in this region. Seawater intrusion has occurred in the Pingtung Plain due to overexploitation of groundwater, especially due to private well pumping (Chang et al. 2017). The Taiwan Environmental Protection Agency (TWEPA) characterises the saltwater with respect to its total dissolved solids (TDS) content and categorises the water quality according to the range of TDS into three groups: contaminated water (TDS > 10,000 mg/L), semi-brackish water (1,000 < TDS < 10,000 mg/L) and freshwater (TDS < 1,000 mg/L) (Huang and Chiu 2018). Based on an early investigation, in 1960 the groundwater in the entire Pingtung Plain aquifer was of good quality, with TDS ranging between 180 and 984 mg/L (Ellis 1999). However, overabstraction of groundwater, primarily for agricultural use, deteriorated the groundwater quality, especially in the wells located around the Kaoping River mouth, causing the inland encroachment of seawater, with TDS ranging between 1,000 and 29,000 mg/L from 1995 to 1996 (Ellis 1999). One of the main factors triggering seawater encroachment is the outcropping of the aquifers along the Kaoping River mouth, which provides a pathway between seawater and the land (Wang 1996). Overabstraction of the aquifer along the coast has led to lowering of the groundwater table below mean sea level (MSL), which created a hydraulic gradient from the sea towards the land and naturally pushed the seawater inland through this pathway. Based on the literature, nearly 30% of the Pingtung Plain area (359 km2) has been subject to seawater intrusion, with an average inland encroachment rate of 500 m/year from 1980 to 1996 (Wang 1996). Therefore, all areas in the vicinity of the shoreline are greatly susceptible to seawater intrusion.
Development of the numerical model
Finite element modelling
The Pingtung Plain aquifer consists of three aquifers separated by two aquitards. To define the two-dimensional (2D) domain, the target geometry maps, captured by ArcGIS, were imported as a polygon shapefile of the plain and 25 points representing the pumping wells into the FEFLOW (Finite Element subsurface FLOW) software (Diersch 2013; Fig. 3). The mesh generation was accomplished as an intermediate step defining inner and outer geometries. A triangular prism mesh was selected because of its capability to discretize irregular geometries containing complex points, lines, and polygons with variable layer thickness and critical areas such as coastlines or well fields (DHI-WASY 2010).
Special attention was paid to designing the finite element mesh of the model in order to minimize distorted elements. For this purpose, local mesh refinement was applied for the polygon domain, increasing the refinement for the coastline zone and the pumping well points in order to fulfil the irregular geometry of the plain, including very narrow sections along the corner of the domain boundary and variable layer thickness. The 2D model was then extended to the 3D multilayer aquifer based on the available elevation data (X, Y, Z) captured by 95 observation wells (Fig. 4).
The neighbourhood-interpolated-regionalisation method was used for assigning the elevation to the nearest node or to a group of nodes adjacent to the original observation well locations. After interpolation, the multilayer aquifer system with seven slices and six layers was created automatically within a domain area of 1,059.48 km2 and volume of 1,918.6 km3). Each layer was discretized into some sublayers in order to prevent vertical mesh disorders (considering the depth of aquifer is about 250 m) based on the thickness of each layer. Finally, the discretized model included 43 slices and 42 layers (Fig. 4) with a total of 947,352 elements and 516,688 nodes.
To the knowledge of the authors, this 3D finite element model of the Pingtung Plain aquifer with its six main layers and seven slices (Fig. 4a) is the first representation of the coastline and natural domain topography due to the flexible unstructured discretisation of the computational domain and local mesh refinements without nesting.
In the developed 3D model, the ground surface elevation (top of the model) lies from 2.3 m to a maximum of 89 m above mean sea level (MSL) and the bottom of the aquifer lies at 197 m below MSL. The surface layer with 10–16 m thickness overlies the first aquifer with 10–121 m thickness. Below the first aquifer, there is a semipervious first aquitard with 10–81 m thickness, overlying the second aquifer, with its thickness varying from 10 to 96 m. Under the second aquifer, lies the second aquitard with 10–63 m thickness, overlying the third aquifer with 10–103 m thickness. Once the model dimensions and mesh generation had been set up, the properties of the model were applied as a fully saturated, standard groundwater model in an unconfined multilayer aquifer with a free surface, where the water table is considered as a mobile material interface. To develop the relationship between the different layers of the aquifer, the top surface layer was assigned as a free surface with variable (movable) mesh. This allowed the mesh to adapt to the changing groundwater level and avoided the problem of dry cells. Additionally, when mass transport is considered, the contaminant can become “frozen” in dry cells and thus unable to move along the water table, which makes the model incorrect from a physical point of view. The top and bottom of the domain were left as unconstrained heads by default and the amount of residual water depth for the unconfined layer was set to 0.01 m. The model was run in steady state and then transient conditions. The collected transient data for water flow are from January 2008 to December 2015. In this study, the observed monthly precipitation data collected by Taiwan’s Water Resource Bureau (MOEA) from January 2008 to the end of December 2015 were used. The average monthly distribution of rainfall at 24 stations within different locations in the Pingtung Plain is presented in Fig. 2. These data were assigned to the top layer of the 3D model using the delogarithmic Kriging interpolation method as a spatial inflow distribution. The time discretisation was defined with automatic time step control by selecting an appropriate time step length according to the changes in the preliminary variable head. The groundwater flows from north east to south west (Fig. 5) and the freshwater is discharged to the sea through the entire depth of the domain. The general flow directions of the groundwater system are shown in Fig. 5. A predictor-corrector approach was used as the basis for the automatic time step control. The hydraulic head values for the three aquifers are presented in Fig. 6.
The default second-order accurate Forward Adams-Bashforth/backward Trapezoid rule (AB/TR) was used, which is standard for flow and flow-transport analyses and suitable for density-dependent models (Diersch 2010). Based on the experimental data (MOEA), only horizontal hydraulic conductivity data (Kx) were measured in observation wells in different layers of the aquifer. The confining layers, comprised of silt and clay, were assumed to have a constant hydraulic conductivity of 0.0001 m/day. The conductivity values varied from 1 to 520 m/day, 5–90 m/day and 1–100 m/day in the first, second and third aquifers, respectively (Fig. 7).
FEFLOW allows assigning axis-parallel anisotropic hydraulic conductivity in such a way that the principal directions of hydraulic conductivities are coincident with the Cartesian coordinates (Kx, Ky, Kz along the X, Y and Z axes; DHI-WASY 2010). Therefore, for the initial set up of the model, it was assumed that Kx = Ky = 10 Kz. The conductivity of each layer was determined by applying the Kriging logarithmic interpolation method to achieve spatial representation in the entire 3D model. Due to the high sensitivity of the model to permeability and the importance of this parameter in natural groundwater recharge from precipitation, it was selected to be calibrated along the X, Y and Z axes.
The first-type constant head (Dirichlet) boundary condition was assigned to the southern boundary, which is bounded by the Taiwan Strait. The saltwater head boundary condition (hs) could not be directly applied as the shoreline boundary condition and had to be transformed to the reference hydraulic head h (DHI-WASY 2010) based on Eq. (1):
where ρf = 1,000 and ρs = 1,025 kg/m3 are densities of the freshwater and saltwater respectively and z is the elevation from mean sea level (MSL) at each point of the model. The second-type (Neumann) boundary condition was assigned as no fluid flux along the east, north, and west of the domain, which is surrounded by low permeability material (Ting et al. 1998a). The coastal line in the southern boundary was assigned a constant mass concentration of 35,000 mg/L as the salt concentration of seawater. Salt is the only contaminant in this model and the adsorption is assumed negligible (Huang and Chiu 2018).
FEFLOW employs the generic governing equations (Bear 1979) covering most types of groundwater flow and solute transport problems. The general forms of these equations (Eqs. 2 and 3) are stated for fluid mass balance as:
and for the solute mass balance as:
where molecular diffusivity (Dm), gravity acceleration (g), fluid viscosity (μ) and porosity (ε) are 0 m2/s, 9.81 m/s2, 97.1 kg/m/day and 0.3, respectively. The other influence parameters are represented and defined in Table 2.
Assuming the molecular diffusivity (Dm) as zero, the hydrodynamic dispersion is a function of dispersivity and average velocity which has higher values in the direction of flow than the lateral and vertical directions (Ogata 1970; Voss 1984). The mean value of elemental diameters is a good approximation for longitudinal dispersivity in FEFLOW which should also guarantee a good convergence (Trefry and Muffels 2007). The mean elemental diameter of this model was 70 m, and hence it was selected as the longitudinal dispersivity. The longitudinal dispersivity for most of the studies ranges between 6 and 150 m (Gelhar et al. 1992; Sherif et al. 2012). The transverse dispersivity was calculated as 10% of this value as 7 m based on the FEFLOW parameter’s definition which is in good agreement with the literature (Bear et al. 1999; Sherif et al. 2012; Huang and Chiu 2018). Based on a recent study (Huang and Chiu 2018), the horizontal transverse dispersivity was assumed to have the same value as the longitudinal dispersivity.
Model calibration and validation
Simulation of a flow and solute transport problem requires a reliable steady-state solution; however, achieving this solution directly is not possible in FEFLOW, due to high sensitivity and nonlinearity of the model to some parameters such as hydraulic conductivity (Boufadel 2000). The time-stepping technique (Diersch and Kolditz 1998; Voss 1984) was utilised for this initial simulation with static boundary conditions for mass and hydraulic head in transient state. The system is steady when the state variables such as hydraulic head and mass concentration are unchanged with time. Due to the lack of observed salinity data, a steady-state model was first developed in order to provide initial salinity data (Gagniuc 2017). Since large-scale computational models require a considerable amount of time for each simulation to reach stable conditions (Sherif et al. 2012), the analysis was simulated initially for 7,300 days to reach its steady condition. An automatic time stepping technique with a predictor-corrector scheme with a time step length of 0.001 day was selected to reach the steady-state condition. The simulated mass concentration results from the steady-state run showed that the aquifer system underwent seawater intrusion throughout the whole depth, but horizontal encroachment in the middle and left side of the plain was highlighted more than the right side, which is in good agreement with the encroachment pattern reported in a recent study (Huang and Chiu 2018). Pingtung undergoes saline water intrusion along the entire width of the aquifer, at all depths from the south along the coastal boundary, and the water circulates back to the Taiwan Strait as brackish water through the upper layers of the aquifer. Initially, seawater intruded into an area of approximately 53 km2 with contaminated water (TDS > 10,000 mg/L). All the townships in the vicinity of the shoreline—Fangliao (T16), Jiadong (T21), Ligang (T09), Donggang (T03), Xinyuan (T17) and Linyuan (E13)—were affected by the SWI.
The large-scale models require multiple runs to reach the best fit between calibration parameters and model outputs (Goretzki et al. 2016). To achieve optimum calibration, PEST software (Doherty 1998) was used to optimize the parameters of the models with their initial conditions. The calibration tool was set up initially based on the adjustable parameters using the Levenberg-Marquardt algorithm (Moré 1978). PEST can change these parameters in such a way to minimize the objective function. In this model, the hydraulic conductivities (Kx, Ky, Kz) of the aquifer layers were selected as the adjustable parameters by assuming an initial relationship between them (Kx = Ky = 10 Kz). Kx and Ky were bounded between 0.1 and 600 m/day (lower and upper bounds) based on the initial range of permeability (Fig. 7). This range was 0.01 and 100 m/day for Kz. Also, Ky and Kz were tied to the changes of Kx using the Kriging interpolation method at 20 random pilot points.
Due to the availability of seawater encroachment trends at the end of 2010, analyzed by one of the most recent studies in this region (Huang and Chiu 2018), this study selected this particular year for the end of the calibration period. The model was calibrated for the first period of (01/01/2008–31/12/2010) against the observed hydraulic heads in all 95 observation wells. Figure 8 shows the comparison between the observed hydraulic head data and the simulated results in scatter plots using the root mean square (RMS) measure. The best fit was achieved when the deviation of the observed and computed heads was less than 1 m in all the observation wells. The RMS value of 0.926 was achieved for the calibrated hydraulic heads (Fig. 8). The hydraulic conductivity values after calibration are shown in Fig. 9.
Validation
The model was analyzed for a second time period of 2011–2015 under transient conditions, employing the resultant mass concentrations at the end of 2010 (Fig. 6), the time variable hydraulic heads of January 2011 as well as the calibrated conductivities, and monthly rainfall data for 2011–2015. In this model, the Dirichlet head (saltwater head computed by Eq. 1) and constant mass concentration of 35,000 mg/L were assigned to the shoreline boundary, while assuming no flux for the northern, eastern and western boundaries. Figure 5 shows the comparison between the computed and observed hydraulic heads at the end of 2015 as scatter plots, with the RMS value of 2.985 (Fig. 10).
Results and discussion
To study the inland encroachment of saline water in the Pingtung Plain, three cross-sections were used; these are cross-sections A–A, B–B and C–C through the right, middle and left side of the plain, respectively (Table 3; Fig. 11). The contour lines of contaminated water with TDS > 10,000 mg/L were used to represent the saline intrusion (highlighted in red to yellow in Figs. 12 and 13). At the end of 2010, the coverage of the contaminated area followed an increasing pattern from the right to the left of the domain. Although the seawater intrusion maintained its forward pattern through all aquifers, an insignificant encroachment along the right-hand side region of the model (A–A section) for the three aquifers was observed (Table 3; Fig. 11), which is in good agreement with the literature (Huang and Chiu 2018). This could be due to the high potential of the eastern part of the plain (proximal fan) for natural recharge, which leads to higher groundwater levels (Fig. 1) in all aquifer layers compared with the left and middle parts of the plain, where the groundwater heads are lower due to overabstraction (Ting et al. 1998a). Increasing the freshwater level due to precipitation percolation in the eastern side of the plain reduced the occupied transition zone (freshwater–saltwater interface) by pushing it back towards the sea. This is the main reason for the relatively insignificant change of SWI in the right side of the plain.
Also, the predicted salinity concentrations at the end of 2010 (December 2010) showed a larger contaminated area in the top and bottom aquifers compared with the middle aquifer, which is in agreement with the permeability distributions in the three aquifers. The second aquifer is comprised of lower permeability soil compared with the first and third aquifers. As the SWI shows more progress in the middle region of the domain, the 2D vertical section of the model is presented through the B–B cross-section for full representation of the SWI behaviour through the entire depth in the middle of the aquifer system (Fig. 14). Considering the thicknesses of the aquitards and based on the literature (Hsu et al. 2007), no leakage was considered between aquifers and aquitards. The significant difference in conductivity of aquitards and aquifers also supports this assumption. The saline water with TDS higher than 10,000 mg/L intruded about 800 m along the first and second aquitards at the end of 2010, mostly under the influence of abstraction along Donggang Township (T03; Table 1). Although the seawater progressively intruded the aquifer during the 5 years of study (end of 2010 to the end of 2015), the transition of saltwater with TDS > 10,000 mg/L was slower than the lower TDS. The saline water with TDS higher than 10,000 mg/L intruded approximately 100 m more landward in this period (Table 3; Fig. 11). However, larger areas covered by freshwaters were superseded with brackish water in this 5-year period. The mass transfer through the aquitards was very slow (less than 15 m for TDS > 10,000 mg/L) and almost negligible during the 5 years of analysis.
The model was employed to predict the SWI for the next 25 years (2016–2040) in order to study the future trends of saltwater intrusion. In this analysis, the hydrological setting and input parameters were maintained from the previous run. In addition, the effects of sea-level rise, a 30% increase in abstraction rate, a 30% decrease in abstraction rate, and a combination of sea-level rise with a 30% increase in abstraction rate were studied (Table 4; Fig. 13).
The model predicts that in 2040, seawater may intrude mostly in the middle region of the domain by approximately 5 km along the cross-section B–B in the top aquifer (Table 4; Fig. 11).
The results show that, in the top aquifer, an SLR of 27 cm during the next 25 years would lead to more than 1 km, 900 m and 50 m additional intrusion along the cross-sections C–C, B–B, and A–A, respectively. Some townships, including Fangliao (T16) and Jiadong (T21), would be affected more by the increased abstraction, with nearly 70 m additional SWI in the bottom aquifer. By 2040, a 30% increase in the abstraction rate, without considering the effects of SLR, would cause approximately 70, 220 and 120 m of additional seawater intrusion along the A–A, B–B and C–C sections in the third aquifer, respectively.
Among the aforementioned factors, the combined effect of SLR and overabstraction would lead to the most severe intrusion of saline water due to the increased seawater head and decreased inland head, resulting in additional hydraulic gradient towards the land. The contaminated water would cover 340 km2 (28% of the entire domain), which is 67.17% more than the situation without SLR or overabstraction (Table 4; Fig. 11).
One of the potential management scenarios for reducing SWI and recovering groundwater resources is to decrease the abstraction rate in order to increase the groundwater table and decrease the landward hydraulic gradient, as one of the suggested scenarios in literature for managing SWI (Hussain et al. 2019). A 30% reduction in the total abstraction rate would lead to about 50, 250 and 1,850 m backward movement (retreat) of saline water in the top aquifer along the A–A, B–B and C–C cross-sections, respectively. For the middle aquifer, this would not lead to any significant backward movement (only 44, 200 and 19 m along the A–A, B–B and C–C sections, respectively). The lower aquifer depicts a 25, 315 and 170 m retreat along the A–A, B–B and C–C cross-sections, respectively; therefore, the top aquifer would be influenced more by a reduction in abstraction. Another possible scenario to control SWI would involve relocating the coastal wells in the vicinity of the shorelines further inland (Hussain et al. 2019) in the regions of Linyuan (E31), Xinyuan (T17), Donggang (T03), Linbian (T19), Jiadong (T21), and Fangliao (T16). The right side of the plain along the A–A cross-section shows a very low response for a 1-km inland relocation of wells with less than 5-m backward movement of seawater at all depths of the aquifer. It maintained this low reaction by increasing the distance of wells from the sea by either 5 km or 10 km with less than 10 m seaward movements in all layers of the aquifer. However, the reaction of the middle part of the plain along the B–B cross-section was more significant, with a minimum of about 365 m and a maximum 375 m backward movement of seawater through the bottom and middle aquifers, respectively, as a response to the 1-km inland relocation of wells. Inland relocation of the wells further away from the sea (5 or 10 km) would not lead to a significant difference in pushing back the seawater in all layers of the aquifer. Inland relocation of the wells 10 km farther pushed the seawater a maximum of about 80 m back to the sea in the middle aquifer (Fig. 15). In the west of the plain in the distal fan, a 1-km inland relocation of pumping wells cleared a minimum of about 50 m to a maximum of 65 m seawater along the C–C cross-section in the bottom and middle aquifers, respectively. Also, this part of the plain did not show a significant difference for the relocation of the wells (either 5 or 10 km away) in all layers of the aquifer. From the predicted results, it can be concluded that the inland relocation of the abstraction wells is a more effective solution at a maximum 1 km distance from the coastal boundary, and any further movement will not change the results in terms of increasing its performance.
Conclusion
A 3D finite element model was developed to simulate the seawater intrusion in the Pingtung Plain coastal aquifer. The developed model can simulate density-dependent flow and allows coupling between the water flow and salt transport by tracing the interface of saltwater and freshwater. The model can address the challenges and complexity of aquifer conditions and parameters (e.g., geology, atmospheric forces, groundwater abstraction, etc.). After rigorous validation, the model was used to study SWI in all layers of the Pingtung Plain aquifer system and to predict the future behaviour of the aquifer. The model showed the relationships between seawater intrusion and aquifer parameters and examined the effectiveness of different management scenarios. Water abstraction near the shoreline is proven to be the main reason for the inland encroachment of seawater, especially in the lower left and middle parts of the plain. Although sea-level rise, the variation of pumping rates and inland relocation of wells were among the other influential parameters, a combination of SLR and increased abstraction exacerbate the situation.
The analysis depicts that the seawater intruded into the entire width of the aquifer in all investigated scenarios, however, less encroachment was observed in the second aquifer. Likewise, seawater intruded less into the lower east of the plain, due to its high potential for natural groundwater recharge and possessing higher groundwater heads.
However, the middle and left side of the plain are more vulnerable to SWI due to overabstraction around the Kaoping River mouth (lower middle) and distal fan (left). Decreasing the abstraction rate and farther inland relocating the wells could be effective solutions with a significant reversal of the seawater intrusion.
This 3D finite element model can potentially be used as an asset to investigate the influential parameters on the SWI to help the decision-makers for establishing policies especially in the era of climate change. Several limitations existed when developing this model. Firstly, the data for the abstraction wells were captured for only one specific year and the same rates were assumed for the consecutive years. Secondly, due to the lack of data, the storativity parameter was assigned as the default value in the software for the entire model.
References
Ababou R, Al-Bitar A (2004) Salt water intrusion with heterogeneity and uncertainty: mathematical modeling and analyses. Dev Water Sci 55:1559–1571
Barazzuoli P, Nocchi M, Rigati R, Salleolini M (2008) A conceptual and numerical model for groundwater management: a case study on a coastal aquifer in southern Tuscany, Italy. Hydrogeol J 16:1557–1576
Bear J (1979) Hydraulics of groundwater. McGraw-Hill, New York
Bear J, Cheng AH-D, Sorek S, Ouazar D, Herrera I (1999) Seawater intrusion in coastal aquifers: concepts, methods and practices. Springer, Heidelberg, Germany
Bobba AG (2002) Numerical modelling of salt-water intrusion due to human activities and sea-level change in the Godavari Delta, India. Hydrol Sci J 47:S67–S80
Boufadel MC (2000) A mechanistic study of nonlinear solute transport in a groundwater–surface water system under steady state and transient hydraulic conditions. Water Resour Res 36:2549–2565
Bricker S (2009) Impacts of climate change on small island hydrology: a literature review. OR/09/025, BGS, Nottingham, UK
Carretero S, Rapaglia J, Bokuniewicz H, Kruse E (2013) Impact of sea-level rise on saltwater intrusion length into the coastal aquifer, Partido de La Costa, Argentina. Cont Shelf Res 61–62:62–70
Chang C, Chang T, Wang C, Kuo C, Chen K (2004) Land-surface deformation corresponding to seasonal ground-water fluctuation, determining by SAR interferometry in the SW Taiwan. Math Comput Simul 67:351–359
Chang SW, Clement TP, Simpson MJ, Lee K-K (2011) Does sea-level rise have an impact on saltwater intrusion? Adv Water Resour 34:1283–1291
Chang F-J, Huang C-W, Cheng S-T, Chang L-C (2017) Conservation of groundwater from over-exploitation: scientific analyses for groundwater resources management. Sci Total Environ 598:828–838
Collins MA, Gelhar LW (1971) Seawater intrusion in layered aquifers. Water Resour Res 7:971–979
Cooper H (1959) A hypothesis concerning the dynamic balance of fresh water and salt water in a coastal aquifer. J Geophys Res 64:461–467
Das A, Datta B (1999) Development of management models for sustainable use of coastal aquifers. J Irrig Drain Eng 125:112–121
DHI-WASY (2010) FEFLOW 6: user’s manual. DHI-WASY, Berlin
Diersch HJG (2006) FEFLOW finite element subsurface flow and transport simulation system-reference manual. User’s manual, White Papers-Release 5.3, DHI-WASY, Berlin
Diersch H (2010) FEFLOW user’s manual. WASY, Berlin
Diersch H-JG (2013) FEFLOW: finite element modeling of flow, mass and heat transport in porous and fractured media. Springer, Heidelberg, Germany
Diersch H-J, Kolditz O (1998) Coupled groundwater flow and transport: 2. thermohaline and 3D convection systems. Adv Water Resour 21:401–425
Diersch H-J, Kolditz O (2002) Variable-density flow and transport in porous media: approaches and challenges. Adv Water Resour 25:899–944
Dogan A, Fares A (2008) Effects of land use changes and groundwater pumping on salt water intrusion in coastal watersheds. Coastal Watershed Management 13:219
Doherty J (1998) Visual PEST: graphical model independent parameter estimation. Watermark, Brisbane, Australia and Waterloo Hydrogeologic, Waterloo, ON
Ellis JB (1999) Impacts of urban growth on surface water and groundwater quality: proceedings of an international symposium held during IUGG 99, the XXII General Assembly of the International Union of Geodesy and Geophysics, Birmingham, UK, 18–30 July 1999, IAHS, Wallingford, UK
Essink GHO (2001) Improving fresh groundwater supply: problems and solutions. Ocean Coast Manag 44:429–449
Ferguson G, Gleeson T (2012) Vulnerability of coastal aquifers to groundwater use and climate change. Nat Clim Chang 2:342
Fitzgerald DM, Fenster MS, Argow BA, Buynevich IV (2008) Coastal impacts due to sea-level rise. Annu Rev Earth Planet Sci 36:601–647
Gagniuc PA (2017) Markov chains: from theory to implementation and experimentation. Wiley, Hoboken, NJ
Gelhar LW, Welty C, Rehfeldt KR (1992) A critical review of data on field-scale dispersion in aquifers. Water Resour Res 28:1955–1974
Goretzki N, Inbar N, Kühn M, Möller P, Rosenthal E, Schneider M, Siebert C, Raggad M, Magri F (2016) Inverse problem to constrain hydraulic and thermal parameters inducing anomalous heat flow in the Lower Yarmouk Gorge. Energ Proced 97:419–426
Hsieh H-H, Lee C-H, Ting C-S, Chen J-W (2010) Infiltration mechanism simulation of artificial groundwater recharge: a case study at Pingtung plain, Taiwan. Environ Earth Sci 60:1353–1360
Hsu T (1961) The artesian water system beneath the Pingtung plain, Taiwan. Proc Geol Soc China 4:73–81
Hsu K-C, Wang C-H, Chen K-C, Chen C-T, Ma K-W (2007) Climate-induced hydrological impacts on the groundwater system of the Pingtung plain, Taiwan. Hydrogeol J 15:903–913
Huang P-S, Chiu Y-C (2018) A simulation-optimization model for seawater intrusion management at Pingtung coastal area, Taiwan. Water 10:251
Hussain MS, Abd-Elhamid HF, Javadi AA, Sherif MM (2019) Management of seawater intrusion in coastal aquifers: a review. Water 11:2467
Kacimov A, Sherif M (2006) Sharp interface, one-dimensional seawater intrusion into a confined aquifer with controlled pumping: analytical solution. Water Resour Res 42:W06501
Kim K-H, Shin J-Y, Koh E-H, Koh G-W, Lee K-K (2009) Sea level rise around Jeju Island due to global warming and movement of groundwater/seawater interface in the eastern part of Jeju Island. J Soil Groundw Environ 14:68–79
Kolditz O, Ratke R, Diersch H-JG, Zielke W (1998) Coupled groundwater flow and transport: 1. verification of variable density flow and transport models. Adv Water Resour 21:27–46
Kooi H, Groen J, Leijnse A (2000) Modes of seawater intrusion during transgressions. Water Resour Res 36:3581–3589
Kopsiaftis G, Mantoglou A, Giannoulopoulos P (2009) Variable density coastal aquifer models with application to an aquifer on Thira Island. Desalination 237:65–80
Kuo C-H, Wang C (2001) Implication of seawater intrusion on the delineation of the hydrogeologic framework of the shallow Pingtung plain aquifer. West Pac Earth Sci 1:459–472
Langevin CD, Guo W (2006) MODFLOW/MT3DMS–based simulation of variable-density ground water flow and transport. Groundwater 44:339–351
Langevin CD, Thorne DT Jr, Dausman AM, Sukop MC, Guo W (2008) SEAWAT version 4: a computer program for simulation of multi-species solute and heat transport. Techniques and Methods, Book 6, Chap A22, US Geological Survey, Reston, VA
Lin I-T, Wang C-H, Lin S, Chen Y-G (2011) Groundwater–seawater interactions off the coast of southern Taiwan: evidence from environmental isotopes. J Asian Earth Sci 41:250–262
Loáiciga HA, Pingel TJ, Garcia ES (2012) Sea water intrusion by sea-level rise: scenarios for the 21st century. Ground Water 50:37–47
Mehnert E, Jennings A (1985) The effect of salinity-dependent hydraulic conductivity on saltwater intrusion episodes. J Hydrol 80:283–297
Moré JJ (1978) The Levenberg-Marquardt algorithm: implementation and theory. Numerical Analysis, Conference Paper, Springer, Heidelberg, Germany
Narayan KA, Schleeberger C, Bristow KL (2007) Modelling seawater intrusion in the Burdekin Delta irrigation area, North Queensland, Australia. Agric Water Manag 89:217–228
Nicholls R J (2010) Impacts of and responses to sea-level rise. In: Understanding sea-level rise and variability, pp 17–51. https://doi.org/10.1002/9781444323276.ch2
Nicholls RJ (2015) Adapting to sea level rise, chap 9. In: Ellis JT, Sherman DJ (eds) Coastal and marine hazards, risks, and disasters. Elsevier, Boston
Ogata A (1970) Theory of dispersion in a granular medium. US Government Printing Office, Washington, DC
Paniconi C, Khlaifi I, Lecca G, Giacomelli A, Tarhouni J (2001a) Modeling and analysis of seawater intrusion in the coastal aquifer of eastern Cap-Bon, Tunisia. Transp Porous Media 43:3–28
Paniconi C, Khlaifi I, Lecca G, Giacomelli A, Tarhouni J (2001b) A modelling study of seawater intrusion in the Korba coastal plain, Tunisia. Phys Chem Earth, B: Hydrol Oceans Atmos 26:345–351
Pool M, Carrera J (2011) A correction factor to account for mixing in Ghyben-Herzberg and critical pumping rate approximations of seawater intrusion in coastal aquifers. Water Resour Res 47:W05506
Priyanka B, Mahesha A (2015) Parametric studies on saltwater intrusion into coastal aquifers for anticipate sea level rise. Aquat Proced 4:103–108
Rasmussen P, Sonnenborg T, Goncear G, Hinsby K (2013) Assessing impacts of climate change, sea level rise, and drainage canals on saltwater intrusion to coastal aquifer. Hydrol Earth Syst Sci 17:421–443
Sefelnasr A, Sherif M (2014) Impacts of seawater rise on seawater intrusion in the Nile Delta aquifer, Egypt. Groundwater 52:264–276
Sherif MM, Singh VP (1999) Effect of climate change on sea water intrusion in coastal aquifers. Hydrol Process 13:1277–1287
Sherif M, Sefelnasr A, Javadi A (2012) Incorporating the concept of equivalent freshwater head in successive horizontal simulations of seawater intrusion in the Nile Delta aquifer, Egypt. J Hydrol 464:186–198
Simmons CT, Fenstemaker TR, Sharp JM Jr (2001) Variable-density groundwater flow and solute transport in heterogeneous porous media: approaches, resolutions and future challenges. J Contam Hydrol 52:245–275
Solomon S, Qin D, Manning M, Averyt K, Marquis M (2007) Climate Change 2007: the physical science basis: Working Group I contribution to the fourth assessment report of the IPCC. Cambridge University Press, Cambridge, UK
Stocker T (2014) Climate Change 2013: the physical science basis: Working Group I contribution to the fifth assessment report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, UK
Tber MH, Talibi MEA, Ouazar D (2008) Parameters identification in a seawater intrusion model using adjoint sensitive method. Math Comput Simul 77:301–312
Ting C (1992) Application of a groundwater model in the dispute among water users in the Pingtung coastal plain, Taiwan. Proceedings of an international workshop on ground water and environment, Seismological Press, Beijing, pp 332–345
Ting C-S, Liu CW, Tsai W-W (1997) Application of geostatistical analysis in the design of a ground water level monitoring network for Pingtung Plain, Taiwan: II. sampling frequency. In: Groundwater: an endangered resource. ASCE, Washington, DC, pp 34–38
Ting C-S, Kerh T, Liao C-J (1998a) Estimation of groundwater recharge using the chloride mass-balance method, Pingtung plain, Taiwan. Hydrogeol J 6:282–292
Ting CS, Zhou Y, Vries JD, Simmers I (1998b) Development of a preliminary ground water flow model for water resources management in the Pingtung plain, Taiwan. Groundwater 36:20–36
Trefry MG, Muffels C (2007) FEFLOW: a finite-element ground water flow and transport modeling tool. Groundwater 45:525–528
Tu Y-C, Ting C-S, Tsai H-T, Chen J-W, Lee C-H (2011) Dynamic analysis of the infiltration rate of artificial recharge of groundwater: a case study of Wanglong Lake, Pingtung, Taiwan. Environ Earth Sci 63:77–85
Uddameri V, Singaraju S, Hernandez EA (2014) Impacts of sea-level rise and urbanization on groundwater availability and sustainability of coastal communities in semi-arid South Texas. Environ Earth Sci 71:2503–2515
Vacher H (1988) Dupuit-Ghyben-Herzberg analysis of strip-island lenses. Geol Soc Am Bull 100:580–591
Voss CI (1984) A finite-element simulation model for saturated-unsaturated, fluid-density-dependent ground-water flow with energy transport or chemically-reactive single-species solute transport. US Geol Surv Water Resour Invest Rep 84-4369
Voss CI, Provost AM (1984) Sutra. In: A finite-element simulation model for saturated-unsaturated, fluid-density-dependent ground-water flow with energy transport or chemically-reactive single-species solute transport. US Geol Surv Water Resour Invest Rep 84-4369
Voss CI, Souza WR (1987) Variable density flow and solute transport simulation of regional aquifers containing a narrow freshwater–saltwater transition zone. Water Resour Res 23:1851–1866
Wang C (1996) The salinization of groundwater in the northern Lan-Yang plain, Taiwan: stable isotope evidence. J Geol Soc China 39:627–636
Werner AD, Simmons CT (2009) Impact of sea-level rise on sea water intrusion in coastal aquifers. Groundwater 47:197–204
Werner AD, Bakker M, Post VE, Vandenbohede A, Lu C, Ataie-Ashtiani B, Simmons CT, Barry DA (2013) Seawater intrusion processes, investigation and management: recent advances and future challenges. Adv Water Resour 51:3–26
Yechieli Y, Shalev E, Wollman S, Kiro Y, Kafri U (2010) Response of the Mediterranean and Dead Sea coastal aquifers to sea level variations. Water Resour Res 46:W12550
Yu P-S, Yang T-C, Kuo C-C (2006) Evaluating long-term trends in annual and seasonal precipitation in Taiwan. Water Resour Manag 20:1007–1023
Zhou X, Chen M, Ju X, Ning X, Wang J (2000) Numerical simulation of sea water intrusion near Beihai, China. Environ Geol 40:223–233
Acknowledgements
The authors thank the DHI group for providing the FEFLOW software, especially Björn Elsäßer for technical support. Also, we thank the anonymous reviewers for their insightful comments and suggestions.
Funding
The authors would like to acknowledge the financial support from the Royal Society (Grant number IE161191) which facilitated this collaborative research.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dibaj, M., Javadi, A.A., Akrami, M. et al. Modelling seawater intrusion in the Pingtung coastal aquifer in Taiwan, under the influence of sea-level rise and changing abstraction regime. Hydrogeol J 28, 2085–2103 (2020). https://doi.org/10.1007/s10040-020-02172-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-020-02172-4