Introduction

The subsurface urban heat island (SUHI) is the phenomenon of elevated subsurface temperatures in urban areas. In part, SUHIs can be regarded as the subsurface thermal imprint of the meteorological urban heat island (UHI) that causes elevated ground-surface temperature, but anthropogenic heat sources such as basement heating, underground thermal energy storage, sewers, and district heating, provide additional control on the development of a SUHI. Temperature-depth (TD) profiles obtained from borehole records allow one to describe the subsurface extent of SUHIs—examples of case studies that use such descriptions include mid-latitude cities in Canada (Ferguson and Woodbury 2004), Japan (Benz et al. 2018; Taniguchi et al. 2007, 2009), and Europe (e.g., Benz et al. 2015; Epting and Huggenberger 2013; Menberg et al. 2013b; Mueller et al. 2018). In contrast to the UHI, the SUHI is a significant store for heat which accumulates at shallow depths and only slowly diffuses deeper into the subsurface. Consequently, the SUHI is often more pronounced than the UHI in terms of thermal intensity (Benz et al. 2017). The heat that is stored in SUHIs could be retrieved by geothermal energy systems (GES) and used for the heating of buildings, and in that way contribute to the offset of carbon emissions (e.g., Allen et al. 2003; Zhu et al. 2010; Menberg et al. 2013b; Menberg et al. 2015; Benz et al. 2015; García-Gil et al. 2015; Bayer et al. 2016; Epting et al. 2017). Bayer et al. (2019) review and categorize available studies on the geothermal potential of the urban subsurface; however, the long-term geothermal potential of a SUHI is expected to depend on the current extent, intensity and processes that maintain the SUHI (Benz et al. 2018). The latter are still poorly quantified because the development of SUHIs underneath major cities has been occurring in many instances over time-scales of centuries during which the evolution of surface heat fluxes and/or subsurface temperatures is typically unknown. Chen et al. (2019), for example, characterize the spatiotemporal dynamics of anthropogenic heat fluxes due to rapid urban expansion over the past 20 years in China.

Groundwater temperature observations are the only means to map the lateral extent of a SUHI, whilst relatively deep (e.g. at least tens of meters) TD profiles taken in boreholes are required to characterize the depth extent of a SUHI. From TD profiles, past fluctuations in surface heat flux can be retrieved using inverse modeling techniques (Beltrami 2002). However, repeated TD observations, ideally separated by decades or more (Kooi 2008; Bense and Kurylyk 2017), allow one to directly estimate site-specific heat fluxes from the surface into the SUHI under a range of urban surface cover types (Benz et al. 2018). At the scale of entire cities, numerical modeling of coupled heat transport and groundwater flow, calibrated with observed temperatures and hydraulic head data, has been used to assess the geothermal potential of the SUHI (e.g., Mueller et al. 2018). The Mueller et al. (2018) study only considered the present-day thermal state using a model period of 2010–2015 CE (common era, hereafter applying to all dates in this article). Zhu et al. (2014) simulated the development of the SUHI of the city of Cologne, Germany, by numerical modeling of groundwater flow and heat transport. However, detailed simulations of spatial development of the city and potential heat sources were beyond the scope of their study and an idealized hot spot of fixed size, representing the city center, was defined. In contrast, the present study uses recent TD observations, not only to define the current thermal state, but to reconstruct the spatiotemporal characteristics of the subsurface temperature field of the city of Amsterdam, The Netherlands, as a function of the history of urban expansion using a transient heat flow model covering a time span of several centuries, between 1350 and 2012 CE.

In order to better understand SUHI development since the onset of urban expansion, a particularly detailed subsurface-temperature data set from the city of Amsterdam has been analyzed. The TD data have all been collected in the same manner, with one instrument, in similar monitoring wells at the same depth of 20 m below ground level (bgl; and deeper). Furthermore, location-specific surface air temperatures, and hydrogeological and auxiliary data have been collected.

Amsterdam was developed in a staged manner over the past centuries, where well-defined periods of urban expansion can be distinguished. Through an analysis of TD profiles inside and outside the city, using a numerical model, it is found that these stages can be identified at the present day as a thermal zonation in subsurface temperature patterns.

The numerical model, coupling groundwater flow and heat transport, covers a two-dimensional (2D) section parallel to the regional groundwater flow direction, stretching 10 km from the city center to the rural outskirts of the city, and to a depth of 750 m.

The numerical model is used to investigate if a heat transport model of the subsurface of Amsterdam, linked to a surface model for the ground surface temperature (GST) that reflects the spatial-temporal development of urban expansion, results in a modelled SUHI that is consistent with the observations. This study provides novel insights into the interplay between urban expansion and the development of a SUHI. These insights will allow improved simulation of the present and future states of SUHIs, which provides important input for the assessment of the geothermal potential of SUHIs.

Study area and thermal data

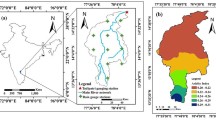
The city of Amsterdam is a medium-sized western European city and the capital of the Netherlands (Fig. 1a). The city currently (2019) has a population size of ~820,000 people. Amsterdam is, compared to many other European cities, a relatively young city, with origins dating to the early fourteenth century.

Fig. 1
figure 1

a Map of the city of Amsterdam (The Netherlands) indicating stages of urban expansion since the eighteenth century and observed groundwater temperatures at 20 m depth (T-20m). b Average annual air temperatures (dots) and 30-year running average of annual air temperatures (solid lines). c Temperature-depth (TD) curves

Full size image

Urban expansion

The first stone building in Amsterdam was erected in 1295 (the Oude Kerk). The fourteenth century city comprised only approx. 40 hectares (ha) and is located in the present-day city center. The city gradually expanded around this city center, south of the River IJ, to approx. 60 ha by 1450. Between 1450 and the end of the sixteenth century, there was virtually no growth of the city. Between the end of the sixteenth century and the first quarter of the eighteenth century, the city grew to almost 700 ha; this forms the present-day historical part of the city with the many concentric canals illustrating the stages of expansion.

The city’s expansion has been carefully recorded by the municipality (Fig. 1a) illustrating how Amsterdam went through a period of bloom in the seventeenth century, experiencing rapid expansion; however, in the 18th and until halfway through the nineteenth century, further expansion was very sparse. Only from the mid-nineteenth century, further urban expansion of the areas surrounding the city occurred, but in a staged manner.

The present-day (2017) built-up surface of Amsterdam comprises approx. 7,900 ha, while paved surfaces occupy approx. 1,700 ha. Green spaces, agricultural terrain and natural habitat account for 6,900 ha, and water bodies account for 5,500 ha, in the municipality of Amsterdam.

Thermal data

Surface air temperature

From two locations in the study area (Fig. 1a), long-term time-series of surface air temperature (SAT) are available (Fig. 1b). One series was recorded in the Amsterdam city center (Stadswaterkantoor) starting in 1785 but which was discontinued in 1961 (KNMI 2014b). At Schiphol airport, air temperature has been recorded since 1951. Additionally, a long-term (1706–Present) temperature reference record (Fig. 1b) has been constructed by the Royal Netherlands Meteorological Institute (KNMI 2014a) for the town of De Bilt, 36 km from the city center (Fig. 1a). van Engelen et al. (2001) constructed average annual temperature data for The Netherlands dating back to the eighth century. Figure 1b shows a section of the Van Engelen et al. (2001) data series and the KNMI (2014a) 1706–Present temperature record.

Auxiliary data

Short-term air temperature records are available from 14 semi-professional amateur stations in the city (see Appendix 1). The long-term (1990–2015) canal water temperature at two locations in the city center is 0.2–0.9 °C higher than the urban SAT (IHW 2019; see Appendix 1). Stichting Bouwresearch (1985) showed that heat losses through uninsulated floors to ventilated crawl spaces resulted in an average crawl space temperature of 12 °C. Due to ventilation with outside air, the crawl space temperature is only slightly higher than the outside temperature (~ urban SAT).

Subsurface temperature data

Groundwater temperature data for the subsurface below Amsterdam and its vicinity were collected in 2012 (Fig. 1a,c). This was possible through the presence of boreholes equipped with piezometers that allowed the collection of TD data. The measurements were done by carefully lowering a temperature probe into a piezometer tube to record temperature at depth intervals of 1 m. The narrow diameter (diameter 50 mm or 38 mm) of the tubes reduced the risk of convection in the bore (Sammel 1968). At six locations (1–6, Fig. 1c), relatively deep TD profiles could be obtained up to 45–115 m.

At 63 other locations in the area (Fig. 1a), temperature was measured, in similar piezometers, at a depth of 20 m below the surface (T–20m). The depth of 20 m is well below the zone where significant seasonal fluctuations of temperature occur for typical conditions in The Netherlands (Bense and Kooi 2004).

Hydrogeology

Amsterdam is set in an essentially flat landscape built upon loosely consolidated sedimentary deposits of Holocene age that have a thickness of 10–20 m. These overlay a stack of Quaternary and Tertiary sedimentary deposits that reach to a depth of ~450 m, where stiff marine clayey deposits of Miocene age are reached (TNO 2012; Beets and Beets 2002). The latter is widely regarded (e.g. Dufour 2000) as the hydrological base, not allowing much, if any, groundwater movement. The subsurface is schematized in Fig. 2a, in which also the hydraulic parameters of the various strata are given.

Fig. 2
figure 2

a Geological cross section along line A–A′ (after TNO 2012), with lithology, hydraulic and thermal parameters of the strata, b polder water levels (= approx. surface-water levels) in m relative to the ordnance datum (NAP = approx. sea level), c isohypses of hydraulic head in m relative to NAP in aquifers 1 and 2 (a) and the inferred groundwater flow direction

Full size image

Surface-water levels and phreatic water levels follow the polder water levels (Fig. 2b) closely. The river IJ runs north of the city center with a water level of 0.4 m below mean sea-level and a water depth of approx. 11 m. At the southwest end of the cross-section line in Fig. 1a, the Haarlemmermeer reclaimed lake area lies about 4.5 m below mean sea level. Before reclamation of the Haarlemmermeer, the regional groundwater flow south of the River IJ was directed to this river. Due to the reclamation of the Haarlemmermeer in the nineteenth century, this gradient was gradually reversed to the southwest (Fig. 2c).

Data analysis

The available data from Amsterdam outlined in the preceding allow one to interpret the evolution of the suburban heat island underneath the city in relation to urban expansion, regional climate warming and groundwater flow.

Suburban temperature distribution

The deep TD data (Fig. 1c) confirm the presence of a SUHI underneath Amsterdam. Temperatures inside the city limits are distinctly elevated as compared to the temperatures outside these limits. Comparison of the historic SAT series for both the Amsterdam city center (Stadswaterkantoor; KNMI 2014b) and De Bilt (KNMI 2014a) shows that between the late eighteenth century and mid-twentieth century the Amsterdam temperatures have consistently risen by an average of 1.1 °C and with a maximum of 1.8 °C (Fig. 1b). The 1951–2014 temperature time series of the Schiphol Airport meteorological station tracks the De Bilt series very closely; the averages for the periods 1951–2014 (9.9 °C) and 1985–2014 (10.4 °C) are just 0.1 °C higher at Schiphol. The substantially higher temperatures in the Amsterdam city center are, therefore, most likely an expression of the UHI effect. The period where SAT was measured at both Schiphol and the Amsterdam city center (1951–1964) shows that the difference between these two stations is also about 1.1 °C. The Schiphol SAT is therefore used to extrapolate the city center temperatures to more recent times using the same offset. Recent measurements of amateur semi-professional Meteo stations in the city center (see Appendix 1) suggest that this is a reasonable approach. The SAT time series are used to reconstruct the GST development in time as is explained in section ‘Numerical modeling’.

The TD profiles (Fig. 1c) show a concave shape, characteristic of increasing ground surface temperatures (Kurylyk and Irvine 2019). For location 6 (Fig. 1a), comparison with an older temperature log shows that temperatures have increased to a depth of approx. 62 m in the period 1979–2012.

The measured minimum and maximum T–20m are respectively 10.8 and 15.1 °C. The mean is 12.5 °C with a 1.1 °C standard deviation, resulting in a 95% reliability interval of approx. 10.3–14.7 °C. T–20m values below 11.0 °C are found near the city limits. These temperatures are only marginally higher than the long-term average SAT for Schiphol and, therefore, considered to be the (rural) background temperature. In this study, the SUHI intensity is defined as the T–20m minus the rural background temperature (11 °C). T–20m values between 11 and 13 °C are found scattered over all built-up areas of the city. All T–20m higher than 13 °C are concentrated in and near the city center.

Figure 3 suggests a degree of correlation between the urban expansion age and the built-up density (fraction of the surface occupied by buildings and pavements) with the T–20m around the observation point. Almost all T–20m > 13 °C are found in the parts of the city that were built before 1900 CE, whilst also highest T–20m values are associated with the higher built-up densities. Figure 3b considers the data from the city quarters that were built after 1870 CE in more detail, further illustrating the T–20m relation with the built-up density. Although the data set is limited in size, the lower T–20m values appear to be related to the lowest built-up densities. This illustrates the interplay between the age of the urban expansion and built-up densities. Thirdly, it can be expected that the UHI effect is the strongest in the city center, where also the oldest quarters are found.

Fig. 3
figure 3

aT–20m plotted against date of urban expansion. The colors of the symbols represent the percentage of the surface in a 100-m radius covered by buildings and paved surfaces. bT–20m for the younger city quarters, built after 1870. The locations built after 2012 have been plotted at 2012

Full size image

This analysis leads to the hypothesis that the development of the SUHI can be construed from the urban expansion history and built-up densities. To do so, the delayed and attenuated temperature rise with depth in response to urban expansion has to be taken into account. The modeling of the development of the SUHI of Amsterdam is presented in the following section.

Numerical modeling

A numerical model to describe the development of the temperature distribution underneath the city of Amsterdam from 1350 to 2012 was considered. A 2D cross-sectional model that is aligned parallel to the regional direction of groundwater flow (cross section location in Fig. 1a) was developed.

Groundwater and heat flow equations

The scriptable finite-element code FlexPDE (PDE Solutions; Bense and Kooi 2004) was used to solve the groundwater flow equations and advection-diffusion equation for heat flow (Stallman 1963; Kurylyk and Irvine 2019).

Model domain and layers

The model domain is 10,300 m wide and stretches to a depth z = −750 m. The ground level is assumed to be constant over the model domain. The model comprises 16 layers of alternating sand and clay with variable hydraulic and thermal properties. A schematic presentation of the layers and their properties is given in Fig. 2a. The thermal properties are based upon literature values (Kooi 2008) or in-situ measurements on similar sediments (Witte et al. 2002). The hydraulic properties are derived from the national hydrogeological database DinoLoket (TNO 2012).

Hydraulic boundary conditions and groundwater flow

Only horizontal flow is modelled. Recharge at the surface is therefore implicitly neglected. This is considered reasonable. The top strata comprise clay and peat layers with a very low vertical hydraulic conductance and a thickness of almost 20 m at the northeastern end of cross section A–A′ to approx. 7 m at the southwestern end. This, in combination with intensive surficial drainage, limits vertical infiltration and makes it negligible compared to the vertical flow qx. This can be shown as follows.

Apart from the River IJ, surface waters comprise mainly shallow canals around the city center. The canals have an average depth of 2.6 m (to 3 m below sea level) and an average water level of 0.4 m below sea level (Fig. 2a). The hydraulic head in the aquifer below the Holocene layers in the city center is approx. 1 m below sea level. This results in a hydraulic gradient below the canals of 0.05 m m−1 over 13 m of Holocene strata. With a vertical permeability of 1.16e−8 m s−1, and an effective porosity of 0.2, this results in a vertical flow (qz) of 2.9e−9 m s−1.

On the other hand, the present-day horizontal hydraulic gradient in the aquifers below the Holocene strata is approx. 5e−4 m m−1, while the minimum horizontal permeability and effective porosity are 7e−5 m s−1 and 0.35, respectively. This results in a horizontal groundwater flow (qx) of 1e−7 m s−1, demonstrating that qx is at least several orders of magnitude larger than qz.

Horizontal groundwater flow is based upon the uniform hydraulic gradient that is determined by the different hydraulic heads at both ends of the domain. A gradient of approx. 10−4 m m−1 is directed towards the River IJ (northeast) between 1350 and 1849. First, this gradient was induced by drainage towards the IJ (north of the cross section). In the early seventeenth century, reclamation of deep polders north of the River IJ increased this gradient. From 1849 to 1852, reclamation of the Haarlemmermeer lake on the southwest end of the cross section gradually reversed the hydraulic gradient into that direction. Nowadays, a groundwater divide is located approximately below the River IJ. The hydraulic heads close to the IJ are well below the river level (>1 m vs. 0.4 m below sea level), indicating a high hydraulic resistance of the deposits at and below the river bottom. The reversal of the hydraulic gradient direction was simulated by stepwise lowering of the hydraulic head on the southwest domain boundary until the hydraulic gradient was about the present-day value of 5 × 10−4 m m−1 to the southeast.

Thermal boundary conditions

The northeastern vertical boundary and the model bottom have been assigned fixed temperatures that are calculated from a constant initial vertical geothermal gradient and initial GST. The initial GST is taken as 9.1 °C, being the average 1,329–1,349 SAT (Van Engelen et al. 2001) minus 0.5 °C. The background geothermal gradient is 0.025 °C m−1. The southwestern model domain edge has a flux (Neumann) boundary condition in the form of ρeceqxT, where ρe [kg m−3] and ce [J kg−1 °C] are respectively the density and specific heat of the solid-fluid medium, T [°C] is the temperature, qx [m s−1]is the x-component of specific discharge.

The model top has been assigned a spatiotemporal variable ground-surface temperature (GST). The GST history is constructed from the following components:

  1. 1.

    The time-dependent autonomous or ‘rural’ SAT

  2. 2.

    The UHI effect, that takes effect after urban expansion. Added to the rural SAT, this yields an ‘urban’ SAT

  3. 3.

    An offset between SAT and GST that depends on the land cover, which varies with time

The rural SAT history is taken from the long-term records given by KNMI (2014a) and van Engelen et al. (2001). From the city margins to the city center, the UHI effect is increased stepwise from 0.7 to 1.1 °C. This graduated UHI effect is based on the average 2014 air temperatures measured along the cross section by semi-professional amateur stations (see Appendix 1) and the consistent difference between the De Bilt, Schiphol and Stadswaterkantoor time series. At the rural southwest extreme of the model domain, the UHI effect is nil.

GST usually tracks the seasonal fluctuation of SAT but tends to be systematically higher than SAT with the offset depending on land surface conditions (Mann and Schmidt 2003). Before the building period, the GST is assumed equal to the average annual SAT plus 0.5 °C, being a reasonable rural SAT-GST offset (e.g. Dědeček et al. 2012; Kooi 2008). After the building period, the offset is assumed to depend on the building period and the position relative to the city center.

The urban SAT-GST offset is based on the ‘built-up density’ history as follows. The model domain is horizontally divided into 400–800-m long sections that coincide with discrete building periods. The SAT-GST offset per top boundary section is time-dependent and calculated as area-weighted values for green spaces (including surface water), roads and buildings (comparable to Taylor and Heinz 2009). Surface water was assumed to have the same SAT-GST offset at green spaces. The water temperature of the canals in the city center is 0.2–0.9 °C higher than the urban SAT (see Appendix 1), which is comparable to that of green spaces.

A radiation-balance-based soil-atmosphere-heat-transport-model has been set up to calculate the SAT-GST offsets and ground heat flux for various pavement types under specific climatological conditions of the Amsterdam city center (see Appendix 2). The inferred offset for brick was used for roads constructed before 1925 and the offset for asphalt was used for roads that were constructed since 1925.

The present-day temperatures in living spaces in The Netherlands average approx. 20 °C. One century ago, an ambient living space temperature of 15 °C was normal. For work spaces the temperatures vary between 12 and 18 °C (e.g. Montijn 2000; Palmer and Cooper 2012; Kuijer and Watson 2017). For uninsulated flooring, the maximum temperature ranged between 14 and 16 °C, due to a 2 °C m−1 vertical temperature gradient in living spaces (Stichting Bouwresearch 1985). Most buildings in Amsterdam have basements, cellars or crawl spaces, whereby the basements and cellars were rarely heated. In fact, these were often used as storage rooms and had temperatures of ~11 °C (Montijn 2000). Only recently, semi-basements of the seventeenth century buildings are being converted into living and working spaces and may be heated.

Only where floor heating is applied with uninsulated floors, the crawl space temperature approaches the living space temperature (Stichting Bouwresearch 1985). Floor heating is not very common; therefore, the ground temperature below buildings is assumed to be approx. 2.5 °C higher than the urban SAT for the building periods before 1960. After that date, central heating became common and it is assumed that this resulted in higher living-space temperatures and a 5.0 °C higher ground temperature below buildings. For the building period after 2000, it must be assumed that better floor insulation resulted in a lower (4.0 °C) difference.

A GST increase due to emplacement of a new urban surface cover (e.g. paving of the surface) or construction of a building propagates into the subsurface primarily by diffusion. This implies that the temperature rise at depth occurs with a delay relative to the surface change and that the amplitude is smaller than, or attenuated relative to the GST change, over long time periods (e.g. Lesperance et al. 2010).

Initial conditions

The initial conditions are calculated as a steady-state simulation representing the pre-1350 temperature distribution and groundwater flow. A horizontal hydraulic gradient of 10−4 m m−1 directed northeast, a surface temperature of 9.1 °C and a geothermal gradient of 0.024 °C m−1 were imposed on a steady-state version of the model. The results of this model run were used as initial conditions for the transient 1350–2012 simulations.

Results

Figure 4 depicts the modelled GST history for various pavement types under the meteorological conditions of the city center of Amsterdam for the period 1990–2014 (method detailed in Appendix 2). Table 1 summarizes the average GSTs for these pavement types over this period together with the modelled component contributions: rural SAT, the UHI effect and the SAT-GST offset. The results show that GST differences associated with pavement type are expected to be about 1.2 °C. The offsets for brick and asphalt were used to represent the SAT-GST offset for roads before and since 1925. Figure 5 presents the calculated area-weighted offset between the rural SAT and the local GST (Fig. 5d) for the model transect.

Fig. 4
figure 4

Calculated annual averages of road surface temperatures for an average city center SAT represented by Schiphol SAT + 1.1 °C. The dashed lines in corresponding colors show the 1990–2014 averages of the temperatures

Full size image
Table 1 Summary of the predicted GST and contributing components for the city center
Full size table
Fig. 5
figure 5

a Cross section line A–A′ plotted on the present-day topographical map, b Building periods of the sections along line A–A′, c Percentages of space occupied by buildings, roads and green space, and d UHI effect and total compounded offset between the rural SAT and GST of the sections along line A–A′

Full size image

The historically minimum rural SAT was 6.4 °C in both 1491 and 1740 (Van Engelen et al. 2001; Fig. 1b). Taking the SAT-GST offset for the oldest part of the city center (Fig. 5b,d) into account, the urban GST in these years would have been 10.1 °C. The present-day compounded SAT-GST offsets vary from 0.9 to 4.5 °C (Fig. 4d). For the period 1990–2014, this results in average GSTs from 11.3 °C at the city margins to 14.9 °C for the section between distances 7,300 and 7,800 m, that were built up around year 2000 (Fig. 5b) with 88% buildings and 6% (asphalt) roads (Fig. 5c).

The spatio-temporal development of the GST has been implemented as the thermal top boundary condition of the coupled groundwater and heat transport model, resulting in TD distributions for the years 1350–2012. Figure 6a–g shows the calculated distribution of temperature in the top 200 m of the model domain at selected times. Figure 6h shows the calculated T–20m values along the cross section at four selected years. At the positions indicated with dashed vertical lines in Fig. 6g, synthetic TD profiles have been calculated for the situation in 2012.

Fig. 6
figure 6

Calculated temperatures at selected times (a–g) along the cross section in Fig. 1. The northeast end of the cross section is on the left, the southwest end is on the right. The dashed vertical lines in panel g are the locations of the synthetic TD profiles in Fig. 5. h Calculated T–20m distribution along the cross section in 4 selected years

Full size image

Figure 7a shows the calculated TD profiles at various distances together with the measured profiles. Figure 7b gives the relative frequency of measured and calculated T–20m values for the year 2012.

Fig. 7
figure 7

a Synthesized TD profiles at selected distances along the cross section (solid lines), and measured TD profiles (dashed lines). The locations of the calculated profiles are indicated in Fig. 6g. The circled numbers at the measured TD profiles correspond to the locations in Fig. 1a. b Relative frequency distributions of the observed T–20m values (n = 63) and calculated T–20m values (n = 103) at 100-m intervals along cross section A–A′

Full size image

Discussion

The Amsterdam T–20m observations (Fig. 1a), with a maximum of 4.1 °C above the background temperature, appear to compare very well with other cities; however, studies in other cities have recorded the subsurface temperatures at variable depths, as well above and below the seasonal zone. This biases the comparison with the present study. The SUHI effects reported are, for example, 5 °C in Winnipeg in Canada (Ferguson and Woodbury 2004; Zhu et al. 2010; Zhu et al. 2014) and 3.5 °C for Istanbul in Turkey (Yalcin and Yetemen 2009). Taniguchi et al. (2007) and Huang et al. (2009) demonstrated that SUHIs exit in various Asian cities. In Basel (Switzerland) the mean temperatures in the saturated zone were found to be approx. 5 °C higher than the average annual SAT (Epting and Huggenberger 2013). In various German cities the inferred difference between highest and lowest observed groundwater temperatures is 4–8 °C (Zhu et al. 2010; Menberg et al. 2013a, b, c; Menberg et al. 2015; Benz et al. 2015). Locally, subsurface temperatures have been raised to an even larger extent by groundwater heat pump systems or warm water injection—e.g. Zaragoza (Spain) at 8 °C and more (García-Gil et al. 2014).

The observed maximum T–20m values are less than the expected maximum GST (Table 1). This may indicate that the propagation of elevated urban GSTs and attenuation with depth constrain the T–20m to values below the maximum of 15.6 °C based on the urban SAT and SAT-GST offset.

The synthetic-road surface temperatures, shown as predicted GST values in Table 1, are probably over-estimations. The low asphalt albedo used is not likely to occur as the asphalt surface is usually covered with chippings with a higher albedo; furthermore, the albedo of asphalt surfaces increases with the age of the surface. In the city, the insolation of the road surfaces is often reduced due to a limited sky view factor and heat may be discharged by surficial run off and evaporation of precipitation. Therefore, the calculated road surface temperatures are maximum values, which may also explain the lower observed T–20m values compared to the maximum GST. It is recommended to collect long-term surface temperature data at various types of surfaces in the city center to validate and fine-tune the modeling approach described in Appendix 2.

The calculated temperature distributions in Fig. 6 clearly reflect the staged urban expansion in the shifting of the front of higher temperatures to the right end (southwest) of the cross section. Between the end of the sixteenth century and the late-nineteenth century, little urban expansion took place. Groundwater flow was directed to the northeast and, therefore, the thermal front only moved marginally due to conduction. After 1900, fast urban expansion raised the subsurface temperatures widely in the model, but over a lesser depth than in the older parts of the city. The effect of the groundwater flow is obvious from a slight rightward tilting of the thermal fronts.

The calculated TD profiles in Fig. 7a show, as expected, the concave deviation of the curves from the straight deeper end of the curves at larger depth for the older urban expansion stages. The calculated TD profiles fit in the measured ranges, supporting the suitability of the approach; however, it is recommended to repeat the TD logging and T–20m measurements in the future to be able to validate the model. Validation of the model would allow the use of the model to predict the future thermal state of the SUHI.

To model and describe the spatiotemporal development of the SUHI, the model domain has been scaled down to generalized sections of 400–800 m long. Therefore, a direct comparison of the measured and synthesized profiles will never result in a ‘perfect’ fit. Site specific developments that cannot be incorporated in such a model influence the local TD profiles. Although no direct comparison is possible, the calculated TD profiles appear to have systematically slightly higher temperatures than the observed TD profiles. A possible over-estimation of the GST, as discussed in the preceding, may play a role in this as well. The high temperatures in the deeper part of the observed curve 4 (Fig. 7a) must have been caused by lateral advection from a deep-seated heat source. This was possibly the subway station, that had been constructed in the years preceding the measurements, only 10 m from the piezometer and at a depth of approx. 25 m bgl, although other sources, like an underground thermal energy storage (UTES) system, cannot be excluded.

The distribution of the T–20m values, as a measure of the SUHI intensity, is rather well explained by the model, as demonstrated by the relative frequency distribution of these observations (Fig. 7b). The distribution of the calculated T–20m values on the cross section compares well with measured T–20m values at random locations. It is remarkable that in both histograms, two peaks occur. The calculated values peak at temperatures that are about 0.5 °C higher than where the peaks in observed values occur, which suggests that the calculated values may be a slight over-estimation of the actual values. The same could be read from the fact that the calculated TD profiles (Fig. 7a) seem to indicate higher temperatures than the observed TD profiles.

The range of the calculated T–20m values is narrower than that of the measured values. Figure 6h shows the calculated T–20m distribution along the cross section, with a maximum of 13.5 °C. The eight observed T–20m values above 14.0 °C were all found in a relatively small area, just south of the city center. The land cover at these locations is not different from comparable observation points and the high T–20m values can, therefore, not be explained by locally higher SAT-GST offsets. All these observation points are located very close (10–20 m) to buildings with deep boiler basements, subway stations or district heating, and a link with these sources can be assumed. These individual anthropogenic heat sources were not included in the model. Four T–20m observations between 13.5 and 14.0 °C are also located near similar potential heat sources, but could not be linked unequivocally to known sources.

This leads to the observation that the maximum T–20m on a regional (model) scale, that can be explained from the urban expansion history and land cover, is 13.5 °C. The TD observations, however, are only representative of a small subsurface volume around the observation well. These differences in scale explain, at least in part, deviations between the maximum modeled and observed T–20m values. The T–20m observations between 13.5 and 14.0 °C may suggest that the lower value is a slight underestimation of the actual maximum. Values above 14 °C can be linked to localized anthropogenic heat sources, and have no great extent. The actual maximum SUHI intensity at 20 m depth is, therefore, only between 2.5 and 3.0 °C for Amsterdam. Locally, e.g. close to buildings with deep boiler basements, the T–20m values are higher, but these are very local effects.

One aspect that may, at least in part, explain the difference with other studies is the observation depths. Menberg et al. (2013a) concluded that elevated GST and heat loss from basements are dominant factors in groundwater temperature anomalies in the city of Karlsruhe (Germany) at the groundwater surface between 3 and 8 m bgl. Ferguson and Woodbury (2004) used the same 20-m observation depth as used in the present study to investigate the Winnipeg SUHI. Based on their measurements and numerical modeling, they concluded that the highest temperatures occur close to buildings, and that several hundreds of meters from these buildings, the difference with the background temperature was only a few tenths of a degree. Their conclusion is that heat loss from buildings is the major source of the Winnipeg SUHI.

Bidarmaghz et al. (2019) studied by numerical modeling the amount of heat from basements released to the ground and concluded that this constitutes a significant percentage of the total heat loss from buildings, particularly in the presence of groundwater flow. In that study, basements were assumed to be kept at 18 °C throughout the year. Benz et al. (2015) used satellite-derived land-surface temperatures in combination with building densities and basement temperatures to estimate regional groundwater temperatures below German cities. Basement temperatures were estimated to be 17.5 ± 2.5 °C. Bayer et al. (2016), by inversion of TD logs from three locations in the suburbs of Zurich (Switzerland), derived temperatures of 15–16 °C below basements of buildings, whereas Zhu et al. (2014) carried out a numerical modeling of groundwater flow and heat transport to simulate the SUHI development of the city of Cologne (Germany) in the past 110 years, and applied a GST increase up to 15 °C for the built-up areas. The basement temperatures in these studies, and therefore the heat loss from buildings, are higher than estimated for Amsterdam, where only semi-basements and crawl spaces prevail, with much lower temperatures. In Amsterdam, therefore, the contribution of buildings to the higher ground temperatures, appears to be much less and in the same range as that of the pavements.

The development of the SUHI of Amsterdam shows that temperatures at depths that are of interest for GES systems (existing systems are located between 25 and 230 m bgl, with averages between 90 and 147 m bgl) are up to 2 °C higher in the parts of the city that were built before 1900 and that these temperatures have increased rapidly in more recently urbanized areas. Increases of these temperatures to 13 °C against a 11 °C background temperature must be expected, thus limiting the cooling capacity of these systems. A lesser cooling capacity may result in higher groundwater demand during the cooling cycle of ATES systems and higher return temperatures. A self-strengthening effect may be the consequence.

Conclusions

Simulation of the SUHI of Amsterdam by modeling the SAT, UHI, GST relations and offsets based on historical data, results in a realistic distribution of subsurface temperatures that compare well to measured TD profiles and T–20m values. This is, to the authors’ knowledge, the first case where a long-term (centuries) urban development, studied in relation to climate change, along with the history of both the surface urban heat-island temperatures and ground surface temperatures, has been modeled to simulate the SUHI of a city.

This simulation sheds light on the relative contributions of the drivers that play a role in this long-term process. It shows that distinction can be made between a regional SUHI effect and localized higher temperature anomalies. The drivers of the regional SUHI are higher GSTs due to pavement and heat loss from buildings. The GST history is related to the SAT history and UHI effect and the history of the land cover (e.g. Kooi 2008; Bayer et al. 2016).

The data illustrate the relationship between T–20m and the age of the urban expansion and building density. It can be expected that the UHI effect is the strongest in the city center, where also the oldest quarters are found. The model results show that these relations and the development of the SUHI can be construed from the urban expansion history and building density.

The maximum regional SUHI intensity in Amsterdam ranges between 2.5 and 3.0 °C, which is much less than for comparable (similar latitudes and sizes) cities around the world. This difference is caused by omitting high subsurface temperatures associated with localized subterranean heat sources like boiler basements, UTES systems etc., as part of the regional SUHI. The local sources are relatively recent features and have a relatively local impact (horizontal and vertical). The regional SUHI is caused by processes that find their origin in urban developments that started centuries ago.

The distinction between a regional SUHI and localized heat sources has implications for the calculations of the (exploitable) geothermal potential of the SUHI, as done in some other studies (e.g. Menberg et al. 2015; Bayer et al. 2019; Epting et al. 2018).