Abstract
A Turonian limestone-dolomite aquifer from the Tadla basin of Morocco was analysed using a multi-tracer approach (δ18O, δ2H, δ13C, 3H, 14C and noble gases) to reconstruct the paleotemperature evolution from the late Pleistocene to the Holocene. The Turonian aquifer was found to be suitable for a groundwater-based paleoclimate reconstruction, representing the Holocene–late Pleistocene epochs. After correction for young water contribution, mean residence times (MRTs) of groundwater were calculated using the Pearson radiocarbon model. Additionally, terrigenic helium content was used as an age indicator. Noble gas temperature (NGT) results from wells with groundwater ages corresponding to glacial periods showed an average of 17.2 ± 1.7°C. In contrast, samples of recent recharge water gave a mean NGT of 25.2 ± 1.3°C. This reveals a temperature difference of 8.0 ± 2.1 °C between the Holocene and late Pleistocene. This significant Pleistocene–Holocene temperature difference observed in Africa has considerable significance and can be extended to address an important topic relating to the nature of the wet epochs during which the fossil aquifers of North Africa were recharged. It is evident that this aquifer was recharged during both interglacial (warm) and glacial (cool) wet periods.
Résumé
L’aquifère des calcaires dolomitiques du Turonien du bassin de Tadla au Maroc a été étudié par une approche multi-isotopique (δ18O, δ2H, δ13C, 3H, 14C et gaz nobles) pour reconstruire l’évolution de la paléotempérature du Pléistocène tardif à l’Holocène. Après correction de la contribution d’eau jeune, le temps moyen de résidence (TMR) des eaux souterraines a été calculé en utilisant, pour le radiocarbone, un modèle de Pearson. De plus, la teneur en hélium géogénique a été utilisée comme un indicateur d’âge. Les résultats de l’estimation de la température par les gaz nobles (TGN) des puits pour les eaux souterraines d’âge correspondant aux périodes glaciaires donnent une moyenne de 17.2 ± 1.7 °C. Au contraire, les eaux de recharge récente ont des TGN moyennes de 25.2 ± 1.3 °C. Ceci indique une différence de température de 8.0 ± 2.1 °C entre l’Holocène et le Pléistocène tardif. Cette différence significative de température de la période Pléistocène - Holocène observée en Afrique a une importance considérable et peut être prise en considération pour aborder un sujet important qui est celui de la nature des époques humides durant laquelle les aquifères fossiles d’Afrique du Nord ont été rechargés. Il est évident que cet aquifère a été rechargé durant les périodes humides interglaciaires (chaudes) et glaciaires (froides).
Resumen
Se analizó un acuífero Turoniano de caliza-dolomita de la cuenca de Tadla, Marruecos, utilizando un enfoque de trazadores múltiples (δ18O, δ2H, δ13C, 3H, 14C y gases nobles) para reconstruir la evolución de la paleotemperatura desde el Pleistoceno tardío hasta el Holoceno. El acuífero Turoniano se consideró adecuado para una reconstrucción del paleoclima basada en las aguas subterráneas, que representa las épocas del pleistoceno tardío holoceno. Después de la corrección para una contribución de agua joven, se calcularon los tiempos medios de residencia (MRT) del agua subterránea usando el modelo de radiocarbono de Pearson. Adicionalmente, se utilizó el contenido de helio terrigénico como indicador de edad. Los resultados de la temperatura de los gases nobles (NGT) de los pozos con edades de agua subterránea correspondientes a períodos glaciales mostraron un promedio de 17.2 ± 1.7 °C. En contraste, las muestras de agua de recarga reciente dieron un NGT medio de 25.2 ± 1.3 °C. Esto revela una diferencia de temperatura de 8.0 ± 2.1 °C entre el Holoceno y el Pleistoceno tardío. Esta importante diferencia de temperatura entre el Pleistoceno y el Holoceno observada en África tiene una importancia considerable y puede ampliarse para abordar un importante tema relacionado con la naturaleza de las épocas húmedas durante las cuales se recargaron los acuíferos fósiles del norte de África. Es evidente que este acuífero se recargó durante los períodos húmedos interglaciares (cálidos) y glaciares (fríos).
摘要
使用多元示踪方法(δ18O, δ2H, δ13C, 3H, 14C和惰性气体)分析了摩洛哥Tadla盆地的Turonian石灰岩-白云岩含水层, 以重建从更新世晚期到全新世的古温度演化。发现Turonian含水层适合基于地下水进行全新世至晚更新世时期的古气候重建。在校正了年轻水的贡献之后, 使用皮尔逊放射性碳模型计算了地下水平均滞留时间(MRT)。此外, 将陆源氦含量用作年龄指标。来自地下水年龄与冰期相对应的井中的惰性气体温度(NGT)平均为17.2 ± 1.7 °C。与之相对的是, 最近补给的水样品的平均NGT为25.2 ± 1.3 °C。这表明全新世与晚更新世之间的温差为8.0 ± 2.1 °C。在非洲发现的更新世-全新世温差具有重大意义, 可以扩展到涉及北非化石含水层得到补给的湿润期性质的重要课题。显然, 在间冰期(温暖)和冰期(干冷)的湿润期, 该含水层都得到了补给。
Resumo
Um aquífero Turoniano calcário dolomitico da bacia de Tadla, no Marrocos, foi analisado usando-se uma abordagem multitraçador (δ18O, δ2H, δ13C, 3H, 14C e gases nobres) para reconstruir a evolução da paleotemperatura do Pleistoceno tardio ao Holoceno. Verificou-se que o aquífero Turoniano é adequado para uma reconstrução paleoclimática à base de águas subterrâneas, representando as épocas do Holoceno e Pleistoceno tardio. Após a correção de uma contribuição de água jovem, os tempos médios de residência (TMRs) das águas subterrâneas foram calculados usando o modelo de radiocarbono de Pearson. Além disso, o conteúdo de hélio terrigênico foi utilizado como indicador de idade. Os resultados da temperatura do gás nobre (TGN) de poços com idade das águas subterrâneas correspondentes a períodos glaciais mostraram uma média de 17.2 ± 1.7 °C. Por outro lado, amostras de água de recarga recente deram um TGN média de 25.2 ± 1.3 °C. Isso revela uma diferença de temperatura de 8.0 ± 2.1 °C entre o Holoceno e o Pleistoceno tardio. Essa diferença significativa de temperatura entre Pleistoceno e Holoceno observada na África tem um significado considerável e pode ser estendida para abordar um tópico importante relacionado à natureza das épocas úmidas durante as quais os aquíferos fósseis do norte da África foram recarregados. É evidente que esse aquífero foi recarregado durante os períodos de chuva interglacial (quente) e glacial (frio).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Valuable paleoclimatic information can be derived from the investigation of environmental isotopes and noble gases in groundwater. Noble gas solubility in groundwater is a useful method to reconstruct the recharge temperature, which together with groundwater dating is a very powerful tool for paleoclimatic reconstruction. This is a direct and quantitative method to reconstruct past mean annual temperature by measuring noble gas concentrations and radiocarbon or other age indicators in groundwater. This approach provides the soil temperature at which the water recharged to the aquifer (Stute and Schlosser 1993; Aeschbach-Hertig et al. 1999; Klump et al. 2007; Varsányi et al. 2011; Aeschbach-Hertig and Solomon 2013). Although such groundwater studies exist for Africa, the data coverage is poor and general knowledge is still scarce on reconstructions of groundwater recharge temperatures (e.g. Rudolph et al. 1984; Heaton et al. 1986; Darling et al. 1987; Fontes et al. 1993; Andrews et al. 1994; Edmunds et al. 1998; Guendouz et al. 1998; Beyerle et al. 2003; Kulongoski et al. 2004; Abouelmagd et al. 2014).
Several paleoclimatological methods have been used to reconstruct past climate on decadal or annual timescales during the last few decades. These are usually based on δ18O records in polar ice cores, or laminated sediments from marine or terrestrial environments. These proxies, such as those in marine sediments accumulating along the margins of the African continent, provide information on African paleoclimate history, and are unique records of past global climate (Stuiver and Grootes 2000; Martrat et al. 2004; Darling 2011; Berke et al. 2012; Loomis et al. 2012; de Menocal 2014; Wu et al. 2017). Temperature reconstruction together with age determination are generally used to study climate conditions and similar paleoclimate records have been published from the continent (Namibia, Oman, Niger, Botswana, Egypt) (Stute and Talma 1998; Weyhenmeyer et al. 2000; Beyerle et al. 2003; Kulongoski et al. 2004; Abouelmagd et al. 2014).
In this paper, a limestone-dolomite aquifer was studied in the Tadla basin, Morocco, where environmental isotopes (δ18O, δ2H, δ13C, 3H, 14C) and noble-gas investigations were used in the Turonian aquifer to determine the annual temperature of the late Pleistocene and Holocene periods. Although similar isotope hydrological studies exist for Tadla basin (Bouchaou et al. 2009; Bouhlassa 2010; Saadi et al. 2017), the data coverage is poor and information about the groundwater recharge conditions in the basin is still incomplete. The multi-layered aquifer system in the Tadla basin constitutes one of the main water resources in Morocco and the purpose of this investigation is to expand the hydrological knowledge of the Turonian aquifer by analysing the recharge conditions, the age distribution and the isotope characteristics of the groundwater. The aim in this study is to interpret the noble gas data in terms of paleoclimate reconstruction, which has the potential to make significant contribution to the discussion on climate evolution and past groundwater dynamics in Morocco.
Study area
The Turonian aquifer is located in central Morocco in the Tadla basin (5,000 km2) and is part of a multi-layer aquifer system (Mio-Plio-Quaternary, the Maastrichtian-Eocene, the Senonian and the Turonian) of the Oum Er-Rabia basin. The Turonian aquifer is formed in the north by karstic limestone and dolomite, and is characterized mostly by dolomite in the south. It is one of the main water resources with high production rates up to 1,300 l/s in the basin, and is among the most important aquifer sources in Morocco (Bouchaou et al. 2009). It is under an impermeable marl formation of Cenomanian. The thickness of the Turonian formation ranges from 50 m (in the north) to 100 m (in the south). Most of the wells and boreholes are in the confined part, except in the locations of well samples 1, 2 and 3, which are in the recharge area located in the unconfined part of the aquifer. The climate is warm and temperate in the basin and it is considered to be a hot-summer Mediterranean climate (Csa) according to the Köppen-Geiger climate classification. The annual precipitation is 550 mm, and the most rainfall occurs between October and April with precipitation of 60–85 mm/month. The driest months are in summer (July, with 2 mm of rainfall). The annual average temperature is about 19 °C. The warmest month of the year is July, with an average temperature of 29.5 °C. The lowest average temperatures in the year occur in January, when it is around 10.5 °C (Climate-data.org, 1982–2012).
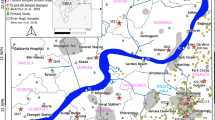
The potential of the Turonian aquifer as a paleoclimate archive was described in detail in a preliminary study of this area (Saadi et al. 2017), where the direction of flow paths to the south and south-west from the outcrop zone, based on stable isotope values, had been confirmed. Moving away from the outcrop zone, the stable isotope values became increasingly depleted along the existing flow lines as radiocarbon and tritium concentrations decrease. It had been concluded there that the Turonian aquifer might be a potential place for late Pleistocene-Holocene paleoclimate reconstruction from groundwater studies, since the mean residence times of water along the flow path was increasing and this confirmed the existence of the paleowater in the Turonian aquifer. To find paleowater, it is desirable to extend groundwater sampling of the aquifer along the direction of the flow-path. The sampled points in the basin used as part of this study covered over 3,500 km2 between Boujad, Oulad Zmam and El Borouj (Fig. 1) and according to the flow paths the screen depth of the sampled points are continuously decreasing (Table 1).
A simplified geological map of the Tadla basin with sampling points of wells and boreholes, and a North-South cross section (Tammal et al. 2014)
Analytical methods
Nineteen groundwater samples were taken for noble gas, tritium, radiocarbon, and stable isotope analyses by researchers from the CNESTEN (Centre National de l’Energie des Sciences et Techniques Nucléaires, Morocco) and ICER (Isotope Climatology and Environmental Research Centre, Hungary) laboratories. The samples were collected from artesian boreholes and wells (Fig. 1). Water temperature, pH, electrical conductivity as well as alkalinity were measured in the field. The major ions were determined at CNESTEN with ion chromatography, atomic spectroscopy and titration, where HCO3− (±1.0%), Cl− (±1.7%), NO3− (±1.9%), SO42−(±2.0%), Ca2+ (±1.1%), K+ (±0.9%), Na+ (±1.3%), and Mg2+ (±0.9%) were measured (the numbers in parenthesis refers to the relative standard deviation RSD of the analyses).
Carbon stable isotope analyses of dissolved inorganic carbon (DIC) from the water samples were carried out with an automated GASBENCH II sample preparation device attached to a Thermo Finnigan DeltaPlus XP mass spectrometer (Vodila et al. 2011) at the ICER laboratory. Hydrogen and oxygen stable isotopes of the water were measured with a Picarro (L2130-i) at CNESTEN and they are expressed as δ2H, δ18O, and δ13C values relative to VSMOW and VPDB, respectively, following the equation: δ = (Rsample/Rstandard – 1; expressed in permil), where R is the 2H/1H, 18O/16O or 13C/12C ratios in the sample or in the international standards. Measurement precision is better than ±0.1‰ for δ18O and δ13C, and ±1‰ for δ2H.
Groundwater samples were treated in vacuum-tight septa-sealed reactors for AMS (accelerator mass spectrometry) 14C analyses. First, 20 ml of the groundwater sample was injected into the evacuated reaction cell and, in a second step, 3 ml of 85% phosphoric acid was introduced into the cell, via the septum by disposable sterile medical plastic syringes. Then the water and acid mixture at the bottom of the reaction cell was heated to 75 °C in a heating block for at least 1 h to increase the rate of reaction and improve CO2 extraction yield from DIC fraction. The CO2 produced off-line was then introduced into the in-line CO2 gas purification system (Molnár et al. 2013a). In a final step, AMS graphite targets were prepared from the purified CO2 samples using a customized sealed tube graphitization method, for 14C analysis by the EnvironMICADAS AMS at ICER (Rinyu et al. 2013). The 14C results are reported as percent modern carbon (pMC), calculated by the BATS software (version 3.66; Wacker et al. 2010). The overall 14C measurement uncertainty for modern samples is <0.3 pMC, including normalization, background subtraction, stable-isotope fractionation correction and counting statistics (Molnár et al. 2013b).
The water samples for dissolved noble gases analysis were collected in copper tubes in the field, sealed by stainless-steel pinch-off clamps. The water samples were introduced into a preparation line, where all the gases were adsorbed in two cryotraps. The heavy gases including argon, krypton, xenon and all chemically active gases (N2, O2, CO2, etc.) were collected in a stainless steel trap (SST) at 25 K, while helium and neon were collected in a charcoal trap (CT) at 10 K. Heating the CT up to 42 and 90 K, allowed the helium and neon fraction to be determined sequentially. After releasing the heavy gases from the SST at 150 K, a tiny amount was purified with a SAES St707 getter cartridge. The pure argon-krypton-xenon fraction was then admitted to the mass spectrometer. The heavy noble gas (Ne-Ar-Kr-Xe) measurements were measured using a VG5400 (Fisons Instruments), while helium and 3He/4He were obtained using a Helix SFT (Thermo Scientific) noble gas mass spectrometer. The whole analysis was calibrated with known air aliquots with an accuracy of 1.0% for He, Ne, Ar concentrations and 3He/4He ratios, and 1.5% for Kr and Xe concentrations (Papp et al. 2012). The accuracies allow for calculation of noble gas temperatures (NGTs) with a precision better than 0.5 °C.
Tritium concentrations were measured using batches of electrolysis cells, which were developed for tritium enrichment in water samples to increase its concentration, followed by liquid scintillation counting using Quantulus 1220 (Perkin Elmer), in CNESTEN (Marah 2007). The results are expressed in tritium units (TU) and the precision of the tritium measurements were better than 0.5 TU.
Results and discussion
Chemical characterisation of the groundwater
The water chemistry is useful for the radiocarbon dating model and also helps understand and demonstrate that the samples come from the same aquifer, have similar groundwater dynamics, and which samples derive from the same flow-path. Both shallow and deep wells were sampled, with water samples collected from the outcrop zone at depths of 27 and 30 m and from deeper parts along the flow path, between depths of 100–650 m. Water temperatures varied between 22.1 and 40.2 °C, and the aquifer is generally characterised by neutral pH ranging from 6.75 to 7.45. The main chemical parameters of the groundwater samples are summarized in Table S1 of the electronic supplementary material (ESM).
Groundwater quality depends on water–rock interaction mechanisms between the Turonian karstic limestone/dolomite and water. General groundwater characteristics based on major ions are illustrated in a Piper diagram (Fig. S1 of the ESM). The groundwater in the Turonian aquifer is mainly characterised by Ca-(Mg)-HCO3 waters. One group, located in the middle part of the study area (samples 7, 8, 9, 10) has slightly more sulphate and chloride. The chemical composition of these waters indicates that the samples come from the same aquifer, which has a unique geochemical character. Sample 17 has SO4-Cl groundwater character based on dissolved anions, with relatively high SO4 content, being the only outlier of the groundwater samples. This water might not belong to the Turonian aquifer. In terms of radiocarbon dating, the carbonate will evolve along the flow path, which is characterized by a slight decrease in HCO3− in the area of the unsaturated zone (samples 1, 2, 3, 4). Further downstream the HCO3− remains almost stable along the flow path (between 5 and 6 mmol/L). Ionic balance was calculated to observe any deviation from electrically neutral water based on all measured anions and cations, with differences less than 5.2% (Table S1 of the ESM). This deviation is partly due to the use of multiple instruments for ion analyses leading to an accrual of analytical errors, and/or the lack of measurement of some ions (such as ammonium ion in this case).
Radiocarbon dating of the groundwater
To estimate groundwater residence time, it is necessary to consider partitioning processes at the boundary of the unsaturated and saturated zone, water–rock interactions and mixing processes to correct for potential addition of nonatmospheric carbon. Over the years, many theories and calculations have been developed to obtain accurate groundwater ages from 14C measurements of dissolved inorganic carbon (Ingerson and Pearson 1964; Fontes and Garnier 1979; Mook 1980; Salem et al. 1980; Blaser et al. 2010; Varsányi et al. 2011; Plummer and Glynn 2013; Han and Plummer 2013). Ideally, radiocarbon dating of groundwater can be performed in cases when the chemical parameters do not change significantly along the flow path within the aquifer. For this study, first the proportion of freshwater (as indicated by the presence of tritium) was calculated and based on the freshwater proportion, a mixing correction has been made for the measured components (δ18O, δ2H, δ13C, 3H, 14C, HCO3− and noble gases). The Pearson model was used for radiocarbon dating of groundwater based on mixing corrected values.
Surprisingly, the natural dynamics of this groundwater system is affected by mixing with freshwater, even at the confined part of the aquifer. This freshwater input is indicated by the presence of tritium, an isotope tracer capable of giving complementary information to understand and quantify freshwater contributions to the aquifer. As one can see in Table 2, the tritium concentrations of most of the samples in the confined aquifer are between 0.5 and 1.9 TU, having 14C concentrations between 12 and 73 pMC. In general, considering the long mean residence time (MRT) based on the Pearson 14C model (Table 2), the aquifer should not contain any trace of freshwater. A possible source of this freshwater contamination is from mixing of shallow groundwater with the Eocene aquifer through faults, incorrect well construction or multiscreen wells (Fig. 1). This contamination may occur due to overexploitation of the aquifer, causing high local water-table depression.
To estimate mixing proportions of groundwater samples, the first step is to calculate the freshwater contribution using the tritium content of the samples (Table 2). The determination of the freshwater/old-water proportion is calculated by the expected initial and measured tritium values of the groundwater sample. The initial tritium content of water is assumed to be 4TU according to the IAEA GNIP station data of Fes Sais and tritium content of Oum Er-Rabia (OER) river (IAEA and WMO 2014; Bouhlassa 2010). In both cases, the average annual precipitation and the average annual river water have a tritium concentration of 4 TU. The GNIP station in Fes Sais is only about 300 km from the Tadla basin, and at the same distance from the Atlantic Ocean; hence, the 4 TU is a reliable estimate for the local precipitation in this study area. However, the freshwater contribution might not be necessarily absolute recent, while tritium might be derived from bomb peak. It might have recharged during the last 0–60 years, when the tritium concentration of the precipitation (mainly in the northern hemisphere and continental areas) was much higher due to the thermonuclear bomb tests. Unfortunately, there are only tritium data for the GNIP station Fes Sais available from 1994 to 2000; earlier values have not been reported. The recent value for the precipitation and the OER river, 4 TU, might be considered as a reliable value for the earlier precipitation, when the radioactive decay is taken into account. However, an uncertainty of 1 TU to the freshwater contribution (4 TU) is therefore added to the calculation. To calculate the mixing ratios, the following equation is applied: freshwater proportion (in %) = (Tritiummeasured/Tritiuminitial) · 100, assuming that the old component has no tritium.
The principle of radiocarbon dating of groundwater is that precipitation enters the aquifer through the unsaturated zone and dissolves CO2 from the soil gas, which is produced by root respiration (Clark and Fritz 1997; Geyh 2000; Mook 2000). Therefore, it is assumed to be modern at 100 pMC 14C. CO2 dissolution forms carbonic acid, which in turn, dissolves carbonate mineral species in the aquifer sediments to produce dissolved inorganic carbon (DIC), which stands for CO2(aq) + HCO3− + CO3−2. The 14C content of DIC in groundwater begins to decrease with a half-life of 5,730 years after the isolation from the modern 14C reservoir, when the groundwater enters the saturated zone. The main questions in radiocarbon age models are the estimation of the initial radiocarbon concentration and what happens along the groundwater flow-line. Because of the dissolution of 14C-free carbonate along the flow-line, the DIC does not reflect the atmospheric 14C activity plus the effect of radioactive decay. Different radiocarbon age models estimate the initial 14C content (A0) of DIC in groundwater at recharge in different ways (Ingerson and Pearson 1964; Fontes and Garnier 1979; Mook 1980; Salem et al. 1980; Plummer and Glynn 2013). The usual way in groundwater hydrology to calculate the groundwater apparent age is to apply the following equation: t = 8267 ln (A0/At), where t is the radiocarbon age, A0 is the initial and At is the measured radiocarbon activity in the dissolved inorganic carbon, where the mean life-time of radiocarbon is 8,267 years.
According to the Pearson model, a dilution factor (q) can be calculated to estimate the proper A0 from the radiocarbon content of atmospheric and soil CO2. This dilution factor (q) can be calculated by using the equation of q = (δ13CDIC – δ13Ccarb)/(δ13Csoil – δ13Ccarb); in respect to this the δ13CDIC is the measured carbon isotope ratio in groundwater, δ13Ccarb is the δ13C of the dissolved carbonate (estimated to be 0‰ vs. VPDB), while δ13Csoil refers to CO2 in the soil gas (estimated to be –16‰ vs. VPDB based on the C4 vegetation cover in the outcrop-zone). The radiocarbon content of the host rock is assumed to be 0 pMC and that of the soil zone is 100 pMC (Ingerson and Pearson 1964; Saadi et al. 2017).
The mixing-corrected values (A) using the Pearson model were also calculated using tritium-based freshwater proportions following this equation: = (100 · Ameasured – freshwater proportion · Ainitial)/(100-freshwater proportion). The initial bicarbonate value was chosen to be 289 mg/L (4.7 mmol/L), which was the average of the values from the Eocene aquifer (Bouchaou et al. 2009). The initial δ13C value is −13.02 (‰ vs. VPDB) which is the average δ13C value of samples in the area of the outcrop zone (samples 1, 2, 3). Although the accuracy of the radiocarbon measurements is just between 0.12 and 0.31 pMC, the uncertainty of the radiocarbon groundwater age is propagated from other factors, mainly from the mixing correction. Using the uncertainties of the individual tritium values as well as the 1 TU uncertainty of the freshwater component, the uncertainty of the freshwater contribution can be calculated. As Table 2 shows, these uncertainties can be significantly high. This latter increases the uncertainty of the corrected radiocarbon content of the old component, and hence the error of the age also increases. These calculations are rather a conservative approach, and might overestimate the overall error; therefore, it is recommended to consider it carefully.
The same mixing correction approach was applied to determine the noble gas and stable isotope compositions of the old component of groundwater samples, where the initial values were chosen to be the average values in the area of the outcrop zone (samples 1, 2, 3). For the Pearson model, the mixing-corrected radiocarbon content was determined using a binary calculation based on the tritium-derived freshwater proportion and the mixing-corrected bicarbonate content. The modern recharge waters close to the outcrop zone (samples 1, 2, 3) are expected to contain tritium and so mixing corrections are not necessary for these waters. It must be noted that the values used in the Pearson model of sample 17 were not corrected for mixing, despite the fact that the water has some tritium, as the mixing correction did not give meaningful results for the mixed radiocarbon age. Additionally, based on the chemical composition, sample 17 is an outlier.
Besides the recently recharged samples from the outcrop zone of the Turonian aquifer, with radiocarbon content between 100 and 112 pMC (samples 1, 2, 3), there are samples from the unconfined and confined part of the aquifer (samples 4, 5, 6, 7, 8, 9, 14, 15, 16, 18) with Holocene ages between 1 and 7 kiloyears (kyr) and there are samples with ages 9.5–24 kyr (samples 10, 11, 12 13, 17, 19) closely correspond to the late Pleistocene. Although the calculated MRTs cover mostly the past 15,000 years, there are samples such as sample 11 with an age of about 25 kyr and sample 17, which has a low radiocarbon content (and no mixing correction was used for sample 17); therefore, these locations might represent older ages between 15 and 25 kyr.
Paleotemperature estimates from noble gases
Noble gas concentrations are suitable temperature indicators at the time of groundwater recharge. In aquifers, the concentrations of Ne, Ar, Kr and Xe are derived from the atmosphere (as soil gas) and after their dissolution into the groundwater, their concentrations remain constant along the flow path, because they do not take part in either chemical or biological processes. The interpretation of noble gas concentrations in groundwater requires inverse modelling, which allows one to determine reliable solubility temperatures (noble gas temperatures, NGTs). As a gas partitioning model, the closed-system equilibration model (CE-model) was applied (Aeschbach-Hertig et al. 1999, 2008; Aeschbach-Hertig and Solomon 2013). The main principle of the CE-model is that excess air is formed when the groundwater level is rising, and the soil gas bubbles are entrapped in the pore space. Afterwards, due to the increased hydrostatic pressure, the entrapped soil gas bubbles are totally or partly dissolved. When calculating the recharge temperature, an inverse modelling approach was used. During inverse modelling, parameters such as temperature, excess air and the fractionation of the excess air are varied, and the corresponding model concentrations are evaluated to determine which parameter setup provides the best estimates of the measured concentrations. In the case of the closed-system equilibration model, the model concentrations are calculated according to the following equation:
In this equation, the model concentration can be divided into two parts: a solubility equilibrium component (Ceq) and an excess air component (Cex). There are parameters that have to be assumed, like salinity (S) and atmospheric pressure of the recharge area (p). In case of recharging water, salinity can be neglected, while the prevailing atmospheric pressure can be calculated from the elevation of the recharge area. In this calculation, an average recharge elevation of 700 m asl has been chosen for all samples. The other parameters like temperature (T), unfractionated excess air amount (or in case of the CE-model, the entrapped air amount in the saturated zone) (A), and the fractionation factor (F) have to be estimated in the inverse modelling process. The index i refers to the four atmospheric noble gases (neon, argon, krypton and xenon). Note that helium does not take part in the calculation, since it often has a significant terrigenic contribution. When searching for the best parameter set of T, A and F, the calculated model concentrations are compared to the measured concentrations until the χ2 values reach a minimum. The χ2 value is defined in the following equation (σi is the analytical uncertainty of noble gas i):
The calculations have been performed with the Noble90 MATLAB routine (Peeters et al. 2003) and the Noblebook excel worksheet (Aeschbach-Hertig et al. 2000, 2008). The noble gas results are given in Table 3 and the mixing-corrected noble gas data can be found in Table 3 in parentheses. These latter datasets were exclusively used in subsequent interpretations. When the uncorrected noble gas concentrations are used in the inverse-fitting procedure, uncertainties of 1.5% for Ne, Kr and Xe, and 1.0% for Ar are included. Uncertainties of the mixing-corrected noble gas concentrations are twice as much than that of uncorrected values; hence, the NGTs calculated from mixing corrected noble gas concentrations have also higher uncertainties (about 1.5 °C instead of 0.9 °C). Both calculations give significant results above the rigorous significance level of 0.1. The mixing corrected noble gas data for all samples were used in the interpretation.
Water temperatures in the recharge area (samples 1, 2, 3) varied between 23.1 and 24.1 °C, as measured in the field, which may reflect soil temperatures. These samples originating from the outcrop zone yielded an average noble gas temperature of 25.7 ± 0.7 °C. This temperature is close to today’s ground temperature (23.6 ± 0.5 °C) (Bouchaou et al. 2009; Saadi et al. 2017), and can be correlated with the corresponding water temperatures which have been measured on the field. The NGTs are about 2 °C in excess of ground temperatures. This phenomenon can also be observed in temperate climate regions, where the soil temperature is slightly higher than the mean annual air temperature (Stute and Schlosser 1993; Stute et al. 1995), due to ground heating by incident solar radiation (Bartlett et al. 2006). In fact, the difference of soil and air temperature can be even higher in arid/semi-arid regions due to the lack of vegetation and the higher heat radiation (Beyerle et al. 2003; Aeschbach-Hertig and Solomon 2013). When evaluating water samples farther from the recharge area, the NGTs for the Holocene samples from modern to 7 kyr (samples 1, 2, 3, 5, 7, 9, 14, 15, 16, 18), show an average of 25.1 ± 1.3 °C. The average NGT of samples between 9.5 and 24 kyr in age is 19.1 ± 1.5 °C (samples 10, 11, 12, 13, 17, 19). These paleotemperatures are likely to correspond to glacial periods as the deduced recharge temperatures are considerably lower than Holocene temperatures in the Tadla basin. Based on the radiocarbon age classification, younger and older water samples can be relatively distinguished although there are some samples where the NGT clearly suggested to warmer (sample 12) or colder (samples 4, 6, 8) periods in the past (Fig. 2a; Table 3), conceivably due to mixing.
In addition to the radiocarbon age classification, the terrigenous helium accumulation in groundwater can help for a distinction between Holocene and Pleistocene recharged waters and can help in questionable samples (4, 6, 8, 12; Torgersen and Stute 2013). Helium represents another groundwater age indicator, which can contribute to a better understanding of MRTs of the groundwater samples. Groundwater samples often contain helium derived from other sources than the atmosphere (helium of crustal or mantle origin), and the ratio R/RA (where R and RA are the 3He/4He ratio of the sample and air, respectively) generally decreases, while the helium concentration increases with longer MRTs (Gardner and Heilweil 2014). Hence, terrestrial 4He (4Heterr) can be used to identifying old groundwater (Solomon 2000). NGTs plotted against the 4Heterr content show that groundwater samples with lower NGTs contain more 4Heterr (Fig. 2b). This can be a useful tool to characterise the old fractions of groundwater especially in mixed samples; therefore, it is expected that groundwater samples with lower NGTs should have longer MRTs and a higher 4Heterr content. Figure 2a,b show a similar pattern: the older the water, the higher the terrigenous helium component, and the lower the NGT. Two groups have been selected based on the radiogenic helium component: the first group with low radiogenic helium consists of samples 1, 2, 3, 5, 7, 9, 12, 15, 16, 18, while the other group with high radiogenic helium consists of samples 4, 6, 8, 11, 13, 14, 17. The average NGTs of the groundwater samples with radiogenic helium concentrations below and above 5 · 10−7 ccSTP/g (defined arbitrarily) are 25.2 ± 1.3 °C and 17.2 ± 1.7 °C. Thus, the samples with the lowest NGTs of 14.2 °C and 14.6 °C (samples 8, 11) indicate that their recharge occurred during the coldest glacial periods. As a result, the temperature difference between the Holocene and the late Pleistocene is 8.0 ± 2.1 °C. Based on the terrigenous helium age classification, younger and older water samples can be more clearly distinguished and samples where the NGT clearly suggested to warmer or colder periods in the past can be more precisely distinguished. The samples are in two groups, one with warm young Holocene recharged water samples and the other with cold old Pleistocene recharged samples.
Similar to this study, past continental climatic changes have been confirmed by NGTs in several areas of Africa and the surrounding regions. A warming of at least 5 °C from the late Pleistocene to the Holocene was reconstructed in other studies in Africa. This signal can be seen in the Uitenhage artesian aquifer in South Africa (Heaton et al. 1986) and in Namibia (Stute and Talma 1998), as well as in groundwater samples from the Kalahari Desert in Botswana (Kulongoski et al. 2004). More intense warming (6–7 °C) was revealed by NGTs in Niger (Beyerle et al. 2003) and in the surrounding region of Africa in Oman (Weyhenmeyer et al. 2000). There are recharge temperatures from the northeastern region of Africa (Egypt), where deglacial warming of a similar magnitude (2–7 °C) was observed (Abouelmagd et al. 2014). These significant Pleistocene-Holocene temperature differences observed in Africa are noteworthy and can address the nature of the wet periods during which the fossil aquifers of North Africa were recharged. These aquifers were largely recharged during interglacial wet periods, as well as glacial wet periods. Previous studies have shown that even Holocene waters can show a cooler recharge (Beyerle et al. 2003). The large temperature difference between recent soil temperature and NGTs has been interpreted as being due to the impact of changes in soil temperature in the early-mid Holocene “green Sahara” period. The “outlier” samples in this study, like samples 4, 6, 8 and 14 (or even 10, 13 and 17), might represent the same effect (Fig. 2a). These samples seem to be recharged during the Holocene, only the mixing correction shifts the ages of these samples to around 10 kyr, and without this correction most of them would be clearly of early Holocene age.
Groundwater stable isotope compositions
Stable isotope values were corrected for mixing using the calculated mixing proportions and the initial values taken as average delta values for the recharge area (samples 1, 2, 3); these mixing corrected values were used in the interpretations. The oxygen stable isotope values are plotted against deuterium values for the whole study area (Fig. 3; Table 1). The majority of points fall on or around the global and the local meteoric water lines (GMWL and LMWL), with the latter defined by the equation δ2H = 7.92 · δ18O + 9.87 (Brahim et al. 2016). Groundwater samples from the area of the outcrop zone (samples 1, 2, 3) with modern recharge display the highest stable isotope compositions, and lie somewhat off the GMWL suggesting a slight degree of surface evaporation. The second group, which includes groundwater samples with terrigenous helium component under 1.92 · 10−7 ccSTP/g is characterised by low δ18O (−5.7 to −6.3‰) and δ2H (−37.5 to −40.8‰) values (samples 5, 7, 9, 12, 15, 18, 19). On the other hand, the most depleted isotopic signatures of wells with terrigenous helium component above 1.92 · 10−7 ccSTP/g are characterised by low δ18O (−6.5 to −8.3‰) and δ2H (−39.6 to −47.4‰) values (samples 4, 6, 8, 10, 11, 13, 14, 16, 17). These waters show markedly different isotopic signatures, which may be explained by recharge during the late Pleistocene or the transition time between the two epochs (Holocene–Pleistocene), otherwise mixing with waters that recharged during the late Pleistocene and the Holocene.
Groundwater evolution characteristics
Besides the clustering of the samples into two groups, one with warm young Holocene recharged water samples and the other with cold old Pleistocene recharged samples, the 4Heterr-NGT plot suggests a more continuous NGT evolution with time. Samples 4, 6, 8 were taken in the eastern part of the aquifer and they noticeably do not fit into the warm young cluster, presumably because they have a different groundwater evolution than the western part. Based on the 4Heterr-NGT (Fig. 2b) plot, two trends of groundwater evolution can be distinguished, where samples 4, 6, 8 represent one group and samples 11, 13, 14, 17 trending towards younger and warmer waters represent another group. These groups can refer to a different component of the aquifer because they can be separated spatially: samples 4, 6, 8 describe the eastern part and samples 11, 13, 14, 17 refer to the western and south-western part of the Turonian aquifer (Fig. 1).
Noble gas groundwater studies in semiarid regions show a correlation between NGTs and excess air amounts (Aeschbach-Hertig et al. 2002; Beyerle et al. 2003; Ingram et al. 2007; Massmann and Sültenfuss 2008; Aeschbach-Hertig and Solomon 2013). When plotting the excess neon concentration (defined as Nemeasured – Nesolubility equilibrium) as the indicator of the excess air amount and the terrigenous helium concentration, a clear positive correlation can be seen (Fig. 4a). The neon excess is calculated by the mixing corrected values. According to the closed-system equilibration model, the explanation of the higher excess air component might be increased fluctuations of the groundwater level due to intense rainfall events. Because an elevated water table can lead to increased hydrostatic pressure on the entrapped air in the quasi-saturated zone, the neon concentration would increase (Stute and Talma 1998). The increased neon concentration can be connected to the increase of recharge due to the higher amount of intermittent precipitation events that occurred in the recharge area of the Turonian aquifer (Stute and Talma 1998).
Plotting the deuterium excess (d = δ2Hcorr – 8 · δ18Ocorr; after Dansgaard 1964) against the NGTs, a clear negative correlation is observed which can be associated to the humidity-related climate indicator (Pfahl and Sodemann 2014; Table 1; Fig. 4b). Higher NGTs correlates with lower deuterium excess in the groundwater. Additionally, there is a clear correlation between deuterium excess and neon excess (Fig. 4c). The deuterium excess of those waters that recharged during late Pleistocene or during or between early and mid Holocene is above 10‰. This high deuterium excess can be explained by reevaporation, which may cause a kinetic isotope enrichment where the fractionation for both 18O and 2H is correlated (Clark and Fritz 1997). This phenomenon could explain the high deuterium excess values as a consequence of reevaporation of surface water at the recharge area of the Turonian aquifer, contrary to the recent recharge where the formation of groundwater takes places through heavier rains (Rozanski 1985). Heavy rains indicate higher water level fluctuations, and hence higher neon excess. If precipitation with an average deuterium excess of 10‰ is reevaporated, the lighter 2H1H16O molecule would be enriched in the vapor phase, resulting in increased deuterium excess in precipitation.
Conclusions
A limestone-dolomite aquifer was studied using a multi-tracer approach (δ18O, δ2H, δ13C, 3H, 14C and noble gases) in the Tadla basin, Morocco. The Turonian aquifer is suitable for a groundwater-based paleoclimate reconstruction, representing the Holocene–late Pleistocene epochs. MRTs of groundwater were calculated using the Pearson radiocarbon model, taking into account the chemical and isotope hydrological parameters and contribution of freshwater. Stable isotope, noble gas and radiocarbon data were used to verify the existence of waters recharged during the late Pleistocene. Noble gas analyses were carried out to determine the temperature difference between the late Pleistocene and Holocene. In addition to the radiocarbon ages, the groundwater samples were clustered into two groups based on Heterr content, one with warm young Holocene recharged water samples and the other with cold old Pleistocene recharged samples. The NGTs derived for the Holocene samples gave an average of 25.2 ± 1.3 °C, while the older samples, representing the late Pleistocene, yield a mean NGT of 17.2 ± 1.7 °C. These ages correspond to glacial periods and the recharge temperatures obtained are significantly lower (8.6 ± 2.1 °C) than the Holocene temperatures in the Tadla basin. This paleotemperature reconstruction confirms previous groundwater-based studies from the African continent and its surroundings, where a deglacial warming of at least 5–7 °C has been inferred. A clear positive correlation can be observed between the neon excess and the terrigenous helium. The neon excess can be connected to increased recharge due to a higher amount of intermittent precipitation events indicating that the older groundwater recharged during a wetter period of the past. Further, a clear negative correlation can be found between the deuterium excess and the NGT, which means the higher the NGT the lower the deuterium excess is in the groundwater sample. This connection also supports a colder and wetter climate of the late Pleistocene and the warmer and wetter climate of early and mid-Holocene.
According to the analysis, these aquifers were recharged during interglacial wet periods and it appears that one part of these aquifers recharged during glacial wet periods. The results of this investigation suggest that a similar approach to groundwater studies can be used to address the nature of wet epochs in other regions of North Africa.
References
Abouelmagd A, Sultan M, Sturchio NC, Soliman F, Rashed M, Ahmed M, Kehew AE, Milewski A, Chouinard K (2014) Paleoclimate record in the Nubian Sandstone aquifer, Sinai Peninsula, Egypt. Quat Res 81(1):158–167
Aeschbach-Hertig W, Solomon DK (2013) Noble gas thermometry in groundwater hydrology. In: Burnard P (ed) The Noble gases as geochemical tracers. Springer, Heidelberg, Germany, pp 81–122
Aeschbach-Hertig W, Peeters F, Beyerle U, Kipfer K (1999) Interpretation of dissolved atmospheric noble gases in natural waters. Water Resour Res 35:2779–2792
Aeschbach-Hertig W, Peeters F, Beyerle U, Kipfer R (2000) Palaeotemperature reconstruction from noble gases in ground water taking into account equilibration with entrapped air. Nature 405:1040–1044
Aeschbach-Hertig W, Beyerle U, Holocher J, Peeters F, Kipfer R (2002) Excess air in groundwater as a potential indicator of past environmental changes. In: Study of environmental change using isotope techniques. IAEA, Vienna, pp 174–183
Aeschbach-Hertig W, El-Gamal H, Wieser M, Palcsu L (2008) Modeling excess air and degassing in groundwater by equilibrium partitioning with a gas phase. Water Resour Res 44:449–461
Andrews JN, Fontes J-C, Aranyossy J-F, Dodo A, Edmunds WM, Joseph A, Travi Y (1994) The evolution of alkaline groundwaters in the Continental Intercalaire aquifer of the Irhazer plain, Niger. Water Resour Res 30:45–61
Bartlett MG, Chapman DS, Harris RN (2006) A decade of ground–air temperature tracking at Emigrant Pass Observatory, Utah. J Clim 19(15):3722–3731
Berke MA, Johnson TC, Werne JP, Grice K, Schouten S, Damsté JSS (2012) Molecular records of climate variability and vegetation response since the late Pleistocene in the Lake Victoria basin, East Africa. Quat Sci Rev 55:59–74
Beyerle U, Rueedi J, Leuenberger M, Aeschbach-Hertig W, Peeters F, Kipfer R, Dodo A (2003) Evidence for periods of wetter and cooler climate in the Sahel between 6 and 40 kyr BP derived from groundwater. Geophys Res Lett 30(4):1173
Blaser PC, Coetsiers M, Aeschbach-Hertig W, Kipfer R, Van Camp M, Loosli HH, Walraevens K (2010) A new groundwater radiocarbon correction approach accounting for palaeoclimate conditions during recharge and hydrochemical evolution: the Ledo-Paniselian aquifer, Belgium. Appl Geochem 25(3):437–455
Bouchaou L, Michelot JL, Qurtobi M, Zine N, Gaye CB, Aggarwal PK, Marah H, Zerouali A, Taleb H, Vengosh A (2009) Origin and residence time of groundwater in the Tadla basin (Morocco) using multiple isotopic and geochemical tools. J Hydrol 379:323–338
Bouhlassa S (2010) Atlas of isotope hydrology – MOROCCO. AIEA, Durham, NC
Brahim YA, Bouchaou L, Sifeddine A, Khodri M, Reichert B, Cruz FW (2016) Elucidating the climate and topographic controls on stable isotope composition of meteoric waters in Morocco, using station-based and spatially-interpolated data. J Hydrol 543:305–315
Clark I, Fritz CI (1997) Environmental isotopes in hydrogeology. Lewis, Boca Raton
Dansgaard W (1964) Stable isotopes in precipitation. Tellus 16(4):436–468
Darling WG (2011) The isotope hydrology of Quaternary climate change. J Hum Evol 60:417–427. https://doi.org/10.1016/j.jhevol.2010.05.006
Darling WG, Edmunds WM, Kinniburgh DG, Kotoub S (1987) Sources of recharge to the basal Nubian sandstone aquifer, Butana region, Sudan. In: Isotope techniques in water resources development, vol 1987. International Atomic Energy Agency, Vienna, pp 205–224
de Menocal PB (2014) Marine sediment records of African climate change: progress and puzzles. In: Reference module in earth systems and environmental sciences, from treatise on geochemistry, vol 14, 2nd edn. Elsevier, Amsterdam, pp 99–108
Edmunds WM, Fellman E, Goni IB, McNeill G, Harkness DD (1998) Groundwater, palaeoclimate and palaeorecharge in the Southwest Chad Basin, Borno State, Nigeria. In: Isotope techniques in the study of environmental change. IAEA, Vienna, pp 693–707
Fontes J-C, Garnier JM (1979) Determination of the initial 14C activity of the total dissolved carbon: a review of the existing models and a new approach. Water Resour Res 15:399–413
Fontes JC, Gasse F, Andrews JN (1993) Climatic conditions of Holocene groundwater recharge in the Sahel zone in Africa. In: Isotope techniques in the study of past and current environmental changes in the hydrosphere and the atmosphere. IAEA, Vienna, pp 231–248
Gardner PM, Heilweil VM (2014) A multiple-tracer approach to understanding regional groundwater flow in the Snake Valley area of the eastern Great Basin, USA. Appl Geochem 45:33–49
Geyh MA (2000) An overview of 14C analysis in the study of groundwater. Radiocarbon 42:99–114
Guendouz A, Moulla AS, Edmunds WM, Shand P, Poole J, Zouari K, Mamou A (1998) Paleoclimatic information contained in groundwaters of the Grand Erg Oriental, North Africa. In: Isotope techniques in the study of environmental change. IAEA, Vienna, pp 555–571
Han LF, Plummer LN (2013) Revision of Fontes & Garnier’s model for the initial 14C content of dissolved inorganic carbon used in groundwater dating. Chem Geol 351:105–114
Heaton THE, Talma AS, Vogel JC (1986) Dissolved gas paleotemperatures and 18O variations derived from groundwater near Uitenhage, South Africa. Quat Res 25:79–88
IAEA, WMO (2014) Global network of isotopes in precipitation. GNIP database, IAEA, Vienna
Ingerson CW, Pearson FJ (1964) Estimation of age and rate of motion of ground-water by the 14C method. In: Recent researches in the field of hydrosphere, atmosphere, and nuclear geochemistry. Sugawara Festival Volume. Maruzen, Tokyo, pp 263–283
Ingram RGS, Hiscock KM, Dennis PF (2007) Noble gas excess air applied to distinguish groundwater recharge conditions. Environ Sci Technol 41:1949–1955
Klump S, Tomonaga Y, Kienzler P, Kinzelbach W, Baumann T, Imboden DM, Kipfer R (2007) Field experiments yield new insights into gas exchange and excess air formation in natural porous media. Geochim Cosmochim Acta 71(6):1385–1397
Kulongoski JT, Hilton DR, Selaolo ET (2004) Climate variability in the Botswana Kalahari from the late Pleistocene to the present day. Geophys Res Lett 31(10)
Loomis SE, Russell JM, Ladd B, Street-Perrott FA, Damsté JSS (2012) Calibration and application of the branched GDGT temperature proxy on East African lake sediments. Earth Planetary Sci Lett 357:277–288
Marah H (2007) Liquid scintillation low level tritium measurement in water. Phys Chem News (37):20–24
Martrat B, Grimalt JO, Lopez-Martinez C, Cacho I, Sierro FJ, Flores JA, Zahn R, Canals M, Curtis JH, Hodell DA (2004) Abrupt temperature changes in the Western Mediterranean over the past 250,000 years. Science 306(5702):1762–1765
Massmann G, Sültenfuss J (2008) Identification of processes affecting excess air formation during natural bank filtration and managed aquifer recharge. J Hydrol 359:235–246
Molnár M, Janovics R, Major I, Orsovszk J, Gönczi R, Veres M, Leonar AG, Castle SM, Lange TE, Wacker L, Hajdas I (2013a) Status report of the new AMS 14 C sample preparation lab of the Hertelendi Laboratory of Environmental Studies (Debrecen, Hungary). Radiocarbon 55(2):665–676
Molnár M, Rinyu L, Veres M, Seiler M, Wacker L, Synal HA (2013b) EnvironMICADAS: a mini 14 C AMS with enhanced gas ion source Interface in the Hertelendi Laboratory of Environmental Studies (HEKAL), Hungary. Radiocarbon 55(2):338–344
Mook WG (1980) Carbon-14 in hydrogeological studies. In: Fritz P, Fontes JC (eds) Handbook of environmental isotope geochemistry. Elsevier, Amsterdam 1:49–74
Mook WG (2000) Environmental isotopes in the hydrological cycle: principles and applications. In: International Hydrological Programme (IHP-V). Technical documents in hydrology, IAEA, Vienna and UNESCO, Paris
Papp L, Palcsu L, Major Z, Rinyu L, Tóth I (2012) A mass spectrometric line for tritium analysis of water and noble gas measurements from different water amounts in the range of microlitres and millilitres. Isot Environ Health Stud 48(1):494–511
Peeters F, Beyerle U, Aeschbach-Hertig W, Holocher J, Brennwald MS, Kipfer R (2003) Improving noble gas based paleoclimate reconstruction and groundwater dating using 20Ne/22Ne ratios. Geochim Cosmochim Acta 67:587–600
Pfahl S, Sodemann H (2014) What controls deuterium excess in global precipitation? Clim Past 10(2):771–781
Plummer LN, Glynn PD (2013) Radiocarbon dating in groundwater systems. In: Isotope methods for dating old groundwaters, chap 4. IAEA, Vienna, pp 33–90
Rinyu L, Molnár M, Major I, Nagy T, Veres M, Kimák Á, Wacke L, Synal HA (2013) Optimization of sealed tube graphitization method for environmental C-14 studies using MICADAS. Nucl Instrum Methods Phys Res, Sect B 294:270–275
Rozanski K (1985) Deuterium and oxygen-18 in European groundwaters: links to atmospheric circulation in the past. Chem Geol 52(3–4):349–363
Rudolph J, Rath HK, Sonntag C (1984) Noble gases and stable isotopes in 14 C dated palaeowaters from Central Europe and the Sahara. In: Isotope hydrology. IAEA, Vienna 1983:467–477
Saadi R, Túri M, Palcsu L, Marah H, Oum KH, Rinyu L, Molnár M, Futó I (2017) A potential groundwater aquifer for palaeoclimate reconstruction: Turonian aquifer, Tadla basin, Morocco. J Afr Earth Sci 132:64–71
Salem O, Visser JH, Dray M, Gonfiantini R (1980) Environmental isotopes used in hydrogeological study of north-eastern Brazil. In: Arid-zone hydrology: investigations with isotope techniques, panel proceedings series (1980). IAEA, Vienna, p 134
Solomon DK (2000) 4He in groundwater, Environmental tracers in subsurface hydrology. Springer, New York, pp 425–439
Stuiver M, Grootes P (2000) GISP2 oxygen isotope ratios. Quat Res 53(3):277–284
Stute M, Schlosser P (1993) Principles and applications of the noble gas paleothermometer. In: AGU monograph on climate change in continental isotopic, records, geophysical monograph, vol 78, pp 89–100
Stute M, Talma AS (1998) Glacial temperatures and moisture transport regimes reconstructed from noble gases and δ18O, Stampriet aquifer, Namibia. In: Isotope techniques in the study of environmental change. IAEA, Vienna
Stute M, Clark JF, Schlosser P, Broecker WS, Bonani G (1995) A 30,000 yr continental paleotemperature record derived from noble gases dissolved in groundwater from the San Juan Basin, New Mexico. Quat Res 43:209–220
Tammal M, Kili M, Gasmi H, El Mridekh A, El Mansouri B (2014) Modélisation multicouche du système aquifère du bassin de Tadla et le plateau des phosphates [Modeling multi-aquifer system of Tadla basin and plateau of phosphates]. Int J Innov Sci Res 6(2):172–180
Torgersen T, Stute M (2013) Helium (and other noble gases) as a tool for understanding long timescale groundwater transport. In: Isotope methods for dating old groundwater, chap 8. IAEA, Vienna
Varsányi I, Palcsu L, Kovács LÓ (2011) Groundwater flow system as an archive of palaeotemperature: noble gas, radiocarbon, stable isotope and geochemical study in the Pannonian Basin, Hungary. Appl Geochem 26(1):91–104
Vodila G, Palcsu L, Futó I, Zs S (2011) A 9-year record of stable isotope ratios of precipitation in eastern Hungary: implications on isotope hydrology and regional palaeoclimatology. J Hydrol 400:144–153
Wacker L, Christl M, Synal HA (2010) BATS: a new tool for AMS data reduction. Nucl Instrum Methods Phys Res, Sect B 268(7–8):976–979
Weyhenmeyer CE, Burns SJ, Waber HN, Aeschbach-Hertig W, Kipfer R, Loosli HH, Matter A (2000) Cool glacial temperatures and changes in moisture source recorded in Oman groundwaters. Science 287(5454):842–845
Wu J, Liu Z, Stuut JBW, Zhao Y, Schirone A, de Lange GJ (2017) North-African paleodrainage discharges to the Central Mediterranean during the last 18,000 years: a multiproxy characterization. Quat Sci Rev 163:95–113
Acknowledgements
The English editing of the manuscript by Prof. Timothy Jull is highly acknowledged.
Funding
Open access funding provided by MTA Institute for Nuclear Research (MTA ATOMKI). The research was supported by the European Union and Hungary, co-financed by the European Regional Development Fund through the GINOP-2.3.2-15-2016-00009 ‘ICER’ project.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
ESM 1
(PDF 761 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Túri, M., Saadi, R., Marah, H. et al. Paleotemperature reconstruction using environmental isotopes and noble gases in groundwater in Morocco. Hydrogeol J 28, 973–986 (2020). https://doi.org/10.1007/s10040-020-02121-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-020-02121-1