Introduction

The capture of groundwater by horizontally arranged screens is an old but often overlooked technique, as most textbooks focus on the much more common vertical wells. Horizontal wells (HWs), including radial collector wells (RCWs), covered drainage trenches and horizontal directionally drilled wells, are, from a hydraulic and economic point of view, an interesting alternative to vertical wells for a variety of hydrogeological situations, e.g. in thin aquifers. The focus here is RCWs pumping groundwater, although many developments of horizontal well techniques and models come from the oil industry.

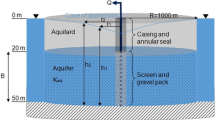
RCWs are generally comprised of a vertical reinforced concrete shaft (caisson) with horizontal well screens (laterals) projected out into the aquifer (Fig. 1). During operation, groundwater enters the well through the slots in the laterals and flows into the caisson, where one or more pumps are installed.

Fig. 1
figure 1

a Cross-section and b plan view of a radial collector well. Ll, Lf, Lbc are total, screened and closed lateral length, respectively; dc diameter of the caisson; Dc caisson depth; gp gravel pack thickness; ds diameter of lateral; H static head; h pumped head (©BGR)

Full size image

Collector wells are more expensive to build than vertical wells, but offer many benefits: practical experience and models have shown that collector wells distribute drawdown over a larger area than equivalent vertical wells and thus produce significantly smaller maximum drawdown (e.g. Huang et al. 2012), fouling of the well screen occurs at a much slower rate, and wells need less frequent cleaning. Collector wells are often used to induce recharge from surface water bodies and are installed close to rivers (Fig. 1), in some cases with laterals that extend beneath the river.

Practically all modeling techniques available in groundwater hydrology have been applied to HWs. Physical sandtank models of RCWs were constructed by Falcke (1962), Kotowski (1982, 1983, 1985, 1988), Chen et al. (2003), Birch et al. (2007) and Kim et al. (2008), of which the earlier studies derived empirical models which were upscaled to field dimensions. Kordas (1961), Milojevic (1961, 1963) and Debrine (1970) used electrical analog models. A myriad of analytical models exist, from the earliest models by Forchheimer (1886) and Polubarinova-Kochina (1955), to models adapted from vertical wells (e.g. Nöring 1953) and, finally, more recent models for predicting drawdown in anisotropic aquifers (e.g. Hunt 2005), well bore storage (e.g. Zhan and Park 2003) or interaction with surface water (e.g. Huang et al. 2011, 2012, 2015; Sun and Zhan 2006). Analytical element models of RCWs were developed by Patel et al. (2010) and Bakker et al. (2005). Several authors have computed numerical models of flow around RCWs (Bischoff 1981; Ophori and Farvolden 1985; Eberts and Bair 1990; Beljin and Losonsky 1992; Zhan et al. 2001; Cunningham et al. 1995; Luther and Haitjema 1999; Mohamed and Rushton 2006; Birch et al. 2007; Haitjema et al. 2010; Lee et al. 2010; Dimkić et al. 2011; Kelson 2012), of which some went beyond the classical assumption of linear laminar Darcy flow and included nonlinear laminar (Forchheimer) and turbulent flow.

The aim of this work is not to review all of these techniques (for a review, see Huang et al. 2012; Yeh and Chang 2013). Instead, the focus is two widely used analytical solutions for an infinite aquifer and the vertical well approximation, in comparison with field observations. The first analytical model (Hantush and Papadopulos 1962) is the most cited and one of the oldest in the literature, and the second (Williams 2013) is newer and less cited, but simple to apply. To the authors’ knowledge, the only comparison of an analytical model with field data in the literature is that of Huang et al. (2012), who compared their analytical model of an RCW next to a river with data from two pumping tests. They found a reasonably good agreement to their model in the caisson and in a single piezometer 20 m from the caisson, but poorer agreement in a second piezometer (>100 m from caisson), which they attributed to heterogeneities in the aquifer. There are also a few examples of field data being compared with more complex, numerical models able to incorporate turbulent flows in the laterals: Lee et al. (2012) were able to reproduce groundwater levels in a single piezometer during a pumping test carried out in an RCW next to a river and Mohamed and Rushton (2006) successfully modelled groundwater level in a number of piezometers around an HW in a shallow aquifer. In this study, a dense network of piezometers in the direct vicinity of two RCWs is used and flowmeter data from inside a lateral to investigate the applicability of more simple analytical models. Analytical models are often viewed with a degree of skepticism and rejected in favor of more complex, numerical models. Numerical models offer flexibility—for example, in assigning boundary conditions or including geological heterogeneity—which analytical models cannot represent. However, the ease with which analytical models can be applied means that they should not be overlooked. Here, the aim is to show how far the analytical approach can be simplified and address whether the main assumption of many analytical models—that of uniform flux along the lateral—is reasonable. The latter aim is approached by comparing the results of solutions using different boundary conditions against flowmeter data from inside a lateral with numerical models.

Methodology

Analytical models

The most frequently cited analytical model is that of Hantush and Papadopulos (1962). They represented the laterals as line sinks of uniform discharge, just as partially penetrating vertical wells had been treated previously (e.g. Hantush and Jacob 1955; Hantush 1957). Further assumptions include a limited drawdown (s < 0.25 H0), a small percentage of water release due to aquifer compaction, and that the caisson radius is significantly smaller than the lateral length (rc < < Ll). The drawdown for the ith of a group of i laterals after a long time of pumping—quasi steady state, valid for t > 2.5 b2/v´ and t > 5 (r2 + Li2)—is then:

$${s}_i=\frac{Q_i/{L}_i}{4\ \pi\ K\ b}\left\{\begin{array}{c}\alpha\ W\left(\frac{\alpha^2+{\beta}^2}{4v\hbox{'}t}\right)-\delta\ W\left(\frac{\delta^2+{\beta}^2}{4v\hbox{'}t}\right)+2{L}_i-2\beta \left({\tan}^{-1}\frac{\alpha }{\beta }-{\tan}^{-1}\frac{\delta }{\beta}\right)\\ {}+\frac{4\ \mathrm{b}}{\pi }{\int}_{n=1}^{\infty}\frac{1}{n}\ \left[L\left(\frac{n\ \pi\ \alpha }{b},\frac{n\ \pi\ \beta }{b}\right)-L\Big(\frac{n\ \uppi\ \delta }{b},\frac{n\ \pi\ \beta }{b}\Big)\right]\cos \frac{n\ \uppi\ z}{b}\cos \frac{n\ \pi\ {z}_i}{b}\end{array}\right\}$$
(1)

with

$$\alpha =r\ \cos \left(\theta -{\uptheta}_i\right)-{r}_{\mathrm{c}}\hbox{'}$$
(2)
$$\beta =r\ \sin \left(\theta -{\theta}_i\right)$$
(3)
$$\delta =r\ \cos \left(\theta -{\theta}_i\right)-l\hbox{'}$$
(4)
$$r=\sqrt{x^{2}+y^{2}}$$
(5)
$$l\hbox{'}={r}_{\mathrm{c}}\hbox{'}+{L}_i$$
(6)
$${r}_{\mathrm{c}}\hbox{'}={r}_{\mathrm{c}}+{L}_{\mathrm{bc}}$$
(7)
$$v\hbox{'}=\frac{K\ b}{S_{\mathrm{y}}}$$
(8)
$$L\left(a,\pm b\right)=-L\left(-a,\pm b\right)={\int}_0^a{K}_0\left(\sqrt{b^{2}+y^{2}}\right)\mathrm{d}y$$
(9)
$$W(u)={\int}_u^{\infty}\frac{{\mathrm{e}}^{-y}}{y}\mathrm{d}y$$
(10)

where K is hydraulic conductivity [L T−1], Qi is pumping rate of ith lateral [L3 T−1], Li is the length of the screened section of the ith lateral (Lf) [L], Lbc is the length of the closed section of the ith lateral [L], b is the thickness of a confined aquifer or initial water-saturated thickness of an unconfined aquifer [L], Sy is specific yield, rc is the radius of the caisson [L], N is the number of laterals, n is an integer counter (1, 2, 3, 4, …), r, z, Θ are cylindrical coordinates (z positive downwards), ri, zi, Θi are cylindrical coordinates of the ith lateral, x, y, z are rectangular coordinates, t is time since the start of pumping [T] and K0(u) is the zero-order modified Bessel function of the second kind. W(u) is the well function (Theis 1935) and can be approximated by

$$W(u)=-0.5772-\ln u+u-\frac{u^2}{2\times 2!}+\frac{u^3}{3\times 3!}-\frac{u^4}{4\times 4!}+\dots$$
(11)

With z = 0, the approximate drawdown of the piezometric surface is obtained. The 2D solution for average drawdown is derived by integrating with respect to z over the aquifer thickness and dividing by the aquifer thickness. The result is Eq. (1) without the integral term. At a distance from the center of the caisson r ≥ (rc + Li + b), the 2D and 3D solutions converge, as the integral in Eq. (1) approaches zero.

An elegantly simple analytical model was devised by Williams (2013), who distributed the total discharge, Q, of a lateral over a number of i point sinks (with Qi each) along the vertical projection of the well screen. The calculated transient drawdown represents that which would be measured in a fully penetrating observation well. The result is thus a 2D drawdown field, unlike the Hantush and Papadopulos (1962) model, with which drawdown can be calculated for any horizontal plane through the aquifer. The approach not only simplifies the calculation of drawdown around an HW/RCW dramatically, but also makes it easy to model wells of any shape, e.g. slant wells of which the horizontal and vertical well are just special cases. The approach has the additional advantage that it is not restricted to a uniform-flux boundary condition, i.e. the point sink strength could be adapted to mimic nonuniform inflow. In practice, however, it is unlikely that flowmeter data from inside the laterals would be available. For the individual point sinks, Williams (2013) adapted the Cooper and Jacob (1946) equation for transient flow to a fully penetrating vertical well:

$$s=\frac{2.3\ Q}{4\ \uppi\ K\ b}\ \log \left(\frac{2.25\ K\ b\ t}{S}\right)-\left(\frac{2}{n_{\mathrm{s}}}\right)\ \log \left({\mathrm{RP}}_1\times {\mathrm{RP}}_2\times {\mathrm{RP}}_3\times \dots \times {\mathrm{RP}}_{n_{\mathrm{s}}}\right)$$
(12)

where ns is the number of point sinks along the vertical projection of the well screen and RPx is the distance from an (arbitrary) observation point to point sink x [L]. It should be noted that Eq. (12) is valid under the same assumptions and simplifications as the Cooper and Jacob (1946) approximation. The goodness of fit of this model to the more explicit Hantush and Papadopulos (1962) solution depends on the number of point sinks employed.

Even simpler than the approach of Williams (2013) is the “ersatzradius” method (ersatz is German for replacement) adapted from analytical models developed for fully penetrating vertical wells. The so-called “ersatzradius” (analogous or equivalent well radius) was defined to replace the length of the HW, defined by the extension of its laterals, by an equivalent, fully penetrating vertical well. The drawdown around the HW in a confined aquifer at steady state is then given by the Thiem (1870) equation, assuming horizontal, radially symmetric flow in an isotropic island aquifer:

$$s=\frac{Q}{2\ \uppi\ K\ b}\ \ln \left(\frac{r_0}{r_{\mathrm{w}}}\right)$$
(13)

where r0 is the radius of the cone of depression (i.e. radial distance from the well center to a location where drawdown is zero [L]). rw is the radius of the (analog) well [L] and is defined as follows:

$${r}_{\mathrm{w}}={F}_{\mathrm{e}}\ {L}_{\mathrm{l}}$$
(14)

where Fe is a correction factor for the ersatzradius [L] and Ll is the (average) length of the laterals [L]. Nöring (1953) proposed:

$${r}_{\mathrm{w}}=0.66\ \frac{\sum {L}_{\mathrm{l}}}{n_{\mathrm{l}}}$$
(15)

where nl [−] is the number of laterals. Correction factors, Fe, suggested in the literature vary between 0.61 and 0.8 (Mikels and Klaer 1956; Hantush and Papadopulos 1962; McWhorter and Sunada 1977).

Alternatively, drawdown around an RCW can be approximated with a vertical well equation without a correction factor. Hantush (1964) stated that at a distance of r > 5 (rc + Li) from an RCW of at least two laterals, drawdown can be described with the Theis (1935) equation without correction. An advantage of this method over the Thiem method is that it allows for transient conditions.

$$s=\frac{Q}{4\ \uppi\ K\ b}\ W\left(\frac{r^2S}{4\ K\ b\ t}\right)$$
(16)

Field data

The Fuhrberger Feld is a rural area located in northern Germany, 30 km north−east of the city of Hanover. Besides agriculture and forestry, the Fuhrberger Feld is used to produce groundwater for the drinking water supply of Hanover. The Quaternary aquifer consists of unconsolidated, mostly sandy sediments with a thickness of 20–30 m, with interspersed thin layers of interglacial silts. The base of the aquifer consists of clay and glacial till. Depth to groundwater varies annually between approximately 0.5 and 2.5 m below ground. The hydraulic conductivity of the aquifer is approximately 45 m/day and its porosity is 0.3. Recharge rates range between 150 mm/a below forest and 250 mm/a below agricultural land. Detailed descriptions of the hydrogeology can be found in Böttcher et al. (1990), Frind et al. (1990), Franken et al. (2009) and Houben et al. (2018).

The first RCW of the Fuhrberger Feld well field, Fuhrberg 3, with eight laterals, was installed in 1964 and has not been altered since. The second well, Fuhrberg 1, was originally installed in 1958 with ten laterals, which were closed and replaced in 2011. The ten new laterals were installed on two levels, four being roughly 2 m higher than the remaining six. All information concerning the dimensions of the collector wells is given in Table 1. The hydraulic conductivity was calibrated manually to fit the observed data, and the calibrated values can also be found in Table 1.

Table 1 Description of the two radial collector wells
Full size table

The two collector wells are surrounded by observation wells at varying depths (10–26 m below ground) with screen lengths 1–10 m. The wells are in near-constant use, but flow rates vary. Prior to measuring groundwater level in the observation wells, the pumping rate had been held constant for 24 h and, therefore, steady-state conditions were assumed. This is a reasonable assumption given that pumping had been continuous and the hydraulic conductivity of the aquifer is high. The head in the caisson was used as a reference head, rather than static water level, due to the difficulties in determining the static water table in a well field. Maximum drawdown at Fuhrberg 3 is 10% of the aquifer thickness, but at Fuhrberg 1 it is 22%. Hantush and Papadopulos (1962) state that the drawdown must be ≤25% of aquifer thickness, when applying their equation to an unconfined aquifer. Fuhrberg 3 is, therefore, very close to the limit of applicability.

Turbulent losses along the laterals were estimated with the Darcy-Weisbach equation (Weisbach 1845) (see ‘Appendix’ for estimation of the friction factor):

$$\Delta h={f}_{\mathrm{D}}\frac{L_l}{D}\frac{u^2}{2g}$$
(17)

where ∆h is head loss [L], fD is the Darcy friction factor, g is gravitational acceleration [L T−2], u is the mean flow velocity in the pipe [L T−1] and D is the hydraulic diameter of the lateral [L].

The spot loss incurred as water flows from the laterals into the caisson was estimated as follows (Munson et al. 1998, cited in Bakker et al. 2005; Lee et al. 2010):

$$\Delta h=\frac{u^2}{2\ g}$$
(18)

The equation is derived from the Bernoulli equation by assuming u − > 0 within the caisson.

Numerical model

The numerical code FEFLOW (Diersch 2014) was used to test the assumption of uniform screen inflow. The 2D model comprises a regular, square 70 × 70 m grid (i.e. 0 ≤ x ≤ 70, 0 ≤ y ≤ 70) with a spatial discretization of 0.5 m and fixed head boundaries at y = 70 m and x = 70 m. The laterals were created with the well boundary condition and, as such, are effectively a series of point sinks with varying strengths. The other parameters can be found in Table 2.

Table 2 Parameters for numerical models in Fig. 4
Full size table

Results

Comparison of analytical models with field data

The models of Hantush and Papadopulos (1962) and Theis (1935) were compared with groundwater level observations around two RCWs in the Fuhrberger Feld well field. Figure 2a compares observed heads around Fuhrberg 3 against the models of Hantush and Papadopulos (1962) and Theis (1935). Hantush and Papadopulos’s (1962) 3D model is solved at a z plane equal to the average mid-point of the screened depth of the piezometers (10.7 m below ground). The angle at which the equation is solved has little effect on the result (< 0.01 m difference in head). There is a good fit between the observations and the Hantush and Papadopulos (1962) model (Fig. 2a). From ~30 m from the center of the caisson, the difference between the two analytical models is less than 10 cm, and at the tips of the laterals the more complex Hantush and Papadopulos (1962) model provides no advantage over the vertical well equation. Figure 2b shows the same comparison for Fuhrberg 1. The Hantush and Papadopulos (1962) model provides a good fit to the observations, apart from the two measurements furthest away from the well center (70 m from center), which are overestimated. The calibrated hydraulic conductivity is much smaller than that of Fuhrberg 3 (33 vs. 95 m/day), which could be artificially low because the drawdown is relatively large with respect to the saturated thickness (~22%). The hydraulic conductivity at Fuhrberg 1 is, however, closer to that previously estimated for the aquifer (45 m/day).

Fig. 2
figure 2

Observed head data against the Hantush and Papadopoulos (1962) analytical model and the Theis (1935) equation for a Fuhrberg 3 and b Fuhrberg 1 radial collector wells. Gradient in b refers to a hydraulic gradient south−north of 0.0076. Solid black line along x axis shows lateral length

Full size image

Whereas Fuhrberg 3 is on the edge of the well field with no direct neighbors, Fuhrberg 1 is within the well field and surrounded by other wells. The pattern in the observations suggests that the heads could be affected by these neighboring wells. If a hydraulic gradient in the direction south–north of 0.0076 obtained from Eq. (19) is superimposed over the observed data, the model is able to reproduce the pattern of the observations close to the caisson (Fig. 2b):

$$\Delta {h}_{\mathrm{lat}}=-\frac{y\ {q}_{\mathrm{y}}}{K}$$
(19)

where ∆hlat is the head “correction” from lateral groundwater flow and qy is the Darcy flux in the y direction.

The model is still unable to reproduce the two observations furthest away from the caisson, and this is likely because of the effect of other wells. Given this, the vertical well model is of little value here, as it provides a reasonable estimate of only the two groundwater levels ~50 m from the caisson.

The uniform-flux assumption

For the sake of mathematical simplicity, many RCW models, including that of Hantush and Papadopulos (1962), assume that the flux (discharge from the aquifer per unit length along the well) is uniformly distributed along the screen (e.g., Hantush 1964; Cleveland 1994; Zhan 1999; Zhan et al. 2001). It is generally agreed that the use of a uniform-head boundary to simulate an HW is closer to physical reality, but this boundary is difficult to incorporate in analytical studies (Rosa and Carvalho 1989). The few available flowmeter measurements in real and physical model wells show that the uniform-flux assumption is probably rarely valid. Krems (1972) used a flowmeter to measure flow along the length of two laterals of an RCW. He found that influx is highest at the tip of the lateral, being more than eight times higher than that close to the caisson wall and more than two times higher than the average flux (Fig. 3). Given that the Hantush and Papadopulos (1962) model compares well with field data (Fig. 2a), it is interesting to see how the uniform-flux boundary differs from uniform head or variable flux based on this field example.

Fig. 3
figure 3

Measured flow velocities and specific flow rates in two laterals of a radial collector well in Tegel-Scharfenberg, Berlin, Germany, in 1956 (modified after Krems 1972) (©BGR)

Full size image

To visualize the likely drawdown around the RCW in Fig. 3, the measured specific flow rates (lateral 10) were digitized and applied to four lateral arms in the 2D steady-state numerical model described in section ‘Numerical model’ and Table 2. Two further identical models with the same total pumping rate were created: in the first, the total pumping rate was distributed evenly among the point sinks, and, in the second, the total pumping rate was assigned to a single node at the caisson (x = 0, y = 0) and the laterals were represented with discrete features (i.e. a dual-continuum approach). The former demonstrates the uniform-flux boundary condition and the latter is an approximation of the uniform-head boundary condition. The Hagen−Poiseuille equation, which estimates head loss for laminar flow through a pipe, was applied to the discrete features. Turbulent pipe losses were not considered. In the uniform- and variable-flux cases, the cells in the bottom left corner were assigned a hydraulic conductivity of 1 × 10−4 m/day, creating a caisson of very roughly 1 m radius (imperfect because square grid cells were used); for the uniform-head approximation, discrete features were connected directly to the well node (Fig. 3b). All three models were appropriately converged: the average errors in hydraulic head were 2.1 × 10−5, 1.26 × 10−6 and 3.5 × 10−7 m for the constant-head, variable-flux and constant-flux models, respectively.

Figure 4 compares drawdown around an RCW for three boundary conditions along the laterals: uniform flux, uniform head and flux varying according to observed data. The boundary condition affects drawdown only between the laterals, with all three models converging just beyond the tips of the laterals. Although data from only a single RCW are used here, these results suggest that the uniform-flux and constant head boundaries are two extremes and that the reality is likely somewhere in between. This result was also changed by neither moving the boundaries further away from the well nor changing the hydraulic conductivity over three orders of magnitude. The fact that the drawdown distribution created from flowmeter data is not closer to the uniform-head case suggests that turbulent losses within the laterals, which were not considered here, are significant. Although an improvement on the vertical well approximation, the Hantush and Papadopulos (1962) model will likely overestimate maximum drawdown.

Fig. 4
figure 4

Hydraulic head (m) around four laterals of a radial collector well with a uniform-flux, b constant head and c variable-flux boundary conditions

Full size image

Vertical well approximation

The ersatzradius method is rather crude, as it simply replaces the well radius by an empirically corrected average lateral length; however, as can be seen in Fig. 2a, the Theis (1935) equation is capable of estimating drawdown around an RCW. The ersatzradius approach can be improved upon by assuming the correction factor is a linear function of the ratio of the radius of the caisson to the length of the lateral, that is:

$${F}_{\mathrm{e}}=a\ \frac{\left({r}_{\mathrm{c}}+{L}_{\mathrm{bc}}\right)}{L_{\mathrm{f}}}+b$$
(20)

where a and b are parameters to be calibrated, and the length of the unscreened lateral is added to the caisson radius. A script was written in Python for comparing drawdown against radial distance from the center of the caisson (directly above a lateral) for the ersatzradius and 2D Hantush and Papadopulos (1962) approaches. Parameters a and b were calibrated using the quasi-Newton optimisation method of Broyden, Flether, Goldfarb and Shanno implemented in the Scipy package (optimize.minimize; Nocedal and Wright 2006) by minimizing the root mean square error between the two methods for distances greater than 0.75 Ll, the point at which the solutions converge. The calibration was repeated for realistic collector well configurations: 6–12 laterals; lateral length 10–100 m; and combined caisson radius and unscreened lateral length 1–6 m.

Figure 5a shows a good correlation between (rc + Lbc)/Lf and Fe (r2 = 0.97) for the selected collector well configurations. The equation of the least squares regression line is as follows:

$${F}_{\mathrm{e}}=1.327\ \frac{\left({r}_{\mathrm{c}}+{L}_{\mathrm{bc}}\right)}{L_{\mathrm{f}}}+0.38$$
(21)
Fig. 5
figure 5

a Correlation between the ratio of the caisson radius and unscreened lateral length (rc + Lbc) to the length of the laterals (Lf) and the correction factor (Fe) and line of least squares. Dashed lines represent 95% confidence intervals for the mean Fe and 95% prediction intervals for a single future observation (Student’s t-distribution). b Dimensionless drawdown against distance from the center of the caisson (x) for an analytical model (Hantush and Papadopoulos 1962) and the ersatzradius method. “Calibrated Fe” refers to dimensionless drawdown calculated with Eq. (21). T transmissivity; Q pumping rate; s drawdown

Full size image

Whereas the correction factors in the literature apply for only a narrow range of caisson radii and lateral lengths, this new equation is able to mimic the 2D Hantush and Papadopulos (1962) analytical solution from radial distances of 0.75 Ll for a range of collector well setups (e.g. Fig. 5b). However, if this equation were used in practice with observed drawdown in the caisson set to the drawdown at rc + Lbc, the equation would likely overestimate drawdown. This is because the model was calibrated to a 2D analytical model with drawdown at rc + Lbc set equal to the maximum 2D drawdown—i.e. the drawdown that would be measured in a fully penetrating observation well at the face of the caisson—which is lower than drawdown inside the caisson. For the Fuhrberg sites, this error would be less than 5%; however, the error would increase above 10% for thick aquifers (>60 m) or short laterals (ca. <30 m, dependent on rc + Lbc).

Hantush (1964) stated that at a distance of r > 5 (rc + Lbc + Lf) from an RCW of at least two laterals, drawdown can be described with the Theis (1935) equation without correction. If laterals are arranged symmetrically around a caisson, as the number of laterals increases, the drawdown should approach that which would be observed around a vertical well. An RCW with an infinite number of laterals is simply a vertical well, if viewed in 2D. For the RCW described in Table 3, the Theis (1935) and 2D Hantush and Papadopulos (1962) models converge at the tips of the laterals (Lf = 40 m; Fig. 6a). Moreover, Fig. 6b shows the relationship between the number of laterals and the difference between the two models at the tip of the lateral. For RCWs with at least six laterals the error in dimensionless drawdown becomes very small. As can be seen in Fig. 6b, the error is insensitive to the configuration of the RCW, the aquifer thickness and the hydraulic conductivity.

Table 3 Parameters for Hantush and Papadopulos (1962), Williams (2013) and Theis (1935) comparisons in Figs. 6 and 7
Full size table
Fig. 6
figure 6

a Drawdown around a radial collector well in a confined aquifer according to the 2D Hantush and Papadopoulos (1962) equation and the Theis (1935) equation for drawdown around a fully penetrating vertical well. Drawdown is along the y = 50 m plane in Fig. 7. b Difference in dimensionless drawdown between Hantush and Papadopoulos (1962) and Theis (1935) equations at the tip of the lateral for different numbers of laterals. Parameters are listed in Table 3

Full size image

The choice of appropriate model, of course, depends on the question being asked. Whereas the 3D Hantush and Papadopulos (1962) model is likely most appropriate for estimating the maximum drawdown, simply replacing the RCW with a fully penetrating vertical well would be appropriate for simulating the impact of an RCW or HW on the aquifer groundwater head field. For estimating aquifer parameters in a pumping test, if observation wells are not in the direct vicinity of the well, the Theis (1935) equation could be used.

Software tool for analytical models

The complexity of the 3D Hantush and Papadopulos (1962) model probably deters many practitioners working with HWs from using it; therefore, a simple piece of software, called HORI, was created from the scripts written for this study. Although written in MATLAB (MATLAB 2016a, The MathWorks, Inc., Natick, MA, USA), a MATLAB license or knowledge of programming is not required to use the software, provided that the user downloads a runtime from the MATLAB homepage (MathWorks 2019). A graphical user interface allows the user to implement not only the models of Hantush and Papadopulos (1962) in 2D or 3D, but also Williams’s (2013) model for an RCW or slant well. Help can be found by clicking on the ‘info’ button. The software is freely available (Collins 2020).

Figure 7 shows a comparison of the 2D Hantush and Papadopulos (1962) and the Williams (2013) methods in a confined aquifer, calculated with HORI (see Table 3 for parameters). For the Williams (2013) approach, the total pumping rate was distributed evenly among 20 point sinks along each lateral. The two methods produce almost identical drawdown distributions, differing slightly only very close to the caisson.

Fig. 7
figure 7

Drawdown (m) around a radial collector well in a confined aquifer according to Hantush and Papadopoulos (1962) (solid line) and Williams (2013) (dotted line). Parameters can be found in Table 3. The laterals are represented by thick solid lines

Full size image

Conclusions

Comparisons in the literature between analytical models of HW/RCWs and field data are limited, and, to the authors’ knowledge, there have been no comparisons of flowmeter data from inside an RCW with models. It has been shown here that these analytical models can perform well. Numerical modelling with flowmeter data suggests that the uniform-flux boundary condition is a reasonable assumption and representing the lateral as a constant-head boundary would not necessarily improve modelled heads close to the caisson, as previously assumed. It should be noted, however, that the field data in this paper all relate to radial collector wells and that the uniform-flux boundary may break down in very long horizontal or slant wells. Future work could investigate the appropriateness of using the Williams (2013) model in these cases. It has also been shown that approximating drawdown around an RCW with a vertical well equation is probably sufficient in some circumstances. In particular, the Theis (1935) vertical well equation is suitable for estimating aquifer properties from a pumping test, if observed groundwater levels at r > Lf + rc are available and drawdown is not affected by other wells. A MATLAB application with graphical user interface, HORI, has been developed to aid practitioners in calculating drawdown around an RCW with the Hantush and Papadopulos (1962) and Williams (2013) methods.