Abstract
The need for regional-scale integrated hydrological models for the purpose of water resource management is increasing. Distributed physically based coupled surface-subsurface models are usually complex and contain a large amount of spatio-temporal information that leads to a relatively long forward runtime. One of the main challenges with regard to regional-scale inverse modeling relates to parameterization and how to adequately exploit the information embedded in the existing observational data while avoiding parameter identifiability issues. This study examined and compared the calibration of a “highly parameterized” model with a “classical” unit-based parameterization scheme in which the dominant geological features were assumed to be known. The physically based coupled surface-subsurface model MIKE SHE was used for conducting the study of five river basins (4,900 km2) in central Jutland in Denmark, characterized by heterogeneous geology and a considerable amount of groundwater flux across topographical catchment boundaries. The results indicated that introducing more flexibility in the parameter estimation process through a regularized approach significantly improved the model performance, in particular head and water balance errors. The highly parameterized calibration results additionally provided very useful insights into the model deficiencies in terms of conceptual model structure and incorrectly imposed boundary conditions. Furthermore, the results from data-worth analysis indicated that the highly parameterized model has more effectively utilized the information in the dataset compared to a traditional unit-based calibration approach.
Résumé
Le besoin de modèles hydrologiques intégrés à l’échelle régionale pour la gestion des ressources en eau est. en augmentation. Les modèles distribués à base physique, couplant surface-souterrain, sont souvent complexes et contiennent un volume d’informations spatio-temporelles important qui entraine des calculs directs relativement longs. Un des principaux défis avec les modèles régionaux inverses concerne la paramétrisation et comment exploiter de manière adéquate l’information comprise dans les données observées existantes tout en évitant les questions d’identification des paramètres. Cette étude a examiné et comparé la calibration d’un modèle « hautement paramétré » avec un schéma de paramétrisation « classique » basé sur des unités dans lesquels les caractéristiques géologiques dominantes ont été supposées connues. Le modèle à base physique couplant les écoulements de surface et souterrains, MIKE-SHE, a été utilisé pour mener l’étude de cinq bassins versants de cours d’eau (4,900 km2) dans la région centrale du Jutlan au Danemark, caractérisée par une géologie hétérogène et un écoulement d’eau souterraine considérable dans les limites topographiques des bassins versants. Les résultats ont indiqué qu’introduire plus de flexibilité dans le processus d’estimation de paramètre au travers d’une approche de régularisation améliorait de manière significative la performance du modèle, en particulier les erreurs de charges hydrauliques et de bilan d’eau. Les résultats d’une calibration hautement paramétrée ont donné en sus des connaissances très utiles à propos des insuffisances du modèle, en termes de structure de modèle conceptuel et des conditions aux limites imposées de manière incorrecte. En outre, les résultats d’analyses de données de valeur ont indiqué que le modèle hautement paramétré a utilisé plus efficacement l’information du jeu de données en comparaison à l’approche de calibration traditionnelle basée sur les unités.
Resumen
La necesidad de modelos hidrológicos integrados a escala regional para la gestión de los recursos hídricos es cada vez mayor. Los modelos distribuidos físicamente acoplados superficie-subsuperficie son generalmente complejos y contienen una gran cantidad de información espacio-temporal que conduce a un tiempo de ejecución hacia delante relativamente largo. Uno de los principales desafíos con respecto a la modelización inversa a escala regional se refiere a la parametrización y a cómo explotar adecuadamente la información contenida en los datos observacionales existentes, evitando al mismo tiempo los problemas de identificabilidad de los parámetros. Este estudio examinó y comparó la calibración de un modelo “altamente parametrizado” con un esquema de parametrización “clásico” basado en unidades en el que se suponía que se conocían las características geológicas dominantes. El modelo físicamente acoplado superficie-subsuperficie MIKE SHE se utilizó para realizar el estudio de cinco cuencas hidrográficas (4,900 km2) en Jutlandia central en Dinamarca, caracterizadas por una geología heterogénea y una cantidad considerable de flujo de agua subterránea a través de los límites topográficos de las cuencas. Los resultados indicaron que la introducción de una mayor flexibilidad en el proceso de estimación de parámetros mediante un enfoque regularizado mejoró significativamente el rendimiento del modelo, en particular los errores en las cargas hidráulicas y en el balance hídrico. Los resultados de calibración altamente parametrizados proporcionaron además una visión muy útil de las deficiencias del modelo en términos de la estructura conceptual del modelo y de las condiciones de contorno impuestas incorrectamente. Además, los resultados del análisis del valor de los datos indicaron que el modelo altamente parametrizado ha utilizado más eficazmente la información del conjunto de datos en comparación con un enfoque de calibración tradicional basado en unidades.
摘要
面向水资源管理的区域尺度综合水文模型的需求日益增加。基于物理基础的分布式地表水地下水耦合模型通常很复杂,模型运行要输入大量的时空信息,在建模前需要相对长时间的准备。区域尺度反演模拟的主要挑战之一是参数化问题以及如何充分利用现有观测数据信息以避免参数识别出现相关问题。本研究检验并比较了“高度参数化”模型的校准与“经典”基于单元的参数化方案,其中假设主要地质条件已知的。采用基于物理基础的地表水地下水耦合模型MIKE SHE对丹麦中部日德兰中部的5个流域(4,900平方公里)开展研究,其特点是非均质地层和跨地形流域边界的相当数量的地下水径流。结果表明,通过正则化方法参数估计过程显得具有更大灵活性,极大改善了模型性能,特别是水头和水平衡误差。高度参数化的校准结果还在概念模型结构和不合适的边界条件处理方面的模型缺陷提供了相关分析途径。此外,数据价值分析结果表明,与传统的基于单元的校准方法相比,高度参数化模型更有效地利用了数据集信息。
Resumo
A necessidade de modelos hidrológicos integrados de escala regional para fins de gestão de recursos hídricos está aumentando. Os modelos distribuídos de subsuperfície-superfície acoplados com bases físicas são geralmente complexos e contêm uma grande quantidade de informações espaço-temporais que levam um tempo relativamente longo de execução. Um dos principais desafios no que diz respeito à modelagem inversa em escala regional refere-se à parametrização e como explorar adequadamente as informações incorporadas nos dados observacionais existentes, evitando problemas na identificação de parâmetros. Este estudo examinou e comparou a calibração de um modelo “altamente parametrizado” com um esquema de parametrização baseado em unidades “clássicas” em que as feições geológicas dominantes foram assumidas como sendo conhecidas. O modelo de superfície-subsuperfície acoplado com bases físicas MIKE SHE foi usado para conduzir o estudo de cinco bacias hidrográficas (4,900 km2) na região central da Jutlândia, na Dinamarca, caracterizado por geologia heterogênea e uma considerável quantidade de fluxo de águas subterrâneas através dos limites topográficos das bacias hidrográficas. Os resultados indicaram que a introdução de maior flexibilidade no processo de estimativa de parâmetros através de uma abordagem regularizada melhorou significativamente o desempenho do modelo, em particular os erros de cargas hidráulicas e balanço hídrico. Os resultados de calibração altamente parametrizados também forneceram compreensões muito úteis sobre as deficiências do modelo em termos de estrutura de modelo conceitual e condições de contorno impostas incorretamente. Além disso, os resultados da análise de dados indicam que o modelo altamente parametrizado utilizou mais efetivamente as informações no conjunto de dados, em comparação com uma abordagem tradicional de calibração baseada em unidades.
Similar content being viewed by others

Avoid common mistakes on your manuscript.
Introduction
Globally, water resources are under increasing pressure due to rapidly growing demands and climate change that has led to an increased competition between ecosystems and socio-economic sectors (UNESCO 2012). In many regions, groundwater is the main source of water supply, for instance, Denmark relies on groundwater abstraction for its entire supply (Højberg et al. 2013). Thus, groundwater management should aim at finding a balanced solution between sustainability and socioeconomic as well as environmental impacts on all groundwater-dependent ecosystems. As referred to by Jakeman et al. (2016), this requires “thinking beyond the aquifer” and considering surface water, economics, energy, climate, agriculture and environmental issues when managing water resources. Moreover, there is a growing demand for management at the regional scale, since only at this scale can the economic, environmental and social problems that are linked to water resources be analyzed and solved in an integrated approach (Barthel and Banzhaf 2016).
Hydrological models are essential tools to support sustainable-water-resources management (Abbaspour et al. 2015) and integrated hydrological models, including physically based dynamically coupled groundwater and surface-water models, are potentially the most suitable tool for integrated-water-resources management (Refsgaard and Henriksen 2004). However, the application of such models, in particular at regional scale, is limited by the understanding of the physical system, data availability, and computational capacity (Barthel and Banzhaf 2016). Another important challenge with regard to integrated-water-resource-management, in particular at the regional scale, is that most of the currently existing hydrological models do not contain dynamic physically based coupling between surface water and groundwater or unsaturated zone and evapotranspiration processes (Jing et al. 2017). Even if the groundwater component is included in the models, they are often calibrated using only surface-water observations (Barthel 2014) or applied under a steady-state assumption (Sonnenborg et al. 2003; Meyer et al. 2018), mainly due to the high computational burden of transient description. The importance of considering dynamic groundwater flow for the proper representation of the hydrological processes at the catchment scale has been emphasized by many researchers (e.g., Brunner et al. 2008; Ghasemizade and Schirmer 2013; Jiang et al. 2017).
Regional-scale groundwater-flow models, in contrast to surface-water models, do allow for an estimation of subsurface flow between topographical subcatchments, which are typically defined as independent in surface hydrology. In some regions, groundwater flow across topographical boundaries constitutes a significant part of the water budget and, as it is impossible to measure, its quantification requires modeling.
A major challenge in regional-scale integrated-surface–subsurface modeling regards the parametrization and optimization. The classical approach is to build a simplified unit-based hydrogeological model based on the available geological information and to identify the optimal parameter values for each unit through model calibration, while maintaining the predefined hydrogeological structure. Another approach is to utilize pilot points (De Marsily et al. 1984) as a spatial parameterization scheme to increase flexibility in the distribution of parameters while increasing the degrees of freedom and thereby the computational burden (Doherty 2003; Fienen et al. 2009; Doherty et al. 2010b). Pilot points can also be applied as a supplement to the traditional unit-based calibration, where major predefined geological units are preserved, while some degree of spatial variability is allowed within each unit.
In this study, a transient, coupled subsurface–surface water flow model for five river catchments in the central part of Jutland in Denmark has been constructed and calibrated in a multi-objective framework. The Central Jutland Catchment (CJC) is characterized by heterogeneous geology, groundwater-dominated streams and a considerable amount of groundwater flow across topographical catchment boundaries. The land use type in the region is predominantly agriculture with extensive irrigation by groundwater. The presence of a west–east regional groundwater flux across the hydrological boundary of the subcatchments has previously been reported for this region (Højberg et al. 2013); however, so far it has not been quantified.
The primary objective of the study is to investigate the suitability of a pilot-point-based optimization scheme across the entire model domain in comparison to a traditional unit-based approach. This is addressed by evaluating the model performances, the degree to which the parametrization schemes utilize the available observational data set, the sensitivity to different weighting schemes and the effect it has on internal subsurface fluxes. A limitation to the traditional unit-based parametrization approach is that its ability to correct structural errors in the geological model or boundary conditions is constrained by too few parameters (Doherty and Welter 2010). The predefined aggregation of uniform hydraulic conductivity (K) values within a unit can significantly limit the ability of the calibration process to utilize the information available in an abundant observational dataset. In contrast, the pilot-point-based parameterization method, while allowing a large degree of freedom, requires precaution regarding overfitting and interpretation of parameters identifiability issues. The current study evaluates a novel combination of a highly parameterized, multi-objective pilot point approach and a transient regional scale surface-subsurface modelling scheme. The hydraulic conductivity field obtained through this pilot-point-based optimization can guide the model building process and help identifying deficiencies in the unit-based approach while utilizing the information content in the observational data to a higher degree.
Methods
Study area and observation data
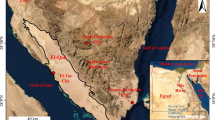
The study area extends over an area of approximately 4,900 km2 in the central part of Jutland in western Denmark (Fig. 1). The hydrological catchment comprises five river catchments with the rivers Karup, Storaa and Skjern flowing towards the west, while the rivers Gudenaa, and Haldsoe flow towards the north-east (Fig. 1b). The topography is characterized by a north–south-oriented divide (Fig. 2) separating the westward flowing and north-eastward flowing rivers. The north–south-oriented topographical divide corresponds to the maximum advancement of the glacier front during the latest glaciation period. The elevation ranges from 2 m asl in the west and north east to 162 m asl along the topographical divide in the central parts. The mean annual temperature is 8.3 ̊C, and the land use in the catchment comprises agriculture (65%), forest (19%), urban (6%) and others (10%). Irrigation is more widespread in the western part of the domain, which is dominated by sandy sediments. Precipitation data used in this study are based on daily 10-km-gridded data, and reference evapotranspiration and temperature data used for the calculation of actual evapotranspiration (ET) by the model are based on 20-km-gridded cells, all provided by the Danish Meteorological Institute (DMI). Observation data consist of groundwater level data from 2,450 wells (Fig. 1a), discharge measurements at 24 locations (Fig. 1b), and abstraction permissions from 4,513 irrigation wells (Fig. 1b). The long-term discharge–rainfall ratios calculated for all discharge stations regardless of their time series length are shown in Fig. 2. Very different ratios varying between 0.2 west and 0.65 east of the topographical divide are observed. This dissimilarity in the ratios cannot be explained by a difference in actual evapotranspiration, as remote-sensing-based estimates show lower evapotranspiration in the west compared to the east (Mendiguren et al. 2017). This strongly suggests that there is a significant groundwater flow across the north–south topographical divide from west to east in this region.
Geological, hydrological and numerical models
The geological model of the CJC is comparable to the one used in the National Water Resource Model of Denmark (DK model; Henriksen et al. 2003). The model has been developed based on a voxel-based geological conceptualization, where the subsurface is discretized into a 1,000 × 1,000 × 10-m grid and a geological unit is assigned to each grid element. The geology is classified into five major units: Quaternary sediments are classified into sand and clay, and pre-Quaternary sediments into quartz sand, mica sand, and clay (Stisen et al. 2012). The geological model is subsequently translated into the hydrological model with four computational layers over the vertical and a horizontal grid size of 500 × 500 m. The uppermost computational layer has a constant thickness of 3 m, whereas the computational layers below have varying spatial thicknesses, depending on the geological configuration. The boundary condition for the subsurface is considered to be a no-flow boundary and corresponds to the topographical divide, while no restriction is applied to the internal subsurface flow between subcatchments. The simulation period is 1990–2007. The period 1990–2000 is used as a warm-up period and the calibration period is 2000–2007.
The model code used in this study is the MIKE SHE modeling system (Abbott et al. 1986). MIKE SHE is an integrated physically based and distributed hydrological model code, which considers all the major terrestrial processes of the hydrological cycle and their interactions including precipitation, evapotranspiration, surface runoff, groundwater recharge, abstraction and irrigation, drainage flow, groundwater flow and river flow (Højberg et al. 2015; Henriksen et al. 2003; Stisen et al. 2012). The model system allows for different formulations of the individual components. The current model setup is based on a three-dimensional (3-D) groundwater flow module coupled with a two-layer water balance module for one-dimensional (1-D) unsaturated flow. The unsaturated zone is divided into an upper zone representing the root zone from where evapotranspiration (ET) can occur and an underlying zone (Yan and Smith 1994). The amount of water available for evapotranspiration and recharge is respectively controlled by the soil hydraulic parameters and the root zone parameters (Butts and Graham 2005). The spatial and seasonal variation of the applied irrigation is not known and is thus simulated by an irrigation module that is part of the modelling system. The scheduling and the amount of applied irrigation is calculated based on the estimated soil water deficit of the different crop types which varies depending on the soil characteristics, the soil moisture status of the root zone, and the climate (Stisen et al. 2011). The river routing is simulated by applying the kinematic routing method and using the MIKE HYDRO code integrated into MIKE SHE (Zhang and Ross 2015).
Calibration methodology
The calibration framework used in this study is based on the nonlinear gradient-based local optimization tool PEST using the Gauss-Marquardt-Levenberg algorithm (Doherty and Hunt 2010a). Two main calibration approaches have been pursued: (1) the unit-based calibration approach in which each hydrostratigraphic unit is assumed to have uniform hydraulic properties: the “classical” calibration approach, (2) the pilot-point-based calibration approach, which introduces pilot points in the individual units where the hydraulic properties are estimated: the “highly parameterized” approach.
Unit-based calibration
The unit-based calibration approach is in line with the parameterization scheme which is applied to the DK model (Højberg et al. 2015). In this approach, the geological information achieved from the geological model is translated and categorized into a limited number of hydrostratigraphic units. The values of the hydraulic properties of each unit are determined by calibration. The unit-based approach strives to use a small number of parameters for the calibration purpose (Doherty et al. 2010a).
Based on a sensitivity analysis, which has been performed prior to calibration, 13 parameters have been chosen for the calibration. Seven of these parameters are the horizontal hydraulic conductivity of each unit with their corresponding vertical hydraulic conductivity tied to the horizontal value with a ratio of 1 to 10. Other calibration parameters are the water deficit factor for irrigation control, leakage coefficient for stream–aquifer interaction, drainage time constant and depth, and root depth. All parameters used for the unit-based calibration approaches are listed in Table 1.
Pilot point calibration and regularization techniques
The pilot point calibration approach is considered to be a tradeoff between estimation of the parameter values at each individual grid of a model and estimation of the parameter values for a few predefined zones or units (Doherty et al. 2010b). In this approach the hydrogeologic properties, most commonly hydraulic conductivity, are estimated in the inverse modeling process at pilot points distributed in the model domain and subsequently interpolated throughout the grid (Doherty 2003). By applying pilot-point-based calibration a great flexibility is added to the parameter estimation process; however, without proper care, overfitting, nonunique solutions, and longer calibration time may occur due to the estimation of higher numbers of parameters (Fienen et al. 2009). The introduction of regularization can constrain the optimization process and provide stability into the parameter estimation (Moore and Doherty 2006). Regularization falls into two broad categories: Tikhonov regularization and subspace regularization. In Tikhonov regularization, the geological knowledge can be incorporated as prior information into the parameter estimation, which allows the inclusion of expert knowledge on parameter values and their spatial variability. Mathematically, the prior information adds additional constraints into the estimation process and can transform an ill-posed problem to a well-posed one; hence, a unique solution to the problem can be achieved (Doherty 2015). Employing the Tikhonov regularization becomes more necessary when the information available for the parameter estimation is limited. Although Tikhonov regularization can provide more trustworthy estimated values, numerical instability can still occur during the calibration process (Doherty et al. 2010a). The numerical stability can be ensured by applying the truncated singular value decomposition (SVD) regularization (Tonkin and Doherty 2005). Based on the weighted Jacobian matrix (parameter sensitivity matrix), the insensitive and correlated parameters (calibration null space) are truncated from the estimable parameters (calibration solution space; Doherty et al. 2010a); however, the high computational burden remains as a limitation of the pilot point method, especially for transient integrated models. The computational efficiency of the SVD process can be increased by using SVD-Assist (SVDA; Tonkin and Doherty 2005) in which the Jacobian matrix for all the parameters is calculated just once at their initial values to define the solution and null subspace. Based on this Jacobian matrix, the so-called “super parameters”, which are linear combinations of sensitive and uncorrelated base parameters, are formed (Anderson et al. 2015). The number of “super parameters” is normally much fewer than the base parameters; therefore, a significant reduction in the parameter estimation process can be obtained (Doherty 2015). This procedure is based on the linearity assumption of the parameter estimation, and its validity can be evaluated by reformulation of the “super parameters” at any iteration intervals (Anderson et al. 2015).
The pilot-point-based-calibration approach used in this study is based on the geological knowledge available from the DK model in the form of the hydrostratigraphic units and their associated initial hydraulic conductivity values combined with the flexibility of pilot points in the parameter estimation process. In this setup, 205 pilot points are placed in each of the four computational layers resulting in 820 pilot points with regular 5-km spacing (Fig. 1a). Additional parameters common to the unit-based approach have been subject to calibration as well (Table 1). Based on the Jacobian matrix of all the base parameters at their initial values, a total of 350 “super parameters” have been defined for the SVDA estimation process. Tikhonov regularization was briefly explored in the early stages of the study in combination with SVD-Assist, but the balance between observation fit and reasonable parameter fields using only SVD-Assist was adequate, obviating the need for additional regularization. In addition, it was desired to explore which K field distribution the pilot point optimization would suggest based on the observation information and without any a priori preference to either uniformity or the initial K field. Interpolation of the values between pilot points is performed using the kriging method based on an exponential variogram model and a nugget of zero.
Parameter set
The main parameter groups describing the hydrological conditions of the study area in both calibration approaches include hydraulic conductivity, drainage characteristics, stream-aquifer leakage coefficient, and available water content for evapotranspiration (Table 1). Hydraulic conductivity in the unit-based calibration approach is categorized into seven hydro-faces units. The distribution of each of these units differs from the classical zones in which there is a piecewise constancy. In the applied unit-based parameterization scheme, a conductivity unit is not required to be a continuous zone, though the value is the same across the whole catchment for the individual unit. In contrast, a spatial variation of the hydraulic conductivity within the unit is allowed for the pilot point approach.
In MIKE SHE code, drainage flow represents both natural and artificial drainage and is activated whenever the simulated water table rises above a specified level (Zhou et al. 2013). The drainage level is a specified parameter, which in this study is set to 0.5 m below ground throughout the catchment. The drainage time constant is assumed to be a semidistributed parameter with one value specified for the western part and another one for the eastern part. Drainage water is routed to the nearest surface-water bodies using a linear reservoir description. The drainage time constants have been included in both calibration approaches. The stream–aquifer interaction in the MIKE SHE model is defined by the leakage coefficient, which is considered uniform for all stream segments.
The available water content (AWC) controls the simulated actual evapotranspiration (ET). AWC is determined by the root depth, water content at field capacity and wilting point. The actual ET is determined as a fraction of reference ET based on the level of soil moisture in the root zone. In this study, the root depth has been defined as the only free parameter for the calibration, while the other parameters are given physically realistic values according to the soil type (Stisen et al. 2012). The seasonal variation of root depth is parametrized based on literature values and experience from the DK Model for the individual vegetation types (Højberg et al. 2015). In the model calibration process, all initial ratios in root depth between vegetation types are maintained and all root depths are scaled uniformly.
The simulation of the irrigation amount in the MIKE SHE model is driven by the water demand of the different crops, implying that irrigation is applied when the water deficit in the root zone drops below a certain threshold. The soil moisture deficit threshold at which irrigation starts or ends is the main controlling parameter. This parameter has been selected for calibration in both approaches.
Objective functions
Calibration by inversion techniques involves minimization of a weighted model-to-measurement misfit, formulated in an objective function (Skahill and Doherty 2006). In a water-resource management context, models are usually designed for multiple purposes; therefore, by applying a multiple-objective calibration approach, the models are simultaneously tuned towards the different aspects for which they are designed (Højberg et al. 2013; Stisen et al. 2018). In this study the total objective function (Фt) comprises five objective functions (Ф). These Ф components are based on three different observation data sets: stream discharge, hydraulic head, and aggregated irrigation records. Table 2 lists the Ф components and their contributions to the total Фt in different calibration approaches. The ME–head (Eq. 1) represents the mean simulation error for all 2,450 observation wells (Fig. 1a).
The Nash-Sutcliffe model efficiency coefficient (NSE; Eq. 2), and water balance error (WBE; Eq. 3) are based on 24 daily discharge stations:
The base flow index (BFI; Gustard et al. 1992) is calculated as the ratio of the area below the separated base flow line to the total area below the hydrograph (Riis et al. 2008). The index is based on 22 discharge stations as two stations did not meet the observational consistency criteria for BFI. As stated by Gupta et al. (2009), NSE tends to emphasize peak flows and underemphasize low flows. To balance this effect, BFI and WBE objective functions were also included as components of Фt. Furthermore, to ensure a correct simulation of the overall irrigation amounts and inter-annual variability in the area the RMSEIrr objective function (Eq. 4) is included in Фt as well. The irrigation information used in this objective function is the estimated annual values of irrigation abstraction provided by different municipalities and is thus aggregated both in space and time.
To balance the spatial and temporal distribution of head observations for the parameter estimation, a systematic weighting strategy is applied. Concerning the temporal distribution of the head observations, it should be noted that in the ME_head objective function, each observation well is represented only once by the mean residual even though the observation well might contain several observations. For each well, this mean residual is calculated external to PEST and the “observation” for the well provided in PEST is 0 (zero), as the target is a mean error of zero. The groundwater head observation wells further tend to be spatially clustered due to a higher density of wells in urban areas, around large infrastructures and in groundwater abstraction zones. Due to uneven distribution of the head observations in time and space, it is desired to weight each observation individually in order to acknowledge the value of time series and to avoid overfitting to spatial clusters of wells. In the applied weighting procedure, the spatial density of observations, defined as the number of observations in a radius of 2,500 m around each observation well, is calculated and wells are grouped according to their density. Likewise, wells are also grouped according to the number of observations in their time series. Subsequently, weights for each observation well have been assigned as a combination of their spatial density and temporal frequency. Wells with more frequent time series receive higher weights relative to the wells that only contain one or few measurements. This approach supports the idea that time series with higher frequency of measurements during the whole calibration period might contain less measurement uncertainty and therefore are more trustworthy. Meanwhile, if many wells are spatially clustered in one area, this area should not dominate the parameter estimation compared to areas with fewer observations. The final weighting assigns initial weights between one (wells with one observation belonging to a spatial cluster) and nine (wells with several observations located in an area of low spatial density) to all head observations.
Similar to head observations, the statistics for the objective functions related to stream flow—i.e. NSE and WBE are calculated external to PEST for each discharge station, and the observations provided to PEST are one for NSE and zero for WBE. Observations from all discharge stations are time series with daily data, and their accuracy are assumed equal. In addition, the discharge stations do not exhibit spatial clustering and no weighting scheme has thus been applied to compensate for temporal or spatial clustering for discharge observations.
Assigning a relative weight between different components of the objective function is a subjective decision. To avoid a situation where one or more components of Фt dominate, a pragmatic approach is to equalize the components that constitute the total objective function (Doherty and Welter 2010). In order to evaluate the impact of different weighting schemes on different objective functions, two different weighting strategies are pursued. First, a relatively balanced weighting strategy between head and discharge components of the objective function has been applied. This is referred to as the balanced weighting strategy and has been applied to both the unit-based calibration approach (unit-B) and pilot-point-based calibration approach (pilot-B). In the next step, a weighting strategy is pursued in which the discharge components of the objective function have been favored with higher weights for both the unit-based approach (unit-D) and the pilot-point-based approach (pilot-D). All the objective function components and their initial weights are listed in Table 2.
Linear prediction uncertainty
In order to access the linear uncertainty, including identifiability, contribution of parameters on prediction uncertainty, and data-worth analysis for both pilot-D and unit-D models, a Python-based framework tool, pyEMU (White et al. 2016) has been utilized. PyEMU is based on first-order, second-moment (FOSM) theory, which is also known as Bayes linear theory. FOSM uncertainty analysis relies on the assumptions of model linearity and multivariate Gaussian distribution of the model variability. The predictive uncertainty variances are therefore calculated as (Fienen et al. 2010).
where \( {\sigma}_s^2 \) is the postcalibration uncertainty of a prediction target, y is a vector of the prediction target’s sensitivity to all the parameters, Cpp is the covariance matrix of the parameter variability (a priori variance), X is sensitivity of parameters to the observations (Jacobian matrix), and Cεε is the covariance matrix of epistemic uncertainty of observations (reflecting the model structural error and measurement error).
Results
Objective function performances
Фt is noteworthy because this is what the optimizer actually tries to minimize. Reduction in Ф is a straightforward metric that can be used as efficiency criteria for evaluating the performances of models during a parameter estimation. In this case, unit-D is compared with unit-B and pilot-D with pilot-B, as their initial errors are the same, and further, the final Ф values are normalized to the initial values (Table 3).
Since the optimization algorithm minimizes the discrepancy between model outputs and observations based on a weighted least squares method, a relative higher weight on an objective function group generates a larger contribution to Фt. Consequently, the parameters controlling that particular observation group become more sensitive. As a matter of fact, a higher percentage of reduction in MEhead objective function group is observed in both unit-B and pilot-B compare to unit-D and pilot-D. Similarly, all the discharge-related objective functions (NSE, WBE, and BFI) are reduced more in discharge-favored weighted calibrations (unit-D and pilot-D) relative to the balanced calibrations (unit-B and pilot-B). Interestingly, there is a general tendency for the pilot-point-based calibrations to be less affected by the weighting scheme than the unit-based calibrations. This is the case across all Ф reductions in Table 3.
However, due to the fact that the optimizer minimizes the squared error of all individual observations (heads or discharge stations), single poorly performing stations or wells can have a large effect on Фt. Therefore, analyzing actual model performance by evaluating the performance statistics for each calibration is perhaps more informative.
Figure 3 illustrates the results for the objective function components NSE, WBE, BFI and ME_head in absolute values. The absolute values of model performances in each calibration approach are ranked from lowest to highest and shown for each discharge station or observation well. This presentation of the results establishes a baseline for comparison of results from different approaches. The stations are ranked separately for each calibration approach according to the absolute values of model performances and their order does not necessarily coincide with each other in different approaches. All the discharge stations had the same weights regardless of their drainage area size.
Regarding the achieved NSE performances, 62% of the stations in the unit-B calibration had an NSE above 0.6, and in the unit-D calibration 67% of the stations had NSE above 0.6. In the pilot-B calibration, only 46% of the stations exhibited NSE values above 0.6, while assigning higher weight to the discharge objective functions in pilot-D increased the percentage of the stations with NSE values above 0.6–67%.
The absolute WBE were generally lower in both pilot-points-based calibrations—58% of the stations in pilot-B showed WBE below 5%. WBE was significantly lower in the pilot-D approach where 79% of the stations had a value below 5%, whereas in both unit-based calibrations, only 33% of the stations had WBE value below 5%.
The model performances of the pilot-D calibration approach for BFI showed that 95% of the stations had an error below 0.033. For the corresponding unit-based approach (unit-D), the error corresponding to the 95% threshold was 0.075. Generally, unit-B showed the poorest results for the BFI among all the calibration approaches.
The performance on the hydraulic head error for the individual wells showed that the lowest absolute head error was achieved through the pilot-B approach. A slightly poorer result has been achieved through the pilot-D approach. Generally, the two pilot-point-based approaches showed a clear improvement of absolute head error compared to unit-based approaches with approximately 85% of wells with errors below 5 m compared to the unit-based approaches where 70% of the wells had errors below 5 m.
Figure 4 shows the agreement between observed and simulated head data averaged to monthly values. For the pilot-D approach a correlation coefficient of 0.97 is obtained while the unit-D approach resulted in a correlation coefficient of 0.89. To evaluate the goodness of fit, the measurement noise of the observations has to be considered. In this study, the weighting strategy for the head observations has been used to account for measurement uncertainties.
To summarize the evaluation of the errors, the RMSE of the heads has been calculated for each layer and compared for different calibration approaches (Table 4). Furthermore, averaged NSE, absolute averaged WBE, and absolute average BFI have been calculated for different calibration approaches (Table 4).
The results showed that the RMSE of all four layers in both pilot-point-based calibration approaches are lower compared to both unit-based calibration approaches. The comparison between the two unit-based approaches showed that RMSE of heads in all four layers are lower in the unit-B calibration approach. However, the RMSE of the first layer in all four approaches does not seem to be affected as much by the weighting strategy. The RMSE that resulted from the pilot-B calibration approach for the layers 2–4 are the lowest compared to other three approaches. The comparison of the absolute average errors in heads and WBE indicated that the performances of pilot-D relative to pilot-B are more similar compared to the difference between performances of unit-D relative to unit-B.
Figure 5a demonstrates the spatial distribution of mean absolute head error (MAE_head) differences between the unit-D and pilot-D calibration approaches (for the second layer which contains the most observation wells). The values greater than zero (warm colors) represent lower MAE_head in the pilot-D approach relative to unit-D, i.e. a better performance of pilot-D, whereas the values less than zero (cold colors) represent poorer performances in the pilot-D relative to unit-D calibration approach. It is evident that there is an overall improvement of MAE_head in the pilot-D calibration approach compared to the unit-D approach. In particular, there is a systematic improvement of simulated heads between 1–8 m in the central region of the domain and around the catchment boundaries between the Karup catchment and the neighboring catchments (Fig. 5a). The locations of subcatchments are shown in Fig. 2. The larger MAE_head in this specific region for the unit-D calibration approach is likely to be a result of inadequacy in the parameterization of the unit-D calibration approach and consequently not having utilized the information embedded in the observational data set to the extent that the pilot-D approach did. Moreover, better head simulations of the pilot-D in observations located adjacent to the external boundaries where a no-flow boundary condition is assumed are apparent. The overall improvement of the MAE_head in the pilot-D calibration approach relative to the unit-D calibration approach is significant (Fig. 5a); however, this improvement can be expected as a result of the increased number of adjustable parameters. Often a very good fit between observed and simulated values can be at an expense of unrealistic parameter values; therefore, in addition to statistical evaluation of the results it is also essential to assess if the estimated parameters have reasonable values and correspond to prior knowledge of the geology. For a highly parameterized model it becomes even more crucial to verify the feasibility of estimated parameter values. As Hill (2007) points out, increasing the flexibility in the parameter space may lead to unrealistic estimated parameter values, a so-called “overfitting” issue (Fienen et al. 2009). This issue primarily stems from the fact that if the dimensions of the parameter space are larger than the number of observations, the unconstrained parameters may remain uninformed and insensitive to the observations and therefore their values can change dramatically without any or with minimal effect on the model outputs, although this is in principle handled by implementing truncated SVD. In Fig. 5b, the difference in the hydraulic conductivity field of unit-D relative to pilot-D is shown. The warm colors indicate an increase and the cold colors indicate a decrease in the hydraulic conductivity values of pilot-D calibration relative to unit-D. It can also be seen in Fig. 5a,b that the maximum error reduction generally corresponds to the maximum deviation in the conductivity field, though these changes do not exceed more than two orders of magnitude and mostly remain within one order of magnitude. Changes in conductivity can therefore be interpreted as being within the typical range across a geological unit.
Optimized hydraulic conductivity fields
The horizontal hydraulic conductivity field resulting from pilot-D and unit-D calibration approaches has been displayed as two cross-sections (Fig. 6) elongated from west to east (a–a′) and north to south (b–b′). In Fig. 5b, the location of these cross-sections is shown. Figure 6 provides a general picture of the geological layering and the distribution of estimated horizontal hydraulic conductivity within each layer. It can be observed that the thickness of the computational layers and geological structures, e.g. buried valleys are kept identical for both calibration approaches, whereas the distribution of K values within each computational layer has been subject to the estimation process. There is an overall agreement between sand and clay formations in both cross-sections for the pilot points and unit-based calibration; however, there is a higher variability of the K values in the pilot-D approach, especially in layers 2 and 4. The pilot-D calibration approach shows a general tendency of producing a smoother K field relative to unit-D calibration approach. That is because in the unit-D approach the K values are categorized into a few distinct units with sharp interfaces between each units, whereas the values between pilot points are interpolated and therefore the boundaries between different hydrofacies are smoothed out. To inspect the variability of the estimated K values in each computational layer, relative frequency histograms for the pilot-D and unit-D calibration approaches have been demonstrated (Fig. 7). In agreement to what has been visually observed in Fig. 6, the relative frequency histograms show that the spatial distribution of K values in the unit-D have few distinct frequency peaks. This is a result of the K values originally being categorized into a few values, in particular corresponding to pure clay units of low K, whereas in the pilot-D approach the values have a smooth distribution due to interpolation of K values. With the exception of the first layer, the range of K value distributions is approximately an order of magnitude wider in the pilot-D approach. The K distribution in layer 2, in both unit-D and pilot-D calibration approaches, exhibits similar conductivity distributions with a relatively higher frequency of K values around 10−4 m s−1, corresponding to hydraulic conductivity of sand; furthermore, both calibrations indicate a smaller range of K values relative to the other layers. The distribution of K values in layers 1, 3 and 4 are gently skewed toward smaller values of K corresponding to a higher clay-content conductivity in the pilot-D calibration approach compared to unit-D.
Cross sections a b–b′ north–south cross-section in unit-D, b b–b′ north–south cross-section in pilot-D, c a–a′ west–east cross-section in unit-D, d a–a′ west–east cross-section in pilot-D. The y-axes show the surface elevation of each cross-section in meters. The conductivities are presented in log-transformed values. The cross-section locations a–a′ and b–b′ are shown in Fig. 5b
Estimated cross-boundary groundwater fluxes
The hydrological subcatchment boundaries are defined by the topographical divides but this may not necessarily be the case for the groundwater flow. The long-term spatial runoff ratio information provided in Fig. 2 supports the earlier modeling efforts (Højberg et al. 2013) and indicates that there is a groundwater flow across the subcatchments with west–east orientation. In order to assess the magnitude of cross-boundary flow relative to other components of the water balance, a complete water balance analysis has been performed for each subcatchment based on the model simulations (Table 5). The computed boundary flow values indicate that the groundwater cross-boundary fluxes are generally of significance and in some cases higher than pumping and irrigation amounts. The inflow flux entering to the catchment Haldsoe comprises 17% of its discharge in the pilot-D calibration and 14% of its discharge in the unit-D calibration, whereas in catchment Storaa, these values are 6 and 5%, respectively. From the catchments Karup, Storaa, and Skjern, there is a significant amount of outflow to the neighboring catchments Gudenaa and Haldsoe. Among all catchments, the Karup catchment has the highest amount of water loss equivalent to 13% of its discharge in the pilot-D calibration and 11% of its discharge in the unit-D calibration. The sources of groundwater inflow and outflow for each subcatchment and the amount of simulated groundwater fluxes across the north–south topographical boundaries have been calculated by the model. In Fig. 7, the simulated groundwater fluxes through subcatchment boundaries have been shown for both unit-D and pilot-D calibration approaches. The estimated fluxes are the sum of all four computational layers averaged in time for the length of the boundaries. Complementary to the information provided in the Table 5, it can be seen in both calibration approaches that the groundwater flow has a dominant west–east orientation where the catchments Gudenaa and Haldsoe are the main receiving catchments, while subcatchments Karup, Storaa, and Skjern are the main losing ones.
Linear model predictive uncertainty analysis
The following sections provides an analysis of pilot-D identifiability followed by analyses of the contribution of parameter groups and data worth to predictive uncertainty for both unit-D and pilot-D models. The predictive uncertainty analysis is exemplified by using the summer water balance at the outlet of the Haldsoe catchment (mfbal_210794; Fig. 2) as prediction target. The summer water balance is calculated as the bias of simulated stream discharge [mm/s] in summer (June–Sep) for the period of 2000–2007. Based on the observed discharge–rainfall ratios (Fig. 2) and estimated cross-boundary groundwater fluxes (Fig. 8), this subcatchment receives a substantial amount of groundwater through its boundary and therefore has been nominated as a prediction target for this study.
Identifiability
In a highly parameterized inversion context, some parameters may not be uniquely estimated due to either insensitivity of the model outputs to the parameters or correlation between parameters, or occurrence of both conditions at the same time (Doherty and Hunt 2009). Parameter identifiability is a linear statistic, calculated based on the SVD of the weighted Jacobian matrix with values ranging between zero (nonidentifiable) and one (completely identifiable; Doherty and Hunt 2009). The parameter identifiability analysis helps to visualize the dimensionality of the inverse problem by separating the parameters which lie in the solution space from the ones that lie in the null space (Doherty and Hunt 2010b) and thereby leads to a better understanding of the algorithm. In this study, by using the truncated SVD regularization technique for the pilot-point-based calibration of CJC, the inverse problem has been efficiently constrained by estimating only the identifiable parameters (super parameters) on the basis of 350 singular value cutoff for both pilot-D and pilot-B.
The identifiability analysis of pilot-D calibration approach indicates that the identifiability of the parameters is to a great extent in accordance with the spatial distribution of observations in each computational layer. In all, 265 pilot points out of 820 display an identifiability value higher than 0.8 and have been defined identifiable for this study, with 97% of all the identifiable pilot points being located in the second and forth computational layers which are predominantly sandy and have a higher concentration of head observations. Due to their lumped parameterization, the six nonconductivity parameters show high identifiability values of above 0.97. Figure 9a illustrates the identifiability of 205 pilot points in the second computational layer overlain on the final errors of hydraulic head simulations after being calibrated via the pilot-D approach. The general pattern in the identifiability map is a high correlation between the identifiability of the pilot points and the number of observations in the vicinity; however, in spite of relatively dense head observations in some areas of the Storaa and Skjern catchments, the pilot points in this area have very low identifiability values. This can be interpreted as either indication of parameter insensitivity, parameter correlations or redundant information in these observations. To investigate further, the identifiability of the pilot points has been mapped on the simulated water-table depth averaged over the calibration period (Fig. 9b). It can be seen that the low identifiable pilot points in areas with dense coverage of the observations coincide with areas with shallow water-table depth less than 0.5 m; however, the average head errors in these areas are low, illustrating a good fit to observations.
Parameter contributions to change in predictive uncertainty
The parameter-group contributions to pre- and post-calibration uncertainty of mfbal_210794 are illustrated in Fig. 10 for unit-D and pilot-D models. The KS group (hydraulic conductivity) has the largest pre-and post-calibration contribution to uncertainty of mfbal_210794 in both unit-D and pilot-D models. It is noteworthy that the post-calibration contribution of the “roo” group (root depth) to the uncertainty of mfbal_210794 has increased in both unit-D and pilot-D. This means that the contribution of the Root parameter group to the uncertainty of mfbal_210794 has not been reduced after calibration to the observation data set. The difference between pre- and post-calibration uncertainty contribution is much larger in unit-D (34%) than in pilot-D (5.6%). This can be explained by the higher degree of flexibility in the pilot-D model parameter space in comparison to unit-D model. The simpler parameterization scheme in unit-D might have resulted in increasing the compensatory role of the root parameter group during the calibration process, whereas in pilot-D, as a result of a more spatial flexible discretization of the hydraulic conductivities field, this compensation might have occurred through some of the pilot points.
Normalized contributions of parameter groups to pre- and post-calibration prediction uncertainty of mfbal_210794 in Haldsoe catchment shown for a pilot-point-based calibration (pilot-D) and for b unit-based calibration (unit-D). The X-axes show parameter groups. The description of each parameter group is given in Table 1
Observation data worth and impact on prediction uncertainty
The data worth analysis of existing observations in changing the prediction uncertainty of mfbal_210794 for both pilot-D and unit-D models were computed through both the addition and subtraction of excising individual observations/observation groups (Fig. 11). The data with high worth would decrease the uncertainty of the prediction when added as a sole member of the observation data set. Alternatively, the data with low worth or redundant information would have no effect or minimum effect on increasing original prediction uncertainty when removed one by one from the observation dataset (Fienen et al. 2010; White et al. 2016).
Data worth of observation groups to prediction of mfbal_210794 (summer water balance of Haldsoe catchment) shown for a pilot-point-based calibration (pilot-D) and b unit-based calibration (unit-D). The black bars correspond to decrease [%] in uncertainty with adding each observation group as a sole member of calibration dataset. The gray bars correspond to increase [%] in uncertainty with removing each observation group one by one from the calibration dataset. The observation groups are described in Table 3
In the unit-D model, all observation groups, except RMSE_Irr, have reduced the prediction uncertainty of Mfbal_210794 to the same extent (approximately 99%). However, the prediction uncertainty of mfbal_210974 does not increase equally by removal of observation groups. The ME_head increases the prediction uncertainty the most (72%) followed by WBE (27%) and BFI (21%).
In the pilot-D model, the ME_head and WBE observation groups contribute as the most and second-most important group to the reduction of prediction uncertainty. By removing ME_head and WBE observation groups, the prediction uncertainty increases up to 82 and 41% respectively. The discrepancy between changes in prediction uncertainty when an observation/observation group is added and subtracted to/from the data set can reveal the level of redundancy or otherwise uniqueness of that observation group.
Given that the head observations have a higher frequency and spatial distribution compared to other observation groups, it is not surprising that the ME_head group has greater contribution to the reduction of prediction uncertainty for both models. However, it appears that the removal of the ME_head increases the prediction uncertainty more in pilot-D than in unit-D. This suggests that the flexibility in the parameterization of pilot-D enabled the model to obtain more unique information from the ME_head observation group. On the other hand, the pilot-D model utilizes the observation dataset more than the unit-D model; therefore, additional head observations might reduce the uncertainty of this prediction more than in the unit-D model, especially considering the fact that there is a relation between the level of information that is provided for the model and the number of super parameters.
Figure 12 depicts the data-worth spatial distribution of individual head observations in the second layer for the prediction of mfbal_210794 in the pilot-D and unit-D models. It can be seen that in the pilot-D case, the head observations with higher contributions to the prediction uncertainty of mfbal_20026 are mainly located in the upstream part of the Haldsoe catchment and between the Karup and Haldsoe catchment boundaries, whereas in the unit-D model, the head observations with higher contribution to prediction uncertainty of mfbal_210794 are distributed throughout the whole CJC catchment and show a less physically meaningful pattern. The resulting differences between spatial data worth pattern of the two models is considerable. However, taking into account their hydraulic conductivity parameterization, this is easily explainable because a given unit in the unit-D model can be informed by head observations anywhere in the catchments where that unit exists.
Data worth of each individual head observation in the second layer for the prediction of mfbal_210794 (summer water balance of Haldsoe catchment) shown for a unit-D and b pilot-D. The sizes of circles correspond to the measure of decrease in prediction uncertainty with adding each individual head observation to the calibration dataset
Discussion
A highly parameterized calibration approach is used to calibrate a regional-scale, transient, coupled surface–subsurface model in order to examine the feasibility of introducing a large number of pilot points in the optimization process given a comprehensive set of observational data. The current study introduces pilot points across the entire model domain and hereby allows the pilot-point-based optimization to generate the horizontal K field distribution in each model layer. This parametrization approach is compared to a more traditional unit-based optimization, where spatial variability of the geological settings is assumed to be known and where the optimization is limited to identifying the optimal parameter values for a given geological unit.
In terms of model performance, the pilot-point-based approaches yield better results by reducing the misfit between all the observation groups and corresponding model outputs; however, the improvements are most prominent in the ME_head and WBE objective functions. The improvement in the ME_head was expected as a result of increased heterogeneity in hydraulic conductivity parameterization, though a better performance in WBE objective function is also achieved due to a better representation of groundwater/surface-water interactions. The less significant improvement of the NSE objective function relative to the ME_head BFI and WBE objective functions could be due to lack of flexibility in the spatial parameterization of overland flow including roughness coefficient, drainage time constant and leakage coefficient, as the main controlling parameters of the surface system. In addition, the NSE is mainly sensitive to the fit of discharge peaks and is therefore less dependent on a more detailed representation of the groundwater system. Due to spatial discontinuity of overland and unsaturated flow parameters and their subsequent insensitivity to the observations, parameterization of these parameters with the pilot point approach is challenging (Maneta and Wallender 2013). This issue has not been the focus of the current study and, therefore, has not been further explored.
Furthermore, in this study, the trade-off between different weighting strategies of several independent objective functions in both parameterization approaches was investigated. The comparison of the two weighting strategies in which higher weights are given either to head or discharge observation groups, reveals that the performances of the models calibrated with the pilot point approach are less affected by changing the weights compared to the traditional calibration approach. The trade-off between different objective functions in the pilot-point-based approaches is smaller compare to the unit-based approaches, which most likely results from an increased capability of the model to accommodate some of the structural inadequacies.
In the pilot-point-based approach the simulated head biases improved up to 8 m (compared to the unit-based approach) around the Karup catchment boundaries with a clear spatial consistency. This reveals that the unit-based parameterization scheme does not utilize all the information embedded in the observations to the extent that the pilot point approach does. This points out that the level of heterogeneity in the hydraulic conductivity of the unit-based approach does not allow the model to represent the observations in those regions as well as the pilot-point-based approach. Moreover, it can been seen that the MAE_head around the external boundaries are significantly improved. This also suggests that the flexibility in the parameterization of pilot point approach allows the model to compensate for the boundary conditions which might have been inaccurately imposed. Compensation for the boundary conditions is often indispensable in the parameter estimating process, as referred to by Doherty and Welter (2010). In a highly parametrized model in which the inverse problem is appropriately constrained with mathematical regularizations, model insufficiency can be locally accommodated through compensatory parameters. Depending on the prediction target, this does not necessarily lead to a better prediction. In the estimated hydraulic conductivity fields that resulted from pilot-point-based approach, some of those compensatory parameters appear in the close vicinity of the external boundary conditions where the pilot-point K values deviate the most from their estimated counterparts resulted from the unit-based approach. However, these deviations do not exceed more than one to two orders of magnitude, and therefore it can be considered feasible as they are in accordance with the uncertainty of the geology. The general pattern of the estimated K field in the pilot-point-based calibration is clearly smoother and has less distinct transition boundaries between different geological units as an outcome of spatial interpolation between pilot points. The more gradual transitions in the K field may be considered appropriate for the description of the sandy outwash plain in the western part of regional-scale model. However, the lack of distinct shifts in geology might be less appropriate in other parts of the model domain. Likewise, the smooth interpolated K-fields resulting from the pilot point application might work well for estimation of hydraulic head and regional-scale groundwater fluxes; however, it can result in significant limitations for other applications such as solute transport modelling. These limitation of are mostly related to the application of Kriging interpolation method which relies on the assumption that the model parameters have a multiGaussian distribution (Kerrou et al. 2008). As expected, the identifiability analysis of pilot-point-based approaches indicate that the identifiability of the pilot points depends largely on the availability of the head observations in their proximity. Another interesting observation from the identifiability analysis regards the regions where the average water table is less than half a meter below the surface, resulting in very low sensitivity of pilot points to the head observations. This is expected since the drainage depth level is set to 0.5 m and therefore at this level the groundwater head is mainly controlled by the drainage time constant and less by hydraulic conductivity.
In this modeling study, several important features of groundwater flow across the hydrological subcatchments boundaries are characterized. The groundwater flow cross the north–south topographical boundary is dominantly present in both calibrated models. Net flux across subcatchments boundaries vary little between the two calibration approaches, indicating that the computed general regional flow patterns are similar; however, as illustrated in Fig. 8, there are some differences in the specific sub-catchments exchange fluxes, primarily around the Karup sub-catchment. These differences coincide with the significant change in simulated groundwater levels and resulting reduction in head biases using the highly parameterized approach (Fig. 5). Owing to the lack of exact measurements of regional groundwater flow, the estimated cross-boundary fluxes cannot be evaluated explicitly; however, in areas of abundant head observations, the model that represents the head observations the best, is assumed to give the best estimate of head gradients and groundwater fluxes. In addition, the direction and proximal magnitude of cross-boundary flow can be indicated by analysis of rainfall–runoff ratio map. In this study, such a map of observation-based long-term runoff–rainfall patterns was produced (Fig. 2) and indicated a clear west–east groundwater flow component similar to the patterns predicted by the groundwater models.
The focus of the current study has been on investigating the benefits, limitations and tradeoffs between a unit-based and a highly parameterized calibration scheme. The pursued pilot point approach has been used for a thorough investigation on the limitations of the unit-based approach, for a re-evaluation of the conceptual model used in the unit-based approach, and for effective use of information from the available calibration dataset to inform the model optimization. Subsequently, the optimized model has been used to quantify the groundwater flow across topographical boundaries.
Conclusions
In this study, a regularized inversion approach with 350 identifiable super-parameters from both surface and subsurface domains has been evaluated for a transient regional-scale surface–subsurface flow model covering five topographically defined river-basins. The limitations of a highly parameterized calibration including the computational burden and nonidentifiable parameters have been minimized by application of a truncated singular-value-decomposition regularization technique. Evaluation of the highly parameterized calibration approach in terms of model performances and feasibility of the estimated parameters indicated that it more effectivity utilized the information in the data compared to a traditional unit-based calibration approach without extending the estimated parameter value ranges further than the uncertainty range of the underlying geology. Especially the model performance regarding hydraulic head and stream water balances improved significantly for the highly parametrized optimization, which was expected due to the larger degree of freedom. Furthermore, the results showed that adopting different weighting strategies for objective function groups, as an acknowledgment of model imperfections, has a larger impact on the more parsimonious unit-based model compared to the model based on a more complex parametrization scheme. This indicates that the more complex parametrization, in our case the pilot-point-based approach, can accommodate the conceptual model deficiencies to some extent through flexible parameter values. The estimated hydraulic conductivity fields from the two calibration approaches exhibited very different distributions due to the sharp geological boundaries of the unit-based approach relative to the interpolated fields resulting from the pilot point approach; however, the values have generally not changed more than an order of magnitude.
Both approaches have limitations regarding lack of variability and lack of contrast which has to be considered for any given application. The regional-scale groundwater-surface water model provided a valuable insight into the complex, regional flow patterns which otherwise would have been impractical to obtain. In this study, the model was used to quantify the subsurface flux between topographically delineated subcatchments. The fluxes through all the internal boundaries constitute from 3 to 16% of the their discharge amount and are quite significant relative to the pumping; therefore, it is important for the water management to consider these cross-boundary flows in the hydrological models as they might have a big impact on the simulation of the head water streams. This furthermore highlights the need for regional-scale coupled surface–subsurface flow models for water management, since most surface-water models assume zero flux boundaries between topographical divides. The results from the data worth study indicates a less physically meaningful pattern for the unit-based model compared to the pilot-point-based model. It can be therefore concluded that in order to identify the spatial worth of observations to a prediction uncertainty, there should be a certain degree of flexibility and variability in the model parameterization.
References
Abbaspour KC, Rouholahnejad E, Vaghefi S, Srinivasan R, Yang H, Kløve B (2015) A continental-scale hydrology and water quality model for Europe: calibration and uncertainty of a high-resolution large-scale SWAT model. J Hydrol 524:733–752. https://doi.org/10.1016/j.jhydrol.2015.03.027
Abbott MB, Bathurst JC, Cunge JA, O’Connell PE, Rasmussen J (1986) An introduction to the European hydrological system - Systeme Hydrologique Europeen, “SHE”, 1: history and philosophy of a physically-based, distributed modelling system. J Hydrol. https://doi.org/10.1016/0022-1694(86)90114-9
Anderson MP, Woessner WW, Hunt RJ (2015) Model calibration: assessing performance, chap 9. In: Anderson MP, Woessner WW, Hunt RJ (eds) Applied groundwater modeling, 2nd edn. Academic Press, San Diego, pp 375–441
Barthel R (2014) HESS opinions “integration of groundwater and surface water research: an interdisciplinary problem?”. Hydrol Earth Syst Sci 18:2615–2628. https://doi.org/10.5194/hess-18-2615-2014
Barthel R, Banzhaf S (2016) Groundwater and surface water interaction at the regional-scale: a review with focus on regional integrated models. Water Resour Manag 30:1–32. https://doi.org/10.1007/s11269-015-1163
Brunner P, Li HT, Kinzelbach W, Li WP, Dong XG (2008) Extracting phreatic evaporation from remotely sensed maps of evapotranspiration. Water Resour Res. https://doi.org/10.1029/2007WR006063
Butts M, Graham D (2005) Flexible integrated watershed modeling with MIKE SHE. In: Watershed models. Taylor and Francis, Boca Raton, FL, pp 245–271. https://doi.org/10.1201/9781420037432.ch10
Doherty J (2003) Ground water model calibration using pilot points and regularization. Ground Water 41:170–177
Doherty JE (2015) Calibration and uncertainty analysis for complex environmental models. Watermark, Brisbane, Australia 227 pp
Doherty J, Hunt RJ (2009) Two statistics for evaluating parameter identifiability and error reduction. J Hydrol 366:119–127. https://doi.org/10.1016/j.jhydrol.2008.12.018
Doherty J, Hunt R (2010a) Approaches to highly parameterized inversion: a guide to using PEST for groundwater-model calibration. US Geol Surv Sci Invest Rep 2010-5211
Doherty J, Hunt RJ (2010b) Response to comment on two statistics for evaluating parameter identifiability and error reduction. J Hydrol 380:489–496. https://doi.org/10.1016/j.jhydrol.2009.10.012
Doherty J, Welter D (2010) A short exploration of structural noise. Water Resour Res. https://doi.org/10.1029/2009WR008377
Doherty J, Hunt R, Tonkin M (2010a) Approaches to highly parameterized inversion: a guide to using PEST for model-parameter and predictive-uncertainty analysis. US Geol Surv Sci Invest Rep 71:2010–5211
Doherty JE, Fienen MN, Hunt RJ (2010b) Approaches to highly parameterized inversion: pilot-point theory, guidelines, and research directions. Us Geol Surv Sci Invest Rep 2010-5168
Fienen MN, Muffels CT, Hunt RJ (2009) On constraining pilot point calibration with regularization in PEST. Ground Water. https://doi.org/10.1111/j.1745-6584.2009.00579.x
Fienen MN, Doherty JE, Hunt RJ, Reeves HW (2010) Using prediction uncertainty analysis to design hydrologic monitoring networks: example applications from the Great Lakes water availability pilot project. US Geol Surv Sci Invest Rep 2010-5159
Ghasemizade M, Schirmer M (2013) Subsurface flow contribution in the hydrological cycle: lessons learned and challenges ahead—a review. Environ Earth Sci 69:707–718. https://doi.org/10.1007/s12665-013-2329-8
Gupta HV, Kling H, Yilmaz KK, Martinez GF (2009) Decomposition of the mean squared error and NSE performance criteria: implications for improving hydrological modelling. J Hydrol. https://doi.org/10.1016/j.jhydrol.2009.08.003
Gustard A, Bullock A, Dixon JM (1992) Low flow estimation in the United Kingdom. IH report no. 108, Institute of Hydrology, Wallingford, UK, 292 pp
Henriksen HJ, Troldborg L, Nyegaard P, Sonnenborg TO, Refsgaard JC, Madsen B (2003) Methodology for construction, calibration and validation of a national hydrological model for Denmark. J Hydrol. https://doi.org/10.1016/S0022-1694(03)00186-0
Hill MC, Tiedeman CR (2007) Effective groundwater model calibration: With analysis of data, sensitivities, predictions, and uncertainty. Hoboken, N.J: Wiley-Interscience.
Højberg AL, Troldborg L, Stisen S, Christensen BBS, Henriksen HJ (2013) Stakeholder driven update and improvement of a national water resources model. Environ Model Softw 40:202–213. https://doi.org/10.1016/j.envsoft.2012.09.010
Højberg AL, Stisen S, Olsen M, Troldborg L, Uglebjerg TB, Jørgensen LF (2015) DK-model2014: Model opdatering og kalibrering [DK-model2014: Model update and calibration]. GEUS report 2015/8, GEUS, Copenhagen
Jakeman AJ, Barreteau O, Rinaudo RJHJ (2016) Integrated groundwater management: an overview of concepts and challenges. In: Integrated groundwater management:concepts, approaches and challenges. Springer, Heidelberg, Germany
Jiang XW, Sun ZC, Zhao KY, Shi FS, Wan L, Wang XS, Shi ZM (2017) A method for simultaneous estimation of groundwater evapotranspiration and inflow rates in the discharge area using seasonal water table fluctuations. J Hydrol. https://doi.org/10.1016/j.jhydrol.2017.03.026
Jing M, Heße F, Wang W, Fischer T, Walther M, Zink M, Zech A, Kumar R, Samaniego L, Kolditz O, Attinger S (2017) Improved regional-scale groundwater representation by the coupling of the mesoscale Hydrologic Model (mHM v5.7) to the groundwater model OpenGeoSys (OGS). Geosci Model Dev Discuss 11:1989–2007. https://doi.org/10.5194/gmd-2017-231
Kerrou J, Renard P, Hendricks Franssen HJ, Lunati I (2008) Issues in characterizing heterogeneity and connectivity in non-multiGaussian media. Adv Water Resour 31:147–159. https://doi.org/10.1016/j.advwatres.2007.07.002
Maneta MP, Wallender WW (2013) Pilot-point based multi-objective calibration in a surface–subsurface distributed hydrological model. Hydrol Sci J 58(2):390–407. https://doi.org/10.1080/02626667.2012.754987
Marsily G, Lavedan G, Boucher M, Fasanino G (1984) Interpretation of Interference Tests in a Well Field Using Geostatistical Techniques to Fit the Permeability Distribution in a Reservoir Model, Geostatistics for natural Resources Characterization, Part 2. 831-849.
Mendiguren G, Koch J, Stisen S (2017) Spatial pattern evaluation of a calibrated national hydrological model: a remote sensing based diagnostic approach. Hydrol Earth Syst Sci Discuss 21:5987–6005. https://doi.org/10.5194/hess-2017-233
Meyer R, Engesgaard P, Høyer A, Jørgensen F, Vignoli G, Sonnenborg TO (2018) Regional flow in a complex coastal aquifer system: combining voxel geological modelling with regularized calibration. J Hydrol 562:544–563. https://doi.org/10.1016/j.jhydrol.2018.05.020
Moore C, Doherty J (2006) The cost of uniqueness in groundwater model calibration. Adv Water Resour 29:605–623. https://doi.org/10.1016/j.advwatres.2005.07.003
Refsgaard JC, Henriksen HJ (2004) Modelling guidelines: terminology and guiding principles. Adv Water Resour 27:71–82. https://doi.org/10.1016/j.advwatres.2003.08.006
Riis T, Suren AM, Clausen B, Sand-Jensen K (2008) Vegetation and flow regime in lowland streams. Freshw Biol 53:1531–1543. https://doi.org/10.1111/j.1365-2427.2008.01987.x
Skahill BE, Doherty J (2006) Efficient accommodation of local minima in watershed model calibration. J Hydrol 329:122–139. https://doi.org/10.1016/j.jhydrol.2006.02.005
Sonnenborg TO, Christensen BSB, Nyegaard P, Henriksen HJ, Refsgaard JC (2003) Transient modeling of regional groundwater flow using parameter estimates from steady-state automatic calibration. J Hydrol 273:188–204. https://doi.org/10.1016/S0022-1694(02)00389-X
Stisen S, McCabe MF, Refsgaard JC, Lerer S, Butts MB (2011) Model parameter analysis using remotely sensed pattern information in a multi-constraint framework. J Hydrol 409:337–349. https://doi.org/10.1016/j.jhydrol.2011.08.030
Stisen S, Hojberg AL, Troldborg L, Refsgaard JC, Christensen BSB, Olsen M, Henriksen HJ (2012) On the importance of appropriate precipitation gauge catch correction for hydrological modelling at mid to high latitudes. Hydrol Earth Syst Sci 16:4157–4176. https://doi.org/10.5194/hess-16-4157-2012
Stisen S, Koch J, Sonnenborg TO, Refsgaard JC, Bircher S, Ringgaard R, Jensen KH (2018) Moving beyond runoff calibration: multi-constraint optimization of a surface-subsurface-atmosphere model. Hydrol Process. https://doi.org/10.1002/hyp.13177
Tonkin MJ, Doherty J (2005) A hybrid regularized inversion methodology for highly parameterized environmental models. Water Resour Res 41. https://doi.org/10.1029/2005WR003995
UNESCO (2012) Managing water under uncertainty and risk. The United Nations World Water Development report 4. UNESCO, Paris
White JT, Fienen MN, Doherty JE (2016) A python framework for environmental model uncertainty analysis. Environ Model Softw 85:217–228. https://doi.org/10.1016/j.envsoft.2016.08.017
Yan J, Smith KR (1994) Simulation of integrated surface water and ground water systems: model formulation. J Am Water Resour Assoc 30:879–890. https://doi.org/10.1111/j.1752-1688.1994.tb03336.x
Zhang J, Ross M (2015) Comparison of IHM and MIKE SHE model performance for modeling hydrologic dynamics in shallow water table settings. Vadose Zo J. https://doi.org/10.2136/vzj2014.03.0023
Zhou X, Helmers M, Qi Z (2013) Modeling of subsurface tile drainage using MIKE SHE. Appl Eng Agric 29:865–873. https://doi.org/10.13031/aea.29.9568
Acknowledgements
The authors would like to acknowledge Mike Fienen for his valuable inputs and all the support with pyEMU. The authors would also like to acknowledge two anonymous reviewers.
Funding
The authors acknowledge the financial support for the SPACE project by the Villum Foundation (http://villumfonden.dk/) through their Young Investigator Program (grant VKR023443).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Danapour, M., Højberg, A.L., Jensen, K.H. et al. Assessment of regional inter-basin groundwater flow using both simple and highly parameterized optimization schemes. Hydrogeol J 27, 1929–1947 (2019). https://doi.org/10.1007/s10040-019-01984-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-019-01984-3