Groundwater salinity mapping using geophysical log analysis within the Fruitvale and Rosedale Ranch oil fields, Kern County, California, USA

Abstract

A method is presented for deriving a volume model of groundwater total dissolved solids (TDS) from borehole geophysical and aqueous geochemical measurements. While previous TDS mapping techniques have proved useful in the hydrogeologic setting in which they were developed, they may yield poor results in settings with lithological heterogeneity, complex water chemistry, or limited data. Problems arise because of assumed values for empirical constants in Archie’s Equation, unrealistic porosity and temperature gradients, or bicarbonate-rich groundwater. These issues become critical in complex geologic settings such as the San Joaquin Valley of California, USA. To address this, a method to map TDS in three dimensions is applied to the Fruitvale and Rosedale Ranch oil fields near Bakersfield, California. Borehole resistivity, porosity, and temperature data are used to derive TDS using Archie’s Equation, and are then kriged to interpolate TDS. Archie’s a and m (tortuosity factor and cementation exponent, respectively) are found by comparing model predictions, after kriging, to TDS measurements, and minimizing the differences via mathematical optimization. Contributions of abundant bicarbonate ions to TDS were corrected using an empirical model. This work was motivated by federal and state law requirements to monitor and protect underground sources of drinking water. Modeling shows the legally significant boundary of 10,000 ppm TDS is at ~1,067 m below sea level in Rosedale Ranch, and deepens into Fruitvale to ~1,341 m. Mapping groundwater TDS at this resolution reveals that TDS is primarily controlled by depth, recharge, stratigraphy, and in some places, by faulting and facies changes.

Résumé

Une méthode est. présentée pour dériver un modèle volumique de la minéralisation totale (MT) à partir de géophysique de puits et d’analyses hydrogéochimiques. Bien que les techniques antérieures de cartographie de la MT aient montré leur utilité dans le contexte hydrogéologique où elles ont été développées, elles peuvent conduire à des résultats erronés dans des contextes d’hétérogénéité lithologique, de chimie de l’eau complexe ou de nombre limité de données. Des problèmes apparaissent à cause des valeurs estimées pour les paramètres empiriques de la Loi d’Archie, de porosités irréalistes et de gradients de température, ou d’eaux souterraines riches en bicarbonates. Ces problèmes deviennent critiques dans des contextes géologique complexes tels que celui de la Vallée de San Joaquin, Californie, USA. Pour faire face à ces problèmes, une méthode pour cartographier la MT en trois dimensions est. appliquée aux champs pétroliers de Fruitvale et Rosedale Ranch, près de Bakersfield, Californie. Des données de résistivité mesurée en forage, de porosité et de température sont utilisées pour calculer la MT en utilisant la loi d’Archie et sont ensuite krigées pour interpoler la MT. Les paramètres a et m d’Archie (respectivement facteur de tortuosité et exposant de cimentation), sont identifiés en comparant les prédictions du modèle, après krigeage, aux mesures de la MT et en minimisant les différences par optimisation mathématique. Les contributions à la MT des teneurs élevées en ions bicarbonates ont été corrigées en utilisant un modèle empirique. Ce travail a été motivé par les exigences réglementaires fédérales et de l’état de Californie en matière de monitorage et de protection des eaux souterraines destinées à l’eau potable. La modélisation montre que la limite réglementaire significative de 10,000 ppm de MT se situe à ~1,067 m sous le niveau de la mer à Rosedale et s’approfondit à Fruitvale à ~1,341 m. La cartographie de la MT des eaux souterraines avec cette résolution révèle que la MT est. contrôlée principalement par la profondeur, la recharge, la stratigraphie et, en certains endroits, par les failles et les changements de faciès.

Resumen

Se presenta un método para derivar un modelo de volumen de sólidos disueltos totales (TDS) en el agua subterránea a partir de mediciones geofísicas y geoquímicas en perforaciones. Si bien las técnicas previas de mapeo de TDS han demostrado ser útiles en el contexto hidrogeológico en el que se desarrollaron, pueden arrojar resultados deficientes en entornos con heterogeneidad litológica, con química del agua compleja o con datos limitados. Los problemas surgen debido a los valores asumidos para las constantes empíricas en la ecuación de Archie, porosidad y gradientes de temperatura poco realistas, o agua subterránea rica en bicarbonato. Estos problemas se vuelven críticos en entornos geológicos complejos como el Valle de San Joaquín de California, EEUU. Para abordar esto, se aplica un método para mapear TDS en tres dimensiones a los campos petrolíferos de Fruitvale y Rosedale Ranch cerca de Bakersfield, California. Los datos de resistividad, porosidad y temperatura de las perforaciones se utilizan para derivar TDS usando la Ecuación de Archie, y luego se combinan para interpolar losTDS. Los factores de Archie a y m de Archie (factor de tortuosidad y exponente de cementación, respectivamente) se encuentran comparando las predicciones del modelo, después de un kriging, con las mediciones de TDS y minimizando las diferencias a través de una optimización matemática. Las contribuciones de iones bicarbonato abundantes a TDS se corrigieron utilizando un modelo empírico. Este trabajo fue motivado por los requisitos de la ley federal y estatal para monitorear y proteger las fuentes subterráneas de agua potable. El modelado muestra que el límite legalmente significativo de 10,000 ppm de TDS está a ~1,067 m por debajo del nivel del mar en Rosedale Ranch, y se profundiza en Fruitvale a ~1,341 m. El mapeo del TDS del agua subterránea en esta resolución revela que el TDS se controla principalmente por profundidad, recarga, estratigrafía y, en algunos lugares, por fallas y cambios de facies.

摘要

这里介绍了一种根据钻孔地球物理测量结果及水中地球化学测量结果获取地下水总溶解固体体积模型的方法。先前的总溶解固体绘图技术证明在这些技术得到开发的水文地质背景中非常有用,但在具有岩性异质性、复杂的水化学条件或者受限的数据背景下可能会得出很差的结果。这些问题的出现是由于Archie方程中经验常数的假定值、不切实际的孔隙度及温度梯度或富含重碳酸盐地下水等原因造成的。这些问题在复杂的地质背景下诸如在美国加利佛尼亚州的San Joaquin河谷显得非常关键。为了强调这一问题,一种绘制三维总溶解固体图的方法应用到了加利佛尼亚州Bakersfield附近的Fruitvale 和Rosedale Ranch油田。根据钻孔电阻率、孔隙度和温度数据采用Archie方程获取总溶解固体,然后这些数据经过克里格法处理插入总溶解固体中。通过比较克里格法之后的模型预测结果和总溶解固体测量结果以及通过数学最优化把两者之间的差减少到最小。利用经验模型修正丰富的重碳酸盐离子对总溶解固体的贡献率。这项工作是根据联邦和州政府监测和保护地下饮用水资源的法律要求而开展的。模拟显示,法律上非常重要的10,000 ppm TDS的界限在Rosedale Ranch为海平面以下大约1,067 m,在Fruitvale深入到海平面以下大约1,341 m。在这个分辨率上绘制地下水总溶解固体图揭示,总溶解固体主要受控于深度、补给量和地层,在有些地方,还受控于断裂和岩相变化。

Resumo

Um método é apresentado derivando um modelo volumétrico de sólidos totais dissolvidos (STD) em águas subterrâneas a partir de medições geofísicas e geoquímicas aquosa em poços. Embora as técnicas de mapeamento de STD anteriores tenham se mostrado úteis no contexto hidrogeológico em que foram desenvolvidas, estas podem produzir resultados ruins em ambientes com heterogeneidade litológica, química da água complexa, ou dados limitados. Os problemas surgem por causa dos valores assumidos para as constantes empíricas na Equação de Archie, porosidade irreal e gradientes de temperatura, ou águas subterrâneas ricas em bicarbonato. Essas questões tornam-se críticas em ambientes geológicos complexos, como o Vale de San Joaquin, na Califórnia, EUA. Para resolver isso, um método para mapear o STD, tridimensional, é aplicado aos campos de petróleo de Fruitvale e Rosedale Ranch, próximo a Bakersfield, Califórnia. Os dados de resistividade, porosidade e temperatura do poço são usados ​​para derivar os STD usando a Equação de Archie e, em seguida, realiza-se interpolação dos STD por krigagem. Os parâmetros a e m de Archie (fator de tortuosidade e fator de cimentação, respectivamente) são encontrados comparando as previsões do modelo, após a krigagem, com as medições de STD, e minimizando as diferenças por meio da otimização matemática. As contribuições de íons de bicarbonato abundantes para os STD foram corrigidas usando um modelo empírico. Este trabalho foi motivado por exigências legais federais e estaduais para monitorar e proteger fontes subterrâneas de água potável. A modelagem mostra que o limite legalmente significativo de 10,000 ppm STD está ~1,067 m abaixo do nível do mar em Rosedale Ranch, e se aprofunda em Fruitvale para ~1,341 m. O mapeamento de STD em água subterrânea nesta resolução revela que os STD são controlado principalmente pela profundidade, recarga, estratigrafia e, em alguns lugares, por falhas e mudanças de fácies.

Introduction

Previous groundwater salinity-mapping efforts based primarily on borehole geophysics have used a variety of approaches. These methods include using geochemical measurements of TDS from sampled wells (Metzger and Landon 2018), formation resistivity/TDS regression models (Fogg et al. 1983; Hamlin and Rocha 2015), the spontaneous potential (SP) method (Lyle 1988; Lindner-Lunsford and Bruce 1995; Schnoebelen et al. 1995), and using Archie’s Equation to derive formation water resistivity (Lyle 1988; Peterson 1991; Lindner-Lunsford and Bruce 1995; Schnoebelen et al. 1995; Hamlin and Rocha 2015; Gillespie et al. 2017).

While these salinity-mapping methods work well in the geological settings for which they were initially developed, they have assumptions and weaknesses that may limit their use in regions with complicated hydrogeology or limited data availability—for example, in many places available geochemical measurements of TDS are not vertically or laterally dense enough to map salinity in detail. Regression models assume constant porosity which may not hold true in areas with complicated lithology (such as shale and diatomite), lateral facies changes, or volumes spanning large depth intervals. Furthermore, geochemical samples of produced water usually come from oil-bearing zones where the resistivity response is affected by variable oil saturation, which results in regression models that reflect the oil zone, therefore it may not be appropriate to apply the model in the water-saturated zones. The SP method is no longer used by most analysts because of its inaccuracy in predicting TDS (Lindner-Lunsford and Bruce 1995; Schnoebelen et al. 1995; Gillespie et al. 2017). Finally, methods using Archie’s Equation (Archie 1942) or the modified version introduced by Winsauer et al. (1952) have had success, but have uncertainties associated with parameter selection (the a and m coefficients). Further challenges arise when mapping fresh or brackish waters because of the different electrical properties of major ions (Alger 1966; Page 1973; Schlumberger 2009).

Deep salinity mapping is difficult in geologically complex areas like the San Joaquin Valley of California, which has mixed siliciclastic- and diatomite-bearing sedimentary sequences with lateral facies changes (Scheirer and Magoon 2007) that, in places, contain waters rich in bicarbonate. In this area, limitations of standard salinity-mapping methods are compounded, necessitating a new approach to salinity mapping.

Here, a new method and workflow that uses borehole geophysical and geochemical measurements to construct an oil-field scale, three-dimensional (3D) salinity map is described. This method addresses several of the issues raised in previous studies: (1) it uses measured TDS geochemistry to find the Archie Equation’s a and m parameters (tortuosity factor and cementation exponent, respectively), yielding optimized values for different zones in the volume of analysis, (2) it allows correction of resistivity responses based on measured major ion aqueous geochemistry, (3) it considers vertical porosity and temperature gradients, and (4) it results in a 3D continuous map that characterizes vertical and lateral salinity gradients.

This method is applied to an example from the Fruitvale and Rosedale Ranch oil fields which cover roughly 96 km² (37 mi²) near Bakersfield, California (Fig. 1). Examination of the 216 direct measurements of TDS available (64 produced water samples from oil wells and 152 groundwater samples from water wells) show they are distributed too sparsely and unevenly to extrapolate to the entire volume. To supplement the direct measurements, borehole geophysics from 50 oil wells are incorporated, which provide continuous geophysical measurements (formation resistivity and porosity) to depths around 1,371 m (4,500 ft) below sea level. A volume model of TDS is constructed by first using Archie’s Equation to infer TDS over the extent of each borehole, correcting the TDS values to account for different water types (i.e. Na-Cl, Na-HCO₃), and then kriging these values to obtain TDS values (with confidence intervals) for all points in the volume of analysis. The parameters of the model (Archie’s a and m, which were allowed to vary by oil field) were found by matching the model’s predictions to the direct measurements of TDS. Mapping groundwater TDS at this resolution has provided a better understanding of relations to controlling factors such as depth, recharge, stratigraphy, and faulting, which can facilitate better predictions in areas with sparse data.

Fig. 1

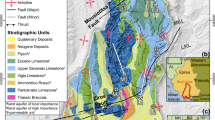
Location of the study area. The Fruitvale Calloway area is the northwest portion of the Fruitvale field while the rest of the field is referred to as the main area. Well location and field boundary data are from the California Division of Oil, Gas, and Geothermal Resources (DOGGR 2017c)

Motivation

Demand for water that is safe for drinking, irrigation, and industrial supply has been steadily growing for decades, leading to increased interest in identifying and protecting fresh and brackish groundwater resources (Cooley et al. 2006; Faunt 2009; BARDEP 2011; EMWD 2013; WaterFX 2014). This has particularly been the case in the State of California in the United States, where population growth and a productive agricultural industry coupled with frequent droughts have led to constrained water supplies and a heavy reliance on finite groundwater resources (Faunt 2009; Scanlon et al. 2012). Consequently, there has been increased use of brackish groundwater resources having TDS of 1,000–10,000 ppm. These waters can be treated for domestic and industrial use at a lower cost than desalination of seawater (GWI 1997; Leitz and Boegli 2011; EMWD 2013). In the southern San Joaquin Valley, one of the most heavily impacted areas in the state, these water resources are often located near oil fields where they are subject to protections from activities such as, water/steam injection, produced water disposal, and hydraulic fracturing.

Historically, state regulators have defined groundwater resources needing specific protection from oil and gas activities as those containing less than 3,000 ppm TDS. Page (1973) mapped the 2,000 ppm TDS boundary in the San Joaquin Valley. However, the 3,000 ppm TDS boundary was usually determined by oil operators on a well-by-well case via water samples or analysis of electric logs. A recent audit by US Environmental Protection Agency (EPA) of California of oil and gas underground injection practices noted that the state has not consistently used federal standards to delineate protected groundwater resources (US EPA 2012). Also, public concerns about hydraulic fracturing and the waste disposal practices of the oil and gas industry in general have led to new legislation (California Senate Bill 4 2013) that implements the federal 10,000 ppm TDS designation (40 Code of Federal Regulations § 144.3) as the threshold for protected waters. Because of these developments, the state needs to systematically map the location of groundwater resources near oil fields containing less than 10,000 ppm TDS to assist in identifying underground sources of drinking water (USDW), defined as nonexempt aquifers containing water with <10,000 ppm TDS (SWRCB Model Criteria 2015). Salinity mapping near oil fields is being conducted by the US Geological Survey and California State University as part of a program of the California State Water Resources Control Board to conduct regional monitoring of water quality in areas of oil and gas production (SWRCB 2014).

Geologic background

Sedimentation in the San Joaquin Basin is controlled by a combination of regional tectonics, sea level change, and sediment supply (Callaway 1990), with significant differences between the west and east sides of the basin. Deposition on the eastside of the basin is dominated by sediment supply from the Mesozoic Sierra Nevada continental arc, with modern altitudes up to 4,390 m (14,400 ft), while sedimentation on the westside of the basin is controlled mainly by development of the Cenozoic San Andreas Fault, northward transport of the faulted Salinian block of southern Sierra Nevada origin, and concomitant folding and thrust faulting (Reid 1995).

The eastside is divided into the Buttonwillow and Maricopa subbasins by Neogene development of the Bakersfield Arch (Kern Arch of Saleeby et al. 2013; Scheirer and Magoon 2007). In the southern Maricopa subbasin, sedimentation began in the Eocene on basement rocks of the Great Valley Ophiolite and Sierra Nevada granitoid metamorphic rocks (Ross et al. 1989; Bartow 1991) that were exhumed during the collapse of the southern Sierra Nevada (Saleeby et al. 2007). The Eocene sedimentary rocks are overlain by primarily marine Oligocene and Miocene sedimentary rocks which are, in turn, overlain by shallow marine and nonmarine deposits of latest Miocene to Pleistocene age.

The Fruitvale (Hluza 1961, 1965) and Rosedale Ranch (Betts 1955) oil fields are on the southern edge of the Bakersfield Arch. The deepest oil producing formation is the shallow marine Santa Margarita sandstone (Hluza 1965; Scheirer and Magoon 2007). It is overlain by the Chanac Formation which consists of nonmarine siliciclastic sediments (Scheirer and Magoon 2007) in three producing zones in the Fruitvale field: the Kernco, Martin, and Mason-Parker (in ascending order; Hluza 1965). The Chanac Formation is also productive in the Rosedale Ranch field where it is not differentiated into producing zones (Betts 1955).

In the study area, (Fig. 2) the Chanac Formation is overlain by the transgressive marine Etchegoin Formation, the basal portion of which is an important oil reservoir in both the Rosedale Ranch and Fruitvale fields. The base of the Etchegoin is marked by discontinuous sand beds that have been given local names (Scheirer and Magoon 2007): Lerdo in Rosedale Ranch (Betts 1955) and Fairhaven in Fruitvale (Miller 1940). These sands are overlain by the transgressive Macoma Claystone (Hoots et al. 1954) that thins and pinches out toward the south and east within the Fruitvale oilfield (Callaway 1990). The Macoma is a regional unit and acts as a hydraulic barrier in places. The Etchegoin Formation thins to the east, pinching out east of the Fruitvale field in the adjacent Kern River oil field (Bartow and Pittman 1983). Terrestrial depositional conditions resumed with the overlying fluvial Kern River Formation that grades basinward (westward) into shallow marine and nonmarine sediments of the Etchegoin, San Joaquin, and Tulare Formations (Scheirer and Magoon 2007).

Fig. 2

Cross section of geophysical well logs along A–A′ from Fig. 1. The black curves are spontaneous potential (SP) and the blue curves are deep-reading resistivity. Select geologic formations are correlated across the section. The Macoma Claystone, within the basal Etchegoin Formation, is a regionally extensive clay unit which acts as a hydraulic barrier

This area has been affected by pervasive Miocene extensional faulting, described by Bartow (1984, 1991) and Saleeby et al. (2016). It is not clear if the faulting is geodynamically linked to Miocene development of the Garlock Fault (Bartow 1991), or reactivation of older faults associated with the collapse of the southern Sierra Nevada (Saleeby et al. 2013; Sousa et al. 2016).

The shallow, unconfined to semi-confined aquifer system within the area is approximately 884 m (2,900 ft) at its thickest in the east and thins toward the west (Shelton et al. 2008). The aquifers occur within the Kern River Formation in the study area. Recharge is largely from the nearby Kern River that runs through the southern part of the Fruitvale field (Fig. 1). Other recharge is from artificial groundwater banking systems that are widespread throughout the region. Additional recharge comes from agriculture and municipal irrigation.

Methods

The following describes the available data sets and how each is used to construct the TDS model. Resistivity, porosity, temperature, and bicarbonate concentration data are used to make TDS predictions at discrete locations in the volume of analysis. Those values are interpolated throughout the entire volume using kriging. The TDS model is parameterized using mathematical optimization with the sum of squared residuals as the objective function to be minimized. Note that a similar method using borehole measurements for salinity estimation has been termed the resistivity-porosity (RP) method in some antecedent literature (Lyle 1988; Peterson 1991; Lindner-Lunsford and Bruce 1995; Schnoebelen et al. 1995; Hamlin and Rocha 2015; Gillespie et al. 2017).

Data

This work relies on the following six datasets, to be discussed in turn:

• 1. TDS measurements from produced water samples from 64 oil wells

• 2. TDS measurements from groundwater samples from 152 water wells

• 3. Borehole logs for formation resistivity from 40 oil wells

• 4. Porosity model inputs from 10 oil wells

• 5. Temperature model inputs from 37 oil wells

• 6. Bicarbonate model inputs from 27 oil wells

Figure S1 of the electronic supplementary material (ESM) shows the date distributions of datasets 1 and 3.

Dataset 1: produced water TDS measurements

Geochemical measurements of produced water samples from Fruitvale and Rosedale Ranch oil fields are used as the ground truth for TDS when setting the first-order parameters of the model (Fig. 1). The data come from a compilation of produced water chemical analyses (DOGGR 2017a), a Division of Oil, Gas, and Geothermal Resources (DOGGR) database for underground injection control (UIC) wells that includes data for the TDS of water for selected wells and zones, and the US Geological Survey National Produced Water Database (Gillespie et al. 2017; Metzger et al. 2018; USGS 2017). These data sources list data collected by well operators.

This dataset consists of 64 data points, each with x and y (denoting well location), z (elevation relative to sea level, as calculated from the depth of the top perforation of the well), and a TDS value. The data are available from Metzger et al. (2018). Counts by oil field and stratigraphic unit are shown in Table 1.

Table 1 Number of TDS measurements by oil field and stratigraphic unit

Dataset 2: water well TDS measurements

Historical geochemical analyses of samples from water wells in the area compiled by Metzger et al. (2018) provide an additional 152 TDS values (Fig. 1). Water wells are shallow compared to oil and gas wells and are typically used for irrigation or as domestic or public water supply. Bottom perforations range from 114 m (375 ft) above sea level to 112 m (367 ft) below sea level. These observations are used only to visualize TDS at shallow depths where the geophysical logs do not provide coverage. They are not used in the setting of model parameters because they are out of the coverage area of geophysical logs.

Dataset 3: borehole logs for formation resistivity

Borehole logs (also known as geophysical well logs or well logs) were obtained from the DOGGR website (DOGGR 2017b) as raster images, which were digitized to convert into numerical values with a commercial software program from Neuralog (Neuralog 2018). Most well logs prior to the 1980s lack the data needed to estimate formation porosity, but older logs such as these comprise the primary dataset due to their availability and spatial distribution in the study area (Fig. 1). These logs have readings for spontaneous potential (SP) and formation resistivity (R_t) with depth. Formation resistivity readings are essentially a depth-continuous measurement but, for this dataset, a discrete number of measurements, at depths that correspond to clay-free (“clean”) sands were chosen to minimize the impact of electrical charges present in clay minerals and associated bound water on the results. The clean sand zones were found by analyzing the SP curve and the deep and shallow resistivity curves (for details see p. 77, Asquith and Krygowski 2004). Measurements were discarded in the oil-bearing zone, which was inferred from the perforation interval, core analyses, mudlogs, and from driller’s notes when available. The presence of oil and gas causes resistivity to increase so that it does not accurately represent the resistivity of the formation water. This allows for the exclusion of the effects of clay and hydrocarbons and for the assumption that all resistivity measurements represent only rock and water.

From 40 wells (27 from Fruitvale and 13 from Rosedale Ranch), 364 data points are derived (Fig. S2 of the ESM), each with x and y (denoting well location), z (denoting elevation relative to sea level), and R_t (formation resistivity). The data are available from Stephens et al. (2018).

Dataset 4: porosity model inputs

TDS is inferred from R_t using Archie’s Equation (Archie 1942). This equation requires a value for the formation porosity, which for these purposes is defined as the relative volume of water in pore spaces, excluding clay-bound water or crystallization water (Ellis and Singer 2007). This quantity can be inferred by combining readings of a gamma-gamma density log and a neutron-porosity log (Asquith and Krygowski 2004). Since these logs are not available for most wells in the primary dataset, a porosity model is constructed for each oil field using logs from 10 wells with porosity logs, 5 for Fruitvale and 5 for Rosedale Ranch. This dataset consists of the continuous logs for each well (Stephens et al. 2018). The construction of the porosity model is discussed in the following section ‘Porosity model’.

Dataset 5: temperature model inputs

Like porosity logs, temperature logs are not plentiful in the study area; however, the maximum temperature within the borehole is generally recorded on well log headers. In zones not affected by thermal enhanced oil recovery operations, which are not used in the study area, the maximum temperature is assumed to be at the bottom of the well and can be used to calculate a temperature gradient within the oil field. This dataset consists of bottom hole temperatures and associated depths from 16 wells in Fruitvale and 21 wells in Rosedale Ranch (Stephens et al. 2018).

Dataset 6: bicarbonate model inputs

Log analysis procedures for determining TDS from resistivity assume the water is a Na-Cl type water. While this is the case for much of the study area, some zones within the Fruitvale field contain Na-HCO₃ type water. Because the electrical properties of chloride and bicarbonate are different, the model must account for elevated concentrations of bicarbonate where it occurs (Alger 1966; Chart Gen-4 in Schlumberger 2009, p. 5). Measurements of HCO₃⁻ concentrations from 27 oil and gas wells (Gans et al. 2018) are used to construct a bicarbonate model that is used within the TDS model to predict TDS within the Fruitvale field.

There are additional bicarbonate data from water wells in the study area, which were not used in the bicarbonate model. As with measurements of TDS from water wells (dataset 2) the bicarbonate data from water wells are out of the coverage area of the geophysical logs.

Porosity model

The porosity model gives predictions for sand bed porosity by depth in each of the two oil fields in the study area. It is constructed in four steps, all of which are conventional in well log interpretation (Asquith and Krygowski 2004; Ellis and Singer 2007).

First, the density log reading is converted into a “density porosity” by assuming the density of the rock matrix is known, via:

$$ {\phi}_{\mathrm{D}}=\frac{\rho_{\mathrm{ma}}-{\rho}_{\mathrm{b}}}{\rho_{\mathrm{ma}}-{\rho}_{\mathrm{fl}}} $$

(1)

where the terms are as defined:

ϕ _D :

Density-derived porosity (dimensionless)

ρ _ma :

Rock matrix density, assumed to be 2.65 g/cm³

ρ _b :

Measured formation density (g/cm³)

ρ _fl :

Fluid density, assumed to be 1 g/cm³

Secondly, density porosity and neutron porosity readings are compared to identify, for each well, the depths at which the sand is most likely to be clean (clay free). This is accomplished by only considering porosity measurements where the neutron and density curves are within 2% of each other, thus yielding 936 “sand points” for Fruitvale and 1267 for Rosedale Ranch.

Thirdly, density porosity (ϕ_D) and neutron porosity (ϕ_N) are combined via the root mean square formula from Asquith and Krygowski (2004) to obtain a composite estimate for porosity (ϕ_N − D) at each sand point, through:

$$ {\phi}_{\mathrm{N}-\mathrm{D}}=\sqrt{\frac{\phi_{\mathrm{N}}^2+{\phi}_{\mathrm{D}}^2}{2}} $$

(2)

Finally, lines are fitted to plots of ϕ_N − D versus depth for each oil field to obtain the porosity model (Fig. 3).

Fig. 3

a,c Porosity data. Many wells in the study area do not have porosity logs, which are needed for the TDS calculations. The porosity logs that are available were used to create a model to use for the wells without porosity readings in lieu of estimating with a constant porosity. b,d Temperature data. Temperature readings are also needed for the TDS model, but temperature logs are not common in the area. Temperature data are from well headers in electrical logs obtained from DOGGR (2017b)

Temperature model

The temperatures and corresponding depths were fit with a linear regression to create a temperature model for each oil field (Fig. 3). The equation of the best fit line was used to calculate a temperature at every depth for each of the wells in the analysis (Gillespie et al. 2017).

Bicarbonate model

The Fruitvale field has elevated levels of bicarbonate in produced water (Fig. S3 of the ESM). This is likely due to meteoric recharge brought into Fruitvale by the Kern River, which is also the reason Rosedale Ranch does not have high concentrations of bicarbonate. The plot of the ratio [HCO₃⁻]/TDS against the logarithm of TDS was fit with a sigmoid curve to model the fact that bicarbonate predominates when TDS is low, and tapers in significance as TDS increases (Fig. 4). The sigmoid’s lower asymptote is set to zero, and the upper asymptote is set to 0.73, which is the value of [HCO₃⁻]/TDS in a sodium bicarbonate solution. The sigmoid function was selected to model the bicarbonate fraction in TDS because the behavior at the lower and upper ranges of TDS could be controlled by setting the asymptotes. As noted already, the fraction of bicarbonate in a solution cannot exceed 0.73, and as TDS increases, chloride becomes the predominant anion and the bicarbonate fraction becomes insignificant (demonstrated by data from Kharaka and Hanor 2004), and this behavior could not be modeled with other functions (i.e. linear, polynomial, etc.).

Fig. 4

The relationship used to model bicarbonate. Generally, HCO₃⁻ predominates in water with lower TDS but, as TDS increases, the ratio between bicarbonate and TDS lowers and therefore bicarbonate has a smaller effect on the TDS predictions. The data were fitted with a sigmoidal function to capture the upper and lower bounds of this relationship properly. The upper bound is set to 0.73, which is the ratio of bicarbonate to TDS in a sodium bicarbonate solution. The lower asymptote was set to zero

The bicarbonate model is used within the TDS model to derive TDS estimations in zones where bicarbonate concentrations are significantly contributing to resistivity responses read from the well logs. TDS would be underestimated in these zones without this correction. The application of the bicarbonate model is discussed further in the following section.

TDS model

The TDS model takes resistivity readings at sand points as input, and incorporates outputs from the porosity, bicarbonate, and temperature models to derive a mean and variance for groundwater TDS at all points in the volume of analysis. It is constructed in multiple steps. To summarize:

• Archie’s law is used to estimate the resistivity of groundwater from formation resistivity, with input from the porosity model.

• Groundwater resistivity is converted to TDS values, with input from the temperature model and the bicarbonate model.

• TDS values are interpolated to the whole volume by kriging.

Using Archie’s law to find groundwater resistivity

Archie (1942) found empirically that in brine-saturated (hydrocarbon-free) sand beds, bulk resistivity and brine resistivity are related as follows:

$$ {R}_0=F\times {R}_{\mathrm{w}} $$

(3)

where the terms are as defined:

R ₀ :

Resistivity of 100% water-saturated rock (ohm-m)

F :

Formation factor

R _w :

Resistivity of the water (ohm-m)

The formation factor is related to the porosity of the rock by,

$$ F=\frac{a}{\phi^m} $$

(4)

where:

a :

Tortuosity factor

ϕ :

Porosity (dimensionless)

m :

Cementation factor

The parameters a and m vary by rock type and location. If they are known, and if porosity is known (or in this case, obtained from a porosity model), brine resistivity can be estimated by:

$$ {R}_{\mathrm{w}}={R}_0\left(\frac{\phi^m}{a}\right) $$

(5)

Ideally a and m are determined by lab analysis of borehole cores, which are not available in the study area. Instead, a and m for each oil field are determined from the optimized solution of the TDS model to fit laboratory TDS values of produced water. This is discussed in section ‘TDS model parameterization’.

From groundwater resistivity to TDS

Deriving TDS from the resistivity of a brine solution is a three-step process. Firstly, calculate the resistivity that the brine would have at 75 °F (Asquith and Krygowski 2004):

$$ {R}_{\mathrm{w}75}={R}_{\mathrm{w}}\times \frac{T+6.77}{75+6.77} $$

(6)

where T = temperature (degrees Fahrenheit).

Next, calculate the TDS (ppm) of a NaCl solution with this resistivity (Bateman and Konen 1978):

$$ {\mathrm{TDS}}_{\mathrm{NaCl}}={10}^{\left[\left(3.562-{\log}_{10}\left({R}_{\mathrm{w}75}-0.0123\right)\right)/0.955\right]} $$

(7)

Lastly, if needed, derive TDS from TDS_NaCl in zones where sodium and chloride are not the predominant ions. Bicarbonate and chloride ions have similar electrical mobility, but the greater molar mass of bicarbonate implies higher TDS for solutions with bicarbonate than for a pure NaCl solution, if resistivity is kept constant (Alger 1966). A conversion chart in conjunction with the bicarbonate model is used to derive TDS from TDS_NaCl.

To approximate the Schlumberger chart (Chart Gen-4 in Schlumberger 2009, p. 5), one can use the equation

$$ {\mathrm{TDS}}_{\mathrm{NaCl}}=\left[\mathrm{Na}\right]+\left[\mathrm{Cl}\right]+0.345\bullet \left[{{\mathrm{HCO}}_3}^{-}\right] $$

(8)

where TDS_NaCl is the concentration of a NaCl solution with the same resistivity as a brine that contains bicarbonate. Elsewhere a function f(TDS) that gives [HCO₃⁻]/TDS for TDS in the domain of interest was constructed (Fig. 4). Combining the two equations gives

$$ {\mathrm{TDS}}_{\mathrm{NaCl}}=\mathrm{TDS}\bullet \left[1-f\left(\mathrm{TDS}\right)\right]+0.345\bullet \mathrm{TDS}\bullet f\left(\mathrm{TDS}\right) $$

(9)

This simplifies to

$$ {\mathrm{TDS}}_{\mathrm{NaCl}}=\mathrm{TDS}\bullet \left[1-0.655\bullet f\left(\mathrm{TDS}\right)\right] $$

(10)

Since the target is TDS in terms of TDS_NaCl, the mathematical inverse of this relationship is desired, but a closed-form mathematical expression does not exist. Thus, fixed-point iteration is used to solve for TDS. This equation can be rearranged to get:

$$ \mathrm{TDS}=\frac{{\mathrm{TDS}}_{\mathrm{NaCl}}}{1-0.655\bullet f\left(\mathrm{TDS}\right)} $$

(11)

An approximation for TDS can be found by substituting for TDS_NaCl for TDS on the right-hand side:

$$ {\mathrm{TDS}}_{\mathrm{approx}}=\frac{{\mathrm{TDS}}_{\mathrm{NaCl}}}{1-0.655\bullet f\left({\mathrm{TDS}}_{\mathrm{NaCl}}\right)} $$

(12)

This approximation can be used to get a better approximation by resubstituting it for TDS:

$$ {\mathrm{TDS}}_{\mathrm{approx}2}=\frac{{\mathrm{TDS}}_{\mathrm{NaCl}}}{1-0.655\bullet f\left({\mathrm{TDS}}_{\mathrm{approx}}\right)} $$

(13)

This process can be repeated until convergence. In practice, five iterations suffice for a good approximation. Note when [HCO₃⁻] is zero, TDS_NaCl equals TDS. Applying this methodology to derive TDS from TDS_NaCl to account for bicarbonate improves the TDS model prediction error (discussed further in section ‘TDS model parameterization’).

Kriging TDS

The TDS values derived from borehole sand points are spatially discrete (Fig. S2 of the ESM). Three-dimensional ordinary kriging was used to interpolate log TDS (the logarithm of TDS), to obtain a mean and variance for this quantity at all points in the volume of analysis. The initial motivation for transforming TDS was to have an interpretation for negative interpolated values. Subsequently, examination of the orthonormal residuals (Kitanidis 1991), showed that log TDS comports with modeling assumptions much better than untransformed TDS, as is discussed in the following.

Kriging requires the analyst to choose a model for how observations (log TDS values) covary as a function of distance. An initial inspection of the measured TDS values helped to determine two aspects of the covariance structure. Firstly, it became apparent that the coordinate system could be made isotropic by scaling z (depth) up by a factor of 10 (Kitanidis 1997; Olea 2012). When measured TDS values are projected onto the A–A′ plane that crosscut both fields (Fig. 1), the TDS trends about as much from top to bottom as from side to side, and this plane has a height-to-width ratio of on the order of 10. Secondly, the apparent TDS trend suggests that log TDS lacks spatial stationarity in the mean, or at least that the volume of analysis was too small to warrant positing a stationary mean. Thus, a linear variogram model was used for log TDS (Kitanidis 1997), which has just two parameters, nugget (y-intercept) and slope. These parameters were set by fitting the experimental variogram (Fig. S4 of the ESM).

Variogram fitting and kriging predictions are performed using the Python software package PyKrige (Murphy 2018). PyKrige was also used to analyze krige residuals (Isaaks and Srivastava 1989; Kitanidis 1991, 1997), to verify the modeling assumption that the values being kriged obey a multivariate normal distribution. In this analysis, data points (x, y, z, log TDS) are put one at a time into the kriging model, but before each data point is put in, the model is used to predict log TDS at that location. The difference (the residual) is scaled by the square root of the prediction variance. If modeling assumptions are correct, the scaled residuals should have a unit normal distribution. By comparing the first four moments of this empirical distribution with that of a unit normal, it can be seen that taking the logarithm of TDS before kriging was correct in this case (Table 2).

Table 2 Scaled residual empirical moments, compared to unit normal moments

TDS model parameterization

As already described, the TDS model consists of four steps: Archie’s Equation, resistivity-to-salinity conversion, accounting for bicarbonate in Fruitvale, and kriging. Only the first part has parameters that cannot be derived from model inputs or set by general geological/geophysical knowledge. Resistivity-to-salinity conversion (the second part) has no parameters. The bicarbonate model (the third part) has two parameters that are used to fit a sigmoidal function to the bicarbonate and TDS data, but they are found by fitting the data with nonlinear least squares. Kriging (the fourth part) has three parameters: a z-scale for anisotropy, the nugget, and the slope of the variogram, but the z-scale was set by inspecting measured TDS values, and the nugget and variogram slope was set by computing the experimental variogram, and therefore kriging parameters are fully determined by model inputs. Archie’s Equation parameters (a and m) are the only parameters of the TDS model that remain free.

When borehole core analyses are unavailable, a common approach to setting a and m is to use values from a previous study where the rocks seem to be similar in description (Winsauer et al. 1952; Carothers 1968; Porter and Carothers 1970; Carothers and Porter 1971). The Humble parameterization (a = 0.62 and m = 2.15), established by Winsauer et al. (1952), is recommended for unconsolidated sands. Other settings often used are the Archie parameterization (a = 1.0, m = 2.0) and the Tixier parameterization (a = 0.81, m = 2.0), which are recommended for consolidated sands (Archie 1942; Lyle 1988; Asquith and Krygowski 2004).

To see how such an approach would fare, the model was run with the Humble parameterization, and made predictions for each of the 64 points of dataset 1. Figure 5a shows a cross-plot of predicted versus observed TDS values. The model tends to underestimate TDS, with a root-mean-square error (RMSE) of 0.42, but not in all parts of the study area. The predictions are fairly accurate in the in the Fruitvale field, but too low in Rosedale Ranch. A higher value for a would have caused predicted TDS values to be higher overall. The model was run with the Archie parameterization (a = 1.0, m = 2.0) and the results are shown in Fig. 5b. The RMSE dropped to 0.37 and the model now slightly overpredicts in the Fruitvale field.

Fig. 5

Cross plots of the measured TDS values (x-axis) and the predicted TDS values (y-axis). The black lines are the one-to-one lines. a Using the Humble parameterization (a = 0.62, m = 2.15). b Using the Archie parameterization (a = 1.0, m = 2.0). c Finding a and m through mathematical optimization to achieve the best fit to the measured TDS data (a and m values in Table 3)

These preliminary analyses suggest that a and m vary within the study area, and that a good model might have separate a and m parameters in each oil field. As for setting these parameters, since it is not known how the lithology of any zone compares to lithologies from previous studies, a practical approach would be to set the parameters by trying to match predicted TDS values with measured produced water TDS values. What needs to be decided, then, is how many a and m parameters there should be, and how to partition the volume of analysis. The zones should be numerous enough to account for any significant variation, but not so many that the calibration data is spread too thin. Two zones were selected by distinguishing between the two oil fields, so that each field is a zone. Each field was assigned a separate a and m.

Mathematical optimization is used to find settings for the four model parameters (a and m in each field). The sum of squared residuals (between predicted TDS and measured produced water TDS values) is the objective function to be minimized. This function incorporates the full TDS model (with Archie’s Equation, resistivity to TDS conversion, the bicarbonate correction, and kriging) and compares model outputs against produced water TDS values. Optimization results are shown in Table 3. With this parameterization, RMSE drops to 0.23, and there is no longer systematic over- or under-prediction of TDS (Fig. 5c).

Table 3 Results of TDS model parameter optimization

The geological justification for this approach is that the environment of deposition and/or sediment sources affects physical rock characteristics, which in turn determines a and m. For example, depositional environment can affect the shale volumes within sand beds, and greater shale content results in lower formation resistivity, which can be modeled by lower a values (Worthington 1993). Partitioning the volume of analysis allows the model to account for not only variable clay content, but also subtle differences in pore geometry and rock cementation that are represented by Archie parameters.

Cross-validation results show the estimated typical relative prediction accuracy for the area of analysis as a whole was found to be 22% (see section S1 in the ESM). Also, as noted before, applying the bicarbonate model within the TDS model improves performance—without the bicarbonate model the RSME is 0.30 compared to 0.23 with the bicarbonate model.

Because the input data set for the TDS model was collected over four decades, one must consider if there is a temporal bias in the data—for example, if groundwater TDS changes through time, older resistivity readings may not reflect later conditions. However, TDS model errors are not correlated with the dates the water samples were collected (Pearson r = −0.13, see Fig S1c in the ESM). This suggests there is no significant temporal bias in the data (see section S2 in the ESM for further discussion).

Results and discussion

Groundwater TDS distributions

To visualize TDS in the Fruitvale and Rosedale Ranch area, TDS values derived from borehole measurements (dataset 3) are combined with measured TDS from both oil wells and water wells (datasets 1 and 2), and are kriged to interpolate over the volume of interest. For visualization, the nugget was set to 0.033, which corresponds to a relative error of 20% in TDS, since this level of accuracy is typical for deriving TDS from borehole log analyses (Kong 2016; Gillespie et al. 2017). Figure 6a shows a cross-sectional view of interpolated TDS on the transect in Fig. 1 where it can be seen that TDS generally increases with depth, but is significantly different at similar depths along the transect. TDS begins to increase rapidly with depth in the Rosedale Ranch area at ~914 m (3,000 ft) below sea level and at ~1,158 m (3,800 ft) in the northwest portion of Fruitvale. Near the Kern River in the southern portion of the Fruitvale field, TDS increases only gradually throughout the depth coverage. To the northwest in the Rosedale Ranch area, groundwater reaches 10,000 ppm TDS at ~1,067 m (3,500 ft), whereas in the Fruitvale area to the southeast, 10,000 ppm TDS is reached at ~1,341 m (4,400 ft).

Fig. 6

a Cross section of groundwater TDS along the transect from Fig. 1. This figure uses measured TDS from oil and gas wells, the values from the TDS model, and TDS measurements from water wells. The field boundaries and location of the Kern River are marked along the cross section. b Kriging prediction certainty for log TDS along the cross section. Cooler colors represent lower kriging prediction standard deviation near the data points. The higher kriging standard deviations along the deeper portion is due to a lack of nearby data. Note the contour interval is not constant throughout the figure. The vertical exaggeration is 3.5

Interpolated values are more reliable when they are close to an observation. Since kriging infers a normal distribution for each interpolation, a more reliable interpolation is represented with a smaller standard deviation. Figure 6b plots the standard deviation of log TDS for the transect in Fig. 6a. When a borehole sand point, produced water sample, or water well sample lies nearer the transect, reliability is higher (cooler color) compared to areas where data are more distant, where reliability is lower (warmer color).

The 10,000 ppm TDS surface is visualized in map view using the TDS volume model (Fig. 7). The surface contours provide a map of the depth of potentially useable groundwater resources. The depth to the 10,000 ppm TDS boundary is ~1,067 m (3,500 ft) below sea level in the Rosedale Ranch area and deepens toward the southeast to ~1,341 m (4,400 ft). The elevation of the surface of the previous protected standard of 3,000 ppm TDS is also contoured in Fig. S5 of the ESM.

Fig. 7

Contoured elevation of the 10,000 ppm TDS surface

Potential controls on TDS structure

The distribution of groundwater salinity (Figs. 6 and 7) is controlled by several factors. Depth, faulting, groundwater recharge, and stratigraphy are the dominant controls (Kharaka and Hanor 2004; Gillespie et al. 2017). Generally, salinity increases with depth due to the water at depth having more time to interact with the rock and being less likely to be flushed by meteoric recharge. Faulting can provide preferential pathways for fluid migration or inhibit fluid flow via fault gouge, or by displacement causing nonpermeable beds to lie adjacent to permeable beds. Bedding planes, especially regionally extensive clay layers, are stratigraphic factors that can influence groundwater flow paths allowing for isolation of aquifer layers from one another. Faulting and stratigraphy can also influence movement of meteoric groundwater recharge, which typically has lower salinity than connate water—particularly in formations deposited in marine environments. Freshwater recharge likely becomes more significant when the recharge source is proximal. Characterizing these factors is necessary for designing data collection and analysis—for example, collecting data above and below low-permeability sediments is vital to model a salinity distribution accurately.

Formation data from Fig. 2 is superimposed onto the groundwater TDS cross section to investigate the factors controlling TDS in the study area (Fig. 8). Contours of groundwater elevation data from the California Department of Water Resources (DWR) show the water table in the study area sloping away from the Kern River, demonstrating that it is a significant source of groundwater recharge in the area (Fig. S6 of the ESM). The deepening of the 10,000 ppm TDS surface toward the river shown in Fig. 7 is consistent with deep hydraulic connections beneath the river, allowing freshwater input to replace the more saline connate water. However, the TDS surface slope is not orthogonal to the river, possibly due to groundwater flow complexities along fault planes and offsets (Fig. S7 of the ESM) and/or the orientation of the Macoma Claystone pinching out to the south-southeast (Figs. 2 and 8).

Fig. 8

Cross section from Fig. 1 showing groundwater TDS values with formation data superimposed from Fig. 2. It appears that TDS is fault controlled in the northwest, stratigraphically controlled in the center of the section, and freshened by meteoric recharge from the Kern River toward the southeast. Vertical exaggeration is 3.7

In the Fruitvale Calloway area (center of the cross section, Fig. 8), the surfaces of equal TDS approximately parallel the stratigraphy, which suggests the TDS structure in this area may be controlled by the stratigraphy. However, it is notable that a large range of TDS values exist laterally within the same formation (Chanac, deepest formation on cross-section); therefore, robust stratigraphic control cannot be assumed to always extend laterally. In this case, the Macoma Claystone in the lower Etchegoin Formation thins to the east (Figs. 2 and 8) and becomes less significant in its role as a confining layer, which may be the reason for stronger stratigraphic control in the west where the Macoma Clay is thicker and more consistent.

The TDS distribution may also be fault controlled toward the northwest. A major normal fault in the area is near the highest TDS lateral gradient between the Calloway area in northwest Fruitvale and the Rosedale Ranch area. A geologic cross section from Bartow (1984) shows a normal fault between the Fruitvale and Rosedale Ranch fields. However, the fault is not shown to penetrate the shallower part of the stratigraphic section shown on the TDS cross section. It may be that the major fault extends further up-section than shown in Bartow’s (1984) cross section, as faults commonly are difficult to map in fluvial sediments due to the lack of lateral continuity of these deposits. More evidence of these faults is explained in Saleeby et al. (2013), where normal faulting in this area is tied to southern Sierra Nevada delamination.

Additionally, Betts (1955) reports that Rosedale Ranch oil accumulations are structurally separated from Fruitvale reservoirs, resulting in Rosedale Ranch being designated as a separate oil field. The faults mapped within the Rosedale Ranch field, where well control is greater, offset layers at the same depths as the abrupt TDS gradient. Vertical displacements and fault gouge likely render these faults fluid barriers (Betts 1955). Low-permeability fault planes are common in low net sand-to-gross interval areas with high shale content. The hydraulic isolation provided by the major and minor faults in the area coupled with the presence of the thick, laterally extensive Macoma Claystone in the western part of the study area likely prevents freshwater recharge into the Rosedale Ranch field. This has resulted in groundwater with higher TDS at more shallow depths than waters in Fruitvale, thus suggesting that the larger Miocene faults within the study area have a significant influence on groundwater TDS structure—particularly in areas with thick, extensive clay layers. Future work could incorporate seismic data to confirm the role of faulting on salinity structure.

Conclusions

Groundwater salinity in the Fruitvale and Rosedale Ranch area varies significantly. The 10,000 ppm TDS boundary is reached at ~1,067 m (3,500 ft) in Rosedale Ranch and deepens to the southeast in Fruitvale to ~1,341 m (4,400 ft). The salinity variations are used to examine the factors that control groundwater salinity distributions. During larger-scale investigations, these variations are difficult to assess, and the factors cannot easily be considered; however, field-scale analyses with denser data sets can reveal the specifics of salinity distributions.

This study provides a realistic and effective approach to quantify formation water TDS with borehole geophysics and produced water geochemistry. Porosity and temperature models can help describe the gradients of these parameters needed to estimate salinity. The bicarbonate model demonstrates a method to estimate TDS using resistivity logs in zones with different water types. Measured geochemical data can be used to find optimal parameterizations for petrophysical equations through comparisons with the ground truth data at specific locations. Facies changes and lateral variability of permeability can require different a and m values—even within field-scale investigations. This study demonstrates faulting can significantly influence groundwater flow paths and thus cause significant salinity differences over relatively short distances. Therefore, it is vital to collect TDS data around known faults and low-permeable layers to ensure an accurate analysis. While the present study maps groundwater salinity in and around oil fields, it is expected that the method will be useful in any area with sufficient borehole geophysical log and water geochemistry coverage, leading to better salinity mapping to support groundwater quality management.