Introduction

Tracer tests are powerful and widely used methods to characterize the hydrogeological subsurface. Besides the detection of flow paths and structures, tracer tests are used to determine, among others, residence times and transport parameters (e.g., Käss 2004). The hydrogeologist can choose from a wide selection of tracer substances, for example salts such as sodium chloride (NaCl), (non-)fluorescent dyes (e.g., uranine, brilliant blue), colloids (e.g., microspheres) as well as isotopes (e.g., krypton-85; e.g., Käss 2004). Commonly, tracers in hydrology are assumed to be ‘ideal’ if their transport behaviour is equivalent to the water flow. This assumption is probably most acceptable for the stable isotopes of the water molecule elements, i.e., hydrogen H and oxygen O, as they represent the transport medium water H2O itself (e.g., Koeniger et al. 2010).

Measurements of naturally occurring stable isotope signatures can provide useful information about the hydro(geo)logy of a catchment (Clark and Fritz 1997). These environmental tracer studies are dealing with, among others, the quantification of groundwater flow and discharge including bidirectional surface-water interactions (e.g., Fette et al. 2005), the tracing of infiltration processes in the vadose zone (e.g., Adomako et al. 2015) and subsequently the estimation of recharge rates (e.g., Blasch and Bryson 2007) as well as the determination of flow and transport parameters (e.g., Sprenger et al. 2015). With focus on catchments in alpine regions, some remarkable studies (e.g., Schmieder et al. 2016; Meng et al. 2015; Ahluwalia et al. 2013; Earman et al. 2006) employed environmental isotopes for quantifying the contribution of seasonally occurring snowmelt to the total groundwater recharge. This hydrograph separation method requires significant isotopic differences between pre-event and event water as well as advanced knowledge about their spatial and temporal distribution and about contributions of other sources (e.g., surface storage, vadose zone; Klaus and McDonnell 2013).

Artificial isotope labelling is an alternative for sites not fulfilling these requirements or when the research question directly requires the active injection of tracers. For this, the isotope signature is commonly shifted by equilibration with deuterium oxide (2H2O, also known as D2O) or water-18O (H218O), i.e., artificially 18O-enriched water. 2H2O has been applied to the vadose zone (e.g., Beyer et al. 2015; Mali et al. 2007), porous aquifers, fractured rock aquifers and karstic aquifers before (e.g., Becker and Shapiro 2000; Luhmann et al. 2012; Maloszewski et al. 1999). In direct contrast, H218O has been employed in a very limited number of field-scale experiments only, mainly owing to the high price and limited availability of the material (e.g., Koeniger et al. 2010). Besides, the intended area of application for artificial pure H218O is human medicine, e.g., as a critically needed component for the synthesis of 18F-fluordesoxyglucose (e.g., Yu 2006), among others, required for positron emission tomography (cancer diagnosis, e.g., Ben-Haim and Ell 2009). Hence, the excessive use of pure H218O for hydro(geo)logical applications should be avoided.

The objective of this work is to provide a cost-effective alternative to the use of pure H218O. It is shown that collected precipitation water (in this study: snowmelt) can be easily applied as an actively injected, but naturally labelled, dual isotope tracer solution, which means that the hydro(geo)logist can employ 18O for artificial tracer tests without wasting precious resources. As numerous studies before demonstrated the water isotopes’ conservativeness in aquifers, this should also apply for the artificial injection of snowmelt. However, being virtually distilled water with low ionic strength, snowmelt provides another traceable signal—a very low electrical conductivity (EC)—therefore, the investigation focuses on the combined usage of δ2H, δ18O and EC. Firstly, column tracer tests under controlled experimental conditions and with well-defined test sediments are described. Secondly, a push-drift-pull tracer test with uranine-labelled snowmelt was performed to demonstrate the ‘active snowtracer’ approach on small field-scale under real-world conditions.

Theoretical background

Natural occurrence of water stable isotopes and snowmelt processes

The water molecule H2O can exist in multiple versions based on either stable or radioactive hydrogen and oxygen isotopes with different abundancies (e.g., Coplen and Shrestha 2016). Here, all stable molecule compositions except 1H216O (most abundant water molecule), 1H2H16O, 1H217O and 1H218O can be ignored in hydro sciences due to their extremely low natural abundancies (e.g., CIAAW 2015; Coplen and Shrestha 2016; Dansgaard 1964). Small mass differences due to different isotopic compositions result in slightly differing water molecule velocities and reaction rates, which leads to isotopic fractionation during meteorologically induced phase-change processes such as evaporation (e.g., Mook and de Vries 2001). The fractionation rate mainly depends on temperature during phase change and, combined with secondary effects (continentality, latitude and altitude), results in regional, seasonal and water-type-specific stable isotope signatures (e.g., Clark and Fritz 1997). On a global scale, isotope signature values for naturally occurring waters can cover an approximate range of ∆(δ2H) = 400‰ for hydrogen and ∆(δ18O) = 40‰ for oxygen (Dansgaard 1964).

Especially snow and meltwater samples are “considerably depleted [...] as compared to the annual mean of precipitation and groundwater” (Kendall and McDonnell 1998) mainly due to lower condensation temperatures during formation of solid precipitation, i.e., snow or hail. The isotopic stratification in new snow covers typically reflects the fluctuations of single precipitation events. Complex processes within the snowpack (recrystallization of snow grains, water-vapour-diffusion in the pore spaces, evaporation in the top layer due to solar radiation, snowmelt percolation to the lower layers) as well as external influences (wind, additional rainfall on the snow) can eventually lead to an isotopic homogenization over time (e.g., Stichler and Schotterer 2000; van der Wel et al. 2015). Besides, a significant enrichment of the snowpack in direct exposure to the atmosphere typically occurs during the melting due to a preferential release of lighter isotopes (e.g., Gustafson et al. 2010; Taylor et al. 2001). To estimate the isotopic signatures of the snowmelt and the remaining snowpack, a wide set of analytical models can be employed (e.g., Lee et al. 2010; Taylor et al. 2001).

The natural infiltration of snowmelt via the vadose zone is delayed due to the storage of the snow on the ground surface and often accompanied by isotopic fractionation due to, e.g., soil water evaporation (Adomako et al. 2015), while isotope signatures typically remain stable within aquifer systems, aside from mixing effects with other sources (Leibundgut et al. 2009).

Methods of stable isotope measurement and linear isotope mixing models

Stable isotope analysis (e.g., Isotope Ratio Mass Spectroscopy (IRMS) or laser-based spectrometers) focuses on the determination of the relative ratios between rare and abundant isotopes, i.e., the abundancy ratios (here: 2H/1H for hydrogen and 18O/16O for oxygen). Obtained ratios are recalculated to Delta notations δ2H for hydrogen and δ18O for oxygen, both given in parts per thousand (‰). Hereby, Eq. (1) (for δ2H) and Eq. (2) (for δ18O) are used for normalizing the values between two international standards: Vienna Standard Mean Ocean Water (VSMOW2) and Standard Light Antarctic Precipitation (SLAP2; e.g., Mook and de Vries 2001):

$$ \updelta {}{}^2\mathrm{H}=\frac{{\left({}{}^2\mathrm{H}/{}{}^1\mathrm{H}\right)}_{\mathrm{Sample}}-{\left({}{}^2\mathrm{H}/{}{}^1\mathrm{H}\right)}_{\mathrm{VSMOW}2}}{{\left({}{}^2\mathrm{H}/{}{}^1\mathrm{H}\right)}_{\mathrm{SLAP}2}-{\left({}{}^2\mathrm{H}/{}{}^1\mathrm{H}\right)}_{\mathrm{VSMOW}2}}\times \updelta {{}{}^2\mathrm{H}}_{\mathrm{SLAP}2} $$
(1)
$$ \updelta {}{}^{18}\mathrm{O}=\frac{{\left({}{}^{18}\mathrm{O}/{}{}^{16}\mathrm{O}\right)}_{\mathrm{Sample}}-{\left({}{}^{18}\mathrm{O}/{}{}^{16}\mathrm{O}\right)}_{\mathrm{VSMOW}2}}{{\left({}{}^{18}\mathrm{O}/{}{}^{16}\mathrm{O}\right)}_{\mathrm{SLAP}2}-{\left({}{}^{18}\mathrm{O}/{}{}^{16}\mathrm{O}\right)}_{\mathrm{VSMOW}2}}\times \updelta {{}{}^{18}\mathrm{O}}_{\mathrm{SLAP}2} $$
(2)

Here, δ2HSLAP2 and δ18OSLAP2 are the Delta notations of SLAP2 and equal to −55.50 and −427.5‰ vs. VSMOW2, respectively. The Delta notations of VSMOW2, i.e., δ2HVSMOW2 and δ18OVSMOW2 are both set to 0.0‰ by definition.

The samples in this study were analysed using a high temperature pyrolysis furnace (HEKAtech) coupled to a high precision IRMS system (Thermo Fisher Scientific). Three internal laboratory standards were periodically analysed alongside the samples and mean IRMS precision was better than ±1.0‰ for δ2H and ±0.15‰ for δ18O.

In a dual isotope system without concentration dependencies and with negligible fractionation processes (e.g., due to reactions), a simplified linear isotope mixing model approach can be employed to distinguish between up to three different water sources contributing to a sample (e.g., Phillips et al. 2005). A possible scenario (Fig. 1a) is the separation of natural groundwater (GW), tracer water (here: precipitation water, PW) and a known extraneous water (EW). In the case described in this article, mixture information of two components can be evaluated independently from each other and used as a mutual plausibility check (Fig. 1b).

Fig. 1
figure 1

Linear dual isotope mixing models for using precipitation waters (PW) as active tracers in groundwater (GW) systems: a with and b without inclusion of extraneous waters (EW)

Full size image

This ‘quality control’ can be done graphically using a δ2H-δ18O plot (e.g., Schmieder et al. 2016); if a sample is not scattered along the direct connection line spanned by the tracer and background signatures, then an (unknown) extraneous water source may have biased the test or the samples are corrupted. Alternatively, the respective water fractions can be calculated for each isotope system and compared to each other. Assuming known isotope signatures of the sample and both contributing sources (GW and PW), Eqs. (3)–(6) can be used (here: 2-component system, e.g., Phillips et al. 2005).

$$ {X}_{Z,\mathrm{Mix}}={f}_{Z,\mathrm{GW}}\times {X}_{Z,\mathrm{GW}}+{f}_{Z,\mathrm{PW}}\times {X}_{Z,\mathrm{PW}} $$
(3)
$$ 1={f}_{Z,\mathrm{GW}}+{f}_{Z,\mathrm{PW}} $$
(4)
$$ {X}_{Z,i}=\frac{R_{Z,i}}{R_{Z,i}+1} $$
(5)

and

$$ {R}_{Z,i}=\left(\updelta {\mathrm{Z}}_i+1\right)\times {R}_{Z,\mathrm{VSMOW}2} $$
(6)

Here, Z denotes the respective element (H or O). XZ,i (given as percentage by the number of atoms in a mixture, atom-%) is the abundancy of the rare isotope of element Z in the volumetric fraction fi (with i being GW or PW), while RZ,i and δZi are the abundancy ratios of a specific isotope in this fraction and its Delta notation. XZ,mix, RZ,mix and δZmix belong to the final mixture.

Experimental design for laboratory and field tests

Study site description

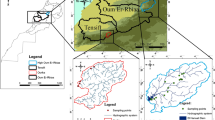
A fluviatile groundwater test site of Technische Universität Dresden (TUD) located in Pirna, Saxony, Germany—see Fig. 2, coordinates: 50°57′57″N and 13°55′25″E (centre of test site), ~20 km southeast of Dresden—was chosen as the study site. It was originally established to observe bidirectional interactions with the nearby Elbe River and is equipped with 1″ and 5″ (~2.5 and ~12.7 cm) groundwater observation wells labelled G and FI (see Fig. 2). Extensive investigations, including sieve analyses, direct-push (DP) injection logs and DP slug tests performed by Dietze and Dietrich (2012), indicate a highly heterogeneous lithology with a permeable lower section (mainly gravel and sand) and an overlying much less permeable section of varying thicknesses (sand, silt and gravel). Hydraulic conductivity (K) values based on the sieve analyses (Dietze and Dietrich 2012) vary over a large range from ~1.5 × 10−3 m/s (aquifer section) to ~2.5 × 10−7 m/s (overlying section), while a short-term pumping test at FI 7 resulted in a significantly higher K value of ~2 × 10−2 m/s for the aquifer section, again demonstrating the high K variability. Groundwater levels and river stages are highly connected with each other, which leads to fast changes of groundwater velocity and even direction (Händel et al. 2016).

Fig. 2
figure 2

Schematic map of Germany, with the location of the TUD groundwater test site in Pirna, Saxony, including a detailed view of the study site itself with locations of groundwater observation points. The two photographs (date: 15 February 2017) show the overall setup of the snowmelt push-drift-pull tracer test (using FI 7 for injection and extraction) and the actual measurement setup in detail. To the right, a simplified borehole profile at FI 7 observation point is depictured

Full size image

A low-maintenance rainwater totalizer with protection against evaporation (combination of the table tennis ball and paraffin oil methods as suggested by IAEA/GNIP 2014) was positioned in the western part of the site for long-term precipitation sampling. Between January and December 2016 (weekly sampling interval), water signature values from −21.1 to −89.1‰ for δ2H and from −3.0 to −12.6‰ for δ18O (vs. VSMOW2) were observed, whereby only rain and naturally melted snow samples were considered (i.e., no solid precipitation sampling). The natural infiltration process via the vadose zone eventually lead to a strong dampening of this amplitude in the groundwater (δ2H: −59.3 to −63.9‰, δ18O: −8.3 to −9.4‰, both vs. VSMOW2, same time scale and sampling interval).

Sediment and water sample collection

For the laboratory experiments (see section ‘Laboratory testing comparing snowmelt isotopes and EC’), two test sediments were mixed using materials obtained from a gravel and sand pit next to the study site for the aim of getting representative samples for the region. The first test substrate, a poorly graded sand with a small silt/clay fraction (hereafter called ‘sand with fines’) is intended to mimic the overlying less permeable section, while the focus of the second test substrate (well graded gravel with sand, hereafter called ‘sandy gravel’) is the aquifer section itself (Table 1).

Table 1 Test sediment composition and characteristics
Full size table

In the nearby city of Dresden, ~1 m3 of snowmelt, hereafter called ‘Dresden snow’, was gathered on 2 January 2017 almost immediately after a snowfall event. For this, ~9 m3 of fresh snow was collected over an area of ~1,500 m2 (coordinates: 51°1′40″N and 13°43′49″E) and melted in a foil-covered basin. This procedure, with reduced atmospheric contact, kept the isotopic shift (enrichment due to the melting process) at a minimum, and conserved the original isotope signature as much as possible. A small portion of the snowmelt was applied in the laboratory experiment (see section ‘Laboratory testing comparing snowmelt isotopes and EC’), while the majority was applied as tracer in the field experiment (see section ‘Field-scale applicability test’). Similarly, groundwater was extracted from observation well FI 5 at the study site, hereafter called ‘Pirna groundwater’, to function as the background solution in the laboratory experiments and as chaser in the field-scale push-drift-pull tracer test.

Laboratory testing comparing snowmelt isotopes and EC

To assess the combined migration performance of snowmelt in respect to δ2H, δ18O and EC under controlled experimental conditions, two laboratory-scale tracer experiments were realized. For this, two columns (inner diameter: 7 cm, length: 40 cm) were filled with the aforementioned sediments under fully water-saturated conditions. Subsequently, each setup was equipped with an EC sensor (flow-through cell, WTW) followed by an automatic system for isotope sampling and placed in a separate laboratory fridge (Liebherr, Viessmann) to simulate groundwater temperatures (~10.5 °C ± 0.5 K). Initially, both sediments were continuously flushed with Pirna groundwater until full ionic equilibrium between pore water and sediment was achieved (stagnant EC at column effluent end, ~20 total pore volumes exchanged). In the first test run, NaCl (~3.3 g/L) was employed as the EC-based reference tracer (see Table 2). After another resaturation period with Pirna groundwater (to restore the initial equilibrium conditions), the Dresden snow sample was injected (see also Table 2). The tracer propulsion was realized using a high-precision peristaltic pump (ISMATEC). Note that the flow rate was increased in the sandy gravel experiments (compared to the less conductive sand-with-fines sample) taking the significant K value difference into account (see Table 3 for further details). Isotope values of the samples taken were analysed using the IRMS setup mentioned in the theory section, and afterwards graphically checked for plausibility as described earlier. A final check regarding conservativeness was performed by inverse parameter estimation based on all observed breakthrough curves (BTCs)—for details, please refer to section S1 of the electronic supplementary material (ESM).

Table 2 Tracer types and measured parameters in the column tracer experiment
Full size table
Table 3 Further setup parameters for the column experiments
Full size table

Field-scale applicability test

Single borehole tracer tests are efficient tools for small-scale exploration and solute transport assessment (e.g., Kim et al. 2004). Here, a common approach is the push-drift-pull tracer method, which consists of up to four successive phases (e.g., Hebig et al. 2015). Firstly, the tracer is injected into the aquifer together with a well-defined amount of water (push), optionally followed by the injection of unlabelled water (chaser). Subsequently, the tracer is transported with natural groundwater flow (drift). Depending on the test’s scope and the parameters intended to be assessed, this phase can be skipped; however, it is quite common to wait until most of the applied tracer mass has entered the aquifer (if not already realized by the chaser). Finally, the former injection well is used for water extraction and concentration measurement (pull).

Using the described method, the collected Dresden snow additionally labelled with uranine was directly injected into the subsurface at the study site and extracted afterwards. Uranine was chosen instead of NaCl (as in the column studies) to enable capturing the low EC of snowmelt as additional tracer information within the same test. The initial difference of the isotope signatures between the snowmelt and groundwater were ∆(δ2H) = 61.0‰ and ∆(δ18O) = 8.2‰, respectively, while the EC difference was ~486 μS/cm (see Table 4).

Table 4 Experimental setup of the push-drift-pull tracer test at the study site in Pirna. Physicochemical properties and isotopic signatures
Full size table

Although a comparable modification of the isotope ratio can be achieved quite easily and inexpensively for δ2H by adding ~11 ml 2H2O (purity of 99.9 atom-%, ~10 USD/ml or less) to 1 m3 injection water, H218O with comparable purities is noticeably more expensive. The price range for H218O (98 atom-%, ~17 ml/m3 required) starts approximately one order of magnitude higher (the lowest rate found was ~80 USD/ml). Hence, minimum hypothetical material costs would be ~1,500 USD (excl. VAT, regionally available distributor, October 2018) for 1 m3 of 2H- and 18O-enriched injection water.

Observation point FI 7 was used for both injection and extraction (5″ inner diameter, screened from 10 to 13 m below surface level, see Fig. 2). Due to the relatively large well diameter and the gravel-filled well annulus, a chaser was applied to force the tracer out of the direct vicinity of the observation point. Water injection/extraction were realized using a rotary pump (Grundfos) and a deep-well submersible pump (Ebara), respectively. Pumping rates were determined using a magnetic flow meter (Endress+Hauser) plus a mechanical water meter (Metron), while several pressure sensors (Solinst) with data logging function were employed to record groundwater levels at surrounding observations points (Fig. 2). More information about the hydraulic and geometrical parameters is listed in Table 5. Isotope samples were analysed using the IRMS method, while uranine fluorescence and EC were determined using a flow-through field spectral fluorimeter (Albilia) and a flow-through EC sensor (WTW), respectively.

Table 5 Experimental setup of the push-drift-pull tracer test at study site in Pirna. Hydraulic and geometrical parameters
Full size table

Besides the evaluation via a δ2H-δ18O plot, all captured BTCs were evaluated for plausibility by reproducing them with a three-dimensional (3D) numerical flow and transport model. Thereby, the combined information of all tracer components was used as constraint; for details, please refer to section S2 of the ESM.

Results and discussion

Breakthrough behaviour of snowmelt in the laboratory experiments

Delta notation isotope values of the samples taken at the column outflows are shown in Fig. 3 (temporal behaviour and δ2H-δ18O plot) and as normalized BTCs in Fig. 4 (using Eqs. 3–6). Note that time is normalized to total pore volumes exchanged. As expected, the observed BTCs of both stable isotope-based tracer components of the snowmelt are nearly equivalent to each other (slight deviations from the theoretical values, see δ2H-δ18O plot) and to the BTC of NaCl (with only slight differences regarding the slope). In contrast, a significantly lower peak as well as a stronger tailing of the snowmelt EC can be observed, especially for the sand-with-fines sample. This may be explained by ion exchange directed from the sediment to the snowmelt filled pores in combination with mineral reactions, i.e., dissolution and precipitation.

Fig. 3
figure 3

a Temporal behaviour of δ2H and δ18O captured at the column outflows and b initial quality control via a δ2H-δ18O plot. IRMS precision is not shown due to the small values. The shown isotope data is available via figshare (Binder et al. 2018)

Full size image
Fig. 4
figure 4

Normalized isotope breakthrough curves (BTCs) of Dresden snow captured at the column outflows in comparison with the snowmelt’s EC and with NaCl. For better visibility, the isotope BTCs (as well as the model simulations) are shown in combined form due to very small differences. Only selected EC values are shown. This figure’s data is also available via figshare (Binder et al. 2018)

Full size image

Assuming the snowmelt water isotopes’ conservativeness within the laboratory experiments and taking the good match of the isotope BTCs with the NaCl BTC as well as the narrow bandwidth of the inversely optimized parameters (see section S1 of the ESM) into account, these first results support the postulated hypothesis, that snowmelt is a valid substitute for classical tracer substances including 2H2O and H218O. Besides, the isotopic shift during breakthrough of snowmelt is directed to a more depleted isotope signature, which allows for realizing an inverse tracer signal (relative to artificially enriched waters) which may be of interest for a more complex series of tracer tests. Similarly, the snowmelt’s EC can be considered as an inverse signal (compared to typical background EC values) as well. However, if EC itself is used as constraint for parameter estimation, possible biases by the aforementioned reactive processes must be considered.

Field-scale applicability test with snowmelt

The isotope ratios for hydrogen and oxygen measured in the samples taken during the pull phase of the field-scale experiment in Pirna are presented in Fig. 5 (Delta notation values including IRMS precision, quality control via δ2H-δ18O plot) as well as in Fig. 6 (normalized values) in comparison to the EC and uranine fluorescence.

Fig. 5
figure 5

a Temporal behaviour of δ2H and δ18O including IRMS precision captured at the extraction well FI 7 during the pull phase of the field-scale experiment. b Scatter plot showing the samples’ δ2H/δ18O data as well as the connection lines spanned by tracer and background. Local/Global Meteoric Water Lines (LMWL/GMWL) are shown for reference. The shown isotope data is available via figshare (Binder et al. 2018)

Full size image
Fig. 6
figure 6

a Normalized isotope data (δ2H, δ18O) during breakthrough of Dresden snow measured at extraction well FI 7 in comparison with the snowmelt’s EC and with uranine fluorescence (corrected with respect to the pH value). b Bandwidth of tracer recovery rates. This figure’s data is available via figshare (Binder et al. 2018)

Full size image

From start to the peak value of the BTC, a clear isotopic depletion in the samples can be observed for δ2H and δ18O, as expected followed by an enrichment after the peak. Only small differences between δ2H and δ18O breakthrough exist (see also the samples’ positions in the δ2H-δ18O plot), mainly due to measurement and sampling uncertainties. At the tracer peak, isotope values of −85.8‰ for δ2H and −11.7‰ for δ18O (both vs. VSMOW2) were observed, which equals ~39% of the initial amplitudes of ∆(δ2H) = 61.0‰ and ∆(δ18O) = 8.2‰. Hence, the signal-to-noise ratios between the observed peak and the precision of the used IRMS setup were ~24 (δ2H) and ~21 (δ18O) which results in a quite good and reliable resolution (see Figs. 5 and 6). Small discrepancies between the last samples and initial background isotope signature indicate that either the recovery of the tracer was not finished completely or that the spatial distribution of the background signature was not constant. Although the normalized peak concentration of the uranine breakthrough (see Fig. 6) is slightly smaller than observed for the isotopes, the rest of the BTC (especially the tailing) matches quite well. Note that the normalized uranine concentration is given in a pH-value-corrected form (according to Käss 2004), as the pH value of the snowmelt tracer (6.7–6.9) differs slightly from the background value (mean pH value of the groundwater in Pirna is ~6.3). Here, online logging without pH-value correction led to an actual fluorescence loss of 20–30%. For the breakthrough of the snowmelt’s EC, significantly smaller peak values were observed in the BTC, eventually leading to a smaller apparent tracer recovery rate. Again, mineral reactions combined with ion exchange are possible explanations for this observation; however, if referenced to the maximum observed value instead of the initial tracer value (not shown in a diagram), all BTCs are almost congruent.

Complementary to the laboratory findings, the observations in the small field-scale experiment in Pirna confirm the assumption of a conservative transport behaviour of snowmelt’s δ2H and δ18O to be valid also for active injections on the field scale. This rating is given based on the good match between both isotope components (as well as with the uranine breakthrough) and the inversely determined transport parameters (see section S2 of the ESM).

Conclusions and outlook

The snowmelt applications realized in this study show a quite conservative behaviour comparable to the established tracer substances NaCl (laboratory experiment) and uranine (field-scale experiment, including pH correction), shown by almost congruent BTCs. This is particularly true for the isotope components. Hence, precipitation water (here: snowmelt) can be used as an active and comparably inexpensive dual isotope tracer for laboratory and field-scale applications. Although subject to slight modifications caused by, among others, mineral reactions resulting in reduced peak values and reduced apparent recovery rates relative to the other tracer signals, the snowmelt’s EC signal can hereby serve as a still quite reasonable and easy-to-measure indicator for the breakthrough to purposefully select samples for later analysis of the more conservative stable isotope signature. This will help to keep the actual number of analyses within the scope of what is economically and technically feasible, at least if a continuously measuring on-site technique such as laser-based spectrometry (e.g., Berman et al. 2009) is not available.

A clear advantage of the proposed tracer method (compared to previous environmental isotope tracer studies and applications with common tracer substances such as dyes) is the detailed knowledge about the tracer input function combined with the conservative stable isotope tracer information. Large amounts of tracer water can be gained quite easily and economically. At the same time, the snow sampling procedure is a limitation as collection is only possible during snowfall season and atmospheric contact must be avoided during the snowmelt process to conserve the signature difference. However, snow can be collected in advance, melted and stored, which enables the application of a snowmelt tracer experiment also during summer time. On condition that the snow is not affected in its water quality during the sampling process (e.g., by using a cleaned collection area) or if the snowmelt is properly treated, the active snowtracer may also be used in areas with increased requirements (e.g., water protection areas), as no toxic or aesthetic impairments should occur.

More research should be done with respect to the modifications of the EC signal. Here, detailed knowledge about the reactive processes may be of interest for a characterization of the porous media. Besides that, further investigations should also be done with respect to other naturally occurring water sources (e.g., rain, surface water, water from alpine or arctic regions) and other sediment types. For both cases, hydrogeochemical modelling should be done to assess possible interactions between injection water quality and groundwater.