Introduction

Human health is at risk when microbes are present in groundwater-fed sources of drinking water. Borchardt et al. (2003) reported that diarrhoea in children in Wisconsin (USA) was correlated with drinking from a household well contaminated with faecal enterococci. Beller et al. (1997) traced an outbreak of gastroenteritis in Alaska (USA) to water consumption from a contaminated well. The disease burden of water-related infectious diseases is the most severe in developing countries (Batterman et al. 2009). In 2010, diarrheal disease caused an estimated 0.8 million deaths in children under the age of 5 years, with approximately half of these occurring in Africa (Liu et al. 2012). Sorensen et al. (2015) detected DNA from the pathogens Vibrio cholerae and Salmonella enterica (cause of typhoid fever) in 41 and 16% of the analysed samples, respectively, in groundwater in the city of Kabwe, Zambia. In developing countries, groundwater often provides the most important sources of drinking water (Pedley and Howard 1997). In Sub-Saharan Africa, where most of the world’s poorest countries are located, understanding of the mechanisms that cause faecal contamination of groundwater sources is still very limited (Kanyerere et al. 2012; Nyenje et al. 2013). It is thus imperative to improve guidelines and practices related to water and sanitation, particularly in Sub-Saharan Africa. For regions that lack water-quality data, the highest priority is to monitor the performance of improved (protected) sources (Abramson et al. 2013). As much as 86% of the population in low-income countries has access to such improved water sources (WHO/UNICEF 2012), which are typically derived from groundwater.

The current study focused on protected groundwater sources used for drinking water in Juba, the capital of South Sudan (Fig. 1). The analysis was based on the incidence of thermotolerant coliforms (TTCs) in samples from boreholes and hand-dug wells, collected in 2010 by the humanitarian aid organisation Médecins Sans Frontières-Belgique (MSF-B). The initial results of these investigations were presented by Engström et al. (2015a): 66% of the investigated sources, including 95 boreholes, were microbiologically contaminated at least once. The local topography and the accumulated long-term antecedent rainfall (5-day and monthly) were statistically associated with contamination events, in contrast with the wellhead drainage efficiency, the distance to the closest latrine, and level of short-term rainfall (Engström et al. 2015a). These findings indicated that the contributing groundwater had been contaminated. Hynds et al. (2014) made the distinction that there are three processes by which well water contamination can occur: generalized aquifer contamination, localized source-specific contamination due to rapid and/or shallow groundwater pathways, or direct ingress at the wellhead. Of these, the study by Engström et al. (2015a) addressed the latter two and the results indicated that direct ingress at the wellhead was not the main process. However, the importance of regional, as opposed to local, factors for groundwater contamination was not investigated. The significance of long-term precipitation suggested that contamination could have been caused by generalized aquifer contamination.

Fig. 1
figure 1

Location map (inset) of the study area based on WHO data (2014b), showing an approximation of actual country borders. Map of Juba from Google (2014), with data on urban subdivisions (purple text) and landmarks (red text) based on WHO (2014b) and Japan International Cooperation Agency (2009a; b) data

Full size image

Statistical models provide means to identify risk factors for groundwater contamination—for example, they can indicate the likely route of contaminant entry, inform future well siting and improve the screening of wells (Hynds et al. 2014). They can also help specify where future monitoring efforts are most needed and the results based on a particular site can be used to guide field investigations in other areas with similar hydrogeology and land use (Mair and El-Kadi 2013). Regression-based models are particularly useful in operational contexts (de Brauwere et al. 2014). Their use is common in the literature in studies on risk factors for microbial groundwater contamination, which have focused on: coliform bacteria in rural wells in Iowa, USA (Glanville et al. 1997), the link between Cryptosporidium and onsite wastewater systems and private wells in New Mexico, USA (Tollestrup et al. 2014), Escherichia coli (E. coli) in 211 wells in the Republic of Ireland (Hynds et al. 2014), E. coli in groundwater sources in northern, rural Malawi (Kanyerere et al. 2012), coliform bacteria in shallow wells in Ibadan, Nigeria (Oguntoke et al. 2013), TTCs and faecal streptococci in shallow groundwater in Kampala, Uganda (Howard et al. 2003), enterococci and TTCs in shallow groundwater sources in Lichinga, Mozambique (Godfrey et al. 2006), and faecal coliform and faecal streptococci in rural areas in Burkina Faso (Guillemin et al. 1991).

Typically, the data used to develop regression models are assumed to be statistically independent, with residuals between observations and model estimates that are independent and identically distributed (iid). However, spatial data have a tendency to be autocorrelated, which implies that the residuals vary systematically over space (LeSage 2000; Mörtberg and Karlström 2005). If spatial effects are ignored, the estimates of the coefficients and the inferences based on such models might be inaccurate. An important characteristic in the current study was that the sources were located relatively close to each other, which might result in spatial interactions between data points, particularly in the event of regional aquifer contamination. Recently, spatial statistics has received increased attention, with applications in geology, economics and epidemiology (Pinkse and Slade 1998). However, to the authors’ knowledge, spatial regression has not been used in research on risk factors for groundwater contamination.

The objectives of the current case study of Juba were to improve understanding of the factors that cause microbiological contamination of protected groundwater sources in areas with tropical climates, low incomes and high population densities and to advance hydrogeological research using statistical modelling as a tool to evaluate mechanisms of urban groundwater pollution. The study investigated the hypothesis that regression models of aquifer pollution should consider spatial autocorrelation when the sources are located near to each other. The risk factor analysis included land use, socio-economic factors and hydrogeological settings.

Methods

Case study area

The investigated groundwater sources were located in Juba, South Sudan, north of the equator in Sub-Saharan Africa. The country is afflicted with conflicts. Juba is segregated with locally dense, transient and low-income populations, as portrayed by the United States Agency for International Development (USAID 2005). Sudan’s Peace Agreement was signed in 2005, after which Juba experienced unprecedented population growth, inducing the expansion and proliferation of informal settlements (McMichael 2016). The area has a tropical climate, with a wet season that normally lasts from April through November and a dry season during the rest of the year. In the wet season, the monthly precipitation typically varies from 100 to 200 mm (Fig. 2). The rainfall events have short durations, lasting approximately 2 h, as described by the Japan International Cooperation Agency (JICA 2009a). In the dry season there is little rainfall, and the mean annual precipitation is approximately 1,000 mm. There is little variation in temperature across the wet season and temperatures do not vary largely between the wet and the dry seasons: the minimum monthly average temperature is approximately 20–25 °C, and the maximum monthly average temperature is 30–40 °C throughout the year; nevertheless, the maximum average monthly temperatures are somewhat lower in the wet season, based on 2006 data (JICA 2009a; Fig. 2).

Fig. 2
figure 2

Average monthly precipitation and temperature data from JICA (2009a), citing the Sudan Meteorological Authority

Full size image

Hydrogeology

Juba is on an alluvial plain that slopes from the Mount Jebel Kujur foothill (550 m a.s.l.) in the south–southwest towards the Bahr-el Jebel (the White Nile) in the north–northeast (450 m a.s.l.), with an average gradient of 0.5% (Fig. 3). During the wet season, flooding affects approximately half of the city and five seasonal streams, or wadis, appear and flow eastward towards the Nile: Luri, Khorbou, Lobulyet, Wallan and Kor Ramula—from north to south (JICA 2009a). At this time, stagnant water typically covers the area along the river, which has alluvial surfaces, wadi fills and swamp deposits (JICA 2009a). The city is underlain by undifferentiated basement complex, and aquifers are typically located in fracture zones in the weathered basement rock (Panagos et al. 2011; Sudan Ministry of Energy and Mines Geological and Mineral Resources Department 1981; Vail 1989). Superficial groundwater also occurs in sand and gravel layers of alluvial deposits and, at greater depths, local perennial or ephemeral aquifers can take place in thin, saturated layers  (JICA 2009a). Groundwater is recharged by rainfall and flooding of river water. As indicated by the sloping topography and the northward flow of the Bahr-el-Jebel, the direction of groundwater flow is expected to be from the south-west towards the north-east. Figure 3 shows a hydrogeological conceptual model of the area with two cross-sections.

Fig. 3
figure 3

Hydrogeological conceptual model of Juba, inferred from JICA (2009a) and borehole logs (MSF-B, unpublished data, 2013). Map of Juba and ground elevation data from Google Earth 7.1.7. 04°48.61596′N, 031°35.08757′E (2016). Lologo, Kator and Gudele are urban subdivisions, PHCC is short for Primary Health Care Corporation facility, and Al Sabah is a children’s hospital

Full size image

Variables and data sources

The spatial risk factor analysis included site-specific information and regional data, reflecting hydrogeological factors, land use, and socio-economics. The Appendix lists the variables used, their measurement units, and the corresponding reference.

Sample collection and analysis

The water quality data were collected by MSF-B during the wet season, from 6 April to 29 October 2010, with the purpose of identifying boreholes that could potentially spread cholera during outbreak events. Most of the sources were tested on two different dates, with approximately 3 months between sampling. Microbiological contamination was defined as >0 CFU/100 ml, in agreement with the WHO (2011) guidelines for drinking-water quality. To assess faecal contamination, water samples were analysed for TTCs using an Oxfam-DelAgua kit (Oxfam-DelAgua 2009). TTCs are considered acceptable indicators of faecal pollution (WHO 2011), because their populations are dominated by E. coli in most environments. The effect of this assumption was previously discussed in Engström et al. (2015a), which further contains a more detailed account of the water sampling procedure and the microbiological analyses.

Hydrogeological variables

The following hydrogeological characteristics were studied: marshlands, the Bahr-el-Jebel river and its tributaries, elevation above sea level, the local topography, and the static water level. The elevation and catchment areas were extracted using topographical data with 30 × 30 m resolution, based on the ASTER Global Digital Elevation Model (NASA Jet Propulsion Laboratory (JPL) 2011). The local topography was based on an on-site assessment by MSF-B at the time of the water sampling. This factor was represented as a Boolean indicator, set to 1 if a water source was located in a lowland area and 0 otherwise. Its importance was investigated using cross-tabulation, which tests the null-hypothesis that a table is independent in each dimension. The static water level was based on data obtained by MSF-B. Independently of the microbiological examination, groundwater sources were examined in 2008, 2009 or 2010 in MSF-B campaigns of boreholes drilling and rehabilitation in cooperation with the government of Southern Sudan, the Ministry of Cooperatives and Rural Development, and the Directorate of Rural Water (MSF-B, unpublished data, 2013). At these evaluations, the static water level was recorded. The static water levels obtained from the rehabilitation and the drilling protocols from 33 sites were used to estimate the depth-to-groundwater elsewhere in Juba (Fig. 3). The groundwater level was calculated by subtracting the static water level from the ground surface elevation, obtained from the ASTER Global Digital Elevation Model. An inverse distance-weighting algorithm was then applied. The resulting raster was subsequently used to extract the static water levels at the borehole locations that were sampled for coliform bacteria.

Land use and socio-economic data

Land cover information was defined via reports by USAID (2005) and JICA (2009a; b). Based on maps in those studies, four land cover categories were identified: bush, open ground or grassland, commercial and market areas, and roads or houses. Furthermore, socio-economic data were included using four land class categories, defined by USAID (2005) as follows: informal Tukul areas, which are low-income areas with squatter housing (532 inhabitants per ha); class 3–4 areas, with a transient, low-income housing mix of permanent and temporary materials (266 inhabitants per ha); class 2 areas, with middle-class cottage homes of simple construction, some with sanitation (200 inhabitants per ha); and Class 1 areas, with permanent structures and colonial-style homes with access to formal sanitation (128 inhabitants per ha). Additionally, the on-site hygiene level was accounted for in the regression. It had been categorized into three levels by MSF-B at the time of water sampling, as presented previously (Engström et al. 2015a). There were 129 water sources accounted for in the current study and 147 locations were evaluated in Engström et al. (2015a); however, spatial data could not be obtained for all sources.

GIS data generation

The spatial features were geographical information system (GIS)-derived using image processing operations on maps. Features were accounted for in variables reflecting shares of circular areas centered on each water source. Different radii were considered to investigate the effect of lateral contaminant transport (30, 100 and 500 m). In some cases, the feature was lacking in the smaller buffers and these radii were omitted from the statistical analysis. The regression also included variables reflecting the Euclidean distance from each water source to the nearest feature.

Statistical analyses

The statistical associations between contamination and the hydrogeological and anthropological risk factors were investigated. These tests were based on the two-sided Wilcoxon rank-sum test (or Mann-Whitney U-test). This identified the most important risk factors, which were subsequently considered in the multivariable models. The variables with individual significance of p < 0.10 were assessed in these models, in agreement with Mair and El-Kadi (2013) and Hynds et al. (2014). A probabilistic (probit) regression model was developed to estimate the probability of contamination related to these predictors. It included only the factors for which the relationship corresponded with prior theories. The occurrence, defined as the presence/absence of TTCs in 100-ml samples, was considered rather than concentrations, in accordance with Hynds et al. (2014), motivating a binary model with unquantifiable variability within the system.

Conventional probabilistic regression

In a probit regression model, the inverse standard normal distribution of the probability is described as a linear combination of the most significant explanatory variables. The conventional probit model assumes that the error terms are iid with constant variance. The probability of contamination of sample i, p i was thus estimated according to (LeSage and Pace 2009; LeSage 2000):

$$ {p}_i = P\left({Y}_i=1\right) = \Phi \left({{\mathbf{x}}_{\mathbf{i}}}^{\prime}\boldsymbol{\upbeta} \right),\;\mathrm{and}\;1-{p}_i = P\left({Y}_i=0\right) = 1-\Phi \left({{\mathbf{x}}_{\mathbf{i}}}^{\prime}\boldsymbol{\upbeta} \right) $$
(1)

for i = 1, …, n, where Y i is a random variable representing contamination, Φ is the cumulative distribution function of the standard normal distribution, x i is a vector of independent explanatory variables for sample i (assumed to be deterministic), β is a vector of parameters to be estimated, and n is the number of observations. Thus:

$$ {\Phi}^{-1}\left({p}_i\ \right) = {{\mathbf{x}}_{\mathbf{i}}}^{\prime}\boldsymbol{\upbeta} $$
(2)

for i = 1, …, n. An equivalent model, with a latent variable Y * i can be formulated as:

$$ {Y}_i^{*} = {{\mathbf{x}}_{\mathbf{i}}}^{\prime}\boldsymbol{\upbeta} +{e}_i $$
(3)

for i = 1, …, n, where the error terms e i are iid, and N(0, σ) and Y i indicates if Y * i is positive: Y i  = 1 if Y * i >0 and Y i  = 0 otherwise. Thus:

$$ {p}_i\left({Y}_i=1\ |\ {x}_i\right)={p}_i\left({Y}_i^{*}>0\right)={p}_i\left({{\mathbf{x}}_{\mathbf{i}}}^{\prime}\boldsymbol{\upbeta} +{e}_i > 0\right)=\Phi \left({{\mathbf{x}}_{\mathbf{i}}}^{\prime}\boldsymbol{\upbeta} /\sigma \right) $$
(4)

for i = 1, …, n.

Model evaluation and selection

The estimated β values maximized the natural log of the likelihood function L(β) considering each selection of explanatory variables, according to:

$$ \log L\left(\mathbf{y}\ |\boldsymbol{\upbeta} \right)={\displaystyle \sum_{i=1}^n}{y}_i \log \left({p}_i\right) + \left(1-{y}_i\right) \log \left(1-{p}_i\right) $$
(5)

where y i is the observed binary dependent variable. In this study, this represents microbiological contamination of sample i. The Akaike information criterion (AIC) Akaike (1973) was used to compare the models:

$$ \mathrm{A}\mathrm{I}\mathrm{C} = -2 \log {L}_{\max }+2k $$
(6)

where L max is the maximized value of the likelihood function and k is the number of covariates in the model. This criterion reflects the information lost when a particular model is used to represent the observations. The AIC decreases with higher goodness-of-fit, and increases with the number of model parameters. All combinations of the variables with individual significance of p < 0.10 were evaluated and the one that resulted in the lowest AIC was selected. This model was thus the optimal estimate in terms of both the selection of explanatory variables and the values of the corresponding coefficients β. To maintain as much information as possible, the whole data set was used for model development, in agreement with Mair and El-Kadi (2013) and Howard et al. (2003). The rationale was that there were relatively few data points and the purpose of the study was to make structural interpretations of the results to infer the key mechanisms that affect contamination, rather than prediction. A cut-off value for the probability of predicted contamination p i was specified at 0.5 by convention.

Testing for spatial autocorrelation

The effect of spatial autocorrelation is particularly important in binary-outcome models such as the probit model. In the presence of spatial interdependence, the standard maximum likelihood estimator of these models is miss-specified if the interdependence is ignored, because the spatial structure affects the error terms (Fleming 2004). Moran’s I (MI) test statistic (Moran 1950) is the most popular test for spatial autocorrelation (Kelejian and Prucha 2001). Kelejian and Prucha (2001) generalized Moran’s I to limited dependent variable models, allowing for heteroscedasticity in the error term, which results in the following probit specification (Amaral et al. 2012):

$$ \mathrm{M}\mathrm{I}=\frac{{\left({\mathbf{e}}^{\mathbf{\prime}}\mathbf{W}\mathbf{e}\right)}^2}{\mathrm{trace}\left(\mathbf{W}\ \Sigma \mathbf{W}\ \Sigma +{\mathbf{W}}^{\mathbf{\prime}}\ \Sigma \mathbf{W}\ \Sigma \right)} $$
(7)

resulting in the I-statistic:

$$ {I}^2=\frac{{\left({\mathbf{e}}^{\mathbf{\prime}}\mathbf{W}\mathbf{e}\right)}^2}{\mathrm{trace}\left(\mathbf{W}\ \Sigma \mathbf{W}\ \Sigma +{\mathbf{W}}^{\mathbf{\prime}}\ \Sigma \mathbf{W}\ \Sigma \right)} $$
(8)

where W is the weight matrix, with entries w ij that specify whether the locations i and j are neighbours and Σ is a diagonal matrix that contain the variances of the individual residual terms, i.e., between the observed values, y i , and the predicted values, \( \hat{\Phi_{\mathbf{i}}}=\Phi \left({{\mathbf{x}}_{\mathbf{i}}}^{\prime}\hat{\boldsymbol{\upbeta}}\right) \), according to \( {\sigma}_i^2 = \hat{\Phi_{\mathbf{i}}}\left(1-\hat{\Phi_{\mathbf{i}}}\right) \), with \( \hat{\boldsymbol{\upbeta}} \) as the Maximum-Likelihood estimated parameters. The variance is not constant because \( \hat{\Phi_{\mathbf{i}}} \) changes with x i . The weight matrix defines the spatial structure and should be specified based on theory (Mörtberg and Karlström 2005). In the current study, it reflected an estimate of the maximum lateral microbial travel distance in the aquifers in Juba. Two different weight matrices, W, were considered: one that accounted for lateral distance only, and one that additionally considered the direction of groundwater flow. In the former case, a source was defined as a neighbour if it was located within a radius of 300 m of the reference source; in the latter, a source was defined as a neighbour if it was located within 300 m and up-gradient or level with the reference but not lower than 2 m below it. By convention, the weight matrix was normalized, summing each row to unity and setting the diagonal to zero. Moran’s I ranges from –1 to 1 and a high value indicates a high positive autocorrelation, whereas a value close to zero indicates spatial independence. For zero spatial autocorrelation, Moran’s I is N(0,1) (Kelejian and Prucha 2001). Amaral et al. (2012) compared three test statistics proposed to reflect spatial error autocorrelation in probit models and found that Kelejian and Prucha’s (2001) generalized Moran’s I statistic performed the best.

Spatial probit regression

To develop the spatial probit model, a spatial autocorrelation parameter, ρ, was included in addition to the explanatory variables selected in the conventional probit models. The spatial error model is based on a spatial autoregressive error term, according to:

$$ {e}_i=\rho {\displaystyle \sum_{\mathrm{j}=1}^n}{w}_{ij}{e}_j+{\mu}_i $$
(9)

for i = 1, …, n, where the error terms are normal and iid μ i  ∼ N(0, 1), and ρ reflects the spatial autocorrelation: ρ = 0 for independent error terms and a positive value indicates positive autocorrelation. In the spatial probit, the probabilities, p i , are not independent and a multidimensional integral needs to be calculated, reflecting the number of observations (LeSage and Pace 2009; LeSage 2000). Thus:

$$ {p}_i\left({Y}_i=1\ |\ {x}_i\right)={p}_i\left({Y}_i^{*}>0\right)={p}_i\left({\mathbf{x}}_i^{\mathbf{\prime}}\boldsymbol{\upbeta} +{e}_i > 0\right)={p}_i\left({e}_i > -{{\mathbf{x}}_i}^{\prime}\boldsymbol{\upbeta} \right)={p}_i\left({e}_i\ /{\sigma}_i<{\mathbf{x}}_i^{\mathbf{\prime}}\boldsymbol{\upbeta} /{\sigma}_i\right)=\Phi \left({{\mathbf{x}}_i}^{\prime}\boldsymbol{\upbeta} /{\sigma}_i\right) $$
(10)

for i = 1, …, n. The individual error terms σ i are heteroscedastic and the vector σ follows a multivariate normal distribution with zero mean and variance-covariance matrix [(I –  ρ W)’(I –  ρ W)–1] (Amaral et al. 2012). The recursive importance sampling algorithm was applied to calculate the n -dimensional integral in the likelihood function and thus estimate the parameters in the spatial probit model. This method uses random draws of truncated normal distributions (Beron and Vijverberg 2004). This simulator is one of the most efficient techniques for estimating the likelihood function (Pace and LeSage 2011). Other alternative methods include Gibbs sampling (LeSage 2000), the generalized method of moments (Pinkse and Slade 1998), and the expectation-maximization algorithm (McMillen 1992). To assess the relevance of a spatial probit model, confidence intervals (95%) and p-levels were evaluated for the spatial parameter, ρ.

Results and discussion

Statistical evaluation

Individual analyses

The exploratory analyses showed that contamination was correlated with several factors, as in prior hypotheses (Table 1). The most important factor was related to the near proximity of Tukul areas. A Tukul is a circular dwelling made of mud with a roof with thatching such as straw and leaves; Tukul areas are low-income zones that are informally occupied by people from rural regions, as described by USAID (2005). Three related variables were significant at the 10% level: the distance to the nearest Tukul area (p = 0.002), the share of a 500 m radius buffer (p = 0.009), and the share of a 100 m radius buffer (p = 0.055). Note that the different z-value signs reflect the situation that a larger share of Tukul areas in the surrounding area was statistically associated with more contamination, whereas a larger distance to the nearest Tukul area was associated with less contamination. The results further indicated that the proximity of rivers or wadis might constitute a risk factor (p = 0.023), in accordance with prior hypothesis. Studying a peri-urban area in Malawi, Palamuleni (2002) found that the surface water was highly polluted and suggested that this might be attributed to the disposal of raw sewage and run-off from townships, the washing of diapers in the rivers, and workers using the river as a disposal system. The proximity of land class 3–4 areas, which have limited or no sanitation, was also associated with contamination (p = 0.059). In the current study, the sign of the correlation indicated that the proximity of open ground or grassland was correlated with a lower risk of contamination (p = 0.070). This agreed with prior hypothesis because open ground indicates fewer residences, which might indicate less sources of human and animal waste. In all but one instance, the evaluated factors followed the predefined hypotheses in terms of the signs of the test statistics (Table 1); however, the results indicated that a long distance to nearest marshland implied a higher risk for contamination (p = 0.096). One explanation could be that an inverse relationship could be seen between the location of Tukul areas and the marshlands, which were mainly found along the Nile, whereas the former were located closer to the Mt. Jebel Kujur (Fig. 1); in Juba, people rarely settle in the marshlands, which are prone to flooding. Nevertheless, all of the factors with p-values < 0.1 were included in the multivariable regression, because the final results were derived based on AIC. This criterion penalizes additional parameters and gives low scores to models with factors that do not add significantly to the variance in the responses.

Table 1 Results from the bivariate risk factor analyses: variables with p-values < 0.10
Full size table

Multivariable regression

In the conventional regression analysis, the model with the lowest AIC (model 1A) included three explanatory variables: the distance to the nearest Tukul area, the local topography, and the share of class 3–4 residence areas within a 100 m radius. The proximity of rivers or wadis was not significant in the multivariable regression, which was likely related to covariation with other factors. Further, these results indicated that the distance to open ground, grasslands and marshlands was not relatively important. Considering the Tukul areas, they showed that the three variables identified in the individual analyses were correlated (Table 1). In model 1A, the proximity of class 3–4 residence areas was not significant at the 5% level; therefore, another model was developed (model 2A), which was the model with the lowest AIC that included only significant explanatory variables at the 5% level. It accounted for the distance to the nearest Tukul area and the local topography. Explanations of the different models can be found in Table 2.

Table 2 Description of the different multivariable probit regression models developed
Full size table

The residuals of the conventional probit models were spatially autocorrelated. For model 1A, Moran’s I was 1.90 (I-stat 3.61) if a source was defined as a neighbour located nearby, and Moran’s I was 2.88 (I-stat 8.29) if a source was defined as neighbor only if it was found both nearby and upstream. Considering model 2A, the corresponding values were 2.08 (I-stat 4.31) for neighbours located nearby, and 3.05 (I-stat 9.28), for neighbours located nearby and upstream. These results indicated that spatial autocorrelation was stronger for the narrower definition of a neighbour, which excluded sources that were located downstream of a reference source. This was anticipated, considering the direction of groundwater flow. These results showed that subject knowledge is important to appropriately define the weight matrix when applying a spatial model.

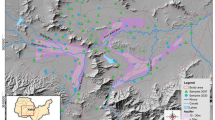
These findings thus indicated the presence of spatial autocorrelation in the residuals of a conventional approach, so spatial versions of models 1A and 2A were developed. Based on the MI values, two different definitions of contiguity were considered in these spatial models: in the first, a water source was specified as a neighbour if it was located nearby another source (models 1B and 2B); in the second, a source was considered as neighbour if it was located both nearby and upstream (models 1C and 2C in Table 2). Table 3 lists the parameter estimates in the different multivariable probit regression models, their standard deviations and t-statistics, as well as the log-likelihood of making the observations given the model parameters and the corresponding AIC. Considering the AIC, the latter models (models 1C and 2C) consistently performed better than former ones (models 1B and 2B). This was anticipated, considering the direction of groundwater flow and the Moran’s I values; the subsequent analysis therefore concentrates on models 1C and 2C. In model 1C, the spatial interaction parameter, ρ, was estimated at 0.48 (standard deviation, SD, 0.16), which was significantly above zero (p-value 0.004). In the case of model 2C, ρ was estimated at 0.50 (SD 0.15 and p-value 0.001). Introducing a spatial parameter improved the models: the lowest AIC obtained using a traditional approach was 158.31 (model 1A), whereas the spatial model with the highest goodness-of-fit was model 2C, with an AIC of 153.20. Furthermore, there was an important difference between the inferences drawn from the traditional and spatial models. The latter emphasized the relative importance of the presence of Tukul areas, whereas it reduced the importance of the local topography; this factor was no longer significant at the 5% level (p-value 0.074 vs. 0.040 for the conventional approach). Figure 4 depicts the location of such Tukul areas as well as the investigated water sources and their TTC contamination levels.

Table 3 The two best conventional models (models 1A and 2A) and the corresponding spatial models (models 1B, 1C, 2B, 2C) for explaining TTC contamination of water sources in Juba
Full size table
Fig. 4
figure 4

Uncontaminated and contaminated water sources (Juba map from Google Maps 2014) and the locations of informal Tukul areas, from USAID (2005)

Full size image

Contamination mechanisms and hydrogeology

The best model, the one with the lowest AIC, thus incorporated two explanatory variables: the distance to the nearest Tukul area (β 3), and the local topography (β 1) (model 2C). The siting of the Tukul areas, as specified by USAID (2005), was clearly approximate, seeing that the zones were circular (Fig. 4); nevertheless, considering the negative sign of β 3, these results reasonably indicated that if a water source was located at a far distance (measured in m) from all of the Tukul areas, then the susceptibility to contamination was substantially reduced. For water sources located in the Tukul areas the effect of the corresponding variable coherently disappears from the equation.

The statistical significance of a factor could either be linked to the presence of contaminant sources or to transport pathways; of these, it was likely that the effect of the near presence of Tukul areas was primarily related to the former. These areas typically have dense populations that reside in squatter housing and lack access to formal sanitation systems and the surrounding land is often used for rotational crops and subsistence farming (USAID 2005). In the proximity of Tukul areas, this suggests the high relative prevalence of animal and human waste, which provides sources of faecal coliforms. The Southern Sudan Commission for Census Statistics and Evaluation (2006) reported that 64% of the household population in the country used open-air spaces to dispose of human wastes. This part of the population is more likely to reside in informal Tukul areas than in the other zones where a larger share of the residents has access to sanitation.

To identify a region of impact of each feature, different buffer zones were considered in the GIS analyses. In the case of Tukul areas, the most significant factor in the regression reflected the Euclidean distance (Table 3); additionally, the shares of Tukul areas within 500 m radii circular areas around each source were more significant than those within 100 m radii areas (Table 1). This suggested that the characteristics of an area further than 100 m from a borehole might influence its level of contamination. This result thus indicated generalized aquifer contamination, a contamination mechanism articulated by Hynds et al. (2014). Consistently, Batterman et al. (2009) found that the spreading of water-related infectious diseases is related to both ecologic and socio-economic processes, and that distal causes should be accounted for to enable sustainable interventions.

Seeing the positive sign of β 1, the results moreover indicated that lowland areas were more prone to contamination than highlands or flatland (Table 3). In the regression model, this factor was represented as a dummy variable, disappearing from the equation for water sources located in highlands or flatlands, and the coefficient would supplement the intercept for water sources located in lowland areas, such as valleys. Assuming the presence of coliforms on the ground, this could be related to ponding in such areas, considering that Engström et al. (2015a) reported that the level of accumulated long-term precipitation was associated with contamination. The hydrogeology in Juba might allow for groundwater pollution. Basement complex aquifers generally imply large variations in groundwater velocities and vulnerability to contamination (Morris et al. 2003). Geological profiles from drilling protocols (MSF-B, unpublished data, 2013) specified that the top soil in Juba contained alluvial sediments with sand, loam, clay and weathered rock, which was underlain by rock of various degrees of weathering, and that the distance to the rock had large local variations. Lineaments in fractured rock do not provide substantial natural protective layers to reduce contamination (Kanyerere et al. 2012). Particularly, laterite zones near the surface can be quite transmissive and unconfined aquifers can enable contaminant transport from the ground towards the water table in a matter of days or weeks, with low attenuation potential and high to extreme pollution vulnerability (Morris et al. 2003).

The water samples considered in this study were collected by MSF-B to monitor the evolution of potential cholera outbreaks and identify high-risk water sources. The sampling focused on areas previously affected by cholera, Kator and Munuki, where all of the water sources were tested. In developing countries, cholera is typically transmitted through water, and infected people could transmit the disease to other individuals via faecal contamination of water (Sack et al. 2004). It is thus reasonable to expect that boreholes contaminated with faecal indicators, such as TTCs, are more likely than clean ones to transmit cholera. Vibrio cholerae and TTCs have important similarities: they are gram-negative, facultatively anaerobic, and have similar size and shape (Cabral 2010), indicating that the strains would be transported in the same manner underground; however, this link requires further research. Nevertheless, the results could support future efforts that aim to reduce diarrheal disease. Cholera outbreaks have taken place in the South Sudan region every year from 2006 to 2009 and in 2014 (WHO 2014a). It remains a public health threat in Sub-Saharan Africa. According to Mengel et al. (2014), Sub-Saharan Africa accounted for 86% of reported cases of cholera and 99% of deaths due to cholera worldwide in 2011 (excluding the Haitian epidemic).

Spatial regression

This is the first study to use spatial regression models to assess risk factors for groundwater contamination, to the authors’ knowledge. Hence, there was no previous literature to refer to when specifying the spatial model. The weight matrix should reflect the distance within which the response data are correlated. In theory, the groundwater in Juba might originate from the whole upstream Nile river basin, which would imply a vast zone of impact for each borehole and the possibility of spatial correlation among boreholes located very far from each other. However, the zone of impact would be limited by the fact that faecal coliforms typically die after 20 days in the field at 20–30 °C temperatures, based on Westcot (1997); nevertheless, it is not obvious how this would translate to distance, as discussed more thoroughly by Engström et al. (2015b). Notably, aquifers in weathered basement complexes often have anisotropic properties related to the orientation of the fractures, and pumping from boreholes could induce constricted and elongated zones of contribution (Tearfund 2007). In the current study, as an approximate approach, the presence of a water source within a fixed 300 m distance from a reference was defined as a neighbour and sources further away were not, which allowed for relatively lengthy transport. Shorter transport distances might also have been relevant. Hynds et al. (2012) estimated that the approximate zone of impact of septic tanks extended up to 110 m up-gradient of the wellhead, if high 120-h prior precipitation rates were considered. Conversely, in a review, Pang (2009) reported that the maximum observed E. coli transport distance was as great as 920 m, for sewage polluted groundwater in gravel aquifers in Burnham, New Zealand, at velocities as high as 56–153 m/day (Sinton 1980). Future studies might investigate the cut-off distance for spatial autocorrelation as related to microbial transport in different hydrogeological environments.

The results in this study indicated that a spatial model might be more adequate than one that assumes all data are independent in space. The findings thus contribute to research on risk factors for urban (or peri-urban) groundwater contamination because sources that provide water in such areas are likely to be densely located. This is especially notable because groundwater provides an important component of the water supply system in 12 of the world’s 23 megacities (>10 million inhabitants) (Hirata et al. 2006); in particular, groundwater is an essential water source in peripheral, poorer parts of many cities, which often do not receive piped water or formal sanitation services (Hirata et al. 2006).

Limitations

The regression resulted in 67% correct predictions using the model with the lowest AIC (model 2C). This was relatively low, indicating that the investigated features did not account for the whole variance in the response variable, which might be an effect of the low resolution of the maps. Other factors than those considered in the current study may have also influenced the water quality.

Data resolution

It is reasonable to expect that microbial contamination of groundwater sources is particularly prevalent in urban areas in developing countries; however, such environments are often relatively disorganized, imposing constraints on access to detailed spatial and temporal data. Batterman et al. (2009) stated that understanding of water-related infectious diseases in developing countries is often limited by knowledge and data gaps and that related analyses are often based on multiple and sparse data sets. The current study also faced some related restrictions. The Comprehensive Peace Agreement was signed between fighting parties in Sudan in 2005, ending decades of civil war. Few records of geological and hydrogeological surveys in Juba were centralized before 2005. The decades of conflict resulted in many internal refugees and very limited resources for systematic monitoring of environmental and socio-economic factors. Therefore, the analysis relied on reports by USAID (2005) and JICA (2009a; b) for spatial information. The resolution in these data varied. Furthermore, the report by USAID (2005) was developed 5 years prior to the sampling in the current study and spatial features could have changed during this time, which means that the exact location of features could not be determined. Instead, inferences need to be based on broad trends in the data.

Missing spatial risk factors

In the regression, it would be preferable to account for the hydrogeological settings in the vicinity of each water source, such as the bedrock and the subsoil characteristics. Fine-resolution spatial data on the location of fracture zones or lithology could not be found, as the accessible hydrological and geological maps were on a country scale. Groundwater levels in Juba had to be estimated based on interpolation of the registered static water level from a limited number of sources. The static water level reported in these protocols varied from 2 m to more than 20 m below ground, with large variations. It was anticipated that the local water table level would be associated with contamination. For example, Kulabako et al. (2007) reported that the level of faecal contaminants increased in areas in Kampala with a higher water table. However, in the current study, the static water level was not significant; nevertheless, the results do not exclude the possibility that local and/or ephemeral aquifers influenced contamination, considering that local variations might not be correctly estimated based on the 33 locations used for estimation of the static water level elsewhere in Juba. Further, the static water level was measured at times other than the microbiological sampling dates and there could be seasonal variations. Future studies would thus preferably account for ephemeral and local aquifers.

Additionally, the results indicated that the proximity of houses or roads was not associated with borehole contamination; however, the map representing their locations did not thoroughly reflect the informal infrastructure in Juba, such as walkways and individual clay huts, which might be important. If possible, future studies should account for such data. Other potential risk factors include the number of users of each source and the locations of small-scale animal farming facilities or cultivated areas where manure might be used for fertilizer. Further, the distance to small ponds near each water source would preferably be included. Studying ponds in rural Bangladesh, Knappett et al. (2011) reported that the water in the majority of the ponds contained unsafe levels of faecal contamination, which was mainly attributed to the proximity of unsanitary latrines (visible effluent or open pits).

Time-variant risk factors

The current study focused on spatial factors, although temporal factors are also likely to be important. Results from Engström et al. (2015a) indicated that both the level of on-site hygiene and contamination of groundwater sources varied considerably with time. The latter was transient in 43% of the investigated sources, and the level of on-site hygiene was a significant factor for contamination in pairwise comparisons of the sources with varying contamination at different times (Engström et al. 2015a). Water sampling was consistently conducted in the wet season in the current study; nevertheless, there are weather variations in this period that might have impact on the susceptibility of wells to contamination. Engström et al. (2015a) found that accumulated long-term antecedent rainfall was associated with contamination events but temperature was not. It is therefore recommended that future studies in similar areas account for time-variant factors that might influence groundwater quality, particularly precipitation, in addition to spatial factors.

Summary and conclusions

This study investigated potential risk factors influencing bacterial contamination of urban groundwater sources. The evaluated variables reflected site-specific information as well as regional land use, hydrogeological setting and socio-economic characteristic data in Juba, South Sudan. A conventional multivariable regression model was developed. This approach resulted in residuals that had significant, positive spatial autocorrelation. Therefore, a spatial model was estimated in which the parameter that reflected spatial interactions was significant (p-value 0.001) and estimated at 0.50 (SD 0.15). This model accounted for the proximity of areas with informal settlements, Tukul areas, as well as the local topography (lowland/no lowland indicator variable). The results indicated that the groundwater below these zones was contaminated. Tukul areas lack formal sanitation systems, rearing animals is common and the surrounding land is often used for subsistence farming, which might explain the increased risk for contamination in their vicinity. The results suggested that generalized aquifer contamination occurred. It is recommended that future remediation efforts and monitoring schemes in cities similar to Juba—in terms of climate, hydrogeology and socio-economic characteristics—focus on such low income and informal settlement areas.

This study contributed to methodological development in the subject area. The results showed that statistical studies of groundwater quality should consider the effects of spatial interactions when the investigated sources are located near to each other. Introducing a spatial term could have important effects on the other parameters in the model. In the current study, the spatial model indicated that the local topography was not significant at the 5% level, in contrast with inferences based on the conventional model. However, when applying spatial regression, it should be emphasized that subject knowledge is important to define the weight matrix that reflects spatial interactions. In this study, the spatial parameter was more significant when the direction of groundwater flow was considered in defining the weight matrix. In the field of groundwater quality, research based on statistical models can inform decision making by identifying priority land-use types and prioritizing remediation efforts. In cities, groundwater quality data are unlikely to be independent in space because the water sources are often located near to each other. Future research should address the mechanisms for urban groundwater contamination; when using statistical models to do so, spatial effects should be accounted for. This is important considering that groundwater provides a large component of the water supply system in a majority of the world’s megacities.