Abstract
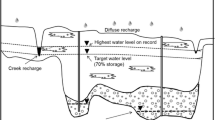
Groundwater has provided 50–90 % of the total water supply in Antelope Valley, California (USA). The associated groundwater-level declines have led the Los Angeles County Superior Court of California to recently rule that the Antelope Valley groundwater basin is in overdraft, i.e., annual pumpage exceeds annual recharge. Natural recharge consists primarily of mountain-front recharge and is an important component of the total groundwater budget in Antelope Valley. Therefore, natural recharge plays a major role in the Court’s decision. The exact quantity and distribution of natural recharge is uncertain, with total estimates from previous studies ranging from 37 to 200 gigaliters per year (GL/year). In order to better understand the uncertainty associated with natural recharge and to provide a tool for groundwater management, a numerical model of groundwater flow and land subsidence was developed. The transient model was calibrated using PEST with water-level and subsidence data; prior information was incorporated through the use of Tikhonov regularization. The calibrated estimate of natural recharge was 36 GL/year, which is appreciably less than the value used by the court (74 GL/year). The effect of parameter uncertainty on the estimation of natural recharge was addressed using the Null-Space Monte Carlo method. A Pareto trade-off method was also used to portray the reasonableness of larger natural recharge rates. The reasonableness of the 74 GL/year value and the effect of uncertain pumpage rates were also evaluated. The uncertainty analyses indicate that the total natural recharge likely ranges between 34.5 and 54.3 GL/year.
Résumé
Les eaux souterraines ont fourni 50–90 % de l’approvisionnement total en eau dans la vallée d’Antelope, en Californie (Etats Unis d’Amérique). Les baisses de niveau des eaux souterraines associées ont conduit la Cour supérieure de Californie du comté de Los Angeles a publié récemment une règle stipulant que le bassin des eaux souterraines de la vallée d’Antelope est dans une situation de surexploitation, à savoir que le pompage annuel excède la recharge annuelle. La recharge naturelle se compose principalement de la recharge sur la chaîne de montagnes et est une composante importante du bilan total des eaux souterraines e la vallée d’Antelope. Par conséquent, la recharge naturelle joue un rôle majeur dans la décision de la Cour. La quantité exacte ainsi que la distribution de la recharge naturelle sont incertaines, les estimations globales des études antérieures étant comprises entre 37 et 200 gigalitres par an (GL/an). Afin de mieux comprendre l’incertitude associée à la recharge naturelle et de fournir un outil pour la gestion des eaux souterraines, un modèle numérique d’écoulement souterrain et des affaissements de terrain a été développé. Le modèle transitoire a été calibré en utilisant PEST avec les données de niveaux d’eau et de subsidence; l’information préalable a été incorporée grâce à l’utilisation de la régularisation de Tikhonov. L’estimation calibrée de la recharge naturelle était de 36 GL/an, ce qui est nettement inférieur à la valeur utilisée par la Cour (74 GL/an). L’effet de l’incertitude des paramètres sur l’estimation de la recharge naturelle a été abordé en utilisant la méthode de Monte Carlo Null-Space. La méthode de compromis de Pareto a également été utilisée pour dépeindre le caractère raisonnable des plus grands taux de recharge naturelle. Le caractère raisonnable de la valeur de 74 GL/an et l’effet des débits incertains des pompages ont également été évalués. Les analyses d’incertitude indiquent que la recharge naturelle totale varie entre 34.5 et 54.3 GL/an.
Resumen
El agua subterránea ha proporcionado el 50–90 % del suministro total de agua en Antelope Valley, California (EE.UU.). Los descensos de nivel de las aguas subterráneas asociados han llevado recientemente a la Los Angeles County Superior Court of California a reglamentar recientemente que la cuenca de agua subterránea Antelope Valley está sobreexplotada, es decir, que bombeo anual excede recarga anual. La recarga natural se compone primariamente de la recarga en el frente montañoso y es una componente importante del balance total de las aguas subterráneas en Antelope Valley. Por lo tanto, la recarga natural juega un papel importante en la decisión de la Corte. La cantidad exacta y la distribución de la recarga natural es incierta, con estimaciones totales en estudios previos que van desde 37 hasta 200 gigalitros por año (GL/año). Con el fin de comprender mejor la incertidumbre asociada a la recarga natural y para proporcionar una herramienta para la gestión de las aguas subterráneas, se desarrolló un modelo numérico de flujo de agua subterránea y de subsidencia del terreno. El modelo transitorio se calibró usando el PEST con datos niveles de agua y de subsidencia; se incorpora información previa mediante el uso de la regularización Tikhonov. La estimación calibrada de la recarga natural fue de 36 GL/año, que es sensiblemente menor que el valor utilizado por la Corte (74 GL/año). El efecto de la incertidumbre de los parámetros en la estimación de la recarga natural fue abordada utilizando el método de Monte Carlo de espacio nulo. Un método de compensación de Pareto se utilizó también para discernir la razonabilidad de las tasas de mayores recarga natural. Se evaluó también la razonabilidad del valor 74 GL/año y el efecto de las tasas de bombeo inciertas. Los análisis de incertidumbre indican que la recarga total natural oscila muy probablemente entre 34.5 y 54.3 GL/año.
摘要
在(美国)加利佛尼亚州羚羊山谷,总供水量的50–90%为地下水。相关联的地下水位下降致使加利佛尼亚州洛杉矶县高等法院最近裁定,羚羊山谷地下水盆地处于超采状态,也就是说,每年的开采量超过了补给量。天然补给主要由山前补给组成,是羚羊山谷中地下水预算总额中重要的组成部分。因此,天然补给在高等法院决定中发挥着主要作用。天然补给的准确数量和分布不确定,根据先前的研究估算为每年37到200 千兆升。为了更好地了解与天然补给相关的不确定性并为地下水管理提供工具,建立了地下水流和地面沉降数值模型。采用PEST用水位和沉降资料对瞬时模型进行校准;通过采用吉洪诺夫正则化合并先验信息。校准过的天然补给估算量为每年36千兆升,明显少于高等法院采用的值(74千兆升/每年)。参数不确定性对天然补给量估算的影响采用零空间蒙特卡洛法进行处理。还采用了帕累托的权衡方法描述较大天然补给量的合理性。还对每年74千兆升值的合理性及不确定抽水量的效果进行了评估。不确定性分析表明,总的天然补给量很可能在每年34.5到54.3千兆升之间。
Resumo
As águas subterrâneas forneceram 50–90 % do total de água de abastecimento no Vale do Antílope, na Califórnia (EUA). O declínio dos níveis das águas subterrâneas associado levou a Corte Superior de Los Angeles na Califórnia a decidir recentemente que a bacia de águas subterrâneas no Vale do Antílope está superexplorada, ou seja o bombeamento anual excede a recarga anual. A recarga natural consiste primariamente da recarga de frente de montanha e é um componente importante do balanço total das águas subterrâneas no Vale do Antílope. Desta forma, a recarga natural teve um maior peso na decisão da Corte. A quantidade exata e distribuição da recarga natural é incerta, com estimativas totais em estudos anteriores variando de 37 a 200 gigalitros por ano (GL/ano). Afim de melhor entender as incertezas associadas com a recarga natural e fornecer uma ferramenta para a gestão das águas subterrâneas, um modelo numérico de fluxo de águas subterrâneas e subsidência do terreno foi desenvolvido. O modelo transiente foi calibrado usando PEST com os dados de níveis d’água e subsidência; a informação anterior foi incorporada através do uso da regularização Tikhonov. A estimativa de recarga calibrada foi de 36 GL/ano, que é apreciavelmente menor que os valores usados pela Corte (74 GL/ano). O efeito da incerteza nos parâmetros de estimativa da recarga natural foi resolvido usando o método de Monte Carlo Espaço Nulo. Um método Pareto de permutação foi também usado para retratar a razoabilidade das altas taxas de recarga naturais. A razoabilidade do valor de 74 (GL/ano) e o efeito da incerteza das taxas de bombeamento foram também avaliadas. As análises das incertezas indicaram que a recarga natural total provavelmente varia entre 34.5 e 54.3 GL/ano.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Prior to 1972, groundwater had provided more than 90 % of the overall water supply in Antelope Valley, California, USA (Fig. 1). During this time, groundwater extraction was primarily used for agricultural purposes and reached a peak of approximately 500 gigaliters per year (GL/year) in 1951 (Leighton and Phillips 2003). Since 1951, urban groundwater use has increased significantly and agricultural use declined. By 1995, groundwater extraction resulted in water-level declines of more than 90 m and land subsidence of about 2 m in some areas of the basin. Even though the introduction of imported surface water in 1972 has alleviated some of the necessity for groundwater extraction, imported surface water is still relatively expensive and difficult to deliver to farms in the basin interior. Total groundwater extraction then declined to approximately 100 GL/year in 1995 (Leighton and Phillips 2003). Additionally, in recent years, agricultural demand has begun to increase once again. Therefore, as both urban population and agricultural practices increase, and if the quantity of imported surface water is limited, the demand for groundwater is likely to rise.
Recent increases in the demand for groundwater in the Antelope Valley, combined with continued storage reductions and land subsidence, have caused several entities, both private and governmental, to take legal action to ensure their rights to water. As a result, the groundwater basin has been adjudicated and the Los Angeles County Superior Court of California has subsequently ruled on a “safe yield” value of 135.7 GL/year (Los Angeles County Superior Court of California 2011) based on an estimate of total average annual natural recharge of 74.0 GL/year (Beeby et al. 2010a, b). As defined by the Court, “safe yield is the amount of annual extractions of water from an aquifer over time equal to the amount of water needed to recharge the groundwater aquifer and maintain it in equilibrium, plus any temporary surplus.” In order for the Court to make appropriate decisions regarding the management and distribution of groundwater extraction, the quantity, spatial and temporal distribution of natural recharge and return flow must be well understood.
The objectives of this study are to provide an improved estimate of groundwater recharge and to thoroughly assess its associated uncertainty. The groundwater-flow and land-subsidence model of Leighton and Phillips (2003) was updated and calibrated for this purpose (Siade et al. 2014). The three-layer model developed by Leighton and Phillips (2003) resulted in an estimate of total natural recharge of 37.4 GL/year and provided no quantitative estimate of the posterior uncertainty of this value.
The updated model developed for this study was calibrated systematically using the Gauss-Marquardt-Levenberg algorithm, which is embedded in PEST (Doherty 2010). The Tikhonov regularization technique was used to impose expert knowledge, or prior information, on the parameter-estimation process (Tikhonov and Arsenin 1977). Sources of non-uniqueness, including parameter correlation and insensitivity, can result in a significant degree of uncertainty associated with the model’s predictions. The primary prediction for this study is the total average annual natural recharge, which consists primarily of the subsurface groundwater flow entering the basin from the mountain fronts.
The nature of the predictive uncertainty of a model is typically explored using a Monte Carlo type of uncertainty analysis with the restriction that each realization reasonably calibrates the model (i.e., calibration-constrained Monte Carlo). However, recalibrating the model for a set of randomly generated parameter vectors can be computationally expensive. The null-space Monte Carlo (NSMC) algorithm, contained in the PEST software (Tonkin and Doherty 2009; Doherty 2010; Keating et al. 2010; Herckenrath et al. 2011; Yoon et al. 2013), reduces this computational burden using knowledge of the calibration null space, i.e., linear combinations of parameters that are not estimable given the chosen parameterization and the observation data provided. It is within this calibration null space that the vast majority of the parameter error or parameter uncertainty resides. The NSMC method was implemented in this study to evaluate the uncertainty associated with natural recharge that stems from parameter error.
The uncertainty associated with natural recharge was also addressed using Pareto techniques (Moore et al. 2010; Doherty 2010). This analysis portrays the degradation in model calibration at larger total volumetric rates of natural recharge. It is considered a Pareto curve because it illustrates a trade-off where decreases in model fit result when predicted values of natural recharge are increased. In addition to the Pareto method, a feasibility analysis was conducted to specifically address the reasonableness of the Court’s value for natural recharge (i.e., 74 GL/year).
Another source of uncertainty when making predictions of natural recharge resides in the structure of the model itself, e.g., coarse spatial and temporal discretization, improper boundary conditions, inappropriate representation of geologic formations, etc. In this study, a potential source of significant structural error resides in the a priori estimates of agricultural groundwater extraction. These rates are quite uncertain as they are not directly measured and are determined indirectly based on crop type, climatic conditions, etc. The effects of this potential structural error on predictions of natural recharge are also addressed in this study by simply considering a range of different scenarios and recalibrating the model for each scenario.
Description of study area
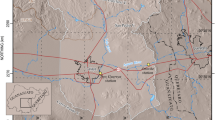
Antelope Valley is a topographically closed basin, about 80 km northeast of Los Angeles, California (Fig. 1). The valley is bounded on the south by the San Gabriel Mountains and on the northwest by the Tehachapi Mountains. Lower hills, ridges, and buttes form the northern and eastern boundaries of the valley. The valley floor slopes gently toward several playas north and east of the center of the basin. Land use in the valley is mainly urban, agricultural, industrial, and military; Lancaster and Palmdale are the largest cities. All natural channels are ephemeral; any surface-water runoff terminates in the playas. The climate in the valley is semiarid to arid. Estimates of precipitation and evapotranspiration (ET) throughout the valley floor indicate that ET significantly exceeds precipitation. Therefore, infiltration on the valley floor is assumed to be negligible and the primary source of natural recharge is the underflow entering the valley from the mountain fronts, along with any infiltrated overland flow along ephemeral stream channels (Siade et al. 2014).
Hydrogeology
Beneath the Antelope Valley floor exist large sediment-filled structural depressions between the Garlock and the San Andreas fault zones (Fig. 1; Leighton and Phillips 2003). The bedrock complex in the valley forms the impervious bottom of the groundwater basin and crops out at higher elevations, surrounding the valley. The bedrock complex is comprised of pre-Cenozoic igneous and Tertiary sedimentary rocks (Hewett 1954; Dibblee 1963). The basin fill consists of a series of unconsolidated deposits of Quaternary age, in some places more than 1,500 m thick (Benda et al. 1960; Mabey 1960; Jachens et al. 2014). Dutcher and Worts (1963) mapped these deposits as either alluvial or lacustrine. The alluvium consists of unconsolidated to moderately indurated, poorly sorted materials with the older, deeper units being more compacted and indurated than the younger shallow units (Dutcher and Worts 1963; Durbin 1978). The fine-grained lacustrine clay deposits consist of interbedded sands, silts, and clays that have accumulated in a large lake that periodically covered large parts of the valley center (Dibblee 1967; Orme 2003). These lacustrine deposits consist primarily of thick layers of a blue-green silty clay and a brown clay which contains interbedded sands and silts. These large clay beds are as much as 30 m thick and are interbedded with lenses of coarser material. The greater lacustrine deposits are overall as much as 90 m thick in some areas (Dutcher and Worts 1963). These lacustrine deposits are covered by as much as 245 m of alluvium in the southern part of the Lancaster subbasin; they become progressively shallower towards the northeast, and are exposed at the land surface near the southern edge of Rogers (dry) Lake (Fig. 2).
Antelope Valley contains numerous faults (Fig. 1), some of which may act as barriers to groundwater flow (Mabey 1960; Dibblee 1960, 1963; Dutcher and Worts 1963; Ward et al. 1993; Nishikawa et al. 2001; Leighton and Phillips 2003). In this study, the aim is to determine which faults act as barriers by estimating their conductance via parameter estimation; faults with a low estimated conductance act as barriers and vice versa.
Pre-development recharge and discharge
The primary source of natural recharge to the basin is infiltration of precipitation in the surrounding mountains, resulting in subsurface flow into the groundwater basin. Natural recharge may also occur as infiltration of runoff originating from the surrounding mountains in ephemeral stream channels. Since these two types of mountain-front recharge comprise the vast majority of natural recharge, they are together referred to, throughout this study, as natural recharge. Precipitation over the valley floor is low (less that 25 cm/year; Rantz 1969) while ET rates are high; therefore, recharge from direct infiltration of precipitation on the valley floor is considered to be negligible (Snyder 1955; Durbin 1978). Precipitation in the mountains is highly variable, but generally greater than 30 cm/year (Rantz 1969).
The quantity of natural recharge in Antelope Valley has been estimated in previous investigations based on rainfall, runoff, channel-geometry data, water-quality data, groundwater age dating, and groundwater-flow modeling. Bloyd (1967) estimated a natural recharge value of about 72 GL/year using the entire valley as the surface-water drainage area (1,445 km2), whereas Durbin (1978) estimated that natural recharge was about 50 GL/year, using only the Antelope Valley groundwater basin as the surface-water drainage area (997 km2). In a more recent study by Leighton and Phillips (2003), the annual natural recharge was estimated to be 37.4 GL/year.
The quantity, distribution and source of groundwater recharge were estimated for this study using the regional-scale basin characterization model (BCM; Flint and Flint 2007). The BCM used a deterministic water-balance approach to estimate recharge and runoff from the adjacent mountains. This approach incorporated the distribution of precipitation, snow accumulation and melt, potential evapotranspiration, soil-water storage, and bedrock permeability to estimate a monthly water balance for the groundwater system. BCM results are useful for providing bounds associated with water-balance results of more detailed models, evaluating long-term climate conditions, illustrating the mechanisms responsible for recharge in a basin, and comparing the locations and volumes of recharge and runoff in different basins on a regional scale (Flint et al. 2013). The BCM-estimated average annual natural recharge was about 63 GL/year.
Because the basin is topographically closed, predevelopment discharge from the Antelope Valley consisted primarily of ET in the lower parts of the valley where the water table was within 3 m of land surface (Lee 1912). Johnson (1911) mapped the areal extent of artesian conditions by observing numerous shallow flowing wells throughout the valley. The areal extent of significant ET is assumed to coincide approximately with this artesian region. A large area of alkali soils (Durbin 1978) and the existence of phreatophytes (e.g., mesquite) in the north central part of the groundwater basin indicate that the water table was near land surface at one time and that ET was significant (Thompson 1929).
Other types of predevelopment discharge from the basin included lateral groundwater underflow to adjacent basins and discharge from springs. Bloyd (1967) and Durbin (1978) claimed that groundwater underflow occurred in the northwest corner of the North Muroc subbasin into the Fremont Valley Basin. Estimates of this underflow were developed by Bloyd (1967) (0.1 to 0.6 GL/year), Durbin (1978) (1.2 GL/year) and Leighton and Phillips (2003) (0.5 GL/year). Discharge by springs was reported to be less than 0.4 GL/year (Johnson 1911; Thompson 1929).
Post-development recharge and discharge
The history of groundwater extraction throughout Antelope Valley has caused significant changes in the amount, distribution, and type of recharge and discharge. In addition to natural recharge, new sources of recharge have emerged including, irrigation return flow and infiltration of treated wastewater. Furthermore, ET has been replaced by groundwater pumping as the primary discharge from the valley.
Since the development of irrigated agriculture in Antelope Valley, large amounts of irrigation water have been applied to crops; a portion of this water may have percolated below the root zone and contributed recharge to the groundwater basin. Infiltration of treated municipal wastewater may also contribute to groundwater recharge, with the largest producers of treated wastewater being the Palmdale Water Reclamation Plant and the Lancaster Water Reclamation Plant (Templin et al. 1995; Fig. 1). Beginning in 1975, treated wastewater has been disposed of in ponds or on spreading grounds such that it either evaporates or infiltrates below the land surface.
Return flows from urban landscape irrigation and septic tanks in urban areas of the Antelope Valley are also potential sources of recharge to the groundwater basin. Previous US Geological Survey (USGS) investigations did not estimate the quantity of recharge contributed from this source; however, as part of the adjudication, return flows from landscape (non-agriculture) irrigation and septic tanks were estimated based on estimates of municipal and industrial water requirements for the period 1919–2006 (Beeby et al. 2010a, b; Appendix D).
The extraction of groundwater for irrigation in the Antelope Valley began in the 1800s; however, the quantity of groundwater pumpage was initially small. Beginning in 1915, the number of wells drilled for agriculture in Antelope Valley increased dramatically, resulting in appreciable increases in annual pumpage. By the 1970s, wells drilled for municipal and industrial use increased significantly (Leighton and Phillips 2003; Templin et al. 1995). Historical pumpage, from 1915 through 1995, was estimated by Leighton and Phillips (2003), who extended the work of Snyder (1955), Durbin (1978), and Templin et al. (1995; Fig. 3), and was used directly for this study. Annual pumpage for 1996 through 2005 was estimated by Siade et al. (2014) to extend the Leighton and Phillips (2003) pumping history. The agricultural component of total pumpage for 1996 through 2005 for Los Angeles County was obtained from the water purveyors themselves or the California State Water Resources Control Board (2011). Where reported data were not available for Los Angeles County, agricultural pumpage was estimated indirectly using irrigated crop acreage and crop consumptive-use data, similar to the techniques used by Leighton and Phillips (2003). Agricultural pumpage for all of Kern County during the 1996–2005 period was estimated indirectly since direct pumpage data was not available (Siade et al. 2014).
Graph comparing estimates of groundwater pumpage in Antelope Valley groundwater basin, California, 1915–2005. The estimates obtained by Leighton and Phillips (2003) were used for this study from 1915 to 1995. The pumpage from 1996 to 2005 was estimated using similar methods (Siade et al. 2014). Modified from Leighton and Philips (2003)
Land subsidence and aquifer-system compaction
Land subsidence is the loss of surface elevation as a result of the removal of subsurface support and is governed by the principle of effective stress and the theory of hydrodynamic consolidation (Terzaghi 1925). One of the principal causes of land subsidence is the gradual compaction of compressible aquifer systems resulting from declines in hydraulic head caused by groundwater pumping (Leake 1990; Galloway et al. 1998, 1999). Some of the detrimental effects of land subsidence include the loss of aquifer storage, increased risk of flooding, cracks and fissures, damage to man-made structures, and other intangible economic costs. The spatial variability in the amount of land subsidence in Antelope Valley is affected by both the magnitude of declines in hydraulic head, as well as the distribution of compressible sediments. Between 1930 and 1992, groundwater pumping in Antelope Valley has resulted in as much as 1.8 m of subsidence and a corresponding loss of groundwater storage capacity (Ikehara and Phillips 1994).
Groundwater flow and subsidence model
The three-layer model developed by Leighton and Phillips (2003) was updated for this study; the resulting model was used to address the uncertainty of natural recharge. The Leighton and Phillips (2003) model was updated to MODFLOW-NWT (Niswonger et al. 2011), which is a Newton formulation of MODFLOW-2005 (Harbaugh 2005) in which an upstream weighted finite-difference method is employed resulting in greater stability when simulating complex nonlinear systems, especially systems containing model cells that transition from dry to wet or vice versa. This is particularly important for this study as most of the natural recharge occurs along the mountain boundaries where the basin fill is relatively thin and the model often contains only one active layer. In these regions, the model is quite susceptible to having cells become dry or inactive during the parameter estimation process, which can lead to associated parameter estimation instability.
Model discretization
The hydrogeologic conceptualization developed by Leighton and Phillips (2003), using stratigraphic, hydrologic, and water-quality data since the early 1990s, was used as a starting point for this study, and is defined as follows. Their model consisted of three primary aquifer systems. The upper aquifer extended from the water table to an elevation of about 594.0 m above sea level (asl) and varied from unconfined to confined depending on the presence and vertical position of the thick lacustrine deposits within the aquifer (Fig. 2). The middle aquifer extends from 594.0 m asl down to 472.0 m asl and is either unconfined or confined by the overlying lacustrine deposits and the discontinuous interbedded aquitards in the upper aquifer. The lower aquifer extends from 472.0 m asl down to the bedrock complex. The lower aquifer is confined by the overlying lacustrine deposits and the discontinuous interbedded aquitards in the middle aquifer.
In order to adequately reproduce measured water levels throughout the north-central region of Lancaster subbasin, in the area of former Lake Thompson (Orme 2003), the three-layer hydrogeologic conceptualization developed by Leighton and Phillips (2003) was modified by dividing the upper aquifer into two aquifers. Data from electrical-resistivity logs in the area and geologic logs from a study of the region (CH2M HILL 2005), along with the findings of Johnson (1911), indicate the presence of a laterally extensive, confining, clay interbed throughout this region. This interbed was simulated in this study by dividing model layer 1, as defined by Leighton and Phillips (2003), into two model layers and assigning relatively low vertical hydraulic conductivity between the new model layers 1 and 2 (Figs. 4 and 5). Siade et al. (2014) describe the details of this layer subdivision.
Groundwater-flow and subsidence model geometry, horizontal discretization, active cells, flow barriers, specified-head and general-head boundary conditions, and zonation patterns for hydraulic conductivity and specific yield for the groundwater-flow and land-subsidence model, Antelope Valley groundwater basin, California: (a) layer 1, (b) layer 2, (c) layer 3, and (d) layer 4
Model-layer 1, therefore, represents the shallow portion of the upper aquifer in the Lancaster subbasin coincident with the area of former Lake Thompson. This layer represents a confining unit, and consists of unsaturated and saturated alluvial, lacustrine, and playa deposits. The bottom elevation of model-layer 1 was set to the approximate top of a 3–15 m thick clay, that occurs at an elevation of about 652–668 m asl, and was spatially distributed (interpolated or extrapolated) based on both the available electrical-resistivity logs and on a study conducted by CH2M HILL (2005) southwest of Rosamond Lake (Fig. 1). The study conducted by CH2M HILL (2005) indicates that water levels in wells perforated above this elevation have higher water levels than wells perforated below this elevation, suggesting that the clay layers above 652 m asl restrict the vertical flow of groundwater.
The uniform bottom elevations of Leighton and Phillips (2003) for layers 2, 3 and 4 (594.0, 472.0, and 305 m, respectively) were used, except where recent gravity surveys (Jachens et al. 2014) provided improved estimates of the lower no-flow boundary. Horizontally, the original model by Leighton and Phillips (2003) used square 1.6 km model cells, which were rediscretized for this study into square 1-km cells (Fig. 5).
The groundwater-flow model was used to simulate both steady-state (i.e., predevelopment) and transient conditions. The simulation period was extended from that of Leighton and Phillips (2003; i.e., 1915–1995) to the period 1915–2005. The steady-state results represent early 1900 conditions, which were assumed to represent predevelopment conditions in Antelope Valley. Simulated hydraulic head results from the steady-state model were then used as the initial conditions for the transient model.
Model boundaries
Recharge and pumping were simulated using specified-flux boundary conditions, and all other groundwater discharge was simulated using head-dependent boundary conditions. Head-dependent flux boundaries were used in the form of a time-variant specified-head (CHD package), general-head boundary (GHB package), ET (EVT package) and drain (DRN package) boundaries to simulate groundwater flowing into or out of the model domain (Harbaugh 2005). A CHD boundary condition was used to simulate flux exchanges with the Fremont Valley due to the presence of high quality hydraulic head data at the boundary itself, whereas, due to a lack of high quality data, a GHB boundary condition was used for exchanges with El Mirage (Fig. 5b). EVT boundary conditions are used to simulate discharge due to ET, and DRN boundary conditions are used to simulate flow through the playa surfaces via evaporation as well as through various springs throughout the valley. Reference-head values for the EVT and DRN packages are based on plant rooting depths and land-surface elevations, respectively (Fig. 6).
Specified-flux boundaries were used in the form of multi-node wells (MNW1 package; Halford and Hanson 2002), unsaturated zone flow (UZF1 package; Niswonger et al. 2006), and recharge (RCH package; Harbaugh 2005). The MNW1 package was used to simulate groundwater pumping. The MNW1 package internally calculates the vertical distribution of pumpage for wells that are perforated through multiple model layers. MNW1 also allows for water flow through boreholes that span multiple model layers. Groundwater recharge from agricultural irrigation is assumed to be 30 % of the water applied to crops (i.e., irrigation efficiency is assumed to be 70 % throughout the model domain). This return flow is applied at land surface using the UZF1 package in order to simulate delays associated with water traveling through the unsaturated zone. Groundwater recharge from imported surface water is assumed to occur near their respective turnouts, and the total annual water delivered to each turnout was obtained from the Antelope Valley East Kern (AVEK) water agency. Similarly, the irrigation efficiency for imported water was assumed to be 70 %. Recharge data from treated wastewater spreading ponds was obtained and modeled as an RCH boundary (Beeby et al. 2010a, b).
Urban groundwater recharge volumes and rates (which are considered to also contribute to return flow) were based solely on the temporal and spatial distribution and extent of the urban areas. That is, if a model cell is considered an urban model cell at a particular stress period, it is assumed to contribute groundwater recharge. This return-flow value is constant for all urban model cells; the assigned value of 182.9 mm/year is based on the estimated total basin-wide urban return flow calculated during the adjudication (Beeby et al. 2010a, b). Urban return flow is applied at land surface and the UZF1 package simulates delays associated with travel time to the water table.
Model calibration
The model-independent parameter estimation software PEST (Doherty 2010) was used to calibrate the groundwater-flow and subsidence model. The algorithm employed in PEST that was chosen for this study is known as the Gauss-Marquardt-Levenberg method (Levenberg 1944; Marquardt 1963). This algorithm is a nonlinear regression algorithm in which parameter values are iteratively updated until the sum of the squared residuals (i.e., the objective function) is minimized as much as possible. Parameter estimation for large-scale nonlinear systems containing many parameters can suffer from issues associated with nonuniqueness and insensitivity. In this case, the inverse problem is referred to as ill-posed or under-determined (Yeh 1986). To alleviate some of the issues associated with under-determination, Tikhonov regularization is employed (Tikhonov and Arsenin 1977). However, it is important to note that the PEST algorithm used in this work is a local-search algorithm and will not guarantee a global solution; therefore, the solution may depend largely on the quality of the initial guess of the parameter values.
Model parameterization
Horizontal and vertical hydraulic conductivity are assumed vertically anisotropic and horizontally isotropic and are assigned a value to each model cell. Horizontal and vertical hydraulic conductivity for layers 1–3 are assigned to model cells using the zonation patterns developed by Siade et al. (2014) depicted in Fig. 5; layer 4 is represented as one homogeneous hydraulic property zone. Specific yield is parameterized using the same zonation pattern as hydraulic conductivity, but specific storage is assumed to be homogeneous for each entire model layer.
Flow through the unsaturated zone is assumed to be vertical and is simulated with a kinematic wave approximation of Richard’s equation (Niswonger et al. 2006). The rate at which water fronts or waves move through, and accumulate in, the unsaturated zone is dependent on the saturated vertical hydraulic conductivity of the unsaturated zone (K uz), the Brooks-Corey coefficient, and the saturated water content of the unsaturated zone (Niswonger et al. 2006). The Brooks-Corey coefficient was set to 3.5 everywhere, which is consistent with the sedimentary deposits found in Antelope Valley (Tindall et al. 1999). The saturated water content was assumed to be a constant 25 %, a value just larger than the specific yield of typical Antelope Valley sediments. K uz was parameterized using zones that are consistent with the zonation patterns of hydraulic conductivity for layers 1 and 2 (Fig. 7).
The SUB Package was used to simulate land subsidence, which, in addition to instantaneous compaction, also allows for the simulation of delayed dewatering of the thicker, fine-grained interbeds (Hoffmann et al. 2003). The simulation of subsidence in the model assumes that compaction occurs from the deformation of the confining clay layers and the fine-grained deposits of the aquifers. The compressible deposits in model-layer 1 consist primarily of the visible playas on land surface; these deposits are assumed to compact instantaneously. The compressible deposits in model-layer 2 consist of the relatively young, thin, shallow interbeds that span most of the Lancaster subbasin and the older, thicker, deeper lacustrine deposits. The former is assumed to compact instantaneously and the latter is assumed delayed. Model-layer 3 consists of the relatively old, thicker lacustrine deposits and is assumed to have delayed compaction. Model-layer 4 was assumed non-susceptible to compaction because the continental deposits of this aquifer range from moderately to very well consolidated.
Storage and other subsidence-related properties must be defined in order to simulate subsidence. These included elastic and inelastic skeletal storage coefficients (S ke and S kv respectively, unitless), preconsolidation head, and the vertical hydraulic conductivity associated with the compressible deposits. S ke is the product of elastic skeletal specific storage and the saturated thickness of the compressible deposits; and, S kv is the product of the inelastic skeletal specific storage and the saturated thickness of the compressible deposits. The spatially distributed thickness of the lacustrine deposits was obtained from an interpolation and extrapolation of well-log data (Fig. 8). Assuming that these deposit thicknesses are known and entered directly as model input, only the specific storage values needed to be parameterized and were assumed homogeneous for each model layer. Because it is unknown, initial preconsolidation head is parameterized using pilot-point interpolation (Doherty et al. 2010) to produce a smoothly varying field; however, this interpolation is zoned based on model faults (Fig. 9).
Simulated thicknesses of compressible geologic units within each layer by type of compaction for the groundwater-flow and subsidence model of Antelope Valley groundwater basin, California: (a) instantaneous compaction thickness (layer 1 and layer 2), and (b) delayed compaction thickness (layer 2 and layer 3)
Pilot-point interpolation (Doherty et al. 2010) was used to distribute average annual natural recharge across the recharge model cells. The values assigned to the pilot points were treated as parameters. Each catchment depicted in Fig. 6 has a pilot-point interpolation zone associated with it. Most of the zones used in this process contain only a single pilot-point and, therefore, no interpolation is conducted (which is equivalent to using a zone for the parameterization). However, some catchments contain distinct channels in which some overland flow is observed during significant rainfall events. In these zones, the natural recharge is interpolated along the channel such that the magnitude of recharge diminishes as the channel extends into the model domain (Fig. 6).
Observation data
Observation data consisted of measured water levels in wells (Fig. 10) and measured changes in land-surface elevation, i.e., land-surface deformations (Fig. 11). Observed water-level data were used in two ways: as direct observations of hydraulic head and as observations of drawdown. Drawdown data were used in this study to highlight information about water-level dynamics by removing the impact of overall hydraulic head magnitudes. Land-surface deformations were measured at selected benchmarks (Fig. 11) by sequential leveling surveys, extensometer measurements, and interferometric synthetic aperture radar (InSAR) data. An extensometer located in Edwards Air Force Base (EAFB), known as the Holly site, directly measures compaction at this location and depth (Fig. 11).
Synthetic observation data are also added to control unreasonably high water levels that could potentially result in discharge to the land surface. Currently, MODFLOW-NWT is designed such that when the water table rises above the land surface elevation, surface leakage will occur (Niswonger et al. 2006). This phenomenon has not occurred in Antelope Valley since pre-development because of the appreciable depth to water in the model domain, with the exception of springs, which are being simulated using the DRN package. The potential for water to be lost to surface leakage presents a problem when conducting parameter estimation due to the fact that an unreasonably large amount of natural recharge can be specified in the model while achieving a reasonable level of calibration, because most of the water is leaving the model as surface leakage. In this study, this phenomenon is controlled by introducing a penalty into the objective function. This penalty is implemented in PEST as a series of above-land-control “observations”. Each model cell, where water should never rise above land surface, contains one of these “observations”. After each steady-state simulation within the parameter-estimation process, the distance between the steady-state water table and land surface is calculated in each model cell outside of the ET and DRN cells. If the steady-state water table is near land surface, a non-zero residual is assigned to the above-land-control “observation”. This residual then increases as the hydraulic head increases.
Tikhonov regularization
Tikhonov regularization (Tikhonov and Arsenin 1977; Doherty 2003) is a form of Bayesian estimation in which a composite objective function is minimized (Yeh 1986). This composite objective function consists of the sum of squared residuals discussed previously, which is often referred to as the least-squares objective function and a Bayesian term that penalizes the composite objective function when parameters deviate from their expected value:
where, Φ is the composite or overall objective function, Φr is the penalty function for parameter deviations from expected values, Φm is the least-squares objective function, and μ is the trade-off or regularization weight factor. Tikhonov regularization determines the optimal regularization weight factor given a modeler-specified level of calibration—that is, a desired value for Φm, denoted as Φ 1m . Therefore, the inverse problem is considered to have converged when Φm ≤ Φ 1m ; however, in practice it is often Φm ≈ Φ 1m . Throughout the process of achieving this, the Tikhonov regularization algorithm contained in PEST will determine the optimal μ such that Φr is minimized as much as possible (Doherty 2010).
Prior estimates, or expected values, of the model parameters throughout the Antelope Valley groundwater-flow and subsidence model are assigned, for the most part, using the values reported in Leighton and Phillips (2003). Additional parameters, resulting from the modifications of the Leighton and Phillips (2003) model made for this study, were assigned values based on professional judgment and geologic knowledge of the area. Prior estimates of natural recharge were obtained from the results of both the BCM model and the results of Leighton and Phillips (2003). The BCM results were important for providing prior information about the relative distribution of natural recharge, which was also used to develop the upper and lower bounds of each natural recharge pilot point. Any remaining parameters without prior information were assigned an expected value similar to nearby parameters of the same type. This association tends toward the use of a simpler model parameterization by interjecting a precondition for local homogeneity. There were a total of 203 independent parameters estimated for this study, which consist of 24 recharge, 92 hydraulic conductivity, 25 storage, 27 fault conductance, and 35 subsidence-related parameters.
Calibrated model simulation results
The comparisons between observations and their corresponding model-simulated equivalents for transient water levels and subsidence are displayed in Figs. 4, 12 and 13, respectively; additionally, detailed calibration results can be found in Siade et al. (2014). Overall, the model reproduces historical observations with a reasonable level of accuracy. Simulated hydraulic head contours for model-layer 2 (the principal aquifer for groundwater extraction) show good agreement with both water-level measurements and total simulated drawdown at the end of the simulation period (Fig. 14). Dividing model-layer 1 of the original 3-layer model by Leighton and Phillips (2003) into two layers allowed for improved simulated water levels in the Lancaster subbasin (Fig. 4). For example, water levels at two neighboring wells, 7 N/11 W-9P2 (9P2) and 7 N/11 W-21E1 (21E1; Figs. 4 and 10), could not have been simulated accurately if the model layer they are perforated in is vertically homogeneous. This is due to the fact that the impedance and confining effects of the shallow clay lenses in this area cannot be simulated with a vertically homogeneous model layer. Simulated total land subsidence also shows good agreement with observed land-surface deformation throughout the simulation period (Fig. 13); contoured results are displayed for conditions in 1951, when pumpage was at its maximum, and 2005 (Fig. 15).
The simulated hydraulic heads deviate from observed water levels in the northwestern region of the Finger Buttes subbasin and along the mountain-front boundaries in the Pearland and Buttes subbasins (Fig. 1). The model underpredicts the transient water levels in the northwestern region of the Finger Buttes subbasin by approximately 33 m at well 10 N/15 W-33D1 (33D1, Fig. 10). The large difference between simulated hydraulic heads and measured water levels could be due to the fact that the bedrock slope in this region is relatively steep, or to the presence of a previously unmapped fault downgradient of well 33D1. Additionally, the model significantly overpredicts the steady-state water level at well 08 N/16 W-10E1 (10E1, Fig. 10); this is also likely due to the steep slope of the bedrock or a misrepresentation of the fault structure in this region.
Discrepancies in the Pearland and Buttes subbasins are likely due to the fact that this entire region is simulated as a single model layer. Some of the observation wells in the Pearland and Buttes subbasins are also located near stream channels where natural recharge occurs (Fig. 10). The measured water levels in observation wells along the stream channels vary in response to wet and dry years; for example well 5 N/9 W-20 K1 (20 K1) in Pearland subbasin and wells 6 N/10 W-17 N1 (17 N1), 6 N/10 W-20P1 (20P1), and 6 N/9 W-30 F1 (30 F1) in Buttes subbasin (Fig. 10). Because natural recharge in the basin is simulated as an average, temporally constant distribution throughout the simulation (which is a valid assumption for this study), it is impossible to reproduce any subtle observed naturally occurring temporal variability in recharge rates.
The estimated total average annual natural recharge was about 36 GL/year. This is consistent with the value of 37.4 GL/year estimated by Leighton and Phillips (2003). However, this value was used as prior information, i.e., as a starting regularization target; therefore, there may be other values or predictions of natural recharge that also reasonably calibrate the model. This issue is addressed in the following section using systematic predictive uncertainty procedures.
Major components of the time-varying groundwater budget are shown in Fig. 16. Prior to significant groundwater development in the valley, the average annual natural discharge due to ET, groundwater underflow, springs, and evaporation through the playa surface was 28.5, 3.1, 1.9, and 0.1 GL/year, respectively. Additionally, at predevelopment (i.e., steady state), a small amount of water (2.3 GL/year) discharges as surface leakage in areas not mapped for spring discharge. This discharge likely did not exist and is perhaps the product of model-structure error; however, this rate of discharge is relatively small compared with the simulated total natural recharge (36 GL/year) and has little effect on the overall model-simulated results and estimated natural recharge.
About 18,500 GL of cumulative groundwater pumpage was specified during the transient simulation period of 1915–2005. The estimated cumulative depletion in groundwater storage is 10,700 GL. The decline in hydraulic head in the groundwater basin (Fig. 14) is the result of this depletion in groundwater storage. In turn, the decline in hydraulic head in the groundwater basin has resulted in a decrease in natural discharge from the basin and caused compaction of aquitards, resulting in land subsidence (Fig. 15).
Uncertainty of natural-recharge estimates
The model developed in this study can be used to help evaluate water-management scenarios throughout Antelope Valley. However, in order to more effectively use this model, the uncertainty associated with its predictions should be estimated. In particular, the prediction of the distribution and quantity of average annual natural mountain-front recharge is important to evaluate because it is the principal source of natural recharge.
Null-space Monte Carlo analysis
Predictive uncertainty stemming from potential parameter error associated with non-uniqueness and insensitivity can be significant, particularly when the parameterization is complex and the observation data is insufficient to uniquely estimate all parameters. To quantitatively assess the resulting predictive uncertainty, one can apply a basic calibration-constrained Monte Carlo analysis; however, this approach can be computationally expensive, especially for highly parameterized models such as the model presented in this study.
The NSMC method reduces the computational burden of conducting calibration-constrained Monte Carlo analysis using subspace techniques (Tonkin and Doherty 2009). This method employs a nonlinear extension of principal components regression (PCR), in which the original parameter vector is projected onto a vector subspace with a reduced dimensionality (Jolliffe 2002). Using PCR in linear regression, the inverse problem is reparameterized based on the eigenvectors that span the row space of the regression matrix. For nonlinear regression and NSMC, the regression matrix (conditioned on a given set of parameter values) becomes the Jacobian matrix containing the sensitivities of each model parameter to the model-simulated equivalent of each observation (Tonkin and Doherty 2009). This Jacobian matrix can be decomposed using singular-value decomposition into its respective singular values and eigenvectors. The mutually orthogonal unit eigenvectors (that span the row space of the Jacobian matrix), whose corresponding singular values are significantly non-zero, are assumed to span the calibration solution space. Therefore, these eigenvectors define the transformed parameters, also known as superparameters, which reside in the solution space. The remaining eigenvectors whose corresponding singular values are zero or near zero, are assumed to span the calibration null space and, therefore, represent superparameters that are relatively inestimable. As a result, parameter perturbations that have been projected onto the calibration null space may have little or no effect on the least-squares objective function thus, maintaining the calibrated state of the model. However, since the inverse problem is nonlinear, the definition of the superparameters is not always valid and parameter perturbations projected onto the null space cannot always be guaranteed to calibrate the model. Therefore, further iterations of the parameter-estimation algorithm may need to be undertaken to achieve an acceptable level of calibration; however, only the superparameters in the solution space are estimated, which are fewer than the original base parameters.
The methodology that was used to conduct the NSMC analysis for the Antelope Valley groundwater-flow and subsidence model using PEST and its suite of utilities is documented in Doherty et al. (2010); however, a brief overview is as follows. First, thousands of random realizations of parameter vectors are obtained based on prior probability distributions. For each realization, the corresponding parameter perturbations from the calibrated parameters are calculated and projected onto the calibration null space. A single iteration of recalibration is conducted if necessary. If the model is sufficiently calibrated, the prediction (i.e., total annual natural recharge) is recorded; if the model is not calibrated, the realization is discarded. The predictions associated with the acceptable realizations are collected and analyzed statistically. In this study, a realization is assumed sufficiently calibrated if the weighted least-squares objective function is below a certain value, which was chosen based on the calibration of each data type (e.g., transient heads, land-surface deformations, etc.); if the weighted least-squares objective for a particular data type was greater than twice that of the calibrated value, the realization was discarded. Additionally, the prior probability distributions for the parameters were assumed log-uniform between upper and lower bounds.
Prior to conducting the analysis described in the preceding, the singular-value truncation level (i.e., the dimension of the solution space and null space) must be determined. Depending on how underdetermined the inverse problem is, there may be many near-zero singular values. Determining where to divide the solution space from the null space is based on the number of near-zero singular values; however, defining “near-zero” is not straightforward. If the truncation level is set too high, the resulting randomly generated, projected parameter perturbations could significantly affect the objective function, requiring several iterations of the PEST algorithm for recalibration, which is often computationally infeasible. However, if the truncation level is set too low, these parameter perturbations may result in an overly narrow exploration of the predictive uncertainty (Tonkin and Doherty 2009). However, based on the assumption of a linear model (about the calibrated parameter vector), the predictive error variance as a function of solution space dimensionality can be approximated using PEST and its utilities (Doherty 2010; Fig. 17). Based on this result, the predictive error variance associated with total natural recharge is minimized when the solution space dimensionality is 186, which is the truncation level chosen for this study.
Due to limited computational resources, only one iteration is conducted in the recalibration step of the NSMC method. This single-iteration approach may not be adequate to achieve a model with an acceptable level of calibration for every Monte Carlo realization. Subsequently, the resulting histogram may not perfectly represent the true histogram (see Tonkin and Doherty (2009)) for an example comparison between one- and two-iteration NSMC results). Of the 4,251 realizations tested in the NSMC process, 1,022 were deemed acceptable. The simulated mean natural recharge for the acceptable realizations was about 40.0 GL/year, with a standard deviation of about 2.5 GL/year. A histogram of the simulated predictions of natural recharge shows an overall range of about 35–49 GL/year (Fig. 18).
The low standard deviation and relatively narrow range of predicted quantities of natural recharge indicate that the predictive uncertainty associated with parameter error is likely to be relatively small. However, it is important to note that many realizations of the NSMC analysis were omitted due to failure to recalibrate the model in a single iteration. Conducting more iterations may result in fewer rejected realizations and a slightly different estimate of the posterior probability distribution for annual natural recharge.
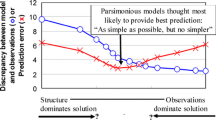
Pareto trade-off uncertainty analysis
In addition to the NSMC method, predictive uncertainty of natural recharge was also analyzed using a feasibility analysis known as a Pareto trade-off analysis (Moore et al. 2010; Doherty 2010). This analysis portrays the degradation in model calibration at larger total volumetric rates of natural recharge, and is conducted by imposing a penalty, within the objective function, that increases as the model-prediction of interest (i.e., total natural recharge) deviates from a modeler-specified value. For example, if the weight on this penalty is high, the parameter-estimation procedure will degrade the model fit in an attempt to match the desired, greater recharge rate as closely as possible. Conversely, if this weight is low, the penalty will have very little effect on the model calibration and the model predicted recharge rate will likely remain at the initial, calibrated value of 36.0 GL/year.
The Pareto analysis contained in the PEST software can begin with a relatively small weight on this penalty and incrementally increase this weight until the specified, greater natural recharge rate is nearly met. For each weight value considered by PEST, the model is recalibrated such that the objective function (which now includes the prediction of interest along with the observations and prior information) becomes as small as possible; for each weight/calibration, PEST records the prediction of interest.
The observations used in this analysis consisted of the calibrated-model outcomes, corresponding to each measured value, rather than the measured values themselves (as suggested by Doherty 2010). The Pareto procedure begins with the calibrated model; therefore, the initial objective function value is, by definition, zero. The maximum prediction for natural recharge was set very large at about 200 GL/year, and for each solution (that is, each point on the curves in Fig. 19), four iterations of the recalibration procedure were conducted. The choice of four iterations was sufficient due to the fact that the model calibration at each point on the Pareto curve stopped improving after only a few iterations.
The Pareto curves indicate that the calibration potential for very large volumes of annual natural recharge is not likely, and is driven primarily by degradation in the model’s ability to fit observations of transient water levels (Fig. 19). A clear inflection point in the “overall” Pareto curve is observed when the natural recharge reaches about 54 GL/year. This value is consistent with the largest value observed during the NSMC analysis of about 49 GL/year, which suggests that the one-iteration approach for the recalibration step of the NSMC procedure may have been sufficient for adequately characterizing the predictive uncertainty associated with natural recharge for this study. As the natural recharge increases from this point, model calibration begins to deteriorate rapidly. The noisy behavior in the Pareto curves associated with extreme values of natural recharge is likely a result of the instability and/or nonlinearity associated with subsidence simulations (Fig. 19).
Natural recharge feasibility tests
The feasibility of the volume of natural recharge used by the Court was also tested directly by attempting to calibrate the model with this value using Tikhonov regularization. The Los Angeles County Superior Court of California ruled a “safe yield” value of 135.7 GL/year based on an estimate of total average annual natural recharge of 74.0 GL/year (Beeby et al. 2010a, b). Using the distribution of natural recharge resulting from the BCM simulation, the corresponding natural recharge pilot point values were calculated such that the total recharge was 74.0 GL/year. These values were then used as both initial values and regularization targets for the parameter-estimation process (i.e., the prior information used in the previous analyses for the natural recharge pilot points has now been altered to support the estimate of natural recharge used by the Court). The initial values for the remaining parameters were set equal to their respective calibrated values. The regularization targets for these remaining parameters also were set equal to their calibrated values (i.e., the prior information associated with the remaining parameters was altered to reflect the calibrated model). In other words, the model was recalibrated in an attempt to produce a total average natural recharge of 74.0 GL/year, while reasonably matching observed historical water levels and land-surface deformations. Additionally, the upper bounds associated with horizontal hydraulic conductivity were also increased to about 305 m/day to allow for greater flexibility in obtaining a calibrated model; however, this also provides the potential for values that are not realistic. This feasibility analysis, or recalibration of the model, differs from the Pareto analysis discussed previously because the prior information (or regularization targets) and some of the upper bounds of the parameters have been changed.
There were two simulations conducted for this exercise. The first simulation consisted of the same formulation of the parameter-estimation process used to calibrate the model originally (with the alterations mentioned previously). This simulation converged to an objective function value similar to the original calibrated model. The resulting estimated natural recharge was about 56 GL/year. This value is less than that associated with the regularization targets, indicating that natural recharge values above 56 GL/year will not likely produce a reasonably calibrated model. Furthermore, this value is consistent with both the inflection point in the Pareto curves and the maximum value observed in the NSMC analysis. However, the horizontal hydraulic conductivity parameters did not change significantly from their starting values and regularization targets. This is likely due to the fact that PEST’s Tikhonov procedure adjusts the inter-regularization group weights independently, which could lead to relatively high weights placed on matching prior values of hydraulic conductivity.
To further address the feasibility of 74 GL/year of natural recharge, a second calibration simulation was conducted in which the greatest emphasis for matching prior information was placed on the natural recharge pilot points. An option in PEST, known as IREGADJ, allows for the relative inter-regularization group weighting to be controlled somewhat by the user (Doherty 2010). For this second simulation, IREGADJ was set to three, which requires PEST, at each iteration, to honor the relative inter-regularization group weights set by the user at the outset of the parameter estimation process. In order to use this option, the inter-regularization weight ratios must now be chosen carefully. Since the objective is to match the 74.0 GL/year total natural recharge rate as closely as possible, the second simulation was conducted such that the weights associated with natural recharge targets were ten times larger than those associated with the rest of the parameters.
This second simulation converged to an objective function value slightly larger than that of the original calibrated model; the largest discrepancy or misfit was that associated with the transient water-level observations. The resulting estimated annual natural recharge was about 66 GL/year. This value is still less than that associated with the regularization targets, indicating that a natural recharge rate of 74.0 GL/year may be overestimated. Furthermore, at 66 GL/year, many of the resulting estimated horizontal hydraulic conductivity values were unreasonably large for the type of geologic deposits in Antelope Valley.
Model structure error — estimated agricultural pumpage
Agricultural pumpage is an uncertain component of groundwater discharge that was assumed known during model calibration. Conceivably, underestimation of the agricultural pumpage used in this study could result in, for example, smaller values of hydraulic conductivity in order to match observed water levels. As a result, attempts at achieving the appropriate initial condition (pre-development or steady state) may result in an underestimation of natural recharge. The converse is also true for overestimation of pumpage. The exact temporal and spatial uncertainty associated with 1916–2005 agricultural pumpage cannot be quantified. Without knowing the details of this uncertainty, magnitudes of agricultural pumpage were explored uniformly in both space and time. Therefore, in this study, predictive uncertainty resulting from agricultural pumpage uncertainty was addressed by uniformly perturbing the agricultural pumpage, in space and time, followed by recalibration of the model.
The estimates of natural recharge made in this study are much smaller than that made by the Court; therefore, we only consider the potential for underestimation of pumpage. Therefore, two increases of 10 and 25 % in agricultural pumpage were considered for this study. The recalibrated models for the 10 and 25 % increase in agricultural pumpage estimated a natural recharge rate of 36.6 and 38.4 GL/year, respectively. As expected, increases in estimated natural recharge were observed as a result of increased agricultural pumpage rates. However, these increases in recharge are relatively small, indicating that uncertainty in agricultural pumpage likely has little effect on the estimates of natural recharge.
This is only a very basic exploration of the effects of underestimated agricultural pumpage on the prediction of natural recharge. Indeed, the regularization targets for natural recharge were set to the same values as during calibration, i.e., the targets are based on both the BCM results and the natural recharge estimate by Leighton and Phillips (2003). Therefore, the results of this analysis only indicate that it is possible to calibrate the model with approximately 37 GL/year of natural recharge and increased agricultural pumpage. This does not indicate that larger volumes of natural recharge are impossible with larger values of agricultural pumpage. Furthermore, the agricultural pumpage in this basic analysis is increased uniformly for only two scenarios. A more sophisticated investigation could be performed in which agricultural pumpage is treated as a random variable, but such an analysis is beyond the scope of this study.
Conclusions
A numerical groundwater-flow and land-subsidence model has been developed based on the model published by Leighton and Phillips (2003) to estimate the natural recharge and its associated uncertainty in the Antelope Valley, California. Mountain-front recharge is assumed to be the primary source of natural recharge. The numerical solution procedure known as the Newton Solver in MODFLOW-NWT has been employed. This solver’s enhanced capability improves the overall numerical stability of MODFLOW with particular improvements in simulating model cells that transition from wet to dry and vice versa. In this study, this is especially important because most of the natural recharge that requires estimation occurs along the mountain front where there is often only a single active layer that could become dry or wet quite easily, depending on the parameter values being implemented by PEST.
The updated model was calibrated using the parameter-estimation and predictive-uncertainty software suite PEST and prior information was incorporated using the Tikhonov regularization functionality in PEST. All model parameters were regularized such that they tend toward expected parameter values, which were based on professional judgment, geologic knowledge of the area, BCM model results, and the results of Leighton and Phillips (2003). The resulting average annual natural recharge estimated in this study is about 36 GL/year, which is very close to the previous estimate by Leighton and Phillips (2003); however, this value is much smaller than the Court-determined value of 74 GL/year.
The estimate of natural recharge was considered as the prediction of the model. Predictive uncertainty analysis was conducted based on both parameter uncertainty and the model-structure errors associated with underestimated agricultural pumpage estimates. The NSMC method was used to explore the likely range of natural recharge given the conceptual model used and observations available for calibration. The mean value result of the NSMC method was about 40 GL/year with a standard deviation of about 2.5 GL/year. Pareto trade-off concepts were also used to show the degradation to model calibration that accompanies increases in natural recharge values. These results indicated that when the natural recharge reaches about 54 GL/year, the model fit degrades dramatically.
The effects on predictive uncertainty resulting from underestimated agricultural pumpage were also considered. The agricultural pumpage was increased uniformly in time and space by 10 and 25 % and recalibrated for both cases. The resulting estimated natural recharge for an increase of 10 and 25 % was 36.6 and 38.4 GL/year, respectively. This indicates that the uncertainty associated with agricultural pumpage has little effect on the estimate of natural recharge.
References
Beeby RG, Durbin TJ, Leever WE, Lefler PM, Scalmanini JC, Wildermuth MJ (2010a) Phase 3: basin yield and overdraft, Antelope Valley area of adjudication. In: Dunn J (ed) Public water suppliers’ expert report: part 1, Santa Clara County Superior Court of California, Antelope Valley groundwater case doc no. 3749, 77 pp. http://www.scefiling.org/document/document.jsp?documentId=35952. Accessed 7 July 2014
Beeby RG, Durbin TJ, Leever WE, Lefler PM, Scalmanini JC, Wildermuth MJ (2010b) Appendices to public water suppliers’ expert report. In: Dunn J (ed) Public water suppliers’ expert report: part 1, Santa Clara County Superior Court of California, Antelope Valley groundwater case doc no. 3745, variously paged. http://www.scefiling.org/document/document.jsp?documentId=35948. Accessed 7 July 2014
Benda WK, Erd RC, Smith WC (1960) Core logs from five test holes near Kramer, California. US Geol Surv Bull 1045-F:319–393
Bloyd RM Jr (1967) Water resources of the Antelope Valley-East Kern Water Agency area, California. US Geol Surv Open-File Rep 67-21, 73 pp
CH2M HILL (2005) Lancaster water reclamation plant groundwater monitoring program: evaluation of phase II investigation results at Piute Ponds. CH2M HILL, Englewood, CO
California State Water Resources Control Board (2011) Groundwater Recordation Program background information available on the World Wide Web. http://www.swrcb.ca.gov/waterrights/water_issues/programs/groundwater_recordation/. Accessed 10 Jan 2012
Dibblee TW Jr (1960) Geology of the Rogers Lake and Kramer quadrangles, California. US Geol Surv Bull 1089-B:73–139
Dibblee TW Jr (1963) Geology of the Willow Springs and Rosamond quadrangles, California. US Geol Surv Bull 1089-C:141–253
Dibblee TW Jr (1967) Areal geology of the western Mojave Desert, California, US Geol Surv Prof Pap 522, 153 pp
Doherty J (2003) Groundwater model calibration using pilot points and regularization. Ground Water 41(2):170–177. doi:10.1111/j.17456584.2003.tb02580.x
Doherty J (2010) PEST, Model-independent parameter estimation: user manual, 5th edn. (and addendum to the PEST manual). Watermark, Brisbane, Australia. Available at www.pesthomepage.org. June 2015
Doherty JE, Fienen MN, Hunt RJ (2010) Approaches to highly parameterized inversion: pilot-point theory, guidelines, and research directions. US Geol Surv Sci Invest Rep 2010–5168, 36 pp
Durbin TJ (1978) Calibration of a mathematical model of the Antelope Valley ground-water basin, California. US Geol Surv Water Suppl Paper 2046, 51 pp
Dutcher LC, Worts GF (1963) Geology, hydrology, and water supply of Edwards Air Force Base, Kern County, California. US Geol Surv Open-File Rep 225 pp
Flint AL, Flint LE (2007) Application of the Basin Characterization Model to estimate in-place recharge and runoff potential in the Basin and Range carbonate-rock aquifer system, White Pine County, Nevada, and adjacent areas in Nevada and Utah. US Geol Surv Sci Invest Rep 2007–5099. http://pubs.water.usgs.gov/sir20075099. June 2015
Flint LE, Flint AL, Thorne JH, Boynton R (2013) Fine-scale hydrological modeling for climate change applications: using watershed calibrations to assess model performance for landscape projections. Ecol Process 2(25):1–21. doi:10.1186/2192-1709-2-25
Galloway DL, Hudnut KW, Ingebritsen SE, Phillips SP, Peltzer G, Rogez F, Rosen PA (1998) Detection of aquifer system compaction and land subsidence using inteferometric synthetic aperture radar, Antelope Valley, Mojave Desert, California. Water Resour Res 34(10):2573–2585
Galloway DL, Jones DR, Ingebritsen SE (eds) (1999) Land subsidence in the United States. US Geol Surv Circ 1182, 175 pp
Halford KJ, Hanson RT (2002) User guide for the drawdown-limited, multi-node well (MNW) package for the U.S. Geological Survey’s modular three-dimensional finite-difference groundwater flow model. US Geol Surv Open-File Rep 02-293, 33 pp
Harbaugh AW (2005) MODFLOW-2005, the U.S. Geological Survey modular groundwater model: the groundwater flow process. US Geol Surv Tech Methods 6-A16
Herckenrath D, Langevin CD, Doherty J (2011) Predictive uncertainty analysis of a saltwater intrusion model using null‐space Monte Carlo. Water Resour Res 47:W05504. doi:10.1029/2010WR009342
Hewett DF (1954) General geology of the Mojave Desert region California. In: Jahns RH, Baily TL (eds) Geology of southern California, chap 2. Bull 170, Cal. Div. of Mines, Sacramento, CA, pp 5–20
Hoffman J, Leake SA, Galloway DL, Wilson AM (2003) MODFLOW-2000 groundwater model: user guide to the Subsidence and Aquifer-System Compaction (SUB) Package. US Geol Surv Open-File Rep 03-233, 44 pp
Ikehara ME, Phillips SP (1994) Determination of land subsidence related to ground-water-level declines using global positioning. system and leveling surveys in Antelope Valley, Los Angeles and Kern counties, California, 1992. US Geol Surv Water Resour Invest Rep 94-4184, 101 pp
Jachens RC, Langenheim VE, Christensen AH (2014) Gravity analysis for groundwater basin definition: western Mojave Desert, California, Appendix 1. US Geol Surv Sci Invest Rep 2014-5166, pp 92–98
Johnson HR (1911) Water resources of Antelope Valley, California. US Geol Surv Water Suppl Paper 278, 92 pp
Jolliffe IT (2002) Principal component analysis, 2nd edn. Springer, New York
Keating HK, Doherty J, Vrugt JA, Kang Q (2010) Optimization and uncertainty assessment of strongly nonlinear groundwater models with high parameter dimensionality. Water Resour Res 46:W10517. doi:10.1029/2009WR008584
Leake SA (1990) Interbed storage changes and compaction in models of regional groundwater flow. Water Resour Res 26(9):1939–1950
Lee CH (1912) An intensive study of the water resources of a part of Owens Valley, California. US Geol Surv Water Suppl Pap 294, 135 pp
Leighton DA, Phillips SP (2003) Simulation of ground-water flow and land subsidence in the Antelope Valley, California. US Geol Surv Water Resour Invest Rep 03-4016, 107 pp
Levenberg K (1944) A method for the solution of certain non-linear problems in least squares. Q J Appl Math 2:164–168
Los Angeles County Superior Court of California (2011) Tentative decision phase three trial of Antelope Valley groundwater litigation (consolidated cases), Los Angeles County Superior Court of California, Lead Case no. BC 325 201, 9 pp. http://www.scefiling.org/filingdocs/194/37311/61093_49053_TentativexDecisionxTrialxPhasex3.pdf. Accessed June 2014
Mabey DR (1960) Gravity survey of the western Mojave Desert, California. US Geol Surv Prof Pap 316-D:51–73
Marquardt DW (1963) An algorithm for least-squares estimation of nonlinear parameters. J Soc Ind Appl Math 11(2):431–441
Moore C, Wöhling T, Doherty JE (2010) Efficient regularization and uncertainty analysis using a global optimization methodology. Water Resour Res 46:W08527. doi:10.1029/2009WR008627
Nishikawa T, Rewis DL, Martin P (2001) Numerical model of ground-water flow and land subsidence for Edwards Air Force Base, Antelope Valley, California. US Geol Surv Water Resour Invest Rep 01-4038, 111 pp
Niswonger RG, Prudic DE, Regan RS (2006) Documentation of the Unsaturated-Zone Flow (UZF1) Package for modeling unsaturated flow between the land surface and the water table with MODFLOW-2005. US Geol Surv Tech Methods, Book 6, Chapter A19, 62 pp
Niswonger RG, Panday S, Ibaraki M (2011) MODFLOW-NWT: a Newton formulation for MODFLOW-2005. US Geol Surv Tech Methods 6-A37, 44 pp
Orme AR (2003) Lake Thompson, Mojave Desert, California: a desiccating late Quaternary lake system. Monograph TR-03, Engineering Research and Development Center and Cold Regions Research and Engineering Laboratory, Hannover, NH, 53 pp
Rantz SE (1969) Mean annual precipitation in the California Region. US Geol Surv Open-File Map, scale 1:1,000,000, 11 sheets, 5 pp
Siade AJ, Nishikawa T, Rewis DL, Martin P, Phillips SP (2014) Groundwater-flow and land-subsidence model of Antelope Valley, California. US Geol Surv Sci Invest Rep 2014–5166, 154 pp
Snyder JH (1955) Ground water in California: the experience of Antelope Valley: Berkeley, California. Giannini Foundation Ground-Water Studies no. 2, Giannini Foundation, Berkeley, CA, 171 pp
Templin WE, Phillips SP, Cherry DE, DeBortoli ML, Haltom TC, McPherson KR, Mrozek CA (1995) Land use and water use in Antelope Valley, California. US Geol Surv Water Resour Invest Rep. 94-4208, 97 pp
Terzaghi K (1925) Principles of soil mechanics: IV, settlement and consolidation of clay. Eng News Record 95(3):874–878
Tikhonov AN, Arsenin VY (1977) Solution of ill-posed problems. Winston, Washington, DC, 271 pp
Tindall JA, Kunkel JR, Anderson DE (1999) Unsaturated zone hydrology for scientists and engineers. Prentice-Hall, Upper Saddle River, NJ
Thompson DG (1929) The Mojave Desert region, California, a geographic, geologic, and hydrologic reconnaissance. US Geol Surv Water Suppl Pap 578, 759 pp
Tonkin M, Doherty JE (2009) Calibration-constrained Monte Carlo analysis of highly parameterized models using subspace techniques. Water Resour Res 45(12):W00B10. doi:10.1029/2007WR006678
Ward AW, Dixon GL, Jachens RC (1993) Geologic setting of the East Antelope Basin, with emphasis on fissuring on Rogers Lake, Edwards AFB, Mojave Desert, California. US Geol Surv Open-File Rep 93-263, 9 pp
Yeh WW-G (1986) Review of parameter identification procedures in groundwater hydrology: the inverse problem. Water Resour Res 22(2):95–108
Yoon H, Hart BH, McKenna SA (2013) Parameter estimation and predictive uncertainty in stochastic inverse modeling of groundwater flow: comparing null-space Monte Carlo and multiple starting point methods. Water Resour Res 49(1):536–553. doi:10.1002/WRCR.20064
Acknowledgements
This work was supported by the US Geological Survey Cooperative Water Program, Los Angeles County Department of Public Works, Antelope Valley–East Kern Water Agency, Palmdale Water District, and Edwards Air Force Base.
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in the theme issue “Optimization for Groundwater Characterization and Management”
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Siade, A., Nishikawa, T. & Martin, P. Natural recharge estimation and uncertainty analysis of an adjudicated groundwater basin using a regional-scale flow and subsidence model (Antelope Valley, California, USA). Hydrogeol J 23, 1267–1291 (2015). https://doi.org/10.1007/s10040-015-1281-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-015-1281-y