1 Introduction

Among complex systems, granular materials have attracted much interest in the past few years in materials sciences. Granular materials can be encountered in a variety of engineering contexts, such as pharmaceutical engineering, food particle storage, geological mass-driven hazards, and civil engineering. It is well recognized that granular materials can exhibit a wide spectrum of emergent properties that have received much interest [1,2,3,4,5,6]. Such properties appear at the specimen scale, whereas they cannot be observed at smaller scales. As an illustration, granular materials are dissipative structures [7, 8]. Thanks to their disordered microstructure, such materials can adapt themselves through microstructural reorganizations to resist against a given external loading on the specimen scale. Such reorganizations mostly entail dissipative mechanisms through grain sliding and rolling at the inter-granular contacts. They act as elementary, microscopic events that are responsible for the whole system to be in mechanical equilibrium. It is worth emphasizing that the notion of mechanical equilibrium should not be confused with that of thermodynamic equilibrium. Indeed, thermodynamic equilibrium means that any fluctuation that takes place stays bounded and eventually vanishes. On the other hand, mechanical equilibrium imposes that the external tractions applied on the boundary of the system are balanced by the internal stress field developing within the system. When a system is in thermodynamic equilibrium, it is automatically in mechanical equilibrium which is a less restrictive equilibrium type. Thus, even at mechanical equilibrium, a given material system can be out of thermodynamic equilibrium. In that case, some fluctuations are expected to develop within the system, making it evolve in an irreversible way from a given state toward another state. Irreversibility means that the system cannot return spontaneously to the previous states without any external exchange, mainly because of internal dissipative processes. Fluctuations at the micro scale, instead of vanishing, can be amplified. In some circumstances, the system can then bifurcate towards a new response mode, with a new topological organization of the energy dissipation. This is what happens on dense granular assemblies under a shear loading (as a drained triaxial loading, for example). It is repeatedly observed that the deviatoric stress reaches a peak value after a monotonous increase (so-called hardening regime), followed by a decrease (so-called softening regime) until the critical state regime takes place. Furthermore, the specimen is no longer homogeneous once the deviatoric stress peak is reached, as a localization pattern (with a single or multiple shear bands) develops. It was recently shown that the development of a shear band pattern during the softening regime corresponds to a phase transition, marked by a break in symmetry in the kinematic field, consisting in a microstructural reorganization to optimize the inter-granular, frictional dissipation processes (optimal dissipative structure), and make the specimen able to resist against the external loading. The appearance of shear bands within granular materials, patterning of the material in several structured zones, has received much attention over the past decades. It is worth mentioning that such features can be observed irrespective of the scale considered: along faults during earthquakes, in large rocky cliffs, or in laboratory test specimens. Focusing on the lab scale, the occurrence of such events is well predicted by the Rice-Mandel criterion [9, 10]. This criterion was shown to be a subset of the second-order work criterion introduced in the middle of the past century by Hill [11]. More recently, the second-order work theory was formalized [12], by relating the occurrence of an outburst in kinetic energy, regarded as a quasi-unbounded fluctuation, and the vanishing of the second-order work. This vanishing corresponds to the loss of the positive definitiveness of the symmetric part of the constitutive operator relating both incremental stress and strain operating on the material point scale. Along a given loading path, all mechanical states corresponding to the non-ellipticity of the symmetric part of the constitutive operator thus define the bifurcation domain. In such a domain, an effective failure of the material can occur according to the loading direction applied, and to the loading control adopted [13].

In Nicot and Darve [14], two material failure modes in granular material are presented: one associated with localization and the other associated with a diffuse mode. Localization has been clarified through the contributions made by Rudnicki and Rice [10] and Vardulakis [15, 16] in which the vanishing of the determinant of the acoustic tensor occurs when a shear band develops. They use an elasto-plastic model with a non-associative plastic flow. More recently, La Ragione et al. [17], based upon a micro-mechanical approach, predict shear band in stressed granular material with a macroscopic stiffness tensor that does not have the major symmetry, consequently with a similar structure of that introduced in [10, 18]. The other failure is associated with a diffusive mode that can anticipate the localization band when the second order work vanishes (e.g. [19]).

Here we focus on the second order work and the possibility that at some stressed states, during the loading path, it becomes negative under proper perturbations [20, 21]. Our analysis involves both a theoretical model and numerical simulations. The merit of the simulations, based upon the distinct element method (DEM), is to reproduce the proper kinematics and statics of every single grain of the sample while both force and moment equilibrium are satisfied at each applied incremental macroscopic strain [22]. In so doing, it is possible to follow the behavior at contact level of the aggregate, including particle deletion, sliding and rolling.

The novelty of our work is the introduction of fluctuations in particles deformation that allows to predict a stressed state in which the second order work vanishes. Following the DEM analysis, it is possible to employ theoretical models that reproduce the behavior of the aggregate as seen in the simulations. The simplest hypothesis is that contacting particles move according with an average deformation. The resulting macroscopic response of the aggregate seems reasonable from the qualitative point of view. Particle sliding and deletion are predicted as well as the deviatoric stress and the volume strain along a monotonic triaxial test (e.g. [23, 24]). On the other hand, the comparison with numerical simulation shows a quantitative difference that is solved by relaxing the kinematics with the introduction of a fluctuation field along with equilibrium [25]. The kinematic of contacting particles with fluctuations also leads to a qualitative difference with respect to the average strain, under particular loading condition: the macroscopic stiffness of the aggregate, \({\mathcal {A}}_{ijkm}\), that relates the increments in stress with the increment in strains, \({\dot{\sigma }}_{ij}={\mathcal {A}}_{ijkm} {\dot{E}}_{km}\), can be characterized by the loss of the major symmetry. This represents a necessary condition to predict localization.

Following this idea, we focus our investigation on a triaxial test conducted at constant pressure conditions. As emphasized in [17], under specific conditions, the incremental response of the aggregate tends to be frictionless on average, resulting in a non-symmetric elasto-plastic stiffness tensor. Within this framework, we show that the second-order work linked with stressed states can vanish.

2 Triaxial loading

We focus on a triaxial test of an aggregate of N identical, frictional, elastic particles with diameter D which deform according to a macroscopic average strain, \({\textbf{E}}\). After an initial isotropic compression, \(p_{0},\) the aggregate is uniaxial compressed, \(E_{33}<0,\) keeping the pressure constant. We define the shear strain \(\gamma =-1/2(E_{33}-E_{11})\), with \(E_{11}=E_{22}\), and the volume strain, \(\varTheta =-( E_{33}+2E_{11}),\) positive in compression, while \(\varTheta _{0}\) is the volume strain associated with the pressure at the isotropic state. Particles interaction is given by a non central contact force with a normal component that follows the Hertz law and a tangential component that has an elasto-plastic response: a bilinear relation with an elastic displacement followed by a frictional sliding. The incremental force between two contacting particles is given by:

$$\begin{aligned} {\dot{F}}_i={\dot{F}}_i^N+{\dot{F}}_i^T \end{aligned}$$
(1)

in which \({\dot{F}}_i^N\) and \({\dot{F}}_i^T\) are, respectively, the incremental normal and tangential component of the contact force. Given \({\dot{\textbf{F}}}\), the incremental average stress \({\dot{\sigma }}\) may be written as the average over all particles in a region of homogeneous deformation that is identified with the continuum point [25]:

$$\begin{aligned} {\dot{\sigma }}_{ij}=\frac{1}{2}\frac{N}{V}\sum _{p=1}^{M^{p}}\frac{M^{p}}{N} \left\langle {\dot{F}}_{i}\right\rangle _{{\hat{\textbf{d}}}^{p}}d_{j}^{p} \end{aligned}$$
(2)

where \(M^p\) is the number of pairs of contacting particles with contact vectors (the vector that joins the particle centers) within the \({p}\)-th element of R equal elements \(\varDelta \varOmega ^p\) of solid angle in which the surface of the unit sphere has been partitioned, V is the total volume of the aggregate and \(\left\langle {\dot{F}}_{i}\right\rangle _{{\hat{\textbf{d}}}^{p}}\) is the average of all the contact forces between pairs whose contact vectors, \(d_i=D\hat{d_i},\) are within a given solid angle centered at \({\hat{\textbf{d}}}^{p}\). We have \(\varDelta \varOmega ^p=4\pi /R\) and \(\sum _{p=1}^R M^p=2N_c\) in which \(N_c\) is the total number of contacts in the aggregate.

In the monotonic triaxial test, the deviatoric stress is \(q=-1/2\left( \sigma _{33}-\sigma _{11}\right)\) and its components are \(q_N\) and \(q_T\); the former is the part of the deviatoric stress associated with the normal component of the contact force, the latter with the tangential component of the contact force. Therefore, the response of the aggregate is characterized by the \(q-\gamma\) and the \(\varTheta - \gamma\) curves.

We investigate the incremental response of the aggregate, at given stressed state along the curve \(q-\gamma\); in particular, we look at the second order work, \(W_2={\dot{\sigma }}_{ij}{\dot{E}}_{ij}\), and the possibility that it may become negative. We do this through numerical simulations and a theoretical model.

2.1 Numerical simulation

We employ a numerical simulation based upon DEM on a sample made of 10.000 elastic particles with the shear modulus \(G=2.9 \times 10^9\) Pa, the Poisson ratio \(\nu =0.2\), and radii 9.5 and \(10.5 \times 10^{-2}\) mm, initially isotropically compressed and then sheared. More detailed about the protocol adopted can be found in [26]. The initial compression is carried out without friction to generate a very dense state, volume fraction \(\phi =\)0.64; next, the aggregate is uniaxial strained at constant pressure, \(p_0=200\) KPa, with friction coefficient \(\mu =0.5\) and increments of deformation, at every cycle, of the order of \(10^{-6}.\) Along the loading path, there are intermediate states in which no external strains are applied and the aggregate relaxes towards the equilibrium. That is, equilibrium is guarantee by fluctuation fields that allow particles deformation to deviate from the applied average strain.

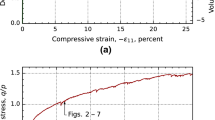
The response of the aggregate is represented by stress–strain and volume strain-strain curves in which the deviatoric stress is normalized by the pressure \(p_0\) while the strains by the volume strain \(\varTheta _0\).

In Fig. 1 we show the response of the aggregate: the evolution of the normalized deviatoric stress and its partition in \(q^N\) and \(q^T\), top; the evolution of the normalized volume strain in which dilatancy is present, bottom. As in Jenkins and Strack [23] and Thorthon and Antony [27], the contribution to the deviatoric stress associated with \(q^N\) and \(q^T\) are illustrative. We can distinguish an initial almost elastic response of the aggregate, for \(0\le \gamma /\varTheta _0\lessapprox 0.2\), followed by an elasto-plastic response in which \(q^T\) does not vary, essentially. In this latter regime, a typical hardening behavior occurs in which the incremental deviatoric stress depends only on the normal contact force while particles slide/roll and irreversibility occurs. Here, the incremental tangential component is assumed to be approximately zero, so \({\dot{q}}_T=0\).

Fig. 1
figure 1

Uniaxial deformation at constant pressure, numerical simulations: normalized deviatoric stress (top), normalized volume strain (bottom)

Full size image

We also consider the network of contact vectors and introduce the fabric tensor (e.g. [27, 28]):

$$\begin{aligned} \varPhi _{ij} = \frac{1}{N_c} \sum _{c=1}^{N^c} \hat{d^c_i}\hat{d^c_j}. \end{aligned}$$
(3)

We measure the evolution of the deviatoric fabric, \({\hat{\varPhi }}=\varPhi _{33}-(\varPhi _{11}+\varPhi _{22})/2\), normalized by the initial fabric \(\varPhi _{iso}=\varPhi _{11}=\varPhi _{22}=\varPhi _{33}\), during the loading. In Fig. 2, top, we show the evolution of the fabric, \({\hat{\varPhi }}/\varPhi _{iso}\).

The fabric tensor, \(\varPhi _{ij}\), is also identified as the second moment of the contact distribution \(f(\hat{{\textbf {d}}})\) whose approximated expression is (e.g. [29]):

$$\begin{aligned} f(\hat{{\textbf {d}}}) = \frac{k}{4\pi }\left[ 1+\frac{15}{2}(\hat{d_i}\hat{d_j}-\frac{1}{3}\delta _{ij})(\varPhi _{ij}-\frac{1}{3}\delta _{ij})\right] \end{aligned}$$
(4)

with \(\int _{\varOmega } f(\hat{{\textbf {d}}}) d\varOmega =k\) and \({\hat{\textbf{d}}}\left( \sin \theta \cos \varphi ,\sin \theta \sin \varphi ,\cos \theta \right)\) in which \(\theta\) is the polar angle with respect to the axis of compression \(y_3\) and k is the coordination number, the average number of contacts per particle. If we knew the contact distribution we could have determined the second moment through the following equation (e.g. [30]):

$$\begin{aligned} \varPhi _{ij}=\int _{\varOmega } {\hat{f}}(\hat{{\textbf {d}}})\hat{d_i}\hat{d_j} d\varOmega \end{aligned}$$
(5)

in which \(d\varOmega =\sin \theta d\theta d\phi .\) In Fig. 2, bottom, we show the normalized contact distribution, \({\hat{f}}(\hat{{\textbf {d}}})=f(\hat{{\textbf {d}}})/k\), at different strain states (for symmetry reason we look at \(0\le \theta \le \pi /2\)). Both Fig. 2, top and bottom, show a development of the structural anisotropy during the loading with a region of increasing contacts around the pole of compression, about \(\theta =0\), and decreasing about \(\theta =\pi /2\) associated with deletion.

In Fig. 3 we show the evolution of the coordination number k, the average number of contacts per particle, whose initial value is \(k_0\approx 6\). We also evaluate a best fit approximation for the evolution of the coordination number, with a polynomial function, which offers the following relation: \(k=a\gamma ^2/\varTheta _0+b\gamma /\varTheta _0+ c\) with \(a=0.5\), \(b=-1.6\) and \(c=6\).

Fig. 2
figure 2

Uniaxial deformation at constant pressure, numerical simulations: fabric evolution (top), contact distribution (bottom)

Full size image
Fig. 3
figure 3

Uniaxial deformation at constant pressure, numerical simulation: evolution of the coordination number with the normalized shear strain (solid line); polynomial approximation (dashed line)

Full size image

At this point, incremental probes are applied at given stressed states. Because of the uniaxial compression, these stressed states are anisotropic and the incremental response depends on the magnitude of the perturbation [31,32,33]: we have an elastic response that corresponds to an unloading condition with respect to the previous triaxial loading, and an elasto-plastic response which corresponds to a forward loading. We are interested to evaluate \(W_2\) when an elasto-plastic increment is applied because we expect to characterize the macroscopic stiffness tensor without the major symmetry [17]. In the last section, we determine \(W_2\) under these particular conditions and test the theory against the simulation data.

2.2 Theory

The model is based on the theory of fluctuations proposed by Jenkins et al. [34] and developed in case of localization by La Ragione et al. [17]. We assume that contacting particles deviate from the applied average strain because of equilibrium. We write the kinematic that governs the problem, we assume the contact law for contacting particles and solve, approximately, equilibrium. With a proper statistical hypothesis, we move from the local pair interaction to the aggregate in order to determine the average stress from which it is possible to obtain an expression for the second order work. It is the nature of the macroscopic stiffness that relates incremental in strain with incremental in stress that provides an explanation of negative second order work.

2.2.1 Kinematics

We phrase the problem incrementally and we restrict our attention to the hardening regime in which, as seen in Fig. 1 (top), the macroscopic response can be approximated as incrementally frictionless. That is, we refer to incremental forward loading. In this regime particles slide, so plasticity occurs but we only have increments in normal components of the contact forces, approximately. Consequently, we focus only on the kinematic of contacting particles related to the motion of their centers. The incremental relative displacement between contacting particles A and B is given by:

$$\begin{aligned} {\dot{u}}_{i}^{\left( BA\right) }={\dot{c}}_{i}^{\left( B\right) }-{\dot{c}} _{i}^{\left( A\right) } \end{aligned}$$
(6)

in which \({\dot{c}}_{i}\) is the incremental particle center displacement. We allow particles to deviate from the average strain and introduce a fluctuation field. So we write

$$\begin{aligned} {\dot{c}}_{i}^{(A)} = \overline{ {\dot{c}}_{i}} + {\tilde{c}}_{i}^{\left( A\right) } \end{aligned}$$
(7)

in which we make explicit the average contribution, \(\overline{ {\dot{c}}_{i}}\), and the fluctuation, \({\tilde{c}}_{i}^{\left( A\right) }\). A simple way to enrich the kinematics is to focus on a pair \(A-B~\) and its neighborhoods (see Fig. 4) and assume that the relative displacement of the contact point of a typical pair \(A-B\) is given by

$$\begin{aligned} {\dot{u}}_{i}^{\left( BA\right) }={\dot{E}}_{ij}d_{j}^{\left( BA\right) }+\dot{ \varDelta }_{i}^{\left( BA\right) } \end{aligned}$$
(8)

while for particle n in contact with A is

$$\begin{aligned} {\dot{u}}_{i}^{\left( nA\right) }={\dot{c}}_{i}^{\left( n\right) }-{\dot{c}} _{i}^{\left( A\right) } \end{aligned}$$
(9)

in which only particle A fluctuates. So

$$\begin{aligned} {\dot{u}}_{i}^{\left( nA\right) }={\dot{E}}_{ij}d_{j}^{\left( nA\right) }+\frac{1 }{2}{\dot{\varDelta }}_{i}^{\left( BA\right) }-\frac{1}{2}{\dot{\varSigma }}_{i}^{\left( BA\right) }. \end{aligned}$$
(10)

The difference in fluctuation is

$$\begin{aligned} {\dot{\varDelta }}_{i}^{\left( BA\right) }={\tilde{c}}_{i}^{\left( B\right) }-\tilde{ c}_{i}^{\left( A\right) } \end{aligned}$$
(11)

while the sum is

$$\begin{aligned} {\dot{\varSigma }}_{i}^{\left( BA\right) }={\tilde{c}}_{i}^{\left( A\right) }+\tilde{ c}_{i}^{\left( B\right) }. \end{aligned}$$
(12)
Fig. 4
figure 4

The pair and its neighboord: particles A and B fluctuate while particle n is constrained to move with the average deformation

Full size image

Similar expressions can be employed for particle B and its neighborhood. The contact vector is indicated by \(d_{j}^{\left( BA\right) }=D\hat{ d}_{j}^{\left( BA\right) }\).

2.2.2 Statics

We write the increment \({\dot{\textbf{F}}}^{(BA)}\)in the contact force exerted by particle B on particle A in terms of the increment \({\dot{\textbf{u}}} ^{(BA)}\)in the relative displacement of the points of contact:

$$\begin{aligned} {\dot{F}}_{i}^{(BA)}=K_{ij}^{(BA)}{\dot{u}}_{j}^{(BA)} \end{aligned}$$
(13)

in which, in case of incremental frictionless behavior, the contact stiffness is

$$\begin{aligned} K_{ij}^{(BA)}=K_{N}{\hat{d}}_{i}^{(BA)}{\hat{d}}_{j}^{\left( BA\right) }. \end{aligned}$$
(14)

The normal contact stiffness depends on the normal component \(\delta\) of the compressive displacement of the centers of the particles, the diameter D of the spheres, and their material properties:

$$\begin{aligned} K_{N}^{(BA)}=\frac{G D^{1/2}}{(1-\nu )}\delta ^{1/2}. \end{aligned}$$
(15)

While the incremental displacement of the centers of contacting particles is given in terms of the averages of the increments, the total normal component, \(\delta =u_i^{(BA)}{\hat{d}}_{i}^{(BA)}\) in Eq. (15), is given in terms of the average strain by

$$\begin{aligned} \delta =-{\hat{d}}_{i}^{(BA)}E_{ij}d_{j}^{(BA)}. \end{aligned}$$
(16)

This is how the stiffness depend upon the existing average strain and it represents a measure of the strain level of the aggregate along the triaxial loading. Equation (16) can be written as:

$$\begin{aligned} \delta =\frac{D}{3}\left( \varTheta -2\gamma +6\gamma \cos ^{2}\theta \right) . \end{aligned}$$
(17)

2.2.3 Equilibrium

We determine the fluctuations that ensure the equilibrium of the pair \(A-B\) through the following equations. For particle A equilibrium is

$$\begin{aligned} \sum _{n\ne B}^{N^{\left( A\right) }}{\dot{F}}_{i}^{\left( nA\right) }+{\dot{F}} _{i}^{\left( BA\right) }=0 \end{aligned}$$
(18)

while for particle B

$$\begin{aligned} \sum _{n\ne A}^{N^{\left( B\right) }}{\dot{F}}^{\left( nB\right) }+{\dot{F}} _{i}^{\left( AB\right) }=0, \end{aligned}$$
(19)

in which, for example, \(N^A\) is the number of particles in contact with particle A. Difference of the equilibrium equations leads to

$$\begin{aligned} {\dot{\varDelta }}_{i}^{\left( BA\right) }=-D\left[ A_{ik}^{{\left( BA\right) }-1}J_{klm}^{\left( BA\right) }-A_{ik}^{{\left( AB\right) }-1}J_{klm}^{\left( AB\right) }\right] {\dot{E}}_{lm} \end{aligned}$$
(20)

in which, for example,

$$\begin{aligned} A_{ik}^{\left( BA\right) }=\sum _{n=1}^{N^{\left( A\right) }}K_{N}^{(nA)}\hat{ d}_{i}^{(nA)}{\hat{d}}_{k}^{\left( nA\right) } \end{aligned}$$
(21)

and

$$\begin{aligned} J_{klm}^{\left( BA\right) }=\sum _{n=1}^{N^{\left( A\right) }}K_{N}^{\left( nA\right) }{\hat{d}}_{k}^{\left( nA\right) }{\hat{d}}_{l}^{(nA)}{\hat{d}} _{m}^{(nA)}. \end{aligned}$$
(22)

We employ the conditional average defined over all pairs whose contact vector is within an increment of solid angle:

$$\begin{aligned} \left\langle A_{ik}\right\rangle _{{\hat{\textbf{d}}}^{\left( BA\right) }}= & {} \left\langle \sum _{n=1}^{N^{\left( A\right) }}K_{N}{\hat{d}}_{i}^{(nA)}\hat{ d}_{k}^{\left( nA\right) }\right\rangle _{{\hat{\textbf{d}}}^{\left( BA\right) }}\nonumber \\= & {} \left\langle \sum _{n=1}^{N^{\left( B\right) }}K_{N}{\hat{d}}_{i}^{(nB)}\hat{ d}_{k}^{\left( nB\right) }\right\rangle _{{\hat{\textbf{d}}}^{\left( AB\right) }} \end{aligned}$$
(23)

and

$$\begin{aligned} \left\langle J_{klm}\right\rangle _{{\hat{\textbf{d}}}^{\left( BA\right) }}= & {} \left\langle \sum _{n=1}^{N^{\left( A\right) }}K_{N}^{\left( nA\right) } {\hat{d}}_{k}^{\left( nA\right) }{\hat{d}}_{l}^{(nA)}{\hat{d}}_{m}^{(nA)}\right\rangle _{{\hat{\textbf{d}}}^{\left( BA\right) }}\nonumber \\ {}= & {} -\left\langle \sum _{n=1}^{N^{\left( B\right) }}K_{N}^{\left( nB\right) }{\hat{d}} _{k}^{\left( nB\right) }{\hat{d}}_{l}^{(nB)}{\hat{d}}_{m}^{(nB)}\right\rangle _{ {\hat{\textbf{d}}}^{\left( AB\right) }} \end{aligned}$$
(24)

because \({\hat{\textbf{d}}}^{\left( BA\right) }=-{\hat{\textbf{d}}}^{\left( AB\right) }.\) Eq. (20) becomes

$$\begin{aligned} \left\langle {\dot{\varDelta }}_{i} \right\rangle _{{\hat{\textbf{d}}} }=-2D\left\langle A_{ik}^{-1}J_{klm}\right\rangle _{{\hat{\textbf{d}}}}{\dot{E}}_{lm} \end{aligned}$$
(25)

with the following representation for the third rank tensor

$$\begin{aligned} \left\langle A_{ik}^{-1}J_{klm}\right\rangle _{{\hat{\textbf{d}}}}= & {} \beta _{1} {\hat{d}}_{i}^{\left( BA\right) }{\hat{d}}_{l}^{\left( BA\right) }{\hat{d}} _{m}^{\left( BA\right) } \nonumber \\ {}+ & {} \beta _{2}\left( \delta _{il}{\hat{d}}_{m}^{\left( BA\right) }+\delta _{lm}{\hat{d}}_{i}^{\left( BA\right) }+\delta _{im}{\hat{d}} _{l}^{\left( BA\right) }\right) . \end{aligned}$$
(26)

The coefficients \(\beta _{1}\) and \(\beta _{2}\) depend on the coordination number k. The summation in the conditional averages employed in Eqs. (23) and (24) are replaced by an integration over all the directions in the neighbors of all pairs characterized by a contact vector \({\hat{\textbf{d}}}\) within an incremental solid angle, assuming an uniform distribution. With a simple statistical model, we obtain

$$\begin{aligned} \beta _{1}=\frac{3}{k}\left( \frac{166-11k}{128}\right) \end{aligned}$$
(27)

and

$$\begin{aligned} \beta _{2}=-\frac{3}{k}\left( \frac{k+14}{128}\right) . \end{aligned}$$
(28)

We are neglecting the contribution of anisotropy through the contact stiffness \(K_N\) so fluctuations depend only on the contacts network. Both \(\beta _1\) and \(\beta _2\) decreases as k increases, or, equivalently, the fluctuations contribution diminishes as the confining pressure increases [35].

Given Eq. (8), we derive:

$$\begin{aligned} \left\langle {\dot{u}}_{i}\right\rangle _{{\hat{\textbf{d}}}^{\left( BA\right) }}= & {} {\dot{E}}_{ij}d_{j}^{\left( BA\right) }-2D\beta _{1}{\hat{d}}_{i}^{\left( BA\right) }{\hat{d}}_{l}^{\left( BA\right) }{\hat{d}}_{m}^{\left( BA\right) } {\dot{E}}_{ml}\nonumber \\ {}- & {} 2D\beta _{2}\left( \delta _{il}{\hat{d}}_{m}^{\left( BA\right) }+\delta _{lm}{\hat{d}}_{i}^{\left( BA\right) }+\delta _{im}{\hat{d}} _{l}^{\left( BA\right) }\right) {\dot{E}}_{ml}. \end{aligned}$$
(29)

Therefore, for a given pair orientated along \({\hat{\textbf{d}},}\) we write the incremental contact force as

$$\begin{aligned} \left\langle {\dot{F}}_{i}\right\rangle _{{\hat{\textbf{d}}}}=K_{N}{\hat{d}}_{i} {\hat{d}}_{j}\left\langle {\dot{u}}_{j}\right\rangle _{{\hat{\textbf{d}}}} \end{aligned}$$
(30)

or

$$\begin{aligned} \left\langle {\dot{F}}_{i}\right\rangle _{{\hat{\textbf{d}}}}=DK_{N}{\hat{d}}_{i} \left[ {\hat{d}}_{q}{\dot{E}}_{qj}{\hat{d}}_{j}\left( 1-2\beta _{1}-4\beta _{2}\right) -2\beta _{2}\delta _{lm}{\dot{E}}_{ml}\right] . \end{aligned}$$
(31)

With respect to the average strain theory, it is the last term in the bracket, proportional to the volume strain and \(\beta _2\), that characterizes the new ingredient in the model from the qualitative point of view, once fluctuations are included.

2.2.4 Incremental stress

An analytical expression for the stress increment may be obtained by employing the continuous analog of Eq. (2). This is phrased in terms of the number of particles per unit volume n and a contact distribution function \(f({\hat{\textbf{d}})}\). In the pre-peak region, range of deformation of our interest, the distribution of contacts is assumed to be isotropic, \(f({\hat{\textbf{d}})} =k/4\pi\), where k is the coordination number that evolves during the loading. Therefore, we account for the induced anisotropy through Eqs. (15) and (17) while we ignore the structural anisotropy which seems reasonable according to Fig. 2 in which, at most, we have, in the region of compression around \(\theta =0\), a slight increments of number of contacts with respect to the isotropic distribution.

The average stress is:

$$\begin{aligned} {\dot{\sigma }}_{ij}=\frac{n}{2}\int _{\varOmega }f({\hat{\textbf{d}})}\left\langle {\dot{F}}_{i}\right\rangle _{{\hat{\textbf{d}}}}d_{j}d\varOmega \end{aligned}$$
(32)

or, given Eqs. (15), (17) and (31),

$$\begin{aligned} {\dot{\sigma }}_{ij}= & {} \omega \left( 1-2\beta _{1}-4\beta _{2}\right) \nonumber \\\times & {} \int _{0}^{2\pi }\int _{0}^{\theta _{1}}R^{1/2}{\hat{d}}_{k}{\hat{d}}_{m}{\hat{d}}_{i}{\hat{d}}_{j}{\dot{E}} _{km}\sin \theta d\theta d\varphi \nonumber \\- & {} 2\omega \beta _{2}\int _{0}^{2\pi }\int _{0}^{\theta _{1}}R ^{1/2}{\hat{d}}_{i}{\hat{d}}_{j}\delta _{km}{\dot{E}}_{km}\sin \theta d\theta d\varphi \end{aligned}$$
(33)

in which \(R=\varTheta -2\gamma +6\gamma \cos ^{2}\theta\), \(\omega \equiv nkGD^{3}/\left[ 4\pi \sqrt{3}(1-\nu )\right]\) and \(\theta _1\) is the angle of deletion, when \(\delta =0\) in Eq. (17):

$$\begin{aligned} \theta _1 = \pi /2 \end{aligned}$$
(34)

if \(\varTheta -2\gamma \ge 0\), otherwise

$$\begin{aligned} \theta _1 = \arccos \sqrt{(2\gamma -\varTheta )/(6\gamma )}. \end{aligned}$$
(35)

The upper limit of the integration, \(\theta _1\), account for deletion when the average contact displacement, \(\delta\), goes to zero.

In compact form,

$$\begin{aligned} {\dot{\sigma }}_{ij}={\mathcal {A}}_{ijkm}{\dot{E}}_{km} \end{aligned}$$
(36)

where the stiffness tensor, \({\mathcal {A}}_{ijkm}\), can be represented through the axial vector \(\textbf{h}=\textbf{y}_3\) and Kronecker delta, \(\delta _{ij}\), with

$$\begin{aligned} {\mathcal {A}}_{ijkm}= & {} \eta _{1}h_{m}h_{k}h_{j}h_{i}+\eta _{2}\delta _{ij}\delta _{km}+\eta _{3}\left( \delta _{ik}\delta _{jm}+\delta _{im}\delta _{jk}\right) \nonumber \\+ & {} \eta _{4}\delta _{km}h_{i}h_{j}+\eta _{5}h_{m}h_{k}\delta _{ij} \nonumber \\+ & {} \eta _{6}\left( \delta _{ik}h_{j}h_{m}+\delta _{jm}h_{k}h_{i}+\delta _{im}h_{k}h_{j}+\delta _{jk}h_{i}h_{m}\right) . \end{aligned}$$
(37)

The six coefficients are

$$\begin{aligned} \eta _{1}= & {} 2\pi \omega \left( 1-2\beta _{1}-4\beta _{2}\right) a_{1}, \\ \eta _{2}= & {} 2\pi \omega \left( 1-2\beta _{1}-4\beta _{2}\right) a_{2}-4\pi \omega \beta _{2}a_{4}, \\ \eta _{3}= & {} 2\pi \omega \left( 1-2\beta _{1}-4\beta _{2}\right) a_{2}, \\ \eta _{4}= & {} 2\pi \omega \left( 1-2\beta _{1}-4\beta _{2}\right) a_{3}-4\pi \omega \beta _{2}\left( a_{5}-a_{4}\right) , \\ \eta _{5}= & {} \eta _{6}=2\pi \omega \left( 1-2\beta _{1}-4\beta _{2}\right) a_{3}, \end{aligned}$$

with

$$\begin{aligned} a_{1}\equiv & {} \int _{0}^{\theta _{1}}R^{1/2}\left( \cos ^{4}\theta -3\sin ^{2}\theta \cos ^{2}\theta +\frac{3}{8}\sin ^{4}\theta \right) \sin \theta d\theta , \\ a_{2}\equiv & {} \int _{0}^{\theta _{1}}R ^{1/2}\frac{1}{8}\sin ^{5}\theta d\theta , \\ a_{3}\equiv & {} \int _{0}^{\theta _{1}}R^{1/2}\left( \frac{1}{2}\sin ^{2}\theta \cos ^{2}\theta - \frac{1}{8}\sin ^{4}\theta \right) \sin \theta d\theta , \\ a_{4}\equiv & {} \int _{0}^{\theta _{1}}R^{1/2}\frac{1}{2}\sin ^{3}\theta d\theta , \end{aligned}$$

and

$$\begin{aligned} a_{5}\equiv \int _{0}^{\theta _{1}}R^{1/2}\cos ^{2}\theta \sin \theta d\theta . \end{aligned}$$
(38)

As suggested by La Ragione et al. [17, 36], it is the presence of fluctuations in the kinematics of contacting particles that leads to \(\eta _4 \ne \eta _5\) which implies the loss of major symmetry for the anisotropic stiffness tensor \({\mathcal {A}}_{ijkm}\). It is the term proportional to \(\beta _2\) and the volume strain in Eq. (31) that makes clear the difference between the simple average strain and the presence of fluctuations. Without fluctuations, \({\mathcal {A}}_{ijkm}\) is symmetric. The asymmetry in \({\mathcal {A}}_{ijkm}\) is a necessary condition for the second order work to vanish at some stressed state, under a particular perturbation.

3 Second-order work

The second order work (e.g. [14]) is

$$\begin{aligned} W_{2}={\dot{\sigma }}_{ij}{\dot{E}}_{ij}. \end{aligned}$$
(39)

or, with Eq. (36)

$$\begin{aligned} W_{2}={\mathcal {A}}_{ijkm}{\dot{E}}_{km}{\dot{E}}_{ij}. \end{aligned}$$
(40)

Given Eq. (37), we obtain

$$\begin{aligned} W_{2}= & {} \eta _{1}h_{m}h_{k}h_{j}h_{i}{\dot{E}}_{km}{\dot{E}}_{ij}+\eta _{2} {\dot{E}}_{qq}{\dot{E}}_{qq}+2\eta _{3}{\dot{E}}_{ij}{\dot{E}}_{ij} \nonumber \\{} & {} +\left( \eta _{4}+\eta _{5}\right) {\dot{E}}_{qq}h_{i}h_{j}{\dot{E}} _{ij}+4\eta _{6}h_{j}h_{m}{\dot{E}}_{sm}{\dot{E}}_{sj}. \end{aligned}$$
(41)

The coefficients \(\eta\)’s depend on the relation between the volume strain \(\varTheta\) and the shear strain \(\gamma\) which are present in the contact stiffness \(K_N.\) Here, following Jenkins and Strack [23], we use the simple average strain and determine the initial pressure

$$\begin{aligned} p=\frac{nGD^2k_0}{27\sqrt{3}(1-\nu )} \varTheta _0^{3/2} \end{aligned}$$
(42)

and then equate it to the pressure when an uniaxial deformation is applied:

$$\begin{aligned} \int _0^{\theta _1} R^{3/2}\sin \theta d\theta - \frac{k_0}{k}\varTheta _0^{3/2}=0. \end{aligned}$$
(43)

Equation (43) provides a relation between \(\gamma\) and \(\varTheta\) and with the evolution of the coordination number, \(k=0.5\gamma ^2/\varTheta _0-1.6\gamma /\varTheta _0+6\), previously derived (see Fig. 3), we can predict \(W_2.\) We focus on the increments that may provide negative values of \(W_2\), according with Hadda et al. [37]. We consider \({\dot{E}}_{33}<0\) and \({\dot{E}}_{11}={\dot{E}}_{22}>0\), so

$$\begin{aligned} W_{2}= & {} \eta _{1}{\dot{E}}_{33}^{2}+\eta _{2}\left( 2{\dot{E}}_{11}+{\dot{E}} _{33}\right) ^{2}+2\eta _{3}\left( 2{\dot{E}}_{11}^{2}+{\dot{E}}_{33}^{2}\right) \nonumber \\+ & {} \left( \eta _{4}+\eta _{5}\right) \left( 2{\dot{E}}_{11}+{\dot{E}}_{33}\right) {\dot{E}}_{33}+4\eta _{6}{\dot{E}}_{33}^{2}. \end{aligned}$$
(44)

In particular, in the Rendulic strain plane, see Fig. 5 (strain positive in compression), we take \({\dot{E}}_{33}=\rho \sin (\alpha _{\epsilon })\) and \({\dot{E}}_{11}={\dot{E}}_{22}=-\rho \cos (\alpha _{\epsilon })/\sqrt{2}\), in which \(\rho\) is a positive constant and \(\alpha _{\epsilon }\) indicates the incremental strain direction in the range \(110 \le \alpha _{\epsilon } \le 160\). These are probes that we identify as forward incremental loadings for which the theory has been developed.

Fig. 5
figure 5

Rendulic strain plane (positive in compression) and the angle \(\alpha _{\epsilon }\)

Full size image

We predict a negative value for \(W_{2}\) when \(\gamma /\varTheta _0=0.93\), with \(\alpha =150^{\circ }\) (see Matlab code in Appendix). This angle is close to what also seen in numerical simulations [37].

We also evaluate \(W_2\) through our numerical simulations. At each stressed states, along the triaxial test, we apply probes to calculate the second order work through Eq. (39). The value of \(\rho\) is crucial as we consider probes associated with an elasto-plastic response [38]. So, we apply \(\rho \approx 10^{-6}\) as in the triaxial test. In Fig. 6 we plot the normalized second order work, \(\left( {\dot{\sigma }}_{ij} {\dot{E}}_{ij} \right) /\left( |{\dot{\sigma }}|\rho \right)\). A first negative value for \(W_2\) occurs at \(\gamma /\varTheta _0 = 0.55\) and \(\alpha _{\epsilon }=130^{\circ }\). Both the strain and the angle are smaller than those predicted by the theory. From simulations, we note an indication of the preferential angle of failure since the first stressed states.

Fig. 6
figure 6

Circular diagrams of the normalized second order work. Focus on the second quadrant. First negative \(W_2\) at \(\alpha _{\epsilon }=130 ^{\circ }\) when \(\gamma /\varTheta _0= 0.55\) according to numerical simulations

Full size image

The evolution of the asymmetry of the stiffnnes tensor \({\mathcal {A}}_{ijkm}\), in the hardening regime, is visualized in Fig. 7.

Fig. 7
figure 7

Evolution of the term responsible of the asymmetry of the stiffnnes tensor \({\mathcal {A}}_{ijkm}\) with the normalized shear strain, see the coefficient \(\eta _4\) in Eq. (37)

Full size image

A possible way to improve the theory is to employ fluctuations in the stiffness, Eq. (16), that will lead to a more complicated relation between \(\gamma\) and \(\varTheta\), now given by Eq. (43), and other terms in the coefficients of the macroscopic stiffness tensor \({\mathcal {A}}_{ijkm}\), without changing the structure of the tensor. It is also possible to include fabric and structural anisotropy in both fluctuations, through Eq. (25) and stress, through Eq. (32). However, we think that the present model is more transparent, and it makes clear and illustrative the role played by the fluctuations in relation to the vanishing of the second order work.

Finally, we take Eq. (44) and dived it by \({\dot{E}}_{11}^2\) and, with \(\chi ={\dot{E}}_{33}/{\dot{E}}_{11}\), we obtain

$$\begin{aligned} \frac{W_{2}}{{\dot{E}}_{11}^2}= & {} \eta _{1}\chi ^2+\eta _{2}\left( 2 +\chi \right) ^{2}+2\eta _{3}\left( 2+\chi ^2\right) \nonumber \\ {}+ & {} \left( \eta _{4}+\eta _{5}\right) \left( 2\chi +\chi ^2\right) +4\eta _{6}\chi ^2 \end{aligned}$$
(45)

or

$$\begin{aligned} \frac{W_{2}}{{\dot{E}}_{11}^2}= A_1 \chi ^2 +A_2 \chi + A_3 \end{aligned}$$
(46)

with

$$\begin{aligned} A_1= & {} \eta _1+\eta _2+2\eta _3+\eta _4+\eta _5+4\eta _6, \end{aligned}$$
(47)
$$\begin{aligned} A_2= & {} 4\eta _2+2\eta _4+2\eta _5, \end{aligned}$$
(48)
$$\begin{aligned} A_3= & {} 4(\eta _2+\eta _3). \end{aligned}$$
(49)

The discriminant is \(A_2^2-4A_1A_3\) and it is zero at \(\gamma /\varTheta _0=0.93\).

4 Conclusion

We have employed a model that characterizes the second work with respect to failure. We have introduced a kinematics of contacting particles that deviates from the average strain and written an explicit but approximate equations of equilibrium for pairs of contacting particles in the aggregate. Because of fluctuations, it is possible, in the hardening regime, to predict a macroscopic stiffness tensor without the major symmetry which is essential to have a stressed, anisotropic state in which \(W_2\) goes to zero. That is, in the context of a simplified model, we have linked the extend kinematics of contacting particles with fluctuations to the asymmetry of the macroscopic stiffness tensor, and to the possibility that the second work \(W_2\) vanishes. The present model overpredicts the angle of failure and the value of the strain when the second order work vanishes. On the other hand, the theory exhibits the important ingredients from the microscopic point of view that may explain failure of the aggregate.