1 Introduction

Centrifuge modelling is a well-established technique in the field of civil engineering, widely employed to investigate common soil stability and soil-structure interaction problems [1]. By rotating a laboratory-scale model at a given angular velocity at the end of a centrifuge arm (Fig. 1), a centripetal acceleration is imposed on the model. When this centripetal acceleration exceeds Earth’s gravity by a scaling factor N, it augments the self-weight of the material within the model, thereby enabling precise control over the gravitational effects in the model [2]. Recently, the technique has been used to simulate the conditions prevalent in geophysical granular mass movements such as landslides and debris flows [e.g. 3, 4, 2].

Fig. 1
figure 1

Schematic of the column collapse experimental configuration loaded on to the geotechnical centrifuge

Full size image

In contrast to traditional laboratory-scale studies of large granular mass movements, which usually rely on Froude scaling to determine the velocity scale [e.g. 5, 6, 7], geotechnical centrifuge modelling offers a unique advantage. This advantage lies in its ability to incorporate stress-related processes that play a critical role in determining the flow’s behaviour and, consequently, the overall dynamics in real-world scenarios [8, 9]. This becomes especially important when examining how the flow interacts with potential mitigation structures [e.g. 10, 11, 12, 13]. Stress-dependent mechanisms also significantly affect the dynamics of partially or fully saturated granular flows. For instance, phenomena such as surface tension effects caused by capillary bridges between adjacent grains [14], or at the surface of the flow itself, can have a significant impact on flow behaviour in laboratory experiments, even though they are relatively minor compared to gravitational forces in natural mass movements [15]. Moreover, in addition to the flow’s particle size distribution, the magnitude of the confining stress at a specific point within the flow greatly influences the buildup and dissipation of excess pore pressures. As previously observed, these pressures can significantly affect flow mobility and dynamics [16,17,18].

Consider a simplified scenario of a centrifuge test as depicted in Fig. 2, where there are three particles in contact with a horizontal surface (i.e. the base of a centrifuge model) of length L that is being spun at a rotational velocity \(\varvec{\omega }\) and at distance of \(R_c\) from the centre of the centrifuge. The Cartesian reference frame xz remains aligned with the horizontal surface and, therefore, spins together with the model. While the central particle remains stationary, the two outer particles move away from the centreline of the model at velocity \(\varvec{u}\). The particle acceleration field can be expressed as the sum of centrifugal acceleration \(\varvec{a}_{cf}\) and the Coriolis acceleration \(\varvec{a}_{co}\)

$$\begin{aligned} \varvec{a} = \varvec{a}_{cf} + \varvec{a}_{co} = -\varvec{\omega } \times (\varvec{\omega } \times \varvec{r}_c) - 2\varvec{\omega } \times \varvec{u}, \end{aligned}$$
(1)

where \(\varvec{r}_c\) is the coordinate direction aligned with the gravity vector. The direction and magnitude of \(\varvec{r}_c\) depend on the position of the objects, in this case, the particles, relative to the centrifuge’s axis of rotation. It is important to note that, for completeness, we should consider the external acceleration vector, gravity \(\varvec{g}\), in Eq. 1. However, if \(\varvec{\omega }\) is sufficiently large, its effects are often considered negligible [19]. As described in Eq. 1, \(\varvec{a}_{cf}\) consistently acts away from the centre of rotation and parallel to \(\varvec{r_c}\), while the direction of \(\varvec{a}_{co}\) depends on both the direction of \(\varvec{u}\) and \(\varvec{\omega }\). To simplify matters, \(\varvec{a}\) is often approximated as an equivalent increased gravity [20]

$$\begin{aligned} a \equiv \omega ^2 R_c \equiv Ng, \end{aligned}$$
(2)

where g is Earth’s gravitational acceleration and N serves as a scale factor. Both \(\varvec{a}_{cf}\) and \(\varvec{a}_{co}\) can impose non-vertical accelerations on the particles, thereby influencing their horizontal velocity. In smaller geotechnical centrifuges, where \(R_c\approx \mathrm{2\,m}\) and \(L\approx \mathrm{0.8\,m}\), the magnitude of the horizontal component of \(\varvec{a}_{cf}\) can equate to 20 % of the presumed increased gravitational acceleration calculated from Eq. 2. While this may have a negligible effect when modelling typical civil engineering applications, it complicates the translation of experimental observations from centrifuge models of granular mass movements, which are inherently more dynamic processes, to natural flows.

To conduct a comprehensive experimental study investigating the impact of centrifugal and Coriolis accelerations on granular flow dynamics, one would need to use multiple centrifuges of varying sizes, considering the dependency on \(R_c\). Therefore, such a study is well-suited for numerical modelling which offers the potential to significantly expand the parameter space of physical experiments. Furthermore, such simulations can serve as effective tools for scaling up our insights from laboratory-scale experiments to these larger geophysical phenomena.

Recent investigations have utilised the Discrete Element Method (DEM) to explore the effects of centrifugal and Coriolis accelerations on both steady [19, 21] and unsteady [12, 22] dry granular flow configurations. Numerical modelling not only facilitates the study of \(\varvec{a}_{cf}\) when varying \(R_c\) but also allows for the independent examination of the effects of \(\varvec{a}_{cf}\) and \(\varvec{a}_{co}\). While these studies represent significant progress in understanding the mechanisms and scaling of centrifuge modelling effects, additional complexities, such as the presence of an interstitial pore fluid, need to be considered.

Fig. 2
figure 2

Schematic of the acceleration forces acting upon particles in the rotating frame of reference of a geotechnical centrifuge experiment

Full size image

The study aims to enhance our understanding by employing numerical modelling to examine a just-saturated granular column collapse configuration within a geotechnical centrifuge. Two recent experimental studies [15, 23] have provided valuable insights into the system, with a strong focus on grain-fluid interaction and its influence on macro-scale flow features. By utilising the Lattice-Boltzmann Method (LBM) to model the fluid phase and coupling it with DEM, this study initially seeks to replicate the flow states observed in these physical experiments. Subsequently, the study investigates the influences of centrifugal and Coriolis accelerations on both grain-scale and macro-scale flow dynamics.

Fig. 3
figure 3

Example of the phase front extraction technique used during the experimental image analysis (available at http://doi.org/10.17639/nott.7277). The raw (dashed) and averaged (line) radial positions of the fluid (green) and granular (red) phase fronts are shown

Full size image

2 Fluid-saturated granular column collapse

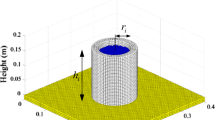
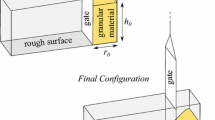
The current research aims to explore the impact of centrifuge modelling on granular-fluid flows by focusing on the dynamics of a simple axisymmetric, just-saturated granular column collapse (see Fig. 1). Although this configuration has been extensively studied under normal laboratory conditions (i.e. \(g=\) 9.81 m s\(^{-2}\)) [e.g. 24, 25, 26, 27, 28], recent investigations [15, 23] have also examined its dynamics within a geotechnical centrifuge. However, theses studies primarily focused on grain-fluid interaction and did not thoroughly investigate the contributions of varying centrifugal and Coriolis accelerations to the collapse dynamics.

To bridge this knowledge gap, we conducted experiments using the same collapse configuration system as in the aforementioned studies, in order to provide empirical data to compare against the numerical model presented in this work (see Sect. 3 and Sect. 4). The collapse of the granular column was initiated using a modified classical weighted-pulley system, designed for hands-free operation within the University of Nottingham’s GT50/1.7 geotechnical beam centrifuge (see Ellis et al. [29] for details). The evolution of the collapses were recorded using two high speed cameras and image processing was used to extract the location of both phase fronts throughout the duration of the experiment (see Fig. 3). A full description of the physical system and image analysis can be found in Webb et al. [15].

Given, that the flow spreads axisymmetrically, specifically, sections of the flow travel ‘upstream’ and ‘downstream’ of centrifuge motion [15], this experimental configuration provides an ideal test case for comprehending the role of centrifugal and Coriolis accelerations in influencing the behaviour of dynamic flows. By using experimental comparison to assess the numerical model, we aim to gain valuable insights into the mechanics of granular-fluid flows in a geotechnical centrifuge setting that would be unachievable from experimental testing alone.

3 The LBM-DEM framework

The numerical tool chosen for the current work was used previously by Cabrera et al. [19] and Leonardi et al. [21] to investigate the behaviour and modelling effects of a granular flow down a rough incline within a geotechnical centrifuge. The code is an extension of the original work by Leonardi et al. [30] which has been modified and extensively used for the study of laboratory- and large-scale fluid-granular flow mechanisms [e.g. 31, 32, 33], and even saturated granular column collapses [34]. The code employs a compound approach to modelling complex granular-fluid systems known as the DEM-LBM method. This method has gained popularity in the last two decades, and can be now considered a standard approach for the simulation of particle-driven flow [35,36,37,38]. The behaviour of the granular and fluid phases are simulated using independent numerical schemes but are coupled together by imposing phase interaction forces. Further additional forces, accounting for the external forces imposed on an object within a rotating domain, are also accounted for.

The code solves the collisions of particle pairs within the flow using a standard Discrete Element Method (DEM) approach. A linear spring-dashpot model is used to determine the surface-normal \(F_n\) and tangential \(F_t\) contact forces through their respective contact stiffness, \(k_n\) and \(k_t\), and damping, \(\alpha _n\) and \(\alpha _t\), coefficients. \(F_n\) is defined as a function of the overlap \(\xi \) between the two colliding bodies

$$\begin{aligned} F_n = k_n \xi + 2 \alpha _n \sqrt{k_n m} \frac{d \xi }{d t}, \end{aligned}$$
(3)

while the magnitude of \(F_t\) is regulated by a Coulomb friction relation

$$\begin{aligned} F_t = \max \left( \mu _s F_n, k_t \zeta + 2 \alpha _t \sqrt{k_t m} \frac{d \zeta }{d t}\right) , \end{aligned}$$
(4)

where m is the grain mass, \(\mu _s\) is the static friction coefficient of the particles, and \(\zeta \) is the elongation of a tangential spring that represents elastic tangential deformations. There are analogous relations for particle-wall interactions where \(\mu _s\) is substituted for the particle-wall friction coefficient \(\mu _{s,w}\).

To ensure that it was possible for the completely spherical particles to form into the stable heaps on the flat surface that were observed in previous experiments (see [33, 34]), an additional torque which opposes the rotational motion of the particles \(M_r\) was also implemented

$$\begin{aligned} M_r = \mu _r F_n \frac{d}{2} \end{aligned}$$
(5)

where \(\mu _r\) is the rolling friction coefficient of the particles and d is the particle diameter. It should be noted that, for collisions between particles that differ in size, m and d should be exchanged for effective values that are representative of the collision (see [33]).

The dynamics of the fluid phase are described using the Lattice Boltzmann method (LBM) which is formulated from kinetic theory at the mesoscopic scale [30]. Fluid advection is expressed using a density function \(f(\varvec{x},\varvec{c},t)\), that describes the probability of finding fluid molecules at a location \(\varvec{x}\), with microscopic velocity \(\varvec{c}\) at time t. f is discretised in space by considering a finite number of advection directions i across a regularly spaced lattice, such that \(f_i(\varvec{x},t) = f(\varvec{x},\varvec{c_i},t)\) where \(\varvec{c_i}\) is the direction dependent weighted lattice velocity for a given fluid cell. The current work uses the D3Q19 lattice configuration, which delineates the lattice into 19 advection directions across 3 dimensions. Also due to the lattice symmetry, it is possible to recover the incompressible Navier-Stokes equations and, hence, obtain the macroscopic fluid density \(\rho _f\) and velocity \(\varvec{u}_f\) at each x for all t. This recovery links the macroscopic viscosity of the fluid to the mesoscopic collision operator. Thus, viscosity can be set by the user by altering the timescale by which the distribution function is relaxed towards thermodynamic equilibrium [39]. Following the work of Leonardi et al. [30], the evolution of the fluid free surface is updated using Janßen and Krafczyk’s [40] volume-of-fluid method, with a full-slip boundary condition, to improve computational efficiency.

The two phases are coupled through the exchange of a drag force \(f_d\), which is calculated as the integral of all the drag contributions between individual fluid points interacting with each granular particle, using the immersed-boundary method [41]. As such, the fluid mesh size \(\Delta _f\) must be smaller than the characteristic DEM particle diameter D. It should be noted that this stipulation on the lattice spacing also implies that the fluid pressure is effectively resolved at the pore scale [34], down to the precision offered by the lattice spacing itself.

The work of Leonardi et al. [21] has been extended so that both the fluid and granular phases can be submitted to an elevated gravitational acceleration field as would be imposed to a model while being spun on a geotechnical centrifuge. This is achieved by imposing both \(\varvec{a}_{cf}\) and \(\varvec{a}_{co}\) on each phase as external forces. Within the LBM framework, the acceleration applied to the fluid phase, which is a function of space, is computed based on the centroid of every lattice node. \(\varvec{a}_{cf}\) and \(\varvec{a}_{co}\) can be imposed independently so that it is possible to investigate the influence of each on collapse dynamics separately.

Fig. 4
figure 4

Schematic of the simulation domain during a column collapse containing 261 particles. The frictional boundaries are shown as grey planes and the insets highlight the direction of the centrifugal and Coriolis accelerations acting on a particle for the defined rotational reference frame

Full size image

In order to model the contacts of colliding grains, the time-step required by the DEM is generally smaller than the time step required for the LBM. Hence, the schemes are staggered so that multiple DEM time steps are run for every LBM time steps. While a complete explanation of the DEM-LBM scheme is out of the scope of the current work, where we have only detailed its most significant components, a comprehensive explanation of the method can be found in Leonardi et al. [31].

4 Simulation methodology

4.1 Simulation parameter space

Similar to the approach taken by Webb et al. [15] in their image analysis, our simulations utilise the axisymmetric nature of the experiment. By modelling only a quarter of the column (see Fig. 4), we significantly reduce computational time for each simulation.

The initial configuration of the granular-fluid column is characterised by two parameters: the initial column height \(h_0\) and radius \(r_0\). As was the case for the two previous studies [15, 23], we set \(h_0=\) 50 mm and \(r_0=\) 54 mm for each phase, resulting in a column aspect ratio of \(a=h_0/r_0=\) 0.93. The granular phase comprises monodispersed particles with a mean diameter \(D=\textrm{8}\times \textrm{10}^{-3}\) m (±10% to prevent crystallisation within the initial configuration [21]) and a particle density \(\rho _p=\) 2650 kg m\(^{-3}\). This is the largest size used in the two previous studies and was selected as it minimises surface tension effects when in contact with a thin film of fluid [15] (see Sect. 5.2 for further discussion). Moreover, the number of particles \(n_p\) that have to be modelled ensures computational efficiency, with \(n_p=\) 261, corresponding to an initial mean solid volume fraction \(\phi _p=\) 0.61. The parameters for modelling the particles using the DEM scheme are summarised in Table 1. Using the real stiffness of the grains would result in unreasonably long simulation times. Since the collapse dynamics of interest are not influenced by particle deformability [42], the linear contact stiffness \(k_n\) has been instead calibrated so that the particles are sufficiently rigid to make elastic deformations negligible.

Table 1 Summary of DEM simulation parameters
Full size table

The three Newtonian fluids used in this study are miscible glycerol-water mixtures, characterised by two parameters: the ratio between the fluid mixture viscosity \(\mu _f\) and the viscosity of water \(\mu _w\) denoted by \(\mu _f^*=\) [50, 100, 150], and the density of the fluid mixture \(\rho _f=\) [1203.8, 1219.7, 1227.5] kg m\(^{-3}\), respectively. The viscosity of the fluids were required to be significantly higher than those used previously by Webb et al. [15] as \(\mu _f\) is directly related to the relaxation time, and, therefore, the stability of the fluid in the LBM scheme [30]. Further details about the preparation of the physical experiments can be found in Webb et al. [15].

The final model considerations are those dictating the relative contribution of centrifugal and Coriolis accelerations to collapse dynamics. Following Cabrera et al.’s [19] approach, we consider the following three external forcing cases

  1. (i)

    A constant acceleration field \(\varvec{a}=N\varvec{g}\) where the far field condition \(R_c \gg h_0\) is assumed, notated as Ng.

  2. (ii)

    A rotating domain that only accounts for the curvature of the acceleration field arising from the centrifugal acceleration (i.e. \(\varvec{a}=\varvec{a}_{cf}\)), notated as \(\omega ^0\).

  3. (iii)

    A complete acceleration field for a rotational domain (i.e. \(\varvec{a}=\varvec{a}_{cf}+\varvec{a}_{co}\)) where contributions of the Coriolis effect in the downstream and upstream direction, notated as \(\omega ^-\) and \(\omega ^+\), respectively, will be considered independently.

To understand how \(\varvec{a}_{cf}\) and \(\varvec{a}_{co}\) can influence collapse dynamics, we explore the parameter space for \(N=\) [5, 8, 10, 12, 15] and \(\log (R_c/h_0)=\) [2, 3, 3.7, 4, 5, 6, 7], where \(\log (R_c/h_0)=\) 3.7 corresponds to the dimensions of the previously conducted physical collapses [15].

4.2 Simulation geometry

The simulation domain is depicted as a rectangular box (Fig. 4) bounded by static frictional walls in the x, y, and z planes. It is characterised by three length parameters [\(x_d\), \(y_d\), \(z_d\)]\(=\)[0.2, 0.2, 0.07] m while the lattice spacing for the fluid phase \(\Delta _f=\textrm{2}\times \textrm{10}^{-3}\) m. Notably, during the column construction process, some adjustments are made to the domain, which will be discussed in Sect. 4.3.

The modelled centrifuge is positioned above the column, with its rotation axis located outside the simulation domain. For simplicity, we define the radius of the centrifuge \(R_c\) as the distance between the axis of rotation and the horizontal plane over which the collapsing material will spread. For the simulations considering the forcing case of the full rotational domain (i.e. \(\varvec{a}=\varvec{a}_{cf}+\varvec{a}_{co}\)), the collapse will be simulated twice so that the flow can be considered in both the \(\omega ^+\) and \(\omega ^-\) directions.

Fig. 5
figure 5

Extraction of the fluid [(a)-(c)] and particle [(d)-(f)] phase fronts for a simulated collapse moving downstream of centrifuge motion where \(\varvec{a}=\varvec{a}_{cf}+\varvec{a}_{co}\), \(R_c=\) 2 m, \(N=\) 5 and \(\mu _f^*=\) 150 at \(t=\) 0 [(a),(d)], 0.1 [(b),(e)] and 0.35 s [(c),(f)]. \(r_v\) (blue), the particle and fluid points making up the phase front (green edge) and the particle and fluid points removed from the phase front (red edge) are all shown. An example of the concentric sectors (grey) splitting up the domain is displayed in (f)

Full size image
Fig. 6
figure 6

Comparison of the raw and filtered phase velocity \(u_v\) and radial position \(r_v\) (insets), where (a) \(v=p\) and (b) \(v=f\) for a simulated collapse moving upstream of centrifuge motion where \(\varvec{a}=\varvec{a}_{cf}+\varvec{a}_{co}\), \(R_c=\) 2.7 m, \(N=\) 5 and \(\mu _f^*=\) 100

Full size image

4.3 Column construction

The dynamics of granular column collapses in both dry and wet conditions are significantly affected by the initial configuration of the column [e.g. 17]. Therefore, it is crucial to closely replicate the physical procedure used in the experiments for the numerical simulations. In this study, we employ a two-step procedure to mimic the experimental conditions.

First, particles are poured into a quarter-cylinder container with a radius of \(r_0\), under a constant natural gravitational field (\(a=g\)) and allowed to settle. To ensure free-fall settling, \(z_d\) was increased to 6 m during the settling simulations.

The column is then consolidated under the acceleration field that will be prescribed for the collapse simulation and allowed to consolidate. It was found that initially pouring the particles into the container under the influence of an elevated acceleration field resulted in a much looser column. Additionally, when the prescribed acceleration field considers a rotating domain (external forcing cases (ii) or (iii)), particles near the top of the column, being less constrained, tended to favour the container edge toward which the fictitious forces pushed them, resulting in an uneven free surface. Hence, this two-stage settling procedure was implemented to limit these effects.

4.4 Front and signal processing

An assessment of the model’s validity was performed by analysing the evolution of the averaged phase front positions \(r_v\) where subscript \(v=p,f\) for the particle and fluid phases, respectively. For the numerical simulations, \(r_v\) was obtained using a two-step procedure. At each saved time-step, the Cartesian domain was divided into n concentric sectors originating from the collapse centre (Fig. 5f) Here, \(n=\) 50 sectors were utilised for the fluid phase, and \(n=\) 16 for the particle phase. The value of n was required to be significantly lower for the granular phase due to it being comprised of far less particles than the fluid phase. The furthest fluid and granular point in each sector were then identified as part of the phase front. Before averaging the radial distance of these points to obtain \(r_v\), points with a radial distance from the origin larger than the 90th percentile of the chosen points were excluded, thereby eliminating points that had escaped from the phase front. While this makes no substantial difference for the fluid phase, removing these points in the case of the granular phase is crucial. It should also be noted that, for the particle phase, the radius of the particle is also considered when calculating the position of the front. An example of this procedure is shown in Fig. 5.

The resulting averaged phase front signal underwent a noise reduction process. Firstly, it was assumed that \(r_v\) monotonically increases with time, allowing the removal of signal sections where \(r_v\) decreased. Secondly, analysis of the phase front velocity, \(u_v = \Delta r_v/\Delta t\), against time (Fig. 6) revealed distinct spikes caused by significant fluctuations in phase front position. These spikes were removed by identifying all peaks in the signal and discarding those with a prominence exceeding 0.001. Notably, filtering was carried out in dimensionless space (see Sect. 5 for further details), facilitating the use of the same prominence value for all simulations, regardless of N. While this processing strategy is not without limitations, unlike methods based on moving average signal reduction, it preserves the magnitude and relative temporal evolution of the signal, resulting in minimal changes to \(r_v\) (see insets of Fig. 6).

5 Model verification

Fig. 7
figure 7

Temporal evolution of the fluid and granular phase fronts in (a) dimensional and (b) \(\rho ^*\)-weighted dimensionless space for a series of simulation conducted with \(\log (R_c/h_0)=\) 3.7 and \(\varvec{a}=N\varvec{g}\)

Full size image

5.1 Family of curves

We begin to evaluate the model’s performance by investigating its ability to reproduce expected behavioural trends under variations in N and \(\mu _f\). The interaction between the two phases will be discussed in Sect. 5.2.

The evolution of \(r_v\) for a set of simulations conducted using the forcing case \(\varvec{a}=N\varvec{g}\) at a constant \(\log (R_c/h_0)=\) 3.7 and varying N and \(\mu _f^*\) are presented in Fig. 7a. Reassuringly, all simulations demonstrate the three sequential stages of motion that are characteristic of an unsteady collapse: acceleration, quasi-steady motion and retardation.

The model also demonstrates consistent adherence to the expected trends as we independently vary N and \(\mu _f^*\). Specifically, we observe that \(r_v\) propagates faster as N increases while its speed of propagation decreases with increasing \(\mu _f^*\). Furthermore, with increasing N, the separation between simulations for a given N reduces, particularly during the acceleration and quasi-steady stages of motion. This observation implies that the influence of flow inertia increases with N which is consistent with previous findings reported by Webb et al. [15] and fundamental scaling principles [e.g. 46].

Following the approach of Webb et al. [47], the anticipated behaviour of the numerically modelled just-saturated column configuration can be characterised using three dimensionless parameters: a, the fluid-grain density ratio \(\rho ^*=\rho _f/\rho _p\) and \(B=(NgD^4\rho ^2)/(h_0\mu _f^2)\). Here \(\rho \) represents the effective column density, defined as \(\rho =\phi _p\rho _p + (1-\phi _p)\rho _f\).

The parameter B, analogous to the square of the ratio of the column Bond and Capillary numbers \((\textrm{Bo}/\textrm{Ca})^2\) [47], quantifies the relative influence of column-scale inertial and viscous forces on collapse dynamics [15]. Since a is held constant, we plot the evolution of the phase radial position in dimensionless density-weighted \(\rho ^* r_v^*\)-\(t^*\) space (Fig. 7b), where \(r_v^*=(r_v-r_0)/r_0\) and \(t^*=t/\sqrt{h_0/(Ng)}\). This transformation results in, approximately, a family of curves dependent on B, with increasing B indicating a higher relative influence of column-scale inertia, leading to the faster propagation of \(r_v^*\rho ^*\). Encouragingly, a similar result was obtained previously when modelling the collapses using a two-phase shallow water model [47].

5.2 Comparison with physical experiments

Fig. 8
figure 8

Comparison of the numerical and experimental evolution of the dimensionless phase front position \(r_v^*\) with dimensionless time \(t^*\) of four column collapses where (a) \(N=\) 5 and \(\mu _f^*=\) 50, (b) \(N=\) 5 and \(\mu _f^*=\) 100, (c) \(N=\) 5 and \(\mu _f^*=\) 150 and (d) \(N=\) 15 and \(\mu _f^*=\) 100

Full size image
Fig. 9
figure 9

Comparison of the numerical and experimental evolution of the dimensionless phase front velocity \(u_v^*\) with dimensionless time \(t^*\) of four column collapses where (a) \(N=\) 5 and \(\mu _f^*=\) 50, (b) \(N=\) 5 and \(\mu _f^*=\) 100, (c) \(N=\) 5 and \(\mu _f^*=\) 150 and (d) \(N=\) 15 and \(\mu _f^*=\) 100

Full size image
Table 2 Summary of experimental test parameters
Full size table

In this section, we further evaluate the performance of the numerical model in replicating the expected dynamics of fluid-saturated granular column collapses. We compare the simulation results with data obtained from four physical experiments (see Table 2). As such, The simulations are conducted with \(\log (R_c/h_0)=\) 3.7, and they are subjected to a complete rotational domain forcing case (\(\varvec{a}=\varvec{a}_{cf}+\varvec{a}_{co}\)). For each test, we perform two simulations to consider both the \(\omega ^-\) and \(\omega ^+\) forcing cases. The analysis is carried out in \(r_v^*\)-\(t^*\) (Fig. 8) and \(u_v^*\)-\(t^*\) (Fig. 9) space, where \(u_v^*\) represents the dimensionless phase front velocity \(u_v^*=u_v/\sqrt{h_0Ng}\) where \(\sqrt{h_0Ng}\) is akin to a scaled characteristic flow velocity equivalent to the local wave speed of the flow [48]. Hence, \(u_v^*\) is equivalent to a temporally evolving, phase specific Froude number [49].

Overall, the model captures many of the experimental observations effectively. In particular, it predicts well the time after release of the phase peak velocity, and achieves runout distances comparable to the physical experiments. However, there are two main sources of discrepancies between the simulations and the physical experiments, as discussed in detail by Webb et al. [47] and summarised below.

5.2.1 Experimental-model discrepancies

The first source of discrepancy, referred to as ‘experimental-model discrepancies’, originates from the process of lifting the cylindrical steel casing to initiate the granular-fluid column collapse. The presence of the casing causes a delay between collapse initiation and a noticeable change in \(r_v^*\) (Fig. 8) because the camera’s view of the collapsing column is initially obstructed. Additionally, the initial value of \(r_v^*\) is larger than \(r_0\) due to the casing’s thickness. The release mechanism also leads to a lag between the initial runout of the granular and fluid phases. The relatively large particle size of the granular phase causes particles to be trapped until the casing displaces far enough to release them, while the fluid can seep out from under the casing. This inter-phase lag increases with decreasing \(\mu _f^*\) due to easier fluid permeation through the granular skeleton and increases with increasing N due to the growing pressure gradient. Moreover, during the lifting process, the acceleration applied to the casing, relative to the collapsing mixture, induces viscous shear stresses, partially lifting the granular-fluid column with the casing. As a result, the initial gravitational potential energy, and, therefore, the peak phase velocity \(u_{v,m}\), \(u_{v,m}^*\) in dimensionless space (Fig. 9), of the physical collapses are larger than the model’s predictions. This discrepancy also increases with increasing N. Furthermore, the delayed collapse of the granular phase may result in it behaving more like a dry material, leading to increased mobility and a larger \(u_{v,m}^*\).

5.2.2 Model simplification discrepancies

The second source of discrepancy, termed ‘model simplification discrepancies’, arises from the simplifications made in the model. Firstly, the model does not consider fluid turbulence, which becomes significant when the fluid height during the horizontal spreading phase reduces to less than a particle diameter. At such small flow heights, fluid turbulence increases due to the increased shear rate imposed on the fluid by the horizontal surface over which it flows [50]. Consequently, the model underestimates the reduction in phase front velocity after \(u_{v,m}^*\) is achieved, resulting in a more gradual retardation compared to the physical experiments (Fig. 9). This effect is more pronounced for tests using higher viscosity fluids, potentially contributing to the overestimation of residual flow runout in simulations conducted at \(N=\) 5. Although Smagorinsky’s turbulence model has been implemented in LBM schemes to account for fine-scale turbulence contributions to macro-scale flow dynamics [e.g. 34, 51], its omission in our study was deemed appropriate given our focus on the acceleration phase and peak flow behaviour, simplifying the model and avoiding calibration of additional parameters. Furthermore, the complexity of potential boundary layer effects and the energy cascade assumption made by the turbulence model raise uncertainties regarding its suitability.

Secondly, the model employs a Darcy-drag style phase interaction term, simplifying the actual interaction occurring in the physical experiments. Notably, the model neglects surface tension, a potentially significant force contribution, which plays a vital role in the macro-scale flow dynamics of laboratory-scale and low N centrifuge tests [e.g. 9, 17, 14, 15]. Surface tension effects can alter flow dynamics in two primary ways. Firstly, during the horizontal spreading phase, capillary bridges can form between contacting or closely situated particles, limiting the granular phase’s ability to surpass the fluid phase front [15] (Fig. 8). In contrast, in numerical simulations, particles can accelerate freely away from the fluid front if their inertia overcomes the inter-phase drag and, for the forcing case \(\omega ^+\), the fictitious retardation due to the rotating reference frame. Secondly, surface tension effects may contribute to the larger separation between downstream and upstream flow fronts observed in the physical experiments during the retardation phase (Fig. 8). The extent of surface tension’s influence on decelerating the flow would be greater for the \(\omega ^+\) forcing case, where \(\varvec{a}_{cf}\) already slows down the flow, and more particles are likely to be in contact due to the higher flow density [21] (see Sect. 6.1).

In conclusion, the numerical model reasonably demonstrates the idealised behaviour of a fluid-saturated granular column collapse within a centrifuge, particularly during the acceleration phase. Although certain discrepancies arise from experimental conditions and model simplifications, we have provided a comprehensive understanding of these sources and their effects. The model’s capability in replicating fundamental dynamics and yielding reasonable results underlines its applicability in studying these complex collapse phenomena.

6 Implications of centrifuge modelling

With the validation of the model complete, the current section investigates the influence of centrifuge modelling on flow dynamics.

Fig. 10
figure 10

Evolution of the coordination number \(n_c\) as a function of the percentage of grains \(P_p\) for a series of collapse simulations with \(\varvec{a}=N\varvec{g}\) where \(N=\) [5,15], \(\log (R_c/h_0)=\) 3.7, and (a) \(\mu _f^*=\) 50 and (b) \(\mu _f^*=\) 150

Full size image
Fig. 11
figure 11

Temporal evolution of the cumulative particle percentage \(P_p\) of particles where \(n_c=\) [0,1], defined as \(P_p^{[0,1]}\). The parameter space considered includes simulations where \(N=\) [5,15], \(\log (R_c/h_0)=\) 3.7, and when the dimensionless fluid viscosity \(\mu _f^*\) is equal to (a) 50 or (b) 150

Full size image

6.1 Coordination number

Before looking at how the acceleration field affects macro-scale flow dynamics, it is important to understand its contribution to dynamics at the grain-scale. Thus, we begin by looking at the temporal evolution of the granular matrix. Specifically, we look at how the distribution of the particle coordination number \(n_c\) (i.e. the number of particles in contact with a particle) evolves as a function of the percentage of grains \(P_p\), where \(P_p\) is the ratio between the number of particles with the same \(n_c\) value and \(n_p\). Figure 10 shows the distribution of \(n_c\) at varying values of \(t^*\) throughout the collapse, with a particular focus on the acceleration stage (i.e. \(t^*<\) 3), for a series of collapses where \(N=\) [5, 15], \(\log (R_c/h_0)=\) 3.7 and \(\mu _f^*=\) [50, 150] exposed to an acceleration field \(\varvec{a}= N\varvec{g}\). Reassuringly, the mean value of \(n_c\) is initially relatively high for all simulations and decreases as the collapsing material accelerates. \(n_c=\) 3 acts as a pivotal point where the \(P_p\) value remains relatively constant throughout the collapse, especially when \(\mu _f^*=\) 150. Independently increasing both N and \(\mu _f^*\) appears to reduce phase separation. This insight is particularly highlighted by the the lower \(P_p\) values at \(n_c=\) [0,1] at each value of \(t^*\). In the case of N, this behaviour is partially attributed to the column construction process (see Sect. 4.3), which results in denser initial column configurations as N increases, as indicated by the peak \(n_c\) values at \(t^*=\) 0.1.

Fig. 12
figure 12

Maximum [(a)-(c)] fluid and [(d)-(e)] particle phase front velocities, \(u_{f,m}\) and \(u_{p,m}\), respectively, against N for [(a), (d)] \(\mu _f^*=\) 50, [(b), (e)] \(\mu _f^*=\) 100, and [(c), (e)] \(\mu _f^*=\) 150. The fitted trend line (black) corresponding to \(u_{v,m}=\alpha _v\sqrt{h_0Ng}\) is also shown for the forcing case \(\varvec{a}=N\varvec{g}\) in each subplot

Full size image

Our primary focus is on phase front dynamics. Therefore, the temporal variation in \(P_p\) values for lower \(n_c\) values is of particular interest, as these particles are likely to contribute to or interact with the granular phase front. As such, it seems worthwhile to analyse how the three different forcing cases contribute to the number of particles with low \(n_c\) values. We capture these variations by plotting the cumulative \(P_p\) value of particles where \(n_c=\) [0,1], defined as \(P_p^{[0,1]}\), against \(t^*\) for the three forcing cases (Fig. 11), where the full rotational domain case considers Coriolis accelerations in both the upstream (\(\omega ^+\)) and downstream (\(\omega ^-\)) directions, for \(N=\) [5, 15], \(\log (R_c/h_0)=\) 3.7 and \(\mu _f^*=\) [50, 150].

Despite the highly unsteady nature of granular matrix compactness, discernible trends emerge within the data. As observed in Fig. 11, generally, \(P_p^{[0,1]}\) increases throughout the acceleration stage until reaching a peak value at \(t^*\approx \) 3.5 aligning well with the time at which \(u_v=u_{v,m}\) for the collapses discussed in Sect. 5.2. Subsequently, \(P_p^{[0,1]}\) stabilises at a residual value as the collapse decelerates. The peak and residual \(P_p^{[0,1]}\) magnitudes are sensitive to the fluid viscosity, decreasing with increasing \(\mu _f^*\). This outcome is fairly logical as the fluid phase interacts with the granular phase through drag meaning that a more viscous fluid would have more control over the behaviour of the granular phase and less particles would ‘escape’ from the bulk. Within the physical experiments, the formation of capillary bridges due to the presence of surface tension would further maintain granular phase connectivity.

Figure 11 also shows the influence of the forcing case on the evolving structure of the granular matrix. While \(P_p^{[0,1]}\) values for the differing cases are initially close, they begin to spread during the acceleration stage. Among simulations with the same N and \(\mu _f^*\), the simulations conducted with the forcing cases \(\omega ^0\) and \(\omega ^-\) typically achieved larger \(P_p^{[0,1]}\) values than the simulations conducted with the forcing cases \(\varvec{a}=N\varvec{g}\) and \(\omega ^+\). This is reassuring given that when \(\varvec{a}=N\varvec{g}\) there is no horizontal acceleration component driving the collapse and while there is a horizontal acceleration component driving the collapse for \(\omega ^+\), \(\varvec{a}_{co}\) is acting in a direction such that it promotes flow densification [21]. Opposing statements can be made for the former two forcing cases. This finding is in agreement with the work of Zhang et al. [22] who stated that the variation in particle coordination number was the main mechanism that allowed Coriolis accelerations to contribute to flow dynamics. For simulations where \(\mu _f^*=\) 50, this trend continues to be the case during the collapse retardation stage while the trend becomes less clear when \(\mu _f^*=\) 150. Independently varying N does not appear to make a significant difference to the behaviour described previously in this section.

6.2 N scaling

In this section, we now explore how macro-scale flow behaviour scales with N. We do this by using the maximum phase front velocity \(u_{v,m}\) as a simplistic indicator of acceleration stage phase front characteristics [15]. We examine the \(u_{v,m}\)-N relationship through a series of simulations, wherein we systematically vary the parameters \(\mu _f^*\), \(\log (R_c/h_0)\), and the applied forcing case. The resulting \(u_{v,m}\)-N space is illustrated in Fig. 12.

A noteworthy observation from Fig. 12 is evident when considering the forcing case where \(\varvec{a}=N\varvec{g}\). The relationship between \(u_{v,m}\) and N can be expressed by the equation

$$\begin{aligned} u_{v,m} = \alpha _v \sqrt{h_0Ng} \end{aligned}$$
(6)

where \(\alpha _v\) is a constant influenced by \(\mu _f^*\) and the phase of interest (i.e. whether \(v=p\) or \(v=f\)). This constant characterises the proportion of the column’s free-fall velocity that is attained by the phase front of interest. Thus, a lower \(\alpha _v\) value suggests that the v phase is experiencing significant confinement from the other phase and the external forcing conditions. In contrast, an \(\alpha _v\) value closer to 1 suggests that the phase is travelling close to its free-fall velocity. The extension of this scaling to the other forcing cases is discussed in Sect. 6.3.

Fig. 13
figure 13

(a) \(\alpha _p\) and (b) \(\alpha _f\) against \(\log (R_c/h_0)\) for all conducted collapse simulations. The mean and standard deviation of the \(\textrm{RMSE}_N\) values characterising the fits to Eq. 6 for the combined dataset are 0.1 and 0.05, respectively

Full size image

Given that \(h_0\) and g are constants within our experimental configuration, Eq. 6 simplifies to reveal that \(u_{v,m}\) scales with \(\sqrt{N}\). This outcome aligns with the theoretical velocity scaling relation for frictional granular materials [19, 52]. It is noteworthy that if the flow was solely comprised a Newtonian fluid, one would anticipate \(u_{f,m}\) to scale linearly with N. Consequently, the observed \(\sqrt{N}\) scaling for \(u_{f,m}\) reinforces the notion that the flow exhibits fluid-granular behaviour, with the fluid’s presence acting as a mediator through drag, as anticipated. It should be noted that Cabrera et al. [19] found that this scaling law had to be adjusted to \(N^{2/3}\) when considering the surface velocity of a steady dry granular flow down an incline due to the variation of the flow’s inertial number with increasing N. However, for simplicity, we choose to maintain the \(\sqrt{N}\) scaling relation. The adequacy of these scaling fits, and those later shown in Sect. 6.3, is also corroborated by their low values of normalised root mean square error \(\textrm{RMSE}_N\).

Furthermore, analysing the \(\alpha _v\) values, as deduced from granular-scale dynamics (as discussed in Sect. 6.1), demonstrates that higher fluid viscosities generally lead to decreased mobility of both granular and fluid phases, resulting in lower values of \(u_{v,m}^*\). Interestingly, for cases with \(\mu _f^*=\) [100, 150], we observe \(u_{p,m} > u_{f,m}\), indicating that the granular phase advances ahead of the fluid phase. However, as discussed in Sect. 5.2, the influence of surface tension makes this behaviour improbable for physical collapses at the laboratory scale.

While the impact of the forcing case and \(\log (R_c/h_0\)) will be elucidated in Sect. 6.3, it is important to highlight that within the \(u_{v,m}\)-N space, forcing cases involving horizontal accelerations (\(\omega ^0\), \(\omega ^-\) and \(\omega ^+\)) manifest a shift in \(\alpha _v\). The magnitude and direction of this shift are contingent on the specific forcing case and the value of \(\log (R_c/h_0)\). Logically, \(u_{v,m}\) values associated with simulations subjected to partially or fully rotational domain forcing cases approach the values observed for \(\varvec{a}=N\varvec{g}\) as \(\log (R_c/h_0)\) increases and the relative magnitude of the horizontal acceleration component diminishes. Additionally, it is observed that this shift is comparatively smaller for the fluid phase compared to the granular phase because the fluid is not frictional and, hence, there is no feedback effect between velocity and pressure (see Sect. 6.3 for further discussion).

6.3 Influence of centrifuge radius

In this section, we delve into an investigation of the influence exerted by the centrifuge’s size, relative to the model’s dimensions, on the dynamics of collapse. Our focus remains on the characteristic quantity of interest \(u_{v,m}\) while introducing the variable \(\log (R_c/h_0)\) as a pertinent factor. However, rather than examining this relationship within the \(u_{v,m}\)-\(\log (R_c/h_0)\) space, where two independent parameters (N and \(\mu _f^*\)) remain, we opt for a more streamlined approach. We introduce \(\alpha _v\)-\(\log (R_c/h_0)\) as our new parameter space, where \(\alpha _v\) is computed using the same methodology outlined in Sect. 6.2 but encompasses all simulated scenarios (refer to Fig. 13). Consequently, the parameter \(\alpha _v\) renders the analysis independent of the parameter N.

Our decision to employ the \(\alpha _v\)-\(\log (R_c/h_0)\) space as the basis for data exploration is fortified by the statistical properties of our findings. Specifically, the mean and standard deviation of the \(\textrm{RMSE}_N\) values, characterising the fits to Eq. 6, are determined to be 0.1 and 0.05, respectively, suggesting that the parameter reduction method is reliable. It is crucial to emphasise that the adoption of \(\alpha _v\) as a surrogate for \(u_{v,m}\) only facilitates a clearer visualisation of the data. Hence, the trends discussed subsequently throughout this section persist when the data is examined within the \(u_{v,m}\)-\(\log (R_c/h_0)\) space for each distinct value of N.

Reiterating the outcomes derived from the preceding sections, Fig. 13 demonstrates the increase in collapse mobility, where \(\alpha _v\) serves as an analogous measure, with decreasing \(\mu _f^*\) for a given forcing case and \(\log (R_c/h_0)\) value. More notably, the examination of data within the \(\alpha _v\)-\(\log (R_c/h_0)\) space highlights the influence of the horizontal acceleration component on phase mobility. Firstly, for given values of \(\mu _f^*\) and \(\log (R_c/h_0)\), \(\alpha _v\) generally decreases with the relative magnitude of the horizontal acceleration component which is defined by the forcing case. Thus, the forcing, \(\omega ^-\) (associated with Coriolis-induced flow expansion), \(\omega ^0\) (lacking Coriolis acceleration contribution), and \(\omega ^+\) (promoting flow densification), achieve descending \(\alpha _v\) values. A reduction in \(\log (R_c/h_0)\) not only enlarges the separation between \(\alpha _v\) values corresponding to distinct forcing cases but also shifts the average \(\alpha _v\) value of these three forcing cases away from the \(\alpha _v\) value obtained when \(\varvec{a}=N\varvec{g}\), a case where centrifuge-induced horizontal accelerations are absent. This result aligns with expectations, as reducing \(\log (R_c/h_0)\)) also increases the relative magnitude of the horizontal acceleration component. Additionally, Fig. 13 suggests that the contribution of horizontal accelerations becomes nearly negligible when \(\log (R_c/h_0)>\) 4, making it suitable to assume \(\varvec{a}=N\varvec{g}\). This finding is consistent with the observations of Cabrera et al. [19], who established the validity of this assumption when \(\log (R_c/h_0)>\) 3.9 for a dry flow travelling down a rough inclined surface.

The less intuitive aspect is the reduced sensitivity of the fluid phase to a decrease in \(\log (R_c/h_0)\). While \(\alpha _f\) generally increases for the forcing cases \(\omega ^0\), \(\omega ^-\) and \(\omega ^+\) as \(\log (R_c/h_0)\) decreases, the rate of this increase is notably less pronounced than that of \(\alpha _p\). We posit that this disparity arises from the fact that the fluid is not frictional. Thus, the influence of the Coriolis force on fluid dynamics is much weaker in comparison to the granular phase when the confining pressure (\(\varvec{a}\)) is varied. This discrepancy may also partially result from the specific conditions prevailing at the juncture of maximum flow velocity, where \(\alpha _v\) is defined. At this critical stage of collapse, it is likely that the particles comprising the particle phase front are predominantly positioned ahead of or in direct contact with the fluid phase front. Consequently, the interplay and consequent drag between the particle phase front and the fluid phase become minimal. In contrast, the fluid phase front continues to engage with numerous particles behind the particle phase front. Consequently, at lower values of \(\log (R_c/h_0)\), \(\alpha _p\) assumes significantly larger values than \(\alpha _f\), primarily attributable to the reduced interaction between the phases along the granular phase front. Further numerical and experimental work would need to be undertaken to truly understand the mechanisms at play. It seems particularly pertinent to assess the influence of the Coriolis acceleration on completely dry and fluid only collapse configurations to remove the additional complexity of the interplay between the phases.

7 Conclusions and further work

In this study, we utilised the DEM-LBM numerical framework to simulate the collapse behaviour of a just-saturated granular column. The model working volume was defined within a rotating frame of reference to replicate the experimental conditions found in a geotechnical centrifuge. By focusing on just-saturated collapses, our research aimed to understand how centrifuge conditions impact granules and pore fluid differently. The primary advantage of a numerical approach is its ability to explore a parameter space that would be impractical in physical experiments. Specifically, we examined the effects of both centrifugal and Coriolis accelerations on flow dynamics by separately considering their contributions and varying the centrifuge radius \(R_c\). We also systematically varied of the fluid viscosity \(\mu _f\) and the gravitational scaling factor N, which are more typical test variables.

The validation of the numerical model consisted of a two-stage approach. Firstly, by ensuring that the predicted temporal evolution of key parameters, including phase front runout \(r_v\) and velocity \(u_v\), conformed to expected trends dictated by variations in N and \(\mu _f\). Secondly, by comparing the numerical predictions to physical collapse experiments. The model exhibited a high degree of accuracy in capturing the complex behaviours observed during the granular column collapse. Discrepancies between the model’s predictions and experimental data could be attributed to specific experimental conditions, such as the lifting of the cylindrical casing during column release, as well as the simplifications inherent in the model’s treatment of fluid-grain and fluid-surface interactions. Despite these limitations, the model reasonably reproduced the idealised behaviour of a fluid-saturated granular column collapse within a centrifuge, particularly during the acceleration phase.

The remainder of the study aimed to understand how acceleration field conditions contribute to collapse dynamics. Its effects on the flow grain-scale behaviour were examined by analysing the temporal evolution of the coordination number \(n_c\). Specifically, the evolution of the number of particles with \(n_c\le \) 1, which are those more likely to interact with the granular phase front. While increasing the fluid viscosity was found to reduce flow dilation, as found in previous studies [21, 22], both the centrifugal acceleration and the Coriolis acceleration significantly influenced the evolution of the granular matrix.

At the macro-scale, the maximum phase front velocity \(u_{v,m}\) was used to characterise acceleration stage phase front dynamics. Under constant acceleration conditions, neglecting centrifugal and Coriolis accelerations, \(u_{v,m}\) scaled with \(\sqrt{N}\) and \(\alpha _v\) which is a phase-specific constant dependent on fluid viscosity. This relationship matches the theoretical velocity scaling for a frictional granular material and was previously observed by Cabrera et al. [19].

Based on the assumption that this relationship holds for all forcing cases, the contributions of \(R_c\) were investigated by utilising the \(\alpha _v\)-\(\log (R_c/h_0)\) parameter space, making it independent of N. It was found that both the centrifugal and Coriolis accelerations had a significant impact on flow mobility, with centrifugal acceleration’s influence increasing as \(R_c\) decreased, resulting in a more pronounced curvature effect. Depending on its direction, Coriolis acceleration either expanded or densified the flow. Moreover, it was found that when \(\log (R_c/h_0)>\) 4, the contribution of horizontal accelerations become almost negligible which is consistent with the findings of Cabrera et al. [19]. Hence, at \(\log (R_c/h_0)\) values greater than 4, it is suitable to assume a constant acceleration field (i.e. \(a=Ng\)). As such, with regards to the design of centrifuge experiments, this could be considered a safe value for considering the Coriolis acceleration to be negligible.

To enhance our comprehension of this subject, forthcoming research should prioritise the investigation of the Coriolis acceleration’s influence on both dry and fluid-only collapses in order to better appreciate the dynamics of the fluid-saturated case, particularly with regards to particle settlement and consolidation. Furthermore, it would be beneficial to explore the influence of a rotating domain on granular flows that contain non-Newtonian interstitial fluids. Additionally, the study of surface tension effects within the phase coupling term holds potential for a deeper understanding of granular flow behaviour in more intricate scenarios.