1 Introduction

Powder-based additive manufacturing, e.g., powder bed fusion, has attracted significant attention due to its advantages of fast prototyping, superior design and geometrical flexibility [27, 46, 48]. This technique allows near-net-shape production, enabling quick production of exact and customized parts, saving time and reducing waste. However, a more extensive usage of this manufacturing technology is still missing due to limitations in process quality control, e.g. getting uniform packing and the limited range of powder materials commercially available. Discrete element method (DEM) simulation is a distinguished technique to examine the structure of layers in powder spreading, in particular for powder-based additive manufacturing. Various types of structural defects are observed which strongly correlates to deficit in quality of sintered parts [10, 14, 18]. Recently, Nasato et al. investigated the influence of vibrating recoating mechanism [32] and effects of particle shape [31, 33] to understand the mechanical behaviour of powders and improving the quality of powder layers in additive manufacturing. Their results showed that a combination of large frequency and moderate amplitude reduces the porosity of the deposited layer. On the other hand, large frequency and large amplitude loosens the granular bed packing. A recent study by Cheng et al. showed that for roller, a forward-rotating roller produces strong compaction increasing coordination number and mass flow rate as compared to a reverse-rotating roller [8]. In addition, the particle dynamics are affected by the frictional force direction, acting opposite to the powder spreading direction. Parteli and Pöschel reported that the bed roughness scales with the square of coating speed [35, 36]. Shaheen et al. recently investigated the influence of material and process parameters on powder spreading in additive manufacturing [47]. Chen et al. studied experimentally and numerically the evolution of angle of repose of particle heap in front of the blade and also the effect of particle cohesion on the angle of repose [6]. He et al. studied the effect of particle cohesion on the degree of particle clustering [21]. As stated here, particle cohesion prohibits the formation of large agglomerates for weakly cohesive powders while promotes the formation of chain-like structures for strongly cohesive powders. Thus, interparticle cohesion, particle size and shape play key roles while strongly influencing the powder yielding and flow behaviour [50]. In this work, we characterise the structure of deposited powder layer in powder spreading for cohesive particles and link the mesoscopic structure with the microscopic properties using various techniques of micromechanical analysis of particle packing.

Heterogeneity of the particle distribution in the constitutive layers of 3D-printed objects strongly influences the properties of the product [1, 25, 55]. The radial distribution functions (RDF) are a metric of local structure and is ideally used to quantify spatial structures of amorphous solids and packings of granular materials [62, 63]. The RDF is found to be strongly determined by the composition of the packing as well as by its degree of heterogeneity which are linked to the properties of the constituent particles. Although, this technique is widely used for structural analysis granular dense packing with respect to spatial structures and particle clustering, it has not been used for analysing structure of quasi-2D thin layer of powder deposition in particular. Therefore, we use RDF function to distinguish structures of powder layers generated from varying particle cohesion in the powder spreading process.

The key aspect of simulation-driven optimization of the layer quality is a good characterization of the packing structure. Despite local packing density being widely used as a measure for characterizing granular packing [8, 21, 31, 33, 35, 36, 47], this parameter alone is not a good indicator to identify structural defects in disordered packing [40] since many packing arrangements correspond to the same local density. A very similar technique is employed for deposition of granular monolayer on substrate by rubbing and horizontal agitation which shows that the degree of orientation is influenced by the rubbing speed and normal pressure [34]. The morphology and orientational order of the obtained monolayers is examined by employing the Voronoi approach [23], a similar technique also used for analysing structural anisotropy of powder layer in additive manufacturing [44]. On the other hand, heterogeneous interparticle forces and contact network are key signatures of disordered granular packings [2, 28, 38, 39] and are associated with important mechanical properties in disordered packing, e.g. jamming [3], mechanical stability [59], shear band formation [19, 20, 56]. Numerous studies have shown that features of interparticle forces and the distribution depend significantly and are susceptible to the specific structure of granular packing [11, 12, 16, 22, 26]. Some of the relevant examples for such studies with different materials in particular are sapphire grains of size \(150-200 ~\mu\)m [22], for nonconvex polymer particles of size 5 mm [9] and cohesive fine particles of size range \(5-1000 ~ \mu\)m [64]. Recent study by Zhang et al. [65] analysed the dynamics of weak and strong force chains in powder spreading process and their distribution, albeit in powder pile during spreading and not on static powder layer. Therefore, in this study, we use topological structure of the force and contact network as a measure to characterize structures of the deposited static powder layer in powder spreading process.

Recently, Fouda et al. observed by numerical simulations that the powder layer packing fraction is always lower than that of the original powder composition due to three mechanicsms, shear-induced dilation, particle rearrangement and particle inertia [15]. Chen et al. investigated the powder layer packing density [5, 7] and found a “stress-dip” region at the bottom front of the spreader and identified “percolation effect” that leads to particle segregation play a critical role and contribute to the packing density of the powder layer. Thus, we present the particle size distribution and the role of interparticle cohesion on segregation in the powder layer as an important aspect of this work.

2 Methods

2.1 Numerical set-up

A small part of the powder bed (width 1 mm) is simulated using periodic boundary conditions in the y-direction.

Fig. 1
figure 1

Numerical setup for powder spreading on a smooth substrate before and during spreading

Full size image

In this numerical set-up, the substrate is assumed to be smooth. We insert particles of mean diameter \(D_{50} = 37 \mathrm {\mu }\)m in front of the spreader tool, at \((x,y,z) \in [0.5,2.5]\) mm \(\times [0,1]\) mm \(\times [0,h]\) mm until the total bulk particle volume equals 0.7 mm\(^3\), which is sufficient material to create a powder layer of 7 mm length, 1 mm width and 0.1 mm height.

We start the simulations by allowing the particles to settle and relax under the effect of gravity. After the particles are settled down and the system is relaxed, the spreading process starts by moving the tool at a constant speed \(v_T = 10\) mm/s. Shaheen et al. studied the effect of varying blade speed on the spreading layer mass and concluded that increasing spreading speed reduced the quality of the powder layer for both non-cohesive and cohesive powders [47]. Fouda et al. also investigated the effect of blade speed on the packing fraction of different sublayers in powder spreading and found that overall the dilation of the sublayers increases with the blade speed [15]. The blade speed in our present study is chosen to be low enough such that there are no inertial effects on the bulk behavior of particles during spreading [29]. On the other hand, a higher blade velocity also limits the achievable powder layer quality which has been reported to decrease with increasing spreading speed [30, 35]. The spreading tool is a blade as shown in Fig. 1. The particles are spread in a layer where the tool gap is set to \(H = 100 \, \mu\)m, which corresponds to about \(2.7\times D_{50}\) in \(z-\)direction. The blade moving at a constant velocity of 10 mm/s takes about 1 s to move through the length of the bed. Particles reaching the end of the powder bed (at \(x = 10\) mm) are not used for the analysis. Finally, the simulation is stopped when the system is static, i.e. the kinetic energy of the system is sufficiently low. Thus, the maximum simulation time is thus chosen as \(t_\textrm{max} = 1.5\) s, taking into account the time for initial settling and relaxation of particles, the spreading time and the time for the system to reach a static state.

2.2 Contact model

The simulations of the spreading process are implemented using MercuryDPM [60]. The interaction of poly-disperse particles is modelled using the computationally inexpensive standard linear spring-dashpot model for normal force. The normal force is composed of a linear elastic, linear dissipative and a linear adhesive force:

$$\begin{aligned} f_{ij}^n = k_n\delta _{ij}^n + \eta _n{\dot{\delta }}_{ij}^n + f_{ij}^\textrm{adh} \end{aligned}$$
(1)

with the normal spring stiffness \(k_n\), the damping coefficient \(\eta _n\), normal deformation between particles \(\delta _{ij}^n\), relative velocity \({\dot{\delta }}_{ij}^n\) and a linear adhesion force \(f_{ij}^\textrm{adh}\).

Many models exist in the DEM that describe dry cohesion of small particles, i.e. the attractive force due to van der Waals interaction between particles close to each other or in contact [37]. According to Parteli et al. [37], a full model including the pure viscoelastic interaction, adhesive interaction as well as van der Waals interaction are required for correct numerical predictions, in particular for smaller particles. We use a linear elastic reversible adhesive force law (acting opposite to the normal elastic repulsive force), which was shown to yield the same bulk rheology as more complicated and realistic non-linear models [43].

$$\begin{aligned}{} & {} f_{ij}^\textrm{adh} \\{} & {} \quad = {\left\{ \begin{array}{ll} -f_\textrm{max}^\textrm{adh},&{} \text {if } \delta _{ij}^n\ge 0;\\ -(f_\textrm{max}^\textrm{adh} + k^\textrm{adh}\delta _{ij}^n),&{} \text {if } -\frac{f_\textrm{max}^\textrm{adh}}{k^\textrm{adh}} \le \delta _{ij}^n < 0;\\ 0, &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$

where \(k^\textrm{adh}\) is the adhesion stiffness during loading and unloading. The maximum adhesion force \(f_\textrm{max}^\textrm{adh}\) is defined identical to the pull-off force of the JKR representation of van der Waals interaction [24]: \(f_\textrm{max}^\textrm{adh} = \frac{3}{2}\pi \gamma (D_\textrm{eff}/2)\), where \(\gamma\) is the surface energy and \(D_\textrm{eff} = \frac{D_iD_j}{D_i + D_j}\) is the effective diameter of two particles i and j. Note that, wetting properties of the powder particles, e.g. interfacial surface tension is comparable to the surface energy \(\gamma\). A detailed analogy between dry cohesive model and wet capillary bridge model is presented by Roy et al. [43].

The tangential forces (sliding and rolling) are modelled using linear elastic and dissipative forces, where the rolling force is a virtual force, used to calculate the rolling torque. The details of the tangential and rolling forces modelling are described in [47]. Both the tangential sliding force \(f^s\) and the rolling torque \(M^r\) have yield criterion as necessary to satisfy \(\vert f^s \vert \le \mu _s \vert f^n_{ij} - f^\textrm{adh}_{ij}\vert\) and \(\mathrm {M^r} = (D/2) \textrm{n} \times \mathrm {f^r}\) with \(\vert \mathrm {f^r} \vert \le \mu _r\vert f^n_{ij} - f^\textrm{adh}_{ij}\vert\), \(\mu _s\) and \(\mu _r\) are the sliding and rolling friction coefficients, respectively. Note, that other significant interactions in granular polymers, e.g., interactions tribo-electric charging which is more relevant at controlled humidity levels [45, 54] are not considered in this study.

2.3 DEM parameters

Figure 2 shows the particle size distribution of Ti-6Al4V powder as implemented in the simulation. The parameters for the particle size distribution are taken from Shaheen et al. [47] which correspond to that of real Ti-6Al4V powder measured using laser diffraction analysis. We assume that the particle shapes are spherical which are favorable in terms of flowability and powder bed packing density. However, non-spherical Ti-6Al4V powders are often present due to satellites, fracture and adhered particles which are of wider particle size distribution, but are not considered in our present studies.

Fig. 2
figure 2

Particle size-distribution of Ti-6Al-4V powder as implemented in simulation

Full size image

To study the effect of particle cohesion, we simulate the powder spreading process on smooth substrate for varying surface energy \(\gamma\) from 0 to 0.8 mJ/m\(^2\) with an interval of 0.1 mJ/m\(^2\). To characterize the ratio between the interparticle cohesion and particle gravity, the Bond number is used, which is calculated as

$$\begin{aligned} Bo = \frac{f_\textrm{max}^\textrm{adh}}{mg} = \frac{9\gamma }{4\rho _pD_{50}^2g}, \end{aligned}$$
(2)

calculated for a mean diameter \(D_{50} = 37 \, \mu\)m, e.g. the Bond number corresponding to \(\gamma = 0.10 ~\textrm{mJ}/\textrm{m}^2\) is \(Bo = 4\). The corresponding range of Bo for the set of surface energy parameters varies from \(Bo = 0\) for non-cohesive materials to \(Bo = 30\) for highly cohesive materials. We also perform simulations of powder spreading on an existing powder layer for \(Bo = 0, 4\) and 8. We run 3 simulations for each set of parameter from different initial configurations to reduce the impact of randomness by increasing sample size for interpreting the results. In order to focus in our studies on the effects of cohesion, we keep the friction parameters \(\mu _s = 0.10\) and \(\mu _r = 0.005\) at a low value. All the other parameters are same as given by Shaheen et al. [47]. Note, that the same parameter values are set for particle-particle, particle-substrate and particle-tool interactions. Adhesion between particles and the substrate will prevent the free flowing of powder over the substrate and as a result we expect the powder to be spread inhomogeneously over the substrate with increasing surface energy.

3 Effect of cohesion

A top view snapshot of the powder layers spread on smooth substrate with \(Bo = 0, 15\) and 30 is illstrated in Fig. 3a, b and c, respectively. The results show that increasingly cohesive powders are characterized by lower packing fractions with particle agglomerates. The results are comparable with Meire et al. [29] with the particle agglomerates within highly cohesive powders resulting in less dense and rather irregular layers in the range of small blade gaps that is deposited. We further characterize the powder layers packing density, radial distribution function, force network distribution and the particle size distribution in the following subsections.

Fig. 3
figure 3

Top view snapshots of the spread powder layer with \(\mu _r = 0.005\) and \(\mu _s = 0.1\) for a \(Bo = 0\), b \(Bo = 15\) and c \(Bo = 30\)

Full size image

3.1 Volume fraction

To characterize the spread powder layer uniformity, we extract the solid volume fraction (\(\phi\)) after spreading from the discrete data by coarse-graining (CG). The macroscopic volume fraction is defined by:

$$\begin{aligned} \varphi (x,y,z) = \sum _{i = 1}^NV_i\psi (r - r_i(t_\textrm{max})), \end{aligned}$$
(3)

where \(V_i\) is the particle volume. The coarse-graining method has the advantage over traditional micro–macro transition by binning method. This method is advantageous; because, by construction, the macroscopic fields derived are consistent with the continuum equations of mass, momentum and energy balance and therefore the local macroscopic volume fraction analyzed in our studies are precise by its definition. A Gaussian coarse-graining function \(\psi\) of width \(w = 40 ~ \mu\)m and a cut-off \(w_c = 3w\) is used. A Gaussian CG function results in smooth fields and is infinitely differentiable and the width of CG is chosen to be approximately the maximum particle radius, which yields \(w-\)independent data with less statistical fluctuations [57, 61]. For details of the CG method, see [17, 57, 61]. Integration in the direction perpendicular to the layer yields a spatial distribution field of averaged powder layer solid volume fraction in the xy-plane,

$$\begin{aligned} \varphi (x,y) = \frac{1}{H}\int _{0}^H\varphi dz, \end{aligned}$$
(4)

where H is the gap height (also expected the optimal layer thickness). The spatial distribution of the depth-averaged solid volume fraction \(\varphi (x,y)\) is used as a quantitative measure of the product layer quality and uniformity.

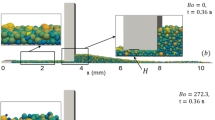
Fig. 4a shows the distribution of the solid volume fractions \(\varphi\) for product layers for different Bond numbers. The width of the probability distributions increases and the peak value decreases with increasing Bo. We further show in Fig. 4b the spatial distribution of the solid volume fraction \(\varphi\) for the two extreme cases of the configurations: a uniform layer (\(Bo = 0\)) and empty patches of layer deposition (\(Bo = 30\)). We see good-quality powder layers with a homogeneous narrow normal distribution at low interparticle cohesion; as the interparticle cohesion increases the spread powder layer uniformity decreases, with empty patches indicated by the dark blue regions in the contour plot of \(\varphi\). Predictably, we observe the highest coefficients of variation and the lowest mean solid volume fraction for nearly empty layers, and the lowest coefficients of variation and the highest mean solid volume fraction for uniform layers.

Fig. 4
figure 4

a The probability distribution of the spread powder layer solid volume fraction \(\varphi\) for different Bo. b Spatial distribution of the solid volume fraction \(\varphi\) of the spread powder layer for \(Bo = 0\) (top) and \(Bo = 30\) (bottom)

Full size image

3.2 Radial distribution function

Fig. 5
figure 5

The radial distribution function g(r) plotted for different Bond numbers

Full size image

The radial distribution function, g(r), describes the probability of finding the center of a particle in a given position at a radial distance r from the center of a reference sphere and is widely used in the study of particle packing as it contains useful information about the interparticle radial correlations [4, 49]. The function g(r) is given by

$$\begin{aligned} g(r) = \frac{\rho (r)}{\rho _o} = \frac{dN(r)}{4\pi r^2dr\rho _o}, \end{aligned}$$
(5)

where N(r) is the average number of particle centers within a sphere of radius r around the center of a reference particle and \(\rho _o\) is the average number of particle per unit volume in the packing. Figure 5 shows the radial distribution function, g(r), for 4 values of Bo, where \(dr = 0.08\). The g(r) curve for \(Bo = 0\) exhibits all the well-known short-range features observed in a random packing of polydisperse system [62]. In particular, in contrast to monodisperse particles that exhibit a sharp peak at \(r = 1\) [62], we observe a rather broad peak at \(r = 1\), the location of the peak being independent of Bo. When cohesion (Bo) increases, the following key changes are identified:

  • The amplitude of the first peak at \(r = 1\) increases as well as the peak becomes broader with increasing Bo.

  • A second peak is located approximately at \(r = 2\) and its amplitude increases with Bo.

  • There is a sharp increase in the first minima as the Bond number Bo increases.

  • The variations in the radial distribution function increases with the Bond number. In fact, for \(Bo = 0\), the variation of the radial distribution function is largely limited to a small distance \((r < 2)\). In contrast, for \(Bo = 30\), the variations in radial contribution function is extended to \(r = 4\). These changes suggest that increasing Bond number can result in a more non-uniform packing.

A similar observation is stated by Yang et al. [64] where the first peak of the radial distribution function, g(r), increases with decreasing particle diameter. While in the work of Yang et al. [64], the interparticle cohesion is varied by changing the particle size and therefore varying van der Waals force, in our present work we change the surface energy \(\gamma\) of the particles to vary cohesion, keeping the particle size distribution the same. Therefore, we show in this work that although the application of radial distribution function in granular packing is not a novel technique in itself, it is used as a new technique in this study to analyze structure of powder layer packing in additive manufacturing.

The radial distribution function (RDF) is a valuable tool in additive manufacturing for understanding and characterizing the microstructure of printed parts. Additive manufacturing involves building three-dimensional objects layer by layer using materials like metals, polymers, or ceramics. The arrangement and distribution of particles within these printed parts impact their mechanical, thermal, and chemical properties. By measuring the distances between particles, the RDF provides insights into the local order, particle packing, and coordination in the material, helping assess structural integrity, density, and porosity. It allows researchers to study the effects of process parameters on microstructure and identify defects, enabling optimization of additive manufacturing processes. Additionally, the RDF aids in comparing the microstructure of additively manufactured components with conventionally manufactured materials, highlighting the unique advantages of additive manufacturing. Overall, the RDF empowers engineers and researchers to improve the quality and performance of additive manufacturing and advance the field as a whole.

3.3 Normal force distribution

The contact forces inside a static packing of grains are organized into highly heterogeneous force networks, and can be characterized by the probability density of contact forces P(f). Here, we probe the tail of P(f) in the force network ensemble of the particle layer deposited on the smooth substrate for the additive manufacturing process. We first examined the distribution of the contact normal force in the non-cohesive configuration, \(Bo = 0\), to compare with the results in the literature. Figure 6a shows a log-linear plot of the distributions of normal contact forces \(P(f^*)\) for the non-cohesive powder configuration, where the forces are scaled by the mean normal force, i.e. \(f^* = f/{\langle f\rangle }\). The PDF is well fitted by a stretched exponential function \(P(f^*) \sim \exp {{(-f^*/f_0)}^\alpha }\) represented by the dashed line [58], with \(\alpha = 1.3\pm 0.1\) and \(f_0 = 1.2\pm 0.1\).

Next, we analyse the effect of particle cohesion on the force network. Figure 6b shows the distribution of normal forces for different Bo. The distribution of forces is strongly affected by Bo and \(P(f^*)\) becomes wider as Bo increases. Therefore, strong cohesion, which leads the system to a mechanically constrained state induces larger fluctuations of positive and negative forces. The cohesive forces modify not only the shape of the PDF, but also their asymptotic behavior, i.e., the morphology of strong force chains. The dynamics of the particle flows and their deposition on the substrate are characterized based on different time scales depending on the local and global variables [41]. For non-cohesive materials, particles subjected to strain and a confining local pressure undergo constant re-arrangement and thus the contact networks re-arrange too by extension, compression and rotation. Finally, the particles are deposited and they relax in absence of external deformation according to the relaxation time scale of the materials. For cohesive materials, the relaxation time is longer due to the interactive adhesive force between the particles, which suppresses the rearrangement of the particles. Hence the particles are deposited before being completely relaxed, which results in more heterogeneities of the stress distribution. We note that similar trends were found by Yang et al. [64] in a static three-dimensional packing of particles of size varying from 5 to \(1000 ~ \mu\)m and by Singh et al. [52] inside the shear band for a mean particle diameter of 2.2 mm. They reported that the PDF gets broader with a decrease in particle size, i.e., with increasing cohesion. While in the work of Yang et al. [64], the interparticle cohesion is varied by changing the particle size and therefore the van der Waals force, in our present work we change the surface energy \(\gamma\) of the particles to vary cohesion, keeping the particle size distribution the same. The two approaches for controlling cohesion in materials, varying cohesion by particle size and varying cohesion by surface energy, provide distinct methods with their own advantages. Varying cohesion by particle size involves using particles of different sizes to influence cohesion, where larger particles decrease cohesion and smaller particles increase it. On the other hand, varying cohesion by surface energy focuses on modifying the surface energy of particles or materials to alter cohesion. The choice between these approaches depends on the application and desired properties of the material, as both methods offer effective means to influence cohesion. The decision should consider the specific context and desired outcome, as well as the materials involved. Ultimately, both approaches provide valuable tools for controlling cohesion in materials.

Fig. 6
figure 6

a Probability distribution of normalized force \(f^*\) for noncohesive \(Bo = 0\). Different colors and markers indicate different sets of simulations and the dashed line corresponds to fitting for all sets of simulations. b Probability distribution of normalized force \(f^*\) for varying cohesion indicated by Bond number Bo

Full size image
Fig. 7
figure 7

Probability distribution of a normal force orientation and b normal deformation between particles. The inset represents the mean deformation between particles as a function of the Bond number Bo and the black dashed line represents a linear fit to the data

Full size image

The effect of cohesion on force structure is further observed from the force orientation pattern. Figure 7a shows the angle distribution of the normal force \(P(\theta )\) for different cohesion, where \(\theta\) is the angle between the force and the horizontal direction with \(\theta \in (0^\circ , 90^\circ ]\). It clearly illustrates the anisotropy of the force network. For configuration with \(Bo = 0\), the effect of gravity results in anisotropy in contact orientation showing the density of contacts increase with increasing \(\theta\) and finally a plateau is reached at \(\theta = 60^\circ\). For configuration with \(Bo = 30\), the plateau appears at \(\theta = 25^\circ\), which reflects the increasing role of the cohesive forces that change the orientation. Thus, we observe slightly more heterogeneous contact orientation distribution for cohesive materials as compared to the non-cohesive materials. Fig. 7a (inset) shows that a peak is observed in the contact orientation at \(\theta = 90^\circ\) for all configurations. This is resulting from the orientations of particle-substrate interactions. This trend is also maintained as the Bo increases. This characteristic of cohesive materials is in good agreement with previous investigations of orientation pattern of contacts in packings of cohesive particles [13, 64].

Furthermore, we investigate the distribution of deformation between particles in contact for \(\delta > 0\) as shown in Fig. 7b. The mean deformation between particles increases linearly as a function of Bond number Bo as shown in Fig. 7b inset. The linear fit function is represented by the dashed line in the figure. Both the heterogeneity in contact orientation as well as in particle overlap is attributed to the characteristic wider stress distribution of the materials with increasing cohesion.

3.4 Particle size distribution

Fig. 8
figure 8

Retained percentage of particles of different sizes in the product layer for different values of the Bond number

Full size image

Figure 8 shows the fraction N of particles of a given diameter remaining in the powder layer after spreading for different values of the Bond number. For example, a value of \(N = 60\%\) indicates that \(40\%\) of the particles have been dragged off the plate by the spreading tool. The fraction of particles retained on the powder layer after spreading decreases with increasing Bo. More importantly, for \(Bo = 0\), the retained percentage of larger particles of diameter \(79 \, \mu\)m is approximately 3% less than that of particles of diameter \(12 \, \mu\)m, indicating particle segregation. This effect is intensified with increasing Bo, e.g. for \(Bo = 30\), the retained fraction for larger particles is approximately 15% less than the smaller particles, indicating that the particle segregation is enhanced by the effect of cohesion. Shaheen et al. reported that the size-segregation effect is less pronunced for strongly cohesive particles [47], primarily for sliding friction \(\mu _s > 0.1\). However, in this study, we observe a strong segregation effect from our results, with a rather lower sliding friction \(\mu _s = 0.1\). For higher Bo, our results show that the retained percentange of particles monotonically decreases with particle size. This is explained by an enhancement of the effect of contact friction with increasing strength of cohesion due to the microstructural changes as reported by Roy et al. [42] and Shi et al. [51]. Thus, in our studies, increasing segregation is observed for higher Bo. With increasing Bo, higher percentage of larger particles are dragged off and hence a higher percenteage of fine particles are retained on the substrate. These fine particles form agglomerates and lead to a more heterogeneous surface of the powder layer, as also observed from the radial distribution function in Sect. 3.2. Similar observations were reported by Parteli and Pöschel [35, 36] where highly polydisperse powders lead to larger powder bed roughness as the smallest particles of the polydisperse powders are most prone to form large agglomerates resulting from cohesive forces thus increasing the packing’s heterogeneity.

4 Deposition on a powder layer

In this section, we study the deposition of particles on a powder layer and compare the structure of deposited layer with that on the smooth substrate.

Fig. 9
figure 9

Numerical setup for spreading on a powder layer before and during spreading

Full size image

The powder layer is constituted of particles and is prepared by depositing a layer of particles on the smooth substrate which is done following a set-up as mentioned in Sect. 2.1. Therefore, the initial configuration for the deposition on a powder layer is prepared from the final configuration of simulations in Sect. 2.1 and thereafter the same procedure is followed as mentioned in Sect. 2.1. In this way, a second layer of particles is created on top of the initial one with an additional thickness of approximately \(2.7 \times D_{50}\). The corresponding spreading setup is shown in Fig. 9. Note that the bottom surface of the blade is always placed at an elevation of the gap height from the maximum surface elevation. The gap height H is thus adjusted to be the gap between the bottom surface of the blade and the maximum surface elevation of the existing powder layer deposited. Our goal here is to differentiate the powder layer structures deposited on a smooth substrate compared to that on a powder layer. Figure 10 shows a top view snapshot of the deposited second powder layer with \(Bo = 0, 4\) and 8. The particles in the system display a sparse distribution, indicating a higher Bond number (Bo) in comparison to lower Bo values. Additionally, upon comparing Fig. 3a with Fig. 10a, both of which correspond to \(Bo = 0\),it is clear that the latter demonstrates an even sparser distribution of particles.

Fig. 10
figure 10

Top view snapshots of the spread second powder layer with \(\mu _r = 0.005\) and \(\mu _s = 0.1\) for a \(Bo = 0\), b \(Bo = 4\) and c \(Bo = 8\)

Full size image

Amongst the parameters that we compare for the deposition on smooth substrate and powder layer in Fig. 11 are the radial distribution function, interparticle normal contact force distribution, distribution of particle overlap and the contact orientation distribution for different cases of \(Bo = 0, 4\) and 8. Figure 11a, b and c show that the radial distribution functions are similar in both spreading on smooth substrate and powder layer for all values of Bo. Figure 11d, e and f show that the force distribution corresponding to deposition on a powder layer is narrower than that corresponding to spreading on a smooth substrate. However, the tail of the force distribution on a powder layer is stretched much wider as we observe in the figure inset. This is true for both non-cohesive and cohesive powders as shown in the figures. This suggests that the contact force network for deposition on a powder layer is less homogeneous. This is in agreement with the observation of Singh et al. [53] where it was shown that the heterogeneity in the contact network also increases with inter-particle friction and the tail of force distribution gets wider. We observe a similar distribution for particle normal overlap in Fig. 11g, h and i where the tail of the distribution corresponding to the spreading on powder layer is also stretched much wider. Figure 11j, k and l show comparisons of the contact orientation distribution for the spreading of powder on smooth substrate and powder layer for different Bo. A stronger anisotropy exists for the deposition on the smooth substrate as compared to spreading on the powder layer. This is contributed to wider and more heterogeneous normal force distribution on the smooth substrate.

Fig. 11
figure 11

Comparison of different parameters for spreading on a smooth substrate and on a powder layer showing the radial distribution function g(r) for a \(Bo = 0\), b \(Bo = 4\) and c \(Bo = 8\), the normal force distribution for d \(Bo = 0\), e \(Bo = 4\) and f \(Bo = 8\), the normal overlap between particles for g \(Bo = 0\), h \(Bo = 4\) and i \(Bo = 8\) and the contact orientation for j \(Bo = 0\), k \(Bo = 4\) and l \(Bo = 8\)

Full size image

Fig. 12a, b and c show the particle size distribution in the deposited powder layer for deposition on the smooth substrate compared with the deposition on the powder layer for different cases of \(Bo = 0, 4\) and 8. The particle deposited on the powder layer has a narrower size distribution and a smaller mean value as compared to the deposition on a smooth substrate for both non-cohesive and cohesive particles. To futher investigate this, we show the percentage of retained particle of different sizes on a smooth substrate and on a powder layer in Fig. 12d, e anf f for \(Bo = 0, 4\) and 8. The retained fraction of larger particles of diameter \(79 \, \mu\)m drops down to as low as 2% for all cases, indicating that almost all the larger particles are dragged off as compared to approximately \(25-40\)% of particle diameter \(12 \, \mu\)m retained on the powder layer. Compared to this, the retained fraction of particles on smooth substrate is only \(3-5\)% less for \(79 \, \mu\)m particles compared to \(12 \, \mu\)m particles and approximately 60% of the raw materials are retained on the substrate. This indicates an intense segregation occurs for deposition on a powder layer for the same gap height and if all the other parameters are kept the same. This is similar to the effect observed by Shaheen et al. [47] where the retained fraction of smaller particles was higher than the fraction of large particles for higher value of particle sliding friction coefficient. In our present work, we can compare the deposition on a powder layer is corresponding to a surface with higher sliding friction coefficient as compared to a smooth substrate. Hence, higher percentages of smaller particles are retained on the powder layer.

Fig. 12
figure 12

Comparison of different parameters for spreading on a smooth substrate and on a powder layer showing the particle size distribution for a \(Bo = 0\), b \(Bo = 4\) and c \(Bo = 8\) and the percentage of particles retained on the deposited layer for (d) \(Bo = 0\), e \(Bo = 4\) and f \(Bo = 8\)

Full size image

The extreme case of \(Bo = 30\) is also studied but the results are not shown in this section. Note, that the percentage of particles retained on the powder layer decreases with increasing interparticle cohesion. For the extreme case of \(Bo = 30\), very few particles were therefore retained in the powder layer and not enough data statistic were available to show the results for this case in Figs 11 and 12.

5 Conclusions

We have simulated the spreading process of powder in additive manufacturing with the discrete element method (DEM) and characterized the powder layer quality for non-cohesive and cohesive powders. The results show that cohesion affects the spreadability of the powder layer and thus influence the powder layer quality. The volume fraction of powder layer decreases and the distribution of volume fraction gets wider with increasing Bond number. The inhomogeneity of the particle size distribution increases with cohesion indicated by the radial distribution function. The force distribution tail can be fitted by a stretched exponential function. The force distribution gets wider with increasing Bond number Bo and hence the heterogeneity in forces increases with increasing Bond number. The mean interparticle deformation increases linearly with Bond number and the distribution also gets wider.

Our observation from the particle size distribution in powder layer suggests that the percentage of retained fraction of larger particles monotonically decreases with increasing Bond number. Hence, cohesion enhances the segregation effect and results in strong segregation as almost all the large size particles are removed from the powder layer. This is different from the observation by Shaheen et al. [47] that size-segregation effect is less pronounced for strongly cohesive particles with higher particle sliding friction coefficient. However, we observed that cohesion strongly enhances segregation for particles with lower sliding friction coefficient and we contribute this to the microstructural changes of the particles.

The quality of the powder layers formed by deposition on a smooth substrate are compared to that of deposition on a powder layer. We found that the radial distribution functions for particle size distribution are nearly overlapping, indicating that the particles are similarly distributed on both the surfaces. The interparticle force and distributions of particle normal overlaps on a powder layer are stretching with a wide tail, indicating that the contact force network is more heterogeneous for powders deposited on another layer. The contact orientation distribution for the deposition on a smooth substrate shows a stronger anisotropy due to the wider and more heterogeneous normal force distribution which is less likely for contacts on a an existing powder layer. Finally, our analysis of the particle size distribution in powder layer suggests a narrower distribution and smaller mean value for deposition on a powder layer. This is also evident from the analysis of particles retained which shows a small percentage of large particles retained in the material deposited on a powder layer which suggests a stronger segregation effect.

Our results can be interpreted for a wider view as follows: Interparticle cohesion adversely affects the powder layer quality in spreading process, resulting in a more heterogeneous structure of the layer. The wider distribution of the solid volume fraction, radial distribution function, normal force distribution as well as the contact overlap are all indicative of non-uniform, heterogeneous packing of cohesive powder layer. Also, interparticle cohesion leads to higher segregation of the constituent particles of the powder layer. Finally, the deposition of a second powder layer is found to have a more heterogeneous structure as well as compared to deposition on a smooth substrate.

Spherical particle shapes are favorable in terms of flowability and powder bed packing density, which is the which is the focus of our current studies. However, recycling of powder changes the chemical and morphological properties and non-sphericity is usually present in powder particles due to fractured and adhered particles. Sintering temperature plays a key role on the structure of powder layer deposited on the substrate. The influence of particle’s temperature, shape and thermal properties has not been investigated yet and is in the scope of our ongoing studies.